A Conservative Four-Dimensional Hyperchaotic Model with a Center Manifold and Infinitely Many Equilibria
Abstract
1. Introduction
- Most existing hyperchaotic systems rely on isolated hyperbolic equilibria; however, systems with infinitely many equilibrium points, particularly with zero eigenvalues, are rarely studied and analytically challenging due to the failure of classical linearization methods.
- Conservative hyperchaotic systems are far less common than their dissipative ones, despite their theoretical importance in energy-preserving dynamics. This work introduces a novel system that combines conservative behavior, infinite equilibria, and center manifold.
- The study of fractional-order dynamical systems has gained momentum for its ability to capture memory effects and enhance system complexity. Extending conservative hyperchaotic systems to the fractional domain introduces new theoretical challenges and richer dynamical behavior.
2. Proposed Model
3. Stability Analysis
- ;
- if
- 1.
- If for all , is stable.
- 2.
- If for all , is asymptotically stable.
- 3.
- If for all , is unstable.
Symmetry and Invariance
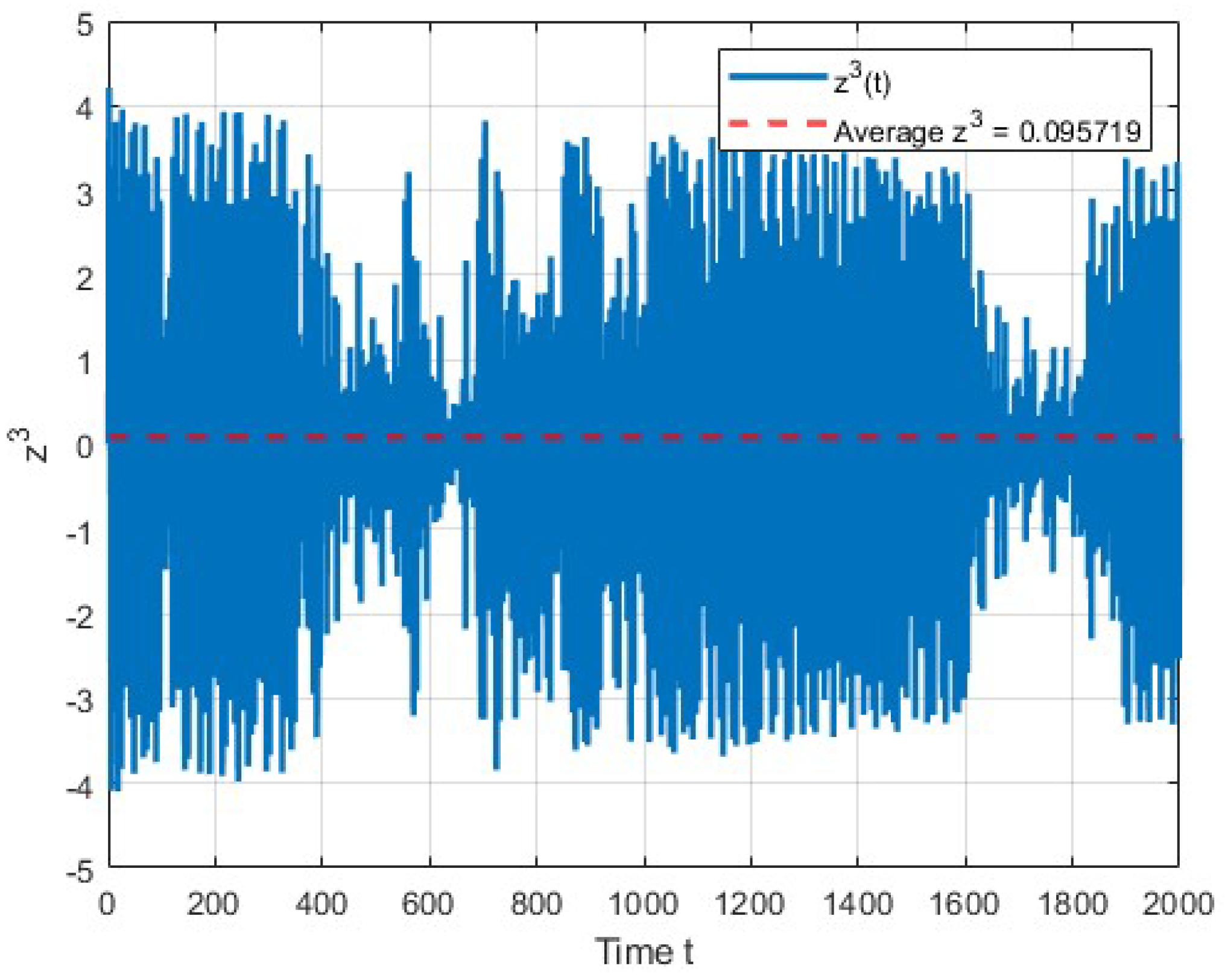
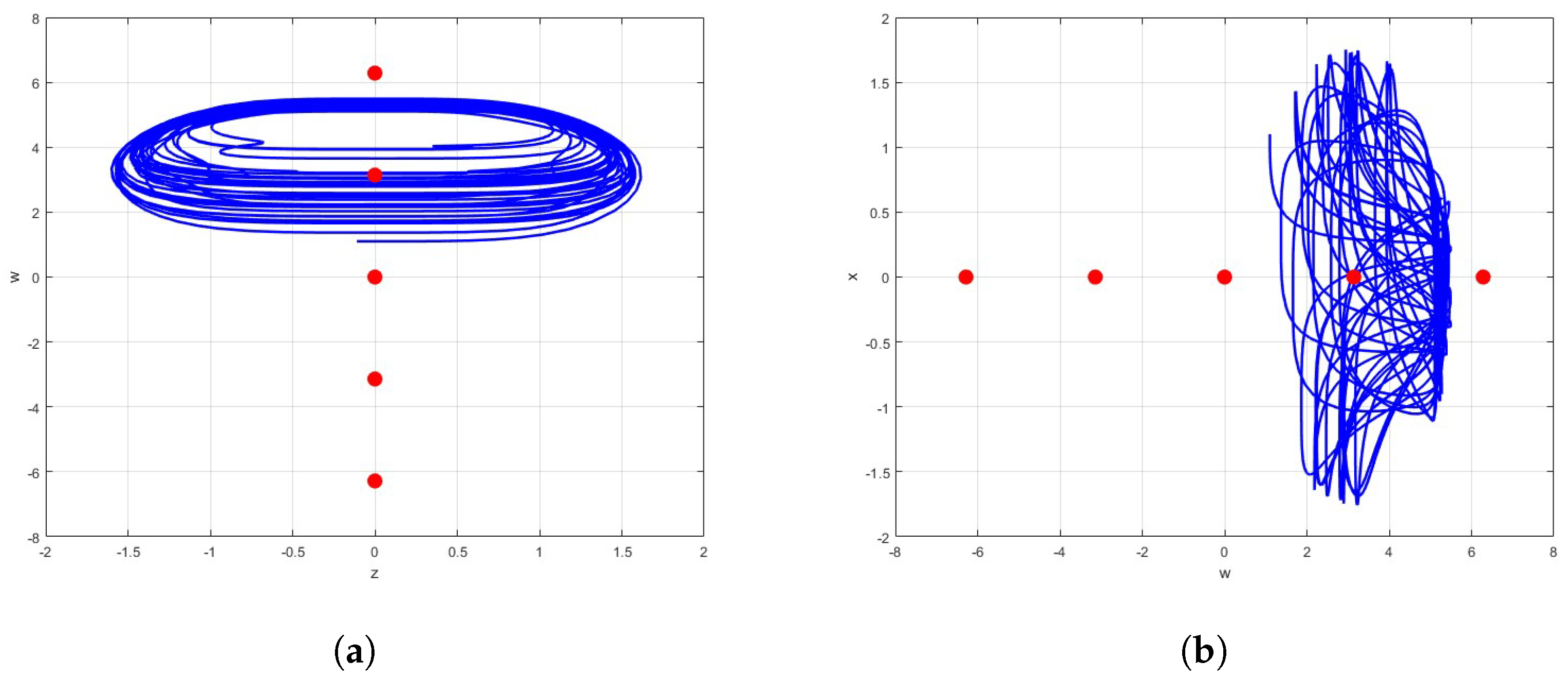
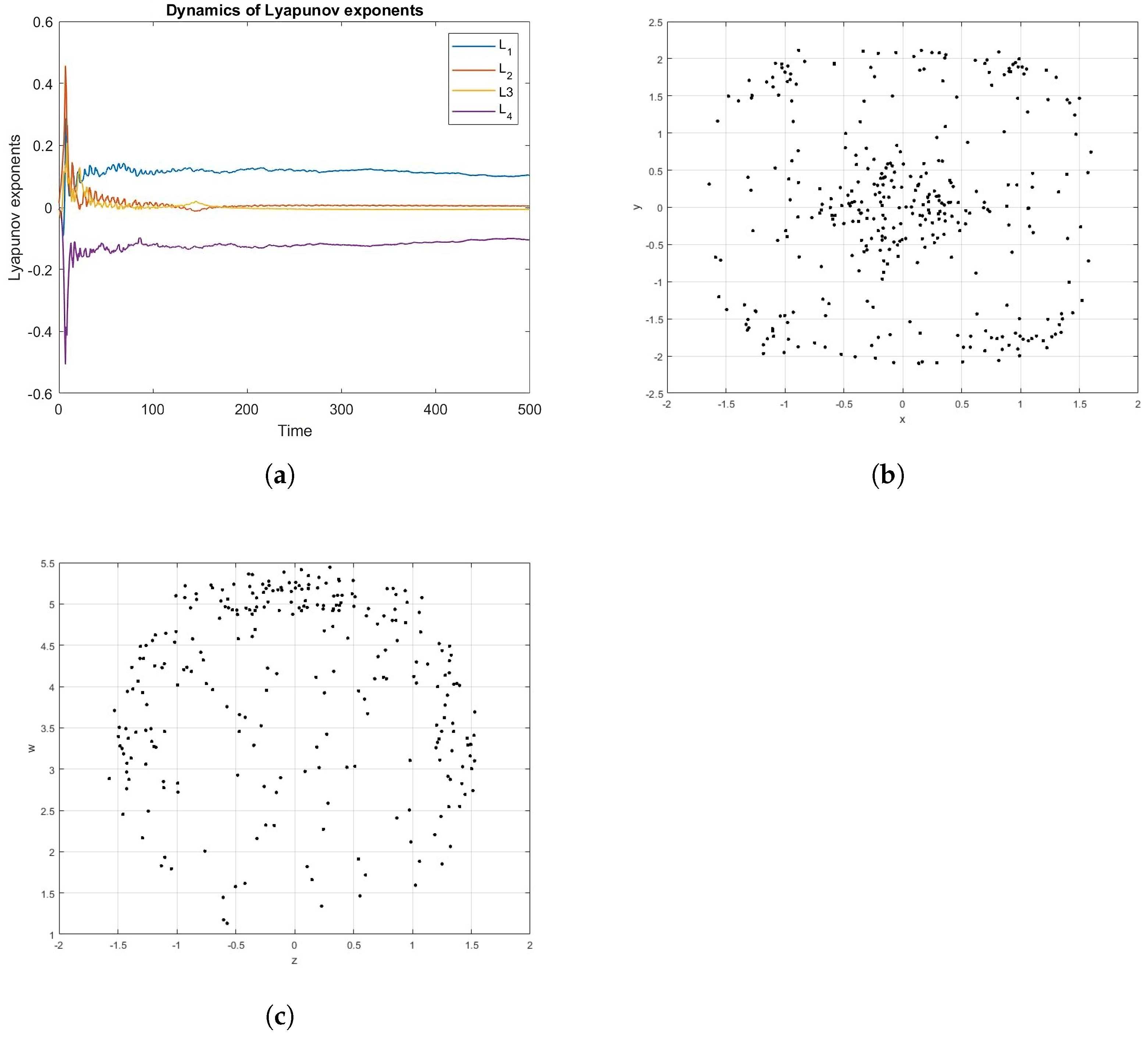
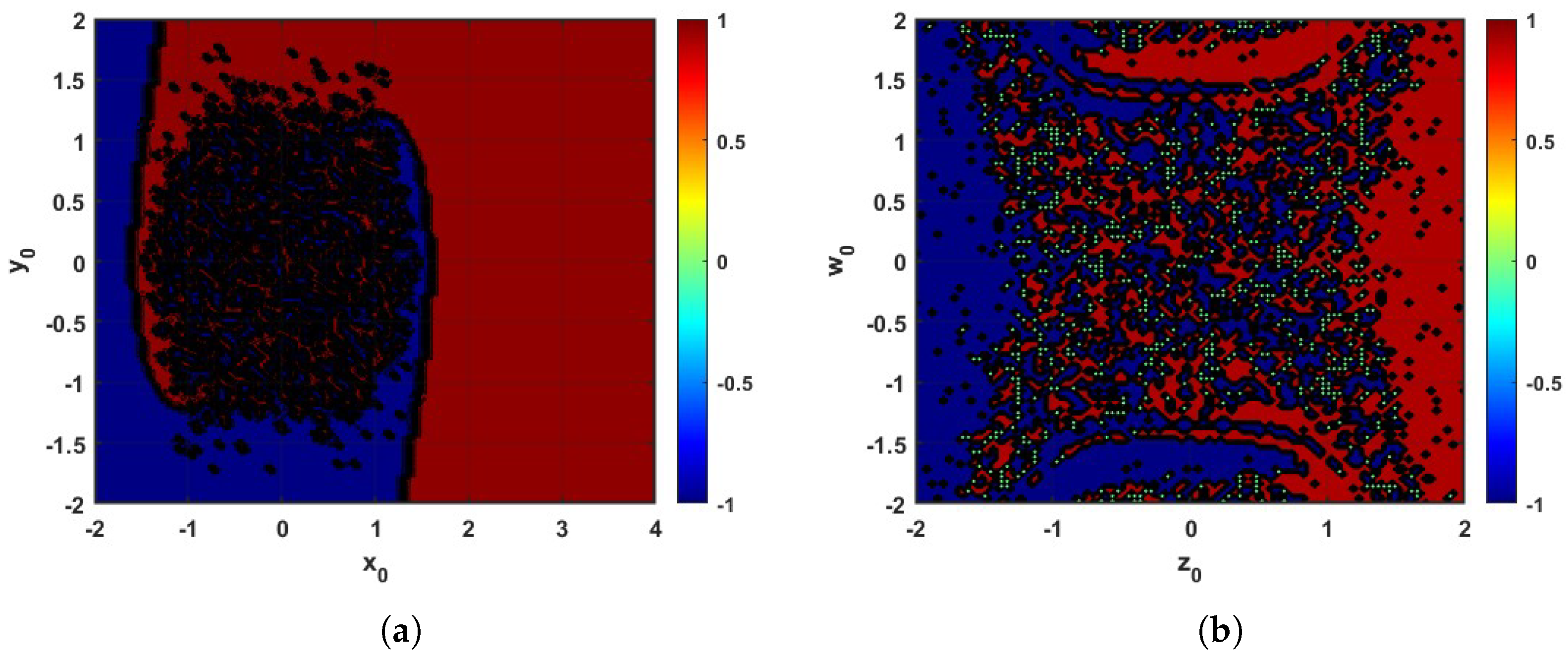
4. Dynamical Analysis
The Complexity of Parameters Variations
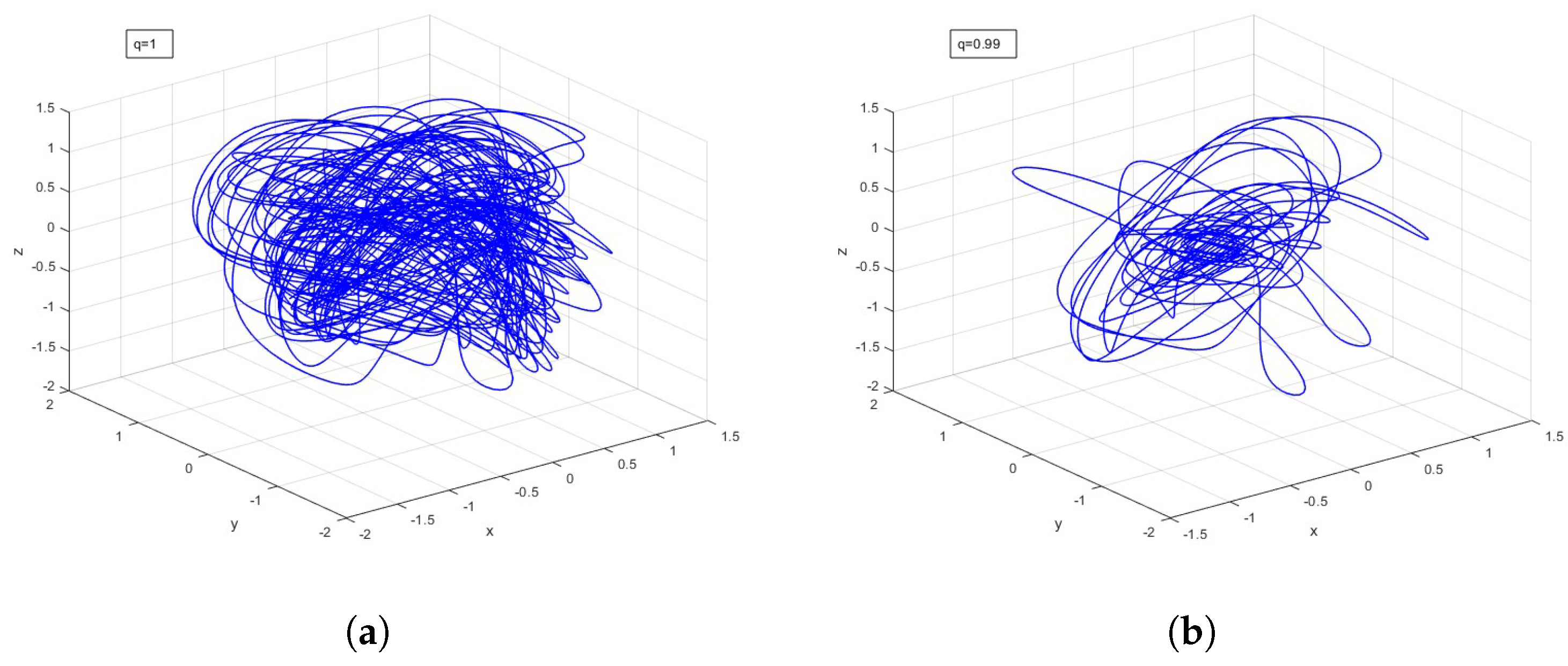
5. Fractional-Order for System (1)
5.1. Existence of a Unique Solution
5.2. Low Effective Order
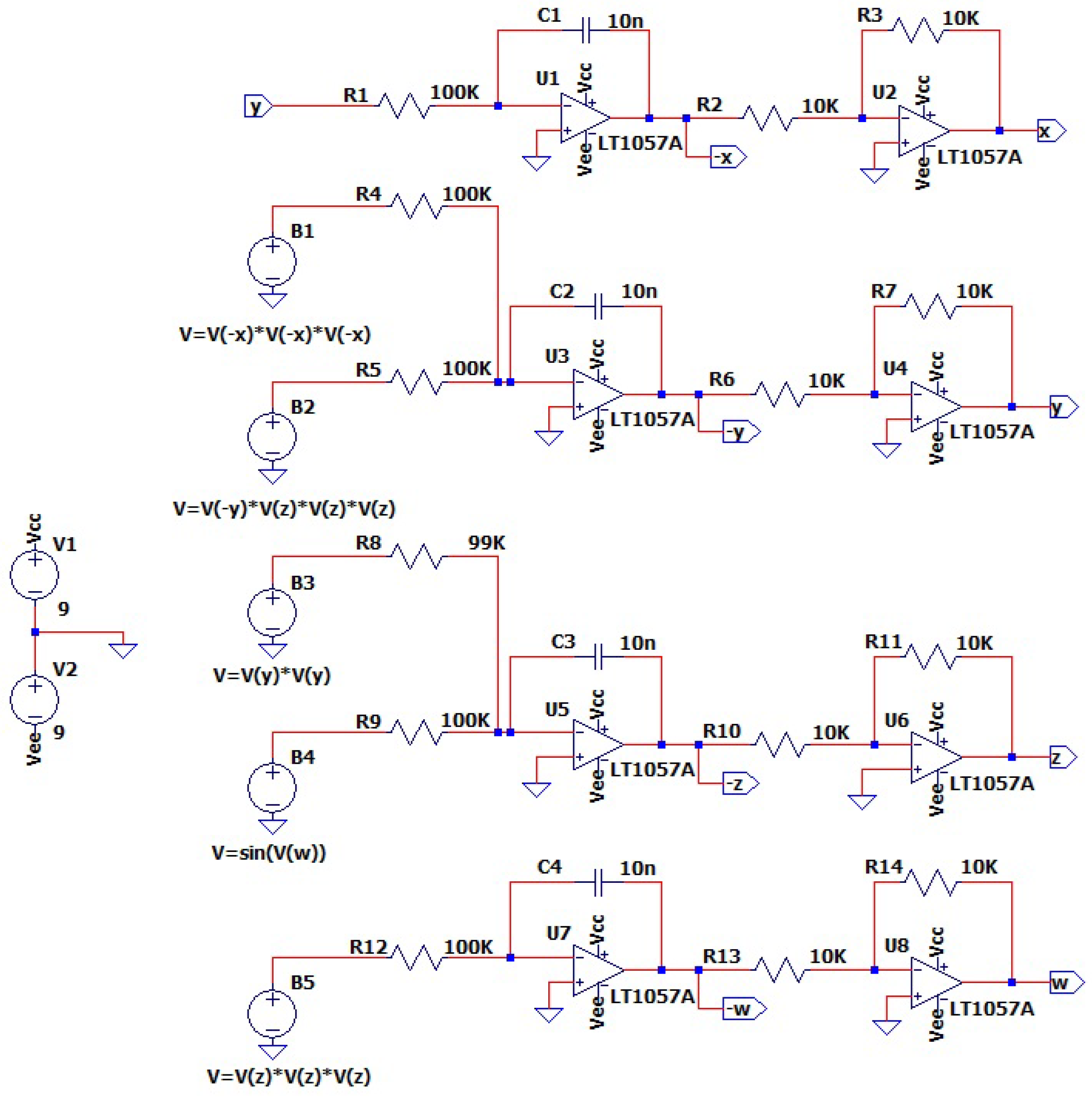
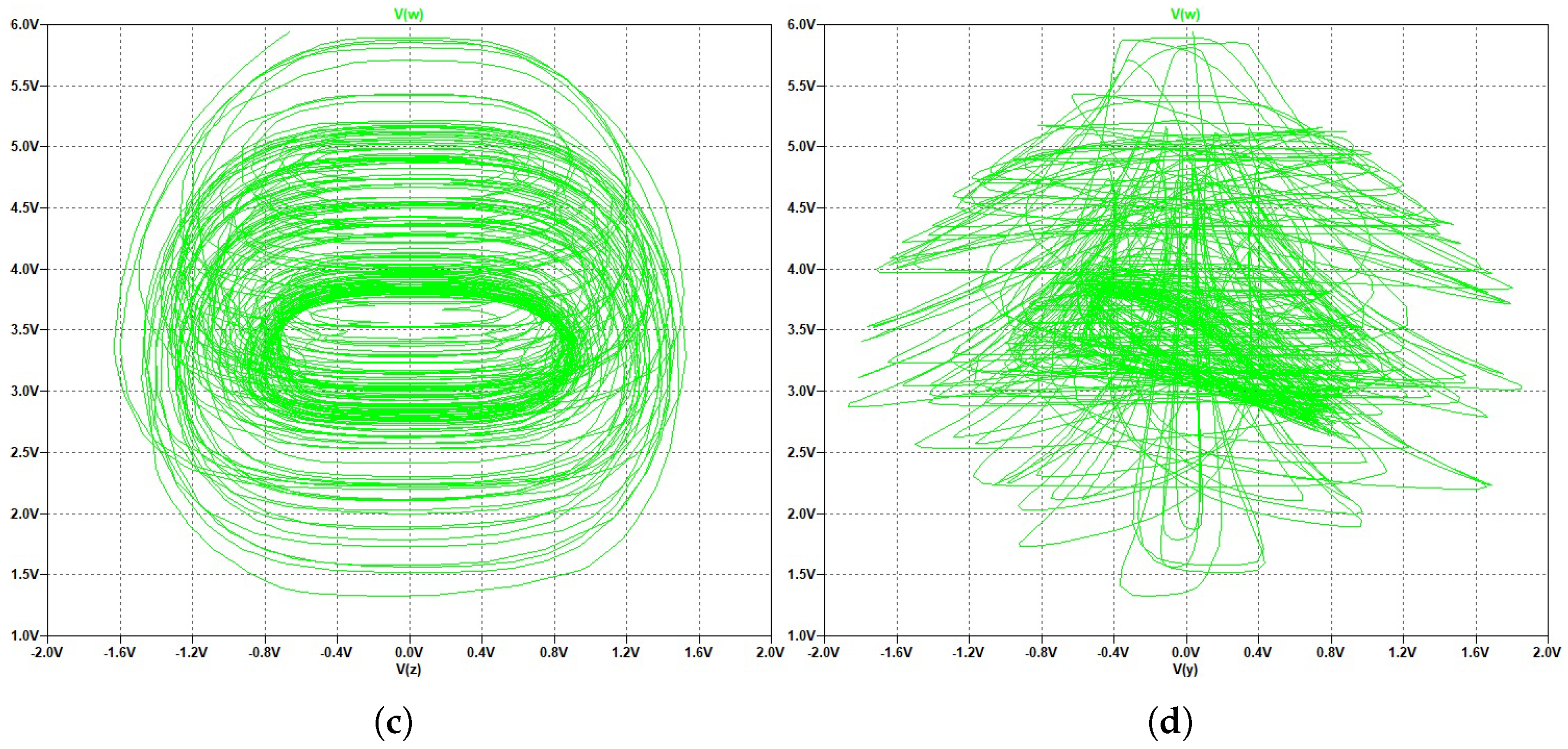
6. Hardware Implementation
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Rössler, O.E.; Letellier, C. Chaos: The World of Nonperiodic Oscillations; Springer Nature: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Jafari, S.; Sprott, J.; Nazarimehr, F. Recent new examples of hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1469–1476. [Google Scholar] [CrossRef]
- Leonov, G.; Kuznetsov, N.; Vagaitsev, V. Localization of hidden Chua’s attractors. Phys. Lett. A 2011, 375, 2230–2233. [Google Scholar] [CrossRef]
- Cang, S.; Li, Y.; Zhang, R.; Wang, Z. Hidden and self-excited coexisting attractors in a Lorenz-like system with two equilibrium points. Nonlinear Dyn. 2019, 95, 381–390. [Google Scholar] [CrossRef]
- Yu, T.; Ma, W.; Wang, Z.; Li, X. Hidden and self-excited attractors in an extended Sprott C system with two symmetric or asymmetric equilibrium points. Eur. Phys. J. Spec. Top. 2023, 96, 1287–1299. [Google Scholar] [CrossRef]
- Shukur, A.A.; AlFallooji, M.A.; Pham, V.T. Asymmetrical novel hyperchaotic system with two exponential functions and an application to image encryption. Nonlinear Eng. 2024, 13, 20220362. [Google Scholar] [CrossRef]
- Tayyab, M.; Sun, K.; Yao, Z.; Wang, H. Dynamics of memristive Liu system and its DSP implementation. Phys. Scr. 2024, 99, 085273. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G. Constructing a chaotic system with any number of equilibria. Nonlinear Dyn. 2013, 71, 429–436. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Wang, X.; Ma, J. A chaotic system with different shapes of equilibria. Int. J. Bifurc. Chaos 2016, 26, 1650069. [Google Scholar] [CrossRef]
- Strogatz, S. Nonlinear Dynamics and Chaos: With Applications to Physics Biology Chemistry and Engineering; Westview Press: Boulder, CO, USA, 2000. [Google Scholar]
- Minati, L. Simulation versus experiment in non-linear dynamical systems. Chaos Solitons Fractals 2021, 144, 110656. [Google Scholar] [CrossRef]
- Fatemeh, P.; Karthikeyan, R.; Anitha, K.; Ahmed, A.; Tasawar, H.; Viet-Thanh, P. Complex dynamics of a neuron model with discontinuous magnetic induction and exposed to external radiation. Cogn. Neurodyn. 2018, 12, 607–614. [Google Scholar] [CrossRef]
- Yang, Y.; Ma, J.; Xu, Y.; Jia, Y. Energy dependence on discharge mode of Izhikevich neuron driven by external stimulus under electromagnetic induction. Cogn. Neurodyn. 2021, 15, 265–277. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, Y.; Chen, B.; Li, Z.; Wang, N. Firing pattern in a memristive Hodgkin-Huxley circuit: Numerical simulation and analog circuit validation. Chaos Solitons Fractals 2023, 172, 113627. [Google Scholar] [CrossRef]
- Sajad, J.; Sprott, J.S.; Golpayegani, S. Elementary quadratic chaotic flows with no equilibria. Phys. Lett. A 2013, 377, 102–108. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G. A chaotic system with only one stable equilibrium. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1264–1272. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J. Simple chaotic flows with a line equilibrium. Chaos Solitons Fractals 2013, 57, 79–84. [Google Scholar] [CrossRef]
- Rajagopal, K.; Karthikeyan, A.; Srinivasan, A. Bifurcation and chaos in time delayed fractional order chaotic oscillator and its sliding mode synchronization with uncertainties. Chaos Solitons Fractals 2017, 103, 347–356. [Google Scholar] [CrossRef]
- Yu, F.; Wang, C. A novel three dimension autonomous chaotic system with a quadratic exponential nonlinear term. Eng. Technol. Appl. Sci. Res. 2012, 2, 209–215. [Google Scholar] [CrossRef]
- Neamah, A.A.; Shukur, A.A. A novel conservative chaotic system involved in hyperbolic functions and its application to design an efficient colour image encryption scheme. Symmetry 2023, 15, 1511. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, M.; Wang, Y.; Tian, H.; Wang, Z. Dynamic Analysis and Degenerate Hopf Bifurcation-Based Feedback Control of a Conservative Chaotic System and Its Circuit Simulation. Complexity 2021, 2021, 5576353. [Google Scholar] [CrossRef]
- Singh, J.P.; Roy, B.K. Five new 4-D autonomous conservative chaotic systems with various type of non-hyperbolic and lines of equilibria. Chaos Solitons Fractals 2018, 114, 81–91. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Ahmed, M. Analysis of chaotic and hyperchaotic conservative complex nonlinear systems. Miskolc Math. Notes 2017, 18, 315–326. [Google Scholar] [CrossRef]
- Faghani, Z.; Nazarimehr, F.; Jafari, S.; Sprott, J.C. A new category of three-dimensional chaotic flows with identical eigenvalues. Int. J. Bifurc. Chaos 2020, 30, 2050026. [Google Scholar] [CrossRef]
- ur Rahman, M.; El-Shorbagy, M.; Alrabaiah, H.; Baleanu, D.; De la Sen, M. Investigating a new conservative 4-dimensional chaotic system. Results Phys. 2023, 53, 106969. [Google Scholar] [CrossRef]
- Zolfaghari-Nejad, M.; Charmi, M.; Hassanpoor, H. A new chaotic system with only nonhyperbolic equilibrium points: Dynamics and its engineering application. Complexity 2022, 2022, 4488971. [Google Scholar] [CrossRef]
- Chen, L.; Nazarimehr, F.; Jafari, S.; Tlelo-Cuautle, E.; Hussain, I. Investigation of early warning indexes in a three-dimensional chaotic system with zero eigenvalues. Entropy 2020, 22, 341. [Google Scholar] [CrossRef]
- Rahman, Z.A.S.; Jasim, B.H.; Al-Yasir, Y.I.; Hu, Y.F.; Abd-Alhameed, R.A.; Alhasnawi, B.N. A new fractional-order chaotic system with its analysis, synchronization, and circuit realization for secure communication applications. Mathematics 2021, 9, 2593. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Liu, J.; Yang, F.; Yan, H.; Zhao, X. Coexistence of multiple attractors for an incommensurate fractional-order chaotic system. Eur. Phys. J. Plus 2020, 135, 1–21. [Google Scholar] [CrossRef]
- Chunhua, W.; Yufei, L.; Gang, Y.; Quanli, D. A Review of Fractional-Order Chaotic Systems of Memristive Neural Networks. Mathematics 2025, 13, 1600. [Google Scholar] [CrossRef]
- Mohamed, S.M.; Sayed, W.S.; Said, L.A.; Radwan, A.G. Reconfigurable fpga realization of fractional-order chaotic systems. IEEE Access 2021, 9, 89376–89389. [Google Scholar] [CrossRef]
- Li, H.; Shen, Y.; Han, Y.; Dong, J.; Li, J. Determining Lyapunov exponents of fractional-order systems: A general method based on memory principle. Chaos Solitons Fractals 2023, 168, 113167. [Google Scholar] [CrossRef]
- Venkataiah, K.; Ramesh, K. On the stability of a Caputo fractional order predator-prey framework including Holling type-II functional response along with nonlinear harvesting in predator. Partial Differ. Equ. Appl. Math. 2024, 11, 100777. [Google Scholar] [CrossRef]
- Abdul-Wahhab, R.D.; Eisa, M.M.; Khalaf, S.L. The study of stability analysis of the Ebola virus via fractional model. Partial Differ. Equations Appl. Math. 2024, 11, 100792. [Google Scholar] [CrossRef]
- Lyapunov, A. The General Problem of Stability of Motion; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Laarem, G. A new 4-D hyper chaotic system generated from the 3-D Rösslor chaotic system, dynamical analysis, chaos stabilization via an optimized linear feedback control, it’s fractional order model and chaos synchronization using optimized fractional order sliding mode control. Chaos Solitons Fractals 2021, 152, 111437. [Google Scholar]
- Zhang, R.; Yang, S. Robust synchronization of two different fractional-order chaotic systems with unknown parameters using adaptive sliding mode approach. Nonlinear Dyn. 2013, 71, 269–278. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, L.; Xiang, J.; Bao, H.; Li, H. Design of multi-wing 3D chaotic systems with only stable equilibria or no equilibrium point using rotation symmetry. AEÜ-Int. J. Electron. Commun. 2021, 135, 153710. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y. Fractional dynamical system and its linearization theorem. Nonlinear Dyn. 2013, 71, 621–633. [Google Scholar] [CrossRef]
- Danca, M.F. Hidden chaotic attractors in fractional-order systems. Nonlinear Dyn. 2017, 89, 577–586. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Moroz, I.; Wei, Z.; Castillo, O. A new multi-stable fractional-order four-dimensional system with self-excited and hidden chaotic attractors: Dynamic analysis and adaptive synchronization using a novel fuzzy adaptive sliding mode control method. Appl. Soft Comput. 2020, 87, 105943. [Google Scholar] [CrossRef]
- Deressa, C.T.; Etemad, S.; Rezapour, S. On a new four-dimensional model of memristor-based chaotic circuit in the context of nonsingular Atangana–Baleanu–Caputo operators. Adv. Differ. Equations 2021, 2021, 444. [Google Scholar] [CrossRef]
- Ahmad, W.M.; Sprott, J.C. Chaos in fractional-order autonomous nonlinear systems. Chaos Solitons Fractals 2003, 16, 339–351. [Google Scholar] [CrossRef]
- Mohammed, B.A.; Messaoud, B. Bifurcation analysis and chaos control for fractional predator-prey model with Gompertz growth of prey population. Mod. Phys. Lett. B 2025, 39, 2550103. [Google Scholar]
- Aida, B.; Rabah, B.; Tarek, H.; Messaoud, B. Nonlinear dynamics and chaos in fractional-order cardiac action potential duration mapping model with fixed memory length. Gulf J. Math. 2025, 19, 369–383. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Ortigueira, M.D.; Machado, J.T. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 84. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Brzeziński, D.W. Accuracy problems of numerical calculation of fractional order derivatives and integrals applying the Riemann-Liouville/Caputo formulas. Appl. Math. Nonlinear Sci. 2016, 1, 23–44. [Google Scholar] [CrossRef]




| Refs | Dim. | No. Systems | Equilibrium Type | Nonlin. Terms-Type |
|---|---|---|---|---|
| [25] | all 3D | 9 | all unstable | 3-all quadratic |
| [26] | 4D | 1 | unstable | 5-cube |
| [27] | 3D | 1 | unstable | 7- trigonometric |
| [28] | 3D | 1 | unstable | 3-quadratic |
| This work | 4D | 1 | stable | 5- trigonometric |
| Order (q) | Kaplan–Yorke | |||||
|---|---|---|---|---|---|---|
| 1 ↓ | 0.0919 | 0.0045 | 0 | −0.0982 | −0.0125 | 3.865 ≃ 4 ↓ |
| 0.99 ↓ | 0.0081 | 0.0149 | 0 | −0.0343 | −0.0218 | 3.364 ↓ |
| 0.98 ↓ | 0.0104 | 0.0077 | 0 | −0.0357 | −0.0365 | 2.958↓ |
| 0.97 ↓ | 0.0085 | 0 | −0.0013 | −0.0330 | −0.0458 | 2.360 ↓ |
| 0.96 ↓ | 0.0097 | 0 | −0.0040 | −0.0468 | −0.0600 | 2.301 ↓ |
| 0.95↓ | 0.0092 | 0 | −0.0038 | −0.0512 | −0.0746 | 2.188 ↓ |
| 0.94 ↓ | 0.0008 | 0 | −0.0055 | −0.0583 | −0.0923 | 1.145 ↓ |
| 0.93 ↓ | 0.0021 | 0 | −0.0181 | −0.0669 | −0.0112 | 1.116 ↓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, S.H.; Shukur, A.A.; Salih, R.H. A Conservative Four-Dimensional Hyperchaotic Model with a Center Manifold and Infinitely Many Equilibria. Modelling 2025, 6, 74. https://doi.org/10.3390/modelling6030074
Ibrahim SH, Shukur AA, Salih RH. A Conservative Four-Dimensional Hyperchaotic Model with a Center Manifold and Infinitely Many Equilibria. Modelling. 2025; 6(3):74. https://doi.org/10.3390/modelling6030074
Chicago/Turabian StyleIbrahim, Surma H., Ali A. Shukur, and Rizgar H. Salih. 2025. "A Conservative Four-Dimensional Hyperchaotic Model with a Center Manifold and Infinitely Many Equilibria" Modelling 6, no. 3: 74. https://doi.org/10.3390/modelling6030074
APA StyleIbrahim, S. H., Shukur, A. A., & Salih, R. H. (2025). A Conservative Four-Dimensional Hyperchaotic Model with a Center Manifold and Infinitely Many Equilibria. Modelling, 6(3), 74. https://doi.org/10.3390/modelling6030074






