An Anisotropic Failure Characteristic- and Damage-Coupled Constitutive Model
Abstract
1. Introduction
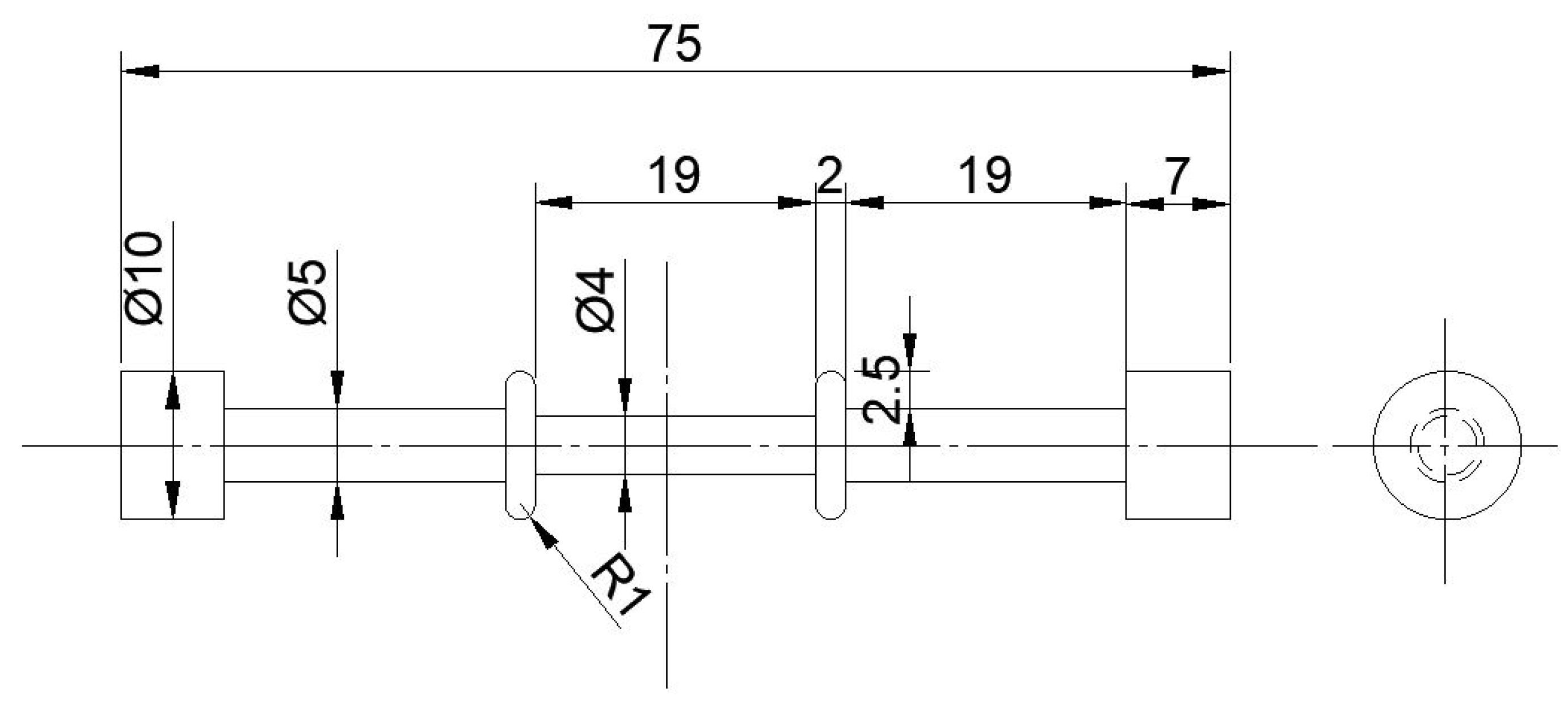
2. Experiment
3. Macroscopic Creep Constitutive Model
4. Results and Discussion
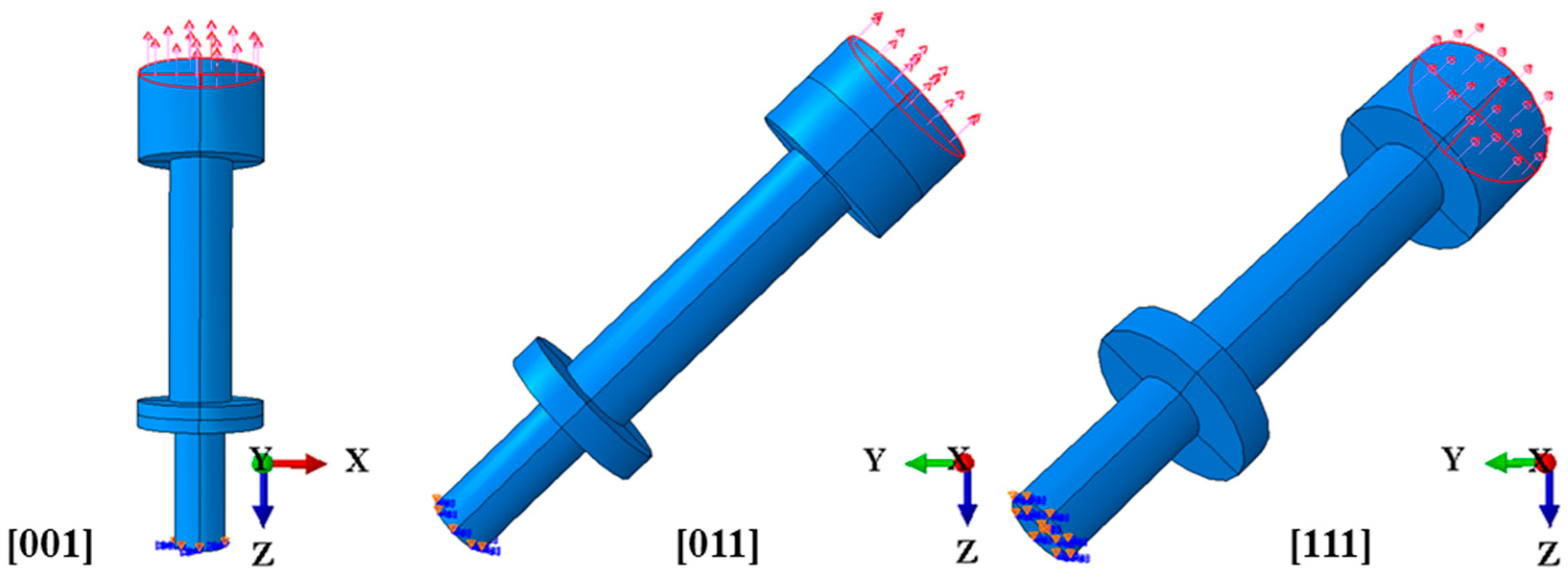
4.1. Finite Element Model Development and Constitutive Parameter Determination Methods
4.1.1. Development of the Macroscopic Model
4.1.2. Constitutive Parameter Determination Methods
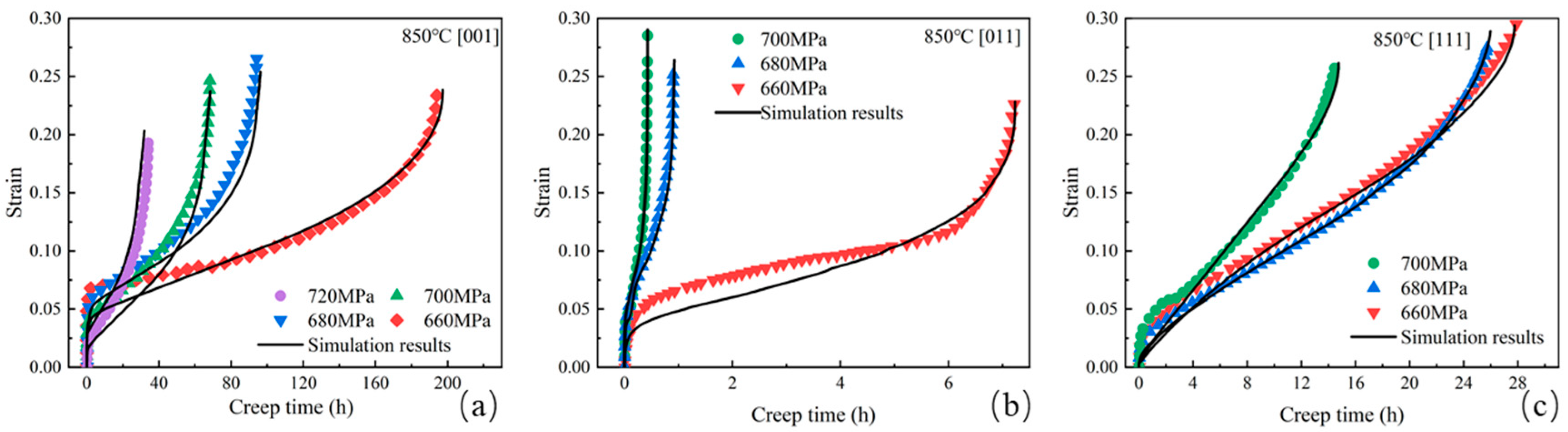
4.2. Creep Curve Fitting Validation of Nickel-Based Single Crystals with Three Orientations Under Different Temperatures and Stresses
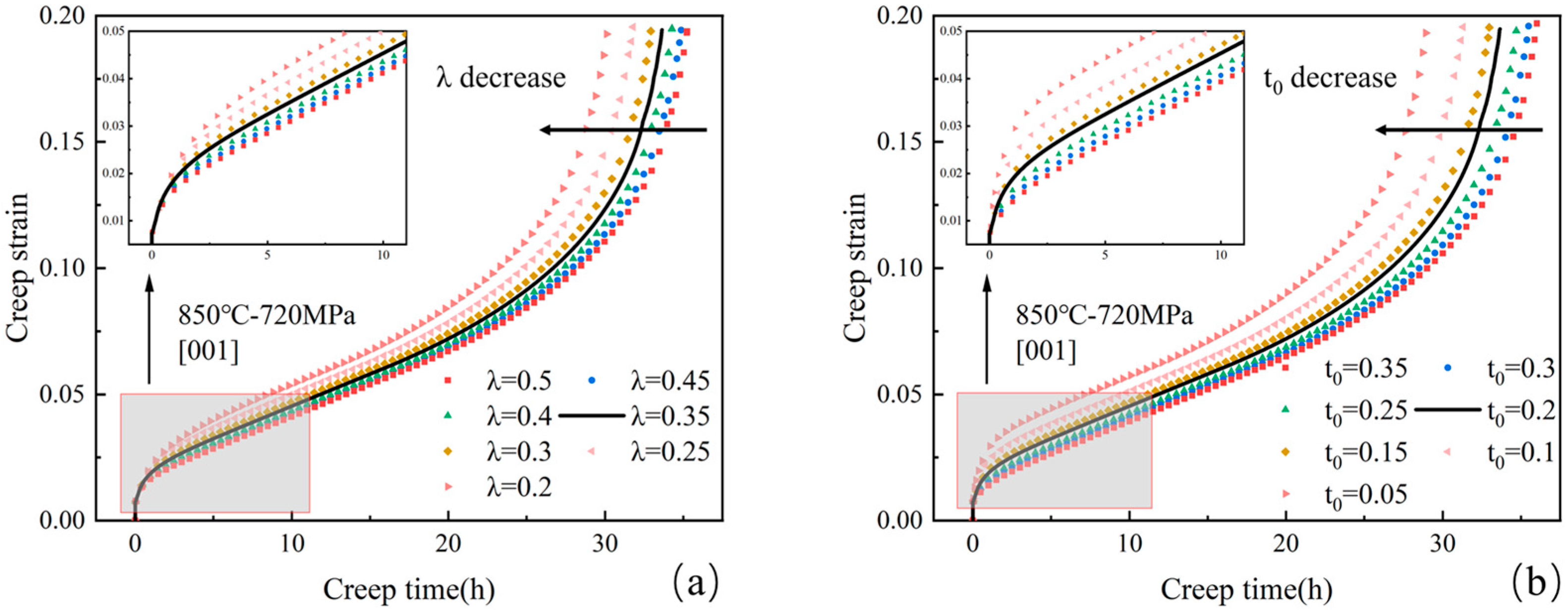
4.3. Model Parameter Analysis
4.4. Prediction of Macroscopic Fracture Surface and Microscopic Morphology
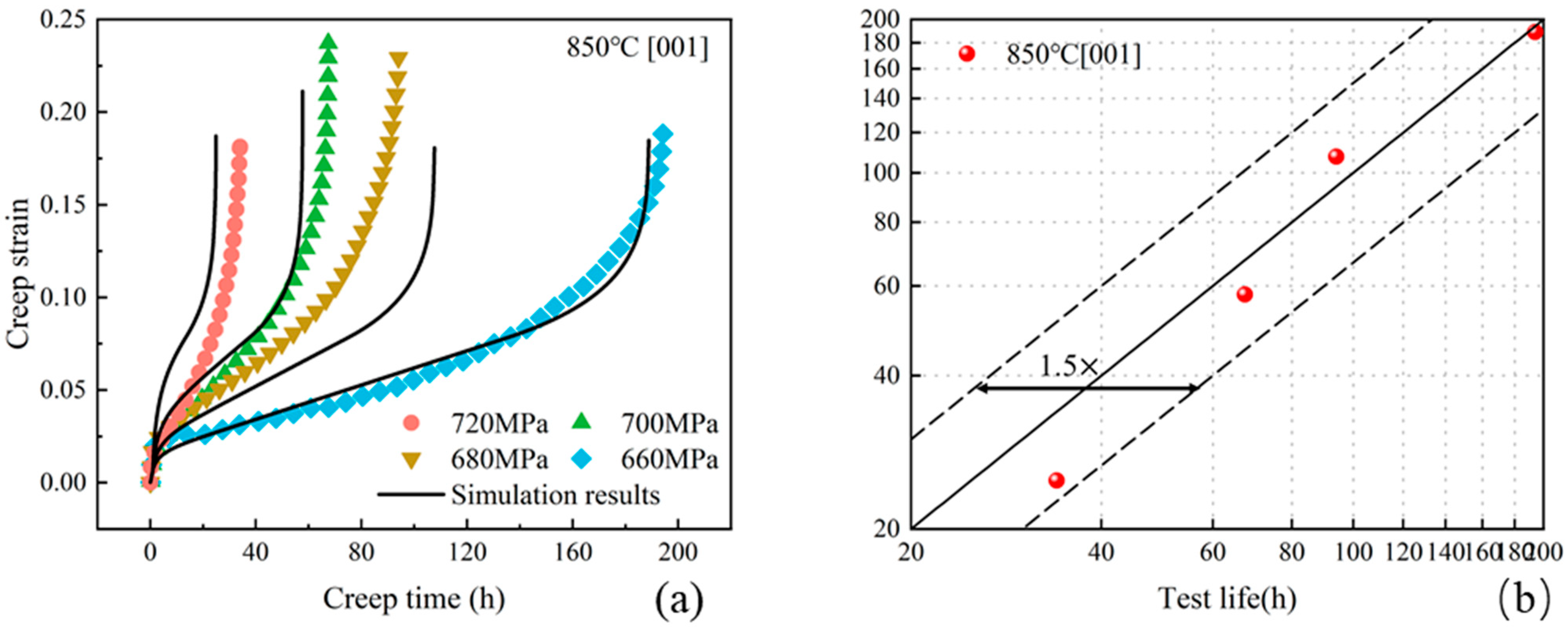
4.5. Life Prediction of the [001] Orientation at 850 °C Under Different Stress Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Temperature/°C | Orientation | Stress/MPa | n | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 850 | [001] | 720 | 0.35 | 0.2 | 0.02 | 1000 | 6 | 0.2 | 0.065 | 0.26 |
| 700 | 0.27 | 0.015 | 0.02 | 1050 | 6 | 0.17 | 0.1 | 0.26 | ||
| 680 | 0.2 | 0.0005 | 0.02 | 1100 | 6 | 0.16 | 0.1 | 0.26 | ||
| 660 | 0.12 | 0.002 | 0.02 | 1150 | 6 | 0.12 | 0.12 | 0.26 | ||
| [011] | 700 | 8 | 0.0044 | 0.1 | 750 | 6 | 0.31 | 0.06 | 0.26 | |
| 680 | 4 | 0.009 | 0.1 | 870 | 6 | 0.15 | 0.04 | 0.24 | ||
| 660 | 1.3 | 0.01 | 0.1 | 990 | 6 | 0.18 | 0.09 | 0.23 | ||
| [111] | 700 | 2 | 0.14 | 0.04 | 900 | 6 | 0.1 | 0.2 | 0.3 | |
| 680 | 0.25 | 0.3 | 0.04 | 950 | 6 | 0.1 | 0.15 | 0.33 | ||
| 660 | 0.035 | 0.35 | 0.04 | 1000 | 6 | 0.1 | 0.17 | 0.33 | ||
| 980 | [001] | 400 | 1 | 20 | 0.1 | 900 | 6 | 0.3 | 0.006 | 0.23 |
| 360 | 1 | 20 | 0.1 | 920 | 6 | 0.35 | 0.004 | 0.26 | ||
| 340 | 1 | 20 | 0.1 | 930 | 6 | 0.38 | 0.004 | 0.25 | ||
| 320 | 1 | 20 | 0.1 | 940 | 6 | 0.4 | 0.003 | 0.29 | ||
| 300 | 1 | 20 | 0.1 | 950 | 6 | 0.42 | 0.002 | 0.29 | ||
| 280 | 1 | 20 | 0.1 | 960 | 6 | 0.42 | 0.002 | 0.3 | ||
| [011] | 360 | 0.07 | 0.0009 | 0.1 | 950 | 6 | 0.6 | 0.036 | 0.11 | |
| 340 | 0.04 | 0.0001 | 0.1 | 1010 | 6 | 0.6 | 0.045 | 0.15 | ||
| 300 | 0.005 | 0.00017 | 0.1 | 1130 | 6 | 0.61 | 0.066 | 0.2 | ||
| [111] | 360 | 0.22 | 0.001 | 0.1 | 800 | 6 | 0.14 | 0.06 | 0.31 | |
| 340 | 0.057 | 0.003 | 0.1 | 860 | 6 | 0.22 | 0.044 | 0.35 | ||
| 300 | 0.01 | 0.004 | 0.1 | 980 | 6 | 0.59 | 0.051 | 0.3 | ||
| 1100 | [001] | 190 | 0.18 | 0.001 | 0.1 | 420 | 6 | 0.36 | 0.045 | 0.23 |
| 170 | 0.07 | 0.0007 | 0.1 | 434 | 6 | 0.5 | 0.048 | 0.23 | ||
| 160 | 0.034 | 0.001 | 0.1 | 441 | 6 | 0.42 | 0.055 | 0.24 | ||
| 140 | 0.01 | 0.001 | 0.1 | 455 | 6 | 0.28 | 0.052 | 0.26 | ||
| [011] | 170 | 0.09 | 0.0009 | 0.1 | 450 | 6 | 0.9 | 0.035 | 0.18 | |
| 160 | 0.032 | 0.0008 | 0.1 | 470 | 6 | 0.88 | 0.045 | 0.15 | ||
| 140 | 0.006 | 0.0007 | 0.1 | 510 | 6 | 0.87 | 0.065 | 0.16 | ||
| [111] | 170 | 0.043 | 0.0013 | 0.1 | 480 | 6 | 0.4 | 0.03 | 0.24 | |
| 160 | 0.02 | 0.0012 | 0.1 | 510 | 6 | 0.5 | 0.034 | 0.27 | ||
| 140 | 0.003 | 0.0011 | 0.1 | 570 | 6 | 0.5 | 0.041 | 0.28 |
References
- Wang, J.; Lu, H.; Wen, Z.; Lian, Y.; Wang, Y.; Yue, Z. Crystal plasticity theory coupled with meso-damage to predict the ratchetting behavior of nickel-based single crystal superalloy. Int. J. Fatigue 2022, 165, 107220. [Google Scholar] [CrossRef]
- Wang, J.; Liu, T.; Yang, L.; Wen, Z.; Yue, Z.; Mao, Q. Stress redistribution and stress triaxiality effect on the fatigue life of notched Ni-based single crystal superalloy at 760 °C. Theor. Appl. Fract. Mech. 2024, 131, 104380. [Google Scholar] [CrossRef]
- Tu, Y.; Wang, J.; Wen, Z.; He, P. Thermomechanical fatigue behavior and lifetime prediction of nickel-based single crystal alloys under varying stress conditions. J. Alloys Compd. 2025, 1023, 180202. [Google Scholar] [CrossRef]
- Wang, J.; Xu, X.; Lu, H.; Zhang, L.; Lian, Y.; Wen, Z.; Yue, Z. Fatigue notch strengthening effect of nickel-based single crystal superalloys under different stress ratios. Eur. J. Mech.-A/Solids 2025, 109, 105471. [Google Scholar] [CrossRef]
- Choi, Y.S.; Parthasarathy, T.A.; Woodward, C.; Dimiduk, D.M.; Uchic, M.D. Constitutive Model for Anisotropic Creep Behaviors of Single-Crystal Ni-Base Superalloys in the Low-Temperature, High-Stress Regime. Metall. Mater. Trans. A 2012, 43, 1861–1869. [Google Scholar] [CrossRef]
- Nörtershäuser, P.; Frenzel, J.; Ludwig, A.; Neuking, K.; Eggeler, G. The effect of cast microstructure and crystallography on rafting, dislocation plasticity and creep anisotropy of single crystal Ni-base superalloys. Mater. Sci. Eng. A 2015, 626, 305–312. [Google Scholar] [CrossRef]
- Leverant, G.R.; Kear, B.H.; Oblak, J.M. Creep of precipitation-hardened nickel-base alloy single crystals at high temperatures. Metall. Trans. 1973, 4, 355–362. [Google Scholar] [CrossRef]
- Kear, B.H.; Oblak, J.M. Deformation Modes γ’ Precipitation Hardened Nickel-Base Alloys. J. Phys. Colloq. 1974, 35, C7-35–C7-45. [Google Scholar] [CrossRef]
- Yang, Q.; Ghosh, S. A crystal plasticity model for porous HCP crystals in titanium alloys under multiaxial loading conditions. Int. J. Solids Struct. 2022, 238, 111400. [Google Scholar] [CrossRef]
- Guo, H.-J.; Ling, C.; Busso, E.P.; Zhong, Z.; Li, D.-F. Crystal plasticity based investigation of micro-void evolution under multi-axial loading conditions. Int. J. Plast. 2020, 129, 102673. [Google Scholar] [CrossRef]
- Yu, Q.M.; Wang, Y.; Wen, Z.X.; Yue, Z.F. Notch effect and its mechanism during creep rupture of nickel-base single crystal superalloys. Mater. Sci. Eng. A 2009, 520, 1–10. [Google Scholar] [CrossRef]
- Lemaitre, J.; Plumtree, A. Application of damage concepts to predict creep-fatigue failures. J. Eng. Mater. Technol. 1979, 101, 284–292. [Google Scholar] [CrossRef]
- Lemaitre, J. How to use damage mechanics. Nucl. Eng. Des. 1984, 80, 233–245. [Google Scholar] [CrossRef]
- Guo, Z.; Song, Z.; Liu, H.; Hu, D.; Huang, D.; Yan, X.; Yan, W. A dislocation-based damage-coupled constitutive model for single crystal superalloy: Unveiling the effect of secondary orientation on creep life of circular hole. Int. J. Plast. 2024, 173, 103874. [Google Scholar] [CrossRef]
- Li, Z.; Wen, Z.; Pei, H.; Yue, X.; Wang, P.; Ai, C.; Yue, Z. Creep life prediction for a nickel-based single crystal turbine blade. Mech. Adv. Mater. Struct. 2022, 29, 6039–6052. [Google Scholar] [CrossRef]
- Chaudhary, S.; Guruprasad, P.J.; Patra, A. Crystal plasticity constitutive modeling of tensile, creep and cyclic deformation in single crystal Ni-based superalloys. Mech. Mater. 2022, 174, 104474. [Google Scholar] [CrossRef]
- Kasar, Ç.; Kaftancıoglu, U.; Bayraktar, E.; Aslan, O. Lifetime Prediction of Single Crystal Nickel-based Superalloys. Appl. Sci. 2024, 15, 201. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Cheng, Y.; Wang, H.; Sha, A.; Duan, H. Modeling of creep in nickel-based superalloy based on microtwinning mechanism. Int. J. Plast. 2024, 174, 103916. [Google Scholar] [CrossRef]
- Gu, S.; Gao, H.; Wen, Z.; Li, Z.; Zhang, C.; Yue, Z. Creep properties and life model of anisotropic Ni-based single crystal superalloys over a wide temperature range. Int. J. Mech. Sci. 2024, 261, 108674. [Google Scholar] [CrossRef]
- Kachanov, L.M. Time of the Rupture Process Under Creep Conditions; Izy Akad; Izvestiia Akademii Nauk SSSR; Otdelenie Teckhnicheskikh Nauk: Moscow, Russia, 1958; Volume 8. [Google Scholar]
- Hyde, T.H.; Xia, L.; Becker, A.A. Prediction of creep failure in aeroengine materials under multi-axial stress states. Int. J. Mech. Sci. 1996, 38, 385–403. [Google Scholar] [CrossRef]
- Jiang, J.; Wang, W.; Zhao, N.; Wang, P.; Liu, Y.; Jiang, P. Application of a creep-damage constitutive model for the rotor of a 1000 MW ultrasupercritical steam turbine. J. Eng. Gas Turbines Power 2015, 138, 022606. [Google Scholar] [CrossRef]
- Luo, Y.; Jiang, W.; Zhang, Y.; Zhou, F.; Tu, S.-T. A new damage evolution model to estimate the creep fracture behavior of brazed joint under multiaxial stress. Int. J. Mech. Sci. 2018, 149, 178–189. [Google Scholar] [CrossRef]
- Wang, W.; Buhl, P.; Klenk, A.; Liu, Y. Influence of high-temperature dwell time on creep-fatigue behavior in a 1000 MW steam turbine rotor. Eng. Fract. Mech. 2016, 166, 1–22. [Google Scholar] [CrossRef]
- Yuan, B.; Liang, J.; Huang, X.; Huang, Q.; Zhang, B.; Yang, G.; Wang, Y.; Yuan, J.; Wang, H.; Yuan, P. Eco-efficient recycling of engineering muck for manufacturing low-carbon geopolymers assessed through LCA: Exploring the impact of synthesis conditions on performance. Acta Geotech. 2024. [Google Scholar] [CrossRef]
- Yuan, B.; Liang, J.; Lin, H.; Wang, W.; Xiao, Y. Experimental Study on Influencing Factors Associated with a New Tunnel Waterproofing for Improved Impermeability. J. Test. Eval. 2024, 52, 20. [Google Scholar] [CrossRef]
- Yuan, B.; Chen, W.; Li, Z.; Zhao, J.; Luo, Q.; Chen, W.; Chen, T. Sustainability of the polymer SH reinforced recycled granite residual soil: Properties, physicochemical mechanism, and applications. J. Soils Sediments 2023, 23, 246–262. [Google Scholar] [CrossRef]
- Lemaitre, J. A Course on Damage Mechanics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar] [CrossRef]
- Becker, A.A.; Hyde, T.H.; Sun, W.; Andersson, P. Benchmarks for finite element analysis of creep continuum damage mechanics. Comput. Mater. Sci. 2002, 25, 34–41. [Google Scholar] [CrossRef]
- Hayhurst, R.J.; Mustata, R.; Hayhurst, D.R. Creep constitutive equations for parent, type IV, R-HAZ, CG-HAZ and weld material in the range 565–640 °C for Cr–Mo–V weldments. Int. J. Press. Vessels Pip. 2005, 82, 137–144. [Google Scholar] [CrossRef]
- Hayhurst, D.R.; Goodall, I.W.; Hayhurst, R.J.; Dean, D.W. Lifetime predictions for high-temperature low-alloy ferritic steel weldments. J. Strain Anal. Eng. Des. 2005, 40, 675–701. [Google Scholar] [CrossRef]
- Nikbin, K. A unified multiscale ductility exhaustion based approach to predict uniaxial, multiaxial creep rupture and crack growth. Eng. Fract. Mech. 2017, 179, 240–259. [Google Scholar] [CrossRef]
- Ma, H.S.; Wang, G.Z.; Liu, S.; Tu, S.T.; Xuan, F.Z. Unified constraint parameter solutions for axial and circumferential surface cracks in pressurized pipes under creep condition. Eng. Fract. Mech. 2018, 189, 307–329. [Google Scholar] [CrossRef]
- Xiong, J.J.; Shenoi, R.A. A two-stage theory on fatigue damage and life prediction of composites. Compos. Sci. Technol. 2004, 64, 1331–1343. [Google Scholar] [CrossRef]
- Dattoma, V.; Giancane, S.; Nobile, R.; Panella, F. Fatigue life prediction under variable loading based on a new non-linear continuum damage mechanics model. Int. J. Fatigue 2006, 28, 89–95. [Google Scholar] [CrossRef]
- Correia, J.A.F.O.; Raposo, P.; Muniz-Calvente, M.; Blasón, S.; Lesiuk, G.; De Jesus, A.M.P.; Moreira, P.M.G.P.; Calçada, R.A.B.; Canteli, A.F. A generalization of the fatigue kohout-věchet model for several fatigue damage parameters. Eng. Fract. Mech. 2017, 185, 284–300. [Google Scholar] [CrossRef]
- Fazlali, B.; Mohammadi, B. A microscale energy-based fatigue damage model for unidirectional composites under multiaxial loading at different stress ratios. Eng. Fract. Mech. 2019, 205, 120–135. [Google Scholar] [CrossRef]
- Kumar, J.; Venugopal Rao, A.; Ganesh Sundara Raman, S.; Kumar, V. Creep-fatigue damage simulation at multiple length scales for an aeroengine titanium alloy. Int. J. Fatigue 2018, 116, 505–512. [Google Scholar] [CrossRef]
- JianPing, J.; Guang, M.; Yi, S.; SongBo, X. An effective continuum damage mechanics model for creep–fatigue life assessment of a steam turbine rotor. Int. J. Press. Vessels Pip. 2003, 80, 389–396. [Google Scholar] [CrossRef]
- Wang, R.-Z.; Zhu, S.-P.; Wang, J.; Zhang, X.-C.; Tu, S.-T.; Zhang, C.-C. High temperature fatigue and creep-fatigue behaviors in a Ni-based superalloy: Damage mechanisms and life assessment. Int. J. Fatigue 2019, 118, 8–21. [Google Scholar] [CrossRef]
- Wu, J.Y.; Li, J.; Faria, R. An energy release rate-based plastic-damage model for concrete. Int. J. Solids Struct. 2006, 43, 583–612. [Google Scholar] [CrossRef]
- Pirondi, A.; Bonora, N.; Steglich, D.; Brocks, W.; Hellmann, D. Simulation of failure under cyclic plastic loading by damage models. Int. J. Plast. 2006, 22, 2146–2170. [Google Scholar] [CrossRef]
- Kuna-Ciskał, H.; Skrzypek, J.J. CDM based modelling of damage and fracture mechanisms in concrete under tension and compression. Eng. Fract. Mech. 2004, 71, 681–698. [Google Scholar] [CrossRef]
- Kaji, Y.; Gu, W.; Ishihara, M.; Arai, T.; Nakamura, H. Development of structural analysis program for non-linear elasticity by continuum damage mechanics. Nucl. Eng. Des. 2001, 206, 1–12. [Google Scholar] [CrossRef]
- Jin, Z.; Liu, C.; Cao, Y.; Lu, Y.; Pan, W.; Ji, D. Research on creep damage model of T91/TP347H dissimilar steel welded joints under overheating condition. Press. Vessel Technol. 2021, 38, 18–26. [Google Scholar]
- Zhang, D.; Lv, M.; Wen, Z. A unified creep life prediction method and fracture mechanism of high-temperature alloys under multiaxial stress. Eng. Fail. Anal. 2023, 149, 107262. [Google Scholar] [CrossRef]
- Ragab, R.; Parker, J.; Li, M.; Liu, T.; Sun, W. Creep crack growth modelling of Grade 91 vessel weldments using a modified ductility based damage model. Eur. J. Mech.-A/Solids 2022, 91, 104424. [Google Scholar] [CrossRef]
- Alang, N.A.; Nikbin, K. An analytical and numerical approach to multiscale ductility constraint based model to predict uniaxial/multiaxial creep rupture and cracking rates. Int. J. Mech. Sci. 2018, 135, 342–352. [Google Scholar] [CrossRef]
- Alang, N.A.; Nikbin, K. A new approach to predict creep rupture of Grade 92 steel under multiaxial stress states. Int. J. Mech. Sci. 2019, 163, 105096. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, Q.; Jiang, W.; Zhang, W.; Xu, S.; Hao, M. Creep failure prediction of brazing joints with double notches. Mater. Des. 2016, 100, 271–279. [Google Scholar] [CrossRef]
- Shigeyama, H.; Takahashi, Y.; Parker, J. Prediction of Creep Life on Notched Bar Specimens of Grade 92 Steel. In Volume 5: High-Pressure Technology, Proceedings of the Rudy Scavuzzo Student Paper Symposium and 24th Annual Student Paper Competition, ASME Nondestructive Evaluation, Diagnosis and Prognosis Division (NDPD), Electric Power Research Institute (EPRI) Creep Fatigue Workshop, Vancouver, BC, Canada, 17–21 July 2016; American Society of Mechanical Engineers: Vancouver, BC, Canada, 2016; p. V005T12A005. [Google Scholar]
- Boehler, J.P.; Sawczuk, A. Application of representation theorems to describe yielding of transversely isotropic solids. Mech. Res. Commun. 1976, 3, 277–283. [Google Scholar] [CrossRef]
- Bonora, N. A nonlinear CDM model for ductile failure. Eng. Fract. Mech. 1997, 58, 11–28. [Google Scholar] [CrossRef]
- Bonora, N.; Gentile, D.; Pirondi, A. Identification of the parameters of a non-linear continuum damage mechanics model for ductile failure in metals. J. Strain Anal. Eng. Des. 2004, 39, 639–651. [Google Scholar] [CrossRef]
- Bonora, N.; Gentile, D.; Pirondi, A.; Newaz, G. Ductile damage evolution under triaxial state of stress: Theory and experiments. Int. J. Plast. 2005, 21, 981–1007. [Google Scholar] [CrossRef]
- Bonora, N. On the effect of triaxial state of stress on ductility using nonlinear CDM model. Int. J. Fract. 1997, 88, 359–371. [Google Scholar] [CrossRef]
- Yue, Z.F.; Lu, Z.Z. Rafting prediction criterion for nickel-base single crvstals under multiaxial stresses and crystallographic orientatione dependence of creep behavior. Acta Met. Sin. 1999, 12, 149–154. [Google Scholar]
- Zhang, C.; Wang, P.; Deng, Y.; Wang, X.; Wen, Z.; Lian, Y.; He, P. Influence of crystal orientations on the creep fracture of a nickel-based single crystal superalloy. Int. J. Solids Struct. 2024, 288, 112614. [Google Scholar] [CrossRef]







| Temperature/°C | Orientation | n | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 850 | 001 | 0.09 | 0.0137 | 0.08 | 900 | 16 | 0.15 | 0.087 | 0.232 |
| Temperature/°C | Orientation | Stress/MPa | Experimental Life/h | Predicted Life/h | Difference/h | Error/% | |
|---|---|---|---|---|---|---|---|
| 850 | 001 | 720 | 0.00234 | 34.0 | 24.9 | 9.1 | 26.8 |
| 700 | 0.0014 | 67.4 | 57.7 | 9.7 | 14.4 | ||
| 680 | 0.00105 | 94.0 | 107.6 | 13.6 | 14.5 | ||
| 660 | 0.00034 | 194.0 | 188.8 | 5.2 | 2.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Dai, J.; Gu, S.; Yang, L.; Long, L.; Wang, J. An Anisotropic Failure Characteristic- and Damage-Coupled Constitutive Model. Modelling 2025, 6, 75. https://doi.org/10.3390/modelling6030075
Chen R, Dai J, Gu S, Yang L, Long L, Wang J. An Anisotropic Failure Characteristic- and Damage-Coupled Constitutive Model. Modelling. 2025; 6(3):75. https://doi.org/10.3390/modelling6030075
Chicago/Turabian StyleChen, Ruiqing, Jieyu Dai, Shuning Gu, Lang Yang, Laohu Long, and Jundong Wang. 2025. "An Anisotropic Failure Characteristic- and Damage-Coupled Constitutive Model" Modelling 6, no. 3: 75. https://doi.org/10.3390/modelling6030075
APA StyleChen, R., Dai, J., Gu, S., Yang, L., Long, L., & Wang, J. (2025). An Anisotropic Failure Characteristic- and Damage-Coupled Constitutive Model. Modelling, 6(3), 75. https://doi.org/10.3390/modelling6030075






