Enhanced Cooling Performance in Cutting Tools Using TPMS-Integrated Toolholders: A CFD-Based Thermal-Fluidic Study
Abstract
1. Introduction
2. Methods
2.1. Geometric Model Construction
2.2. CFD Modeling and Boundary Settings
2.3. Grid Independence and Model Validation
2.4. Thermal–Hydraulic Evaluation Parameters
3. Results and Discussion
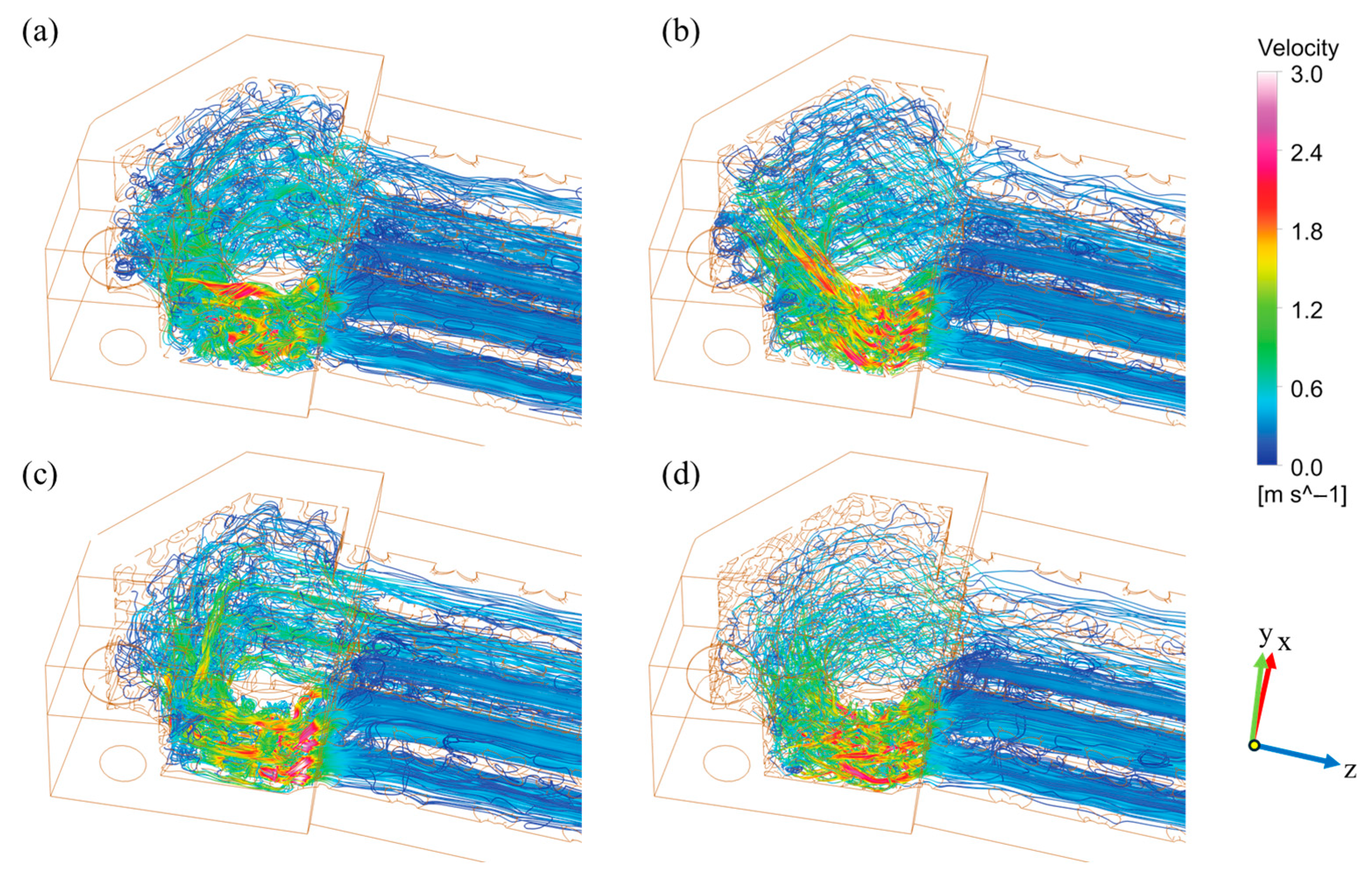
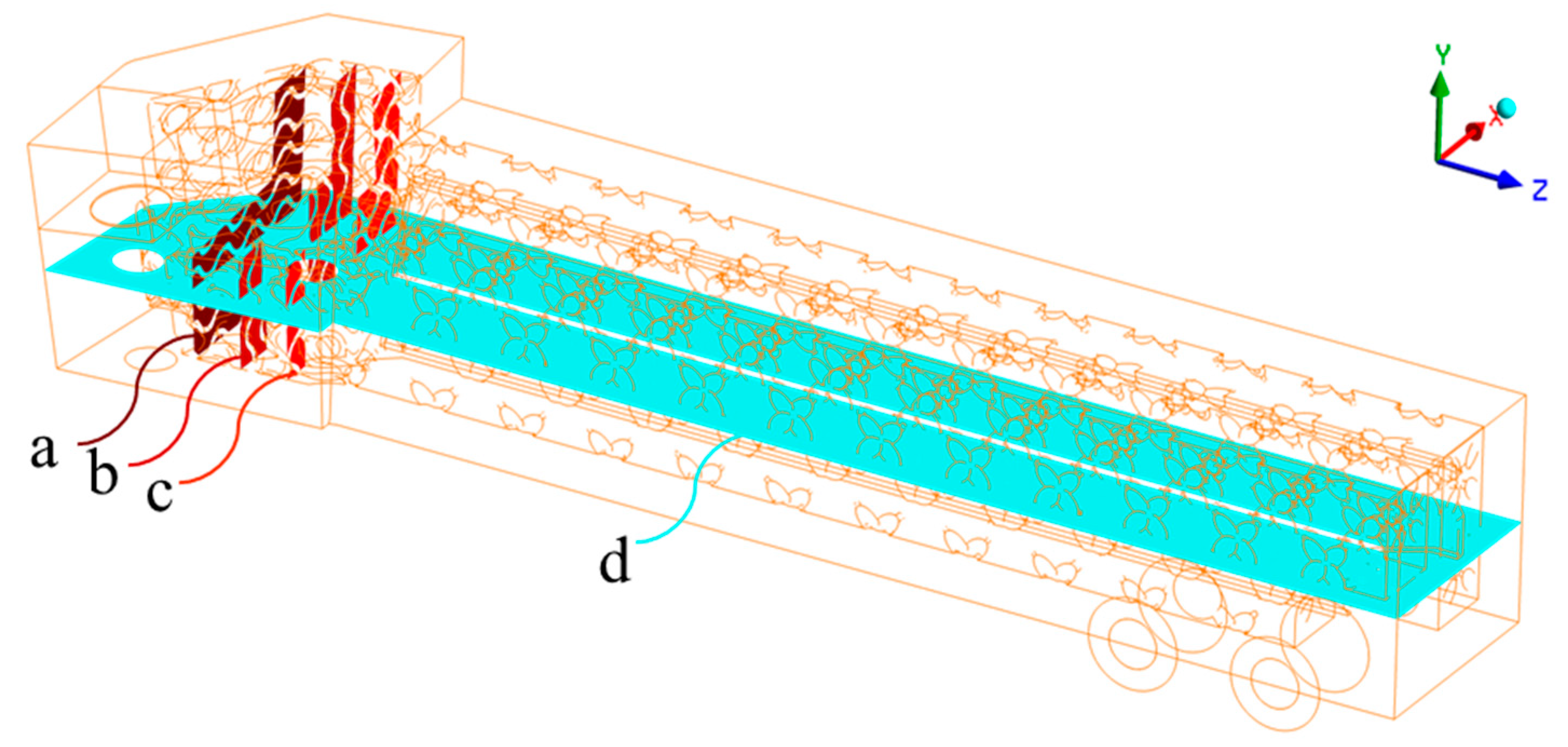
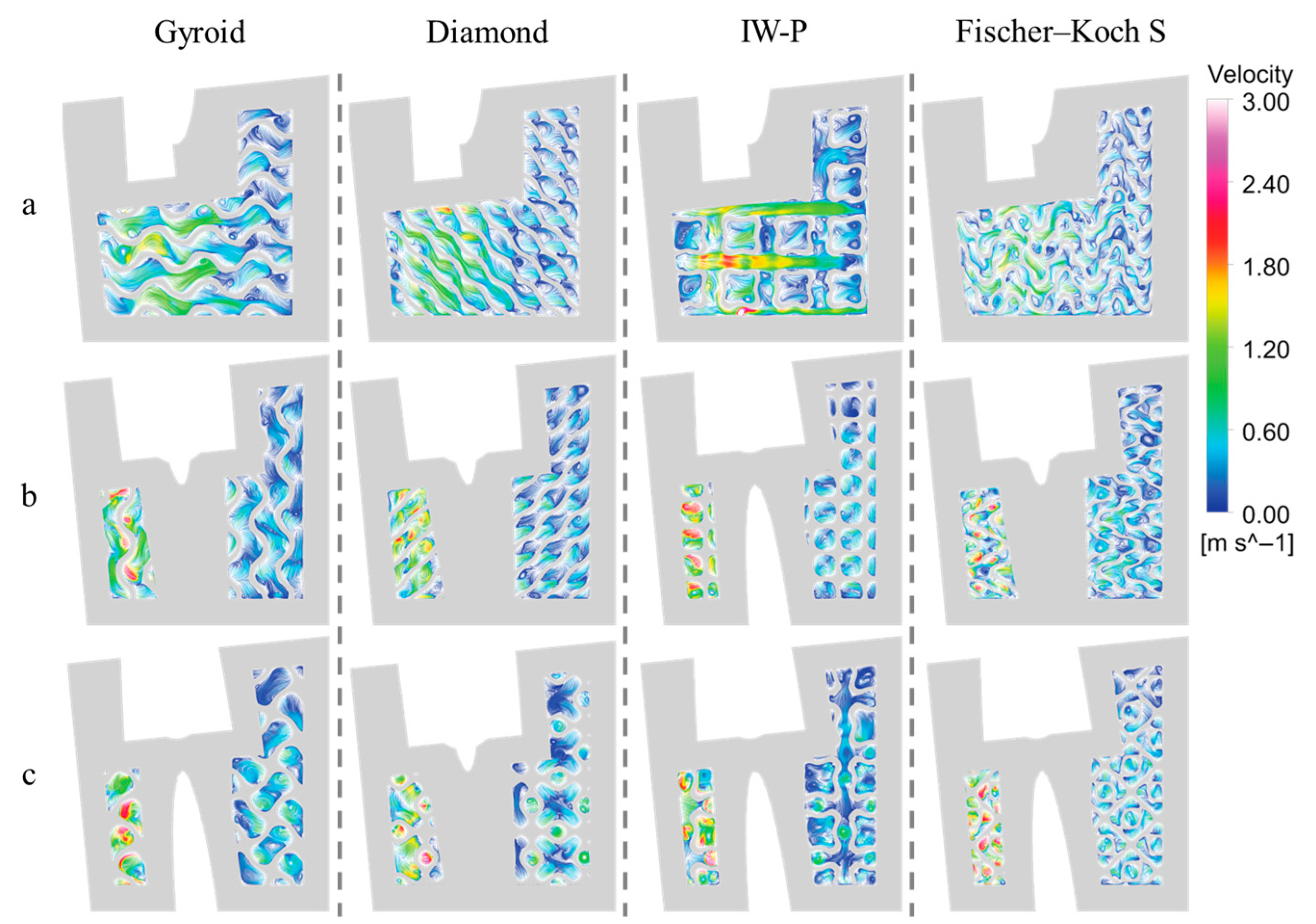
3.1. Flow Field Characteristics and Internal Mixing
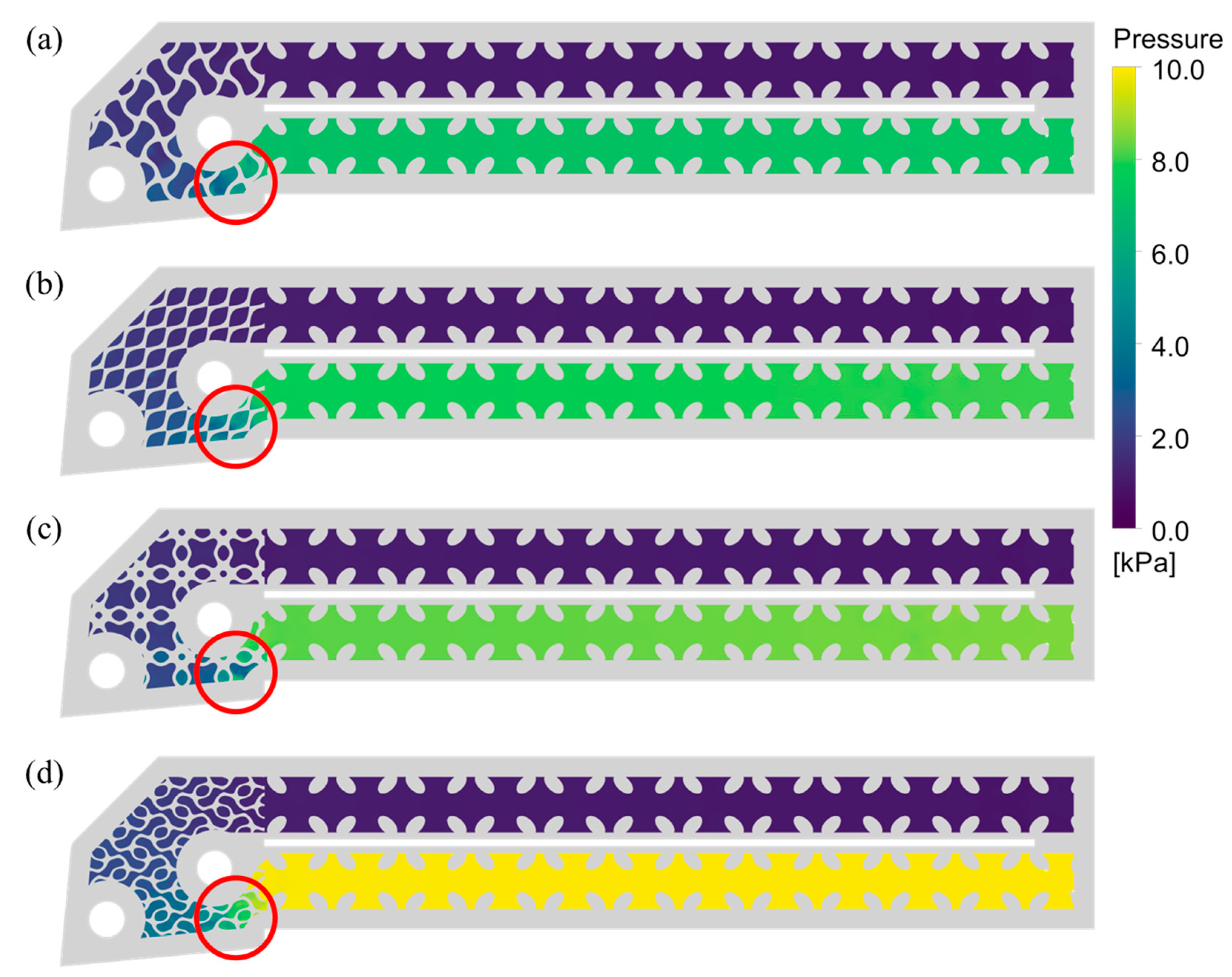
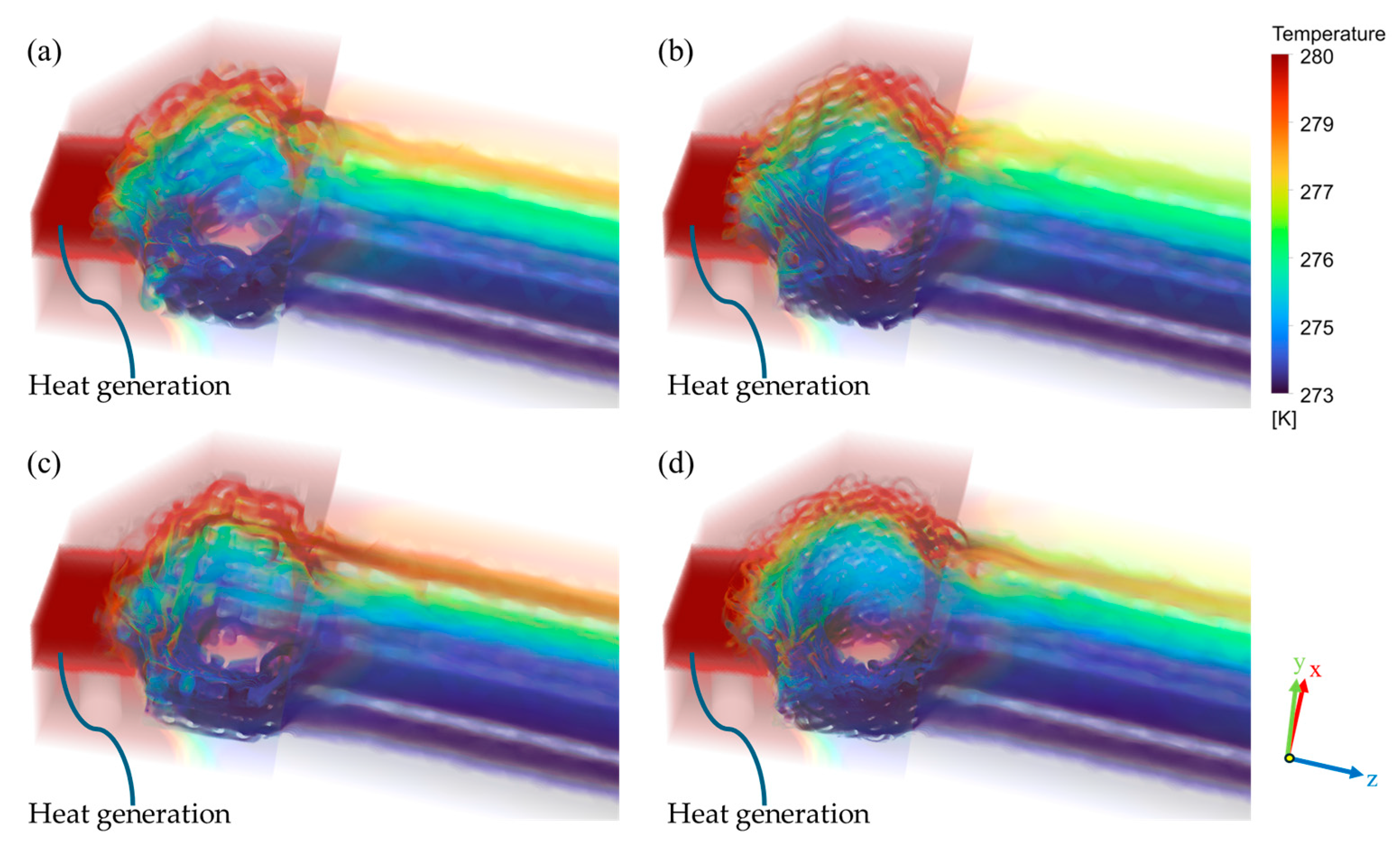
3.2. Temperature Distribution and Thermal Field Analysis
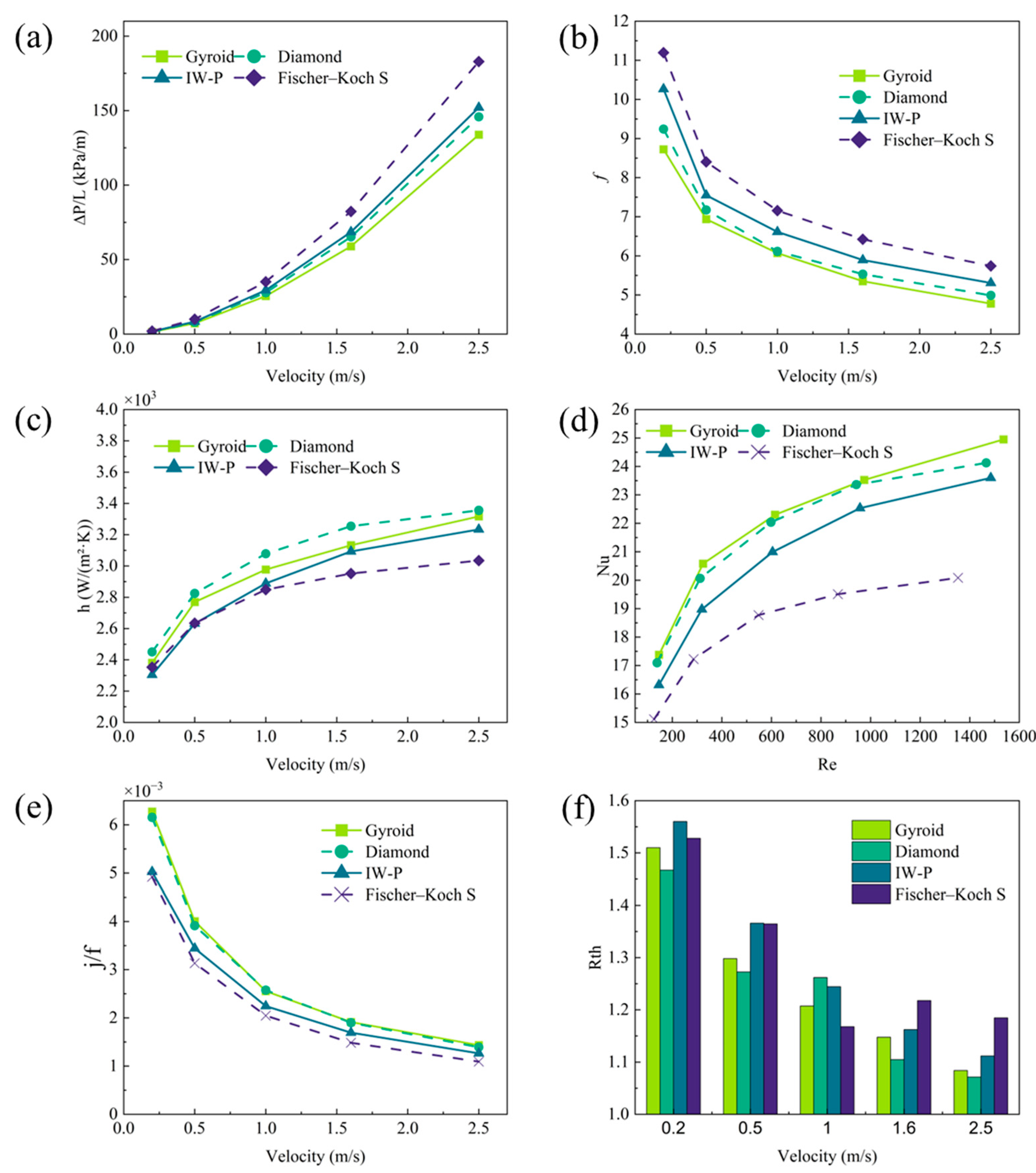
3.3. Evaluation of Thermo-Hydraulic Performance
4. Conclusions
- The complex three-dimensional curvature of TPMS structures effectively disturbs the coolant flow, promoting vortex formation and enhancing turbulence intensity. This leads to improved convective heat transfer through boundary layer disruption.
- Among the four TPMS topologies, the Fischer–Koch S structure exhibits the highest flow resistance and pressure drop, resulting in poorer thermal performance. In contrast, the Gyroid and Diamond structures demonstrate superior hydraulic efficiency with lower pressure losses.
- The Diamond structure achieves the highest convective heat transfer coefficients and the lowest thermal resistance across the tested velocity range, indicating its outstanding cooling effectiveness. Gyroid performs closely behind Diamond, both outperforming the I-WP and Fischer–Koch S structures.
- Thermal isolation between the inlet and outlet channels in TPMS toolholders effectively reduces thermal mixing, thereby enhancing overall cooling efficiency. The trade-off metric confirms that Gyroid and Diamond topologies provide the best balance between heat transfer enhancement and flow resistance, making them the most promising designs for advanced internal cooling tools.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TPMS | Triply Periodic Minimal Surface |
| CFD | Computational Fluid Dynamics |
| I-WP | Infinite Periodic Wrapped Package |
| BCC | Body-Centered Cubic |
| SSA | Specific Surface Area |
| WC-Co | Tungsten Carbide–Cobalt Composite |
| QUICK | Quadratic Upstream Interpolation for Convective Kinematics |
| SST | Shear Stress Transport |
References
- Vieira, J.M.; Machado, A.R.; Ezugwu, E.O. Performance of cutting fluids during face milling of steels. J. Mater. Process Technol. 2001, 116, 244–251. [Google Scholar] [CrossRef]
- Shaw, M.C.; Cookson, J.O. Metal Cutting Principles. Tribol. Int. 1985, 18, 55. [Google Scholar] [CrossRef]
- Abukhshim, N.A.; Mativenga, P.T.; Sheikh, M.A. Heat generation and temperature prediction in metal cutting: A review and implications for high speed machining. Int. J. Mach. Tools Manuf. 2006, 46, 782–800. [Google Scholar] [CrossRef]
- Arrazola, P.J.; Özel, T.; Umbrello, D.; Davies, M.; Jawahir, I.S. Recent advances in modelling of metal machining processes. CIRP Ann. Manuf. Technol. 2013, 62, 695–718. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, X.; Zhang, D. Performance evaluation of high-speed ultrasonic vibration cutting for improving machinability of Inconel 718 with coated carbide tools. Tribol. Int. 2021, 155, 106766. [Google Scholar] [CrossRef]
- Liu, D.; Liu, Z.; Wang, B. Effect of Cutting Parameters on Tool Chipping Mechanism and Tool Wear Multi-Patterns in Face Milling Inconel 718. Lubricants 2022, 10, 218. [Google Scholar] [CrossRef]
- Korkmaz, M.E.; Gupta, M.K.; Ross, N.S.; Sivalingam, V. Implementation of green cooling/lubrication strategies in metal cutting industries: A state of the art towards sustainable future and challenges. Sustain. Mater. Technol. 2023, 36, e00641. [Google Scholar] [CrossRef]
- Wang, Y.; Murga, A.; Long, Z.; Yoo, S.J.; Ito, K. Experimental study of oil mist characteristics generated from minimum quantity lubrication and flood cooling. Energy Built Environ. 2021, 2, 45–55. [Google Scholar] [CrossRef]
- Kuram, E.; Ozcelik, B.; Demirbas, E.; Şik, E.; Tansel, I.N. Evaluation of new vegetable-based cutting fluids on thrust force and surface roughness in drilling of AISI 304 using Taguchi method. Mater. Manuf. Process. 2011, 26, 1136–1146. [Google Scholar] [CrossRef]
- Fang, Z.; Obikawa, T. Turning of Inconel 718 using inserts with cooling channels under high pressure jet coolant assistance. J. Mater. Process Technol. 2017, 247, 19–28. [Google Scholar] [CrossRef]
- Fang, Z.; Obikawa, T. Cooling performance of micro-texture at the tool flank face under high pressure jet coolant assistance. Precis. Eng. 2017, 49, 41–51. [Google Scholar] [CrossRef]
- Bai, X.; Jiang, J.; Li, C.; Dong, L.; Ali, H.M.; Sharma, S. Tribological Performance of Different Concentrations of Al2O3 Nanofluids on Minimum Quantity Lubrication Milling. Chin. J. Mech. Eng. 2023, 36, 1–12. [Google Scholar] [CrossRef]
- Liu, M.; Li, C.; Zhang, Y.; An, Q.; Yang, M.; Gao, T.; Mao, C.; Liu, B.; Cao, H.; Xu, X.; et al. Cryogenic minimum quantity lubrication machining: From mechanism to application. Front. Mech. Eng. 2021, 16, 649–697. [Google Scholar] [CrossRef]
- Shu, S.; Zhang, Y.; He, Y.; Zhang, H. Design of a novel turning tool cooled by combining circulating internal cooling with spray cooling for green cutting. J. Adv. Mech. Des. Syst. Manuf. 2021, 15, JAMDSM0003. [Google Scholar] [CrossRef]
- Shokoohi, Y.; Khosrojerdi, E.; Rassolian Shiadhi, B.H. Machining and ecological effects of a new developed cutting fluid in combination with different cooling techniques on turning operation. J. Clean. Prod. 2015, 94, 330–339. [Google Scholar] [CrossRef]
- Venkateshan, S.P. Heat Transfer; Springer International Publishing: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Dixit, T.; Al-Hajri, E.; Paul, M.C.; Nithiarasu, P.; Kumar, S. High performance, microarchitected, compact heat exchanger enabled by 3D printing. Appl. Therm. Eng. 2022, 210, 118339. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Z.; Li, S.; Yan, G.; Li, H.; Dong, H.; Sun, M.; Zhang, Y.; Song, Y. Enhanced melting behavior of phase change materials using anisotropic Primitive sheet-networks triply periodic minimal surface structure. Energy 2025, 328, 136624. [Google Scholar] [CrossRef]
- Yang, Z.L.; Walvekar, R.; Wong, W.P.; Sharma, R.K.; Dharaskar, S.; Khalid, M. Advances in phase change materials, heat transfer enhancement techniques, and their applications in thermal energy storage: A comprehensive review. J. Energy Storage 2024, 87, 111329. [Google Scholar] [CrossRef]
- Yu, S.; Sun, J.; Bai, J. Investigation of functionally graded TPMS structures fabricated by additive manufacturing. Mater. Des. 2019, 182, 108021. [Google Scholar] [CrossRef]
- Lee, J.W.; Oh, S.H.; Jeon, E.; Kim, J.; Park, K. Functional gradation of the morphological properties of TPMS channel for enhanced flow performance. Mater. Des. 2022, 224, 111413. [Google Scholar] [CrossRef]
- Feng, J.; Fu, J.; Yao, X.; He, Y. Triply periodic minimal surface (TPMS) porous structures: From multi-scale design, precise additive manufacturing to multidisciplinary applications. Int. J. Extrem. Manuf. 2022, 4, 022001. [Google Scholar] [CrossRef]
- Tang, W.; Zhou, H.; Zeng, Y.; Yan, M.; Jiang, C.; Yang, P.; Li, Q.; Li, Z.; Fu, J.; Huang, Y.; et al. Analysis on the convective heat transfer process and performance evaluation of Triply Periodic Minimal Surface (TPMS) based on Diamond, Gyroid and Iwp. Int. J. Heat Mass. Transf. 2023, 201, 123642. [Google Scholar] [CrossRef]
- Baobaid, N.; Ali, M.I.; Khan, K.A.; Abu Al-Rub, R.K. Fluid flow and heat transfer of porous TPMS architected heat sinks in free convection environment. Case Stud. Therm. Eng. 2022, 33, 101944. [Google Scholar] [CrossRef]
- Yeranee, K.; Rao, Y. A Review of Recent Investigations on Flow and Heat Transfer Enhancement in Cooling Channels Embedded with Triply Periodic Minimal Surfaces (TPMS). Energies 2022, 15, 8994. [Google Scholar] [CrossRef]
- Li, J.; Fan, H.; Hua, L.; Du, J.; He, Y.; Jin, Y. Bone implants with triply periodic minimal surface architectures: Design, fabrication, and biological performance. Biodes Manuf. 2025, 8, 672–704. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Chen, X.; Yang, W.; Chen, H.; Che, S.; Han, L. Mechanical Properties of 3D-Printed Polymeric Cellular Structures Based on Bifurcating Triply Periodic Minimal Surfaces. Adv. Eng. Mater. 2025, 27, 2402507. [Google Scholar] [CrossRef]
- Qiu, N.; Wan, Y.; Shen, Y.; Fang, J. Experimental and numerical studies on mechanical properties of TPMS structures. Int. J. Mech. Sci. 2024, 261, 108657. [Google Scholar] [CrossRef]
- Wu, S.; Yang, L.; Wang, C.; Yan, C.; Shi, Y. Si/SiC ceramic lattices with a triply periodic minimal surface structure prepared by laser powder bed fusion. Addit. Manuf. 2022, 56, 102910. [Google Scholar] [CrossRef]
- Wu, Y.; Li, X.; Li, S.; Wang, H.W.; Wang, P.; Li, W. Bending behavior of additively manufactured short fiber reinforced composite sandwich structures based on triply periodic minimal surface. Polym. Test. 2025, 146, 56–70. [Google Scholar] [CrossRef]
- Yuan, L.; Ding, S.; Wen, C. Additive manufacturing technology for porous metal implant applications and triple minimal surface structures: A review. Bioact. Mater. 2019, 4, 56–70. [Google Scholar] [CrossRef]
- Schoen, A.H. Infinite Periodic Minimal Surfaces Without Self-Intersections; National Aeronautics and Space Administration: Washington, DC, USA, 1970; Volume 5541. [Google Scholar]
- Gandy, P.J.F.; Cvijović, D.; Mackay, A.L.; Klinowski, J. Exact computation of the triply periodic D (‘diamond’) minimal surface. Chem. Phys. Lett. 1999, 314, 543–551. [Google Scholar] [CrossRef]
- Fischer, W.; Koch, E. Spanning minimal surfaces. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1996, 354, 2105–2142. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W.; Orsi, G.; Ferziger, J.H.; Date, A.W.; Anderson, J.D. An Introduction to Computational Fluid Dynamics-The Finite Volume Method; Pearson Education India: Noida, Uttar Pradesh, India, 1995. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]




| Type | Gyroid | Diamond | I-WP | Fischer–Koch S |
|---|---|---|---|---|
| Vc (mm3) | 32,809.8 | 32,785.1 | 32,829.9 | 32,817.0 |
| Ac (mm2) | 31,318.6 | 32,744.5 | 32,302.0 | 35,599.1 |
| VTPMS (mm3) | 64.5 | 64.5 | 64 | 64.3 |
| ATPMS (mm3) | 213.8 | 270.1 | 245.5 | 376.2 |
| SSA (mm−1) | 3.31 | 4.19 | 3.84 | 5.85 |
| Thickness (mm) | 0.6405 | 0.4897 | 0.4518 | 0.2659 |
| Dh (mm) | 4.19 | 4.00 | 4.07 | 3.69 |
| Material | Density ρ (kg/m3) | Thermal Conductivity λ (W/(m·K)) | Specific Heat Capacity cp (J/(kg·K)) |
|---|---|---|---|
| Liquid water | 999.8 | 0.6 | 4182 |
| 316 L stainless steel | 8000 | 16.2 | 500 |
| WC-Co | 14,500 | 85 | 200 |
| Boundary Region | Type | Value/Description |
|---|---|---|
| Inlet | Velocity inlet | 0.2–2.5 m/s, water at 273.15 K |
| Outlet | Pressure outlet | 0 Pa gauge pressure |
| Insert region | Volumetric heat source | 200 W |
| Insert–toolholder interface | Thermal contact resistance | 10,000 (m2·K)/W |
| Outer surfaces | Convective boundary | Air convection boundary (Tair = 300 K) |
| Type | Cell Count (Million) | ΔP (Pa) | ErrorP (%) | ΔT (K) | ErrorT (%) |
|---|---|---|---|---|---|
| Gyroid | 9.65 | 7.132 | 8.38 | 1.801 | 5.88 |
| 13.82 | 7.647 | 1.76 | 1.719 | 1.06 | |
| 22.34 | 7.784 | - | 1.701 | - | |
| Diamond | 8.73 | 7.697 | 8.77 | 1.561 | 2.90 |
| 14.08 | 8.356 | 0.96 | 1.492 | 1.65 | |
| 19.71 | 8.437 | - | 1.517 | - | |
| I-WP | 9.28 | 8.107 | 7.91 | 1.817 | 4.37 |
| 13.97 | 8.825 | 0.25 | 1.725 | 0.92 | |
| 19.64 | 8.803 | - | 1.741 | - | |
| Fischer–Koch S | 9.86 | 9.612 | 9.79 | 1.522 | 6.21 |
| 16.02 | 10.522 | 1.25 | 1.457 | 1.67 | |
| 23.2 | 10.655 | - | 1.433 | - |
| Flow Rate (m3/h) | Inlet Velocity (m/s) | Measured Temp (K) | Simulated Temp (K) | Absolute Error (K) |
|---|---|---|---|---|
| 0.030 | 0.2947 | 310.45 | 304.75 | 5.7 |
| 0.042 | 0.4126 | 307.85 | 300.55 | 7.3 |
| 0.054 | 0.5305 | 304.05 | 297.75 | 6.3 |
| 0.066 | 0.6484 | 298.35 | 292.95 | 5.4 |
| 0.078 | 0.7663 | 293.65 | 288.35 | 5.3 |
| 0.090 | 0.8842 | 290.95 | 286.15 | 4.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, H.; Liu, Z.; Zhao, J.; Wang, B. Enhanced Cooling Performance in Cutting Tools Using TPMS-Integrated Toolholders: A CFD-Based Thermal-Fluidic Study. Modelling 2025, 6, 73. https://doi.org/10.3390/modelling6030073
Ji H, Liu Z, Zhao J, Wang B. Enhanced Cooling Performance in Cutting Tools Using TPMS-Integrated Toolholders: A CFD-Based Thermal-Fluidic Study. Modelling. 2025; 6(3):73. https://doi.org/10.3390/modelling6030073
Chicago/Turabian StyleJi, Haiyang, Zhanqiang Liu, Jinfu Zhao, and Bing Wang. 2025. "Enhanced Cooling Performance in Cutting Tools Using TPMS-Integrated Toolholders: A CFD-Based Thermal-Fluidic Study" Modelling 6, no. 3: 73. https://doi.org/10.3390/modelling6030073
APA StyleJi, H., Liu, Z., Zhao, J., & Wang, B. (2025). Enhanced Cooling Performance in Cutting Tools Using TPMS-Integrated Toolholders: A CFD-Based Thermal-Fluidic Study. Modelling, 6(3), 73. https://doi.org/10.3390/modelling6030073









