SpatioConvGRU-Net for Short-Term Traffic Crash Frequency Prediction in Bogotá: A Macroscopic Spatiotemporal Deep Learning Approach with Urban Factors
Abstract
1. Introduction
2. Materials and Methods
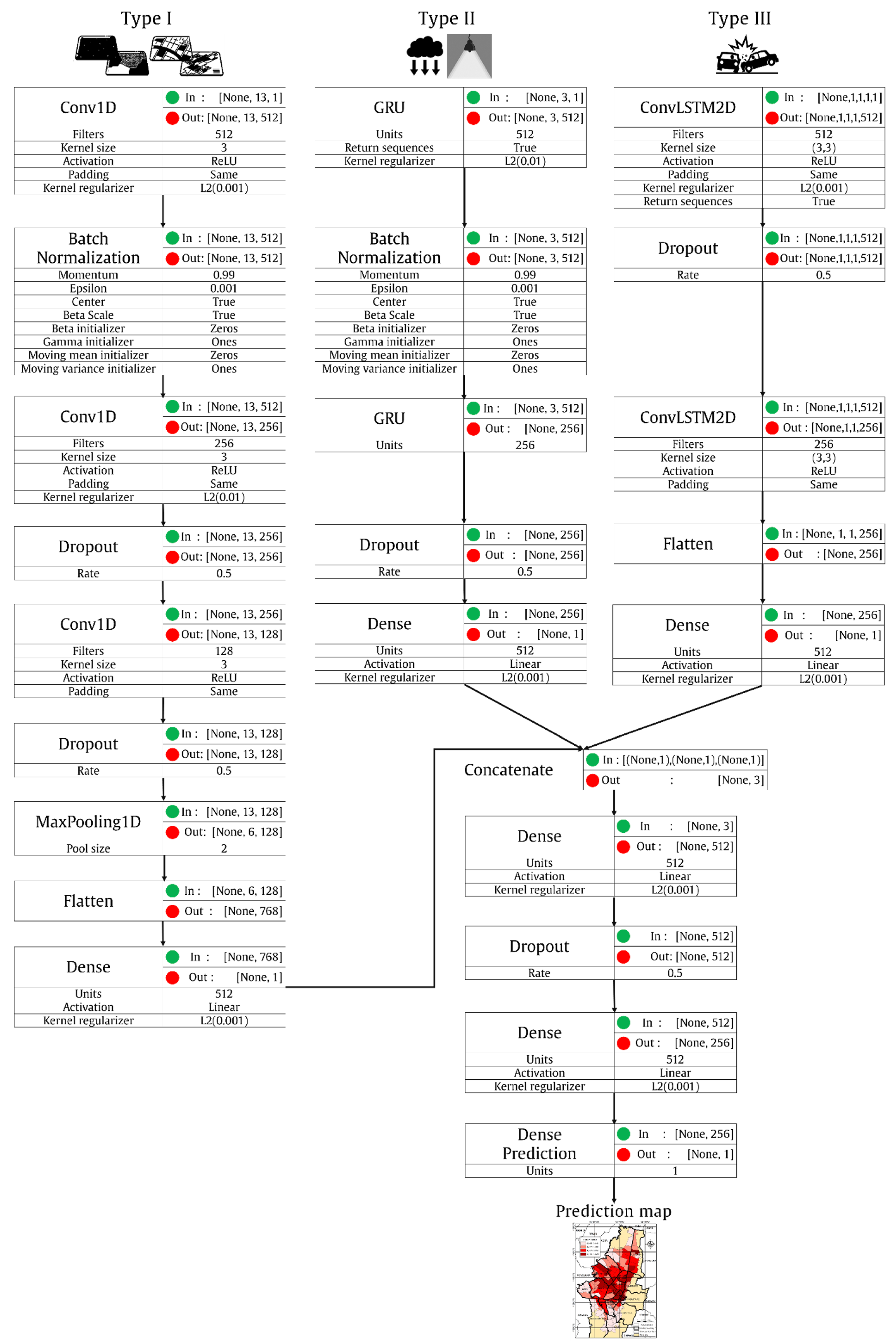
2.1. SpatioConvGru-Net Ensemble Model Structure
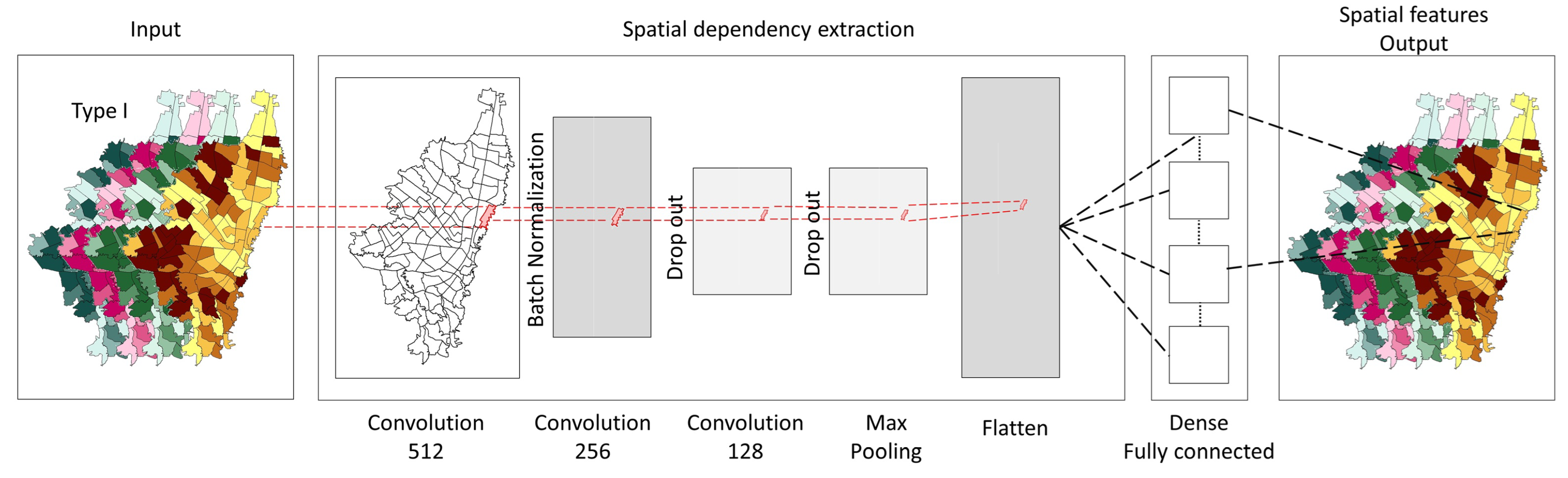
- Type I Variables: These vary spatially but are static in the time of the study period, since they were originally collected during an annual period. For this type of variable, the spatial dependence present between spatial units is considered. Examples include population density, land use, socioeconomic stratification, among others.
- Type II Variables: These vary temporally but are spatially static over the time of the study. This study considers environmental variables such as precipitation and illumination that are constant in space throughout the study area and for which temporal dependence is considered.
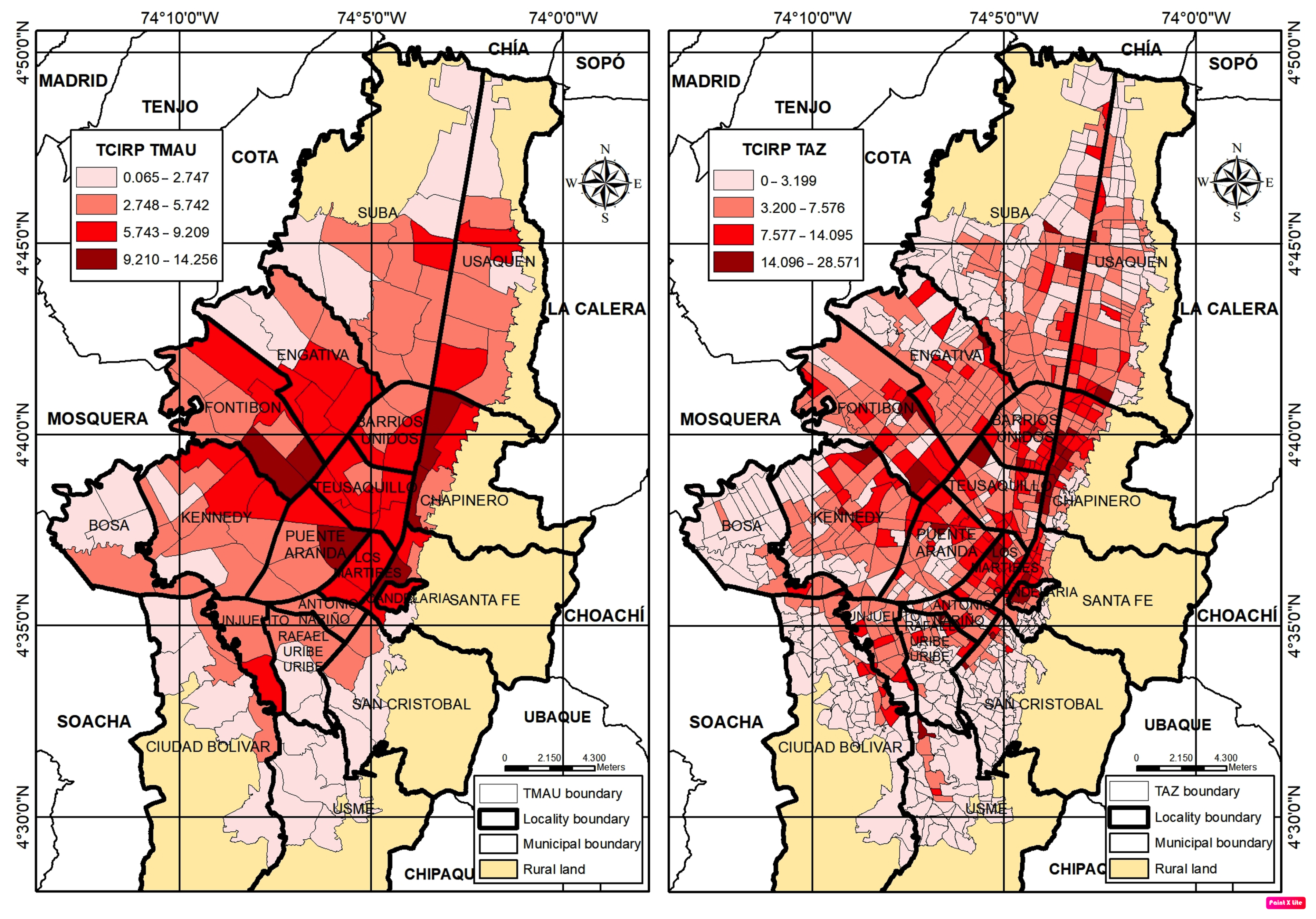
- Type III Variables: These vary spatially and temporally over the study period. This category includes only the variable of interest, the Traffic Crashes Index on the road perimeter, as it exhibits both local and spatial dependence simultaneously.
2.2. Data
Spatiotemporal Cross-Validation Approach
2.3. Proposed Model
2.3.1. Feature Engineering for Spatial Data Using CNN
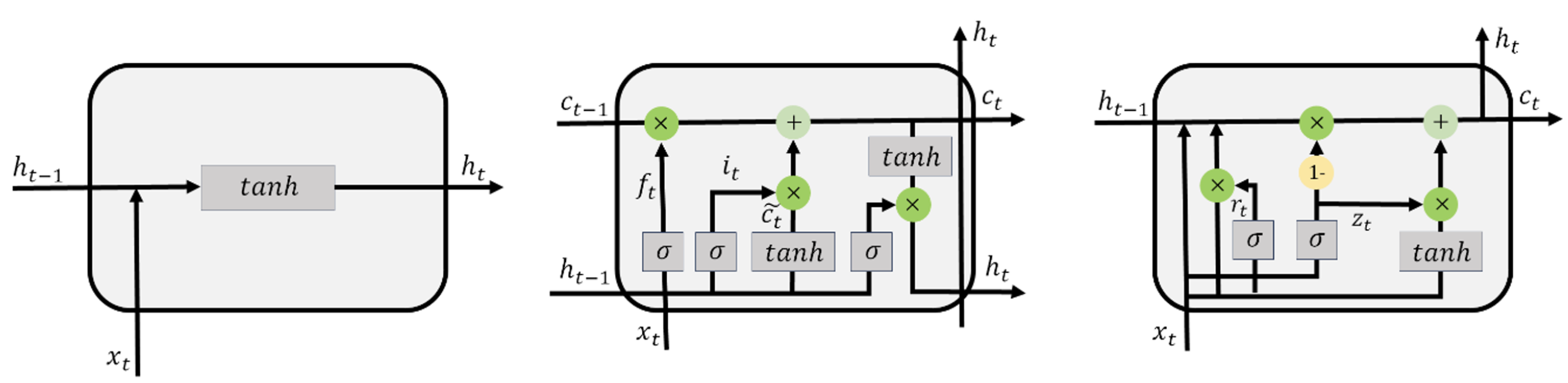
2.3.2. Feature Engineering for Temporal Data Using GRU
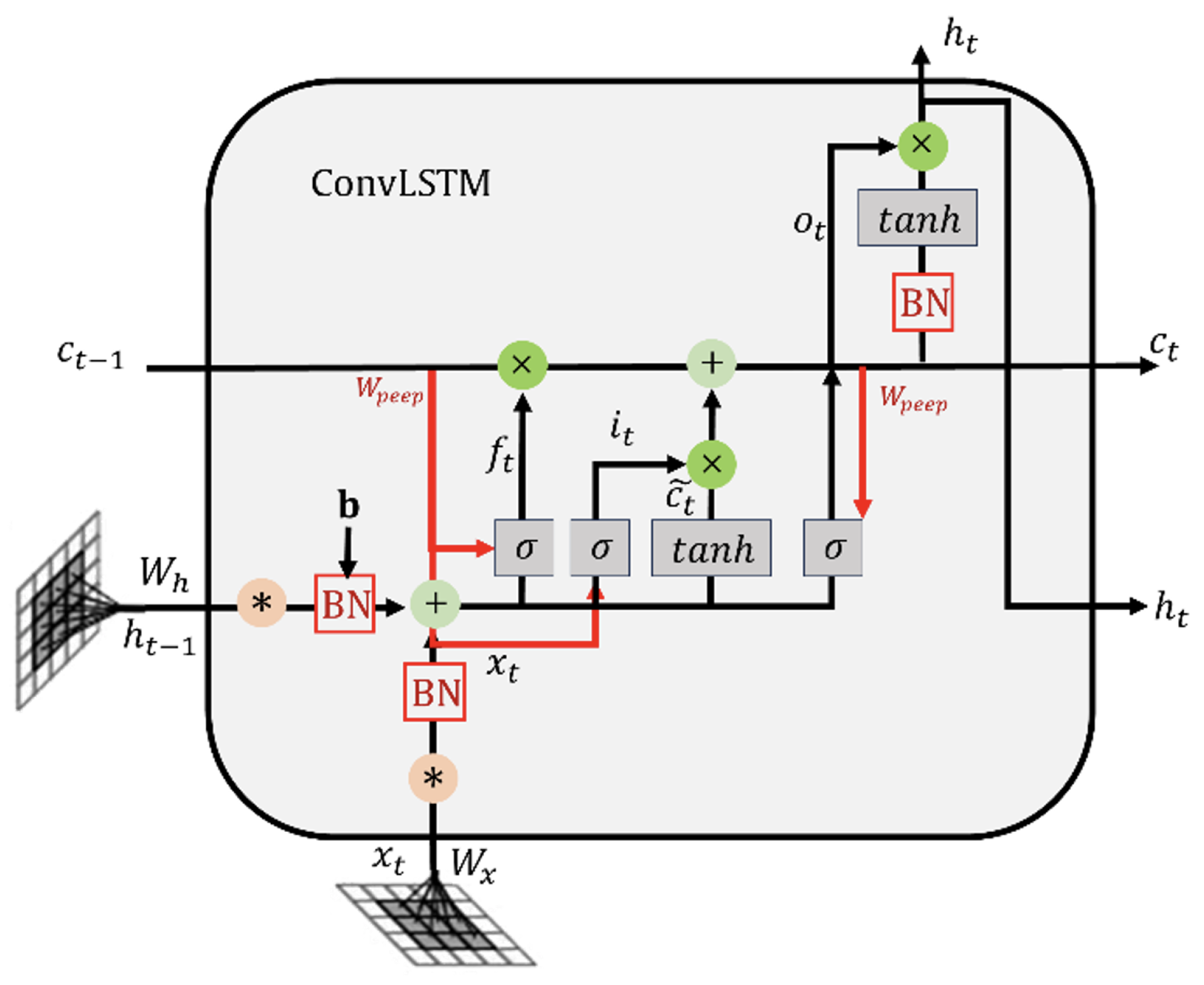
2.3.3. Spatiotemporal Features Extracted from ConvLSTM
2.3.4. Multimodal Fusion and Refinement
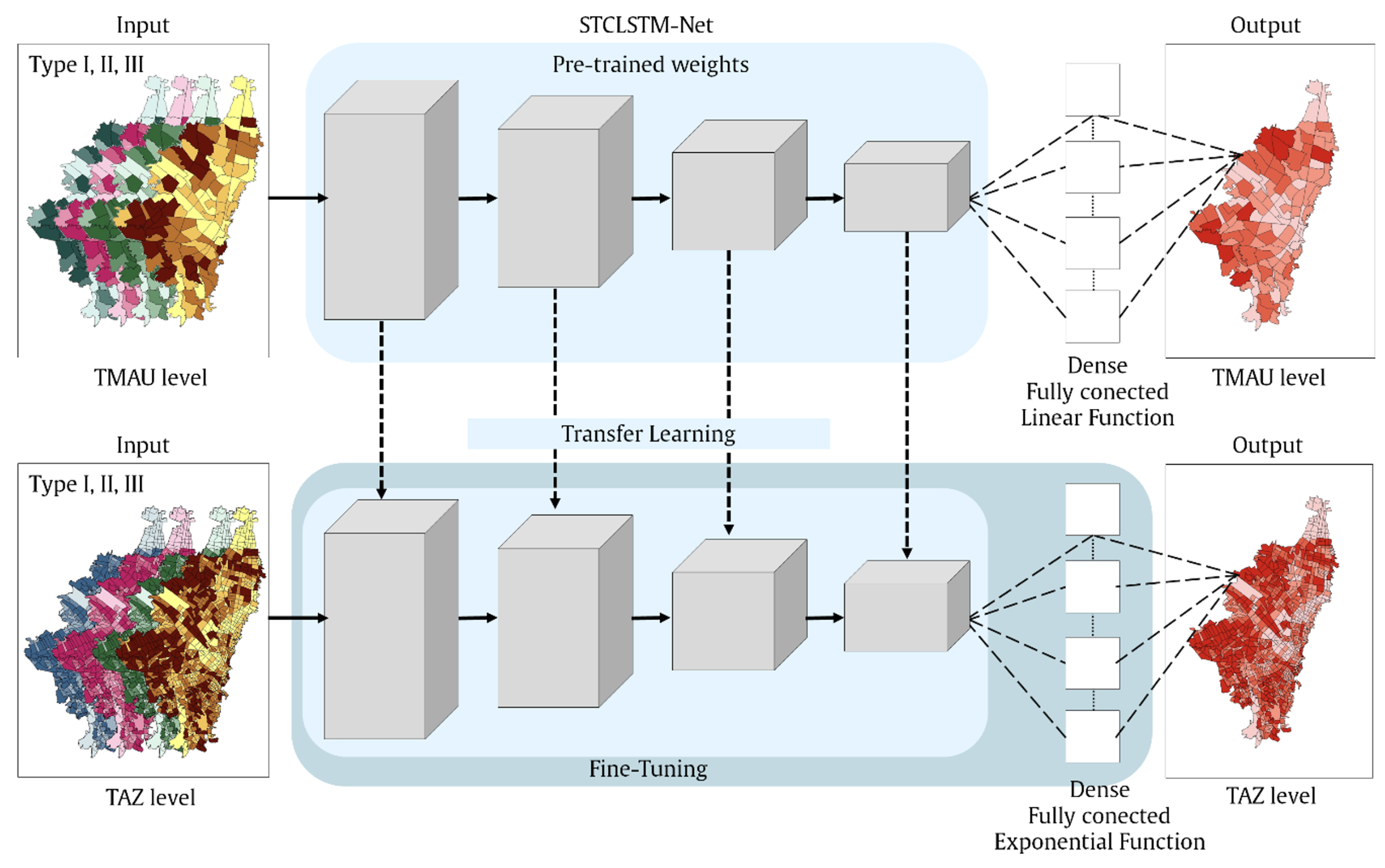
2.3.5. Fine-Tuning with Transfer Learning for Small Areas
2.3.6. Training
2.3.7. Evaluation
3. Results
3.1. Preparation and Exploration Data Analysis
3.2. SpatioConvGru-Net Results
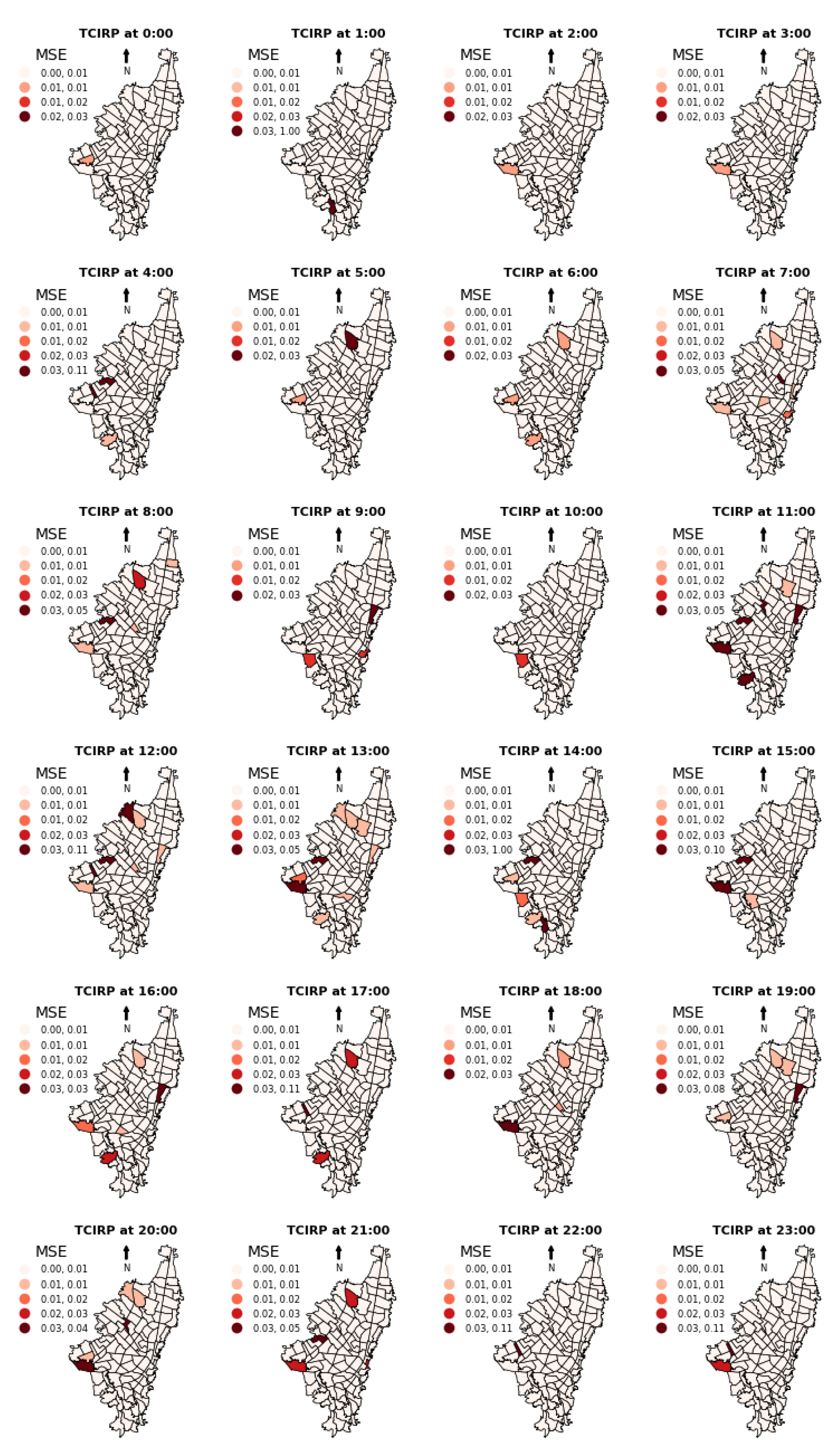
3.3. Evaluating Model Performances
4. Discussion
4.1. Model Performance and Spatiotemporal Patterns
4.2. Spatial Resolution Challenges
4.3. Methodological Limitations
4.4. Implications for Urban Management
- Risk area anticipation: Identification of zones with higher crash probability facilitates implementation of preventive measures and resource allocation.
- Emergency resource planning: Accurate predictions enable advanced planning and optimization of response in case of crashes.
- Traffic policy development: Results can inform long-term policies, including infrastructure planning and road safety measures.
- Associated cost minimization: Crash prediction can reduce the costs of emergency care, infrastructure repair, and compensation.
4.5. Future Directions
- Integrating econometric models with zero-inflated components (Zero-Inflated Hurdle Model, Zero-Inflated Mixed Effects Model)
- Exploring attention-based architectures (Transformer blocks) to capture long-range dependencies
- Implementing explicit seasonal analysis to improve interpretability
- Developing geographically stratified validation to assess spatial robustness
- Including comparisons with existing municipal intervention programs
4.6. Implementation Considerations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Network |
| GRU | Gated Recurrent Unit |
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| ConvLSTM | Convolutional Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MSE | Mean Squared Error |
| R2 | Coefficient of Determination |
| ADAM | Adaptive Moment Estimation |
| FT | Fine-Tuning |
| TL | Transfer Learning |
| ReLU | Rectified Linear Unit |
| TMAU | Territorial Mobility Analysis Unit |
| TAZ | Transportation Analysis Zone |
| TCIRP | Traffic Crashes Index on the Road Perimeter |
| LU | Land Use |
| ST | Socioeconomic Stratification |
| PD | Population Density |
| NH | Number of Households |
| RMMV | Rate of Motorization of Motor Vehicles |
| RPTP | Rate of Pedestrian Trips per Person |
| RTPPT | Rate of Trips per Person in Public Transport |
| RTPT | Rate of Trips per Person by Taxi |
| RTPC | Rate of Trips per Person by Car |
| RTPM | Rate of Trips per Person on Motorcycle |
| RTPB | Rate of Trips per Person by Bicycle |
| TTDOD | Trips in a Typical Day Origin - Destination |
| TRPTM | Travel Rate per Person in BRT System |
| AMSA | Average Maximum Speed Allowed |
| PCP | Precipitation |
| ILLUM | Illumination |
References
- Aguero-Valverde, J.; Jovanis, P.P. Analysis of Road Crash Frequency with Spatial Models. Transp. Res. Rec. J. Transp. Res. Board 2008, 2061, 55–63. [Google Scholar] [CrossRef]
- Bao, J.; Liu, P.; Ukkusuri, S.V. A Spatiotemporal Deep Learning Approach for Citywide Short-Term Crash Risk Prediction with Multi-Source Data. Accid. Anal. Prev. 2019, 122, 239–254. [Google Scholar] [CrossRef]
- Li, Z.; Liu, P.; Wang, W.; Xu, C. Using Support Vector Machine Models for Crash Injury Severity Analysis. Accid. Anal. Prev. 2012, 45, 478–486. [Google Scholar] [CrossRef]
- Hadayeghi, A.; Shalaby, A.S.; Persaud, B.N. Safety Prediction Models: Proactive Tool for Safety Evaluation in Urban Transportation Planning Applications. Transp. Res. Rec. 2007, 2019, 225–236. [Google Scholar] [CrossRef]
- Huang, H.; Song, B.; Xu, P.; Zeng, Q.; Lee, J.; Abdel-Aty, M. Macro and Micro Models for Zonal Crash Prediction with Application in Hot Zones Identification. J. Transp. Geogr. 2016, 54, 248–256. [Google Scholar] [CrossRef]
- Pulugurtha, S.S.; Duddu, V.R.; Kotagiri, Y. Traffic Analysis Zone Level Crash Estimation Models Based on Land Use Characteristics. Accid. Anal. Prev. 2013, 50, 678–687. [Google Scholar] [CrossRef]
- Tasic, I.; Porter, R.J. Modeling Spatial Relationships Between Multimodal Transportation Infrastructure and Traffic Safety Outcomes in Urban Environments. Saf. Sci. 2016, 82, 325–337. [Google Scholar] [CrossRef]
- Wier, M.; Weintraub, J.; Humphreys, E.H.; Seto, E.; Bhatia, R. An Area-Level Model of Vehicle-Pedestrian Injury Collisions with Implications for Land Use and Transportation Planning. Accid. Anal. Prev. 2009, 41, 137–145. [Google Scholar] [CrossRef]
- Abdel-Aty, M.; Siddiqui, C.; Huang, H.; Wang, X. Integrating Trip and Roadway Characteristics to Manage Safety in Traffic Analysis Zones. Transp. Res. Rec. 2011, 2213, 20–28. [Google Scholar] [CrossRef]
- Dong, N.; Huang, H.; Zheng, L. Support Vector Machine in Crash Prediction at the Level of Traffic Analysis Zones: Assessing the Spatial Proximity Effects. Accid. Anal. Prev. 2015, 82, 192–198. [Google Scholar] [CrossRef]
- Mohammadi, M.; Shafabakhsh, G.; Naderan, A. Macro-Level Modeling of Urban Transportation Safety: Case-Study of Mashhad (Iran). Transp. Telecommun. 2017, 18, 282–288. [Google Scholar] [CrossRef][Green Version]
- Quddus, M.A. Modelling Area-Wide Count Outcomes with Spatial Correlation and Heterogeneity: An Analysis of London Crash Data. Accid. Anal. Prev. 2008, 40, 1486–1497. [Google Scholar] [CrossRef] [PubMed]
- Sandoval-Pineda, A.; Pedraza, C.; Darghan, A.E. Macroscopic Spatial Analysis of the Impact of Socioeconomic, Land Use and Mobility Factors on the Frequency of Traffic Accidents in Bogot’a. Computers 2022, 11, 180. [Google Scholar] [CrossRef]
- Guevara, F.L.D.; Washington, S.P.; Oh, J. Forecasting Crashes at the Planning Level: Simultaneous Negative Binomial Crash Model Applied in Tucson, Arizona. Transp. Res. Rec. 2004, 1897, 191–199. [Google Scholar] [CrossRef]
- Hadayeghi, A.; Shalaby, A.S.; Persaud, B.N. Macrolevel Accident Prediction Models for Evaluating Safety of Urban Transportation Systems. Transp. Res. Rec. 2003, 1840, 87–95. [Google Scholar] [CrossRef]
- Wang, J.; Huang, H.; Zeng, Q. The Effect of Zonal Factors in Estimating Crash Risks by Transportation Modes: Motor Vehicle, Bicycle and Pedestrian. Accid. Anal. Prev. 2017, 98, 223–231. [Google Scholar] [CrossRef]
- Zhang, C.; Yan, X.; Ma, L.; An, M. Crash Prediction and Risk Evaluation Based on Traffic Analysis Zones. Math. Probl. Eng. 2014, 2014, 987978. [Google Scholar] [CrossRef]
- Hezaveh, A.M.; Arvin, R.; Cherry, C.R. A Geographically Weighted Regression to Estimate the Comprehensive Cost of Traffic Crashes at a Zonal Level. Accid. Anal. Prev. 2019, 131, 15–24. [Google Scholar] [CrossRef]
- Fuentes, C.; Hern’andez, V. The Urban Spatial Structure and the Incidence of Traffic Accidents in Tijuana, Baja California (2003–2004). Front. Norte 2009, 21, 5. [Google Scholar] [CrossRef]
- Alrajhi, M.; Kamel, M. A Deep-Learning Model for Predicting and Visualizing the Risk of Road Traffic Accidents in Saudi Arabia: A Tutorial Approach. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 475–483. [Google Scholar] [CrossRef]
- Chen, Q.; Song, X.; Yamada, H.; Shibasaki, R. Learning Deep Representation from Big and Heterogeneous Data for Traffic Accident Inference. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, Phoenix, Arizona, 12–17 February 2016. [Google Scholar]
- Lee, J.; Chae, J.; Yoon, T.; Yang, H. Traffic Accident Severity Analysis with Rain-Related Factors Using Structural Equation Modeling—A Case Study of Seoul City. Accid. Anal. Prev. 2018, 112, 1–10. [Google Scholar] [CrossRef]
- Theofilatos, A. Incorporating Real-Time Traffic and Weather Data to Explore Road Accident Likelihood and Severity in Urban Arterials. J. Saf. Res. 2017, 61, 9–21. [Google Scholar] [CrossRef]
- Kashifi, M.T.; Al-Turki, M.; Sharify, A.W. Deep Hybrid Learning Framework for Spatiotemporal Crash Prediction Using Big Traffic Data. Int. J. Transp. Sci. Technol. 2023, 12, 793–808. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F. Traffic Flow Prediction with Big Data: A Deep Learning Approach. IEEE Trans. Intell. Transp. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
- Integrated Information System on Regional Urban Mobility. Open Data Portal-SIMUR, 2025. Bogotá, Colombia. Available online: https://www.movilidadbogota.gov.co/web/simur (accessed on 13 July 2025).
- Institute of Hydrology, Meteorology and Environmental Studies. Atención al Ciudadano-DHIME, 2025. Colombia. Available online: https://www.ideam.gov.co/transparencia/datos-abiertos (accessed on 13 July 2025).
- Alcaldía Mayor de Bogotá. Datos Abiertos Bogotá, 2025. Colombia. Available online: https://datosabiertos.bogota.gov.co/ (accessed on 13 July 2025).
- Zhu, L.; Guo, F.; Krishnan, R.; Polak, J.W. The Use of Convolutional Neural Networks for Traffic Incident Detection at a Network Level. In Proceedings of the Transportation Research Board 97th Annual Meeting, Washington, DC, USA, 7–11 January 2018. [Google Scholar]
- Salehin, I.; Kang, D.K. A Review on Dropout Regularization Approaches for Deep Neural Networks within the Scholarly Domain. Electronics 2023, 12, 3106. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Volume 25, pp. 1007–1105. [Google Scholar]
- Nanni, L.; Brahnam, S.; Paci, M.; Ghidoni, S. Comparison of Different Convolutional Neural Network Activation Functions and Methods for Building Ensembles for Small to Midsize Medical Data Sets. Sensors 2022, 22, 6129. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B. Severity Prediction of Traffic Accidents with Recurrent Neural Networks. Appl. Sci. 2017, 7, 476. [Google Scholar] [CrossRef]
- Shaik, M.E.; Islam, M.M.; Hossain, Q.S. A Review on Neural Network Techniques for the Prediction of Road Traffic Accident Severity. Asian Transp. Stud. 2021, 7, 100040. [Google Scholar] [CrossRef]
- Elman, J.L. Finding Structure in Time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- ArunKumar, K.E.; Kalaga, D.V.; Kumar, C.M.S.; Kawaji, M.; Brenza, T.M. Comparative Analysis of Gated Recurrent Units (GRU), Long Short-Term Memory (LSTM) Cells, Autoregressive Integrated Moving Average (ARIMA), Seasonal Autoregressive Integrated Moving Average (SARIMA) for Forecasting COVID-19 Trends. Alex. Eng. J. 2022, 61, 7585–7603. [Google Scholar] [CrossRef]
- Ma, X.; Yu, H.; Wang, Y. Large-Scale Transportation Network Congestion Evolution Prediction Using Deep Learning Theory. PLoS ONE 2015, 10, e0119044. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W. Convolutional LSTM Networks IEEE Transactions on Pattern Analysis and Machine Intelligence. arXiv 2015, arXiv:1506.04214. [Google Scholar] [CrossRef]
- Li, P.; Abdel-Aty, M.; Yuan, J. Real-Time Crash Risk Prediction on Arterials Based on LSTM-CNN. Accid. Anal. Prev. 2020, 135, 105371. [Google Scholar] [CrossRef]
- Tan, C.; Sun, F.; Kong, T.; Zhang, W.; Yang, C.; Liu, C. A Survey on Deep Transfer Learning. Int. Conf. Artif. Neural Netw. 2018, 9, 270. [Google Scholar]
- Weiss, K.; Khoshgoftaar, T.; Wang, D. A Survey of Transfer Learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Elassad, Z.E.A.; Mousannif, H.; Moatassime, H.A. A Real-Time Crash Prediction Fusion Framework: An Imbalance-Aware Strategy for Collision Avoidance Systems. Transp. Res. Part C Emerg. Technol. 2020, 118, 102708. [Google Scholar] [CrossRef]
- Man, C.K.; Quddus, M.; Theofilatos, A. Transfer Learning for Spatio-Temporal Transferability of Real-Time Crash Prediction Models. Accid. Anal. Prev. 2022, 165, 106511. [Google Scholar] [CrossRef]
- Shew, C.; Pande, A.; Nuworsoo, C. Transferability and Robustness of Real-Time Freeway Crash Risk Assessment. J. Saf. Res. 2013, 46, 83–90. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the ICLR, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 1976. [Google Scholar]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression. The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Xie, K.; Ozbay, K.; Kurkcu, A.; Yang, H. Analysis of Traffic Crashes Involving Pedestrians Using Big Data: Investigation of Contributing Factors and Identification of Hotspots. Risk Anal. 2017, 37, 1459–1476. [Google Scholar] [CrossRef]
- Hadayeghi, A.; Shalaby, A.S.; Persaud, B.N. Development of Planning Level Transportation Safety Tools Using Geographically Weighted Poisson Regression. Accid. Anal. Prev. 2010, 42, 676–688. [Google Scholar] [CrossRef]
| Category | Variable | Name | Description |
|---|---|---|---|
| Type I | Land use factors | ||
| LU | Land uses | Allocation of land use according to the activities that can be developed there: residential, commercial, and industrial. | |
| ST | Socioeconomic stratification | Predominant classification of residential properties: 1 (low-low), 2 (medium-low), 3 (medium-medium), 4 (medium), 5 (medium-high) and 6 (high). | |
| Type I | Socioeconomical Factors | ||
| PD | Population density | Demographic distribution of the number of inhabitants per km2. | |
| RMMV | Rate of motorization of motor vehicles | Number of motorized vehicles with license plates per 1.000 inhabitants (reflects the number of vehicles owned by the population in the territory). | |
| NH | Number of households | Number of households (residential units) per spatial unit. | |
| Mobility factors | |||
| RPTP | Rate of pedestrian trips per person | Hourly average of pedestrian trips equal to or greater than 15 min per person | |
| RTPPT | Rate of trips per person in public transport | Hourly average of public transportation trips per person | |
| RTPT | Rate of trips per person by taxi | Hourly average of taxi trips per person | |
| RTPC | Rate of trips per person by car | Hourly average of automobile trips (light vehicles: sedan, compact, sport utility, camper, truck, pick up and van) per person. | |
| RTPM | Rate of trips per person on motorcycle | Hourly average of motorcycle trips per person | |
| RTPB | Rate of trips per person by bicycle | Hourly average of bicycle trips per person | |
| TTDOD | Trips in a typical day origin-destination | Total of origin (produced) and destination (attracted) trips per hour across all available modes of transportation. | |
| TRPTM | Travel rate per person in BRT system | Hourly average of BRT system trips per person. | |
| AMSA | Average maximum speed allowed | Average maximum allowable speed in km/h of the total number of road segments contained in each spatial unit. | |
| Type II | Environmental factors | ||
| PCP | Precipitation | Total hourly precipitation in millimeters (mm). One millimeter means that one liter of water fell on each square meter of land. | |
| ILLUM | Illumination | Presence of ambient light in an environment. It can vary according to the time of day: optimal during daylight hours and limited during the night. | |
| Type III | Response variable | ||
| TCIRP | Traffic Crashes Index on the road perimeter | Rate of traffic crashes per hour in total kilometers of roadway per one spatial unit. | |
| Spatial Unit | Moran’s I | Z-Score | p-Value |
|---|---|---|---|
| TMAU | 0.018 | 0.742 | 0.457 |
| TAZ | −0.012 | −0.594 | 0.552 |
| Variable | Name | Mean | Median | S.D. | Min | Max | Kurt | Skew | V.C. |
|---|---|---|---|---|---|---|---|---|---|
| Land use factors | |||||||||
| LU_ST | Land uses & Socioeconomic stratification | 0.60 | 0.59 | 0.30 | 0.29 | 1.78 | 0.92 | 0.99 | 49.84 |
| Socioeconomical Factors | |||||||||
| PD | Population density | 18,963.10 | 19,553.30 | 11,538.55 | 0 | 53,668.60 | 4.67 × 103 | 0.43 | 60.85 |
| RMMV | Rate of motorization of motor vehicles | 236.60 | 212.46 | 139.03 | 0 | 753.43 | 1.24 | 1.09 | 58.76 |
| NH | Number of households | 19,411.18 | 15,936.50 | 14,959.57 | 0 | 85,108.00 | 2.63 | 1.31 | 77.07 |
| Mobility factors | |||||||||
| RPTP | Rate of pedestrian trips per person | 8.88 × 102 | 8.93 × 102 | 1.50 × 102 | 0 | 1.16 × 101 | 19.54 | −3.56 | 16.92 |
| RTPPT | Rate of trips per person in public transport | 2.44 × 102 | 2.51 × 102 | 7.58 × 103 | 0 | 4.39 × 102 | 1.53 | −0.77 | 31.00 |
| RTPT | Rate of trips per person by taxi | 4.26 × 103 | 3.25 × 103 | 2.96 × 103 | 0 | 1.23 × 102 | −0.19 | 0.80 | 69.42 |
| RTPC | Rate of trips per person by car | 1.39 × 102 | 1.12 × 102 | 1.18 × 102 | 0 | 6.27 × 102 | 1.59 | 1.26 | 85.01 |
| RTPM | Rate of trips per person on motorcycle | 3.32 × 103 | 3.30 × 103 | 1.82 × 103 | 0 | 1.03 × 102 | 1.38 | 0.89 | 54.77 |
| RTPB | Rate of trips per person by bicycle | 4.02 × 103 | 3.48 × 103 | 2.71 × 103 | 0 | 1.37 × 102 | 0.76 | 0.90 | 67.37 |
| TTDOD | Trips in a typical day origin-destination | 9517.41 | 8440.91 | 6254.29 | 46.00 | 32,909.30 | 1.67 | 1.18 | 65.71 |
| TRPTM | Travel rate per person in BRT system | 0.19 | 6.51 × 102 | 0.46 | 0 | 4.29 | 55.52 | 6.86 | 246.42 |
| AMSA | Average maximum speed allowed | 38.88 | 38.61 | 6.00 | 30.27 | 56.50 | 0.24 | 0.87 | 15.44 |
| Environmental factors | |||||||||
| PCP | Precipitation | 3.70 × 102 | 0 | 0.45 | 0 | 21.60 | 926.60 | 25.85 | 1203.01 |
| ILLUM | Illumination | — | — | — | — | — | — | — | — |
| Response variable | |||||||||
| TCIRP | Traffic Crashes Index on the road perimeter | 5.31 × 104 | 0 | 3.72 × 103 | 0 | 1.48 × 101 | 213.03 | 11.43 | 700.59 |
| Variable | Name | Mean | Median | S.D. | Min | Max | Kurt | Skew | V.C. |
|---|---|---|---|---|---|---|---|---|---|
| Land use factors | |||||||||
| LU_ST | Land uses & Socioeconomic stratification | 0.58 | 0.45 | 0.33 | 0.29 | 1.83 | 1.46 | 1.44 | 56.86 |
| Socioeconomical Factors | |||||||||
| PD | Population density | 2386.66 | 1788.78 | 2388.28 | 0 | 19,364.71 | 9.84 | 2.59 | 100.07 |
| RMMV | Rate of motorization of motor vehicles | 29.78 | 19.57 | 35.35 | 0 | 405.99 | 33.19 | 4.62 | 118.72 |
| NH | Number of households | 2443.04 | 1862.50 | 2251.64 | 0 | 19,314.00 | 9.70 | 2.42 | 92.17 |
| Mobility factors | |||||||||
| RPTP | Rate of pedestrian trips per person | 1.12 × 102 | 8.79 × 103 | 9.57 × 103 | 0 | 0.10 | 17.66 | 3.22 | 85.59 |
| RTPPT | Rate of trips per person in public transport | 3.08 × 103 | 2.29 × 103 | 2.85 × 103 | 0 | 3.36 × 102 | 27.45 | 3.75 | 92.66 |
| RTPT | Rate of trips per person by taxi | 5.37 × 104 | 3.57 × 104 | 6.02 × 104 | 0 | 4.66 × 103 | 13.08 | 3.08 | 112.10 |
| RTPC | Rate of trips per person by car | 1.75 × 103 | 9.12 × 104 | 2.70 × 103 | 0 | 3.65 × 102 | 56.70 | 6.04 | 153.82 |
| RTPM | Rate of trips per person on motorcycle | 4.18 × 104 | 2.96 × 104 | 4.98 × 104 | 0 | 8.60 × 103 | 89.27 | 6.91 | 119.09 |
| RTPB | Rate of trips per person by bicycle | 5.06 × 104 | 3.27 × 104 | 5.68 × 104 | 0 | 5.19 × 103 | 14.37 | 3.12 | 112.22 |
| TTDOD | Trips in a typical day origin-destination | 1197.84 | 931.27 | 966.96 | 4.26 | 6907.87 | 5.34 | 1.90 | 80.73 |
| TRPTM | Travel rate per person in BRT system | 2.35 × 102 | 7.59 × 103 | 7.95 × 102 | 0 | 1.46 | 188.27 | 12.42 | 338.74 |
| AMSA | Average maximum speed allowed | 38.44 | 36.62 | 7.59 | 30.00 | 60.00 | 0.24 | 0.97 | 19.74 |
| Environmental factors | |||||||||
| PCP | Precipitation | 3.68 × 102 | 0 | 4.43 × 101 | 0 | 21.60 | 926.68 | 25.83 | 1203.94 |
| ILLUM | Illumination | — | — | — | — | — | — | — | — |
| Response variable | |||||||||
| TCIRP | Traffic Crashes Index on the road perimeter | 5.39 × 104 | 0 | 1.17 × 102 | 0 | 2.59 | 2510.65 | 39.13 | 2177.57 |
| Spatial Unit | Sample Size | Training Sample | Testing Sample | Evaluation Sample | Spatial Units | Average Area (Km2) |
|---|---|---|---|---|---|---|
| TMAU | 963,600 | 674,520 | 192,720 | 96,360 | 110 | 3.67 |
| TAZ | 7,656,240 | 5,359,368 | 1,531,248 | 765,624 | 874 | 0.46 |
| TMAU | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Training | Testing | Validation | |||||||||||||
| Models | MSE | MAE | MAPE | R2 | PD | MSE | MAE | MAPE | R2 | PD | MSE | MAE | MAPE | R2 | PD |
| SpatioConvGru-Net | 0.018 | 0.023 | 5.54 | 0.982 | 0.026 | 0.018 | 0.022 | 5.50 | 0.981 | 0.027 | 0.017 | 0.023 | 5.54 | 0.983 | 0.025 |
| CNN | 0.036 | 0.033 | 7.07 | 0.852 | 0.058 | 0.039 | 0.035 | 7.07 | 0.851 | 0.059 | 0.041 | 0.040 | 7.08 | 0.841 | 0.060 |
| LSTM | 0.028 | 0.025 | 6.32 | 0.889 | 0.044 | 0.032 | 0.026 | 6.33 | 0.887 | 0.046 | 0.034 | 0.028 | 6.34 | 0.880 | 0.045 |
| GRBT | 0.038 | 0.038 | 7.45 | 0.842 | 0.056 | 0.041 | 0.041 | 7.46 | 0.839 | 0.057 | 0.040 | 0.045 | 7.46 | 0.813 | 0.058 |
| ARIMA | 0.037 | 0.027 | 7.09 | 0.874 | 0.048 | 0.036 | 0.025 | 7.07 | 0.871 | 0.047 | 0.038 | 0.029 | 7.08 | 0.853 | 0.049 |
| GWR | 0.051 | 0.043 | 8.00 | 0.828 | 0.065 | 0.054 | 0.046 | 8.12 | 0.813 | 0.066 | 0.052 | 0.055 | 8.13 | 0.796 | 0.067 |
| TAZ | |||||||||||||||
| Training | Testing | Validation | |||||||||||||
| Models | MSE | MAE | MAPE | R2 | PD | MSE | MAE | MAPE | R2 | PD | MSE | MAE | MAPE | R2 | PD |
| SpatioConvGru-Net | 0.032 | 0.067 | 99.74 | 0.690 | 0.062 | 0.029 | 0.065 | 99.77 | 0.683 | 0.061 | 0.032 | 0.067 | 99.74 | 0.687 | 0.063 |
| CNN | 0.042 | 0.077 | 101.79 | 0.582 | 0.078 | 0.046 | 0.079 | 101.79 | 0.572 | 0.079 | 0.044 | 0.077 | 101.79 | 0.569 | 0.077 |
| LSTM | 0.046 | 0.071 | 100.98 | 0.601 | 0.074 | 0.045 | 0.074 | 100.99 | 0.595 | 0.075 | 0.046 | 0.073 | 100.98 | 0.583 | 0.076 |
| GRBT | 0.043 | 0.075 | 101.47 | 0.573 | 0.076 | 0.048 | 0.081 | 101.47 | 0.569 | 0.078 | 0.045 | 0.079 | 101.47 | 0.561 | 0.077 |
| ARIMA | 0.042 | 0.075 | 100.63 | 0.592 | 0.075 | 0.042 | 0.082 | 100.64 | 0.589 | 0.076 | 0.042 | 0.080 | 100.63 | 0.580 | 0.075 |
| GWR | 0.048 | 0.089 | 101.98 | 0.529 | 0.080 | 0.049 | 0.090 | 101.98 | 0.501 | 0.082 | 0.048 | 0.091 | 101.98 | 0.499 | 0.081 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandoval-Pineda, A.; Pedraza, C. SpatioConvGRU-Net for Short-Term Traffic Crash Frequency Prediction in Bogotá: A Macroscopic Spatiotemporal Deep Learning Approach with Urban Factors. Modelling 2025, 6, 71. https://doi.org/10.3390/modelling6030071
Sandoval-Pineda A, Pedraza C. SpatioConvGRU-Net for Short-Term Traffic Crash Frequency Prediction in Bogotá: A Macroscopic Spatiotemporal Deep Learning Approach with Urban Factors. Modelling. 2025; 6(3):71. https://doi.org/10.3390/modelling6030071
Chicago/Turabian StyleSandoval-Pineda, Alejandro, and Cesar Pedraza. 2025. "SpatioConvGRU-Net for Short-Term Traffic Crash Frequency Prediction in Bogotá: A Macroscopic Spatiotemporal Deep Learning Approach with Urban Factors" Modelling 6, no. 3: 71. https://doi.org/10.3390/modelling6030071
APA StyleSandoval-Pineda, A., & Pedraza, C. (2025). SpatioConvGRU-Net for Short-Term Traffic Crash Frequency Prediction in Bogotá: A Macroscopic Spatiotemporal Deep Learning Approach with Urban Factors. Modelling, 6(3), 71. https://doi.org/10.3390/modelling6030071









