Thermo-Hydro-Mechanical–Chemical Modeling for Pressure Solution of Underground sCO2 Storage
Abstract
1. Introduction
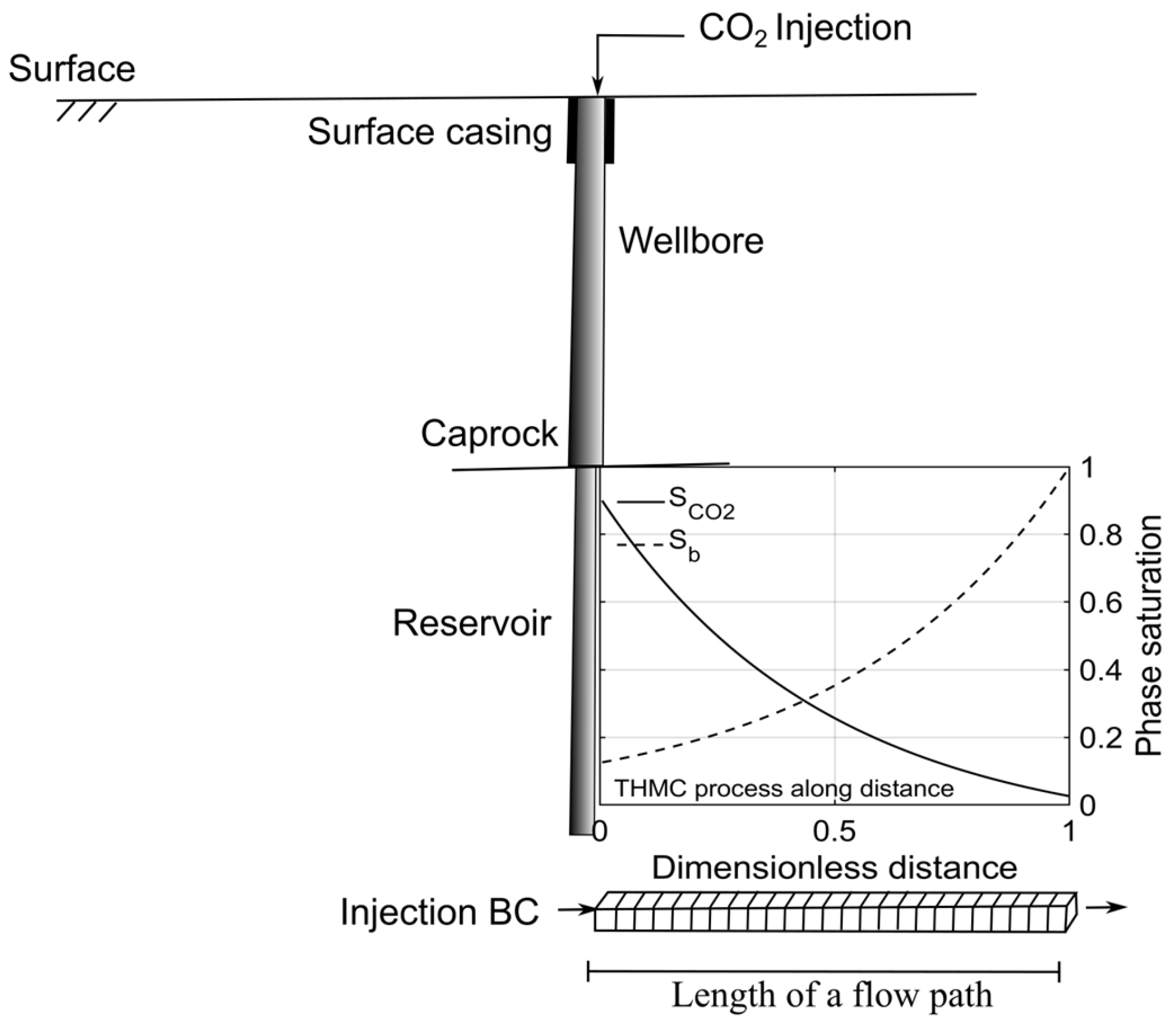
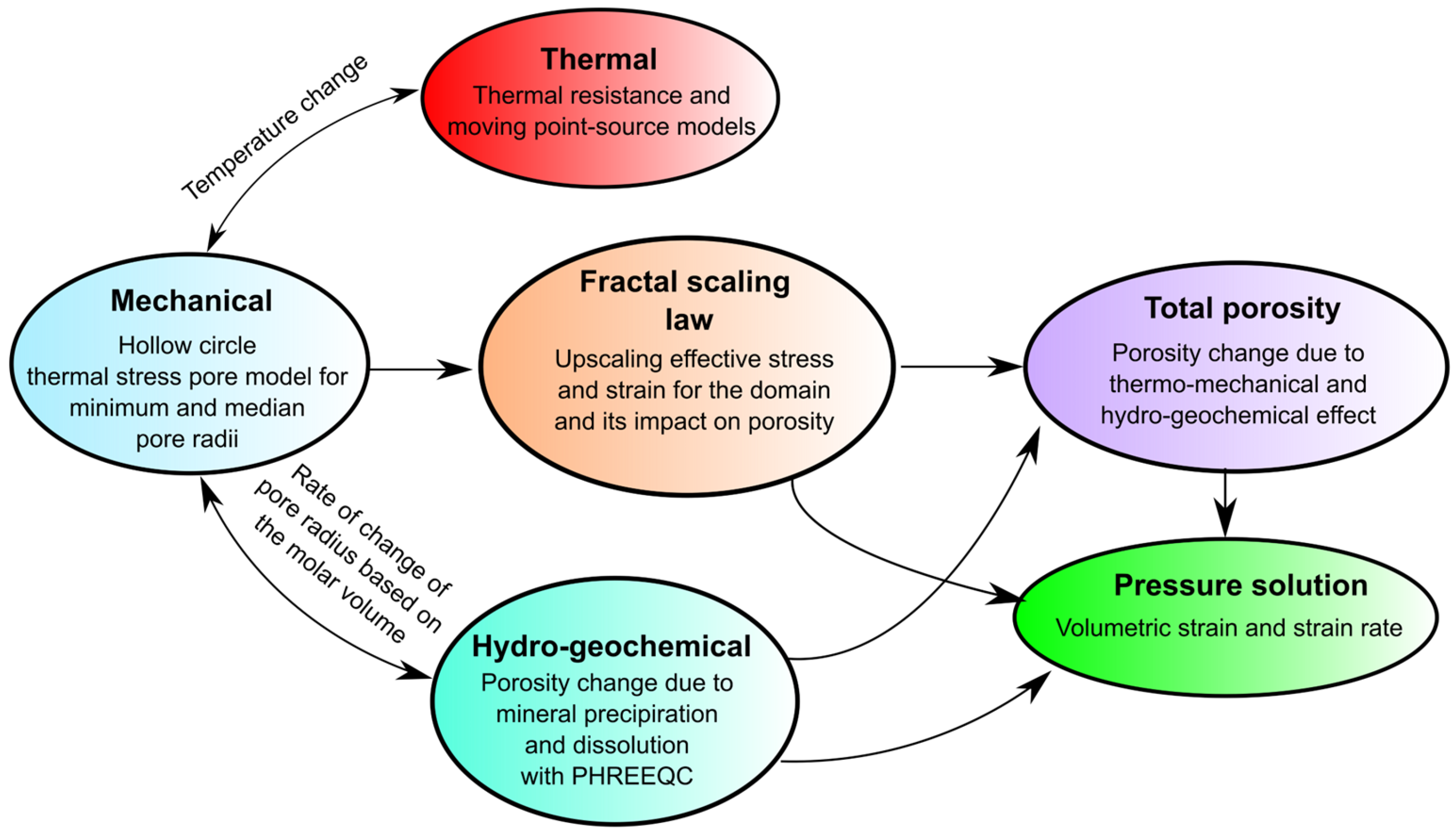
2. Methods
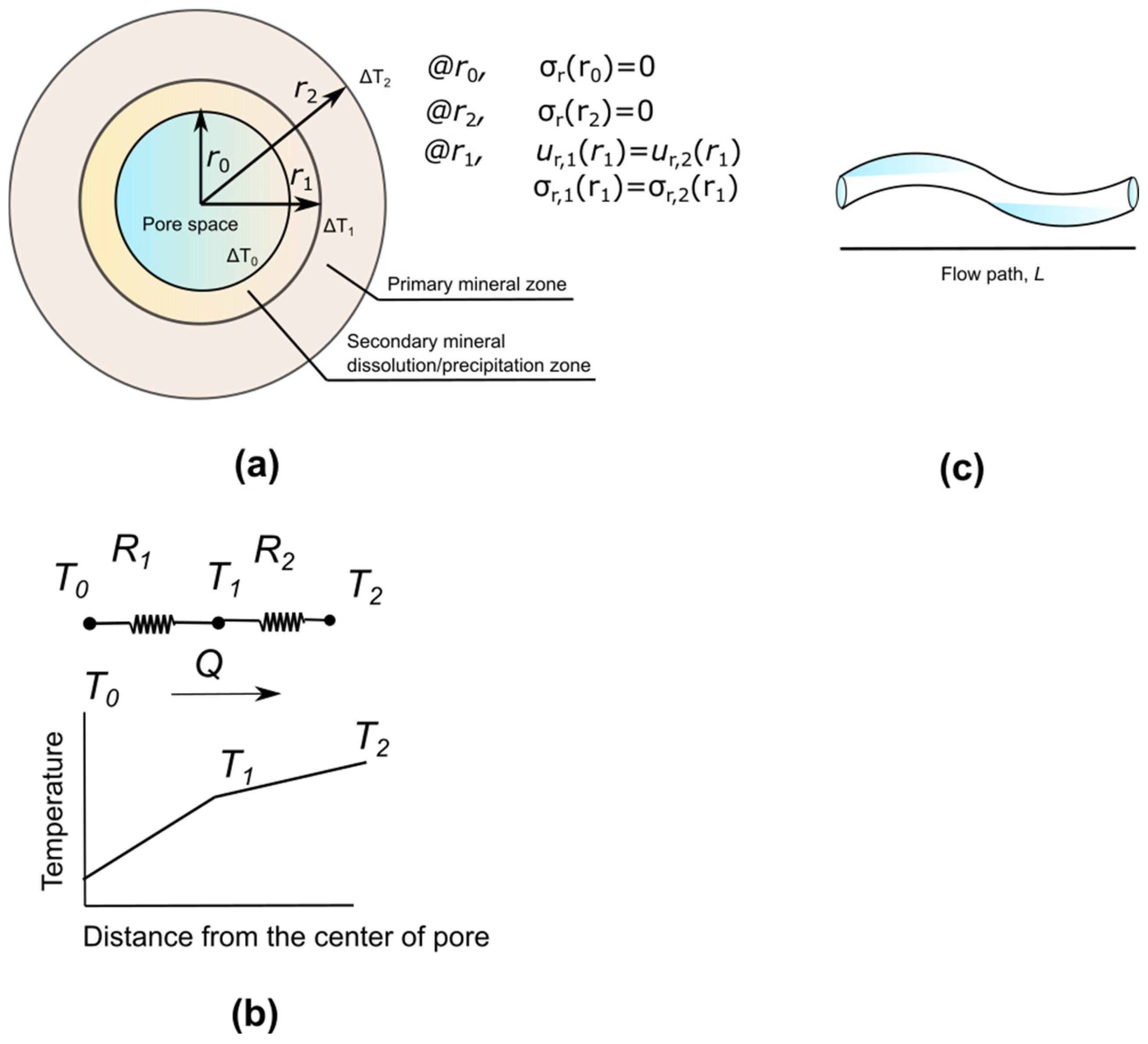
2.1. Thermo-Mechanical
2.2. Fractal Scaling Law
2.3. Hydrochemical
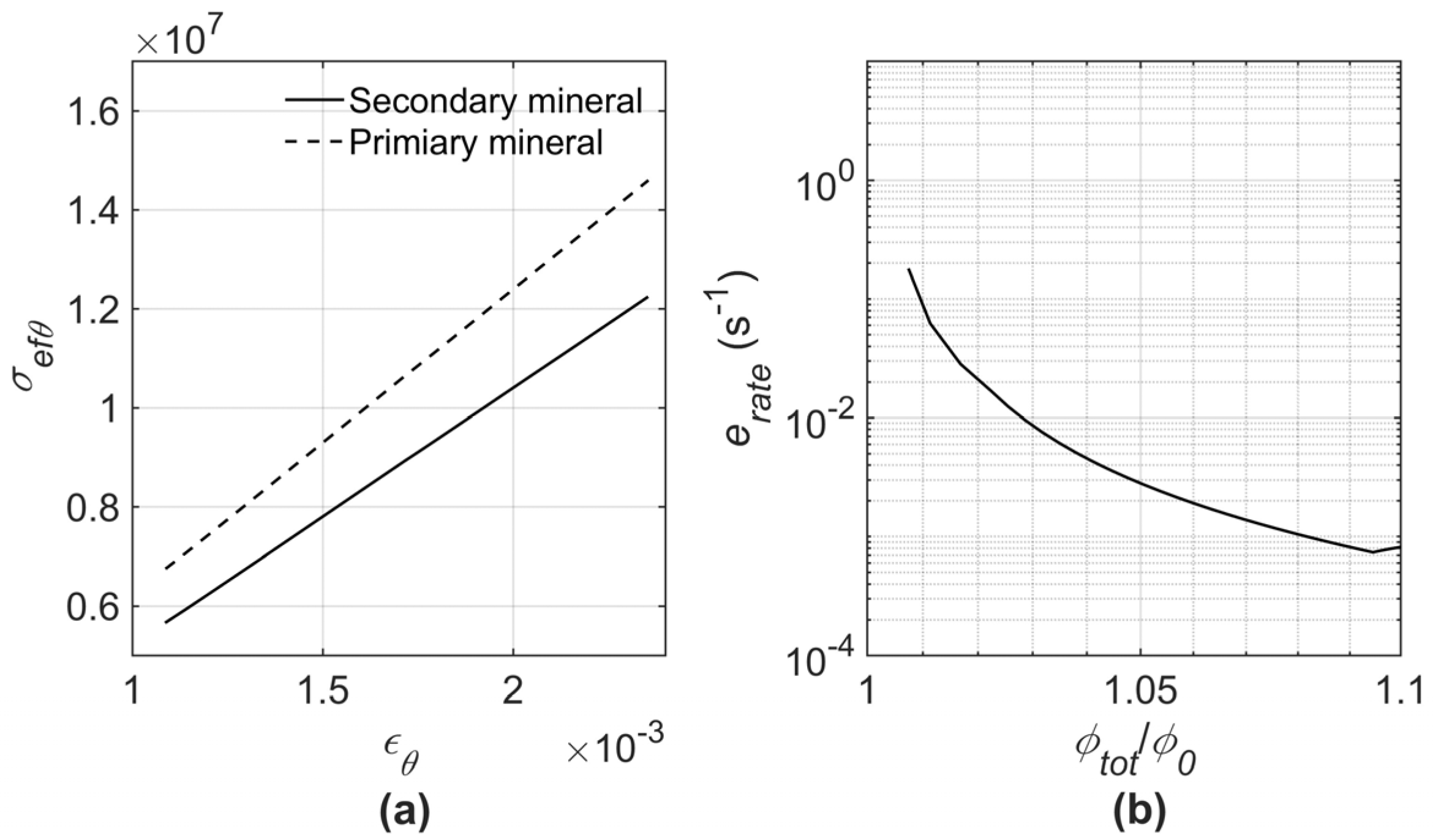
2.4. Total Porosity and Strain Rate
2.5. Conventional IPS Model
3. Validation
4. Results
5. Comparison of Conventional IPS Theory
6. Discussion
7. Conclusions
- It was demonstrated that the strain rate first increased as a consequence of the rapid CO2 saturation, then gradually decreased as a result of the geochemical interactions between the minerals and the CO2–brine solution. This suggests that a major part of the process involves mineral dissolution.
- The results show that the dissolution of clay minerals, particularly undersaturated smectite, during the CO2 injection procedure considerably increased porosity. This alteration in porosity is crucial for understanding the dynamics of CO2 storage in geological formations.
- This study primarily investigates isotropic poro-elasticity, geochemical interaction, and flow and ignores anisotropic conditions.
- An important aspect of this study is the reliance on saturation data during the CO2-fluid core flooding process. The accuracy of estimating the total volume of injected CO2 can be affected by the errors in residual gas and residual liquid saturation.
- The proposed algorithm simplifies calculations employing a fractal approximation to estimate the total pore area based on pore diameter distributions and considers a rock consisting of only two minerals using the hollow cylinder approach. When accounting for multiple mineral systems, minerals can be segregated into groups, which may increase the computation time.
- The results indicate that more inspection is required to better understand how mechanical and chemical processes interact with CO2 sequestration and to improve the model so it can predict the long-term behavior of CO2 in geological formations.
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | thermal diffusivity [m2 s−1] |
| b | Biot’s coefficient |
| d | hydraulic diameter [m] |
| Df | fractal dimension of the porous medium |
| E | elasticity modulus [Pa] |
| Ea | activation energy [J mol−1] |
| h | heat transfer coefficient [W m−2] |
| ki25 | kinetic rate constant of mineral at 25 °C [mol m−2 s−1] |
| K0 | bulk modulus of medium [Pa] |
| Ks | solid grain modulus of medium [Pa] |
| L | length of flow path [m] |
| P | pressure [Pa] |
| Rm | kinetic rate [mol s−1] |
| Rgas | gas constant [J K−1 mol−1] |
| Q | heat exchange rate [W m−1] |
| r0 | pore radius [m] |
| r1 | inner hollow circle radius (secondary mineral) [m] |
| r2 | outer hollow circle radius (primary mineral) [m] |
| Sb | saturation ratio of brine |
| SCO2 | saturation ratio of sCO2 |
| t | time [s] |
| T | temperature [K] |
| TCO2 | injected sCO2 temperature [K] |
| Tref | undisturbed pore system temperature [K] |
| ΔT0 | temperature difference between TCO2 and T1 at r1 [K] |
| ΔT1 | temperature difference at the outer wall of the grout material [K] |
| ΔT2 | temperature difference at the outer wall of the pipe [K] |
| δT | Laplacian temperature difference [K] |
| u | displacement [m] |
| vy | flow velocity of sCO2 in y-direction [m s−1] |
| vT | thermal transport velocity [m s−1] |
| y, z | space coordinates [m] |
| Greek symbols | |
| α | linear thermal expansion coefficient [K−1] |
| εθ | tangential strain |
| εr | radial strain |
| ϕ | porosity |
| κ | permeability [m2] |
| λm | bulk thermal conductivity of fluid and minerals [W m−1 K−1] |
| (ρc)CO2 | volumetric heat capacity of sCO2 [J m−3 K−1] |
| ρmcm | bulk volumetric heat capacity of pore system [J m−3 K−1] |
| σθ | tangential stress [Pa] |
| σr | radial stress [Pa] |
| σT | total stress [Pa] |
| τ | tortuosity |
| υ | Poisson’s ratio |
| ψT | total thermal resistance in hollow circles [K m W−1] |
| ψc | convective thermal resistance of injected sCO2 [K m W−1] |
| ψ1 | conductive thermal resistance of secondary mineral [K m W−1] |
| ψ2 | conductive thermal resistance of primary mineral [K m W−1] |
| ωm | surface area of mineral [m2] |
| Ω | saturation index of mineral |
| Subscripts | |
| inner | |
| outer | |
| c | chemical |
| ef | effective |
| r | radial |
| p | pore |
| T | total |
| TM | thermo-mechanical |
| θ | tangential |
Appendix A
Appendix B
Appendix C
- The internal boundary condition at the inner circle r = r0, and the outer circle of the primary mineral r = r2 are free of stress.
- The radial displacement and radial stress of the primary and secondary minerals are equivalent at r = r1. The two thermo-mechanical problems are coupled as a result of this combined boundary condition, which transforms the mechanical equilibrium between the primary and secondary minerals.
- At the inner radius r0, the temperature is fixed. Equations (15)–(17) are used to evaluate the temperature variations at the outer radius r1 of the secondary mineral and the outer radius r2 of the primary mineral.


References
- Ogata, S.; Yasuhara, H.; Kinoshita, N.; Kishida, K. Coupled thermal–hydraulic–mechanical–chemical modeling for permeability evolution of rocks through fracture generation and subsequent sealing. Comput. Geosci. 2020, 24, 1845–1864. [Google Scholar] [CrossRef]
- Viswanathan, H.S.; Ajo-Franklin, J.; Birkholzer, J.T.; Carey, J.W.; Guglielmi, Y.; Hyman, J.D.; Karra, S.; Pyrak-Nolte, L.J.; Rajaram, H.; Srinivasan, G.; et al. From Fluid Flow to Coupled Processes in Fractured Rock: Recent Advances and New Frontiers; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Barbot, S. A Rate-, State-, and Temperature-Dependent Friction Law With Competing Healing Mechanisms. J. Geophys. Res. Solid Earth 2022, 127, e2022JB025106. [Google Scholar] [CrossRef]
- Pachalieva, A.; Hyman, J.D.; O’Malley, D.; Viswanathan, H.; Srinivasan, G. Learning the Factors Controlling Mineralization for Geologic Carbon Sequestration. arXiv 2023, arXiv:2312.13451. [Google Scholar]
- Eigbe, P.A.; Ajayi, O.O.; Olakoyejo, O.T.; Fadipe, O.L.; Efe, S.; Adelaja, A.O. A general review of CO2 sequestration in underground geological formations and assessment of depleted hydrocarbon reservoirs in the Niger Delta. Appl. Energy 2023, 350, 121723. [Google Scholar] [CrossRef]
- Dehghani, M.R.; Kafi, M.; Nikravesh, H.; Aghel, M.; Mohammadian, E.; Kazemzadeh, Y.; Azin, R. Data driven models for predicting pH of CO2 in aqueous solutions: Implications for CO2 sequestration. Results Eng. 2024, 24, 102889. [Google Scholar] [CrossRef]
- Massarweh, O.; Abushaikha, A.S. CO2 sequestration in subsurface geological formations: A review of trapping mechanisms and monitoring techniques. Earth-Sci. Rev. 2024, 253, 104793. [Google Scholar] [CrossRef]
- Zhuang, X.; Wang, W.; Su, Y.; Shi, M.; Dai, Z. Life-cycle prediction and optimization of sequestration performance in CO2 mixture huff-n-puff development for tight hydrocarbon reservoirs. Appl. Energy 2025, 388, 125618. [Google Scholar] [CrossRef]
- Li, L.; Jia, C.; Yao, J.; Sepehrnoori, K.; Abushaikha, A.; Liu, Y. An Investigation of Gas-Fingering Behavior during CO2 Flooding in Acid Stimulation Formations. SPE J. 2024, 29, 3369–3386. [Google Scholar] [CrossRef]
- Giovannetti, R.; Gambelli, A.M.; Rossi, A.; Castellani, B.; Minicucci, M.; Zannotti, M.; Nicolini, A.; Rossi, F. Thermodynamic assessment and microscale Raman spectroscopy of binary CO2/CH4 hydrates produced during replacement applications in natural reservoirs. J. Mol. Liq. 2022, 368, 120739. [Google Scholar] [CrossRef]
- Zhang, X.; Spiers, C.J.; Peach, C.J. Compaction creep of wet granular calcite by pressure solution at 28 °C to 150 °C. J. Geophys. Res. Solid Earth 2010, 115, B09217. [Google Scholar] [CrossRef]
- Rathnaweera, T.D.; Ranjith, P.G.; Perera, M.S.A. Experimental investigation of geochemical and mineralogical effects of CO2 sequestration on flow characteristics of reservoir rock in deep saline aquifers. Sci. Rep. 2016, 6, 19362. [Google Scholar] [CrossRef] [PubMed]
- Mérit, L.; Soret, M.; Dubacq, B.; Agard, P.; Précigout, J.; Stünitz, H. Grain-scale feedback between deformation mechanisms and metamorphic reactions: Dissolution-precipitation processes in the lower crust (Kågen gabbros). Earth Planet. Sci. Lett. 2025, 656, 119275. [Google Scholar] [CrossRef]
- van den Ende, M.P.A.; Niemeijer, A.R.; Spiers, C.J. Influence of Grain Boundary Structural Evolution on Pressure Solution Creep Rates. J. Geophys. Res. Solid Earth 2019, 124, 10210–10230. [Google Scholar] [CrossRef]
- Van Oosterhout, B.G.A.; Hangx, S.J.T.; Spiers, C.J. A threshold stress for pressure solution creep in rock salt: Model predictions vs. observations. In Mechanical Behavior of Salt; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Malvoisin, B.; Baumgartner, L.P. Mineral Dissolution and Precipitation Under Stress: Model Formulation and Application to Metamorphic Reactions. Geochem. Geophys. Geosystems 2021, 22, e2021GC009633. [Google Scholar] [CrossRef]
- Yasuhara, H.; Kinoshita, N.; Ogata, S.; Cheon, D.S.; Kishida, K. Coupled thermo-hydro-mechanical-chemical modeling by incorporating pressure solution for estimating the evolution of rock permeability. Int. J. Rock Mech. Min. Sci. 2016, 86, 104–114. [Google Scholar] [CrossRef]
- Zhu, T.; Wei, X.; Zhang, Z. Numerical simulation of hydraulic-mechanical-chemical field coupled acid fracturing in complex carbonate reservoir. Comput. Geotech. 2023, 156, 105277. [Google Scholar] [CrossRef]
- McDermott, C.; Bond, A.; Harris, A.F.; Chittenden, N.; Thatcher, K. Application of hybrid numerical and analytical solutions for the simulation of coupled thermal, hydraulic, mechanical and chemical processes during fluid flow through a fractured rock. Environ. Earth Sci. 2015, 74, 7837–7854. [Google Scholar] [CrossRef]
- Bernabé, Y.; Evans, B. Numerical modelling of pressure solution deformation at axisymmetric asperities under normal load. Geol. Soc. Lond. Spec. Publ. 2007, 284, 185–205. [Google Scholar] [CrossRef]
- Jiao, K.; Han, D.; Wang, B.; Chen, Y.; Bai, B.; Gong, L.; Yu, B. Pore-scale modeling of thermal-hydro-mechanical-chemical coupled rock dissolution and fracturing process. J. Clean. Prod. 2023, 421, 138391. [Google Scholar] [CrossRef]
- Yang, X.-S. Pressure solution in sedimentary basins: Effect of temperature gradient. Earth Planet. Sci. Lett. 2000, 176, 233–243. [Google Scholar] [CrossRef]
- Yang, X.-S. A unified approach to mechanical compaction, pressure solution, mineral reactions and the temperature distribution in hydrocarbon basins. Tectonophysics 2001, 330, 141–151. [Google Scholar] [CrossRef][Green Version]
- Hu, M.; Steefel, C.I.; Rutqvist, J. Microscale Mechanical-Chemical Modeling of Granular Salt: Insights for Creep. J. Geophys. Res. Solid Earth 2021, 126, e2021JB023112. [Google Scholar] [CrossRef]
- Schneider, F.; Potdevin, J.L.; Wolf, S.; Faille, I. Mechanical and chemical compaction model for sedimentary basin simulators. Tectonophysics 1996, 263, 307–317. [Google Scholar] [CrossRef]
- Rutter, E.H. The kinetics of rock deformation by pressure solution. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1976, 283, 203–219. [Google Scholar]
- Renard, F.; Ortoleva, P.; Gratier, J.P. Pressure solution in sandstones: Influence of clays and dependence on temperature and stress. Tectonophysics 1997, 280, 257–266. [Google Scholar] [CrossRef]
- Tokunaga, T.K. DLVO-based estimates of adsorbed water film thicknesses in geologic CO2 reservoirs. Langmuir 2012, 28, 8001–8009. [Google Scholar] [CrossRef]
- Desarnaud, J.; Bonn, D.; Shahidzadeh, N. The Pressure induced by salt crystallization in confinement. Sci. Rep. 2016, 6, 30856. [Google Scholar] [CrossRef]
- van Noort, R.; Spiers, C.J. Kinetic effects of microscale plasticity at grain boundaries during pressure solution. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Gundersen, E.; Renard, F.; Dysthe, D.K.; Bjørlykke, K.; Jamtveit, B. Coupling between pressure solution creep and diffusive mass transport in porous rocks. J. Geophys. Res. Solid Earth 2002, 107, ECV 19-1–ECV 19-19. [Google Scholar] [CrossRef]
- Spiers, C.J.; de Meer, S.; Niemeijer, A.R.; Zhang, X.D. Kinetics of rock deformation by pressure solution and the role of thin aqueous films. In Physicochemistry of Water in Geological and Biological Systems: Structures and Properties of Thin Aqueous Films; Nakashima, S., Spiers, C.J., Mercury, L., Fenter, P.A., Hochella, M.F., Jr., Eds.; Universal Academy Press: Tokyo, Japan, 2004; pp. 129–158. [Google Scholar]
- Lang, P.S.; Paluszny, A.; Zimmerman, R.W. Hydraulic sealing due to pressure solution contact zone growth in siliciclastic rock fractures. J. Geophys. Res. Solid Earth 2015, 120, 4080–4101. [Google Scholar] [CrossRef]
- Yasuhara, H.; Elsworth, D. Compaction of a rock fracture moderated by competing roles of stress corrosion and pressure solution. Pure Appl. Geophys. 2008, 165, 1289–1306. [Google Scholar] [CrossRef]
- Wheeler, J. Dramatic effects of stress on metamorphic reactions. Geology 2014, 42, 647–650. [Google Scholar] [CrossRef]
- Gratier, J.; Guiguet, R.; Renard, F.; Jenatton, L.; Bernard, D. A pressure solution creep law for quartz from indentation experiments. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Robin, P.-Y.F. Letter Section Determination of geologic strain using randomly oriented strain markers of any shape. Tectonophysics 1977, 42, T7–T16. [Google Scholar] [CrossRef]
- Launeau, P.; Bouchez, J.-L.; Benn, K. Shape preferred orientation of object populations: Automatic analysis of digitized images. Tectonophysics 1990, 180, 201–211. [Google Scholar] [CrossRef]
- Mulchrone, K.F.; Meere, P.A. Shape fabric development in rigid clast populations under pure shear: The influence of no-slip versus slip boundary conditions. Tectonophysics 2015, 659, 63–69. [Google Scholar] [CrossRef]
- Wassmann, S.; Stöckhert, B. Low stress deformation of garnet by incongruent dissolution precipitation creep. J. Struct. Geol. 2013, 46, 200–219. [Google Scholar] [CrossRef]
- Wassmann, S.; Stöckhert, B. Rheology of the plate interface—Dissolution precipitation creep in high pressure metamorphic rocks. Tectonophysics 2013, 608, 1–29. [Google Scholar] [CrossRef]
- Wang, Z.; Gilbert, B. A Unified Analytical Model for Pressure Solution With Fully Coupled Diffusion and Reaction. Geophys. Res. Lett. 2025, 52, e2024GL112975. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3: A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations. In Modeling Techniques; U.S. Geological Survey: Reston, VA, USA, 2013. [Google Scholar] [CrossRef]
- Pruess, K.; Oldenburg, C.; Moridis, G. TOUGH2 User’s Guide, Version 2.0; LBNL-43134; Earth Sciences Division, Lawrence Berkeley National Laboratory University of California: Berkeley, CA, USA, 1996. [Google Scholar]
- Kolditz, O.; McDermott, C.; Yoon, J.S.; Mollaali, M.; Wang, W.; Hu, M.; Sasaki, T.; Rutqvist, J.; Birkholzer, J.; Park, J.-W.; et al. A systematic model- and experimental approach to hydro-mechanical and thermo-mechanical fracture processes in crystalline rocks. Geomech. Energy Environ. 2025, 41, 100616. [Google Scholar] [CrossRef]
- Birkholzer, J.T.; Graupner, B.J.; Harrington, J.; Jayne, R.; Kolditz, O.; Kuhlman, K.L.; LaForce, T.; Leone, R.C.; Mariner, P.E.; McDermott, C.; et al. DECOVALEX-2023: An international collaboration for advancing the understanding and modeling of coupled thermo-hydro-mechanical-chemical (THMC) processes in geological systems. Geomech. Energy Environ. 2025, 42, 100685. [Google Scholar] [CrossRef]
- Liu, T.; Shi, Y.; Liu, T.; Lin, B. Dynamic Response of Gas Recovery Enhancement Efficiency in Coalbed Methane Displacement by Hot Flue Gas: From the Perspective of Thermo-Hydro-Mechanical-Chemical Coupling. Energy Fuels 2024, 38, 6962–6981. [Google Scholar] [CrossRef]
- Zhang, W.; Han, D.; Wang, B.; Chen, Y.; Jiao, K.; Gong, L.; Yu, B. Research on the solution of the thermo-hydro-mechanical-chemical coupling model based on the unified finite volume method framework. Therm. Sci. Eng. Prog. 2024, 55, 102889. [Google Scholar] [CrossRef]
- Taron, J.; Elsworth, D. Coupled mechanical and chemical processes in engineered geothermal reservoirs with dynamic permeability. Int. J. Rock Mech. Min. Sci. 2010, 47, 1339–1348. [Google Scholar] [CrossRef]
- Ciantia, M.O.; Hueckel, T. Weathering of submerged stressed calcarenites: Chemo-mechanical coupling mechanisms. Geotechnique 2013, 63, 768–785. [Google Scholar] [CrossRef]
- Ilgen, A.G.; Newell, P.; Hueckel, T.; Espinoza, D.N.; Hu, M. Coupled chemical-mechanical processes associated with the injection of CO2 into subsurface. In Science of Carbon Storage in Deep Saline Formations: Process Coupling Across Time and Spatial Scales; Elsevier: Amsterdam, The Netherlands, 2018; pp. 337–359. [Google Scholar] [CrossRef]
- Putnis, A. Mineral replacement reactions. Rev. Mineral. Geochem. 2009, 70, 87–124. [Google Scholar] [CrossRef]
- Vafaie, A.; Cama, J.; Soler, J.M.; Kivi, I.R.; Vilarrasa, V. Chemo-hydro-mechanical effects of CO2 injection on reservoir and seal rocks: A review on laboratory experiments. Renew. Sustain. Energy Rev. 2023, 178, 113270. [Google Scholar] [CrossRef]
- Vilarrasa, V.; Rutqvist, J. Thermal effects on geologic carbon storage. Earth-Sci. Rev. 2017, 165, 245–256. [Google Scholar] [CrossRef]
- Slaughter, W.S. The Linearized Theory of Elasticity; Birkhaeuser: Boston, MA, USA, 2002. [Google Scholar]
- Boley, A.A.; Weiner, J.H. Theory of Thermal Stresses; John Wiley & Sons: New York, NY, USA, 1960; Volume 270, p. 586. [Google Scholar] [CrossRef]
- Kasani, H.A.; Selvadurai, A.P.S. A Review of Techniques for Measuring the Biot Coefficient and Other Effective Stress Parameters for Fluid-Saturated Rocks. Appl. Mech. Rev. 2023, 75, 020801. [Google Scholar] [CrossRef]
- Li, K. Analytical derivation of Brooks-Corey type capillary pressure models using fractal geometry and evaluation of rock heterogeneity. J. Pet. Sci. Eng. 2010, 73, 20–26. [Google Scholar] [CrossRef]
- Lian, P.Q.; Tan, X.Q.; Ma, C.Y.; Feng, R.Q.; Gao, H.M. Saturation modeling in a carbonate reservoir using capillary pressure based saturation height function: A case study of the Svk reservoir in the Y Field. J. Pet. Explor. Prod. Technol. 2016, 6, 73–84. [Google Scholar] [CrossRef]
- Coussy, O. Mechanics and Physics of Porous Solids; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford University Press: New York, NY, USA, 1959. [Google Scholar]
- Molina-Giraldo, N.; Blum, P.; Zhu, K.; Bayer, P.; Fang, Z. A moving finite line source model to simulate borehole heat exchangers with groundwater advection. Int. J. Therm. Sci. 2011, 50, 2506–2513. [Google Scholar] [CrossRef]
- Erol, S.; François, B. Multilayer analytical model for vertical ground heat exchanger with groundwater flow. Geothermics 2018, 71, 294–305. [Google Scholar] [CrossRef]
- Bejan, A.; Kraus, A.D. Heat Transfer Handbook; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2003; p. 1480. [Google Scholar] [CrossRef]
- Huang, X.; Sun, J.; Shi, C.; Du, Y.; Xu, G. Fractal Analysis of the Penetration Flow Through Micro-nano Porous Gaskets with Effects of Slippage and Stress-Sensitivity. Fractals 2019, 27, 1950031. [Google Scholar] [CrossRef]
- Tan, X.-H.; Li, X.-P.; Liu, J.-Y.; Zhang, L.-H.; Fan, Z. Study of the effects of stress sensitivity on the permeability and porosity of fractal porous media. Phys. Lett. A 2015, 379, 2458–2465. [Google Scholar] [CrossRef]
- Erol, S.; Fowler, S.J.; Harcouët-Menou, V.; Laenen, B. An Analytical Model of Porosity—Permeability for Porous and Fractured Media. Transp. Porous Media 2017, 120, 327–358. [Google Scholar] [CrossRef]
- Katz, A.J.; Thompson, A.H. Fractal sandstone pores: Implications for conductivity and pore formation. Phys. Rev. Lett. 1985, 54, 1325–1328. [Google Scholar] [CrossRef]
- Li, W.; Zhao, H.; Li, S.; Sun, W.; Wang, L.; Li, B. A fractal model of effective stress of porous media and the analysis of influence factors. Results Phys. 2018, 8, 920–925. [Google Scholar] [CrossRef]
- Palandri, J.L.; Kharaka, Y.K. A Compilation of Rate Parameters of Water-Mineral Interaction Kinetics for Application to Geochemical Modeling; USGS Report 2004-1068; USGS: Menlo Park, CA, USA, 2004.
- Lasaga, A.C. Chemical kinetics of water-rock interactions. J. Geophys. Res. Solid Earth 1984, 89, 4009–4025. [Google Scholar] [CrossRef]
- Emmanuel, S.; Berkowitz, B. Effects of pore-size controlled solubility on reactive transport in heterogeneous rock. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef]
- Shi, J.Q.; Xue, Z.; Durucan, S. Supercritical CO2 core flooding and imbibition in Tako sandstone-Influence of sub-core scale heterogeneity. Int. J. Greenh. Gas Control 2011, 5, 75–87. [Google Scholar] [CrossRef]
- Harbert, W.; Goodman, A.; Spaulding, R.; Haljasmaa, I.; Crandall, D.; Sanguinito, S.; Kutchko, B.; Tkach, M.; Fuchs, S.; Werth, C.J.; et al. CO2 induced changes in Mount Simon sandstone: Understanding links to post CO2 injection monitoring, seismicity, and reservoir integrity. Int. J. Greenh. Gas Control 2020, 100, 103109. [Google Scholar] [CrossRef]
- Shi, Z.; Sun, L.; Haljasmaa, I.; Harbert, W.; Sanguinito, S.; Tkach, M.; Goodman, A.; Tsotsis, T.; Jessen, K. Impact of Brine/CO2 exposure on the transport and mechanical properties of the Mt Simon sandstone. J. Pet. Sci. Eng. 2019, 177, 295–305. [Google Scholar] [CrossRef]
- Hangx, S.; van der Linden, A.; Marcelis, F.; Bauer, A. The effect of CO2 on the mechanical properties of the Captain Sandstone: Geological storage of CO2 at the Goldeneye field (UK). Int. J. Greenh. Gas Control 2013, 19, 609–619. [Google Scholar] [CrossRef]
- Bagdassarov, N. Thermal Properties of Rocks and Minerals. In Fundamentals of Rock Physics; Cambridge University Press: Cambridge, UK, 2021; pp. 455–504. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, Z.; Park, H.; Shi, J.; Kiyama, T.; Lei, X.; Sun, Y.; Liang, Y. Tracking CO2 Plumes in Clay-Rich Rock by Distributed Fiber Optic Strain Sensing (DFOSS): A Laboratory Demonstration. Water Resour. Res. 2019, 55, 856–867. [Google Scholar] [CrossRef]
- Cama, J.; Ganor, J. Dissolution Kinetics of Clay Minerals. Dev. Clay Sci. 2015, 6, 101–153. [Google Scholar] [CrossRef]
- Cosenza, P.; Giot, R.; Hedan, S. Elastic moduli of clay minerals and their aggregates: A review. Appl. Clay Sci. 2023, 236, 106878. [Google Scholar] [CrossRef]
- Ilgen, A.G.; Cygan, R.T. Mineral dissolution and precipitation during CO2 injection at the Frio-I Brine Pilot: Geochemical modeling and uncertainty analysis. Int. J. Greenh. Gas Control 2016, 44, 166–174. [Google Scholar] [CrossRef]
- Liteanu, E.; Spiers, C.J. Influence of pore fluid salt content on compaction creep of calcite aggregates in the presence of supercritical CO2. Chem. Geol. 2009, 265, 134–147. [Google Scholar] [CrossRef]
- Zheng, Z.; Ma, Q.; Hu, P.; Song, Y.; Wang, D. Uncertainty and sensitivity analysis of relative permeability curves for the numerical simulation of CO2 core flooding. Greenh. Gases Sci. Technol. 2020, 10, 519–530. [Google Scholar] [CrossRef]
- Shi, J.Q.; Xue, Z.; Durucan, S. History matching of CO2 core flooding CT scan saturation profiles with porosity dependent capillary pressure. Energy Procedia 2009, 1, 3205–3211. [Google Scholar] [CrossRef]
- Blanc, P.; Lassin, A.; Piantone, P.; Azaroual, M.; Jacquemet, N.; Fabbri, A.; Gaucher, E. Thermoddem: A geochemical database focused on low temperature water/rock interactions and waste materials. Appl. Geochem. 2012, 27, 2107–2116. [Google Scholar] [CrossRef]



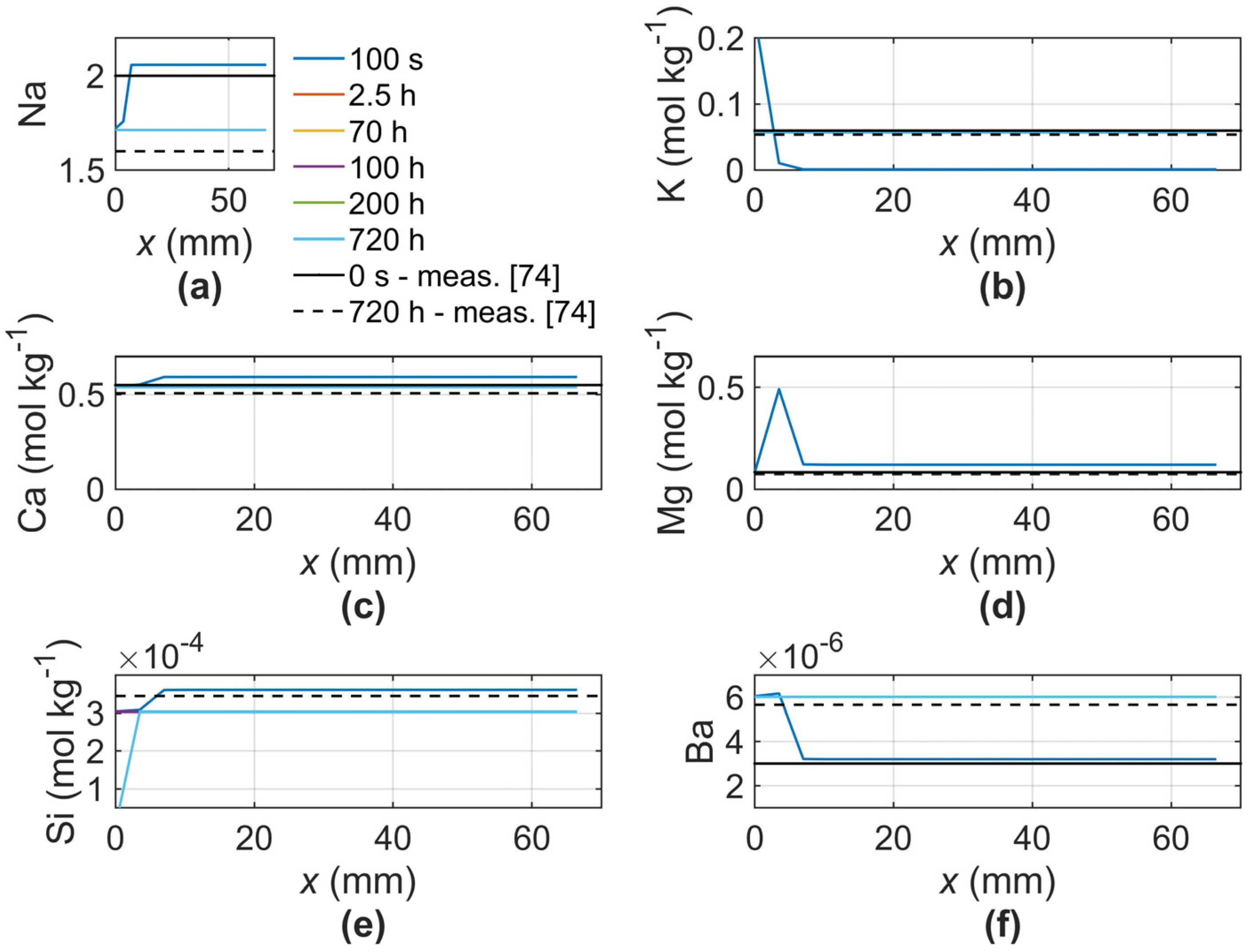


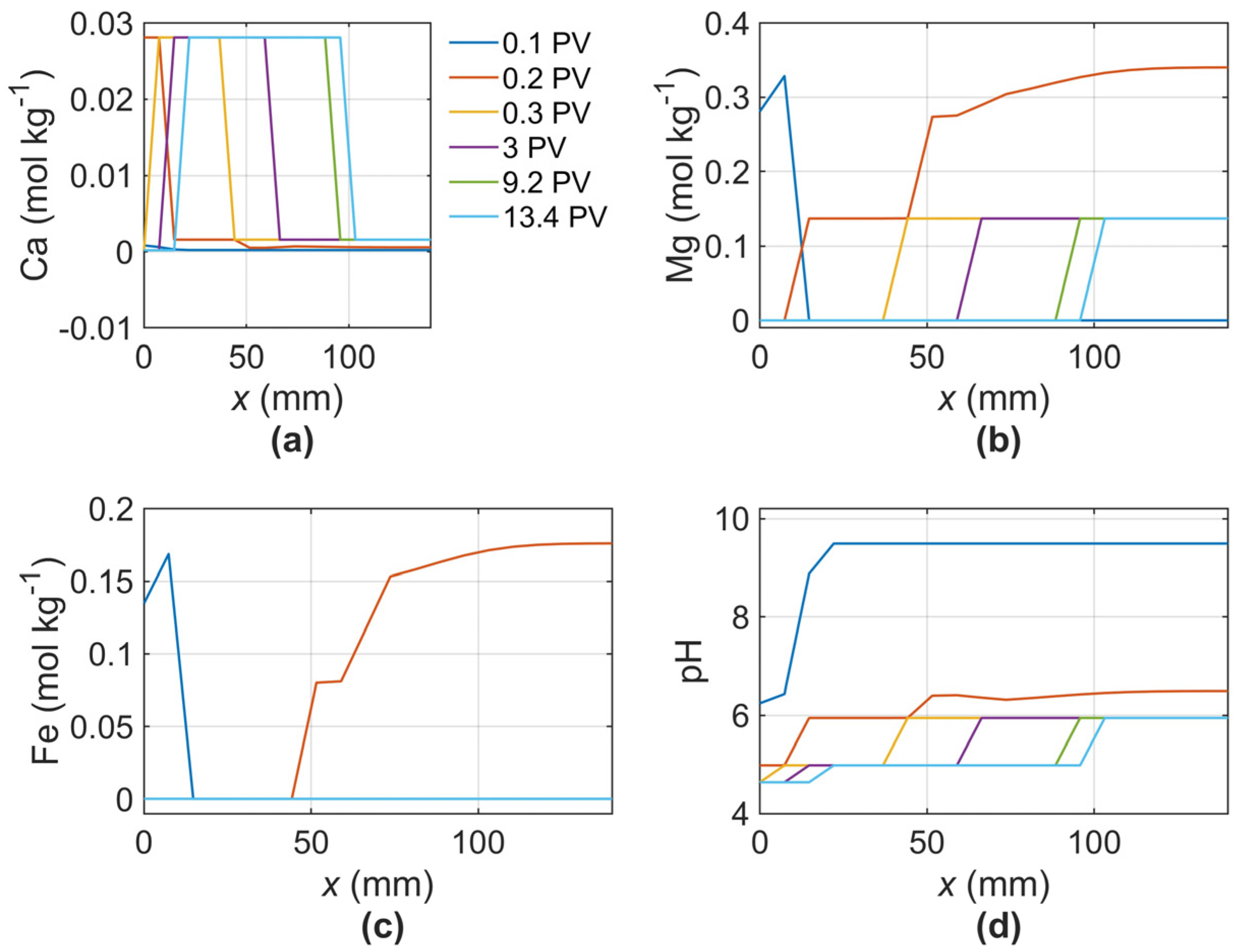

| Ion | Sample VW1-6926 [mol kg−1] | |
|---|---|---|
| Before the Test | After the Test (720 h) | |
| Ca | 0.552 | 0.5067 |
| K | 0.058 | 0.0537 |
| Mg | 0.082 | 0.0752 |
| Na | 1.91 | 1.607 |
| Ba | 2.97 × 10−6 | 5.66 × 10−6 |
| Fe | 2.18 × 10−6 | 2.18 × 10−6 |
| SiO2 | Below detection limit | 3.45 × 10−4 |
| Mineral | Volume Fraction of the Core Sample (%) | Moles in the Core Sample Based on the Solid Volume (2.852 × 10−5 m3) |
|---|---|---|
| Quartz (Primary) | 88 | 1.01 |
| K-feldspar (Secondary) | 12 | 0.3 |
| Parameter | Sample VW1-6919 | |
|---|---|---|
| Before the Test | After the Test | |
| Porosity | 0.236 | 0.214 |
| Parameter | Value |
|---|---|
| Total pore volume [m3] | 5.8412 × 10−6 |
| Reference temperature Tref [K] | 326.15 |
| Injection pressure of sCO2 [Pa] | 13.1 × 106 |
| Injection temperature Tinj [K] | 326.15 |
| Injection volumetric flow rate [m3 s−1] | 4.5 × 10−7 |
| Calculated flow velocity [m s−1] | 9.16 × 10−4 |
| Parameter | Quartz | K-Feldspar |
|---|---|---|
| Ratio of expansion of compacted power (Poisson’s ratio) | 0.13 a | 0.05 b |
| Elasticity modulus of compacted powder E [Pa] | 16.2 × 109 a | 12 × 109 b |
| Thermal expansion coefficient α [K−1] c | 1.5 × 10−5 | 1.5 × 10−5 |
| Density of solid [kg m−3 K−1] c | 2750 | 2550 |
| Thermal conductivity [W m−1 K−1] c | 6 | 4 |
| Kinetic rate constant [mol m−2 s−1] d | 1 × 10−14 | 3.9 × 10−13 |
| Activation energy Ea [kJ mol−1] d | 87.6 | 38 |
| Parameter | Sample T36-14.5 | |
|---|---|---|
| Before the Test | After the Test | |
| Permeability [m2] | 3.6 × 10−15 | 39.5 × 10−15 |
| Porosity | ~0.25 | ~0.285 |
| Minimum pore radius [m] | 0.1 × 10−7 | |
| Maximum pore radius [m] | 1 × 10−6 | |
| Total pore volume [m3] | 4.161 × 10−5 | |
| Reference temperature Tref [K] | 298.15 | |
| Injection pressure of sCO2 [Pa] | 10 × 106 | |
| Injection temperature Tinj [K] | 313.15 | |
| Injection volumetric flow rate [m3 s−1] Injected pore volume [PV] | 1.66 × 10−9 between 0.1 and 2.9 PV 5 × 10−8 between 5 and 13.4 PV | |
| Calculated flow velocity [m s−1] | 1.5 × 10−6 between 0.1 and 2.9 PV 4.55 × 10−5 between 5 and 13.4 PV | |
| Ionic strength of the brine in the saturated core sample | ~3 | |
| Parameter | Quartz | Kaolinite |
|---|---|---|
| Ratio of expansion of compacted power (Poisson’s ratio) | 0.08 a | 0.05 b |
| Elasticity modulus of compacted powder E [Pa] | 7 × 109 a | 10 × 109 b |
| Thermal expansion coefficient α [K−1] c | 1.5 × 10−5 | 1.5 × 10−5 |
| Density of solid [kg m−3 K−1] c | 2750 | 2600 |
| Thermal conductivity of quartz [W m−1 K−1] c | 6 | 4 |
| Kinetic rate constant of quartz [mol m−2 s−1] d | 1 × 10−14 | 1 × 10−13 |
| Activation energy of quartz Ea [kJ mol−1] d | 87.6 | 22.2 |
| Parameter | Value at 80 °C |
|---|---|
| Dissolution velocity Rdis | 8.49 × 10−10 [m s−1] |
| Precipitation velocity Rpre | 3.81 × 10−9 [m s−1] |
| Diffusion coefficient D | 5.98 × 10−10 [m2 s−1] |
| Water film thickness S | 1 × 10−9 [m] |
| Applied effective stress σe | 30 × 106 [Pa] |
| Molar volume of calcite Φ | 3.62 × 10−5 [m3 mol−1] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erol, S. Thermo-Hydro-Mechanical–Chemical Modeling for Pressure Solution of Underground sCO2 Storage. Modelling 2025, 6, 59. https://doi.org/10.3390/modelling6030059
Erol S. Thermo-Hydro-Mechanical–Chemical Modeling for Pressure Solution of Underground sCO2 Storage. Modelling. 2025; 6(3):59. https://doi.org/10.3390/modelling6030059
Chicago/Turabian StyleErol, Selçuk. 2025. "Thermo-Hydro-Mechanical–Chemical Modeling for Pressure Solution of Underground sCO2 Storage" Modelling 6, no. 3: 59. https://doi.org/10.3390/modelling6030059
APA StyleErol, S. (2025). Thermo-Hydro-Mechanical–Chemical Modeling for Pressure Solution of Underground sCO2 Storage. Modelling, 6(3), 59. https://doi.org/10.3390/modelling6030059






