Video Stabilization: A Comprehensive Survey from Classical Mechanics to Deep Learning Paradigms
Abstract
1. Introduction
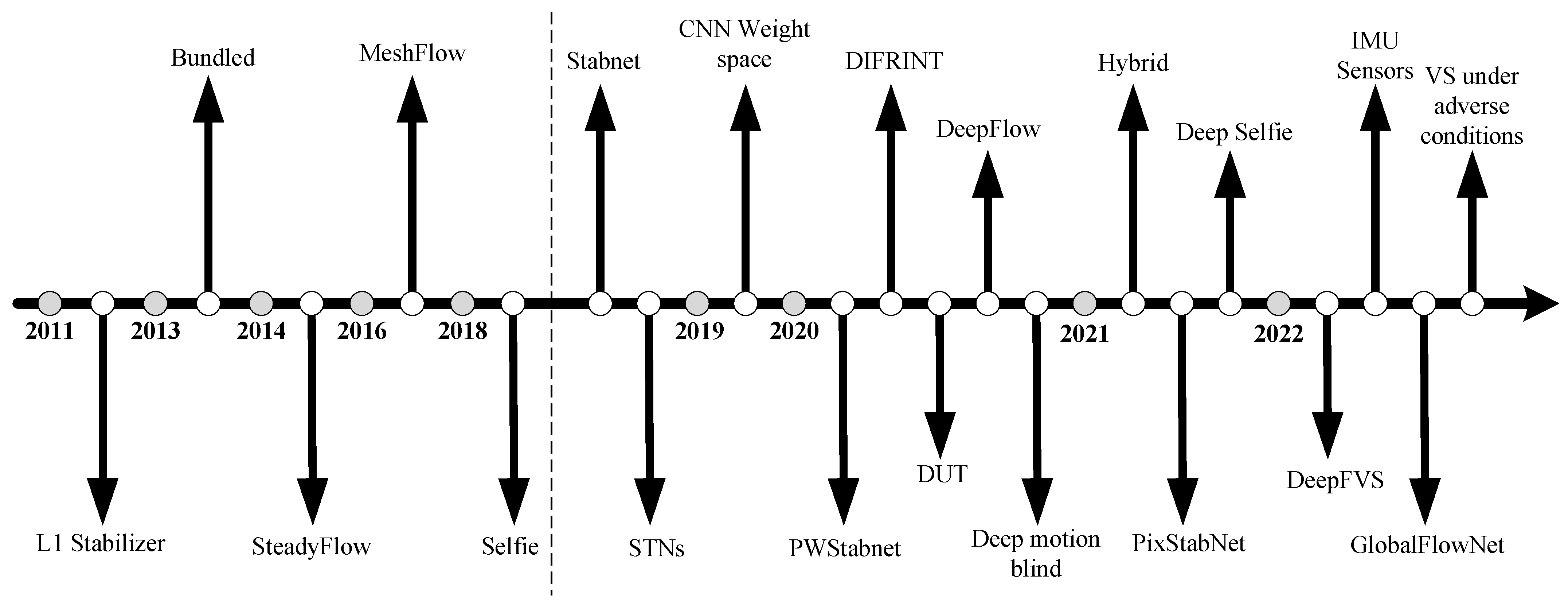
2. Advances in Video Stabilization
2.1. Algorithms of Traditional Digital Video Stabilization
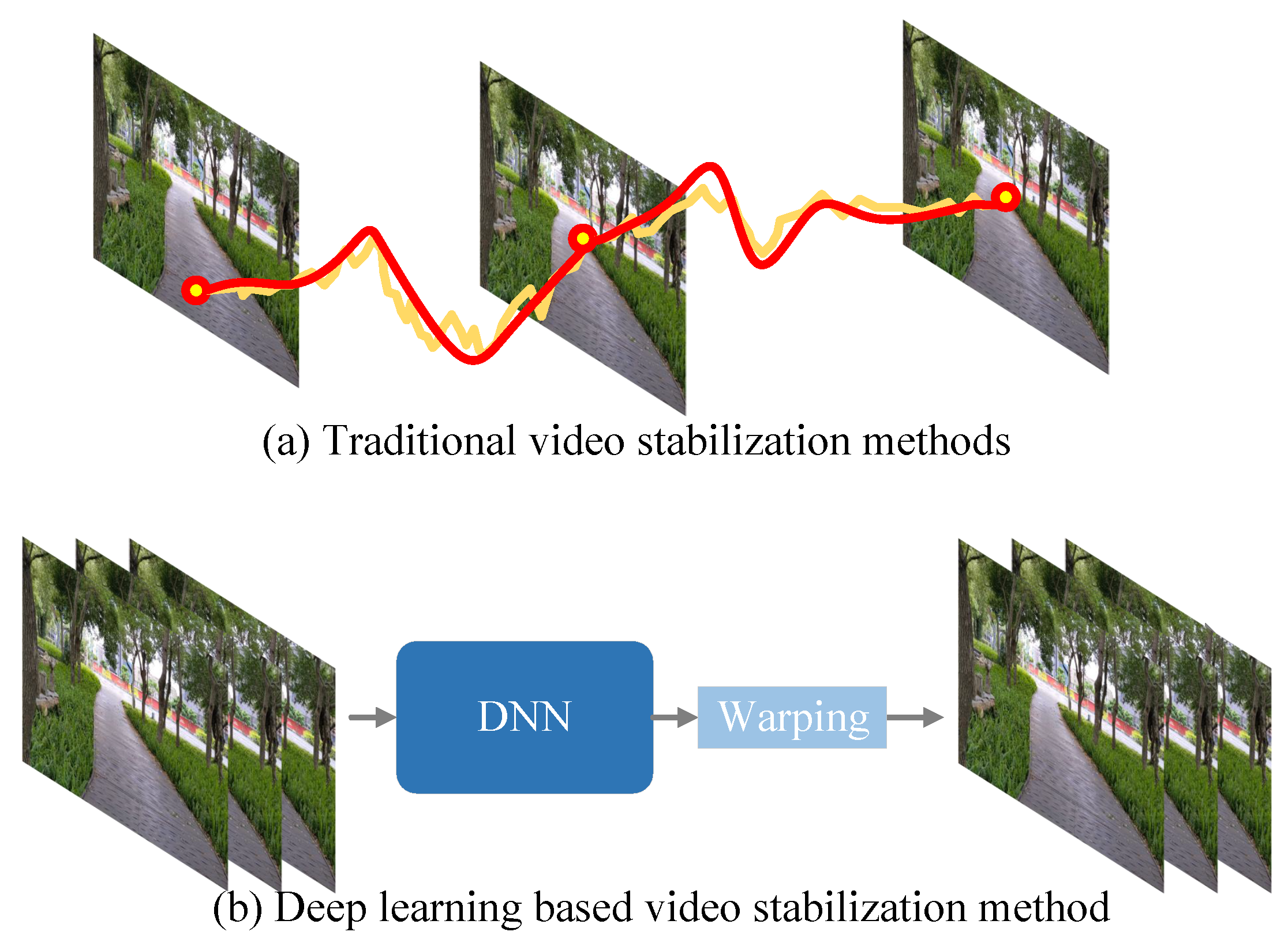
2.2. Video Stabilization Methods Based on Deep Learning
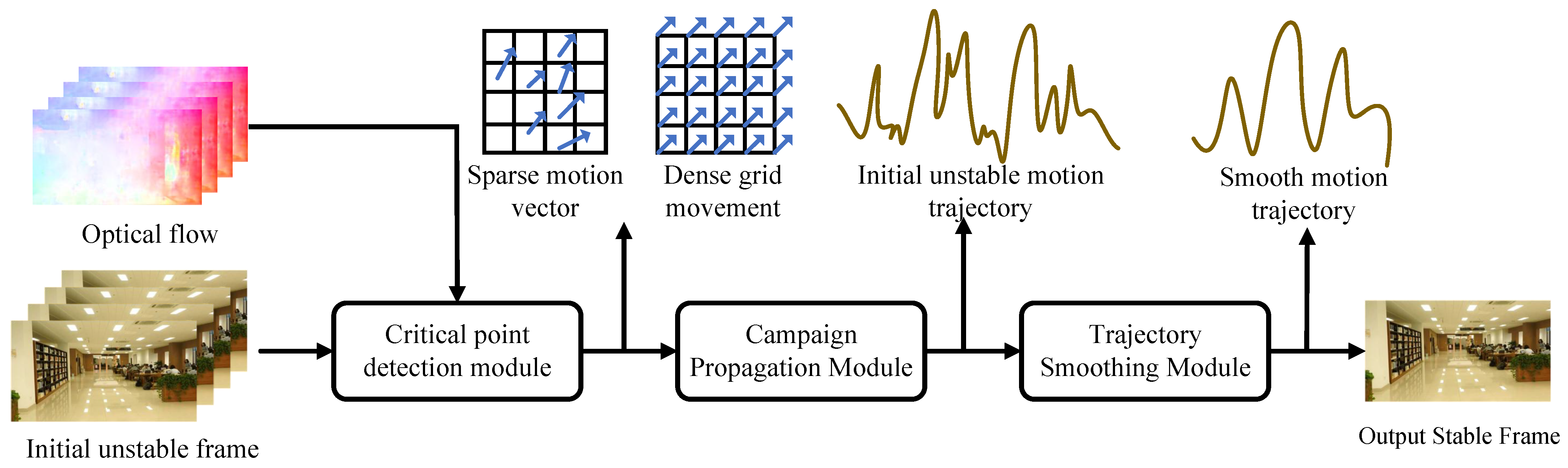
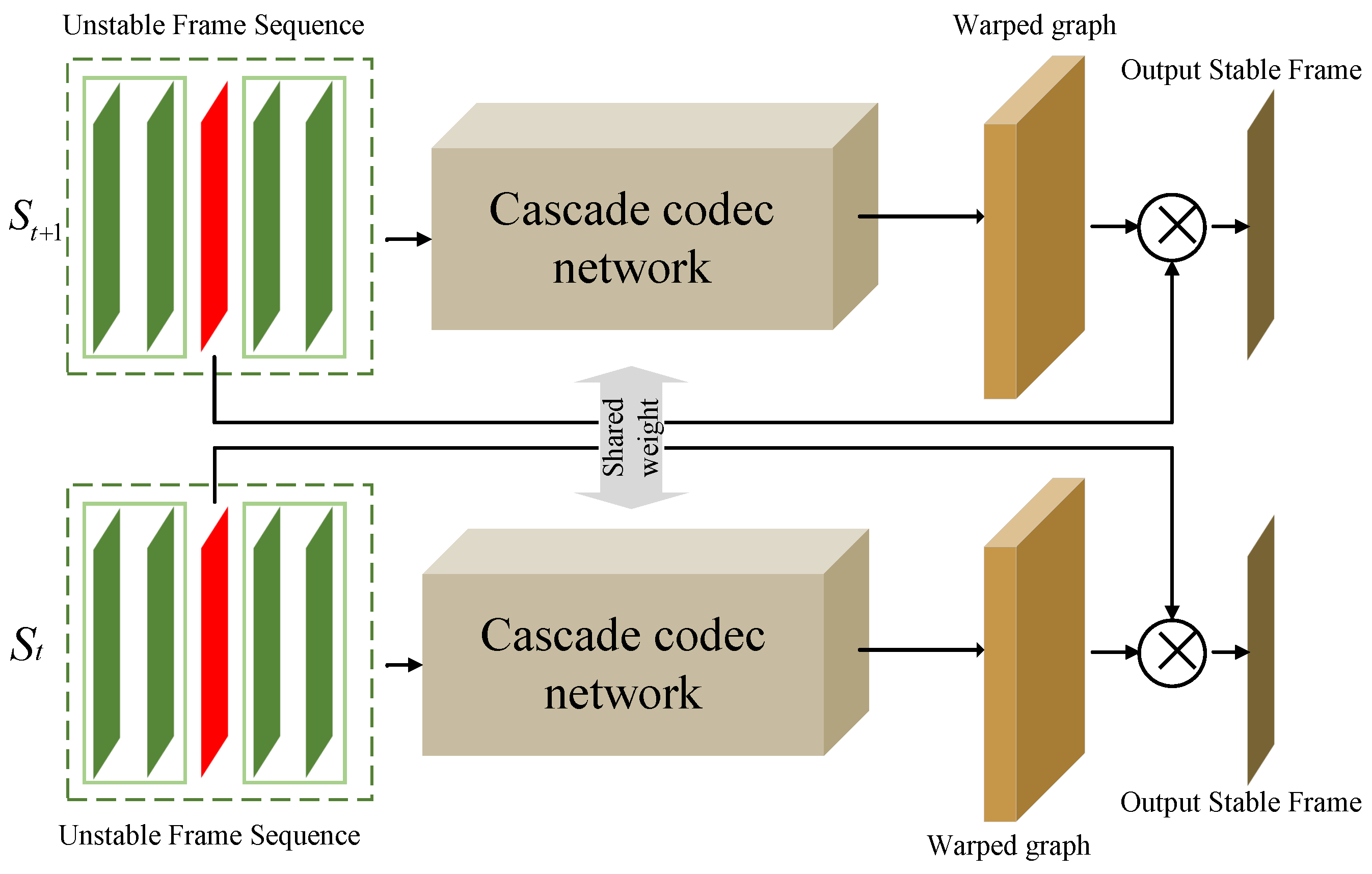
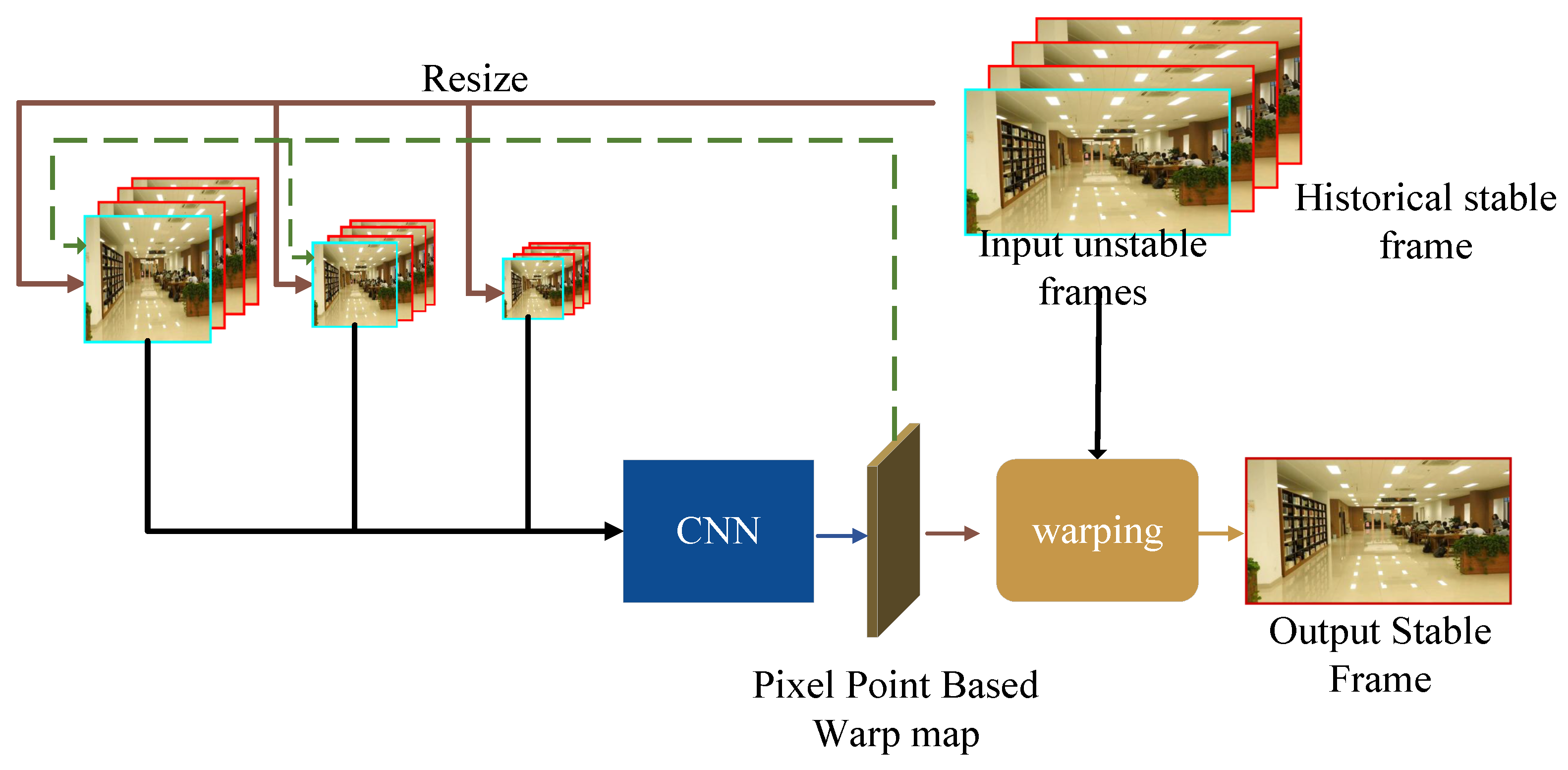
2.2.1. Two-Dimensional Video Stabilization
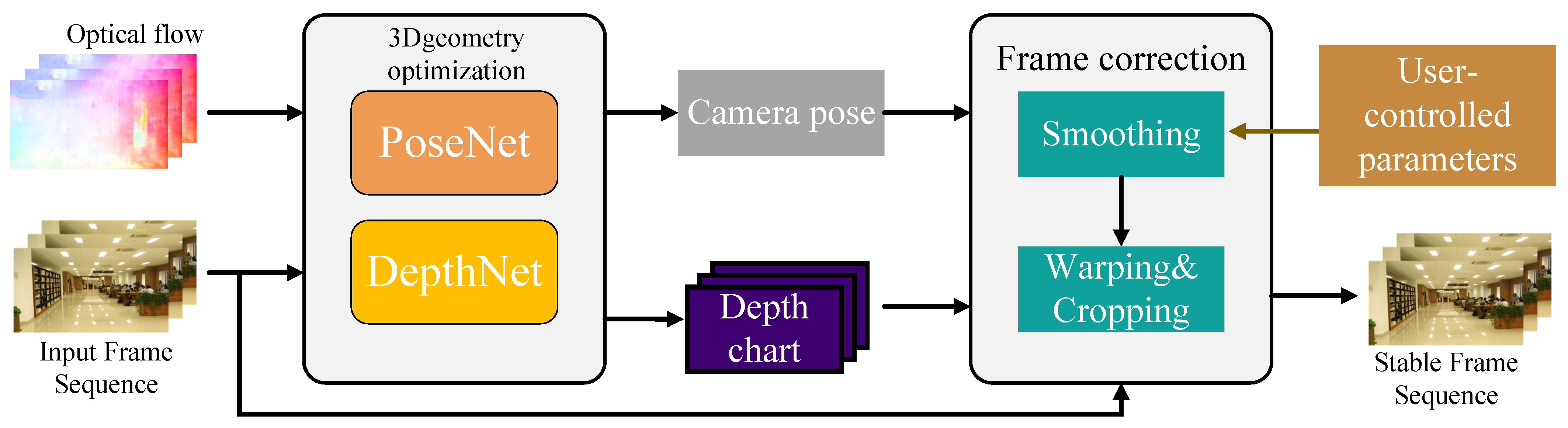
2.2.2. Three-Dimensional Video Stabilization
2.2.3. Two-and-a-Half-Dimensional Video Stabilization
2.3. Comparison of Methods
3. Assessment Metrics for Video Stabilization Algorithms
3.1. Subjective Quality Assessment
3.2. Objective Quality Assessment
3.2.1. Full-Reference Quality Assessment
3.2.2. No-Reference Quality Assessment
4. Benchmark Datasets for Video Stabilization
5. Challenges and Future Directions
5.1. Current Challenges
5.2. Future Directions
5.3. Multi-Disciplinary Applications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baker, C.L.; Hess, R.F.; Zihl, J. Residual motion perception in a “motion-blind” patient, assessed with limited-lifetime random dot stimuli. J. Neurosci. 1991, 11, 454–461. [Google Scholar] [CrossRef] [PubMed]
- Ling, Q.; Zhao, M. Stabilization of traffic videos based on both foreground and background feature trajectories. IEEE Trans. Circuits Syst. Video Technol. 2018, 29, 2215–2228. [Google Scholar] [CrossRef]
- Sharif, M.; Khan, S.; Saba, T.; Raza, M.; Rehman, A. Improved video stabilization using SIFT-log polar technique for unmanned aerial vehicles. In Proceedings of the 2019 International Conference on Computer and Information Sciences (ICCIS), Sakaka, Saudi Arabia, 3–4 April 2019; pp. 1–7. [Google Scholar]
- Li, X.; Xu, F.; Yong, X.; Chen, D.; Xia, R.; Ye, B.; Gao, H.; Chen, Z.; Lyu, X. SSCNet: A spectrum-space collaborative network for semantic segmentation of remote sensing images. Remote Sens. 2023, 15, 5610. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Li, L.; Xu, N.; Liu, F.; Yuan, C.; Chen, Z.; Lyu, X. AAFormer: Attention-Attended Transformer for Semantic Segmentation of Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Yu, J.; Wu, Z.; Yang, X.; Yang, Y.; Zhang, P. Underwater target tracking control of an untethered robotic fish with a camera stabilizer. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6523–6534. [Google Scholar] [CrossRef]
- Cardani, B. Optical image stabilization for digital cameras. IEEE Control Syst. Mag. 2006, 26, 21–22. [Google Scholar]
- e Souza, M.R.; de Almeida Maia, H.; Pedrini, H. Rethinking two-dimensional camera motion estimation assessment for digital video stabilization: A camera motion field-based metric. Neurocomputing 2023, 559, 126768. [Google Scholar] [CrossRef]
- Ke, J.; Watras, A.J.; Kim, J.J.; Liu, H.; Jiang, H.; Hu, Y.H. Efficient online real-time video stabilization with a novel least squares formulation and parallel AC-RANSAC. J. Vis. Commun. Image Represent. 2023, 96, 103922. [Google Scholar] [CrossRef]
- Li, X.; Mo, H.; Liu, F. A robust video stabilization method for camera shoot in mobile devices using GMM-based motion estimator. Comput. Electr. Eng. 2023, 110, 108841. [Google Scholar] [CrossRef]
- Raj, R.; Rajiv, P.; Kumar, P.; Khari, M.; Verdú, E.; Crespo, R.G.; Manogaran, G. Feature based video stabilization based on boosted HAAR Cascade and representative point matching algorithm. Image Vis. Comput. 2020, 101, 103957. [Google Scholar] [CrossRef]
- Kokila, S.; Ramesh, S. Intelligent software defined network based digital video stabilization system using frame transparency threshold pattern stabilization method. Comput. Commun. 2020, 151, 419–427. [Google Scholar]
- Cao, M.; Zheng, L.; Jia, W.; Liu, X. Real-time video stabilization via camera path correction and its applications to augmented reality on edge devices. Comput. Commun. 2020, 158, 104–115. [Google Scholar] [CrossRef]
- Dolly, D.R.J.; Peter, J.D.; Josemin Bala, G.; Jagannath, D.J. Image fusion for stabilized medical video sequence using multimodal parametric registration. Pattern Recognit. Lett. 2020, 135, 390–401. [Google Scholar] [CrossRef]
- Huang, H.; Wei, X.X.; Zhang, L. Encoding Shaky Videos by Integrating Efficient Video Stabilization. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 1503–1514. [Google Scholar] [CrossRef]
- Siva Ranjani, C.K.; Mahaboob Basha, S. Video Stabilization using SURF-CNN for Surveillance Application. In Proceedings of the 2024 8th International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 6–8 November 2024; pp. 1118–1123. [Google Scholar] [CrossRef]
- Wei, S.; Xie, W.; He, Z. Digital Video Stabilization Techniques: A Survey. J. Comput. Res. Dev. 2017, 54, 2044–2058. [Google Scholar]
- Guilluy, W.; Oudre, L.; Beghdadi, A. Video stabilization: Overview, challenges and perspectives. Signal Process. Image Commun. 2021, 90, 116015. [Google Scholar] [CrossRef]
- Roberto e Souza, M.; Maia, H.d.A.; Pedrini, H. Survey on Digital Video Stabilization: Concepts, Methods, and Challenges. ACM Comput. Surv. 2022, 55, 47. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Q.; Jiang, C.; Liu, J.; Shang, M.; Miao, Z. Video stabilization: A comprehensive survey. Neurocomputing 2023, 516, 205–230. [Google Scholar] [CrossRef]
- Huang, Q.; Lu, H.; Liu, W.; Wang, Y. Scalable Motion Estimation and Temporal Context Reinforcement for Video Compression using RGB sensors. IEEE Sens. J. 2025, 25, 18323–18333. [Google Scholar] [CrossRef]
- Huang, Q.; Liu, W.; Shang, M.; Wang, Y. Fusing angular features for skeleton-based action recognition using multi-stream graph convolution network. IET Image Process. 2024, 18, 1694–1709. [Google Scholar] [CrossRef]
- Ravankar, A.; Rawankar, A.; Ravankar, A.A. Video stabilization algorithm for field robots in uneven terrain. Artif. Life Robot. 2023, 28, 502–508. [Google Scholar] [CrossRef]
- e Souza, M.R.; Maia, H.d.A.; Pedrini, H. NAFT and SynthStab: A RAFT-based Network and a Synthetic Dataset for Digital Video Stabilization. Int. J. Comput. Vis. 2024, 133, 2345–2370. [Google Scholar] [CrossRef]
- Ren, Z.; Zou, M.; Bi, L.; Fang, M. An unsupervised video stabilization algorithm based on gyroscope image fusion. Comput. Graph. 2025, 126, 104154. [Google Scholar] [CrossRef]
- Wang, N.; Zhou, C.; Zhu, R.; Zhang, B.; Wang, Y.; Liu, H. SOFT: Self-supervised sparse Optical Flow Transformer for video stabilization via quaternion. Eng. Appl. Artif. Intell. 2024, 130, 107725. [Google Scholar] [CrossRef]
- Gulcemal, M.O.; Sarac, D.C.; Alp, G.; Duran, G.; Gucenmez, S.; Solmaz, D.; Akar, S.; Bayraktar, D. Effects of video-based cervical stabilization home exercises in patients with rheumatoid arthritis: A randomized controlled pilot study. Z. Rheumatol. 2024, 83, 352–358. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Dong, Z.; Li, H.; Yue, Y.; Fu, M.; Yang, Y. Unified Vertex Motion Estimation for integrated video stabilization and stitching in tractor–trailer wheeled robots. Robot. Auton. Syst. 2025, 191, 105004. [Google Scholar] [CrossRef]
- Dong, L.; Chen, L.; Wu, Z.C.; Zhang, X.; Liu, H.L.; Dai, C. Video Stabilization-Based elimination of unintended jitter and vibration amplification in centrifugal pumps. Mech. Syst. Signal Process. 2025, 229, 112500. [Google Scholar] [CrossRef]
- Grundmann, M.; Kwatra, V.; Essa, I. Auto-directed video stabilization with robust L1 optimal camera paths. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 225–232. [Google Scholar]
- Bradley, A.; Klivington, J.; Triscari, J.; van der Merwe, R. Cinematic-L1 video stabilization with a log-homography model. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Virtual, 5–9 January 2021; pp. 1041–1049. [Google Scholar]
- Liu, S.; Yuan, L.; Tan, P.; Sun, J. Bundled camera paths for video stabilization. ACM Trans. Graph. (TOG) 2013, 32, 78. [Google Scholar] [CrossRef]
- Liu, S.; Yuan, L.; Tan, P.; Sun, J. Steadyflow: Spatially smooth optical flow for video stabilization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 4209–4216. [Google Scholar]
- Liu, S.; Tan, P.; Yuan, L.; Sun, J.; Zeng, B. Meshflow: Minimum latency online video stabilization. In Computer Vision–ECCV 2016: Proceedings of the 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part VI 14; Springer: Berlin/Heidelberg, Germany, 2016; pp. 800–815. [Google Scholar]
- Zhang, L.; Xu, Q.K.; Huang, H. A global approach to fast video stabilization. IEEE Trans. Circuits Syst. Video Technol. 2015, 27, 225–235. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, X.Q.; Kong, X.Y.; Huang, H. Geodesic video stabilization in transformation space. IEEE Trans. Image Process. 2017, 26, 2219–2229. [Google Scholar] [CrossRef]
- Wu, H.; Xiao, L.; Lian, Z.; Shim, H.J. Locally low-rank regularized video stabilization with motion diversity constraints. IEEE Trans. Circuits Syst. Video Technol. 2018, 29, 2873–2887. [Google Scholar] [CrossRef]
- Chereau, R.; Breckon, T.P. Robust motion filtering as an enabler to video stabilization for a tele-operated mobile robot. In Proceedings of the Electro-Optical Remote Sensing, Photonic Technologies, and Applications VII; and Military Applications in Hyperspectral Imaging and High Spatial Resolution Sensing, Dresden, Germany, 24–26 September 2013; Kamerman, G.W., Steinvall, O.K., Bishop, G.J., Gonglewski, J.D., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2013; Volume 8897, p. 88970I. [Google Scholar] [CrossRef]
- Franz, G.; Wegner, D.; Wiehn, M.; Keßler, S. Evaluation of video stabilization metrics for the assessment of camera vibrations. In Proceedings of the Infrared Imaging Systems: Design, Analysis, Modeling, and Testing XXXV, National Harbor, MD, USA, 21–26 April 2024; Haefner, D.P., Holst, G.C., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2024; Volume 13045, p. 130450D. [Google Scholar] [CrossRef]
- Yang, C.; He, Y.; Zhang, D. LSTM based video stabilization for object tracking. In Proceedings of the AOPC 2021: Optical Sensing and Imaging Technology, Beijing, China, 20–22 June 2021; Jiang, Y., Lv, Q., Liu, D., Zhang, D., Xue, B., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2021; Volume 12065, p. 120653D. [Google Scholar] [CrossRef]
- Takeo, Y.; Sekiguchi, T.; Mitani, S.; Mizutani, T.; Shirasawa, Y.; Kimura, T. Video stabilization method corresponding to various imagery for geostationary optical Earth observation satellite. In Proceedings of the Image and Signal Processing for Remote Sensing XXVII, Online, 6 October 2021; Bruzzone, L., Bovolo, F., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2021; Volume 11862, p. 1186205. [Google Scholar] [CrossRef]
- Voronin, V.; Frantc, V.; Marchuk, V.; Shrayfel, I.; Gapon, N.; Agaian, S.; Stradanchenko, S. Video stabilization using space-time video completion. In Proceedings of the Mobile Multimedia/Image Processing, Security, and Applications 2016, Baltimore, MD, USA, 17–21 April 2016; Agaian, S.S., Jassim, S.A., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2016. [Google Scholar] [CrossRef]
- Mehala, R.; Mahesh, K. An effective absolute and relative depths estimation-based 3D video stabilization framework using GSLSTM and BCKF. Signal Image Video Process. 2025, 19, 412. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, P.; Ju, M.; Hu, Q. Motion Intent Analysis-Based Full-Frame Video Stabilization. IEEE Signal Process. Lett. 2025, 32, 1685–1689. [Google Scholar] [CrossRef]
- Buehler, C.; Bosse, M.; McMillan, L. Non-metric image-based rendering for video stabilization. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2001), Kauai, HI, USA, 8–14 December 2001; Volume 2, p. II. [Google Scholar]
- Liu, S.; Wang, Y.; Yuan, L.; Bu, K.; Tan, P.; Sun, J. Video stabilization with a depth camera. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 89–95. [Google Scholar]
- Liu, F.; Gleicher, M.; Jin, H.; Agarwala, A. Content-preserving warps for 3D video stabilization. In Seminal Graphics Papers: Pushing the Boundaries, Volume 2; ACM: New York, NY, USA, 2023; pp. 631–639. [Google Scholar]
- Smith, B.M.; Zhang, L.; Jin, H.; Agarwala, A. Light field video stabilization. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 341–348. [Google Scholar]
- Liu, F.; Gleicher, M.; Wang, J.; Jin, H.; Agarwala, A. Subspace video stabilization. ACM Trans. Graph. (TOG) 2011, 30, 4. [Google Scholar] [CrossRef]
- Lee, K.Y.; Chuang, Y.Y.; Chen, B.Y.; Ouhyoung, M. Video stabilization using robust feature trajectories. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 1397–1404. [Google Scholar]
- Wang, M.; Yang, G.Y.; Lin, J.K.; Zhang, S.H.; Shamir, A.; Lu, S.P. Deep online video stabilization with multi-grid warping transformation learning. IEEE Trans. Image Process. 2018, 28, 2283–2292. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J.; Maybank, S.J.; Tao, D. Dut: Learning video stabilization by simply watching unstable videos. IEEE Trans. Image Process. 2022, 31, 4306–4320. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, Y.; Cheng, J.; Lu, H. Two-stream adaptive graph convolutional networks for skeleton-based action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 12026–12035. [Google Scholar]
- Yu, J.; Ramamoorthi, R. Learning video stabilization using optical flow. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 8159–8167. [Google Scholar]
- Wulff, J.; Black, M.J. Efficient sparse-to-dense optical flow estimation using a learned basis and layers. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 120–130. [Google Scholar]
- Choi, J.; Kweon, I.S. Deep iterative frame interpolation for full-frame video stabilization. ACM Trans. Graph. (TOG) 2020, 39, 4. [Google Scholar] [CrossRef]
- Liu, Y.L.; Lai, W.S.; Yang, M.H.; Chuang, Y.Y.; Huang, J.B. Hybrid neural fusion for full-frame video stabilization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2299–2308. [Google Scholar]
- Lee, Y.C.; Tseng, K.W.; Chen, Y.T.; Chen, C.C. 3D video stabilization with depth estimation by CNN-based optimization. In Proceedings of theIEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 10621–10630. [Google Scholar]
- Li, C.; Song, L.; Chen, S.; Xie, R.; Zhang, W. Deep online video stabilization using IMU sensors. IEEE Trans. Multimed. 2022, 25, 2047–2060. [Google Scholar] [CrossRef]
- Peng, Z.; Ye, X.; Zhao, W.; Liu, T.; Sun, H.; Li, B.; Cao, Z. 3D Multi-frame Fusion for Video Stabilization. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 7507–7516. [Google Scholar] [CrossRef]
- Goldstein, A.; Fattal, R. Video stabilization using epipolar geometry. Acm Trans. Graph. (TOG) 2012, 31, 126. [Google Scholar] [CrossRef]
- Grundmann, M.; Kwatra, V.; Castro, D.; Essa, I. Calibration-free rolling shutter removal. In Proceedings of the 2012 IEEE International Conference on Computational Photography (ICCP), Seattle, WA, USA, 28–29 April 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Wang, Y.S.; Liu, F.; Hsu, P.S.; Lee, T.Y. Spatially and Temporally Optimized Video Stabilization. IEEE Trans. Vis. Comput. Graph. 2013, 19, 1354–1361. [Google Scholar] [CrossRef]
- Zhao, M.; Ling, Q. Pwstablenet: Learning pixel-wise warping maps for video stabilization. IEEE Trans. Image Process. 2020, 29, 3582–3595. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.T.; Tseng, K.W.; Lee, Y.C.; Chen, C.Y.; Hung, Y.P. Pixstabnet: Fast multi-scale deep online video stabilization with pixel-based warping. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; pp. 1929–1933. [Google Scholar]
- Yu, J.; Ramamoorthi, R. Robust video stabilization by optimization in CNN weight space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3800–3808. [Google Scholar]
- Ali, M.K.; Im, E.W.; Kim, D.; Kim, T.H. Harnessing Meta-Learning for Improving Full-Frame Video Stabilization. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 12605–12614. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Z.; Liu, Z.; Tan, P.; Zeng, B. Minimum Latency Deep Online Video Stabilization and Its Extensions. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 1238–1249. [Google Scholar] [CrossRef]
- Sánchez-Beeckman, M.; Buades, A.; Brandonisio, N.; Kanoun, B. Combining Pre- and Post-Demosaicking Noise Removal for RAW Video. IEEE Trans. Image Process. 2025. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Chen, X.; Wang, Z. IMU-Assisted Gray Pixel Shift for Video White Balance Stabilization. IEEE Trans. Multimed. 2025, 1–14. [Google Scholar] [CrossRef]
- Balakirsky, S.B.; Chellappa, R. Performance characterization of image stabilization algorithms. In Proceedings of the 3rd IEEE International Conference on Image Processing, Lausanne, Switzerland, 19 September 1996; Volume 2, pp. 413–416. [Google Scholar]
- Morimoto, C.; Chellappa, R. Evaluation of image stabilization algorithms. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP’98 (Cat. No. 98CH36181), Seattle, WA, USA, 15 May 1998; Volume 5, pp. 2789–2792. [Google Scholar]
- Tanakian, M.J.; Rezaei, M.; Mohanna, F. Camera motion modeling for video stabilization performance assessment. In Proceedings of the 2011 7th Iranian Conference on Machine Vision and Image Processing, Tehran, Iran, 16–17 November 2011; pp. 1–4. [Google Scholar]
- Cui, Z.; Jiang, T. No-reference video shakiness quality assessment. In Computer Vision–ACCV 2016: Proceedings of the 13th Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016; Revised Selected Papers, Part V 13; Springer International Publishing: Cham, Switzerland, 2017; pp. 396–411. [Google Scholar]
- Karpenko, A.; Jacobs, D.; Baek, J.; Levoy, M. Digital video stabilization and rolling shutter correction using gyroscopes. CSTR 2011, 1, 13. [Google Scholar]
- Streijl, R.C.; Winkler, S.; Hands, D.S. Mean opinion score (MOS) revisited: Methods and applications, limitations and alternatives. Multimed. Syst. 2016, 22, 213–227. [Google Scholar] [CrossRef]
- Hore, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Wang, Z.; Bovik, A.C. Mean squared error: Love it or leave it? A new look at signal fidelity measures. IEEE Signal Process. Mag. 2009, 26, 98–117. [Google Scholar] [CrossRef]
- Ye, F.; Pu, S.; Zhong, Q.; Li, C.; Xie, D.; Tang, H. Dynamic gcn: Context-enriched topology learning for skeleton-based action recognition. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA USA, 12–16 October 2020; ACM: New York, NY, USA, 2020; pp. 55–63. [Google Scholar]
- Offiah, M.C.; Amin, N.; Gross, T.; El-Sourani, N.; Borschbach, M. An approach towards a full-reference-based benchmarking for quality-optimized endoscopic video stabilization systems. In Proceedings of the Eighth Indian Conference on Computer Vision, Graphics and Image Processing, Mumbai, India, 16–19 December 2012; ACM: New York, NY, USA, 2012; pp. 1–8. [Google Scholar]
- Zhang, L.; Zheng, Q.Z.; Liu, H.K.; Huang, H. Full-reference stability assessment of digital video stabilization based on riemannian metric. IEEE Trans. Image Process. 2018, 27, 6051–6063. [Google Scholar] [CrossRef]
- Niskanen, M.; Silven, O.; Tico, M. Video Stabilization Performance Assessment. In Proceedings of the 2006 IEEE International Conference on Multimedia and Expo, Toronto, ON, Canada, 9–12 July 2006; pp. 405–408. [Google Scholar] [CrossRef]
- Ito, M.S.; Izquierdo, E. A dataset and evaluation framework for deep learning based video stabilization systems. In Proceedings of the 2019 IEEE Visual Communications and Image Processing (VCIP), Sydney, NSW, Australia, 1–4 December 2019; pp. 1–4. [Google Scholar]
- Liu, S.; Li, M.; Zhu, S.; Zeng, B. Codingflow: Enable video coding for video stabilization. IEEE Trans. Image Process. 2017, 26, 3291–3302. [Google Scholar] [CrossRef]
- Yu, J.; Ramamoorthi, R. Selfie video stabilization. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 551–566. [Google Scholar]
- Kerim, A.; Marcolino, L.S.; Jiang, R. Silver: Novel rendering engine for data hungry computer vision models. In Proceedings of the 2nd International Workshop on Data Quality Assessment for Machine Learning, Virtual, 14–18 August 2021. [Google Scholar]
- Huang, Q.; Sun, H.; Wang, Y.; Yuan, Y.; Guo, X.; Gao, Q. Ship detection based on YOLO algorithm for visible images. IET Image Process. 2024, 18, 481–492. [Google Scholar] [CrossRef]
- Thivent, D.J.; Williams, G.E.; Zhou, J.; Baer, R.L.; Toft, R.; Beysserie, S.X. Combined Optical and Electronic Image Stabilization. U.S. Patent 9,596,411, 14 March 2017. [Google Scholar]
- Liang, C.K.; Shi, F. Fused Video Stabilization on the Pixel 2 and Pixel 2 xl; Tech. Rep.; Google: Mountain View, CA, USA, 2017. [Google Scholar]
- Ye, J.; Pan, E.; Xu, W. Digital Video Stabilization Method Based on Periodic Jitters of Airborne Vision of Large Flapping Wing Robots. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 2591–2603. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Q.; Tang, B.; Sun, H.; Guo, X. FGC-VC: Flow-Guided Context Video Compression. In Proceedings of the IEEE International Conference on Image Processing, ICIP 2023, Kuala Lumpur, Malaysia, 8–11 October 2023; IEEE: Kuala Lumpur, Malaysia, 2023; pp. 3175–3179. [Google Scholar] [CrossRef]








| Methods | FPS | Datasets |
|---|---|---|
| Bundle | 3.5 | NUS (test) |
| L1Stabilizer | 10.0 | NUS (test) |
| MeshFlow | 22.0 | NUS (test) |
| StabNet | 35.5 | NUS (test), DeepStab (train) |
| Methods | FPS | Datasets |
|---|---|---|
| Hybrid | 2.6 | NUS (test) |
| Deep3D | 34.5 | NUS (test) |
| DIFRINT | 14.3 | NUS (test) |
| DUT | 14 | NUS (test), DeepStab (train) |
| PWStableNet | 56 | NUS (test), DeepStab (train) |
| PixStabNet | 54.6 | NUS (test), DeepStab (train) |
| Method | Year | C | D | S |
|---|---|---|---|---|
| L1Stabilize | 2011 | 0.641 | 0.905 | 0.826 |
| Bundle | 2013 | 0.758 | 0.886 | 0.848 |
| StableNet | 2018 | 0.751 | 0.850 | 0.840 |
| PWStableNet | 2020 | 0.937 | 0.971 | 0.830 |
| DeepFlow | 2020 | 0.792 | 0.851 | 0.845 |
| DIFRINT | 2021 | 1.000 | 0.880 | 0.787 |
| Datasets | Type | Scenario | Features |
|---|---|---|---|
| HUJ | Real-world | General | Driving/zooming/walking scenarios |
| MCL | Real-world | General | 7 scenarios |
| BIT | Real-world | General | Includes low-light/large parallax |
| QMUL | Real-world | General | Largest scale |
| NUS | Real-world | General | Deep learning validation |
| DeepStab | Real-world | General | Dual-camera synchronization |
| Video+Sensor | Real-world | General | Paired with gyroscope and OIS sensor logs |
| IMU_VS | Real-world | General | IMU sensor data augmentation |
| Selfie | Real-world | Special (selfie) | Continuous face tracking |
| VSAC105Real | Synthetic | Special (weather) | Weather simulation |
| ISDS | Real-world | Special (maritime) | Small-target detection optimization |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Huang, Q.; Jiang, C.; Li, X.; Wang, Y. Video Stabilization: A Comprehensive Survey from Classical Mechanics to Deep Learning Paradigms. Modelling 2025, 6, 49. https://doi.org/10.3390/modelling6020049
Xu Q, Huang Q, Jiang C, Li X, Wang Y. Video Stabilization: A Comprehensive Survey from Classical Mechanics to Deep Learning Paradigms. Modelling. 2025; 6(2):49. https://doi.org/10.3390/modelling6020049
Chicago/Turabian StyleXu, Qian, Qian Huang, Chuanxu Jiang, Xin Li, and Yiming Wang. 2025. "Video Stabilization: A Comprehensive Survey from Classical Mechanics to Deep Learning Paradigms" Modelling 6, no. 2: 49. https://doi.org/10.3390/modelling6020049
APA StyleXu, Q., Huang, Q., Jiang, C., Li, X., & Wang, Y. (2025). Video Stabilization: A Comprehensive Survey from Classical Mechanics to Deep Learning Paradigms. Modelling, 6(2), 49. https://doi.org/10.3390/modelling6020049








