Modeling Skin Thermal Behavior with a Cutaneous Calorimeter: Local Parameters of Medical Interest
Abstract
1. Introduction
2. Materials and Methods
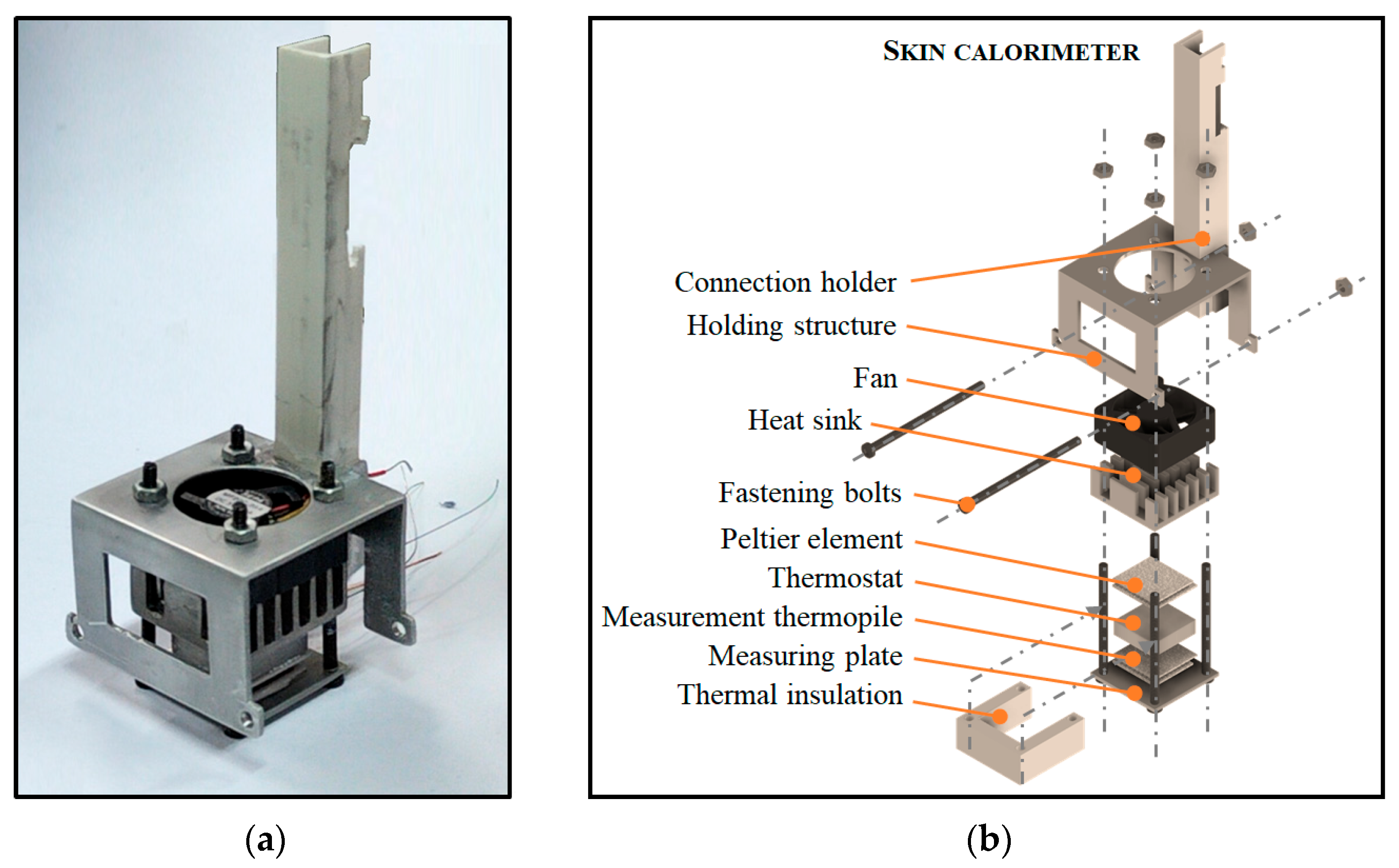
2.1. Skin Calorimeter
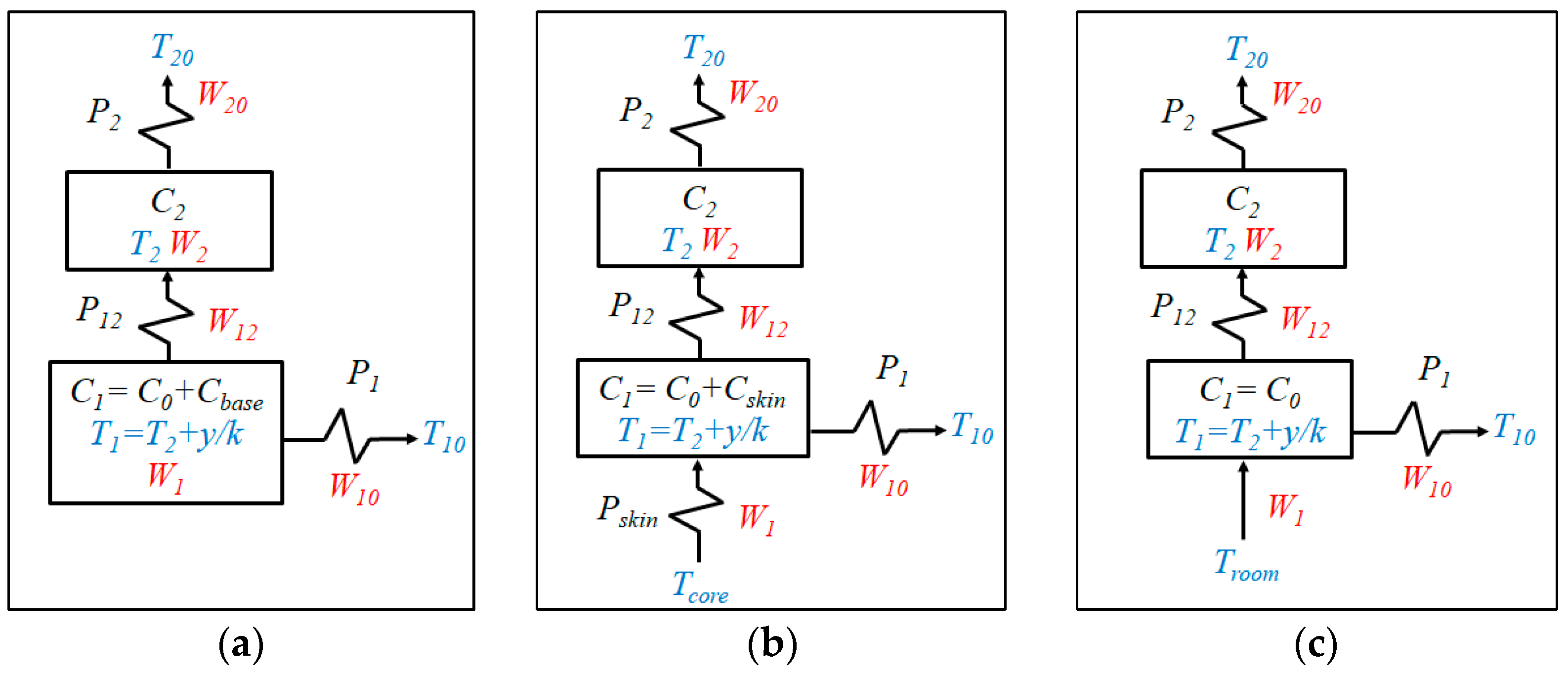
2.2. Calorimetric Model
2.3. Measurement and Control System
2.4. Identification of Model Parameters
3. Results
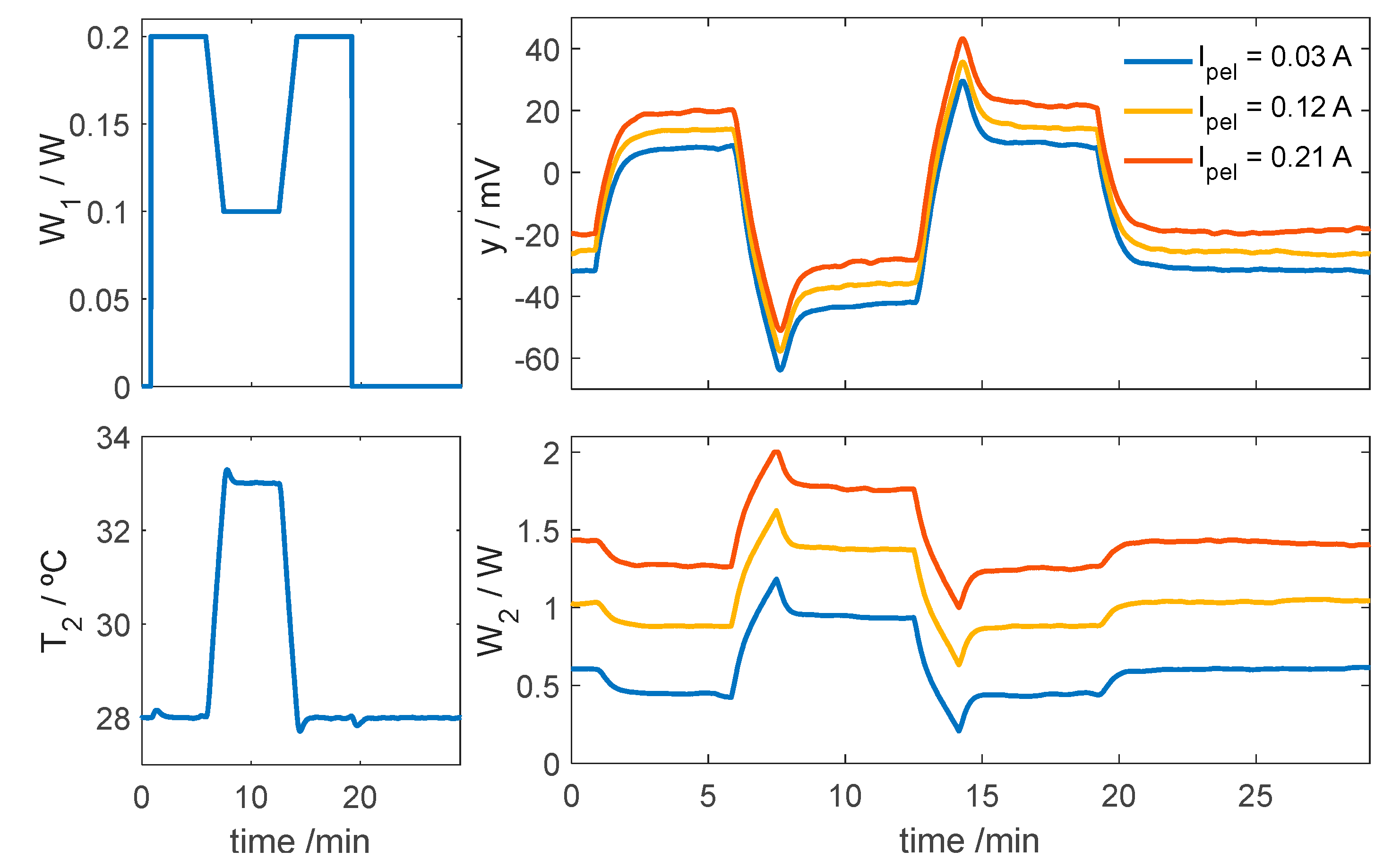
3.1. Parameters of the Calorimetric Model
3.2. Simulations
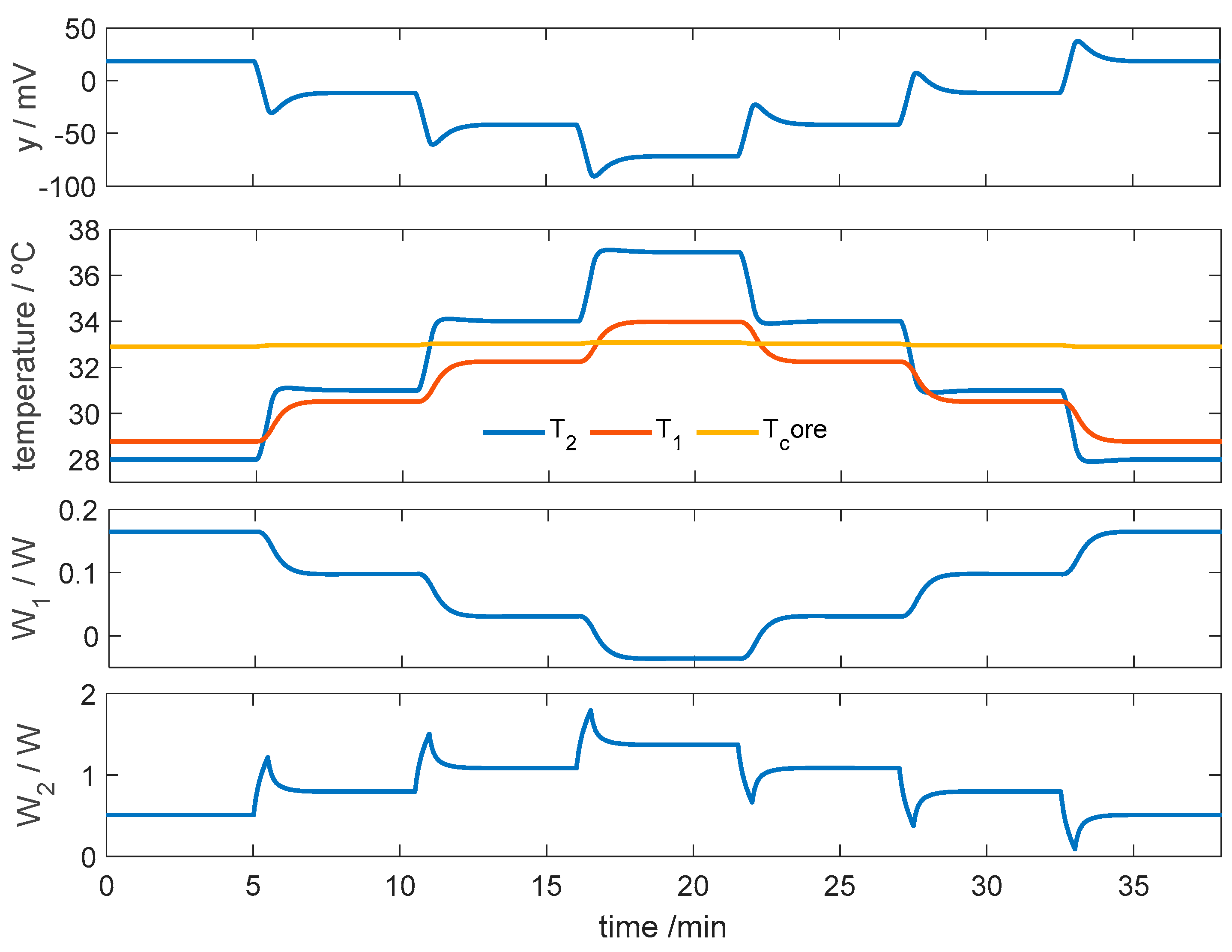
- PI controller and thermal regulation: simulations allow the PI controller parameters to be adjusted and to verify that the thermostat temperature accurately follows the programmed thermal profile;
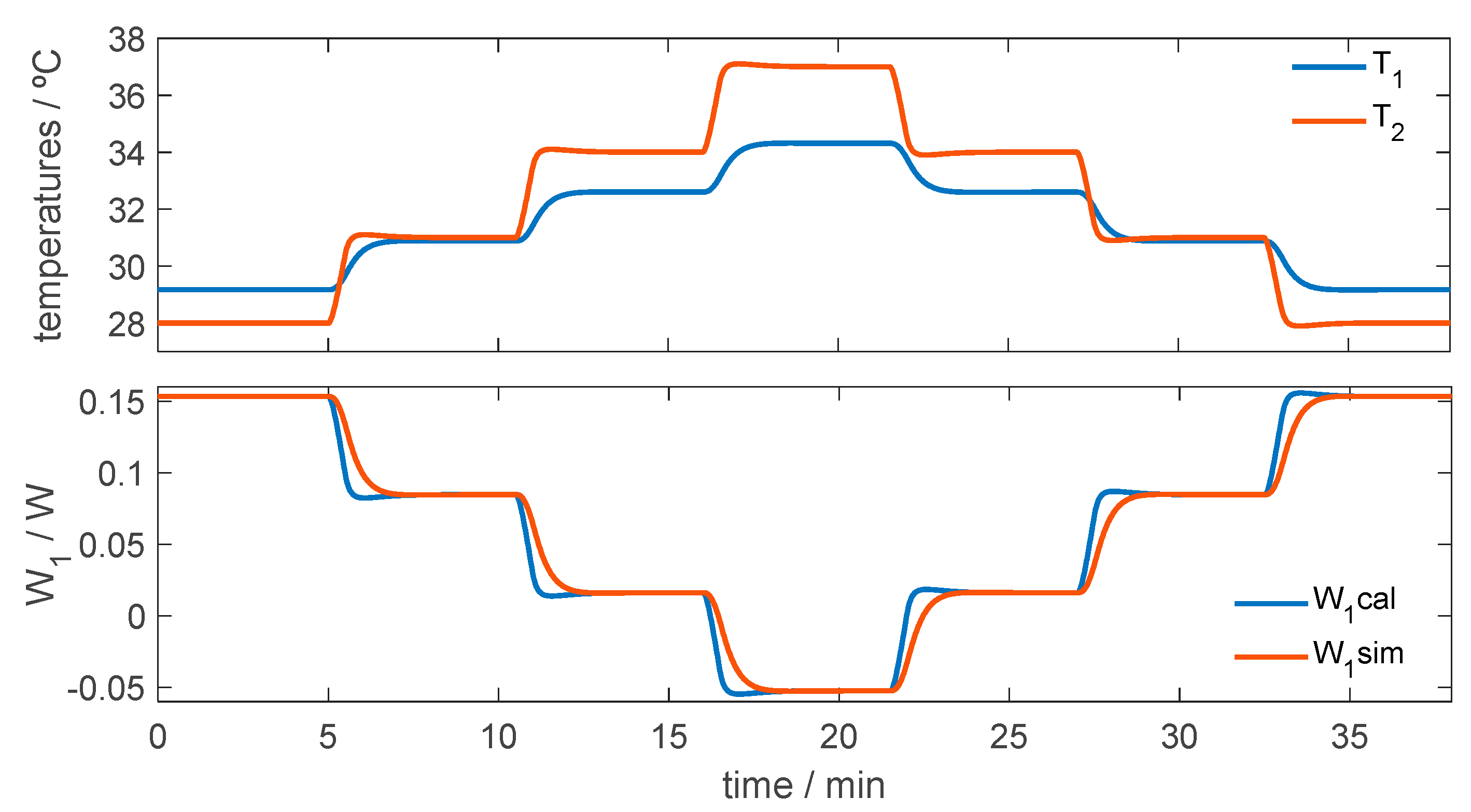
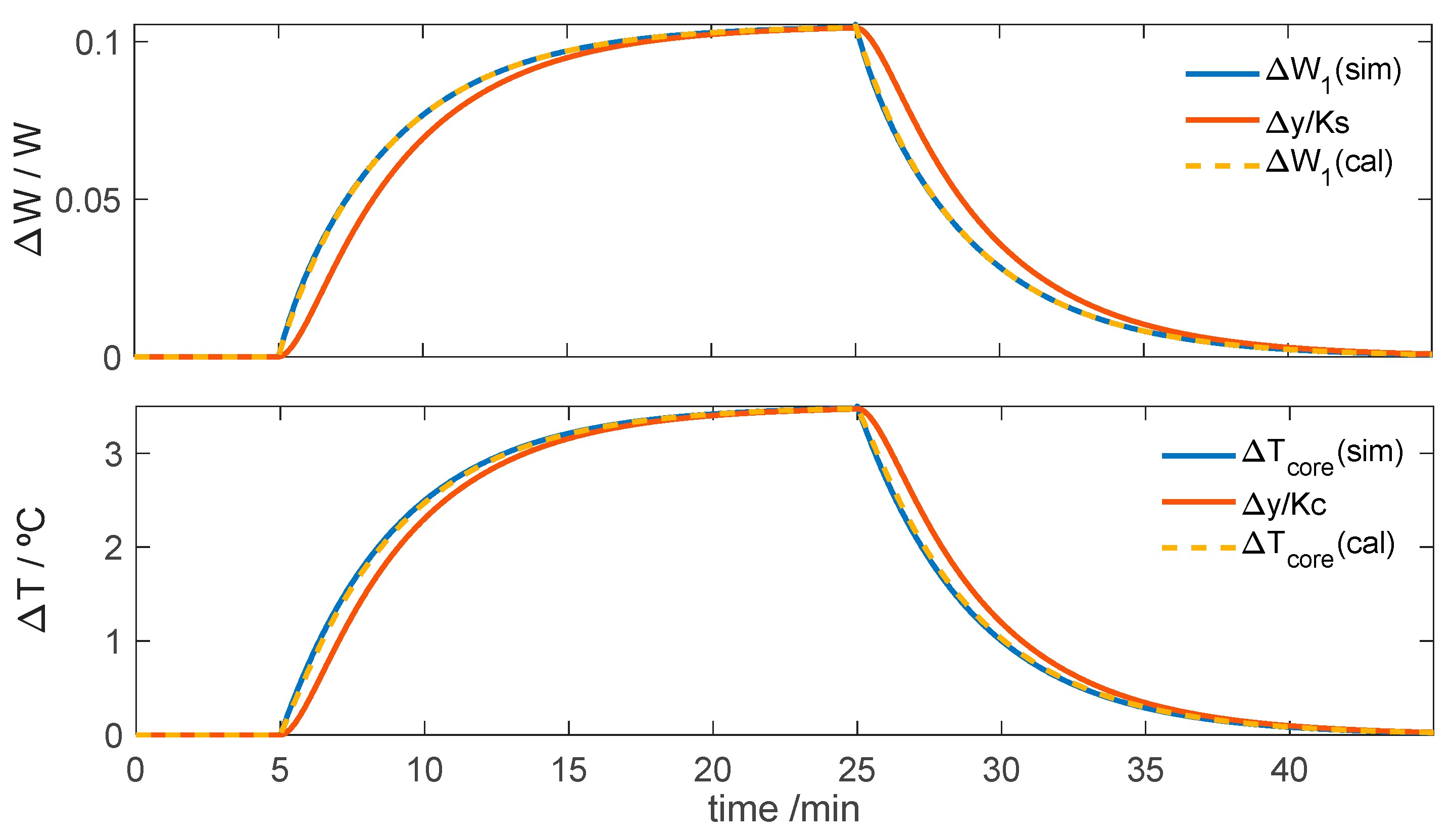
- Calorimetric response under resting conditions: simulations are used to analyze the behavior of the calorimeter when it is applied to the skin at rest;
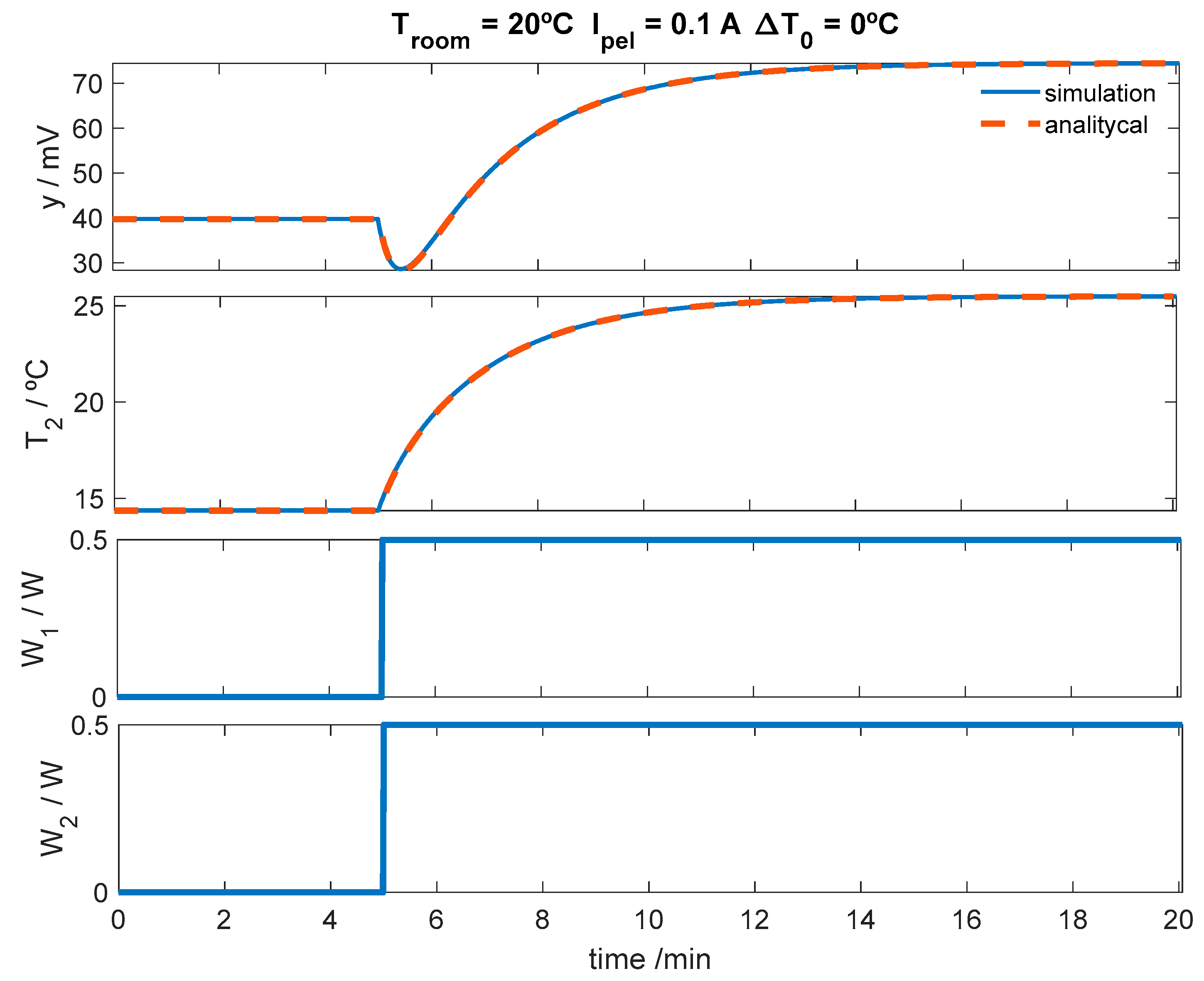
- Calorimetric response during physical activity: Simulations also allow evaluation of the response when the subject performs physical exercise, which generates transient heat fluxes.
3.2.1. Control of Thermostat Temperature
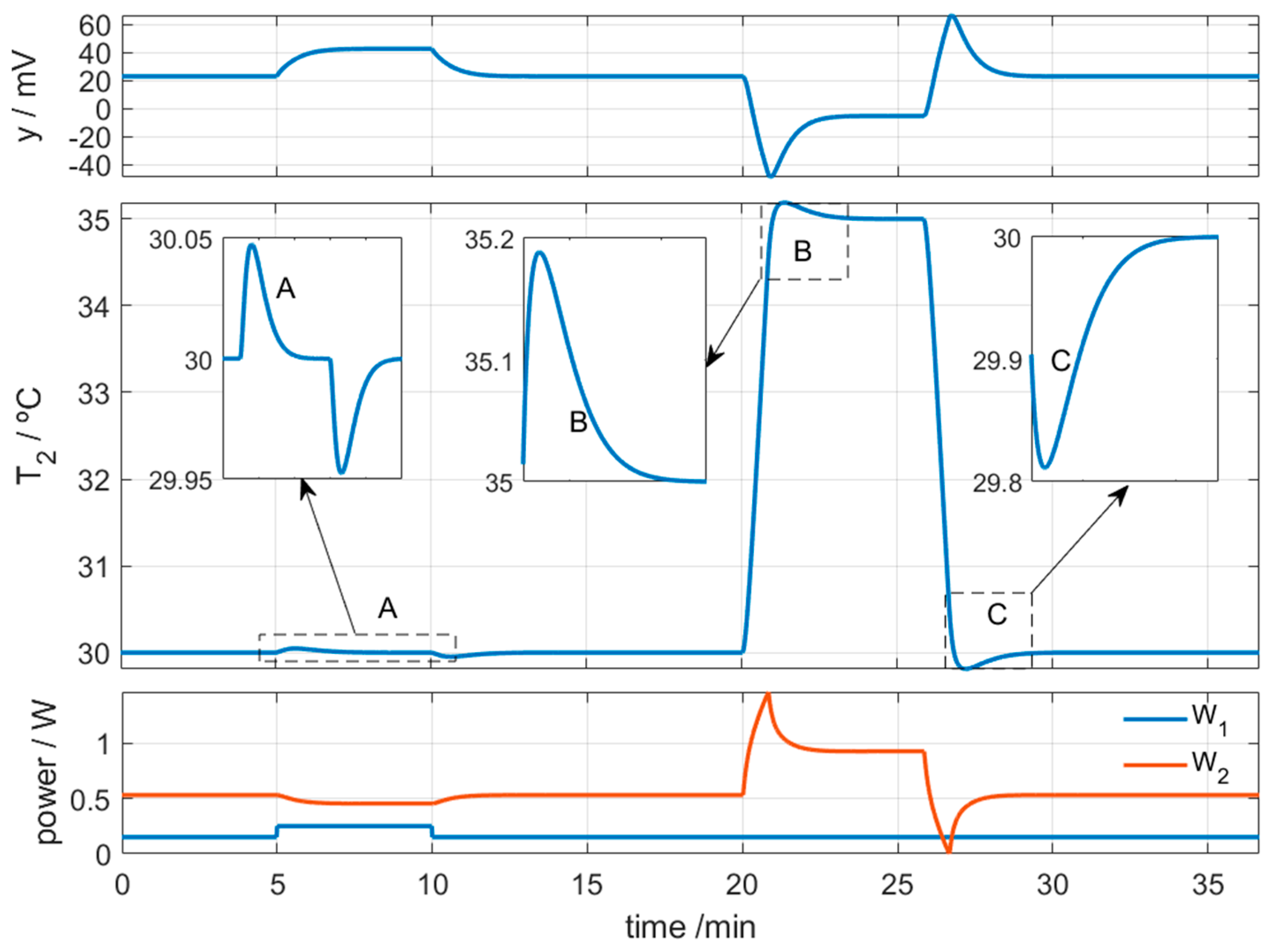
3.2.2. Simulation of the Calorimeter’s Operation for Skin Application at Rest
3.2.3. Simulation of the Calorimeter’s Operation for Skin Application During Exercise
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RC model | Model of thermal Resistances and heat Capacities |
| HFS | Heat flux sensor |
| FEM | Finite element method |
| EPS | Expanded polystyrene |
| PI control | Proportional–integral controller |
| RMSE | Root mean square error |
| GPIB | General Purpose Interface Bus |
| PT100 | Platinum Resistance temperature detector |
| TF | Transfer function |
References
- Available online: https://sea.omega.com/th/pptst/HFS-3_HFS-4.html#description (accessed on 7 April 2025).
- Available online: https://es.omega.com/pptst/UHF-HFS-SERIES.html#description (accessed on 7 April 2025).
- Available online: https://www.hukseflux.com/products/heat-flux-sensors/heat-flux-sensors (accessed on 7 April 2025).
- Tanaka, Y.; Matsunaga, D.; Tajima, T.; Seyama, M.; Kato, I.; Nagashima, K. Skin-Attachable Sensor for Continuous Core Body Temperature Monitoring. IEEE Sens. J. 2024, 24, 38708–38714. [Google Scholar] [CrossRef]
- Okabe, T.; Fujimura, T.; Okajima, J.; Aiba, S.; Maruyama, S. Non-invasive Measurement of Effective Thermal Conductivity of Human Skin with a Guard-Heated Thermistor Probe. Int. J. Heat Mass Transf. 2018, 126, 625–635. [Google Scholar] [CrossRef]
- Kharalkar, N.M.; Hayes, L.J.; Valvano, J.W. Pulse-Power Integrated-Decay Technique for the Measurement of Thermal Conductivity. Meas. Sci. Technol. 2008, 19, 075104. [Google Scholar] [CrossRef]
- Madhvapathy, S.R.; Ma, Y.; Patel, M.; Krishnan, S.; Wei, C.; Li, Y.; Xu, S.; Feng, X.; Huang, Y.; Rogers, J.A. Epidermal Electronic Systems for Measuring the Thermal Properties of Human Skin at Depths of up to Several Millimeters. Adv. Funct. Mater. 2018, 28, 1802083. [Google Scholar] [CrossRef]
- Zubiaga, A.; Kirsch, C.; Boiger, G.; Bonmarin, M. A Simple Instrument to Measure the Thermal Transport Properties of the Human Skin. In Proceedings of the 2021 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Lausanne, Switzerland, 23–25 June 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, X.; Bontozoglou, C.; Xiao, P. In Vivo Skin Characterizations by Using Opto-Thermal Depth-Resolved Detection Spectra. Cosmetics 2019, 6, 54. [Google Scholar] [CrossRef]
- Grenier, E.; Gehin, C.; McAdams, E.; Lun, B.; Gobin, J.-P.; Uhl, J.-F. Effect of Compression Stockings on Cutaneous Microcirculation: Evaluation Based on Measurements of the Skin Thermal Conductivity. Phlebology 2014, 31, 101–105. [Google Scholar] [CrossRef]
- Wang, L.; Chong, D.; Di, Y.; Yi, H. A Revised Method to Predict Skin’s Thermal Resistance. Therm. Sci. 2018, 22, 1795–1802. [Google Scholar] [CrossRef]
- Webb, R.C.; Pielak, R.M.; Bastien, P.; Ayers, J.; Niittynen, J.; Kurniawan, J.; Manco, M.; Lin, A.; Cho, N.H.; Malyrchuk, V.; et al. Thermal Transport Characteristics of Human Skin Measured In Vivo Using Ultrathin Conformal Arrays of Thermal Sensors and Actuators. PLoS ONE 2015, 10, e0118131. [Google Scholar] [CrossRef]
- Webb, R.C.; Bonifas, A.P.; Behnaz, A.; Zhang, Y.; Yu, K.J.; Cheng, H.; Shi, M.; Bian, Z.; Liu, Z.; Kim, Y.S.; et al. Ultrathin Conformal Devices for Precise and Continuous Thermal Characterization of Human Skin. Nat. Mater. 2013, 12, 938–944. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, Y.; Malyarchuk, V.; Jia, L.; Jang, K.; Webb, R.C.; Fu, H.; Shi, Y.; Zhou, G.; Shi, L.; et al. Epidermal Photonic Devices for Quantitative Imaging of Temperature and Thermal Transport Characteristics of the Skin. Nat. Commun. 2014, 5, 4938. [Google Scholar] [CrossRef]
- Rodríguez de Rivera, P.J.; Rodríguez de Rivera, M.; Socorro, F.; Rodríguez de Rivera, M. In Vivo Measurement of Skin Heat Capacity: Advantages of the Scanning Calorimetric Sensor. J. Therm. Anal. Calorim. 2022, 147, 12155–12163. [Google Scholar] [CrossRef]
- Rodríguez de Rivera, P.J.; Rodríguez de Rivera, M.; Socorro, F.; Calbet, J.A.L.; Rodríguez de Rivera, M. Advantages of In Vivo Measurement of Human Skin Thermal Conductance Using a Calorimetric Sensor. J. Therm. Anal. Calorim. 2022, 147, 10027–10036. [Google Scholar] [CrossRef]
- Rodríguez de Rivera, M.; Rodríguez de Rivera, P.J. New, Optimized Skin Calorimeter Version for Measuring Thermal Responses of Localized Skin Areas during Physical Activity. Sensors 2024, 24, 5927. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Clarendon-Press: Oxford, UK, 2008. [Google Scholar]
- Wissler, E.H. Pennes’ 1948 Paper Revisited. J. Appl. Physiol. 1998, 85, 35–41. [Google Scholar] [CrossRef]
- Lakhssass, A.; Kengne, E.; Semmaoui, H. Modified Pennes’ Equation Modeling Bio-Heat Transfer in Living Tissues: Analytical and Numerical Analysis. Nat. Sci. 2010, 2, 1375–1385. [Google Scholar] [CrossRef]
- Deng, Z.S.; Liu, J. Blood Perfusion-Based Model for Characterizing the Temperature Fluctuation in Living Tissues. Physica A 2001, 300, 521–530. [Google Scholar] [CrossRef]
- Sarkar, D.; Haji-Sheikh, A.; Jain, A. Temperature Distribution in Multi-Layer Skin Tissue in Presence of a Tumor. Int. J. Heat Mass Transf. 2015, 91, 602–610. [Google Scholar] [CrossRef]
- Agrawal, M.; Pardasani, K.R. Finite Element Model to Study Temperature Distribution in Skin and Deep Tissues of Human Limbs. J. Therm. Biol. 2016, 62, 98–105. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez de Rivera, P.J.; Rodríguez de Rivera, M.; Socorro, F.; Rodríguez de Rivera, M. Study of the Thermal Measurement Depth of a Skin Calorimeter Using Simple RC and TF Models. Int. J. Heat Mass Transf. 2025, 236, 126256. [Google Scholar] [CrossRef]
- Yuan, L.; Yu, J.; Qian, S. Revisiting Thermal Penetration Depth for Caloric Cooling System. Appl. Therm. Eng. 2020, 178, 115605. [Google Scholar] [CrossRef]
- D’Esposito, R.; Balanethiram, S.; Battaglia, J.-L.; Frégonèse, S.; Zimmer, T. Thermal Penetration Depth Analysis and Impact of the BEOL Metals on the Thermal Impedance of SiGe HBTs. IEEE Electron. Device Lett. 2017, 38, 1457–1460. [Google Scholar] [CrossRef]
- Zielenkiewicz, W. Calorimetric Models. J. Therm. Anal. 1988, 33, 7–13. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Available online: https://es.mathworks.com/help/matlab/ref/fminsearch.html. (accessed on 7 April 2025).
- Rodríguez de Rivera, P.J.; Rodríguez de Rivera, M.; Socorro, F.; Rodríguez de Rivera, M. Monitoring of some minor human skin lesions using a skin calorimeter. J. Therm. Anal. Calorim. 2024, 149, 5257–5264. [Google Scholar] [CrossRef]



| Measurement Area (cm2) | Thickness (mm) | Thermal Resistance (K/W) | Sensitivity (mV/W) | |
|---|---|---|---|---|
| Film Heat flux HFS-4 [1] | 10.0 | 0.18 | 1.8 | 2.1 |
| Film Heat flux HFS-5 [2] | 6.3 | 0.36 | 1.4 | 2.2 |
| Film Heat flux FHF05 [3] | 1.0 | 0.40 | 11.0 | 10.0 |
| Film Heat flux FHF05 [3] | 4.5 | 0.40 | 2.4 | 6.6 |
| Heat flux plate HFP01 [3] | 8.0 | 5.40 | 8.9 | 75.0 |
| Skin Calorimeter 1 (this work) | 4.0 | 2.20 | 11.0 | 195.5 |
| Calorimeter S1 | Calorimeter S2 | ||
|---|---|---|---|
| Parameters | Mean ± std | Mean ± std | Units |
| RC model | |||
| C0 | 2.31 ± 0.07 | 2.31 ± 0.07 | J/K |
| C1 | 4.02 ± 0.09 | 3.91 ± 0.09 | J/K |
| C2 | 3.8 ± 0.2 | 3.7 ± 0.3 | J/K |
| P1 | 0.029 ± 0.002 | 0.029 ± 0.002 | W/K |
| P2 | 0.057 ± 0.005 | 0.055 ± 0.005 | W/K |
| P12 | 0.092 ± 0.008 | 0.089 ± 0.009 | W/K |
| k | 23.7 ± 1.1 | 23.0 ± 1.4 | mV/K |
| Cooling system | |||
| α 1 | 13.6 | 17.4 | °C/A |
| β 1 | –83.5 | –83.8 | °C/A |
| T0 2 | 0.45 | 0.36 | °C |
| RMSE values | |||
| εy | 16.5 ± 2.5 | 16.2 ± 2.4 | µV |
| εT2 | 3.9 ± 2.0 | 3.8 ± 2.0 | mK |
| Troom | T1 | T01 | T2 | T02 | W1 | W10 | W12 | W2 | W20 |
|---|---|---|---|---|---|---|---|---|---|
| 20 | 28.448 | 23.59 | 28 | 15.820 | 0.18210 | 0.1409 | 0.0412 | 0.6531 | 0.6943 |
| 20 | 30.162 | 23.59 | 31 | 15.820 | 0.11353 | 0.1906 | −0.0771 | 0.9424 | 0.8653 |
| 20 | 31.876 | 23.59 | 34 | 15.820 | 0.04496 | 0.2404 | −0.1954 | 1.2317 | 1.0363 |
| 20 | 33.590 | 23.59 | 37 | 15.820 | −0.02362 | 0.2901 | −0.3137 | 1.5209 | 1.2072 |
| 24 | 29.168 | 27.59 | 28 | 19.820 | 0.15328 | 0.0458 | 0.1075 | 0.3588 | 0.4663 |
| 24 | 30.882 | 27.59 | 31 | 19.820 | 0.08471 | 0.0955 | −0.0108 | 0.6481 | 0.6373 |
| 24 | 32.597 | 27.59 | 34 | 19.820 | 0.01613 | 0.1452 | −0.1291 | 0.9374 | 0.8083 |
| 24 | 34.311 | 27.59 | 37 | 19.820 | −0.05243 | 0.1950 | −0.2474 | 1.2267 | 0.9793 |
| y/mV | T2/°C | T01/°C | Tcore/°C |
|---|---|---|---|
| 59.31 | 25.0 | 27.86 | 33.0 |
| 8.53 | 30.0 | 27.86 | 33.0 |
| –42.26 | 35.0 | 27.86 | 33.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez de Rivera, P.J.; Rodríguez de Rivera, M.; Socorro, F.; Rodríguez de Rivera, M. Modeling Skin Thermal Behavior with a Cutaneous Calorimeter: Local Parameters of Medical Interest. Modelling 2025, 6, 42. https://doi.org/10.3390/modelling6020042
Rodríguez de Rivera PJ, Rodríguez de Rivera M, Socorro F, Rodríguez de Rivera M. Modeling Skin Thermal Behavior with a Cutaneous Calorimeter: Local Parameters of Medical Interest. Modelling. 2025; 6(2):42. https://doi.org/10.3390/modelling6020042
Chicago/Turabian StyleRodríguez de Rivera, Pedro Jesús, Miriam Rodríguez de Rivera, Fabiola Socorro, and Manuel Rodríguez de Rivera. 2025. "Modeling Skin Thermal Behavior with a Cutaneous Calorimeter: Local Parameters of Medical Interest" Modelling 6, no. 2: 42. https://doi.org/10.3390/modelling6020042
APA StyleRodríguez de Rivera, P. J., Rodríguez de Rivera, M., Socorro, F., & Rodríguez de Rivera, M. (2025). Modeling Skin Thermal Behavior with a Cutaneous Calorimeter: Local Parameters of Medical Interest. Modelling, 6(2), 42. https://doi.org/10.3390/modelling6020042






