A Review of Dynamic Operating Envelopes: Computation, Applications and Challenges
Abstract
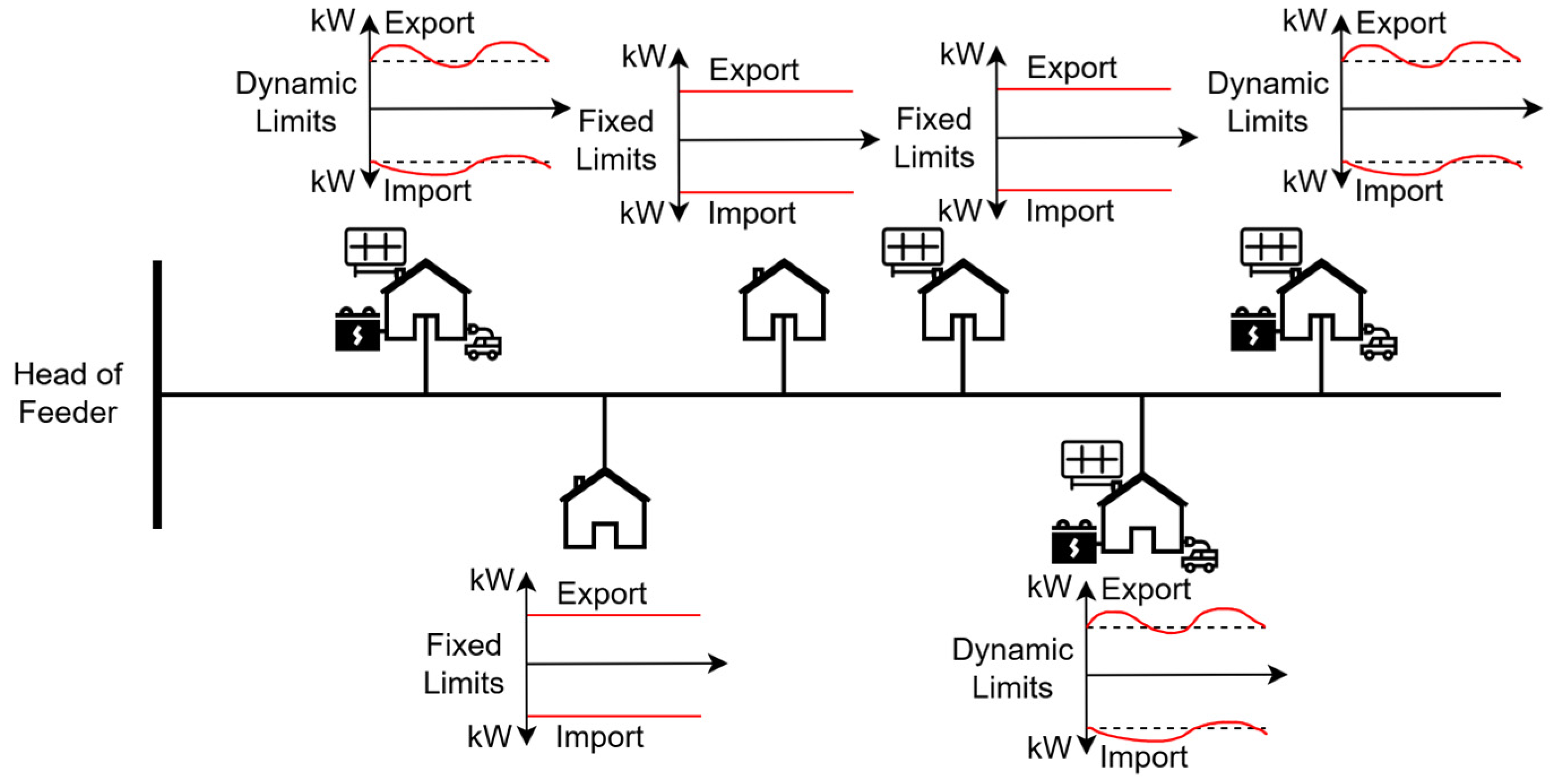
1. Introduction
1.1. Stakeholders Associated with Dynamic Operating Envelopes
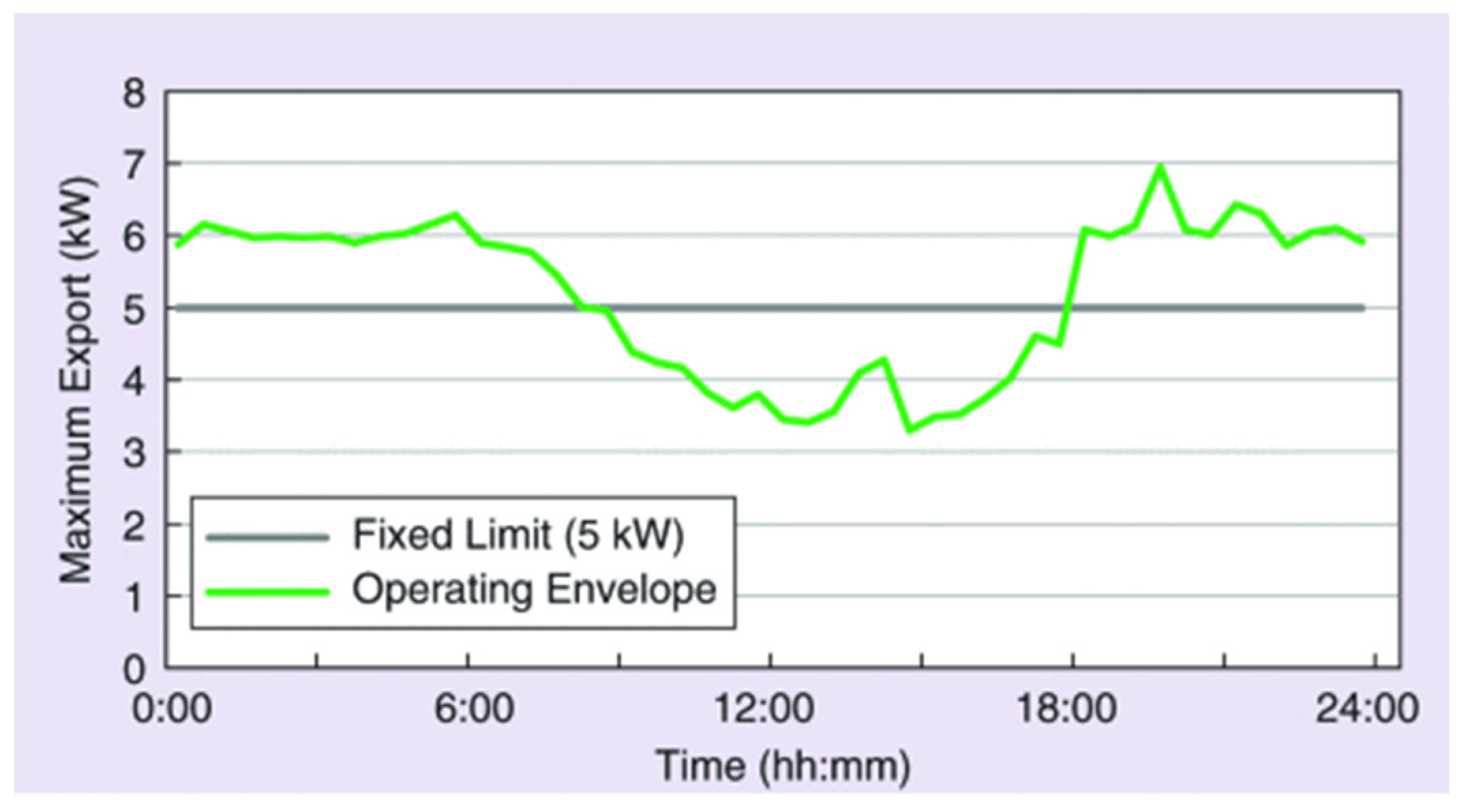
1.2. Maximum and Minimum Dynamic Limits
1.3. Temporal Resolution for Dynamic Operating Envelopes
2. DOE Calculation Methodologies
2.1. Model-Aware Dynamic Operating Envelopes
2.1.1. Iterative Approaches
2.1.2. Optimization Based Approaches
- Objective function
- Maximize DOE
- Fair Allocation Approaches
- 2.
- Constraints
- Voltage constraints
- Thermal constraints
- Line constraints
- Active Power Balance and reactive power balance
- Voltage unbalance constraint
2.2. Model Free Dynamic Operating Envelopes
2.2.1. Machine-Learning Based Approaches
2.2.2. Impedance Estimation Approaches
3. Utilization of Alternating Current (AC) OPF for DOE Calculation
Impact of Using Relaxations for DOE Calculation
4. Case Study
4.1. Network Model
4.2. Formulation of OPF
4.2.1. Objective Functions
4.2.2. Constraints
4.2.3. Comparison of Results
5. Issues Associated with DOE Calculations
5.1. Centralized DOE Calculations
5.2. Accurate Forecasts
5.3. Network Models Used for DOE Calculation
5.4. Uncertainties Associated with DOE Calculation
5.5. Data Privacy Issues
6. Application of Dynamic Operating Envelopes
6.1. Local Energy Markets and DOE
6.2. Demand Response Schemes and DOE
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOE | Dynamic Operating Envelopes |
| DER | Distributed Energy Resources |
| OPF | Optimal Power Flow |
| PV | Photo-Voltaic |
| BESS | Battery Energy Storage Systems |
| EV | Electric Vehicles |
| DSO | Distribution Service Operators |
| OLTC | On-Load Tap Changer |
| DNSP | Distribution Network Service Providers |
| EDGE | Energy Demand and Generation Exchange |
| EVOLVE | Project Energy Value Optimization Leveraging Envelopes |
| ARENA | Australian Renewable Energy Agency |
| ACOPF | Alternating Current Optimal Power Flow |
| AEMO | Australian Energy Market Operator |
| SOE | Static Operating Envelopes |
| NEM | National Electricity Market |
| DSSE | Distribution System State Estimation |
| VUF | Voltage Unbalance Factor |
| ML | Machine Learning |
| NN | Neural Networks |
| SOCP | Second-Order Cone Programming |
| MPC | Model Predictive Control |
| PCE | Polynomial Chaos Expansion |
| UTOPF | Unbalanced Three-Phase Optimal Power Flow |
| FR | Feasible Region |
| MTT | Motzkin Transposition Theorem |
| UTPF | Unbalanced Three-Phase Power Flow |
| IDS | Intrusion Detection Systems |
| ADMM | Alternating Direction Method of Multipliers |
| LEM | Local Energy Markets |
| P2P | Peer-to-Peer |
| CCG | Canonical Coalition Game |
| DR | Demand Response |
| AMI | Advanced Metering Infrastructure |
| LHS | Latin Hypercube Sampling |
References
- DEIP Dynamic Operating Envelopes Workstream. Available online: https://arena.gov.au/assets/2021/09/doe-workshop-summary.pdf (accessed on 21 March 2024).
- Haque, M.M.; Wolfs, P. A review of high PV penetrations in LV distribution networks: Present status, impacts and mitigation measures. Renew. Sustain. Energy Rev. 2016, 62, 1195–1208. [Google Scholar] [CrossRef]
- Chathurangi, D.; Jayatunga, U.; Perera, S.; Agalgaonkar, A.P.; Siyambalapitiya, T. Comparative evaluation of solar PV hosting capacity enhancement using Volt-VAr and Volt-Watt control strategies. Renew. Energy 2021, 177, 1063–1075. [Google Scholar] [CrossRef]
- Dynamic Standard for Small IES Connections. Available online: https://www.energex.com.au/__data/assets/pdf_file/0008/1072592/STNW3510-Dynamic-Standard-for-Small-IES-Connections.pdf (accessed on 5 June 2024).
- Bozalakov, D.; Mnati, M.J.; Laveyne, J.; Desmet, J.; Vandevelde, L. Battery Storage Integration in Voltage Unbalance and Overvoltage Mitigation Control Strategies and Its Impact on the Power Quality. Energies 2019, 12, 1501. [Google Scholar] [CrossRef]
- Alajrash, B.H.; Salem, M.; Swadi, M.; Senjyu, T.; Kamarol, M.; Motahhir, S. A comprehensive review of FACTS devices in modern power systems: Addressing power quality, optimal placement, and stability with renewable energy penetration. Energy Rep. 2024, 11, 5350–5371. [Google Scholar] [CrossRef]
- On the Calculation and Use of Dynamic Operating Envelopes. Available online: https://arena.gov.au/assets/2020/09/on-the-calculation-and-use-of-dynamic-operating-envelopes.pdf (accessed on 27 June 2024).
- Petrou, K.; Procopiou, A.T.; Gutierrez-Lagos, L.; Liu, M.Z.; Ochoa, L.F.; Langstaff, T.; Theunissen, J.M. Ensuring Distribution Network Integrity Using Dynamic Operating Limits for Prosumers. IEEE Trans. Smart Grid 2021, 12, 3877–3888. [Google Scholar] [CrossRef]
- Liu, M.Z.; Ochoa, L.N.; Riaz, S.; Mancarella, P.; Ting, T.; San, J.; Theunissen, J. Grid and Market Services from the Edge: Using Operating Envelopes to Unlock Network-Aware Bottom-Up Flexibility. IEEE Power Energy Mag. 2021, 19, 52–62. [Google Scholar] [CrossRef]
- Project EDGE (Energy Demand and Generation Exchange)—Australian Renewable Energy Agency (ARENA). Available online: https://arena.gov.au/projects/project-edge-energy-demand-and-generation-exchange/ (accessed on 28 January 2025).
- “Evolve—Battery Storage and Grid Integration Program”. Battery Storage and Grid Integration Program—An initiative of the Australian National University. Available online: https://bsgip.com/research/evolve/ (accessed on 2 March 2025).
- Home-Australian Renewable Energy Agency. Available online: https://arena.gov.au/ (accessed on 2 March 2025).
- Open Energy Networks Project-Energy Networks Australia Position Paper. Available online: https://www.energynetworks.com.au/resources/reports/2020-reports-and-publications/open-energy-networks-project-energy-networks-australia-position-paper/ (accessed on 7 September 2024).
- Energex-About Dynamic Connections. Available online: https://www.energex.com.au/our-services/connections/residential-and-commercial-connections/solar-connections-and-other-technologies/dynamic-connections-for-energy-exports/about-dynamic-connections (accessed on 17 May 2024).
- Accelerating the Implementation of Operating Envelopes Across Australia—Milestone 4: Final Report. Available online: https://www.csiro.au/-/media/EF/Files/GPST-Roadmap/Stage3-Final/Topic-8Distributed-Energy-Resources-DERs.pdf (accessed on 4 November 2024).
- NEM Data Dashboard. Available online: https://aemo.com.au/energy-systems/electricity/national-electricity-market-nem/data-nem/data-dashboard-nem (accessed on 2 March 2025).
- Assessing the Benefits of Using Operating Envelopes to Orchestrate DERs Across Australia. Available online: https://www.csiro.au/-/media/EF/Files/GPST-Roadmap/Final-Reports/Topic-8-GPST-Stage-2.pdf (accessed on 5 August 2024).
- Alam, M.R.; Nguyen, P.T.H.; Naranpanawe, L.; Saha, T.K.; Lankeshwara, G. Allocation of Dynamic Operating Envelopes in Distribution Networks: Technical and Equitable Perspectives. IEEE Trans. Sustain. Energy 2023, 15, 173–186. [Google Scholar] [CrossRef]
- Milford, T.; Krause, O. Managing DER in Distribution Networks Using State Estimation & Dynamic Operating Envelopes. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Brisbane, Australia, 5–8 December 2021. [Google Scholar]
- Liu, B.; Braslavsky, J.H. Sensitivity and Robustness Issues of Operating Envelopes in Unbalanced Distribution Networks. IEEE Access 2022, 10, 92789–92798. [Google Scholar] [CrossRef]
- Moring, H.; Mathieu, J.L. Inexactness of Second Order Cone Relaxations for Calculating Operating Envelopes. In Proceedings of the 2023 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Glasgow, UK, 31 October–3 November 2023. [Google Scholar]
- Yi, Y.; Verbič, G. Fair operating envelopes under uncertainty using chance constrained optimal power flow. Electr. Power Syst. Res. 2022, 213, 108465. [Google Scholar] [CrossRef]
- Lankeshwara, G. A Real-Time Control Approach to Maximise the Utilisation of Rooftop PV Using Dynamic Export Limits. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Brisbane, Australia, 5–8 December 2021. [Google Scholar]
- Decision Regulatory Impact Statement 2017. Available online: https://cabinet.qld.gov.au/documents/2017/Sep/Voltage/Attachments/DecisionRIS.PDF (accessed on 2 August 2024).
- A Gentle Introduction to Power Flow. Available online: https://invenia.github.io/blog/2020/12/04/pf-intro/ (accessed on 2 March 2025).
- Farivar, M.; Low, S.H. Branch Flow Model: Relaxations and Convexification—Part I. IEEE Trans. Power Syst. 2013, 28, 2554–2564. [Google Scholar] [CrossRef]
- Antić, T.; Geth, F.; Capuder, T. The Importance of Technical Distribution Network Limits in Dynamic Operating Envelopes. In Proceedings of the 2023 IEEE Belgrade PowerTech, Belgrade, Serbia, 25–29 June 2023. [Google Scholar]
- Bassi, V.; Ochoa, L.F.; Alpcan, T.; Leckie, C. Electrical Model-Free Voltage Calculations Using Neural Networks and Smart Meter Data. IEEE Trans. Smart Grid 2022, 14, 3271–3282. [Google Scholar] [CrossRef]
- Final Report: Model-Free Operating Envelopes. 2023. Available online: https://c4net.com.au/wp-content/uploads/2023/09/UoM-C4NET-Model-Free_OEs-FinalReport_v02.pdf (accessed on 2 May 2024).
- Kumarawadu, A.; Azim, M.I.; Khorasany, M.; Razzaghi, R.; Heidari, R. Smart meter data-driven dynamic operating envelopes for DERs. Appl. Energy 2025, 384, 125469. [Google Scholar]
- Carpentier, J.L. Optimal Power Flows: Uses, Methods and Developments. IFAC Proc. Vol. 1985, 18, 11–21. [Google Scholar] [CrossRef]
- Xia, X.; Elaiw, A.M. Optimal dynamic economic dispatch of generation: A review. Electr. Power Syst. Res. 2010, 80, 975–986. [Google Scholar] [CrossRef]
- Liu, M.Z.; Ochoa, L.F.; Wong, P.K.C.; Theunissen, J. Using OPF-Based Operating Envelopes to Facilitate Residential DER Services. IEEE Trans. Smart Grid 2022, 13, 4494–4504. [Google Scholar] [CrossRef]
- Lavaei, J.; Low, S.H. Zero Duality Gap in Optimal Power Flow Problem. IEEE Trans. Power Syst. 2011, 27, 92–107. [Google Scholar]
- Low, S.H. Convex Relaxation of Optimal Power Flow—Part I: Formulations and Equivalence. IEEE Trans. Control Netw. Syst. 2014, 1, 15–27. [Google Scholar] [CrossRef]
- Wang, L.; Yan, R.; Bai, F.; Saha, T.; Wang, K. A Distributed Inter-Phase Coordination Algorithm for Voltage Control with Unbalanced PV Integration in LV Systems. IEEE Trans. Sustain. Energy 2020, 11, 2687–2697. [Google Scholar] [CrossRef]
- Australian Photovoltaic Institute. Available online: https://pv-map.apvi.org.au/ (accessed on 17 December 2024).
- Flexible Exports. Available online: https://www.ausnetservices.com.au/flexible-exports (accessed on 17 May 2024).
- Review of Dynamic Operating Envelope Adoption by DNSPs. Available online: https://arena.gov.au/assets/2022/07/review-of-dynamic-operating-envelopes-from-dnsps.pdf (accessed on 15 November 2024).
- Project EDGE—Determining the Impact of Update Frequency on Operating Envelope Efficacy. Available online: https://aemo.com.au/initiatives/major-programs/nem-distributed-energy-resources-der-program/der-demonstrations/project-edge/project-edge-reports/dynamic-operating-envelopes (accessed on 25 September 2024).
- Lanas, F.; Liu, M.; Ochoa, L.F. Understanding the Role of Forecast Errors on the Effectiveness of Operating Envelopes. In Proceedings of the 2024 IEEE Power & Energy Society General Meeting (PESGM), Seattle, WA, USA, 21–25 July 2024. [Google Scholar]
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Hooshmand Pakdel, G.; He, Y.; Chen, X. Predicting customer demand with deep learning: An LSTM-based approach incorporating customer information. Int. J. Prod. Res. 2015, 1–13. [Google Scholar]
- Rodríguez, F.; Fleetwood, A.; Galarza, A.; Fontán, L. Predicting solar energy generation through artificial neural networks using weather forecasts for microgrid control. Renew. Energy 2018, 126, 855–864. [Google Scholar] [CrossRef]
- Cavus, M.; Allahham, A. Enhanced Microgrid Control through Genetic Predictive Control: Integrating Genetic Algorithms with Model Predictive Control for Improved Non-Linearity and Non-Convexity Handling. Energies 2024, 17, 4458. [Google Scholar] [CrossRef]
- Petrou, K.; Liu, M.Z.; Procopiou, A.T.; Ochoa, L.F.; Theunissen, J.; Harding, J. Operating Envelopes for Prosumers in LV Networks: A Weighted Proportional Fairness Approach. In Proceedings of the 2020 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), The Hague, The Netherlands, 26–28 October 2020. [Google Scholar]
- Koirala, A.; Geth, F.; Van Acker, T. Day-ahead dynamic operating envelopes using stochastic unbalanced optimal power flow. Sustainable Energy, Grids and Networks 2024, 40, 101528. [Google Scholar] [CrossRef]
- Liu, B.; Braslavsky, J.H.; Mahdavi, N. Linear OPF-Based Robust Dynamic Operating Envelopes with Uncertainties in Unbalanced Distribution Networks. J. Mod. Power Syst. Clean Energy 2023, 12, 1320–1326. [Google Scholar]
- Liu, B.; Braslavsky, J.H. Robust Dynamic Operating Envelopes for DER Integration in Unbalanced Distribution Networks. IEEE Trans. Power Syst. 2023, 39, 3921–3936. [Google Scholar] [CrossRef]
- Liu, B.; Braslavsky, J.H. Robust Dynamic Operating Envelopes via Superellipsoid-Based Convex Optimisation in Unbalanced Distribution Networks. IEEE Trans. Power Syst. 2024, 39, 4775–4778. [Google Scholar]
- Liu, B.; Braslavsky, J.H. Computation of robust dynamic operating envelopes based on non-convex OPF for unbalanced distribution networks. CSEE J. Power Energy Syst. 2024; early access. [Google Scholar]
- Diaba, S.Y.; Shafie-Khah, M.; Elmusrati, M. Cyber-physical attack and the future energy systems: A review. Energy Rep. 2024, 12, 2914–2932. [Google Scholar] [CrossRef]
- Implementing Certificates, TLS, HTTPS and Opportunistic TLS. Available online: https://www.cyber.gov.au/sites/default/files/2023-03/PROTECT%20-%20Implementing%20Certificates%2C%20TLS%2C%20HTTPS%20and%20Opportunistic%20TLS%20%28October%202021%29.pdf (accessed on 20 March 2025).
- Anomaly Detection in Intrusion Detection Systems. Available online: https://www.intechopen.com/chapters/88343 (accessed on 20 March 2025).
- What Is Blockchain? Available online: https://www.ibm.com/think/topics/blockchain#:~:text=Blockchain%20is%20a%20shared%2C%20immutable,patents%2C%20copyrights%2C%20branding) (accessed on 20 March 2025).
- Azim, M.I.; Lankeshwara, G.; Tushar, W.; Sharma, R.; Alam, M.R.; Saha, T.K.; Khorasany, M.; Razzaghi, R. Dynamic Operating Envelope-Enabled P2P Trading to Maximize Financial Returns of Prosumers. IEEE Trans. Smart Grid 2024, 15, 1978–1990. [Google Scholar] [CrossRef]
- Dyda, A.; Purcell, M.; Curtis, S.; Field, E.; Pillai, P.; Ricardo, K.; Weng, H.; Moore, J.C.; Hewett, M.; Williams, G.; et al. Differential privacy for public health data: An innovative tool to optimize information sharing while protecting data confidentiality. Patterns 2021, 2, 100366. [Google Scholar]
- Lankeshwara, G.; Sharma, R. Dynamic Operating Envelopes-enabled Demand Response in Low-voltage Residential Networks. In Proceedings of the 2022 IEEE PES 14th Asia-Pacific Power and Energy Engineering Conference (APPEEC), Melbourne, Australia, 20–23 November 2022. [Google Scholar]
- Dudjak, V.; Neves, D.; Alskaif, T.; Khadem, S.; Pena-Bello, A.; Saggese, P.; Bowler, B.; Andoni, M.; Bertolini, M.; Zhou, Y.; et al. Impact of local energy markets integration in power systems layer: A comprehensive review. Appl. Energy 2021, 301, 117434. [Google Scholar] [CrossRef]
- Capper, T.; Gorbatcheva, A.; Mustafa, M.A.; Bahloul, M.; Schwidtal, J.M.; Chitchyan, R.; Andoni, M.; Robu, V.; Montakhabi, M.; Scott, I.J.; et al. Peer-to-peer, community self-consumption, and transactive energy: A systematic literature review of local energy market models. Renew. Sustain. Energy Rev. 2022, 162, 112403. [Google Scholar] [CrossRef]
- Jogunola, O.; Ajagun, A.S.; Tushar, W.; Olatunji, F.O.; Yuen, C.; Morley, C.; Adebisi, B.; Shongwe, T. Peer-to-Peer Local Energy Market: Opportunities, Barriers, Security, and Implementation Options. IEEE Access 2024, 12, 37873–37890. [Google Scholar] [CrossRef]
- Hoque, M.M.; Khorasany, M.; Azim, M.I.; Razzaghi, R.; Jalili, M. Dynamic Operating Envelope-Based Local Energy Market for Prosumers with Electric Vehicles. IEEE Trans. Smart Grid 2023, 15, 1712–1724. [Google Scholar] [CrossRef]
- Hoque, M.M.; Khorasany, M.; Azim, M.I.; Razzaghi, R.; Jalili, M. A framework for prosumer-centric peer-to-peer energy trading using network-secure export–import limits. Appl. Energy 2024, 361, 122906. [Google Scholar] [CrossRef]
- Azim, M.I.; Hoque, M.M.; Khorasany, M.; Razzaghi, R.; Jalili, M.; Hill, D.J. Dynamic Operating Envelope-Integrated Cooperative Energy Trading: A Fair Allocation Approach. IEEE Trans. Power Syst. 2024; early access. [Google Scholar]
- Lankeshwara, G.; Sharma, R.; Alam, M.R.; Yan, R.; Saha, T.K. Development and validation of a dynamic operating envelopes-enabled demand response scheme in low-voltage distribution networks. Appl. Energy 2025, 382, 125150. [Google Scholar] [CrossRef]
- Lankeshwara, G.; Sharma, R.; Yan, R.; Saha, T.K.; Milanović, J.V. Time-Varying Operating Regions of End-Users and Feeders in Low-Voltage Distribution Networks. IEEE Trans. Power Syst. 2023, 39, 4600–4611. [Google Scholar] [CrossRef]








| References | Objective Function |
|---|---|
| [21,22] | Maximise the smallest DOE |
| [23] | Minimize the squared difference between the calculated DOE and the forecasted PV generation |
| [8] | Maximize the multiplication between the customer inverter capacity and logarithmic value of the calculated DOE |
| Australian LV Standard | Voltage |
|---|---|
| Nominal Voltage | 230 V |
| Upper Limit (+10%) | 253 V |
| Lower Limit (−6%) | 216 V |
| Objective Function | Export Envelopes | Voltage Limits | Total Exports (MW) |
|---|---|---|---|
| (3a) | 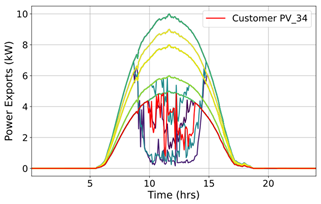 |  | 20.398 |
| (3b) | 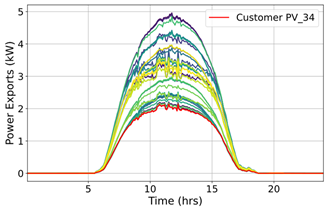 | 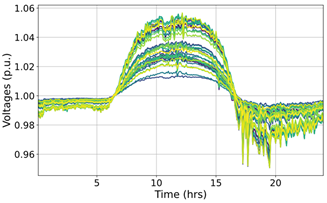 | 10.091 |
| (3c) |  | 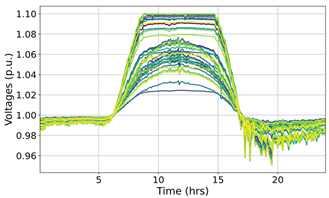 | 19.970 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wickramasinghe, A.; Vilathgamuwa, M.; Nourbakhsh, G.; Corry, P. A Review of Dynamic Operating Envelopes: Computation, Applications and Challenges. Modelling 2025, 6, 29. https://doi.org/10.3390/modelling6020029
Wickramasinghe A, Vilathgamuwa M, Nourbakhsh G, Corry P. A Review of Dynamic Operating Envelopes: Computation, Applications and Challenges. Modelling. 2025; 6(2):29. https://doi.org/10.3390/modelling6020029
Chicago/Turabian StyleWickramasinghe, Anjala, Mahinda Vilathgamuwa, Ghavameddin Nourbakhsh, and Paul Corry. 2025. "A Review of Dynamic Operating Envelopes: Computation, Applications and Challenges" Modelling 6, no. 2: 29. https://doi.org/10.3390/modelling6020029
APA StyleWickramasinghe, A., Vilathgamuwa, M., Nourbakhsh, G., & Corry, P. (2025). A Review of Dynamic Operating Envelopes: Computation, Applications and Challenges. Modelling, 6(2), 29. https://doi.org/10.3390/modelling6020029






