Recent Trends in Proxy Model Development for Well Placement Optimization Employing Machine Learning Techniques
Abstract
:1. Introduction
1.1. Well Placement Optimization Problem Formulation
- Geological information (porosity, permeability, dimensions);
- PVT data (formation volume factors and fluid properties such as viscosity, density, compressibility);
- Existing wells and their types (producers/injectors, vertical/horizontal, gas/water injectors) and locations;
- Well control parameters (maximum injection rates for injectors, minimum bottom-hole pressures for producers);
- Operational constraints (well spacing, geological limitations—e.g., faults, barriers)
- Maximize the objective function (NPV, oil recovery, CO2 storage potential).
- Optimal location of the new production/injection wells;
- The commonly used objective function is the net present value for the optimization problem. Ref. [3] provided a simple mathematical formulation of NPV for a two-phase flow reservoir model as:
1.2. Well Placement Optimization Workflow
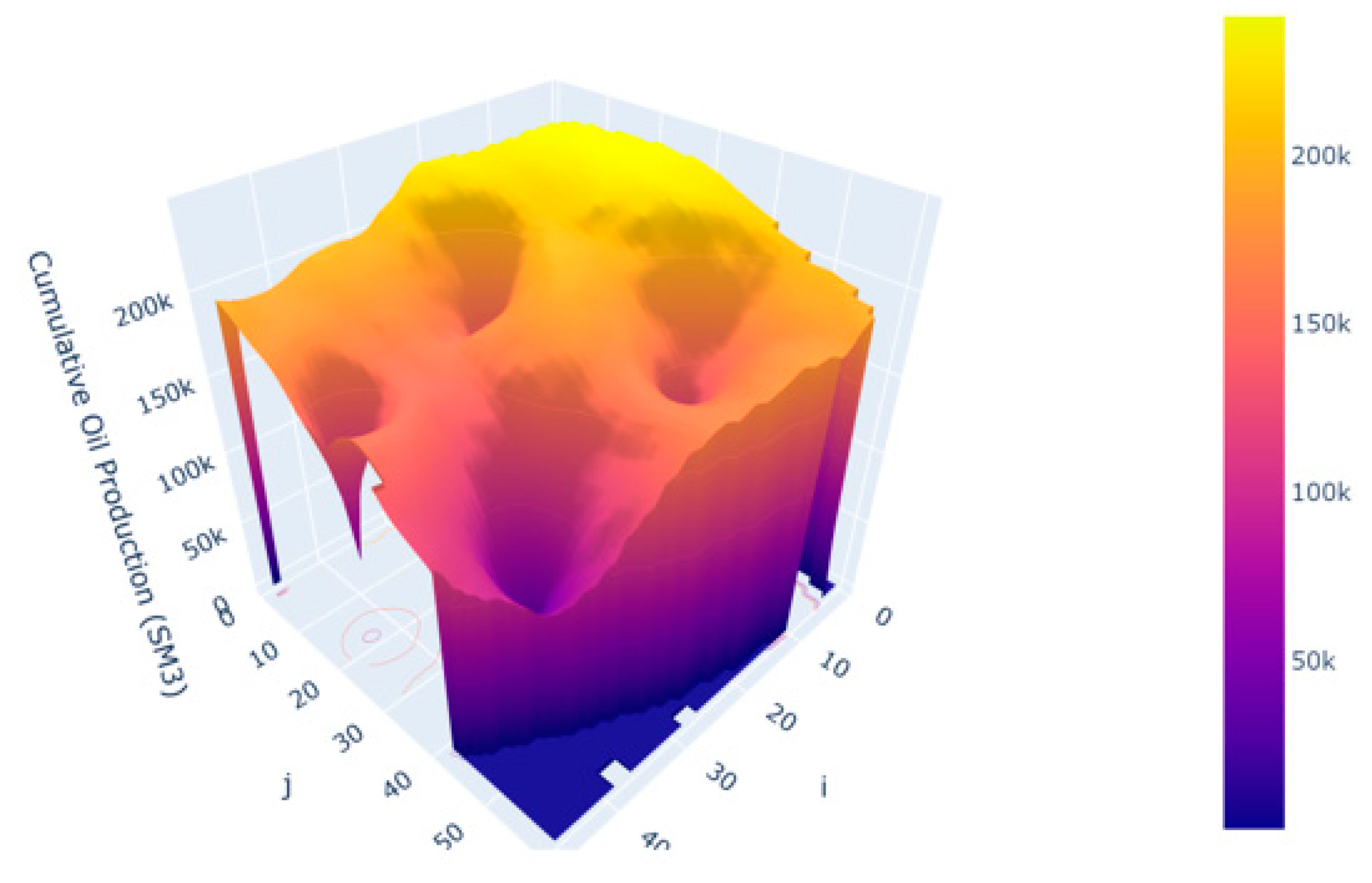
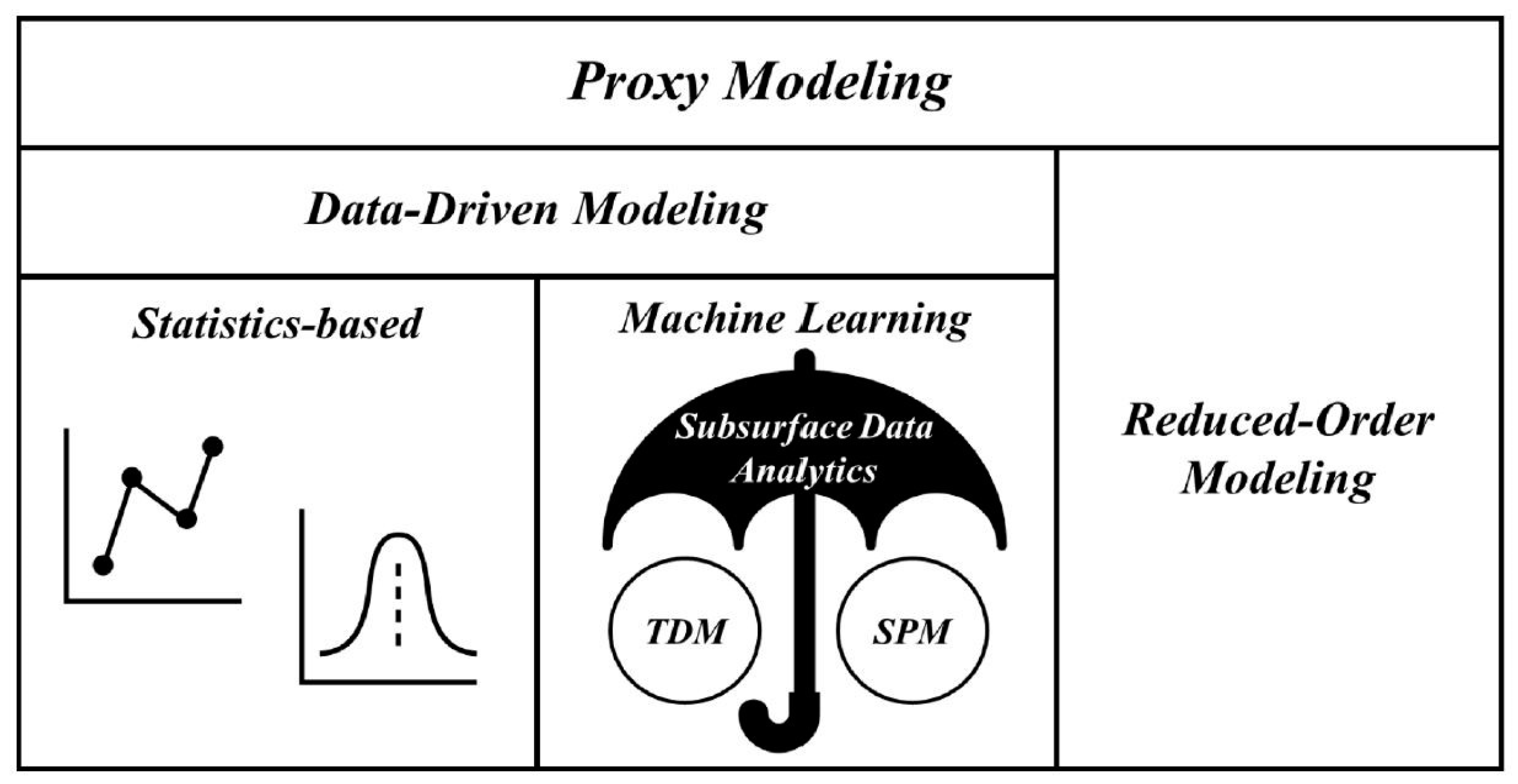
2. Summary of Proxy Models Development
3. Applications of Proxy Models for Well Placement Optimization
3.1. Data-Driven Proxy Models
3.1.1. Mathematical/Statistical-Based Models
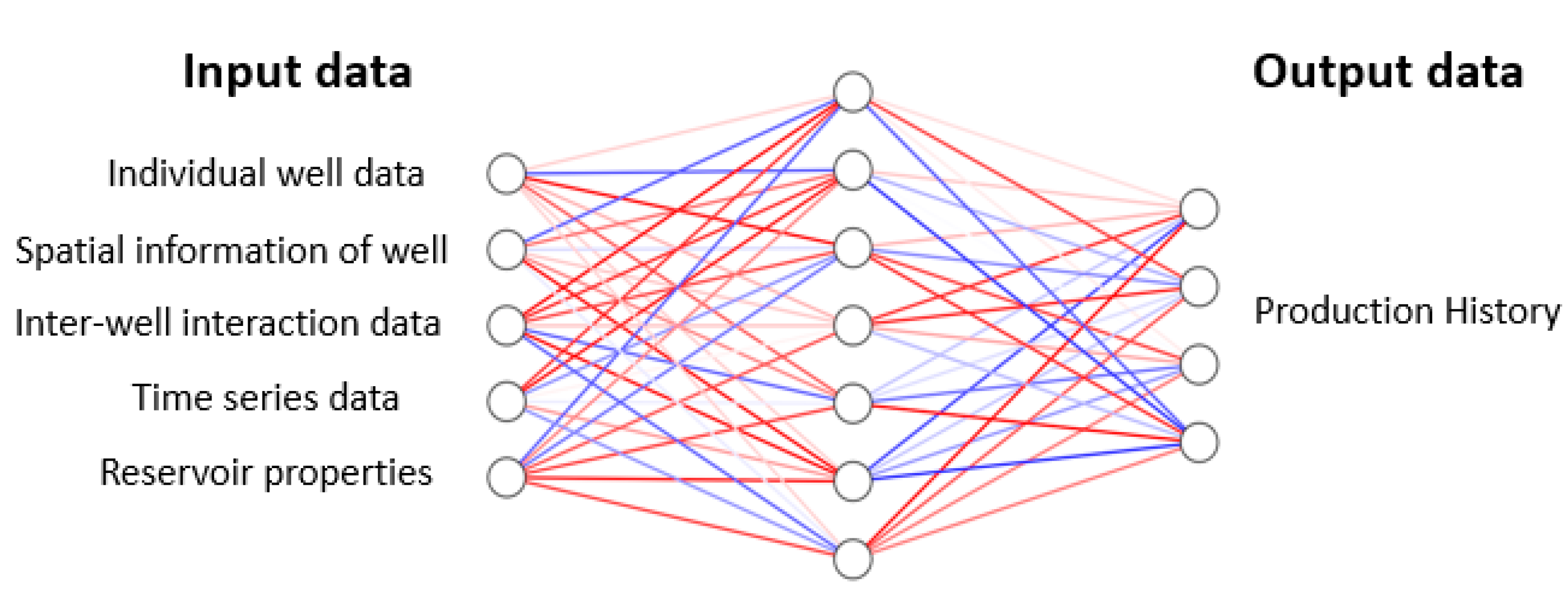
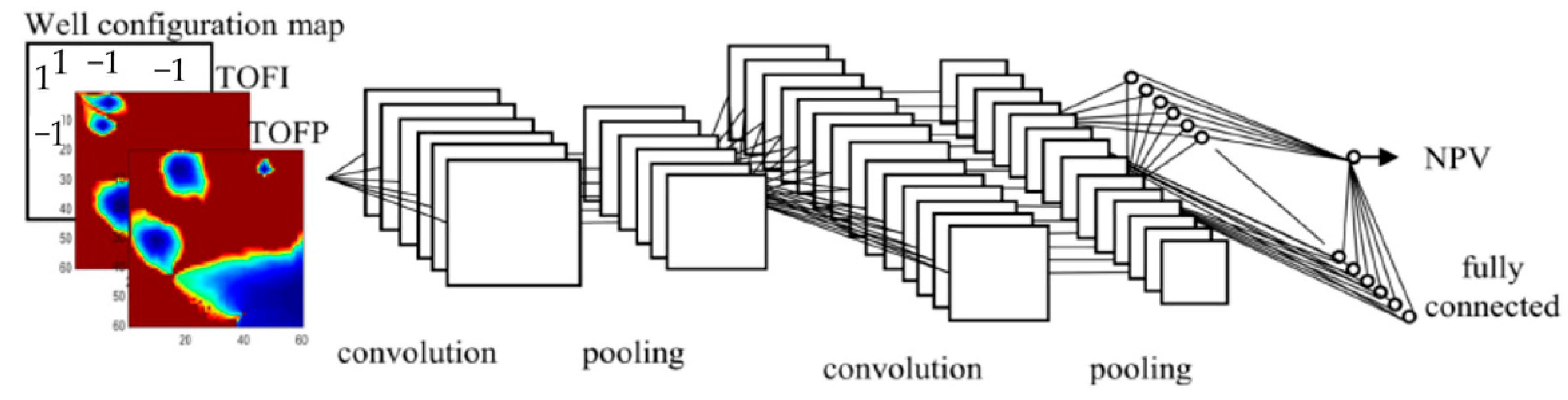
3.1.2. Machine Learning Proxy Models
Neural Networks
| Literature | Method | Objective | Findings |
|---|---|---|---|
| [37] | Artificial neural network | Optimization of CO2 injection and brine production well placement in geological CO2 storage using artificial neural networks to reduce the simulation runs | ANN was coupled with genetic algorithm to optimize the well locations. Total number of runs were reduced by 80.7% from 622 to 120. |
| [5] | V-Net NN | V-Net NN with GA for well placement optimization | Physics-guided V-Net with skip connections, 3D convolutional filters, and a residual learning structure to handle 3D parameter fields results in 30 times faster processing. |
| [41] | Artificial neural network | Application of artifical neural networks trained in time-dependent manner to optimize well placement | Efficient dynamic, time dependent proxy with genetic algorithm comparable with commercial reservoir simulation |
| [30] | Convolutional neural network | Combination of theory guided convolutional neural network with genetic algorithm | Theory-guided neural network framework achieved better accuracy compared to purely data-driven models, even with limited training data. Time was also reduced from 142,595 s (simulation) to 133 s (proxy). |
| [42] | SimProxy | Simproxy to integrate reservoir and surface behavior to reduce computational cost in well placement optimization | Multilayer perceptron (MLP) was used to develop the NN-based proxy. Training samples obtained with principal component analysis (PCA) and Latin hypercube sampling (LHS) showed best results. Some drawbacks as the number of wells grows. |
| [36] | Artificial neural network | Combination of ANN with a covariance matrix adaptation evolution strategy (CMA-ES) | The ANN provides the average NPV and standard deviation of the NPV of an ensemble of geological realization for a given well configuration |
| [43] | LSTM | Well placement and well control optimization with multiple development objectives using LSTM surrogate model | Computational time was reduced by 82% and 95% in the 2D and 3D models, respectively. However, geological uncertainty was not considered. |
| [44] | Graph Neural Surrogate Model (GNSM) | Optimize well placement and well control using GNSM | Demonstrated high accuracy with relative errors of 1–2% for pressure and saturation. The model provided 5–7% median errors for well rates prediction. Longer training time (30 h) is one of the major limitations. The model was only designed for a 2D unstructured reservoir model. |
Autoencoders (AEs)
3.2. Reduced Order Models
4. Future Work: Challenges and Directions
5. Conclusions
- Data-driven models, such as machine learning-based techniques, transform complex nonlinear reservoir simulation problems into simpler linear representation and provide quick and efficient approximations of the objective functions. Current ML-based models have shown promising results by predicting objective functions for various well placement scenarios, featuring above 90% accuracy in many cases.
- Data-driven models do not incorporate the underlying physical principles and theories governing subsurface flow processes, which limits their performance in terms of fully capturing complex reservoir behavior.
- Recently, neural network-based proxy models have gained significant importance and have shown potential for future use in well placement optimization problems due to their capabilities of capturing the nonlinearity and complexities involved in the WPO problem.
- Reduced order models use proper orthogonal decomposition (POD) to reduce dimensionality, capturing solutions in a lower-dimensional sub-space, and, while effective in continuous problems like well control optimization, they are less applicable to the well placement optimization problem due to its highly nonlinear and discrete nature.
- Possible future trends in proxy model development for well placement include physics-informed neural networks (PINNs) for incorporating physical principles, recurrent neural networks (RNNs) for capturing temporal dynamics and Fourier Neural Operators (FNO) for dynamical system learning.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AE | Autoencoder |
| ANN | Artificial neural network |
| CMA-ES | Covariance matrix adaptation evolution |
| CNN | Convolutional neural network |
| CRM | Capacitance–resistance model |
| FNN | Feedforward neural network |
| FNO | Fourier neural operator |
| GA | Genetic algorithm |
| LHS | Latin hypercube sampling |
| LSTM | Long short-term memory |
| MLP | Multilayer perceptron |
| NN | Neural network |
| NPV | Net present value |
| PCA | Principal component analysis |
| PMOR | Parametric model order reduction |
| POD | Proper orthogonal decomposition |
| PSO | Particle swarm optimization |
| RNN | Recurrent neural network |
| ROM | Reduced order model |
| RSMs | Response surface models |
| SPE10 | Society of Petroleum Engineers—10th Comparative Solution Project |
| SPMs | Smart proxy models |
| SVM | Support vector machine |
| TPMs | Traditional proxy models |
| TPWL | Trajectory piecewise linearization |
| WPO | Well placement optimization |
| XGBoost | Extreme gradient-boosting |
References
- Thakur, G.C. Distinguished Author Series What Is Reservoir Management? J. Pet. Technol. 1996, 48, 520–525. [Google Scholar] [CrossRef]
- Ng, C.S.W.; Nait Amar, M.; Jahanbani Ghahfarokhi, A.; Imsland, L.S. A Survey on the Application of Machine Learning and Metaheuristic Algorithms for Intelligent Proxy Modeling in Reservoir Simulation. Comput. Chem. Eng. 2023, 170, 108107. [Google Scholar] [CrossRef]
- Islam, J.; Vasant, P.M.; Negash, B.M.; Laruccia, M.B.; Myint, M.; Watada, J. A Holistic Review on Artificial Intelligence Techniques for Well Placement Optimization Problem. Adv. Eng. Softw. 2020, 141, 102767. [Google Scholar] [CrossRef]
- Kim, J.; Yang, H.; Choe, J. Robust Optimization of the Locations and Types of Multiple Wells Using CNN Based Proxy Models. J. Pet. Sci. Eng. 2020, 193, 107424. [Google Scholar] [CrossRef]
- Xu, R. Physics-Guided V-Net: An Efficient Surrogate Model for Well Placement Optimization in Petroleum Reservoirs. SPE J. 2024, 29, 21–34. [Google Scholar] [CrossRef]
- Kani, J.N.; Elsheikh, A.H. Reduced Order Modeling of Subsurface Multiphase Flow Models Using Deep Residual Recurrent Neural Networks. Transp. Porous Media 2018, 126, 713–741. [Google Scholar] [CrossRef]
- Kim, Y.D.; Durlofsky, L.J. Convolutional-Recurrent Neural Network Proxy for Robust Optimization and Closed-Loop Reservoir Management. Comput. Geosci. 2022, 27, 179–202. [Google Scholar] [CrossRef]
- Tavallali, M.S.; Karimi, I.A.; Teo, K.M.; Baxendale, D.; Ayatollahi, S. Optimal Producer Well Placement and Production Planning in an Oil Reservoir. Comput. Chem. Eng. 2013, 55, 109–125. [Google Scholar] [CrossRef]
- Tavallali, M.S.; Karimi, I.A. Integrated Oil-Field Management: From Well Placement and Planning to Production Scheduling. Ind. Eng. Chem. Res. 2016, 55, 978–994. [Google Scholar] [CrossRef]
- Alqahtani, G.; Vadapalli, R.; Siddiqui, S. Well Optimization Strategies in Conventional Reservoirs. In Proceedings of the SPE Saudi Arabia Section Technical Symposium and Exhibition, Al-Khobar, Saudi Arabia, 8–11 April 2012. [Google Scholar]
- Sarma, P.; Chen, W.H. SPE 112257. Efficient Well Placement Optimization with Gradient-Based Algorithms and Adjoint Models. In Proceedings of the Intelligent Energy Conference and Exhibition, Amsterdam, The Netherlands, 25–27 February 2008. [Google Scholar]
- Zhang, L.; Zhang, K.; Chen, Y.; Li, M.; Yao, J.; Li, L.; Lee, J. Smart Well Pattern Optimization Using Gradient Algorithm. J. Energy Resour. Technol. Trans. ASME 2016, 138, 012901. [Google Scholar] [CrossRef]
- Onwunalu, J.E. Optimization of Field Development Using Particle Swarm Optimization and New Well Pattern Descriptions. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2010. [Google Scholar]
- Guyaguler, B. Optimization of Well Placement. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2000. [Google Scholar]
- Guyaguler, B. Optimisation of Well Placement and Assessment of Uncertainty. Ph.D. Thesis, Department of Petroleum Engineering, Standford University, Stanford, CA, USA, 2002. [Google Scholar]
- Cristiano Stabile, C.; Barbiero, M.; Fighera, G.; Dovera, L. SPE-207233-MS. Robust Well Placement Optimization Through Universal Trace Kriging with Adaptive Sampling. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 15–18 November 2021. [Google Scholar]
- Zubarev, D.I. SPE 124815. Pros and Cons of Applying Proxy-Models as a Substitute for Full Reservoir Simulations. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar]
- AlQahtani, G.; Alzahabi, A.; Kozyreff, E.; Farias, I.R.d., Jr.; Soliman, M. A Comparison between Evolutionary Metaheuristics and Mathematical Optimization to Solve the Wells Placement Problem. Adv. Chem. Eng. Sci. 2013, 3, 38550. [Google Scholar] [CrossRef]
- Bahrami, P.; Sahari Moghaddam, F.; James, L.A. A Review of Proxy Modeling Highlighting Applications for Reservoir Engineering. Energies 2022, 15, 5247. [Google Scholar] [CrossRef]
- Amini, S.; Mohaghegh, S. Application of Machine Learning and Artificial Intelligence in Proxy Modeling for Fluid Flow in Porous Media. Fluids 2019, 4, 126. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K. Optimization of Multiple Hydraulically Fractured Horizontal Wells in Unconventional Gas Reservoirs. In Proceedings of the SPE Production and Operations Symposium, Oklahoma City, OK, USA, 23–26 March 2013. [Google Scholar]
- Arouri, Y.; Echeverría Ciaurri, D.; Sayyafzadeh, M. A Study of Simulation-Based Surrogates in Well-Placement Optimization for Hydrocarbon Production. J. Pet. Sci. Eng. 2022, 216, 110639. [Google Scholar] [CrossRef]
- Kleijnen, J.P.C. Kriging Metamodeling in Simulation: A Review. Eur. J. Oper. Res. 2009, 192, 707–716. [Google Scholar] [CrossRef]
- Badru, O.; Kabir, C.S. Well Placement Optimization in Field Development. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003. [Google Scholar]
- Khademi, G.; Karimaghaee, P. Hybrid FDG Optimization Method and Kriging Interpolator to Optimize Well Locations. J. Pet. Explor. Prod. Technol. 2016, 6, 191–200. [Google Scholar] [CrossRef]
- Gladchenko, E.S.; Gubanova, A.E.; Orlov, D.M.; Koroteev, D.A. Kriging-Boosted CR Modeling for Prompt Infill Drilling Optimization. Petroleum 2024, 10, 39–48. [Google Scholar] [CrossRef]
- Du, X.; Salasakar, S.; Thakur, G. A Comprehensive Summary of the Application of Machine Learning Techniques for CO2-Enhanced Oil Recovery Projects. Mach. Learn. Knowl. Extr. 2024, 6, 917–943. [Google Scholar] [CrossRef]
- Mousavi, S.M. Optimal Well Placement Using Machine Learning Methods: Multiple Reservoir Scenarios. In Proceedings of the SPE Norway Subsurface Conference, Virtual, 2–3 November 2020. [Google Scholar]
- Alpak, F.O.; Jain, V. Support-Vector Regression Accelerated Well Location Optimization: Algorithm, Validation, and Field Testing. Comput. Geosci. 2021, 25, 2033–2054. [Google Scholar] [CrossRef]
- Wang, N.; Chang, H.; Zhang, D.; Xue, L.; Chen, Y. Efficient Well Placement Optimization Based on Theory-Guided Convolutional Neural Network. J. Pet. Sci. Eng. 2022, 208, 109545. [Google Scholar] [CrossRef]
- Fraces, C.G.; Tchelepi, H. SPE-203934-MS. Physics Informed Deep Learning for Flow and Transport in Porous Media. In Proceedings of the SPE Reservoir Simulation Conference, Online, 26 October 2021. [Google Scholar]
- Han, J.X.; Xue, L.; Wei, Y.S.; Qi, Y.D.; Wang, J.L.; Liu, Y.T.; Zhang, Y.Q. Physics-Informed Neural Network-Based Petroleum Reservoir Simulation with Sparse Data Using Domain Decomposition. Pet. Sci. 2023, 20, 3450–3460. [Google Scholar] [CrossRef]
- Mohaghegh, S.D. Smart Proxy Modeling; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Sampaio, T.P.; Ferreira Filho, V.J.M.; De, A. SPE 122148. An Application of Feed Forward Neural Network as Nonlinear Proxies for the Use During the History Matching Phase. In Proceedings of the Latin American and Caribbean Petroleum Engineering Conference, Cartagena de Indias, Colombia, 31 May–30 June 2009. [Google Scholar]
- Kida, M.M.; Sarkinbaka, Z.M.; Abubakar, A.M.; Abdul, A.Z. Neural Network Based Performance Evaluation of a Waterflooded Oil Reservoir. Int. J. Recent Eng. Sci. 2021, 8, 1–6. [Google Scholar] [CrossRef]
- Bruyelle, J.; Guérillot, D. SPE-198656-MS. Well Placement Optimization with an Artificial Intelligence Method Applied to Brugge Field. In Proceedings of the SPE Gas & Oil Technology Showcase and Conference, Dubai, United Arab Emirates, 21–23 October 2019. [Google Scholar]
- Musayev, K.; Shin, H.; Nguyen-Le, V. Optimization of CO2 Injection and Brine Production Well Placement Using a Genetic Algorithm and Artificial Neural Network-Based Proxy Model. Int. J. Greenh. Gas Control. 2023, 127, 103915. [Google Scholar] [CrossRef]
- Min, B.H.; Park, C.; Kang, J.M.; Park, H.J.; Jang, I.S. Optimal Well Placement Based on Artificial Neural Network Incorporating the Productivity Potential. Energy Sources Part A Recovery Util. Environ. Eff. 2011, 33, 1726–1738. [Google Scholar] [CrossRef]
- Pennel, M.; Hsiung, J. SPE-190090-MS. Detecting Failures and Optimizing Performance in Artificial Lift Using Machine Learning Models. In Proceedings of the SPE Western Regional Meeting, Garden Grove, CA, USA, 22–26 April 2018. [Google Scholar]
- Chu, M.g.; Min, B.; Kwon, S.; Park, G.; Kim, S.; Huy, N.X. Determination of an Infill Well Placement Using a Data-Driven Multi-Modal Convolutional Neural Network. J. Pet. Sci. Eng. 2020, 195, 106805. [Google Scholar] [CrossRef]
- Kolajoobi, R.A.; Niri, M.E.; Amini, S.; Haghshenas, Y. A Data-Driven Proxy Modeling Approach Adapted to Well Placement Optimization Problem. J. Energy Resour. Technol. Trans. ASME 2023, 145, 013401. [Google Scholar] [CrossRef]
- Kohler, M.; Vellasco, M.; Silva, E.; Figueiredo, K. SimProxy Decision Support System: A Neural Network Proxy Applied to Reservoir and Surface Integrated Optimization. IEEE Syst. J. 2020, 14, 5111–5120. [Google Scholar] [CrossRef]
- Zhuang, X.; Wang, W.; Su, Y.; Yan, B.; Li, Y.; Li, L.; Hao, Y. Multi-Objective Optimization of Reservoir Development Strategy with Hybrid Artificial Intelligence Method. Expert. Syst. Appl. 2024, 241, 122707. [Google Scholar] [CrossRef]
- Tang, H.; Durlofsky, L.J. Graph Network Surrogate Model for Subsurface Flow Optimization. J. Comput. Phys. 2024, 512, 113132. [Google Scholar] [CrossRef]
- Chen, S.; Guo, W. Auto-Encoders in Deep Learning—A Review with New Perspectives. Mathematics 2023, 11, 1777. [Google Scholar] [CrossRef]
- Mendez, M.A. Linear and Nonlinear Dimensionality Reduction from Fluid Mechanics to Machine Learning. Meas. Sci. Technol. 2023, 34, 042001. [Google Scholar] [CrossRef]
- Qi, J.; Liu, Y.; Ju, Y.; Zhang, K.; Liu, L.; Liu, Y.; Xue, X.; Zhang, L.; Zhang, H.; Wang, H.; et al. A Transfer Learning Framework for Well Placement Optimization Based on Denoising Autoencoder. Geoenergy Sci. Eng. 2023, 222, 211446. [Google Scholar] [CrossRef]
- Illarionov, E.; Temirchev, P.; Voloskov, D.; Gubanova, A.; Koroteev, D. SPE-201924-MS. 3D Reservoir Model History Matching Based on Machine Learning Technology. In Proceedings of the SPE Russian Petroleum Technology Conference, Virtual, 26–29 October 2020. [Google Scholar]
- Temirchev, P.; Gubanova, A.; Kostoev, R.; Gryzlov, A.; Voloskov, D.; Koroteev, D.; Simonov, M.; Akhmetov, A.; Margarit, A.; Ershov, A. SPE-196864-MS. Reduced Order Reservoir Simulation with Neural-Network Based Hybrid Model. In Proceedings of the SPE Russian Petroleum Technology Conference, Moscow, Russia, 22–24 October 2019. [Google Scholar]
- Navrátil, J.; King, A.; Rios, J.; Kollias, G.; Torrado, R.; Codas, A. Accelerating Physics-Based Simulations Using End-to-End Neural Network Proxies: An Application in Oil Reservoir Modeling. Front. Big Data 2019, 2, 471450. [Google Scholar] [CrossRef] [PubMed]
- Jansen, J.D.; Durlofsky, L.J. Use of Reduced-Order Models in Well Control Optimization. Optim. Eng. 2017, 18, 105–132. [Google Scholar] [CrossRef]
- Doren, J.F.M.; Markovinović, R.; Jansen, J.D. Reduced-Order Optimal Control of Water Flooding Using Proper Orthogonal Decomposition. Comput. Geosci. 2006, 10, 137–158. [Google Scholar] [CrossRef]
- Astrid, P.; Papaioannou, G.; Vink, J.; Jansen, J. SPE 141922. Pressure Preconditioning Using Proper Orthogonal Decomposition. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 21–23 February 2011. [Google Scholar]
- Cardoso, M.A.; Durlofsky, L.J.; Sarma, P. Development and Application of Reduced-Order Modeling Procedures for Subsurface Flow Simulation. Int. J. Numer. Methods Eng. 2009, 77, 1322–1350. [Google Scholar] [CrossRef]
- Yang, Y.; Ghasemi, M.; Gildin, E.; Efendiev, Y.; Calo, V. Fast Multiscale Reservoir Simulations with POD-DEIM Model Reduction. SPE J. 2016, 21, 2141–2154. [Google Scholar] [CrossRef]
- Heijn, T.; Markovinovic, R.; Jansen, J. Generation of Low-Order Reservoir Models Using System-Theoretical Concepts. SPE J. 2004, 9, 202–218. [Google Scholar] [CrossRef]
- Krogstad, S. A Sparse Basis POD for Model Reduction of Multiphase Compressible Flow. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 21–23 February 2011. [Google Scholar]
- Markovinović, R.; Jansen, J.D. Accelerating Iterative Solution Methods Using Reduced-Order Models as Solution Predictors. Int. J. Numer. Methods Eng. 2006, 68, 525–541. [Google Scholar] [CrossRef]
- Vermeulen, P.T.M.; Heemink, A.W.; Te Stroet, C.B.M. Reduced Models for Linear Groundwater Flow Models Using Empirical Orthogonal Functions. Adv. Water Resour. 2004, 27, 57–69. [Google Scholar] [CrossRef]
- Zalavadia, H.A. Parametric Model Order Reduction for Optimization in Closed Loop Field Development Using Machine Learning Techniques. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2019. [Google Scholar]
- Kwon, S.; Park, G.; Jang, Y.; Cho, J.; Chu, M.G.; Min, B. Determination of Oil Well Placement Using Convolutional Neural Network Coupled with Robust Optimization under Geological Uncertainty. J. Pet. Sci. Eng. 2021, 201, 108118. [Google Scholar] [CrossRef]
- Kristoffersen, B.S.; Silva, T.; Bellout, M.; Berg, C.F. An Automatic Well Planner for Efficient Well Placement Optimization Under Geological Uncertainty. In Proceedings of the ECMOR XVII, Virtual, 14 September 2020; Volume 2020, pp. 1–16. [Google Scholar]
- Kristoffersen, B.S.; Silva, T.L.; Bellout, M.C.; Berg, C.F. Efficient Well Placement Optimization under Uncertainty Using a Virtual Drilling Procedure. Comput. Geosci. 2022, 26, 739–756. [Google Scholar] [CrossRef]
- Wen, G.; Hay, C.; Benson, S.M. CCSNet: A Deep Learning Modeling Suite for CO2 Storage. Adv. Water Resour. 2021, 155, 104009. [Google Scholar] [CrossRef]
- Pan, Y.; Horne, R.N. SPE 49055. Improved Methods for Multivariate Optimization of Field Development Scheduling and Well Placement Design. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 27–30 September 1998. [Google Scholar]
- Salehian, M.; Sefat, M.H.; Muradov, K. A Robust, Multi-Solution Framework for Well Placement and Control Optimization. Comput. Geosci. 2022, 26, 897–914. [Google Scholar] [CrossRef]
- Xiong, X.; Lee, K.J. Data-Driven Modeling to Optimize the Injection Well Placement for Waterflooding in Heterogeneous Reservoirs Applying Artificial Neural Networks and Reducing Observation Cost. Energy Explor. Exploit. 2020, 38, 2413–2435. [Google Scholar] [CrossRef]
- Selveindran, A.; Zargar, Z.; Razavi, S.M.; Thakur, G. Fast Optimization of Injector Selection for Waterflood, CO2-EOR and Storage Using an Innovative Machine Learning Framework. Energies 2021, 14, 7628. [Google Scholar] [CrossRef]
- Jang, I.; Oh, S.; Kim, Y.; Park, C.; Kang, H. Well-Placement Optimisation Using Sequential Artificial Neural Networks. Energy Explor. Exploit. 2018, 36, 433–449. [Google Scholar] [CrossRef]
- Sayyafzadeh, M. SPE-176468-MS. A Self-Adaptive Surrogate-Assisted Evolutionary Algorithm for Well Placement Optimization Problems. In Proceedings of the SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, Nusa Dua, Bali, Indonesia, 20–22 October 2015. [Google Scholar]
- Zarei, F.; Daliri, A.; Alizadeh, N. The Use of Neuro-Fuzzy Proxy in Well Placement Optimization. In Proceedings of the Intelligent Energy Conference and Exhibition, Amsterdam, The Netherlands, 25–27 February 2008. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salasakar, S.; Prakash, S.; Thakur, G. Recent Trends in Proxy Model Development for Well Placement Optimization Employing Machine Learning Techniques. Modelling 2024, 5, 1808-1823. https://doi.org/10.3390/modelling5040094
Salasakar S, Prakash S, Thakur G. Recent Trends in Proxy Model Development for Well Placement Optimization Employing Machine Learning Techniques. Modelling. 2024; 5(4):1808-1823. https://doi.org/10.3390/modelling5040094
Chicago/Turabian StyleSalasakar, Sameer, Sabyasachi Prakash, and Ganesh Thakur. 2024. "Recent Trends in Proxy Model Development for Well Placement Optimization Employing Machine Learning Techniques" Modelling 5, no. 4: 1808-1823. https://doi.org/10.3390/modelling5040094
APA StyleSalasakar, S., Prakash, S., & Thakur, G. (2024). Recent Trends in Proxy Model Development for Well Placement Optimization Employing Machine Learning Techniques. Modelling, 5(4), 1808-1823. https://doi.org/10.3390/modelling5040094






