Abstract
Based on the solutions of deterministic fracture mechanics and the methods of probability theory, the algorithm for calculating the probabilistic strength characteristics of plate elements of structures with an arbitrary stochastic distribution of surface defects is outlined. On the plate surface, there are uniformly distributed cracks that do not interact with each other, the plane of which is normal to the surface, and the depth is much less than its length on the surface. The cracks’ depth and angle of orientation are random values, and their joint distribution density is specified. Plates made of this material are under the influence of biaxial loading. The probability of failure, along with the mean value, the dispersion, and the variation coefficient of the plate’s strength, taking into account the surface defects under different types of stress, were determined. Their dependence on the type of loading, the size of the plate, and the surface structural heterogeneity of the material were studied graphically. Joint consideration of the influence of the interrelated properties of real materials, such as defectiveness and stochasticity, on strength and fracture, opens up new opportunities in creating a theory of strength and fracture of deformable solids.
1. Introduction
Several works are known in the literature, in which the methods of probability theory and mathematical statistics are applied to the problems of the mechanics of deformable solids. This is explained by the increasing role of probabilistic (statistical) methods as a means of scientific forecasting, given the growing use of new materials and structures with little experience in their operation. The behavior of these materials often depends on several poorly studied and difficult-to-control random factors, such as heterogeneity and defectiveness in the material structure, which as a result lead to heterogeneity in their deformation and strength properties, deviations in the sizes and shapes of structures, and variability of external influences.
When manufacturing thin-walled structural elements from some brittle materials, it was found that structural and technological defects are localized mainly on the surface, or that more dangerous defects are formed on the surface than in the inner layers. Mostly, the failure of such structural elements starts from the surface. These materials include glass and ceramics. Ground and polished glass products have low strength due to microcracks and scratches on the surface. The essence of the method of improving surface quality comes down to reducing the number and depth of surface microcracks and/or increasing the radius of curvature at their tips. It has been experimentally confirmed that the removal of the defective surface layer by etching in aqueous solutions of hydrofluoric acid (HF) significantly increases the strength of glass products from 5–20 MPa (structural strength) to 200–400 MPa [1,2,3].
The calculation of the brittle structural element’s reliability and strength, taking into account the randomness of surface defect characteristics, is an urgent task. The combination of deterministic fracture mechanics solutions and the methods of probability theory and mathematical statistics makes it possible to explain the difference between the theoretical and technical value of the strength of real bodies. These methods, used to study the strength of materials with surface defects, have been developed in recent years by several authors.
In paper [4], uniaxial and biaxial bending tests of sintered aluminum oxide and silicon nitride samples were performed, and the influence of surface defects was studied. Batdorf’s statistical theory of failure and two different deterministic destruction criteria were applied. The influence of surface defects on the strength of ceramic springs was studied in [5]. Analytically obtained ratios and numerical results provide a prediction of the investigated ceramic materials’ reliability with different structural parameters.
In work [6], an algorithm of probabilistic fracture mechanics is proposed, which makes it possible to estimate the probability of failure-free operation of structural elements with cracks. This algorithm takes into account the uncertainty in the defect geometry. Various probabilistic methods have been proposed to assess the reliability of the studied elements. Numerical examples confirm the accuracy of the considered method. An analysis of the sensitivity to the shape of the stress intensity coefficient was carried out. The solution to the problem of finding the probability of failure of a solid body with randomly oriented microcracks under arbitrary multi-axial loading, using the normal tensile stress criterion, was obtained [7]. It is considered that the distribution of microcracks in a solid body is random in shape, size, orientation, and location. Estimating the probability of failure for a randomly oriented defect under arbitrary loading improves the statistical approach to the brittle failure of materials.
The paper [8] describes an integrated model for simulating cracks and assessing structural elements’ reliability. The studied element is under two-dimensional plane load conditions. The Monte Carlo simulation was used to analyze the probability of failure-free operation. A failure criterion that takes into account only axial stresses is proposed. It was established that the probability of failure of the studied structural elements under different types of applied loading was in good agreement with the analytical solutions. In the article [9], the numerical method is applied to model the failure stress and failure location in a double-glazed unit with surface cracks subjected to different bending. It is based on the principle of the weakest link. The magnitude of strength and the location of fracture are stochastic and depend on the state of the surface defects. Correlation of the strength distribution with the Weibull distribution was carried out. A numerical method for modeling strength and fracture sites, which takes into account the state of surface defects of glass samples under the conditions of double-ring bending, is considered in [10]. A comparison of analytical results with experimental data was made. The method implements the principle of the weakest link and the Weibull distribution for strength, and the stochastic distribution of crack sizes is taken into account. Various destruction criteria are applied. The method is a promising means for modeling the strength of glass samples.
In article [11], an analysis of the integrity of a pipeline with a semi-elliptical crack on the outer surface was carried out. The Monte Carlo simulation was used for reliability calculations, covering a variety of geometries, from shallow to deep cracks. To calculate the stress intensity factor, the surface and depth of defects and the influence of the change in the crack shape factor during its development were taken into account. The obtained results increase the accuracy of predicting the probability of failure-free operation (reliability) of the studied structural elements. In work [12], the power law is used to describe the spatial distribution of microdefects in the structural material. The research is based on the hypothesis of the weakest link. Statistical scaling of the tensile strength of irregularly shaped particles in samples made of different materials was carried out. It is taken into account that Weibull’s theory of statistical strength is a special case of the model of the weakest link, based on the uniform spatial distribution of defects.
A statistical model of cracks developed for use in an engineering modeling program is considered [13]. The influence of local crack interactions on failure was studied. Statistical integration of the failure process was carried out. The studied material contains a large number of microcracks, which vary in size and orientation. Under loading, the largest cracks begin to grow, and the distribution of size and orientation of the defects changes. In [14], the stochastic nature of the nucleation, propagation, and coalescence of surface cracks under conditions of cyclic loading was investigated. A comprehensive approach combining numerical modeling and methods of brittle fracture mechanics is applied. A probabilistic study of the propagation and coalescence of surface defects was carried out using the Monte Carlo simulation, which includes experimental data related to the crack distribution density and the distribution of their lengths. The residual service life of the samples from their initial state to destruction was evaluated. In paper [15], the investigation of semi-elliptical surface cracks in pipes under internal pressure loading using the finite element method is proposed. The reliability is determined through statistical analysis of uncertainties regarding material properties, loading, structural reliability, and crack size. The study of the distribution function of the mechanical response was carried out using the Monte Carlo method. An analysis of changes in stress and crack sizes was made.
Paper [16] considers the strength effect of brittle materials under different conditions of applied loading. A model for the variation in strength relative to the loaded volume of the body has been obtained. The distribution of defect sizes is modeled using the largest distribution of extreme values. A model for the volume-dependent strength variation independent of the test method has been obtained. The failure of a plate with a crack under compressive point loading along the crack was investigated in work [17]. The reliability and safety of plate structural elements are considered, taking into account their structure stochasticity, in particular voids, inclusions, and crack presence. The plate fracture analysis was carried out using the finite element method. The proposed method was used to study of the numerous materials strength.
In paper [18], the process of formation, propagation, and orientation of cracks on the surface of the concrete coating is considered a random process that requires a probabilistic approach to research. The study is based on the actual probabilities of crack propagation and orientation using Markov chains. A three-term Markov chain was used for theoretical and numerical calculations. To confirm the correctness of the proposed probabilistic approach, a number of numerical simulation examples were given. Article [19] deals with the assessment of the development of cracks in structural elements, which is based on the approach of probabilistic fracture mechanics. A new law of the differential probability distribution function for nonlinearly growing cracks is written. The proposed method determines the probability of defect size over time, and the computational efficiency of the proposed method is proven.
The fracture of dispersed composite materials was investigated in [20]. The proposed probabilistic model uses a cumulative probability function corresponding to the Weibull distribution. Several mechanical parameters of the material were used to assess the composite fracture. The obtained analytical calculations were compared with the experimental data known in the literature. In paper [21], a probabilistic approach for predicting the reliability of polymer composite materials under biaxial stress is presented. The reliability was determined based on an experimental-numerical approach. Good agreement was observed between the fracture toughness of the composites in transverse shear and in-plane shear. Article [22] proposes a method for researching the strength of brittle materials under tensile conditions. The finite element method was used to evaluate the experimental test, with the results confirmed by evaluating the tensile strength of brittle materials. The proposed method was verified for several brittle materials. The results of the method showed a good agreement with values known in the literature.
An experimental study of welded steel joints with surface defects was conducted in [23]. Defects were characterized by size, shape, and location. The method of magnetic powder testing with an electromagnet, with a change in test conditions, was applied. An increase in the probability of detecting defects, along with their size, was established. In work [24], several experimental tests were conducted to assess the reliability of thin-walled tubes, which are used as energy-absorbing elements of structures, and finite element modeling was carried out. The studies that were conducted confirmed the main mechanical characteristics of the proposed modular self-locking system. In article [25], explicit analytical solutions for the electrostatic stresses resulting from the interaction between a semi-infinite anti-crack and a helical dislocation under anti-plane mechanical and planar electric loading were obtained using the complex variable and conformal mapping methods. The behavior of defects such as cracks, dislocations, cavities, and inclusions under various mechanical loads was analyzed.
This paper represents another development in the statistical theory of strength and brittle failure of structural materials weakened by random surface defects, such as cracks, which have been studied since the 1970s and 1980s. In this publication, new opportunities are provided through a combined consideration of the influence of interconnected properties—defectiveness and stochasticity—on the strength and failure of a structure. The main focus of this study is the construction, along with the graphical and numerical analysis, of the probability of failure, mean value, dispersion, and coefficient of strength variation of plates with random surface cracks under different types of stress states and different numbers of cracks (representing surface heterogeneity of the material). The failure loading distribution function , which is used to determine the probability of failure of a plate with surface defects is proposed in the form of the Weibull type.
The application of a complex approach, based on the principles of the isolated defect development theory, such as cracks, and the methods of the theory of probabilities, makes it possible to obtain a high-quality method for calculating the strength of structural materials. Therefore, the relevance of the work is determined by the importance of taking into account the statistical nature of material failure due to surface defects.
2. Materials and Methods
Consider the deterministic solution to the problem of brittle fracture mechanics for a plate with a surface crack that extends to some depth (Figure 1).
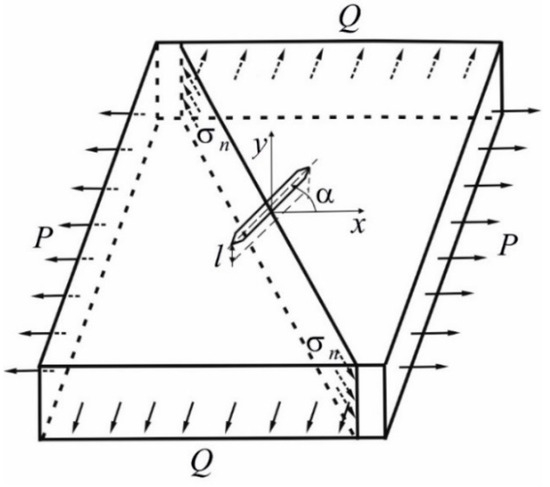
Figure 1.
Model of a plate weakened by a surface crack extending to a certain depth .
The plate has an area and a thickness and is under the conditions of action of a load uniformly distributed along the edges and . We consider the plane of the crack to be normal to the surface of the plate. The crack forms an angle with the direction of the loading .
If the length of the crack on the surface significantly exceeds its depth, then the development of the crack occurs primarily in the depth of the plate [26]. At an arbitrary angle around the crack front, which limits its depth, under the action of the loading under consideration, deformations of normal rupture and longitudinal shear occur [26]. In this case, we accept the condition that the crack propagation is the result of a normal rupture, which is caused by stresses normal to its plane , which are determined by the formula
A crack can develop according to , i.e., for all (arbitrary crack orientation), if ; for if ; in the case of (biaxial compression), a crack with an arbitrary orientation cannot develop.
The condition for crack development in depth is reduced to the condition of the growth of a marginal crack with a length in a strip with a width equal to the thickness of the plate under the action of tensile stresses (Figure 2) [26].

Figure 2.
Marginal crack in the strip of width equal to the thickness of the plate under the action of tensile stresses .
Then, the stress intensity factor based on the approximation of the numerical results is determined by the relation [26]
Let us write Formula (2) in the form
For shallow cracks , we consider that and . Neglecting higher-order small terms, we obtain a simplified expression from Formula (3)
In the case of (very shallow cracks), we get a significant simplification:
Taking into account that the condition for the crack development is reduced to the form , where is the critical value of the stress intensity factor [27], according to Formulas (1)–(5), we find the value of the failure loading for cracks of different depths using
where .
3. Results
3.1. Failure Loading Integral Probability Distribution Function
Let consider the algorithm for determining the failure loading probability distribution function, knowing which allows one to find several failure loading probability characteristics (strength) for plates with stochastically distributed surface defects: the mean and the most probable values, the value of loading corresponding to a given probability of failure, dispersion, coefficient of variation, etc.
Let there be uniformly distributed cracks on the plate surface under the loading conditions and parameters specified above, which do not interact with each other (Figure 3).
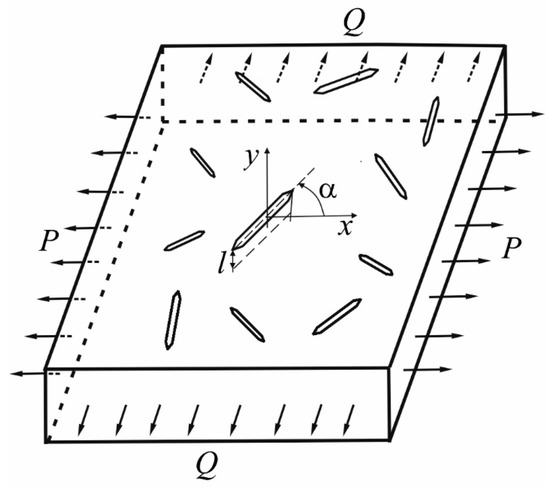
Figure 3.
A plate model with stochastically distributed surface defects of random size and orientation, which are uniformly scattered in such a way that they do not interact with each other.
We introduce as the probability density of the distribution of a random variable , and is the probability density of the distribution of a random variable . In real products, the depth of cracks and the angle of their orientation are statistically independent random variables [28,29]. Then, the density of their joint distribution is [30]
We consider the plate material to be isotropic. Under this assumption, all possible crack orientations, , are equally probable. Then, the probability density of the distribution of a random variable will be written as: [31].
We assume that the interval limits the random depth of cracks, , where is the finite structural characteristic of the material. According to expressions (6)–(8), the following options for changing parameter are possible: , or .
When choosing the law of distribution for defects by depth, it is necessary to take into account the following circumstances. Despite the presence in the material of a very wide spectrum of surface defect depths, with an increase in the depth of the defect beyond a certain value, the probability of encountering a defect of an even greater depth decreases sharply. On the other hand, the probability of encountering defects with a very small depth decreases slowly and monotonically.
The distribution of the depth of defects is described by the law (generalized -distribution) [31]. Then, the integral distribution function is . The physical meaning of parameter is as follows: the larger its value, the higher the likelihood of shallow surface defects being present.
Then, the density of the joint distribution of random variables and , according to (9), can be written as follows:
Using relations (6)–(8), we write
The intervals of change of the random value of the failure loading () are determined by Formulas (11)–(13).
Conditionally, we divide the plate into area elements, each containing one surface defect crack. To interpret the statistical nature of brittle failure, we will use the model of the weakest link. We believe that due to the development of a crack, the first stage of the plate failure process ends with its final failure.
The failure loading integral probability distribution function for a plate element with one surface defect has the following form [29]:
The density of the joint distribution of random variables and can be obtained from (10). The region of integration is a two-dimensional region consisting of all admissible values of and , for which, according to the depth of the cracks, one of the conditions obtained from (6)–(8) is fulfilled.
Let us write the double integral in Formula (14) through the repeated integral
where is the set of possible values of the random parameter for which the condition must be fulfilled for the given values of and .
The value is a positive parameter value satisfying conditions (6), (7) or (8). In particular, is analytically determined, respectively, from expressions (7) and (8) as follows:
Using relation (9), entering the integral probability distribution function , and taking into account that , from Formula (18) we find
Let us stop at the case . Then, using expressions and , from Formula (21), we write as follows:
According to relation (19), takes different values depending on the values of and .
For the case of uniaxial or biaxial tension
In the case of tension-compression (), we obtain from Formula (1) that only defects with orientation can develop.
Then we have
Since the orientation of defects does not affect the magnitude of the failure loading at the same biaxial tension, we obtain a significant simplification of expression (22)
Using expressions (15)–(17), and (20), we obtain a significant simplification in Formulas (20)–(25).
3.2. Statistical Characteristics of a Plate Strength with Surface Defects
Expressions of the failure loading distribution function (22)–(25) form the basis for determining the statistical characteristics of the investigated plate strength.
Let us choose the failure loading distribution function , which determines the probability of failure of a plate with surface defects, in the form of the Weibull type [32]
Here, and are the distribution parameters; in particular, is the material homogeneity parameter (the material becomes more homogeneous as it increases), which is related by a certain ratio to the parameter , which will be shown below. Expression (26) is based on the hypothesis of the weakest link, which is that the strength of a brittle body is completely determined by the strength of its weakest element, with the failure of this element leading to the body’s failure as a whole. Then, the mean value, dispersion, and coefficient of variation of the failure loading are determined by the formulas [30]
where is the gamma function .
To determine the parameters in distribution (26), we use the relation [30]
We introduce the dimensionless loading in expressions (19), and (22)–(25) and get the following expressions:
For the case of uniaxial or biaxial tension
In the case of tension-compression (), we obtain from Formula (1) that only defects with orientation can develop.
Then we have
In the case of failure loading at the same biaxial tension
Using the Maple computer mathematics system [33], and according to expressions (26), and (30)–(35), the dependence of the probability of plate failure for a given loading on the number of surface cracks and the type of stress state is shown in Figure 4.
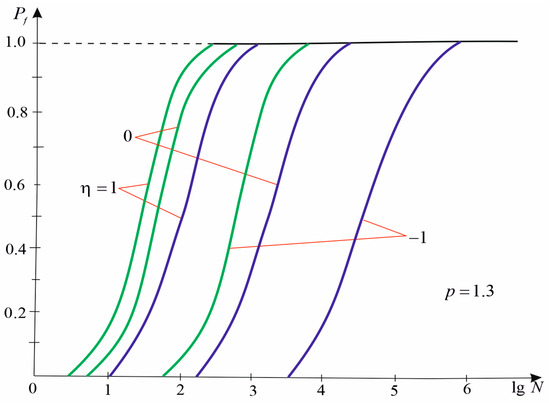
Figure 4.
Probability of failure ( for the green line, for the purple line) for a given loading on the number of surface cracks and the type of stress state ().
According to expressions (27)–(29) and (30)–(35) in Figure 5, Figure 6 and Figure 7, graphs of the statistical characteristics of the failure loading under different types of stress states for materials with different numbers of defects and different heterogeneity are plotted.
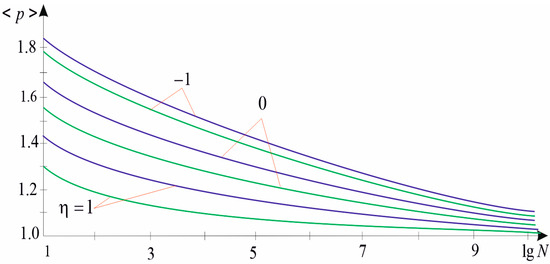
Figure 5.
Failure loading mean value ( for the green line, for the purple line) for different types of stress states (—equal biaxial tension, —uniaxial tension, —tension-compression).
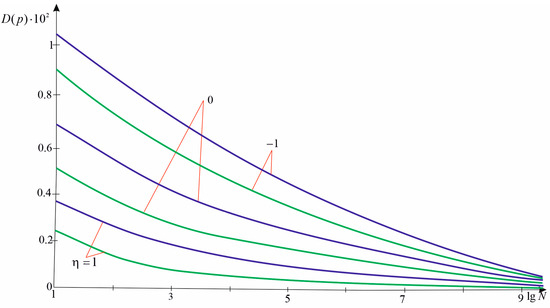
Figure 6.
Dispersion of failure loading ( for the green line, for the purple line) for different types of stress states (—equal biaxial tension, —uniaxial tension, —tension-compression).
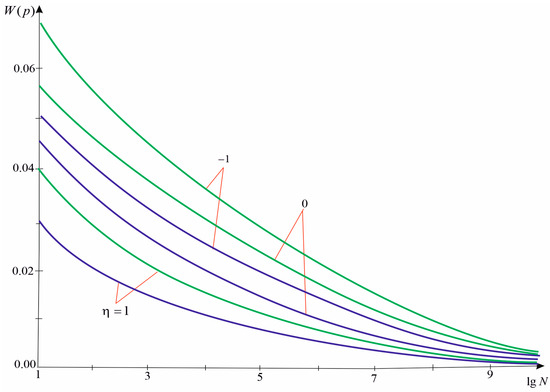
Figure 7.
Coefficient of strength variation ( for the green line, for purple line) for different types of stress states (—equal biaxial tension, —uniaxial tension, —tension-compression).
Article [34] discusses the method of selecting the parameters of the probabilistic failure model of materials, taking into account the stochasticity of their structure to describe the experimental data. This method showed good agreement between the theoretical and experimental results known from the literature [35]. A probabilistic description of several experimental characteristics of the failure loading was carried out. The proposed algorithm for studying materials with randomly distributed surface defects is consistent with the results obtained in [34].
4. Discussion
Several statistical approaches are known in the mechanics of deformable solids, in particular when considering the problem of strength and brittle failure. However, in most cases, with the statistical approach to the theory of strength, defects in the structure of a solid body were not explicitly considered. The calculation of the probability of failure and strength statistical characteristics was carried out based on a given distribution of the limits of the strength or tension of the body’s elements.
Therefore, the impact of interconnected properties of real materials—defectiveness and stochasticity—on the strength and failure of the structure were studied separately, using different methods.
Our proposed approach to assessing the strength of materials with randomly distributed surface defects, such as cracks, in which the specified properties are jointly considered, has advantages from a theoretical point of view. The physical sources and carriers of the failure process—structural defects—are presented in an explicit form. In contrast to previously used expressions for the distribution function of the failure loading in plates containing stochastically distributed internal defects, we propose a Weibull-type distribution function for plates with a surface distribution of defects. This serves as the basis for recording several statistical characteristics of the material’s strength.
In analyzing the obtained numerical results and constructed curves, we see that the value of the probability of failure depends on the number of cracks on a given surface of the plate, the distribution law of the size of cracks (parameter ), the level of loading (), and the type of stress state (from ). The probability of failure increases with an increase in the number of cracks (area of the plate). Each homogeneity of the material and type of stress state corresponds to a certain range of plate sizes, within which a sharp change in magnitude is observed. We can see the effect of the number of cracks, the type of loading, and the homogeneity of the material on the mean value of the failure loading . The value increases with increasing homogeneity of the material. Under the same conditions, the lowest strength of the plate will be at the same all-round tension. Such regularities were also observed in paper [35]. As the number of cracks in the body increases, the mean value of strength decreases, asymptotically approaching its minimum value and, within a certain range, is almost independent of the number of defects.
We can see the dependence of the failure loading dispersion on the number of cracks, the ratio of the applied loading, and the homogeneity of the material. The dispersion of strength is a decreasing function of the number of cracks in the body, and the nature of this decrease does not depend on the homogeneity of the material and the type of loading. With a change in parameter , the dispersion of strength changes by a value that is almost independent of the type of stress state. In a certain range of plate sizes, as in the case of , there is a certain range of plate sizes for which the strength dispersion is almost independent of the number of defects. The dependence of the strength variation coefficient on the number of cracks, the homogeneity of the material plate surface, and the type of stress state is investigated. The value decreases with an increase in parameter and the number of cracks . In a certain range of plate sizes, we observe a sharp decrease in the change in magnitude and an asymptotic approach to zero. These regularities do not depend on the type of stress state. The conducted studies are in good agreement with the results of the works [36,37,38].
5. Conclusions
- In this work, taking into account the stochasticity of brittle materials with surface cracks structure, a new class of problems for the failure study is considered,
- It is stated that the dependence of the plate failure probability on the applied loading P (type of strength state) and the number of surface cracks (plate sizes) have the same features as those observed for a plate with internal cracks.
- The probability of the plate failure under a given loading P increases sharply with an increase in the number of defects, and decreases with an increase in the uniformity of the plate material.
- In all cases, the probability of failure is greatest with the same biaxial tension.
- It is necessary to pay attention to reducing the probability of failure under a given loading .
- If one component of the loading is unchanged, with a decrease in the second, the probability of failure decreases.
- Similar probabilistic strength studies can be applied to construction elements made from glass and ceramics.
Author Contributions
Conceptualization, R.K. and P.P.; methodology R.K., M.V., and T.S.; software, T.S.; validation, M.V. and T.S.; investigation, P.P. and M.V.; writing—original draft preparation, M.V. and T.S.; writing—review and editing, R.K. and P.P.; visualization, M.V. and T.S.; project administration, R.K. and P.P.; funding acquisition, P.P. and M.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pukh, V. The Strength and Failure of Glass; Nauka: Leningrad, Russia, 1973. [Google Scholar]
- Pavelchek, E.; Doremus, R. Fracture strength of soda-lime glass after etching. J. Mater. Sci. 1974, 9, 1803–1808. [Google Scholar] [CrossRef]
- Starchevskyy, V.; Bernatska, N.; Typilo, I.; Oliynyk, L.; Kvit, R. Determination of the cavitation influence on the destruction process of microorganism cells agglomerates. Chem. Chem. Technol. 2018, 12, 462–465. [Google Scholar] [CrossRef]
- Chao, L.Y.; Shetty, D. Reliability Analysis of Structural Ceramics Subjected to Biaxial Flexure. J. Am. Ceram. Soc. 1991, 74, 333–344. [Google Scholar] [CrossRef]
- Nohut, G.; Schneider, A. Failure Probability of Ceramic Coil Springs. J. Eur. Ceram. Soc. 2009, 29, 1013–1019. [Google Scholar] [CrossRef]
- Chowdhury, M.S.; Song, C.; Gao, W. Probabilistic fracture mechanics with uncertainty in crack size and orientation using the scaled boundary finite element method. Comp. Struct. 2014, 137, 93–103. [Google Scholar] [CrossRef]
- Lei, W.S. Fracture probability of a randomly oriented microcrack under multi-axial loading for the normal tensile stress criterion. Theor. Appl. Fract. Mech. 2016, 85, 164–172. [Google Scholar] [CrossRef]
- Choi, W.; Yoon, S.; Lee, L.J. Crack simulation and probability analysis using irregular truss structure modeling equivalent to a continuum structure. Int. J. Agric. Biol. Eng. 2017, 10, 234–247. [Google Scholar] [CrossRef]
- Kinsella, D.T.; Persson, K. Analysis of Glass Fracture Statistics. In Challenging Glass 6: Proceedings of Conference on Architectural and Structural Applications of Glass; Delft University of Technology: Delft, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Kinsella, D.T.; Persson, K. A numerical method for analysis of fracture statistics of glass and simulations of a double ring bending test. Glass Struct. Eng. 2018, 3, 139–152. [Google Scholar] [CrossRef]
- Guillal, A.; Abdelbaki, N.; el Amine Bensghier, M.; Kopei, B.; Bettayeb, M. Effect of shape factor on structural reliability analysis of a surface cracked pipeline-parametric study. Frat. Ed Integr. Strut. 2019, 13, 341–349. [Google Scholar] [CrossRef]
- Qian, G.; Lei, W.S.; Yu, Z.; Berto, F. Statistical size scaling of breakage strength of irregularly-shaped particles. Theor. Appl. Fract. Mech. 2019, 102, 51–58. [Google Scholar] [CrossRef]
- Margolin, L. Damage and failure in a statistical crack model. Appl. Sci. 2020, 10, 8700. [Google Scholar] [CrossRef]
- Zhu, S.P.; Hao, Y.Z.; Liao, D. Probabilistic modeling and simulation of multiple surface crack propagation and coalescence. Appl. Math. Model. 2020, 78, 383–398. [Google Scholar] [CrossRef]
- Mechab, B.; Medjahdi, M.; Salem, M.; Serier, B. Probabilistic elastic-plastic fracture mechanics analysis of propagation of cracks in pipes under internal pressure. Frat. Integr. Struc. 2020, 54, 202–210. [Google Scholar] [CrossRef]
- Pagnoncelli, A.P.; Tridello, A.; Paolino, D.S. Static strength of brittle materials under multiaxial nonuniform stress states: A novel statistical model for assessing size effects. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 997–1013. [Google Scholar] [CrossRef]
- Mishra, K.; Lal, A.; Sutarial, B.M. Fracture analysis of edge cracked FGM plate under compressive load along crack. Proceeding of the IOP Conference Series: Materials Science and Engineering, International Conference on “Advances in Materials Processing & Manufacturing Applications”, Jaipur, India, 5–6 November 2020; 2020; Volume 1017, p. 012018. [Google Scholar] [CrossRef]
- Leblouba, M.; Tarabin, M.; Zahri, M. Probabilistic analysis and simulation of crack propagation in concrete pavements and surfaces. Sci. Rep. 2022, 12, 14157. [Google Scholar] [CrossRef]
- Saifi, Q. Novel probabilistic crack growth assessment method: Based on the realized PDF law for growing cracks. Eng. Fract. Mech. 2022, 276, 108931. [Google Scholar] [CrossRef]
- Mieczkowski, G.; Szymczak, T.; Szpica, D.; Borawski, A. Probabilistic Modelling of Fracture Toughness of Composites with Discontinuous Reinforcement. Materials 2023, 16, 2962. [Google Scholar] [CrossRef]
- Wan, L.; Ullah, Z.; Yang, D.; Falzon, B.G. Probability embedded failure prediction of unidirectional composites under biaxial loadings combining machine learning and micromechanical modelling. Compos. Struct. 2023, 312, 116837. [Google Scholar] [CrossRef]
- Pagnoncelli, A.P.; Paolino, D.S.; Peroni, L.; Tridello, A. Innovative tensile test for brittle materials: Validation on graphite R4550. Int. J. Mech. Sci. 2024, 261, 108679. [Google Scholar] [CrossRef]
- Vera, J.; Caballero Garcia, L.F.; Taboada Neira, M.; Valverde Flores, J.F. Probability of Defects Detection in Welded Joints using the Magnetic Particle Method. Arch. Metall. Mater. 2024, 69, 607–612. [Google Scholar] [CrossRef]
- Yang, K.; Hu, X.; Pan, F.; Qiao, C.; Ding, B.; Hu, L.; Hu, X.; He, Z.; Chen, Y. An on-demand tunable energy absorption system to resolve multi-directional impacts. Int. J. Solids Struct. 2023, 271, 112257. [Google Scholar] [CrossRef]
- Chen, B.; Xiao, Z.; Liew, K. On the interaction between a semi-infinite anti-crack and a screw dislocation in piezoelectric solid. Int. J. Solids Struct. 2002, 39, 1505–1513. [Google Scholar] [CrossRef]
- Cherepanov, G. Mechanics of Brittle Fracture; McGraw Hill: New York, NY, USA, 1979. [Google Scholar]
- Erdogan, F.; Sih, G. On the crack extension in plates under plane loading and transverse shear. ASME J. Bas. Eng. 1963, 85, 519–527. [Google Scholar] [CrossRef]
- Johari, A.; Fazeli, A.; Javadi, A. An investigation into application of jointly distributed random variables method in reliability assessment of rock slope stability. Comp. Geotech. 2013, 47, 42–47. [Google Scholar] [CrossRef]
- Guo, S.; Chidiac, S.E. Probability characteristics of a crack hitting spherical healing agent particles: Application to a self-healing cementitious system. Materials 2022, 15, 7355. [Google Scholar] [CrossRef]
- Vitvitskii, P.; Popina, S. Strength and Criteria of Brittle Fracture of Stochastically Defective Bodies; Naukova Dumka: Kyiv, Ukraine, 1980. [Google Scholar]
- Pukach, P.; Kvit, R.; Salo, T.; Vovk, M. A probable approach to reliability assessment of reinforced plates. Appl. Syst. In. 2023, 6, 73. [Google Scholar] [CrossRef]
- Weibull, W. A statistical theory of the strength of materials. Proc. Roy. Swed. Inst. Eng. Res. 1939, 151, 5–45. [Google Scholar]
- Melnyk, R.; Kalychak, Y.; Kvit, R. Analysis of cloudiness by segmentation and monitoring of satellite map images. Int. J. Comp. 2019, 18, 169–180. [Google Scholar] [CrossRef]
- Vitvitskii, P.; Kvit, R. Probabilistic description of experimental statistical strength characteristics. Sov. Mater. Sci. 1992, 28, 83–86. [Google Scholar] [CrossRef]
- Pisarenko, G.; Lebedev, A. Deformation and Strength of Materials at a Complex Stress State; Naukova Dumka: Kyiv, Ukraine, 1976. [Google Scholar]
- Kvit, R. Investigation of probabilistic aspects reliability of isotropic bodies with internal defects. J. Appl. Math. Comput. Mech. 2022, 21, 73–84. [Google Scholar] [CrossRef]
- Matsuo, Y. The formulation of the multiaxial distribution function for a brittle fracture having location parameters and its application. Trans. Jpn. Soc. Mech. Eng. 1983, 49, 437. [Google Scholar] [CrossRef]
- Matsuo, Y.; Kitakami, K. On the statistical theory of fracture location combined with competing risk theory. Frac. Mech. Cer. 1986, 7, 223–235. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).