Author Contributions
Software, formal analysis, data curation validation, and writing—original draft: H.M.N. and M.A.; conceptualization, methodology, and supervision: T.O.; conceptualization, data curation, and visualization: M.S.; resources, supervision, and writing—review and editing: D.J. All authors have read and agreed to the published version of the manuscript.
Figure 1.
A three-dimensional model of the crankshaft.
Figure 1.
A three-dimensional model of the crankshaft.
Figure 2.
Mesh sensitivity.
Figure 2.
Mesh sensitivity.
Figure 3.
Variation of pressure with crank angle.
Figure 3.
Variation of pressure with crank angle.
Figure 4.
Finite element model of the crankshaft.
Figure 4.
Finite element model of the crankshaft.
Figure 5.
Comparison between crankshaft designs: (
a) design within the reference study [
11], Solidworks (
b) design within this study CATIA V5 R18.
Figure 5.
Comparison between crankshaft designs: (
a) design within the reference study [
11], Solidworks (
b) design within this study CATIA V5 R18.
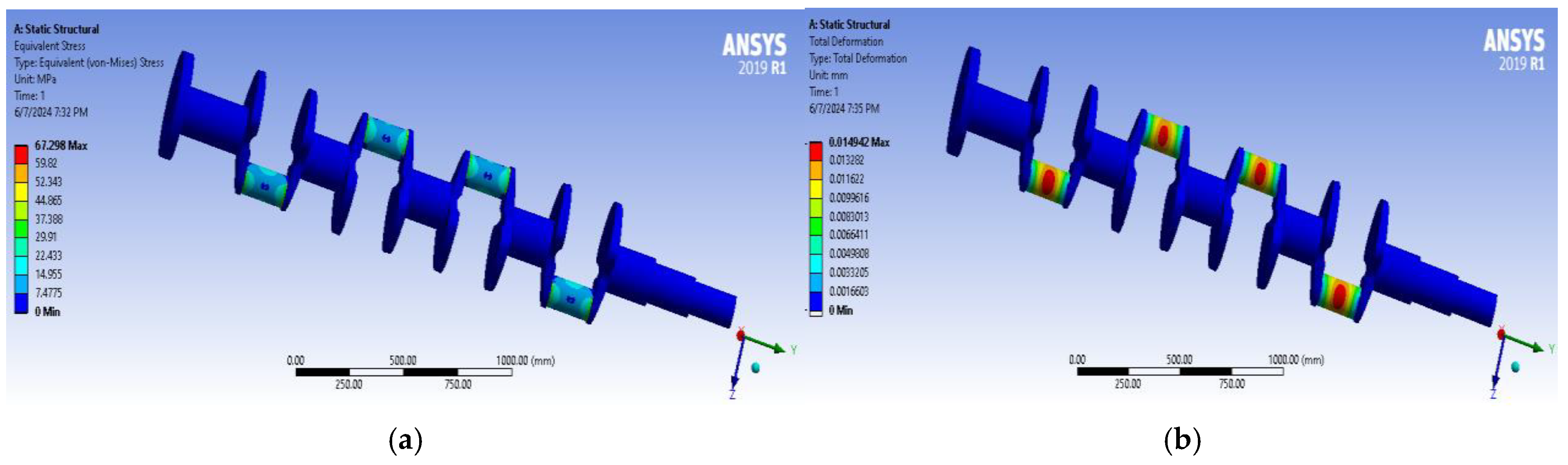
Figure 6.
Von-Mises stress analysis results for the crankshaft.
Figure 6.
Von-Mises stress analysis results for the crankshaft.
Figure 7.
Von Mises stress of the studied materials.
Figure 7.
Von Mises stress of the studied materials.
Figure 8.
Results of displacement analysis of the crankshaft.
Figure 8.
Results of displacement analysis of the crankshaft.
Figure 9.
Displacement analysis results for the studied crankshaft materials.
Figure 9.
Displacement analysis results for the studied crankshaft materials.
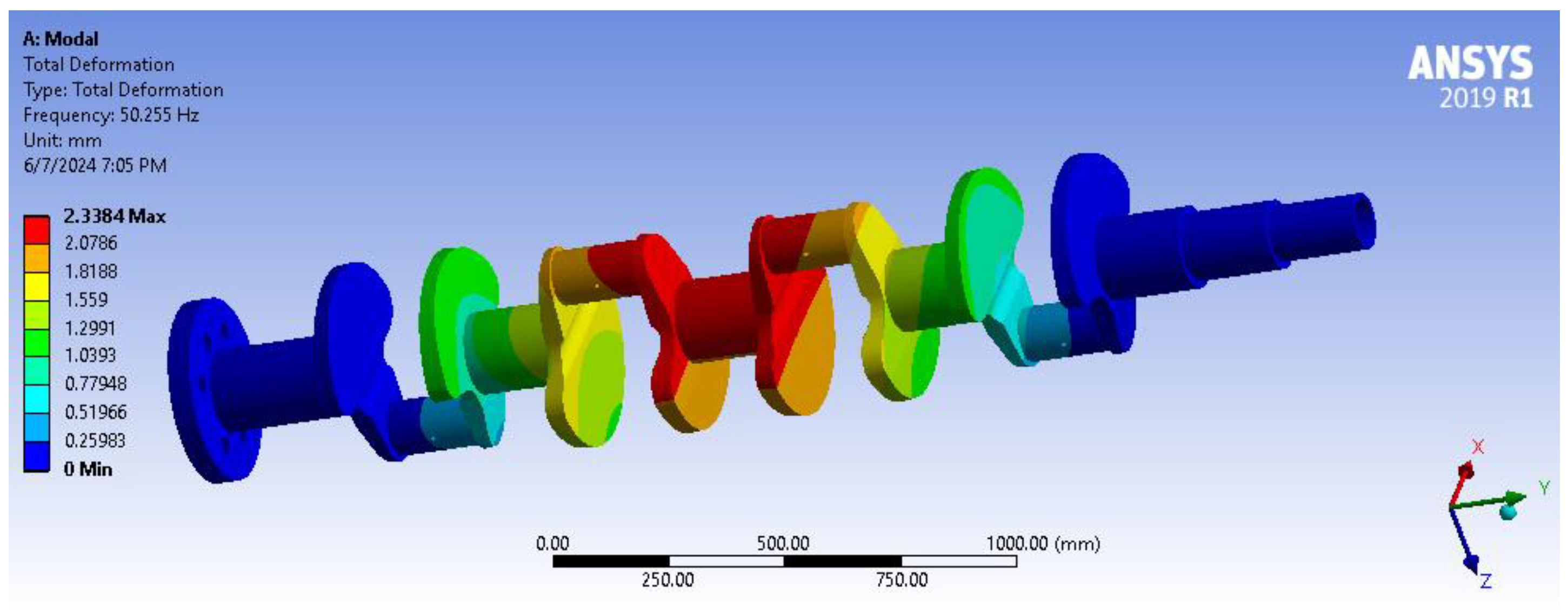
Figure 10.
Boundary conditions for vibratory behavior.
Figure 10.
Boundary conditions for vibratory behavior.
Figure 11.
Vibrational analysis of the four materials.
Figure 11.
Vibrational analysis of the four materials.
Figure 12.
Boundary conditions for thermal behavior.
Figure 12.
Boundary conditions for thermal behavior.
Figure 13.
Output temperature of the studied materials.
Figure 13.
Output temperature of the studied materials.
Figure 14.
Heat flow of materials used for the crankshaft.
Figure 14.
Heat flow of materials used for the crankshaft.
Figure 15.
Advanced concepts for weight loss.
Figure 15.
Advanced concepts for weight loss.
Figure 16.
Crankshaft analysis results (a) von Misses stress and (b) displacement.
Figure 16.
Crankshaft analysis results (a) von Misses stress and (b) displacement.
Figure 17.
Vibration analysis of Structural Steel.
Figure 17.
Vibration analysis of Structural Steel.
Figure 18.
Thermal behavior analysis (a) Output temperature, and (b) Heat flow.
Figure 18.
Thermal behavior analysis (a) Output temperature, and (b) Heat flow.
Table 1.
Mechanical and thermal properties (Aluminum Alloy 7475, Cast Iron, Stainless steel EN 308, Structural Steel).
Table 1.
Mechanical and thermal properties (Aluminum Alloy 7475, Cast Iron, Stainless steel EN 308, Structural Steel).
| Material Properties | Stainless Steel EN 308 | Cast Iron | Aluminum Alloy 7475 | Structural Steel |
|---|
| Density (kg/m3) | 7850 | 7200 | 2810 | 7850 |
| Poisson’s ratio | 0.29 | 0.28 | 0.33 | 0.3 |
| Young’s modulus (GPa) | 205 |
110
| 71.7 | 200 |
| Yield stress (MPa) | 240 | 220 | 490 | 280 |
| Thermal conductivity (W/m°C) | 426 |
50
| 163 |
60.5
|
| Specific heat capacity (J/kg°C) | 473 |
540
| 880 |
434
|
Table 2.
Dimensions of the crankshaft.
Table 2.
Dimensions of the crankshaft.
| Parameter | Value |
|---|
| Crank pin radius | 60 mm |
| Shaft diameter | 90 mm |
| Thickness of the crank web | 50 mm |
| Length of the crank pin | 197 mm |
| Maximum pressure | 35 bar |
Table 3.
Convergence and grid independence.
Table 3.
Convergence and grid independence.
| Solution | Von Mises Stress Max (MPa) | Change Percentage | Nodes | Elements |
|---|
| 1 | 15.5964 | - | 30,149 | 10,311 |
| 2 | 28.8821 | 46% | 98,115 | 30,789 |
| 3 | 42.4741 | 32% | 139,611 | 80,936 |
| 4 | 51.8863 | 18.14% | 213,150 | 103,628 |
| 5 | 56.7250 | 5.83% | 427,888 | 249,630 |
| 6 | 57.7201 | 0.84% | 762,351 | 563,821 |
Table 4.
Comparison of displacement values, maximum stress, and safety factor for the crankshaft under pressure 35 bar.
Table 4.
Comparison of displacement values, maximum stress, and safety factor for the crankshaft under pressure 35 bar.
| Crank Angle (Deg) | Pressure
(bar) | The Design within This Study | Design within the Reference Study [11] | Low Percentage
Von Mises Stress Max (MPa) | Low Percentage
Deformation Max (mm) |
|---|
| Deformation Max (mm) | Von Mises Stress Max (MPa) | Safety Factor | Deformation Max (mm) | Von Mises Stress Max (MPa) | Safety Factor |
|---|
| Structural Steel | Structural Steel |
|---|
| 0 | 35 | 0.0145 | 56.725 |
4.9360
| 0.0146 | 66.82 |
4.1903
| 17.7% | 0.6% |
| 30 | 30.3 | 0.0125 | 49.108 |
5.7017
| 0.0125 | 57.27 |
4.8891
| 16.6% | 0% |
| 60 | 17.5 | 0.0073 | 28.363 |
9.872
| 0.0073 | 33.41 |
8.3807
| 17.7% | 0% |
| 90 | 0 |
0
|
0
| - | 0 | 0 | - | 0% | 0% |
| 120 | −17.5 | 0.0073 | 28.363 | 9.872 | 0.0073 | 33.41 | 8.3807 | 17.7% | 0% |
| 150 | −30.3 | 0.0126 | 49.108 | 5.7017 | 0.0125 | 57.27 | 4.8891 | 16.6% | 0% |
| 180 | −35 | 0.0145 | 56.725 | 4.9360 | 0.0146 | 66.82 | 4.1903 | 17.7% | 0.6% |
| 210 | −30.3 | 0.0126 | 49.108 | 5.7017 | 0.0125 | 57.27 | 4.8891 | 16.6% | 0% |
| 240 | −17.5 | 0.0073 | 28.363 | 9.872 | 0.0073 | 33.41 | 8.3807 | 17.7% | 0% |
| 270 | 0 |
0
|
0
| - | 0 | 0 | - | 0% | 0% |
| 300 | 17.5 | 0.0073 | 28.363 | 9.872 | 0.0073 | 33.41 | 8.3807 | 17.7% | 0% |
| 330 | 30.3 | 0.0126 | 49.108 |
5.7017
| 0.0125 | 57.27 | 4.8891 | 16.6% | 0% |
| 360 | 35 | 0.0145 | 56.725 | 4.9360 | 0.0146 | 66.82 | 4.1903 | 17.7% | 0.6% |
Table 5.
Comparison between the Theoretical and practical results.
Table 5.
Comparison between the Theoretical and practical results.
| Type of Stress | The Design within this Study Using ANSYS | Design within the Reference Study of Sandya et al. [11] Using ANSYS | Theoretical
Results |
|---|
| Von-Mises stress (N/mm2) | 56.725 | 66.82 | 80.56 |
Table 6.
The effect of the type of crankshaft material on the maximum values of stresses and displacements.
Table 6.
The effect of the type of crankshaft material on the maximum values of stresses and displacements.
| Crank Angle (Deg) | Pressure (bar) | Material | Max Deformation (mm) | Von Mises Stress (MPa) Max |
|---|
| 0 | 35 | Structural Steel | 0.0145 | 56.725 |
| Aluminum Alloy 7475 | 0.0041 | 55.071 |
| Stainless Steel EN 308 | 0.0141 | 57.273 |
| Cast Iron | 0.0263 | 57.795 |
| 30 | 30.3 | Structural Steel | 0.0125 | 49.108 |
| Aluminum Alloy 7475 | 0.0035 | 47.675 |
| Stainless Steel EN 308 | 0.0122 | 49.582 |
| Cast Iron | 0.0227 | 50.034 |
| 60 | 17.5 | Structural Steel | 0.0073 | 28.363 |
| Aluminum Alloy 7475 | 0.0021 | 27.535 |
| Stainless Steel EN 308 | 0.0071 | 28.637 |
| Cast Iron | 0.0131 | 28.897 |
| 90 | 0 | Structural Steel | 0 | 0 |
| Aluminum Alloy 7475 | 0 | 0 |
| Stainless Steel EN 308 | 0 | 0 |
| Cast Iron | 0 | 0 |
| 120 | −17.5 | Structural Steel | 0.0073 | 28.363 |
| Aluminum Alloy 7475 | 0.0035 | 47.675 |
| Stainless Steel EN 308 | 0.0071 | 28.637 |
| Cast Iron | 0.0131 | 28.897 |
| 150 | −30.3 | Structural Steel | 0.0126 | 49.108 |
| Aluminum Alloy 7475 | 0.0035 | 47.675 |
| Stainless Steel EN 308 | 0.0122 | 49.582 |
| Cast Iron | 0.0227 | 50.034 |
| 180 | −35 | Structural Steel | 0.0145 | 56.725 |
| Aluminum Alloy 7475 | 0.0041 | 55.071 |
| Stainless Steel EN 308 | 0.0141 | 57.273 |
| Cast Iron | 0.0263 | 57.795 |
| 210 | −30.3 | Structural Steel | 0.0126 | 49.108 |
| Aluminum Alloy 7475 | 0.0035 | 47.675 |
| Stainless steel EN 308 | 0.0122 | 49.582 |
| Cast Iron | 0.0227 | 50.034 |
| 240 | −17.5 | Structural Steel | 0.0073 | 28.363 |
| Aluminum Alloy 7475 | 0.0021 | 27.535 |
| Stainless Steel EN 308 | 0.0071 | 28.637 |
| Cast Iron | 0.0131 | 28.897 |
| 270 | 0 | Structural Steel | 0 | 0 |
| Aluminum Alloy 7475 | 0 | 0 |
| Stainless Steel EN 308 | 0 | 0 |
| Cast Iron | 0 | 0 |
| 300 | 17.5 | Structural Steel | 0.0073 | 28.363 |
| Aluminum Alloy7475 | 0.0021 | 27.535 |
| Stainless Steel EN 308 | 0.0071 | 28.637 |
| Cast Iron | 0.0131 | 28.897 |
| 330 | 30.3 | Structural Steel | 0.0126 | 49.108 |
| Aluminum Alloy 7475 | 0.0035 | 47.675 |
| Stainless steel EN 308 | 0.0122 | 49.582 |
| Cast Iron | 0.0227 | 50.034 |
| 360 | 35 | Structural Steel | 0.0145 | 56.725 |
| Aluminum Alloy 7475 | 0.0041 | 55.071 |
| Stainless Steel EN 308 | 0.0141 | 57.273 |
| Cast Iron | 0.0263 | 57.795 |
Table 7.
Safety factor for the studied materials.
Table 7.
Safety factor for the studied materials.
| Crank Angle (Deg) | Pressure (bar) | Material | Safety Factor
|
|---|
| 0 | 35 | Structural Steel |
4.9360
|
| Aluminum Alloy 7475 | 8.897 |
| Stainless steel EN 308 | 4.1904 |
| Cast Iron | 3.8065 |
Table 8.
Frequency and total distortion values Structural Steel.
Table 8.
Frequency and total distortion values Structural Steel.
| Modal No. | Frequency (Hz) | Total Deformation (mm) |
|---|
| 1 | 60.309 | 2.2185 |
| 2 | 95.419 | 2.0404 |
| 3 | 106.77 | 3.2644 |
| 4 | 142 | 3.7015 |
| 5 | 162.94 | 2.3977 |
| 6 | 214.46 | 2.453 |
Table 9.
Frequency and total distortion values Aluminum Alloy 7475.
Table 9.
Frequency and total distortion values Aluminum Alloy 7475.
| Modal No. | Frequency (Hz) | Total Deformation (mm) |
|---|
| 1 |
190.37
| 3.7133 |
| 2 |
303.58
| 3.4104 |
| 3 |
339.74
| 5.4568 |
| 4 |
445.53
| 6.1975 |
| 5 |
514.22
| 4.021 |
| 6 |
682.46
| 4.0997 |
Table 10.
Frequency and total distortion values cast iron.
Table 10.
Frequency and total distortion values cast iron.
| Modal No. | Frequency (Hz) | Total Deformation (mm) |
|---|
| 1 | 46.791 | 2.3143 |
| 2 | 73.654 | 2.1305 |
| 3 | 82.397 | 3.4083 |
| 4 | 110.61 | 3.8606 |
| 5 | 126.43 | 2.498 |
| 6 | 165.52 | 2.5615 |
Table 11.
Frequency and total distortion values Stainless Steel EN 308.
Table 11.
Frequency and total distortion values Stainless Steel EN 308.
| Modal No. | Frequency (Hz) | Total Deformation (mm) |
|---|
| 1 |
61.115
| 2.2174 |
| 2 |
96.447
| 2.0404 |
| 3 |
107.91
| 3.2643 |
| 4 |
144.19
| 3.6994 |
| 5 |
165.13
| 2.395 |
| 6 |
216.76
| 2.4531 |
Table 12.
Materials comparison table for thermal analysis.
Table 12.
Materials comparison table for thermal analysis.
| Material | Structural Steel | Aluminum Alloy 7475 | Cast Iron | Stainless Steel EN 308 |
|---|
| Temperature (°C) |
225
|
225
|
225
| 225 |
| Convection (W/mm2) | 1.6982 | 4.3723 | 1.4105 | 10.361 |
Table 13.
Summary of results for stresses and displacements of the crankshaft.
Table 13.
Summary of results for stresses and displacements of the crankshaft.
| Crank Angle (Deg) | Pressure (bar) | Max Deformation (mm) | Max von Mises Stress (MPa) |
|---|
| 0 | 35 | 0.0149 | 67.298 |
| 30 | 30.3 | 0.0129 | 58.261 |
| 60 | 17.5 | 0.0075 | 33.649 |
| 90 | 0 |
0
|
0
|
| 120 | −17.5 | 0.0075 | 33.649 |
| 150 | −30.3 | 0.0129 | 58.261 |
| 180 | −35 | 0.0149 | 67.298 |
| 210 | −30.3 | 0.0129 | 58.261 |
| 240 | −17.5 | 0.0075 | 33.649 |
| 270 | 0 |
0
|
0
|
| 300 | 17.5 | 0.0075 | 33.649 |
| 330 | 30.3 | 0.0129 | 58.261 |
| 360 | 35 | 0.0149 | 67.298 |
Table 14.
Frequency and total distortion values of Structural Steel.
Table 14.
Frequency and total distortion values of Structural Steel.
| Modal Orders | Frequency (Hz) | Total Deformation (mm) |
|---|
| 1 | 50.255 | 2.3384 |
| 2 | 72.994 | 2.1074 |
| 3 | 77.479 | 3.5969 |
| 4 | 134.13 | 4.0507 |
| 5 | 138.95 | 2.5467 |
| 6 | 153.4 | 2.6443 |