Seismic Resilience of Emergency Departments: A Case Study
Abstract
1. Introduction
2. Proposed Metamodel and Edsh Functionality
2.1. Case Study: Emergency Department of the Sansepolcro Hospital (EDSH)
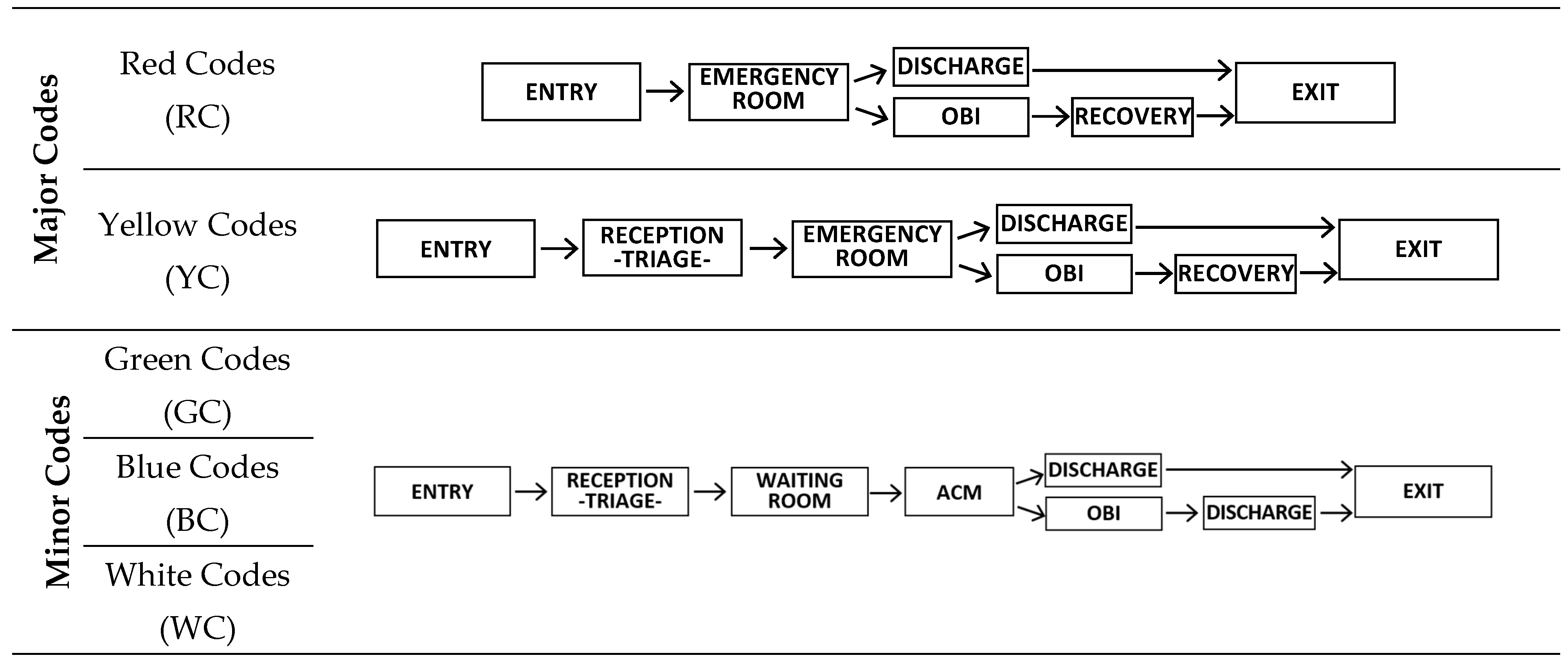
2.2. The EDSH Functions and Selection of Response Parameter
- -
- Reception (REC), where the patients arrive;
- -
- Waiting Room (WR), where patients classified as “Minor Codes” wait for assistance.
- -
- Minor Codes Ambulatory (ACM), where patients classified as “Minor Codes” are visited.
- -
- Short Intensive Observation (OBI), where the patients are left to check their response to the treatment.
- -
- Emergency Room (ER), where patients classified as “Major Codes” receive the first rescue.
- -
- Recovery, where patients classified as “Major Codes” are recovered.
2.3. Systems Affecting the EDSH’s Functionality
2.3.1. The Structure
2.3.2. The Nonstructural Components
2.3.3. The Organizational System
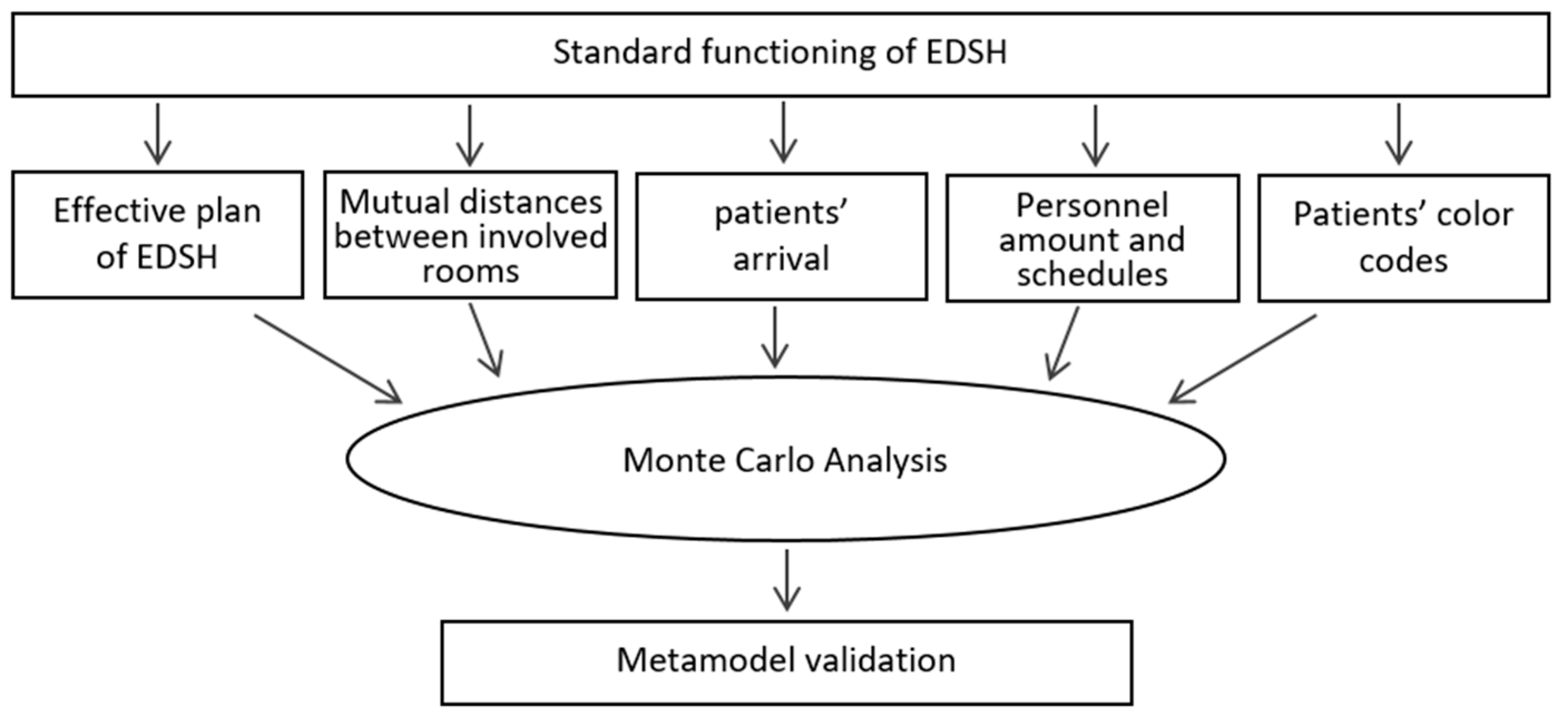
2.4. The Metamodel
2.4.1. Assessment of the WT in Standard Conditions
2.4.2. Assessment of the WT in Emergency Conditions
3. The Seismic Response of the Edsh
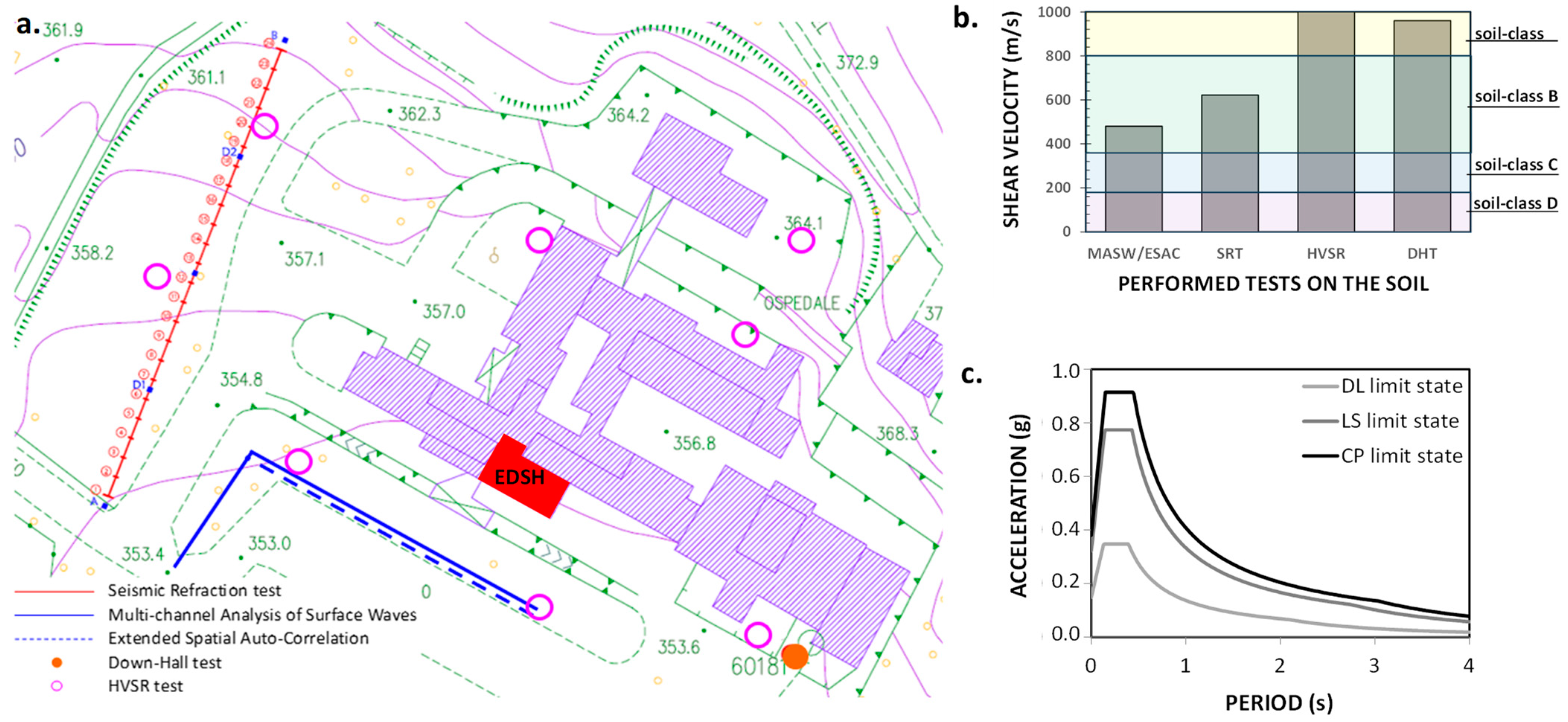
3.1. Seismic Hazard of the Area
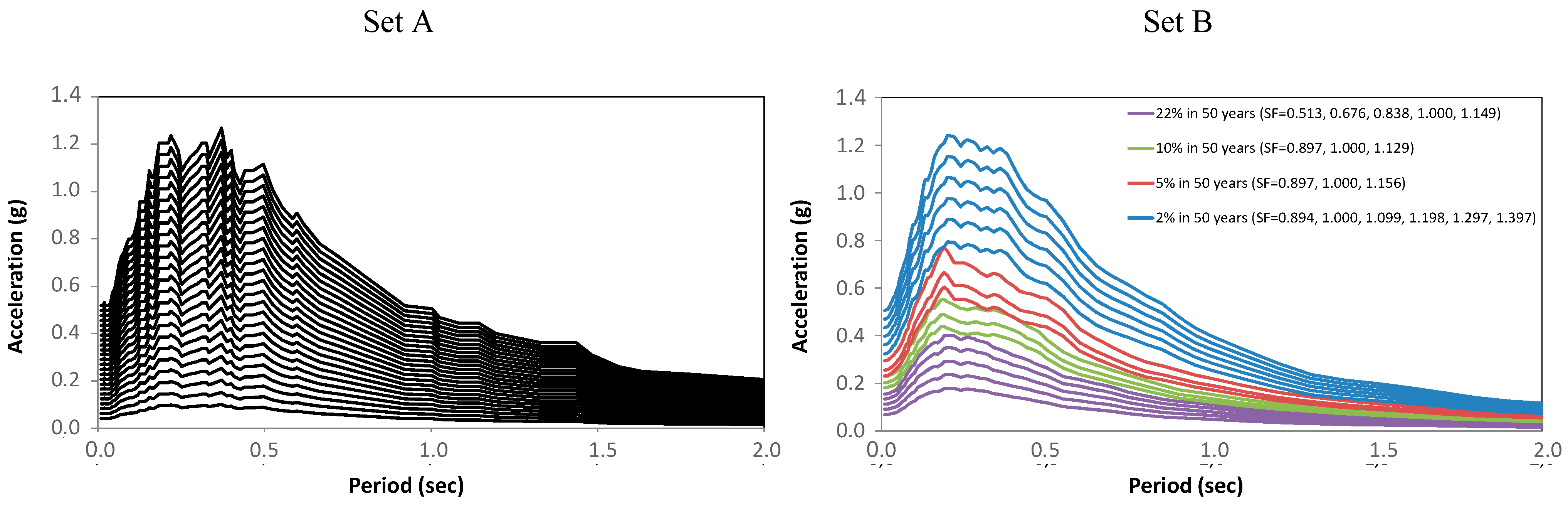
3.2. The Seismic Input
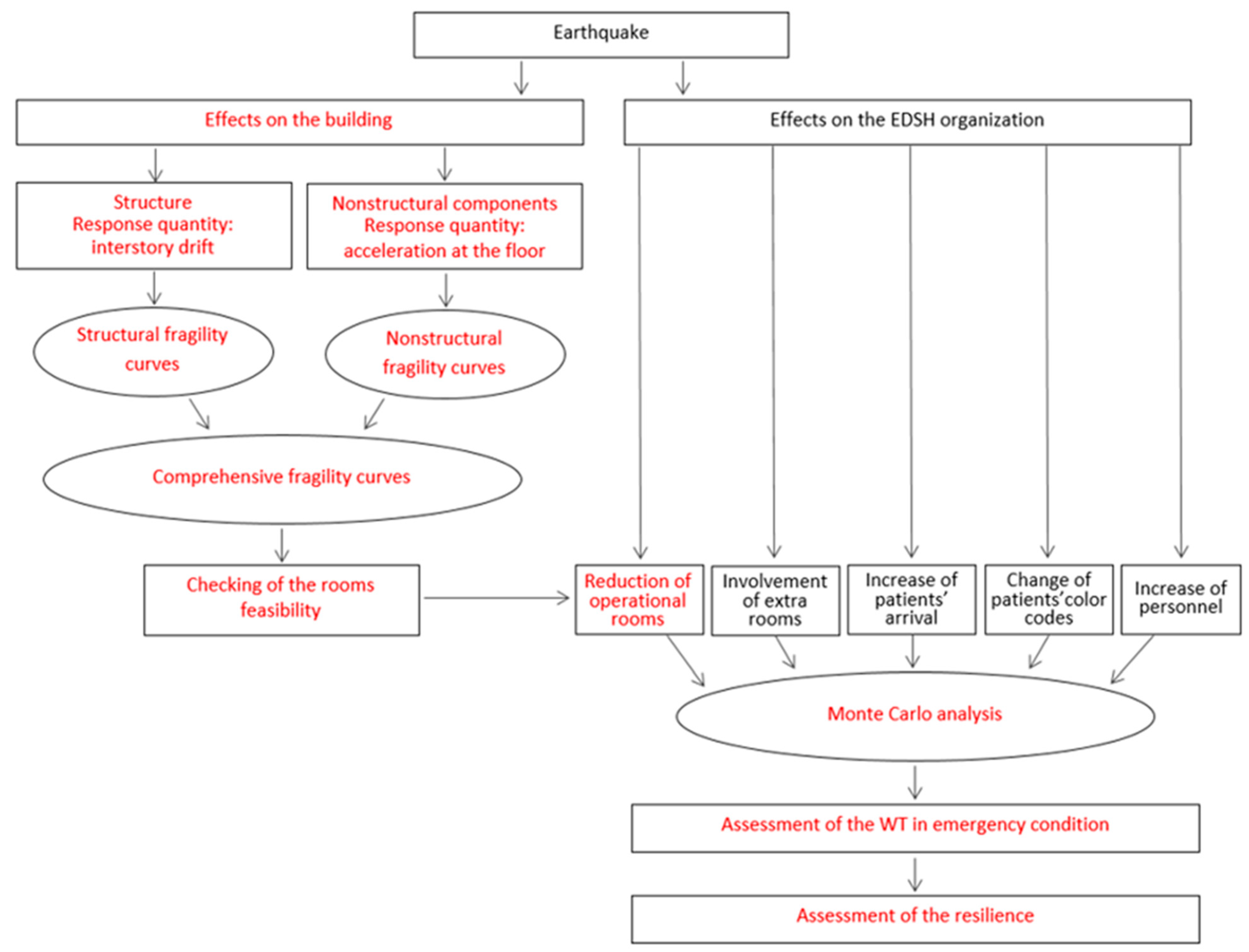
3.3. Effect of the Earthquake on the Physical Systems
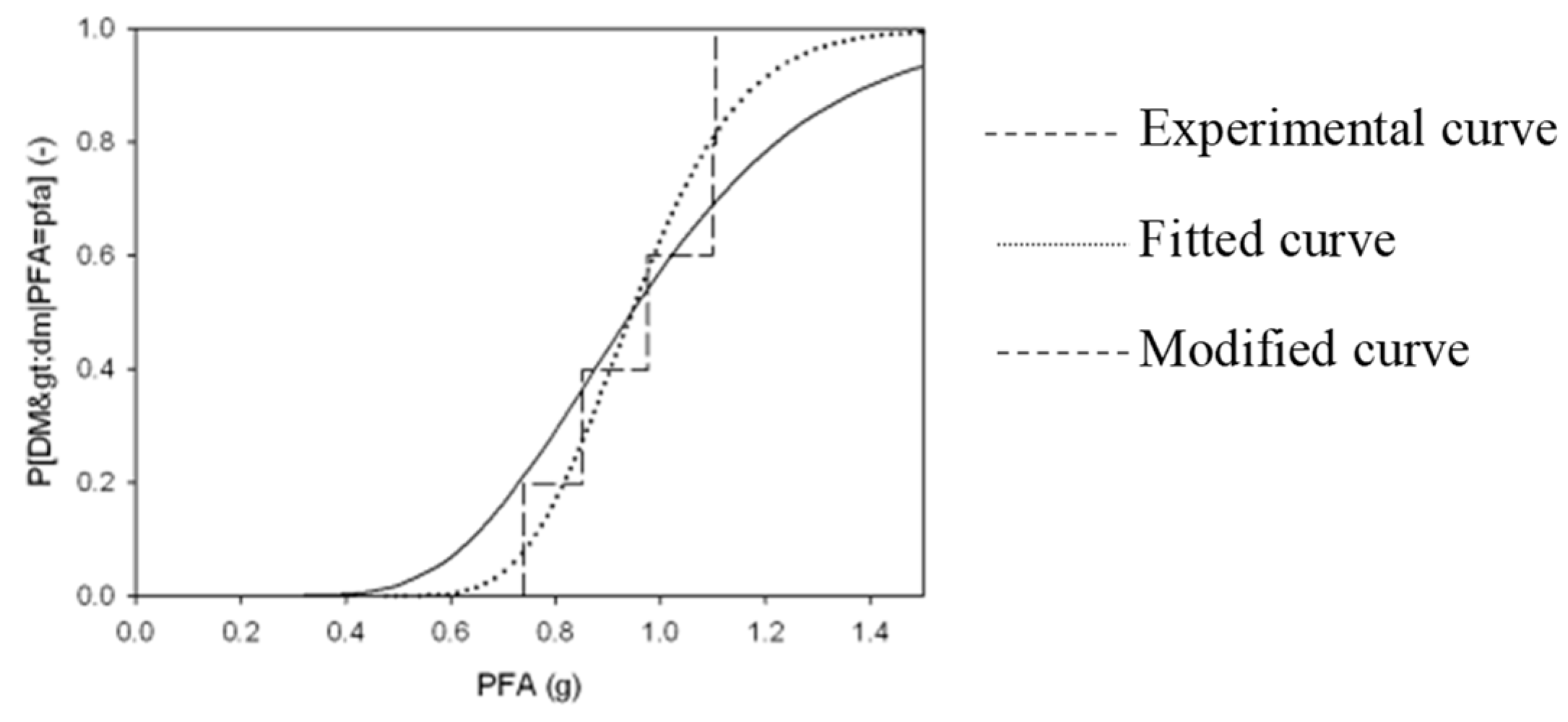
3.3.1. Fragility Curves of the Structure
3.3.2. Fragility Curves of the Nonstructural Components
3.3.3. Damages Scenarios at the Occurring of Seismic Excitation
3.4. Effects of the Earthquake on the Organizational System
3.4.1. Changes in the Demand for Rescue Operations
3.4.2. Changes in the EDSH Organization
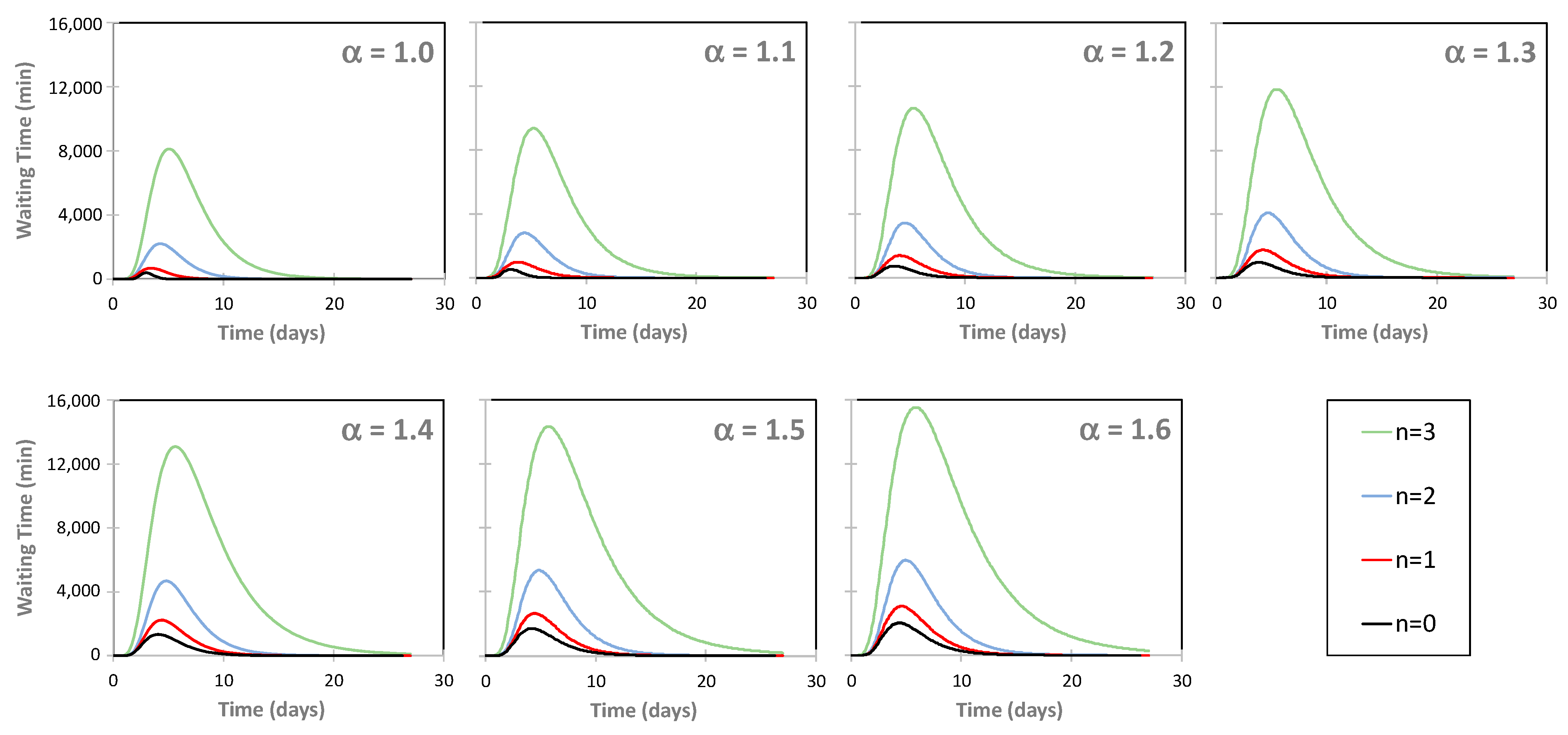
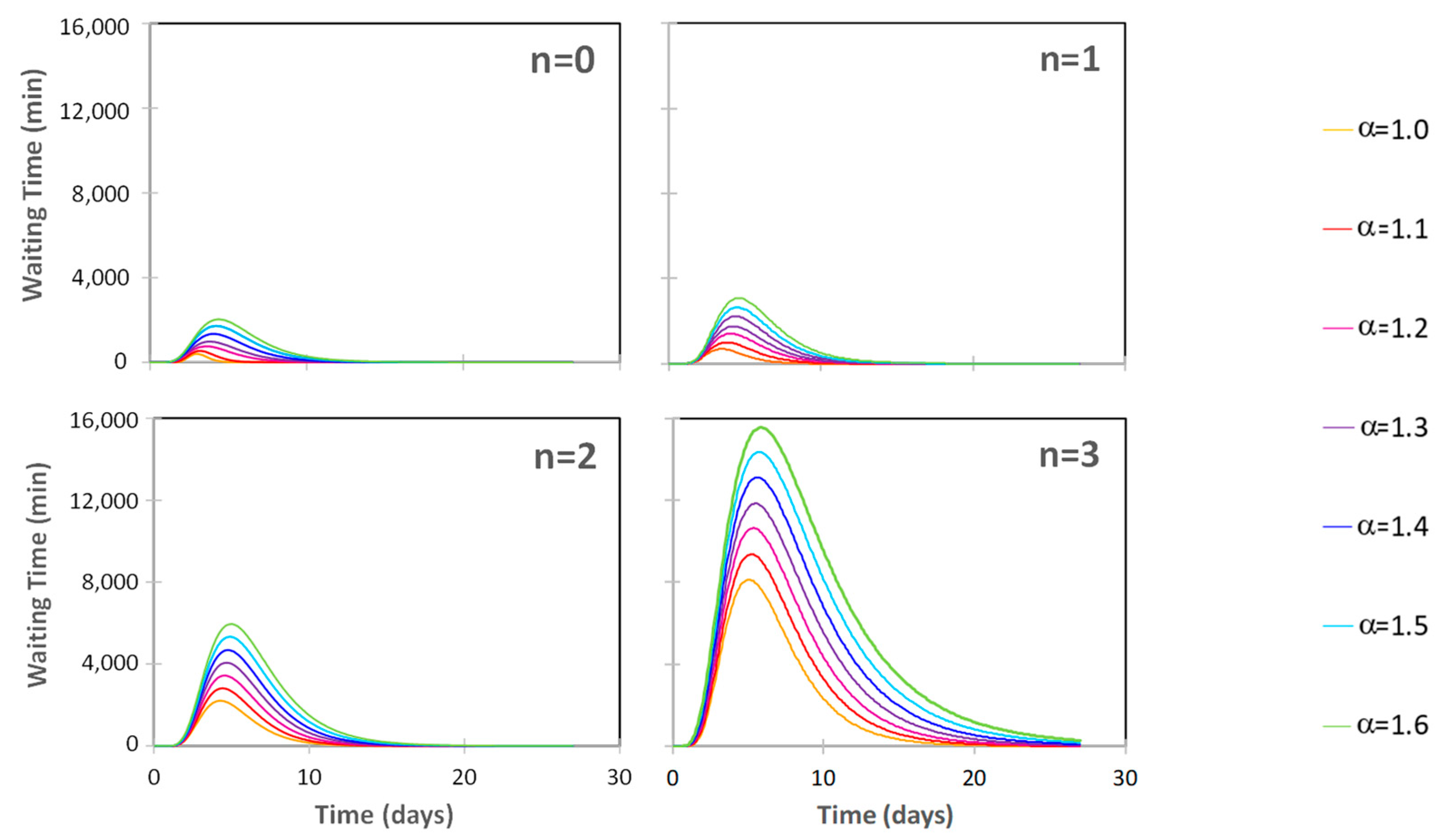
3.5. The EDSH’s Functionality during a Seismic Emergency
4. EDSH Resilience
4.1. Resilience Modeling
4.2. Resilience of the EDSH
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bruneau, M.; Reinhorn, A.M. Overview of the Resilience Concept. In Proceedings of the 8th US National Conference on Earthquake Engineering, San Francisco, FL, USA, 18–22 April 2006; p. 2040. [Google Scholar]
- Bruneau, M.; Reinhorn, A.M. Exploring the Concept of Seismic Resilience for Acute Care Facilities. Earthq. Spectra 2007, 23, 41–62. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Reinhorn, A.M.; Bruneau, M. Framework for analytical quantification of disaster resilience. Eng. Struct. 2010, 32, 3639–3649. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Reinhorn, A.M.; Bruneau, M. Performed-based metamodel for healthcare facilities. Earthq. Eng. Struct. Dyn. 2011, 40, 1197–1217. [Google Scholar] [CrossRef]
- Liu, J.; Zhai, C.; Yu, P. A probabilistic framework to evaluate seismic resilience of hospital buildings using baysian networks. Reliab. Eng. Syst. Saf. 2022, 226, 1086444. [Google Scholar] [CrossRef]
- Chang, S.; Shinozuka, M. Measuring improvements in the disaster resilience of communities. Earthq. Spectra 2004, 20, 739–755. [Google Scholar] [CrossRef]
- Ardagh, M.W.; Richardson, S.K.; Robinson, V.; Than, M.; Gee, P.; Henderson, S.; Khodaverdi, L.; McKie, J.; Robertson, G.; Schroeder, P.P.; et al. The initial health-system response to the earthquake in Christchurch, New Zealand, in February 2011. Lancet 2012, 379, 2109–2115. [Google Scholar] [CrossRef] [PubMed]
- Bruneau, M.; Chang Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Masanobu Shinozuka, M.; Tierney, K.; Wallace, W.A.; Winterfeldt, D. A Framework to Quantitatively Assess and Enhance the Seismic Resilience of Communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Ceferino, L.; Mitrani-Reiser, J.; Kiremidjian, A.; Deierlein, G.; Bambarén, C. Effective plans for hospital system response to earthquake emergencies. Nat. Commun. 2020, 11, 4325. [Google Scholar] [CrossRef]
- Tariverdi, M.; Miller-Hooks, E.; Kirsch, T. Strategies for improved hospital response to mass casualty incidents. Disaster Med. Public Health Prep. 2018, 12, 778–790. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Piquet, M. Resilience of a hospital emergency department under seismic event. Adv. Struct. Eng. 2016, 19, 825–836. [Google Scholar] [CrossRef]
- Hassan, E.M.; Mahmoud, H. An integrated socio-technical approach for postearthquake recovery of interdependent healthcare system. Reliab. Eng. Syst. Saf. 2020, 201, 106953. [Google Scholar] [CrossRef]
- Viti, S.; Cimellaro, G.P.; Reinhorn, A.M. Retrofit of hospital through strength reduction and enhanced damping. Smart Struct. Syst. 2006, 2, 339–355. [Google Scholar] [CrossRef]
- Nuti, C.; Vanzi, I. Assessment of post-earthquake availability of hospital system and upgrading strategies. Earthq. Eng. Struct. Dyn. 1998, 27, 1403–1423. [Google Scholar] [CrossRef]
- WHO. Health Facility Seismic Health Facility Seismic Vulnerability Evaluation; WHO: Geneva, Switzerland, 2006. [Google Scholar]
- Badillo-Almarez, H.; Reinhorn, A.M.; Whittaker, A. Seismic Fragility of Suspended Ceiling Systems. Earthq. Spectra 2007, 23, 21–40. [Google Scholar] [CrossRef]
- Myrtle, R.C.; Masri, S.F.; Nigbor, R.L.; Caffrey, J.P. Classification and prioritization of essential systems in hospitals under extreme events. Earthq. Spectra 2005, 21, 779–802. [Google Scholar] [CrossRef]
- Miniati, R.; Iasio, C. Methodology for rapid seismic risk assessment of health structures: Case study of the hospital system in Florence, Italy. Int. J. Disaster Risk Reduct. 2012, 2, 16–24. [Google Scholar] [CrossRef]
- Masi, A.; Santarsiero, G.; Chiauzzi, L. Vulnerability Assessment and Seismic Risk Reduction Strategies of Hospitals in Basilicata Region (Italy). In Proceedings of the 15th World Conference on Earthquake Engineering—WCEE, Lisbon, Portugal, 24–28 September 2012; pp. 1–10. [Google Scholar]
- Uma, S.R.; Beattie, G.J. Seismic Assessment of Engineering Systems in Hospitals—A Challenge for Operational Continuity. In Proceedings of the New Zealand Society for Earthquake Engineering Annual Meeting, Auckland, New Zealand, 14–16 April 2010. [Google Scholar]
- Davenport, P.N. Review of seismic provisions of historic New Zealand loading codes. In New Zealand Society for Earthquake Engineering Annual Meeting; National Academies Press: Washington, DC, USA, 2004. [Google Scholar]
- IoM. Hospital-Based Emergency Care: At the Breaking Point; Project Retrofitting Studies; IPDED, I.P.D. and E.D.: Washington, DC, USA, 2010. [Google Scholar]
- ASPR. Hospital Preparedness Program. 2013. Available online: http://www.phe.gov/preparedness/plann (accessed on 6 January 2020).
- Hossain, L.; Kit, D.C. Modeling coordination in hospital emergency departments through social network analysis. Disasters 2012, 36, 338–364. [Google Scholar] [CrossRef]
- Fawcett, W.; Oliveira, C.S. Casualty treatment after earthquake disasters: Development of a regional simulation model. Disasters 2000, 24, 271–287. [Google Scholar] [CrossRef]
- Porter, K.; Ramer, K. Estimating earthquake-induced failure probability and downtime of critical facilities. J. Bus. Contin. Emerg. Plan. 2012, 5, 352–364. [Google Scholar]
- Unanwa, C.O.; McDonald, J.R.; Mehta, K.C.; Smith, D.A. The development of wind damage bands for buildings. J. Wind Eng. Ind. Aerodyn. 2000, 84, 119–149. [Google Scholar] [CrossRef]
- Jacques, C.C.; McIntosh, J.; Giovinazzi, S.; Kirsch, T.D.; Wilson, T.; Mitrani-Reiser, J. Resilience of the Canterbury Hospital System to the 2011 Christchurch Earthquake. Earthq. Spectra 2014, 30, 533–554. [Google Scholar] [CrossRef]
- Alowad, A.; Samaranayake, P.; Ahshan, K.B.; Karim, A. Enhancing patient flow in emergency department (ED) using lean strategies–an integrated voice of customer and voice of process perspective. Bus. Process Manag. J. Bus. 2020, 27, 75–105. [Google Scholar] [CrossRef]
- Sabir, S.M.; Mustafa, F.A. Performance-based building design: Impact of emergency department layout on its functional performance efficiency—The case of Erbil hospitals. Open House Int. 2023, 48, 840–862. [Google Scholar] [CrossRef]
- Setola, R. Availability of healthcare services in a networkbased scenario. Int. J. Netw. Vis. Organ. 2007, 4, 130–144. [Google Scholar]
- Kuwata, Y.; Takada, S. Seismic risk assessment of lifeline considering hospital functions. Asian J. Civ. Eng. 2007, 21, 315–328. [Google Scholar]
- Yao, G. Identification of earthquake damaged operational and functional components in hospital buildings. J. Chin. Inst. Eng. 2000, 23, 409–416. [Google Scholar] [CrossRef]
- Lupoi, G.; Franchin, P.; Lupoi, A.; Pinto, P.E.; Calvi, G.M. Probabilistic Seismic Assessment for Hospitals and Complex-Social Systems; IUSS Press: Pavia, Italy, 2008. [Google Scholar]
- Leontief, W.W. Input-Output Economics, 2nd ed.; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Haimes, Y.Y.; Horovitz, B.M.; Lambert, J.H.; Santos, J.R.; Lian, C.; Crowther, K.G. Inoperability input–output model for interdependent infrastructures sectors. I: Theory and methodology. J. Infrastruct. Syst. 2005, 11, 67–79. [Google Scholar] [CrossRef]
- Lee, E.E., II; Mitchell, J.E.; Wallace, W.A. Restoration of Services in Interdependent Infrastructure Systems: A Network Flows Approach. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2007, 37, 1303–1317. [Google Scholar] [CrossRef]
- Arboleda, C.A.; Abraham, D.M.; Lubitz, R.M. Simulation as a tool to assess the vulnerability of the operation of a health care facility. J. Perform. Constr. Facil. 2007, 21, 302–312. [Google Scholar] [CrossRef]
- Yavari, S.; Chang, S.E.; Elwood, K.J. Modeling post-earthquake functionality of regional health care facilities. Earthq. Spectra 2010, 26, 869–892. [Google Scholar] [CrossRef]
- McCabe, O.L.; Barnett, D.J.; Taylor, H.G.; Links, J.M. Ready, willing, and able: A framework for improving the public health emergency preparedness system. Disaster Med. Public Health Prep. 2010, 4, 161–168. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Fumo, C.; Reinhorn, A.M.; Bruneau, M. Seismic resilience of health care facilities. In Proceedings of the 14th World Conference on Earthquake Engineering (14WCEE), Beijing, China, 12–17 October 2008. [Google Scholar]
- Miles, S.B.; Chang, S.E. Modeling community recovery from earthquakes. Earthq. Spectra 2006, 22, 439–458. [Google Scholar] [CrossRef]
- Pianigiani, M.; Viti, S. Functionality analysis of emergency departments: A case study. J. Build. Eng. 2021, 40, 1–13. [Google Scholar] [CrossRef]
- McCarthy, K.; McGee, H.M.; O’Boyle, C.A. Outpatient clinic waiting times and nonattendance as indicators of quality. Psychol. Health Med. 2000, 5, 287. [Google Scholar] [CrossRef]
- Thompson, D.A.; Yarnold, P.R. Relating patient satisfaction to waiting time perceptions and expectations: The disconfirmation paradigm. Acad. Emerg. Med. Off. J. Soc. Acad. Emerg. Med. 1995, 2, 1057–1062. [Google Scholar] [CrossRef] [PubMed]
- Thompson, D.A.; Paul, R.; Yarnold, P.R.; Williams, D.R.; Adams, S.L. Effects of actual waiting time, perceived waiting time, information delivery, and expressive quality on patient satisfaction in the emergency department. Ann. Emerg. Med. 1996, 28, 657. [Google Scholar] [CrossRef]
- Richards, M.E.; Crandall, C.S.; Hubble, M.W. Influence of ambulance arrival on emergency department time to be seen. Prehospital Emerg. Care 2006, 12, 440–446. [Google Scholar] [CrossRef]
- Przelazloski, K. Collapse Fragility Analysis on Sansepolcro Hospital Structure. Master’s Dissertation, Università degli Studi di Pavia, Pavia, Italy, 2014. [Google Scholar]
- NTC. Norme Tecniche per le Costruzioni; Decreto Ministeriale 14 gennaio 2008; Ministero Infrastrutture e Trasporti G.U.R.I. 4 Febbraio: Roma, Italy, 2008. (In Italian) [Google Scholar]
- Pianigiani, M. Seismic Resilience of Hospital Systems. Ph.D. Dissertation, Università degliu Studi di Firenze, Firenze, Italy, 2016. [Google Scholar]
- Price, R.N. ProModel Manufacturing Simulation Software: Reference Guide; Version 4.2; ProModel Corporation: Orem, UT, USA, 1999. [Google Scholar]
- NTC. Aggiornamento delle Norme Tecniche per le Costruzioni; Decreto Ministeriale 17 gennaio 2018; Ministero delle Infrastrutture e dei Trasporti, G.U.R.I. n. 42 del 20 febbraio: Roma, Italy, 2018. (In Italian) [Google Scholar]
- Viti, S.; Tanganelli, M.; D’Intinosante, V.; Baglione, M. Effects of Soil Characterization on the Seismic Input. J. Earthq. Eng. 2017, 23, 487–511. [Google Scholar] [CrossRef]
- FEMA. Quantification of Building Seismic Performance Factors, FEMA P-695; Applied Technology Council for the Federal Emergency Management Agency: Washington, DC, USA, 2009. [Google Scholar]
- Pianigiani, M.; Przelazloski, K.; Christovasilis, I.P.; Cimellaro, G.P.; De Stefani, M.; Filiatrault, A.; Sullivan, T.J.; Tanganelli, M. A comprehensive methodology for evaluating the seismic resilience of health care facilities considering nonstructural components and organizational models. In Second European Conference on Earthquake andn Seismology; European Association for Earthquake Engineering (EAEE): Istanbul, Turkey, 2014; pp. 1–4. [Google Scholar]
- Cosenza, E.; Di Sarno, L.; Maddaloni, G.; Maddaloni Magliulo, G.; Petrone, C.; Prota, A. Shake table tests for the seismic fragility evaluation of hospital rooms. Earthq. Eng. Struct. Dyn. 2014, 44, 23–40. [Google Scholar] [CrossRef]
- Aroni, S.; Durkin, M. Injuries and Occupant Behavior in Earthquakes; Samuel Aroni and Romulus Constantinescu: Washington, DC, USA, 1987. [Google Scholar]
- Cheu, D.H. Northridge Earthquake, 17 January 1994: California Seismic Safety Commission, Sacramento, The Hospital Response. 1994. Available online: https://www.govinfo.gov/content/pkg/GOVPUB-C13-80b021981b7845eb8e7d09b3aa8d4c7f/pdf/GOVPUB-C13-80b021981b7845eb8e7d09b3aa8d4c7f.pdf (accessed on 9 February 2024).
- Durkin, M.E. Fatalities, Non-Fatal Injuries and Medical Aspects of a Northridge Earthquake; EEFIT: L’Aquila, Italy, 2009; pp. 1–54. [Google Scholar]
- Olson, R.A.; Alexander, D.E. Summary of Proceedings. In Second National Workshop on Modelling Earthquake Casualties for Planning and Response; Jesuit Retreat House: Los Altos, CA, USA, 1996. [Google Scholar]
- Salinas, C.; Salinas, C.; Kurata, J. The effects of Northridge Earthquake on the Pattern of Emergency Department Care. Am. J. Emerg. Med. 1998, 16, 254–256. [Google Scholar] [CrossRef] [PubMed]
- Kafali, C.; Grigoriu, M. Rehabilitation decision analysis. In Proceedings of the 9th International Conference on Structural Safety and Reliability, Rome, Italy, 19–23 June 2005. [Google Scholar]
- Chang, S.; Svekla, W.D.; Shinouza, M. Linking infrastructure and urban economy—Simulation of water disruption impacts in Earthquakes. Environ. Plan. B Plan. Des. 2002, 29, 281–301. [Google Scholar] [CrossRef]





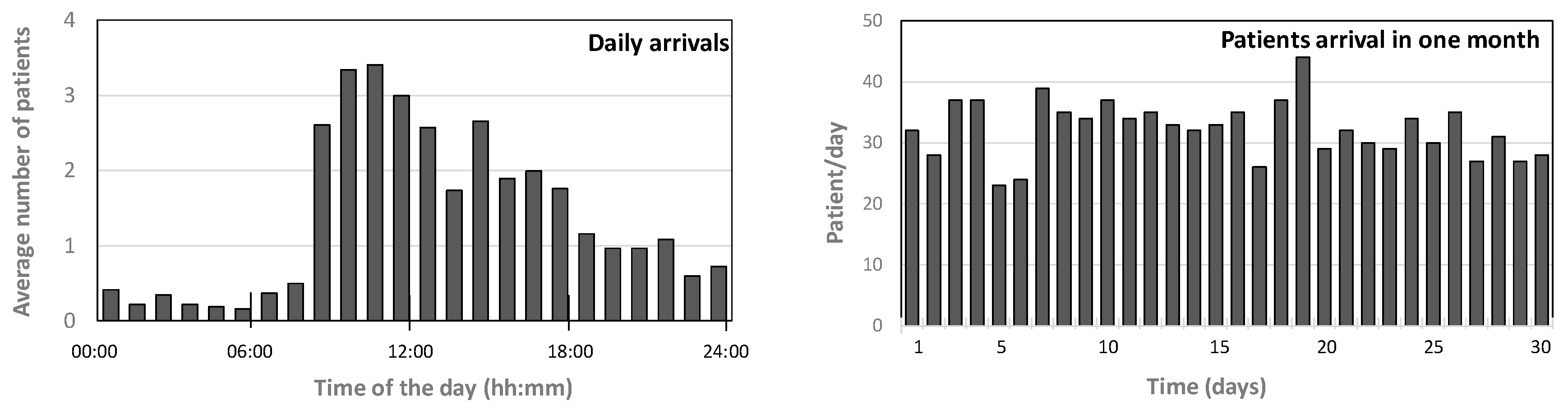












| Estimated Time (in min) of Stay for Each Color Code | Mutual Distances (in meters) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Red | Yellow | Green | Blue | White | Entry | REC | ER | WR | ACM | OBI | ||
| (0.5%) | (10.6%) | (45.1%) | (1.72%) | (41.8%) | Entry | 0 | 20 | 9 | 25 | 25 | 25 | |
| Entry | REC | 0 | 10 | 3 | 10 | 10 | ||||||
| REC | 2–5 | 2–5 | 5–10 | 5–10 | 5–10 | ER | 0 | 12.5 | 17.5 | 13 | ||
| ER | 15–30 | 15–30 | WR | 0 | 12 | 12 | ||||||
| ACM | 10–20 | 10–15 | 5–10 | ACM | 0 | 18 | ||||||
| OBI | 240–2880 | OBI | 0 | |||||||||
| ID | Event Name | Recording Station | PGA | ID | Event Name | Recording Station | PGA |
|---|---|---|---|---|---|---|---|
| 1 | Northridge, CA | Beverly Hills—14145 Mulhol | 0.52 | 12 | Lander, CA | Coolwater | 0.42 |
| 2 | Northridge, CA | Canyon Country—W Lost Cany | 0.48 | 13 | Loma Prieta, CA | Capitola | 0.53 |
| 3 | Duzce, Turkey | Bolu | 0.82 | 14 | Loma Prieta, CA | Gilroy Array #3 | 0.56 |
| 4 | Hector Mine, CA | Hector | 0.34 | 15 | Manjil, Iran | Abbar | 0.51 |
| 5 | Imperial Valley, CA | Delta | 0.35 | 16 | Superstition Hills, CA | El Centro Imp. Co. Cent | 0.36 |
| 6 | Imperial Valley, CA | El Centro Array #11 | 0.38 | 17 | Superstition Hills, CA | Poe Road (temp) | 0.45 |
| 7 | Kobe, Japan | Nishi-Akashi | 0.51 | 18 | Cape Mendocino, CA | Rio Dell Overpass—FF | 0.55 |
| 8 | Kobe, Japan | Shin-Osaka | 0.24 | 19 | Chi-Chi, Taiwan | CHY101 | 0.44 |
| 9 | Kocaelia, Turkey | Duzce | 0.36 | 20 | Chi-Chi, Taiwan | TCU045 | 0.51 |
| 10 | Kocaelia, Turkey | Arcelik | 0.22 | 21 | San Fernando, CA | LA—Hollywood Stor FF | 0.21 |
| 11 | Lander, CA | Yermo Fire Station | 0.24 | 22 | Friuli, Italy | Tolmezzo | 0.35 |
| 22% in 50 Years | 10% in 50 Years | ||||||
|---|---|---|---|---|---|---|---|
| No | Event Name | Recording Station | PGA | No | Event Name | Recording Station | PGA |
| 1 | Northridge, CA | LA—N Figueroa St | 0.29 | 1 | Coalinga, CA | Palmer Ave | 0.29 |
| 2 | Whittier Narrows, CA | LA—Baldwin Hills | 0.18 | 2 | Chi-Chi, Taiwan | CHY032 | 0.18 |
| 3 | Northridge, CA | Burbank—Howard Rd. | 0.20 | 3 | Northridge, CA | Manhattan Beach—Manhattan | 0.20 |
| 4 | Northwest China | Jiashi | 0.37 | 4 | Coalinga, CA | Skunk Hollow | 0.37 |
| 5 | Northridge, CA | Newhall—Fire Station | 0.45 | 5 | Sierra Madre, CA | Altadena—Eaton Canyon | 0.45 |
| 6 | Northridge, CA | Santa Barbara—UCSB Goleta | 0.23 | 6 | Northridge, CA | Downey—Co Maint Bldg | 0.23 |
| 7 | Hector Mine, CA | Fun Valley | 0.22 | 7 | Chi-Chi, Taiwan | TCU075 | 0.22 |
| 8 | Chi-Chi, Taiwan | CHY088 | 0.34 | 8 | Chi-Chi, Taiwan | TCU079 | 0.34 |
| 9 | Landers, CA | Fort Irwin | 0.28 | 9 | Sierra Madre, CA | Pasadena—USGS/NSMP Office | 0.28 |
| 10 | Chi-Chi, Taiwan | CHY015 | 0.49 | 10 | Northridge, CA | LA—Univ. Hospital | 0.49 |
| 11 | Taiwan SMART1 | SMART1 M07 | 0.18 | 11 | Mammoth Lakes, CA | Convict Creek | 0.18 |
| 12 | Chi-Chi, Taiwan | TCU129 | 0.14 | 12 | Taiwan SMART1 | SMART1 E02 | 0.14 |
| 13 | Irpinia, Italy | Rionero In Vulture | 0.20 | 13 | Hollister, CA | Hollister City Hall | 0.20 |
| 14 | Northridge, CA | Compton—Castlegate St | 0.14 | 14 | Northridge, CA | Lakewood—Del Amo Blvd | 0.14 |
| 15 | Imperial Valley, CA | Niland Fire Station | 0.27 | 15 | Prarkfield, CA | Cholame—Shandon Array #8 | 0.27 |
| 16 | Whittier Narrows, CA | La Habra—Briarcliff | 0.21 | 16 | Northridge, CA | LA—116th St School | 0.21 |
| 17 | Chi-Chi, Taiwan | HWA058 | 0.26 | 17 | Northridge, CA | San Gabriel—E Grand Ave | 0.26 |
| 18 | Whittier Narrows, CA | San Marino—SW Academy | 0.27 | 18 | Kalamata, Greece | Kalamata | 0.27 |
| 19 | Mammoth Lakes, CA | Mammoth Lakes H. S. | 0.19 | 19 | Loma Prieta, CA | Fremont—Emerson Court | 0.19 |
| 20 | Sierra Madre, CA | Cogswell Dam-Right Abutment | 0.23 | 20 | Whittier Narrows, CA | El Monte—Fairview Av | 0.23 |
| 21 | Northridge, CA | Northridge—17645 Saticoy St | 0.61 | 21 | Coalinga, CA | Coalinga-14th & Elm (Old CHP) | 0.61 |
| 22 | Northwest China | Jiashi | 0.18 | 22 | Northridge, CA | Moorpark—Fire Station | 0.18 |
| 5% in 50 Years | 2% in 50 Years | ||||||
| No | Event Name | Recording Station | PGA | No | Event Name | Recording Station | PGA |
| 1 | Prarkfield, CA | Cholame—Shandon Array #5 | 0.44 | 1 | Tabas, Iran | Dayhook | 0.41 |
| 2 | Northridge, CA | Pacific Palisades—Sunset | 0.47 | 2 | North Palm Springs, CA | Desert Hot Springs | 0.33 |
| 3 | Northridge, CA | LA—N Westmoreland | 0.40 | 3 | Northridge, CA | Beverly Hills—12520 Mulhol | 0.62 |
| 4 | Whittier Narrows, CA | Downey—Birchdale | 0.30 | 4 | Northridge, CA | LA 00 | 0.39 |
| 5 | Kern County, CA | Taft Lincoln School | 0.18 | 5 | Chi-Chi, Taiwan | TCU080 | 0.54 |
| 6 | Chi-Chi, Taiwan | TCU075 | 0.22 | 6 | Coalinga, CA | Cantua Creek School | 0.28 |
| 7 | Chi-Chi, Taiwan | CHY088 | 0.26 | 7 | Coyote Lake, CA | Gilroy Array #6 | 0.43 |
| 8 | San Fernando, CA | LA—Hollywood Stor FF | 0.21 | 8 | Northwest China | Jiashi | 0.30 |
| 9 | Chi-Chi, Taiwan | CHY010 | 0.23 | 9 | Northridge, CA | Stone Canyon | 0.39 |
| 10 | Chi-Chi, Taiwan | CHY047 | 0.14 | 10 | Chalfant Valley, CA | Bishop—LADWP South St | 0.25 |
| 11 | San Fernando, CA | Castaic—Old Ridge Route | 0.32 | 11 | Chi-Chi, Taiwan | TCU078 | 0.47 |
| 12 | Chalfant Valley, CA | Bishop—LADWP South St | 0.25 | 12 | Managua, Nicaragua | Managua, ESSO | 0.42 |
| 13 | Imperial Valley, CA | Calexico Fire Station | 0.27 | 13 | Chi-Chi, Taiwan | TCU078 | 0.39 |
| 14 | Northridge, CA | LA—Fletcher Dr | 0.24 | 14 | Northridge, CA | LA—Chalon Rd | 0.23 |
| 15 | Kobe, Japan | Tadoka | 0.29 | 15 | Corinth, Greece | Corinth | 0.30 |
| 16 | Chi-Chi, Taiwan | ILA067 | 0.20 | 16 | Imperial Valley, CA | SAHOP Casa Flores | 0.51 |
| 17 | Whittier Narrows, CA | LA—Fletcher Dr | 0.21 | 17 | Friuli, Italy | Tolmezzo | 0.35 |
| 18 | Whittier Narrows, CA | Garvey Res.—Control Bldg | 0.46 | 18 | North Palm Springs, CA | Whitewater Trout Farm | 0.61 |
| 19 | Loma Prieta, CA | Gilroy—Gavilan Coll. | 0.36 | 19 | Coalinga, CA | Oil City | 0.87 |
| 20 | Chi-Chi, Taiwan | TCU129 | 0.95 | 20 | Chi-Chi, Taiwan | TCU095 | 0.71 |
| 21 | Prarkfield, CA | Cholame—Shandon Array #5 | 0.29 | 21 | Northridge, CA | Pacoima Dam (downstream) | 0.43 |
| 22 | Northridge, CA | Pacific Palisades—Sunset | 0.39 | 22 | Yountville, CA | Napa Fire Station #3 | 0.51 |
| WT Curve | Functionality Curve | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Point | X-Coordinate (Days) | Y-Coordinate (Minutes) | Point | X-Coordinate (Days) | Y-Coordinate (%) | ||||
| General | α = 1, n = 3 | General | α = 1, n = 3 | General | α = 1, n = 3 | General | α = 1, n = 3 | ||
| A | 0 | 0 | 0 | 0 | A | 0 | 0 | 100 | 100 |
| B | t0 | 2 | 0 | 0 | B | t0 | 2 | 100 | 100 |
| C | t0 | 2 | WT peak | 8195.8 | C | t0 | 2 | Residual functionality | 0 |
| D | t0 + normalized recovery time | 10.636 | 0 | 0 | D | t0 + equivalent recovery time | 10.636 | 100 | 100 |
| E | Simulation end | 27.77 | 0 | 0 | E | Simulation end | 27.77 | 0 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pianigiani, M.; Viti, S.; Tanganelli, M. Seismic Resilience of Emergency Departments: A Case Study. Modelling 2024, 5, 315-338. https://doi.org/10.3390/modelling5010017
Pianigiani M, Viti S, Tanganelli M. Seismic Resilience of Emergency Departments: A Case Study. Modelling. 2024; 5(1):315-338. https://doi.org/10.3390/modelling5010017
Chicago/Turabian StylePianigiani, Maria, Stefania Viti, and Marco Tanganelli. 2024. "Seismic Resilience of Emergency Departments: A Case Study" Modelling 5, no. 1: 315-338. https://doi.org/10.3390/modelling5010017
APA StylePianigiani, M., Viti, S., & Tanganelli, M. (2024). Seismic Resilience of Emergency Departments: A Case Study. Modelling, 5(1), 315-338. https://doi.org/10.3390/modelling5010017








