Analytical Modeling of Residual Stress in Laser Powder Bed Fusion Considering Volume Conservation in Plastic Deformation
Abstract
1. Introduction
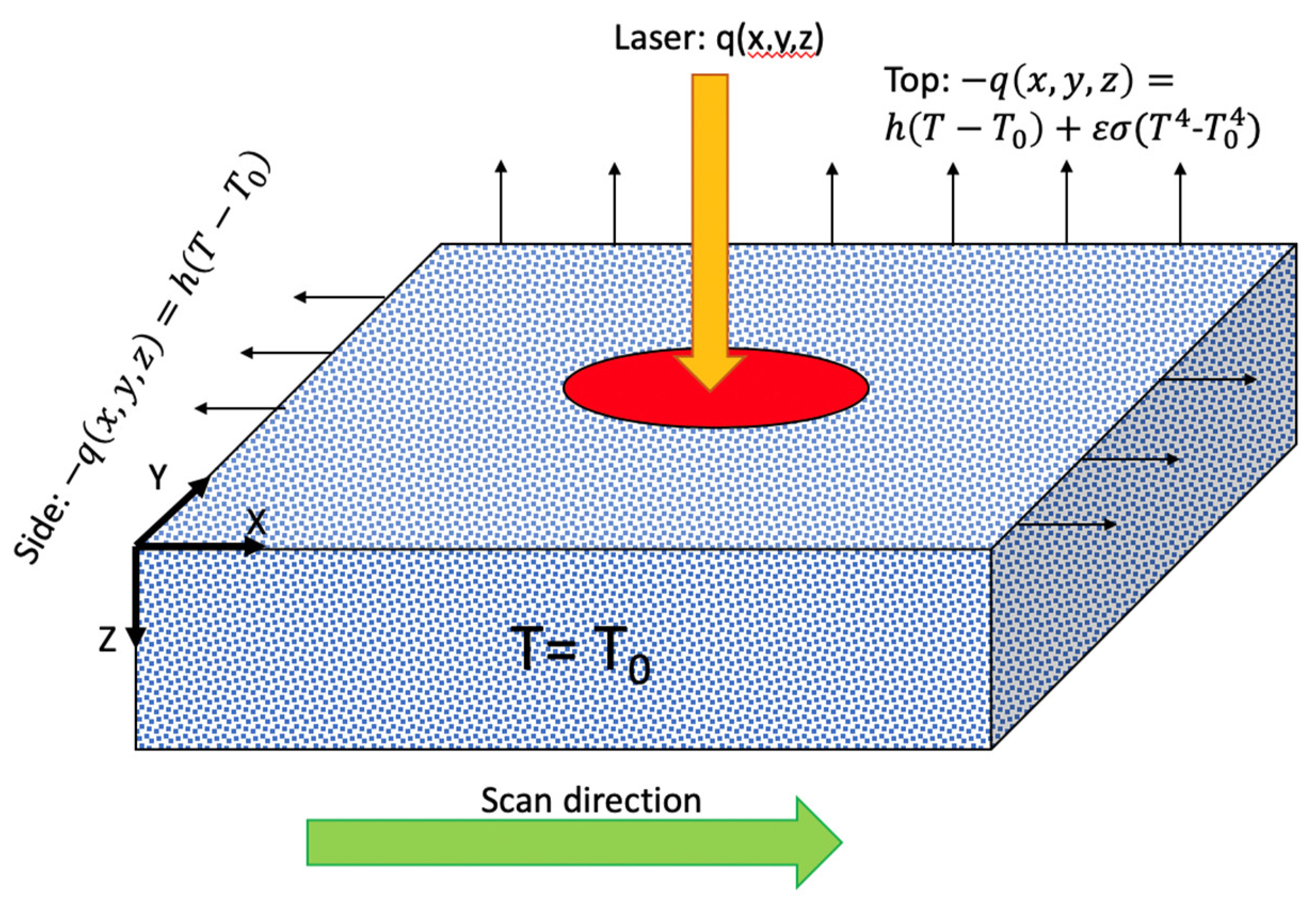
2. Process Modeling
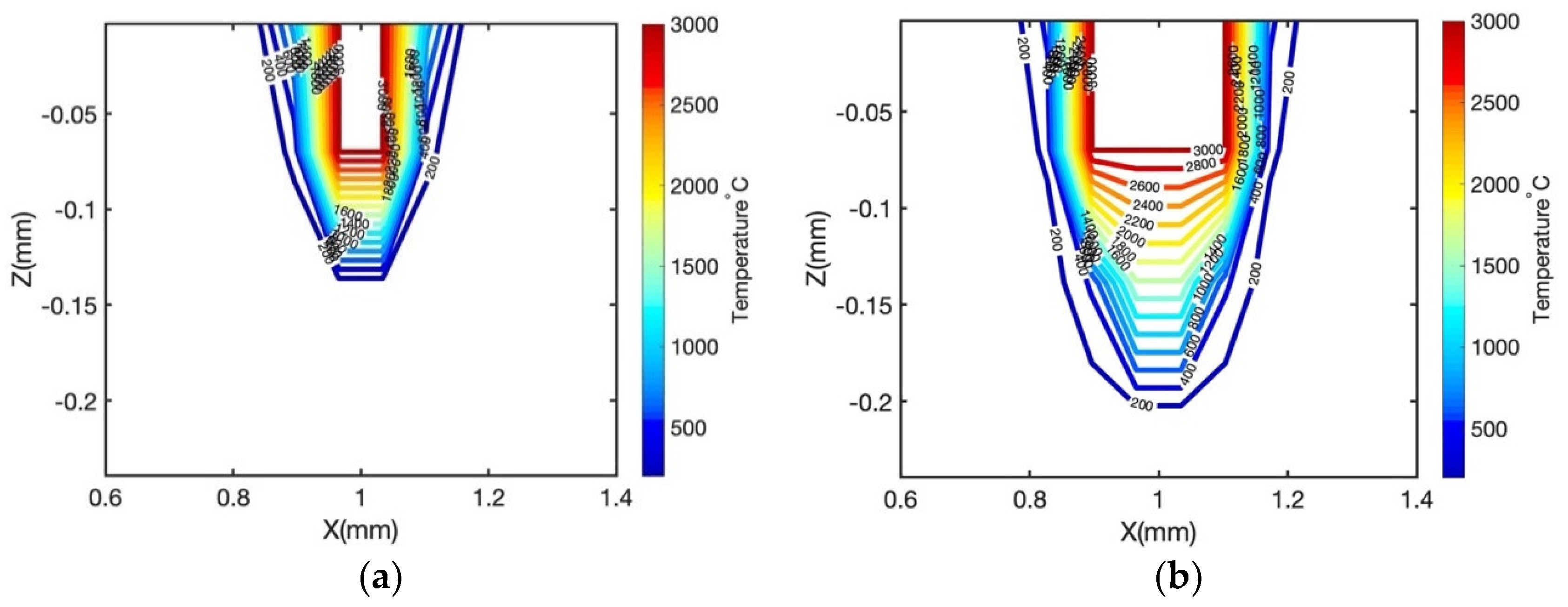
2.1. Thermal Analysis
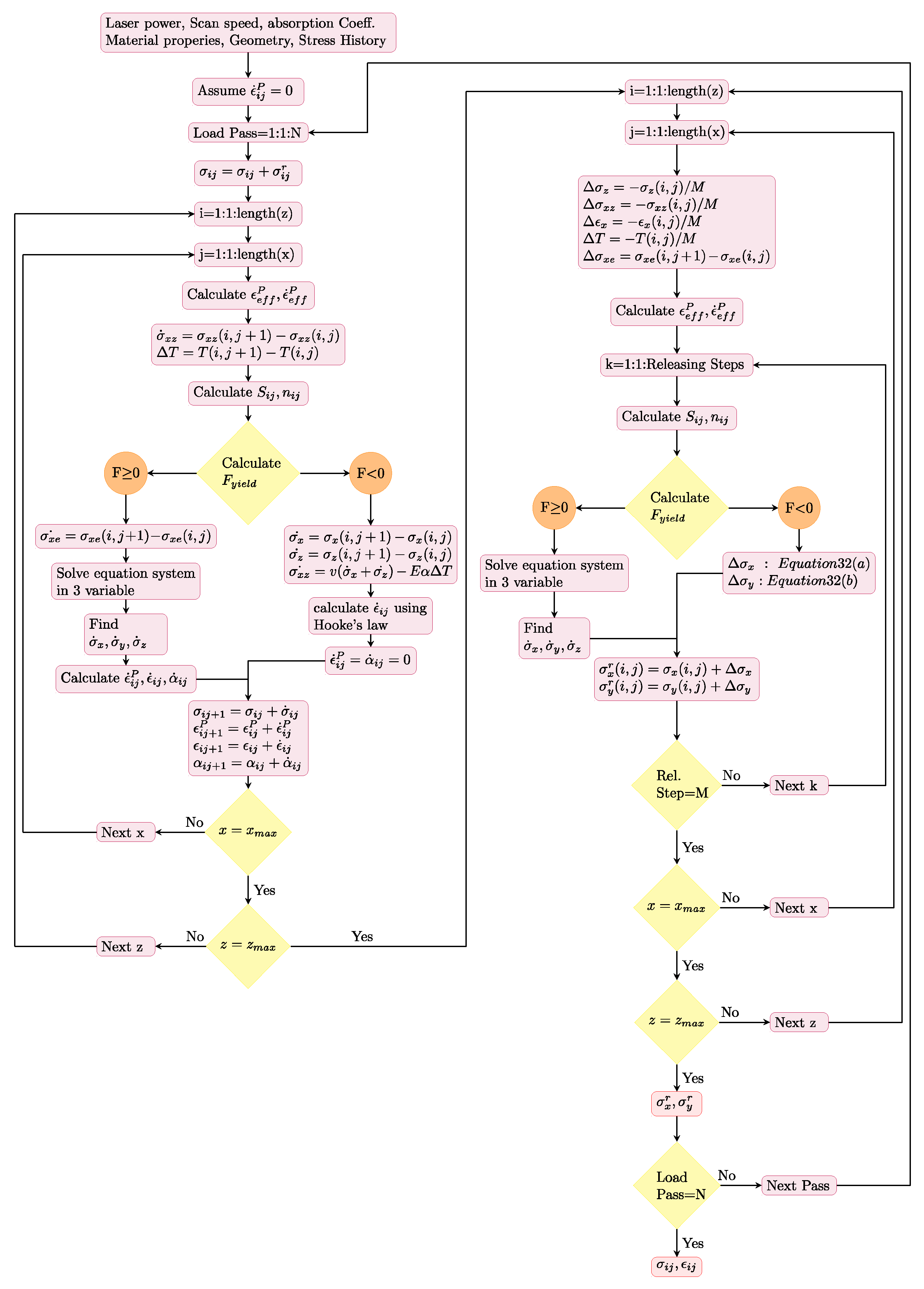
2.2. Mechanical Analysis
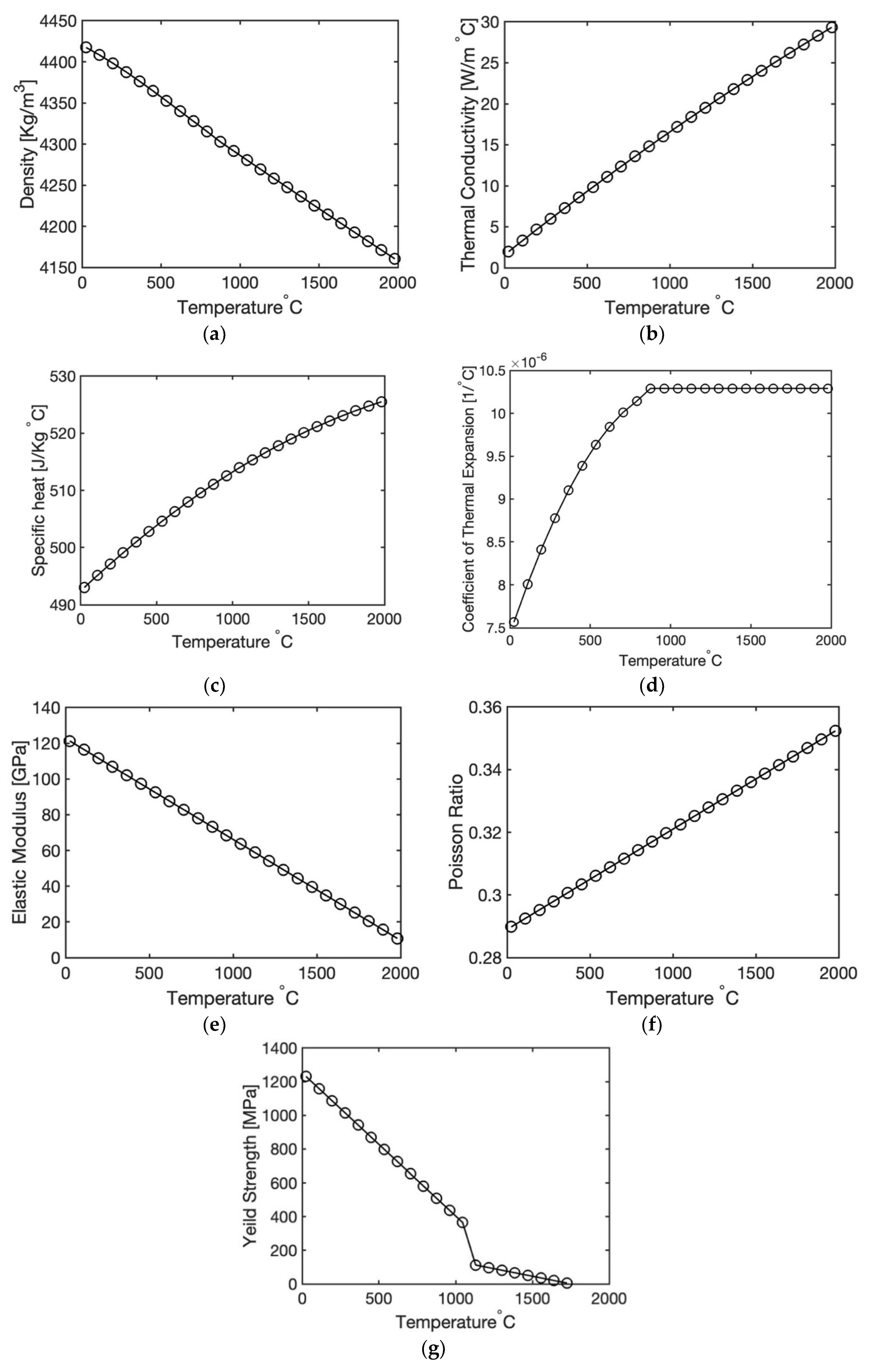
3. Temperature Dependent Material Properties
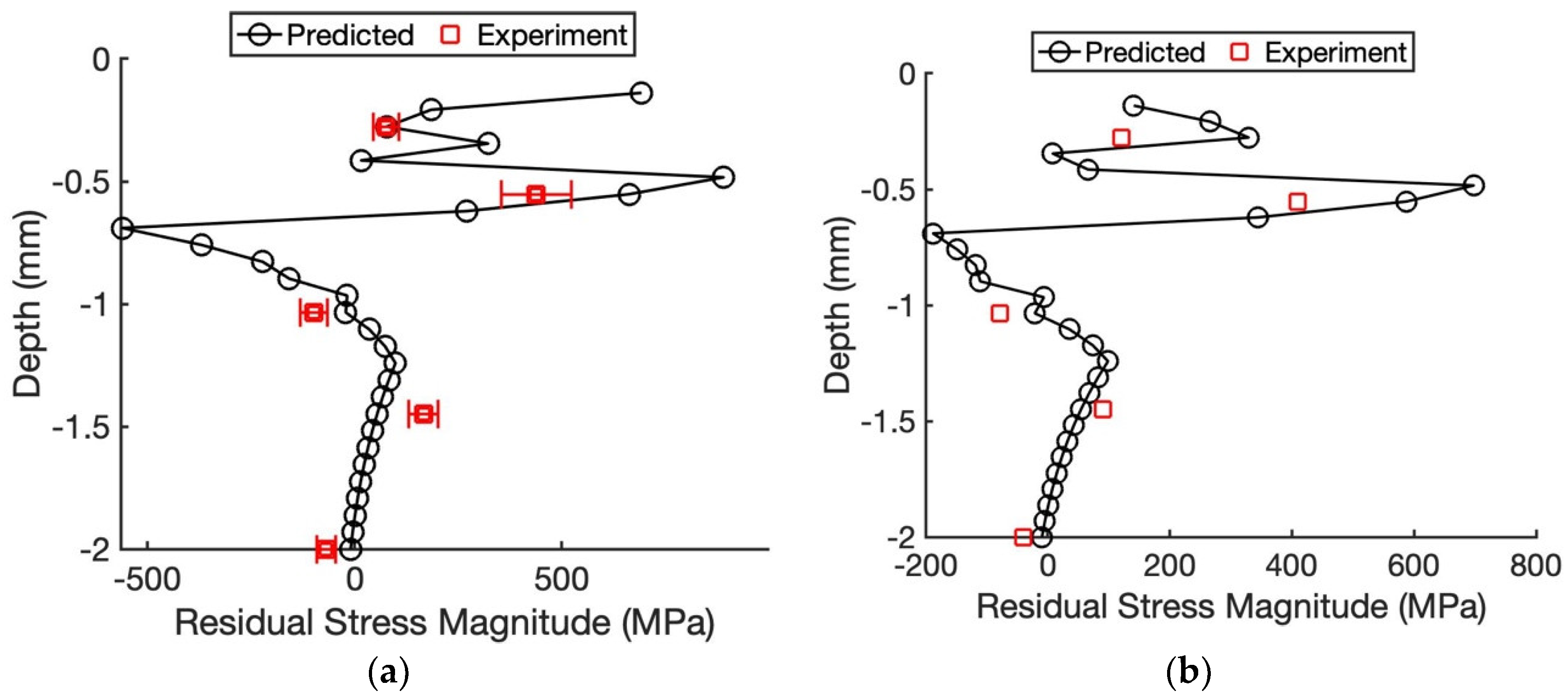
4. Experimental Residual Stress Analysis
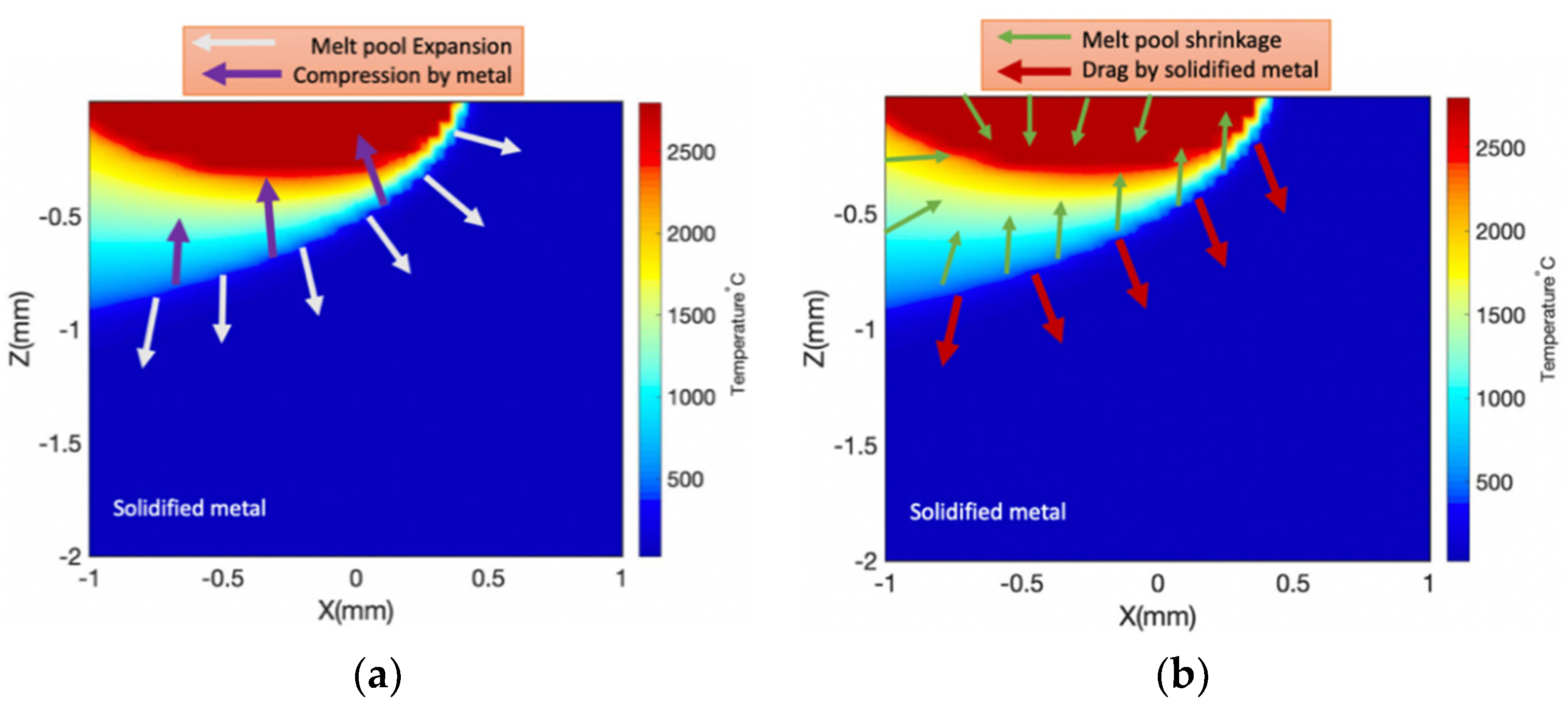
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Herderick, E. Additive manufacturing of metals: A review. Mater. Sci. Technol. 2011, 2, 1413–1425. [Google Scholar]
- Namatollahi, M.; Jahadakbar, A.; Mahtabi, M.J.; Elahinia, M. Additive manufacturing (AM). In Metals for Biomedical Devices; Elsevier: Amsterdam, The Netherlands, 2019; pp. 331–353. [Google Scholar]
- Camacho, D.D.; Clayton, P.; O’Brien, W.J.; Seepersad, C.; Juenger, M.; Ferron, R.; Salamone, S. Applications of additive manufacturing in the construction industry—A forward-looking review. Autom. Constr. 2018, 89, 110–119. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Ji, X.; Mirkoohi, E.; Ning, J.; Liang, S.Y. Analytical modeling of post-printing grain size in metal additive manufacturing. Opt. Lasers Eng. 2020, 124, 105805. [Google Scholar] [CrossRef]
- Tabei, A.; Mirkoohi, E.; Garmestani, H.; Liang, S. Modeling of texture development in additive manufacturing of Ni-based superalloys. Int. J. Adv. Manuf. Technol. 2019, 103, 1057–1066. [Google Scholar] [CrossRef]
- Bartlett, J.L.; Croom, B.P.; Burdick, J.; Henkel, D.; Li, X. Revealing mechanisms of residual stress development in additive manufacturing via digital image correlation. Addit. Manuf. 2018, 22, 1–12. [Google Scholar] [CrossRef]
- Roehling, J.D.; Smith, W.L.; Roehling, T.T.; Vrancken, B.; Guss, G.M.; McKeown, J.T.; Hill, M.R.; Matthews, M.J. Reducing residual stress by selective large-area diode surface heating during laser powder bed fusion additive manufacturing. Addit. Manuf. 2019, 28, 228–235. [Google Scholar] [CrossRef]
- Wang, Z.; Denlinger, E.; Michaleris, P.; Stoica, A.D.; Ma, D.; Beese, A.M. Residual stress mapping in Inconel 625 fabricated through additive manufacturing: Method for neutron diffraction measurements to validate thermomechanical model predictions. Mater. Des. 2017, 113, 169–177. [Google Scholar] [CrossRef]
- An, K.; Yuan, L.; Dial, L.; Spinelli, I.; Stoica, A.D.; Gao, Y. Neutron residual stress measurement and numerical modeling in a curved thin-walled structure by laser powder bed fusion additive manufacturing. Mater. Des. 2017, 135, 122–132. [Google Scholar] [CrossRef]
- Denlinger, E.R.; Heigel, J.C.; Michaleris, P. Residual stress and distortion modeling of electron beam direct manufacturing Ti-6Al-4V. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 1803–1813. [Google Scholar] [CrossRef]
- Zhao, X.; Iyer, A.; Promoppatum, P.; Yao, S.-C. Numerical modeling of the thermal behavior and residual stress in the direct metal laser sintering process of titanium alloy products. Addit. Manuf. 2017, 14, 126–136. [Google Scholar] [CrossRef]
- Romano, S.; Brückner-Foit, A.; Brandão, A.; Gumpinger, J.; Ghidini, T.; Beretta, S. Fatigue properties of AlSi10Mg obtained by additive manufacturing: Defect-based modelling and prediction of fatigue strength. Eng. Fract. Mech. 2018, 187, 165–189. [Google Scholar] [CrossRef]
- Noronha, P.; Wert, J. An ultrasonic technique for the measurement of residual stress. J. Test. Eval. 1975, 3, 147–152. [Google Scholar]
- Chung, D. Thermal analysis of carbon fiber polymer-matrix composites by electrical resistance measurement. Thermochim. Acta 2000, 364, 121–132. [Google Scholar] [CrossRef]
- Krause, T.W.; Clapham, L.; Pattantyus, A.; Atherton, D.L. Investigation of the stress-dependent magnetic easy axis in steel using magnetic Barkhausen noise. J. Appl. Phys. 1996, 79, 4242–4252. [Google Scholar] [CrossRef]
- Ager, J.W., III; Drory, M.D. Quantitative measurement of residual biaxial stress by Raman spectroscopy in diamond grown on a Ti alloy by chemical vapor deposition. Phys. Rev. B 1993, 48, 2601. [Google Scholar] [CrossRef]
- Prime, M.B. Cross-sectional mapping of residual stresses by measuring the surface contour after a cut. J. Eng. Mater. Technol. 2001, 123, 162–168. [Google Scholar] [CrossRef]
- Aggarangsi, P.; Beuth, J.L. Localized preheating approaches for reducing residual stress in additive manufacturing. In Proceedings of the 2006 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 14–16 August 2006; pp. 709–720. [Google Scholar]
- Panda, B.K.; Sahoo, S. Numerical simulation of residual stress in laser based additive manufacturing process. IOP Conf. Ser. Mater. Sci. Eng. 2018, 338, 012030. [Google Scholar] [CrossRef]
- Chen, Q.; Liang, X.; Hayduke, D.; Liu, J.; Cheng, L.; Oskin, J.; Whitmore, R.; To, A.C. An inherent strain based multiscale modeling framework for simulating part-scale residual deformation for direct metal laser sintering. Addit. Manuf. 2019, 28, 406–418. [Google Scholar] [CrossRef]
- Ganeriwala, R.; Strantza, M.; King, W.; Clausen, B.; Phan, T.; Levine, L.; Brown, D.; Hodge, N. Evaluation of a thermomechanical model for prediction of residual stress during laser powder bed fusion of Ti-6Al-4V. Addit. Manuf. 2019, 27, 489–502. [Google Scholar] [CrossRef]
- Ding, H.; Shin, Y.C. A metallo-thermomechanically coupled analysis of orthogonal cutting of AISI 1045 steel. J. Manuf. Sci. Eng. 2012, 134, 051014. [Google Scholar] [CrossRef]
- Mirkoohi, E.; Seivers, D.E.; Garmestani, H.; Liang, S.Y. Heat source modeling in selective laser melting. Materials 2019, 12, 2052. [Google Scholar] [CrossRef] [PubMed]
- Mirkoohi, E.; Sievers, D.E.; Garmestani, H.; Chiang, K.; Liang, S.Y. Three-dimensional semi-elliptical modeling of melt pool geometry considering hatch spacing and time spacing in metal additive manufacturing. J. Manuf. Process. 2019, 45, 532–543. [Google Scholar] [CrossRef]
- Mirkoohi, E.; Ning, J.; Bocchini, P.; Fergani, O.; Chiang, K.-N.; Liang, S. Thermal modeling of temperature distribution in metal additive manufacturing considering effects of build layers, latent heat, and temperature-sensitivity of material properties. J. Manuf. Mater. Process. 2018, 2, 63. [Google Scholar] [CrossRef]
- Fergani, O.; Berto, F.; Welo, T.; Liang, S. Analytical modelling of residual stress in additive manufacturing. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 971–978. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Goldak, J. A Double Ellipsoid Finite Element Model for Welding Heat Sources. IIW Doc. No. 212-603-85. 1985. Available online: https://ci.nii.ac.jp/naid/10003823699/ (accessed on 1 June 2020).
- Saif, M.; Hui, C.; Zehnder, A. Interface shear stresses induced by non-uniform heating of a film on a substrate. Thin Solid Films 1993, 224, 159–167. [Google Scholar] [CrossRef]
- Mirkoohi, E.; Dobbs, J.R.; Liang, S.Y. Analytical mechanics modeling of in-process thermal stress distribution in metal additive manufacturing. J. Manuf. Process. 2020, 58, 41–54. [Google Scholar] [CrossRef]
- Mirkoohi, E.; Sievers, D.E.; Garmestani, H.; Liang, S.Y. Thermo-mechanical modeling of thermal stress in metal additive manufacturing considering elastoplastic hardening. CIRP J. Manuf. Sci. Technol. 2020, 28, 52–67. [Google Scholar] [CrossRef]
- Mirkoohi, E.; Dobbs, J.R.; Liang, S.Y. Analytical modeling of residual stress in direct metal deposition considering scan strategy. Int. J. Adv. Manuf. Technol. 2020, 106, 4105–4121. [Google Scholar] [CrossRef]
- Mirkoohi, E.; Tran, H.-C.; Lo, Y.-L.; Chang, Y.-C.; Lin, H.-Y.; Liang, S.Y. Analytical mechanics modeling of residual stress in laser powder bed considering flow hardening and softening. Int. J. Adv. Manuf. Technol. 2020, 107, 4159–4172. [Google Scholar] [CrossRef]
- Mirkoohi, E.; Tran, H.-C.; Lo, Y.-L.; Chang, Y.-C.; Lin, H.-Y.; Liang, S.Y. Analytical Modeling of Residual Stress in Laser Powder Bed Fusion Considering Part’s Boundary Condition. Crystals 2020, 10, 337. [Google Scholar] [CrossRef]
- McDowell, D. An approximate algorithm for elastic-plastic two-dimensional rolling/sliding contact. Wear 1997, 211, 237–246. [Google Scholar] [CrossRef]
- Qi, Z.; Li, B.; Xiong, L. An improved algorithm for McDowell’s analytical model of residual stress. Front. Mech. Eng. 2014, 9, 150–155. [Google Scholar] [CrossRef]
- Lesuer, D. Experimental Investigation of Material Models for Ti-6Al-4V and 2024-T3. 2000. Available online: https://e-reports-ext.llnl.gov/pdf/236167.pdf (accessed on 29 December 2015).
- Khan, A.S.; Huang, S. Continuum Theory of Plasticity; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Welsch, G.; Boyer, R.; Collings, E. Materials Properties Handbook: Titanium Alloys; ASM International: Almere, The Netherlands, 1993. [Google Scholar]
- Heigel, J.; Michaleris, P.; Reutzel, E.W. Thermo-mechanical model development and validation of directed energy deposition additive manufacturing of Ti–6Al–4V. Addit. Manuf. 2015, 5, 9–19. [Google Scholar] [CrossRef]
- Jamshidinia, M.; Kong, F.; Kovacevic, R. Numerical modeling of heat distribution in the electron beam melting® of Ti-6Al-4V. J. Manuf. Sci. Eng. 2013, 135, 061010. [Google Scholar] [CrossRef]
- Li, J.J.; Johnson, W.L.; Rhim, W.-K. Thermal expansion of liquid Ti–6Al–4V measured by electrostatic levitation. Appl. Phys. Lett. 2006, 89, 111913. [Google Scholar] [CrossRef]
- Mills, K.C. Recommended Values of Thermophysical Properties for Selected Commercial Alloys; Woodhead Publishing: Cambridge, UK, 2002. [Google Scholar]
- Murgau, C.C. Microstructure Model for Ti-6Al-4V Used in Simulation of Additive Manufacturing. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2016. [Google Scholar]
- Nadammal, N.; Kromm, A.; Saliwan-Neumann, R.; Farahbod, L.; Haberland, C.; Portella, P.D. Influence of support configurations on the characteristics of selective laser-melted inconel 718. JOM 2018, 70, 343–348. [Google Scholar] [CrossRef]
- Prevey, P.S. X-ray diffraction residual stress techniques. ASM Int. ASM Handb. 1986, 10, 380–392. [Google Scholar]
- Selvan, J.S.; Subramanian, K.; Nath, A.; Kumar, H.; Ramachandra, C.; Ravindranathan, S. Laser boronising of Ti–6Al–4V as a result of laser alloying with pre-placed BN. Mater. Sci. Eng. A 1999, 260, 178–187. [Google Scholar] [CrossRef]




| A (MPa) | B (MPa) | C | n | m | |
|---|---|---|---|---|---|
| 997.9 | 653.1 | 0.025 | 0.45 | 0.6 | 1 |
| Density [kg/ | |
| Thermal conductivity [W/m | |
| Specific heat [J/kg | |
| Thermal expansion [1/] | |
| Elastic modulus [GPa] | |
| Poisson’s ratio | |
| Yield strength [MPa] |
| Laser Power (W) | Scan Speed (mm/s) | Feed Rate (gram/s) | Layer Height | Hatch Spacing |
|---|---|---|---|---|
| 206 | 25 | 1 | 250 | 105 |
| 385 | 40 | 0.5 | 250 | 105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirkoohi, E.; Li, D.; Garmestani, H.; Liang, S.Y. Analytical Modeling of Residual Stress in Laser Powder Bed Fusion Considering Volume Conservation in Plastic Deformation. Modelling 2020, 1, 242-259. https://doi.org/10.3390/modelling1020015
Mirkoohi E, Li D, Garmestani H, Liang SY. Analytical Modeling of Residual Stress in Laser Powder Bed Fusion Considering Volume Conservation in Plastic Deformation. Modelling. 2020; 1(2):242-259. https://doi.org/10.3390/modelling1020015
Chicago/Turabian StyleMirkoohi, Elham, Dongsheng Li, Hamid Garmestani, and Steven Y. Liang. 2020. "Analytical Modeling of Residual Stress in Laser Powder Bed Fusion Considering Volume Conservation in Plastic Deformation" Modelling 1, no. 2: 242-259. https://doi.org/10.3390/modelling1020015
APA StyleMirkoohi, E., Li, D., Garmestani, H., & Liang, S. Y. (2020). Analytical Modeling of Residual Stress in Laser Powder Bed Fusion Considering Volume Conservation in Plastic Deformation. Modelling, 1(2), 242-259. https://doi.org/10.3390/modelling1020015







