Modeling and Simulation of Head Trauma Utilizing White Matter Properties from Magnetic Resonance Elastography
Abstract
1. Introduction
2. Model Formulation
2.1. MRE Acquisition and Inversion
2.2. Finite Element Mesh Generation
2.3. Material Properties
2.4. Interface and Boundary Conditions
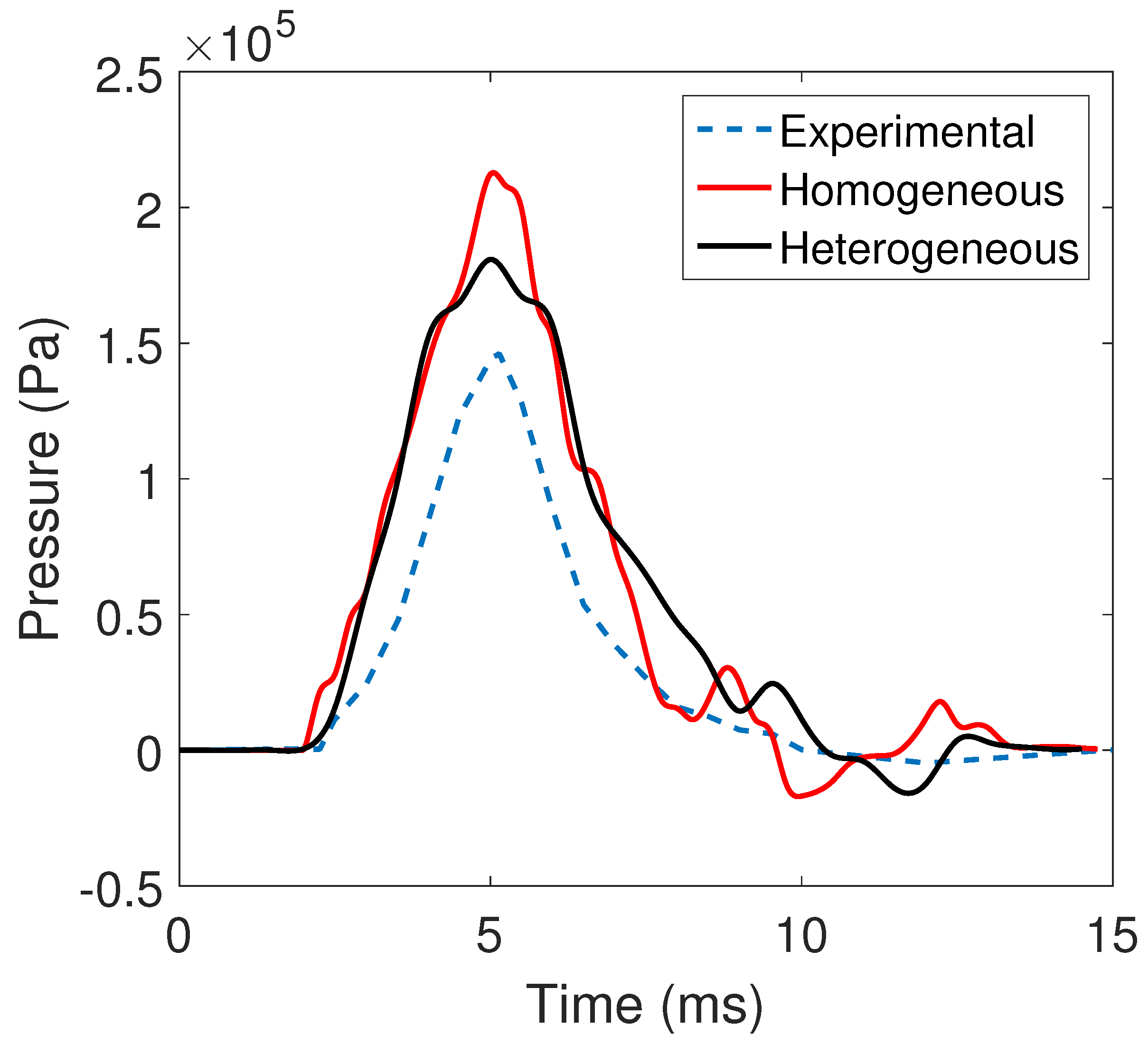
2.5. Experimental Verification
3. Results and Discussion
3.1. Simulation of Impact
3.2. Stochastic Wave Propagation
3.3. Limitations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Taylor, C.A.; Bell, J.M.; Breiding, M.J.; Xu, L. Traumatic Brain Injury-Related Emergency Department Visits, Hospitalizations, and Deaths-United States, 2007 and 2013. MMWR Surveill Summ. 2017, 66, 1–16. [Google Scholar] [CrossRef]
- Gennarelli, T.A.; Thibault, L.E.; Adams, J.H.; Graham, D.I.; Thompson, C.J.; Marcincin, R.P. Diffuse axonal injury and traumatic coma in the primate. Ann. Neurol. 1982, 12, 564–574. [Google Scholar] [CrossRef]
- Gentry, L.R.; Godersky, J.C.; Thompson, B.; Dunn, V.D. Prospective comparative study of intermediate-field MR and CT in the evaluation of closed head trauma. Am. J. Roentgenol. 1988, 150, 673–682. [Google Scholar] [CrossRef] [PubMed]
- Gentry, L.R.; Godersky, J.C.; Thompson, B. MR imaging of head trauma: Review of the distribution and radiopathologic features of traumatic lesions. Am. J. Roentgenol. 1988, 150, 663–672. [Google Scholar] [CrossRef] [PubMed]
- Ng, H.; Mahaliyana, R.; Poon, W. The pathological spectrum of diffuse axonal injury in blunt head trauma: assessment with axon and myelin stains. Clin. Neurol. Neurosurg. 1994, 96, 24–31. [Google Scholar] [CrossRef]
- Arfanakis, K.; Haughton, V.M.; Carew, J.D.; Rogers, B.P.; Dempsey, R.J.; Meyerand, M.E. Diffusion tensor MR imaging in diffuse axonal injury. Am. J. Neuroradiol. 2002, 23, 794–802. [Google Scholar]
- Arbogast, K.B.; Margulies, S.S. Material characterization of the brainstem from oscillatory shear tests. J. Biomech. 1998, 31, 801–807. [Google Scholar] [CrossRef]
- Madhukar, A.; Ostoja-Starzewski, M. Finite element methods in human head impact simulations: A review. Ann. Biomed. Eng. 2019, 47, 1832–1854. [Google Scholar] [CrossRef]
- Chatelin, S.; Constantinesco, A.; Willinger, R. Fifty years of brain tissue mechanical testing: From in vitro to in vivo investigations. Biorheology 2010, 47, 255–276. [Google Scholar] [CrossRef]
- Johnson, C.L.; McGarry, M.D.; Gharibans, A.A.; Weaver, J.B.; Paulsen, K.D.; Wang, H.; Olivero, W.C.; Sutton, B.P.; Georgiadis, J.G. Local mechanical properties of white matter structures in the human brain. Neuroimage 2013, 79, 145–152. [Google Scholar] [CrossRef]
- Muthupillai, R.; Lomas, D.; Rossman, P.; Greenleaf, J.F.; Manduca, A.; Ehman, R.L. Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science 1995, 269, 1854–1857. [Google Scholar] [CrossRef] [PubMed]
- Sack, I.; Streitberger, K.J.; Krefting, D.; Paul, F.; Braun, J. The influence of physiological aging and atrophy on brain viscoelastic properties in humans. PLoS ONE 2011, 6, e23451. [Google Scholar] [CrossRef] [PubMed]
- Murphy, M.C.; Huston, J., III; Jack, C.R., Jr.; Glaser, K.J.; Manduca, A.; Felmlee, J.P.; Ehman, R.L. Decreased brain stiffness in Alzheimer’s disease determined by magnetic resonance elastography. J. Magn. Reson. Imaging 2011, 34, 494–498. [Google Scholar] [CrossRef] [PubMed]
- Murphy, M.C.; Huston, J.; Glaser, K.J.; Manduca, A.; Meyer, F.B.; Lanzino, G.; Morris, J.M.; Felmlee, J.P.; Ehman, R.L. Preoperative assessment of meningioma stiffness using magnetic resonance elastography. J. Neurosurg. 2013, 118, 643–648. [Google Scholar] [CrossRef]
- Boulet, T.; Kelso, M.L.; Othman, S.F. Microscopic magnetic resonance elastography of traumatic brain injury model. J. Neurosci. Methods 2011, 201, 296–306. [Google Scholar] [CrossRef]
- Van Houten, E.E.; Miga, M.I.; Weaver, J.B.; Kennedy, F.E.; Paulsen, K.D. Three-dimensional subzone-based reconstruction algorithm for MR elastography. Magn. Reson. Med. 2001, 45, 827–837. [Google Scholar] [CrossRef]
- Chen, Y.; Ostoja-Starzewski, M. MRI-based finite element modeling of head trauma: Spherically focusing shear waves. Acta Mech. 2010, 213, 155–167. [Google Scholar] [CrossRef]
- Chen, Y.; Sutton, B.; Conway, C.; Broglio, S.P.; Ostoja-Starzewski, M. Brain Deformation Under Mild Impact: Magnetic Resonance Imaging-Based Assessment and Finite Elmenent Study. Int. J. Numer. Anal. Model. Ser. B 2012, 3, 20–35. [Google Scholar]
- Madhukar, A.; Chen, Y.; Ostoja-Starzewski, M. Effect of cerebrospinal fluid modeling on spherically convergent shear waves during blunt head trauma. Int. J. Numer. Methods Biomed. Eng. 2017, 33. [Google Scholar] [CrossRef]
- Johnson, C.L.; McGarry, M.D.J.; Van Houten, E.E.W.; Weaver, J.B.; Paulsen, K.D.; Sutton, B.P.; Georgiadis, J.G. Magnetic resonance elastography of the brain using multishot spiral readouts with self-navigated motion correction. Magn. Reson. Med. 2013, 70, 404–412. [Google Scholar] [CrossRef]
- Glover, G.H. Simple analytic spiral K-space algorithm. Magn. Reson. Med. 1999, 42, 412–415. [Google Scholar] [CrossRef]
- McGarry, M.D.J.; Van Houten, E.E.W. Use of a Rayleigh damping model in elastography. Med. Biol. Eng. Comput. 2008, 46, 759–766. [Google Scholar] [CrossRef] [PubMed]
- Bradshaw, D.; Morfey, C. Pressure and shear response in brain injury models. In Proceedings of the 17th International Technical Conference on the Enhanced Safety of Vehicles, Amsterdam, The Netherlands, 4–7 June 2001. [Google Scholar]
- Prange, M.; Margulies, S. Regional, directional, and age-dependent properties of the brain undergoing large deformation. J. Biomech. Eng. 2002, 124, 244–252. [Google Scholar] [CrossRef] [PubMed]
- Khalil, T.B.; Hubbard, R.P. Parametric study of head response by finite element modeling. J. Biomech. 1977, 10, 119–132. [Google Scholar] [CrossRef]
- Wang, F.; Han, Y.; Wang, B.; Peng, Q.; Huang, X.; Miller, K.; Wittek, A. Prediction of brain deformations and risk of traumatic brain injury due to closed-head impact: Quantitative analysis of the effects of boundary conditions and brain tissue constitutive model. Biomech. Model. Mechanobiol. 2018, 17, 1165–1185. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.; Chinzei, K. Mechanical properties of brain tissue in tension. J. Biomech. 2002, 35, 483–490. [Google Scholar] [CrossRef]
- Budday, S.; Sommer, G.; Birkl, C.; Langkammer, C.; Haybaeck, J.; Kohnert, J.; Bauer, M.; Paulsen, F.; Steinmann, P.; Kuhl, E.; et al. Mechanical characterization of human brain tissue. Acta Biomater. 2017, 48, 319–340. [Google Scholar] [CrossRef]
- Kleiven, S. Predictors for Traumatic Brain Injuries Evaluated through Accident Reconstructions. 2007. Available online: https://saemobilus.sae.org/content/2007-22-0003 (accessed on 10 December 2020).
- Franceschini, G.; Bigoni, D.; Regitnig, P.; Holzapfel, G.A. Brain tissue deforms similarly to filled elastomers and follows consolidation theory. J. Mech. Phys. Solids 2006, 54, 2592–2620. [Google Scholar] [CrossRef]
- Nahum, A.M.; Smith, R.; Ward, C.C. Intracranial Pressure Dynamics during Head Impact. 1977. Available online: https://www.sae.org/publications/technical-papers/content/770922/ (accessed on 10 December 2020).
- Hardy, W.N.; Foster, C.D.; Mason, M.J.; Yang, K.H.; King, A.I.; Tashman, S. Investigation of head injury mechanisms using neutral density technology and high-speed biplanar X-ray. Stapp Car Crash J. 2001, 45, 337–368. [Google Scholar]
- Hardy, W.N.; Mason, M.J.; Foster, C.D.; Shah, C.S.; Kopacz, J.M.; Yang, K.H.; King, A.I.; Bishop, J.; Bey, M.; Anderst, W.; et al. A study of the response of the human cadaver head to impact. Stapp Car Crash J. 2007, 51, 17. [Google Scholar]
- Bozzali, M.; Falini, A.; Franceschi, M.; Cercignani, M.; Zuffi, M.; Scotti, G.; Comi, G.; Filippi, M. White matter damage in Alzheimer’s disease assessed in vivo using diffusion tensor magnetic resonance imaging. J. Neurol. Neurosurg. Psychiatry 2002, 72, 742–746. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.E.; Danielian, L.E.; Thomasson, D.; Baker, E.H. Normal regional fractional anisotropy and apparent diffusion coefficient of the brain measured on a 3 T MR scanner. Neuroradiology 2009, 51, 3–9. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Posnansky, O.; Hirsch, S.; Scheel, M.; Taupitz, M.; Braun, J.; Sack, I. Fractal network dimension and viscoelastic powerlaw behavior: II. An experimental study of structure-mimicking phantoms by magnetic resonance elastography. Phys. Med. Biol. 2012, 57, 4041. [Google Scholar] [CrossRef] [PubMed]
- Wedeen, V.J.; Rosene, D.L.; Wang, R.; Dai, G.; Mortazavi, F.; Hagmann, P.; Kaas, J.H.; Tseng, W.Y.I. The geometric structure of the brain fiber pathways. Science 2012, 335, 1628–1634. [Google Scholar] [CrossRef]
- Ji, S.; Zhao, W.; Ford, J.C.; Beckwith, J.G.; Bolander, R.P.; Greenwald, R.M.; Flashman, L.A.; Paulsen, K.D.; McAllister, T.W. Group-wise evaluation and comparison of white matter fiber strain and maximum principal strain in sports-related concussion. J. Neurotrauma 2015, 32, 441–454. [Google Scholar] [CrossRef]
- Giordano, C.; Kleiven, S. Connecting fractional anisotropy from medical images with mechanical anisotropy of a hyperviscoelastic fibre-reinforced constitutive model for brain tissue. J. R. Soc. Interface 2014, 11, 20130914. [Google Scholar] [CrossRef]
- Giordano, C.; Cloots, R.; Van Dommelen, J.; Kleiven, S. The influence of anisotropy on brain injury prediction. J. Biomech. 2014, 47, 1052–1059. [Google Scholar] [CrossRef]
- Garimella, H.T.; Kraft, R.H. Modeling the mechanics of axonal fiber tracts using the embedded finite element method. Int. J. Numer. Methods Biomed. Eng. 2017, 33. [Google Scholar] [CrossRef]
- Arbogast, K.B.; Margulies, S.S. A fiber-reinforced composite model of the viscoelastic behavior of the brainstem in shear. J. Biomech. 1999, 32, 865–870. [Google Scholar] [CrossRef]
- Wedeen, V.J.; Hagmann, P.; Tseng, W.Y.I.; Reese, T.G.; Weisskoff, R.M. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn. Reson. Med. 2005, 54, 1377–1386. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M.; Costa, L. Shock waves in random viscoelastic media. Acta Mech. 2012, 223, 1777–1788. [Google Scholar] [CrossRef]
- Nishawala, V.; Ostoja-Starzewski, M.; Leamy, M.; Porcu, E. Lamb’s problem on random mass density fields with fractal and Hurst effects. Proc. R. Soc. Math. Phys. Eng. Sci. 2016, 472, 20160638. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Ostoja-Starzewski, M. Impact force and moment problems on random mass density fields with fractal and Hurst effects. Philos. Trans. R. Soc. A 2020, 378, 20190591. [Google Scholar] [CrossRef] [PubMed]
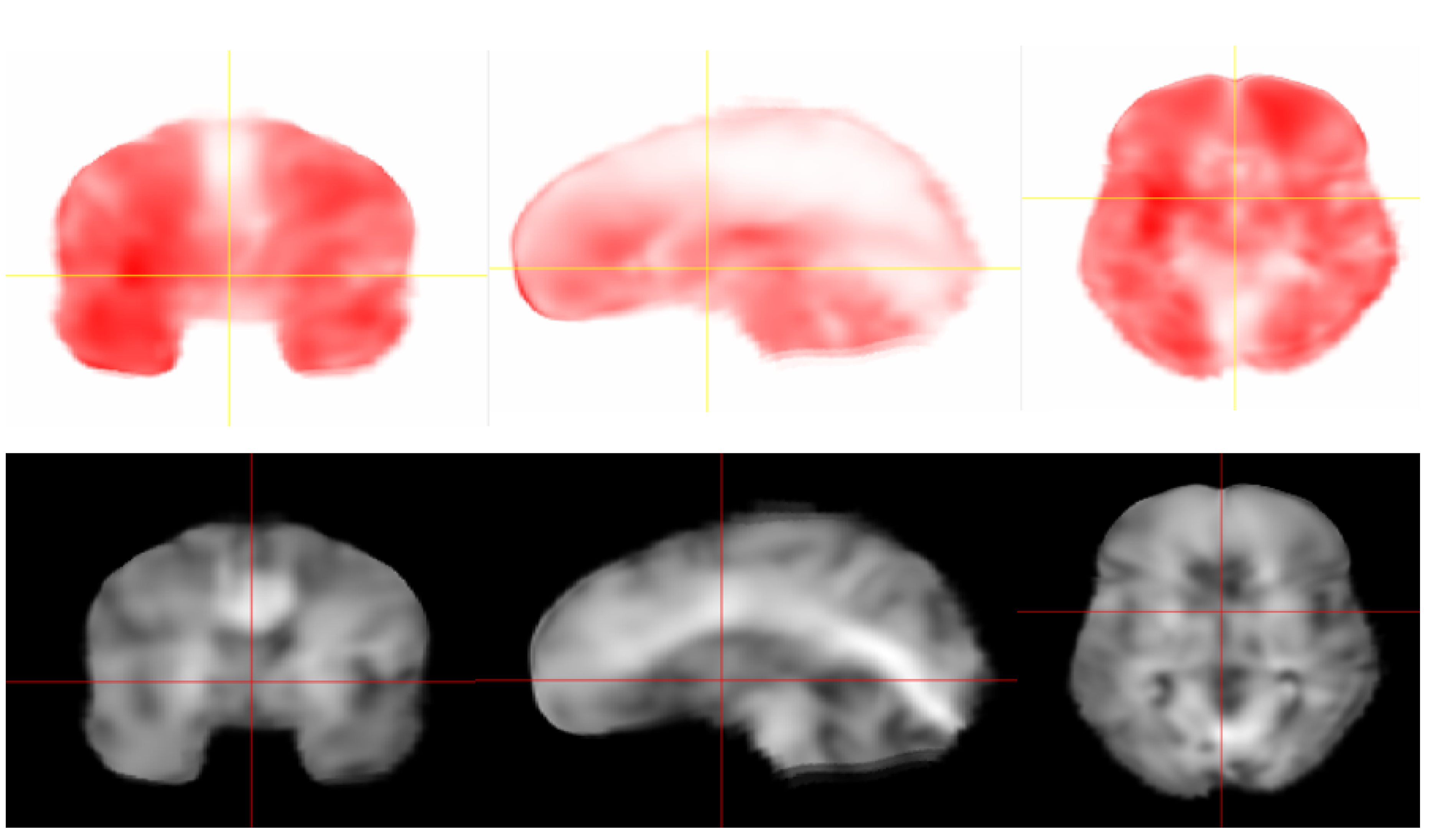





| GM | WM | CC | CR | |
|---|---|---|---|---|
| G (kPa) | ||||
| G (kPa) | ||||
| Tissue | Mass Density (kg/m) | Bulk Modulus K (Pa) | Shear Modulus G (Pa) |
|---|---|---|---|
| Skull [25] | 2070 | 3.61 × | 2.7 × |
| Grey Matter | 1040 | Hyperviscoelastic | |
| White Matter | 1040 | Hyperviscoelastic | |
| Mass Density (kg/m) | Young’s Modulus E (Pa) | Poisson Ratio | |
| CSF [26] | 1000 | 160 | 0.49 |
| ‘Compliant’ | ‘Average’ | ‘Stiff’ | |
|---|---|---|---|
| (Pa) | 26.9 | 53.8 | 107.6 |
| (Pa) | −60.2 | −120.4 | −240.8 |
| 10.1 | 10.1 | 10.1 | |
| −12.9 | −12.9 | −12.9 | |
| 160 | 320 | 640 | |
| 39 | 78 | 156 | |
| 3.1 | 6.2 | 12.4 | |
| 4.0 | 8.0 | 16.0 | |
| 0.05 | 0.10 | 0.20 | |
| 1.5 | 3.0 | 6.0 | |
| ⋮ | ⋮ | ⋮ | ⋮ |
| Location | Experiment | Homogeneous | Heterogeneous |
|---|---|---|---|
| A1 | 9.24 | 7.47 | 9.02 |
| A2 | 8.04 | 4.22 | 6.88 |
| P1 | 12.42 | 7.66 | 8.76 |
| P2 | 9.80 | 4.01 | 10.14 |
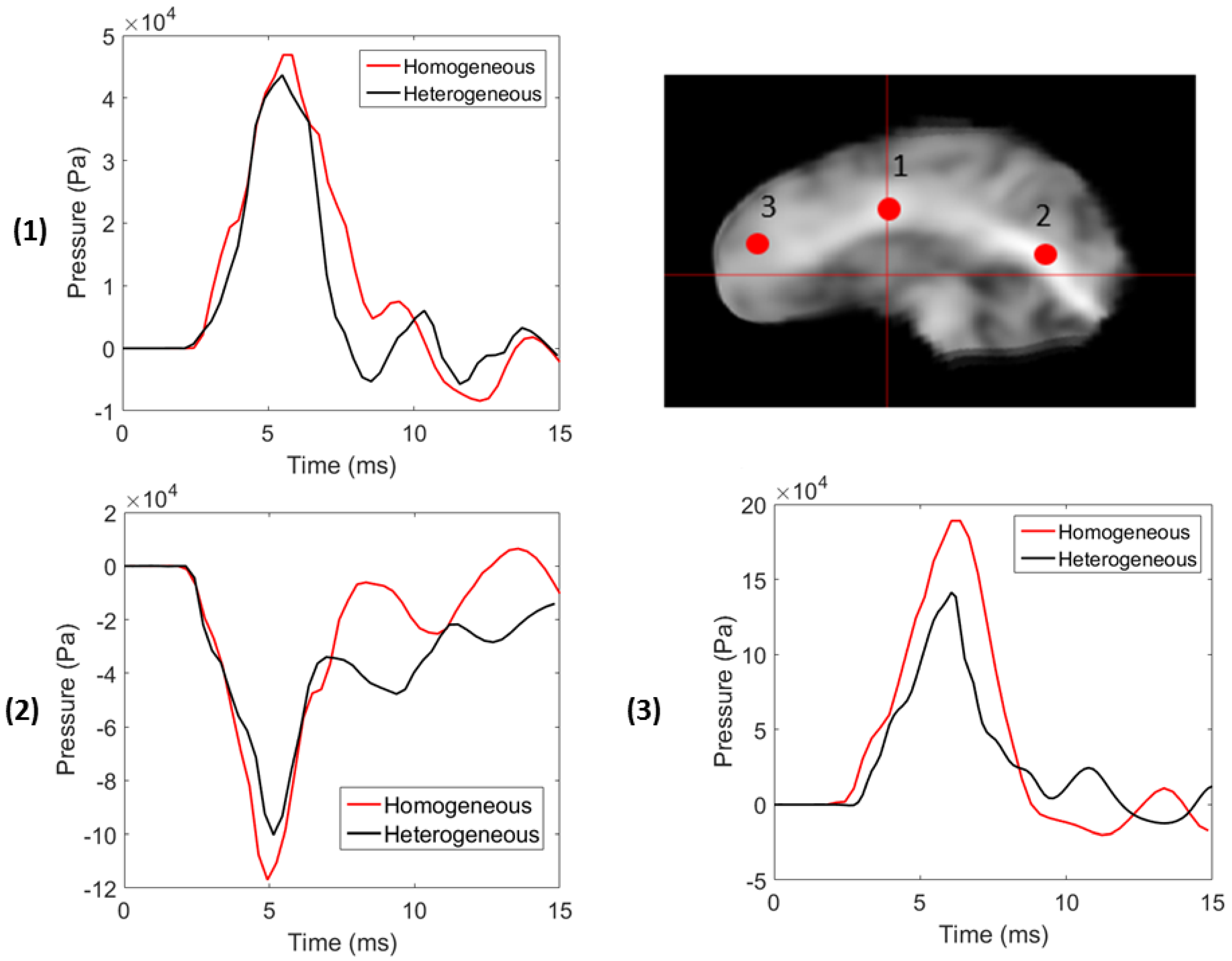
| Location | % Difference in Shear Modulus () | % Difference in Peak Pressure | % Difference in Peak Displacement |
|---|---|---|---|
| 1 | 12.11 | −9.12 | −3.16 |
| 2 | 24.75 | −13.91 | −6.62 |
| 3 | 18.67 | −29.05 | −12.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madhukar, A.; Ostoja-Starzewski, M. Modeling and Simulation of Head Trauma Utilizing White Matter Properties from Magnetic Resonance Elastography. Modelling 2020, 1, 225-241. https://doi.org/10.3390/modelling1020014
Madhukar A, Ostoja-Starzewski M. Modeling and Simulation of Head Trauma Utilizing White Matter Properties from Magnetic Resonance Elastography. Modelling. 2020; 1(2):225-241. https://doi.org/10.3390/modelling1020014
Chicago/Turabian StyleMadhukar, Amit, and Martin Ostoja-Starzewski. 2020. "Modeling and Simulation of Head Trauma Utilizing White Matter Properties from Magnetic Resonance Elastography" Modelling 1, no. 2: 225-241. https://doi.org/10.3390/modelling1020014
APA StyleMadhukar, A., & Ostoja-Starzewski, M. (2020). Modeling and Simulation of Head Trauma Utilizing White Matter Properties from Magnetic Resonance Elastography. Modelling, 1(2), 225-241. https://doi.org/10.3390/modelling1020014







