Assessing the Characteristics of Modern Valvuloplasty Balloons Using a Robotic Non-Contact Optical Approach

Abstract

Background: Balloon aortic valvuloplasty is a procedure for treating aortic stenosis, as well as being a preliminary step before transcatheter aortic valve implantation. Balloon aortic valvuloplasty requires inserting a balloon catheter into the aortic valve and repeatedly inflating it to widen the narrowed valve. With a wide range of equipment, operators rely on manufacturer data to guide the balloon use during surgery. However, such data can have variations of up to 10%, which can affect the procedures’ efficacy. Methods: In this paper, we report a bench-top proof-of-concept, automated, non-contact optical system that combines a linear delta robot (ROMI) equipped with a bright-field microscopy system, image stitching, and passive autofocusing algorithms to measure the diameters of aortic valvuloplasty balloons inflated using clinically relevant pressures. The system also introduces a laser projection system, enabling the use of passive autofocus algorithms to allow measuring transparent balloons. We evaluate three balloon brands (TRUE Dilatation, Edwards, and Z-MED II) across commonly used sizes and compare the measured diameters with vendor specifications. The developed system allows us to systematically determine the balloons’ diameters with submillimeter-level accuracy. Results: The experimental data shows that the TRUE Dilatation balloon presented the smallest deviations from the manufacturers’ data, even though the 22 and 24 mm balloons exceeded the 1% tolerance by +2.26% (over-inflation) and −1.56% (under-inflation), respectively. The Edwards Lifesciences and Z-MED II balloons presented inflation diameter variations ranging from −5.97% to + 8.81%, which led to a deviation of the specified balloon diameter of 1.76 mm. The standard error value obtained within our measurements revealed that the balloon diameters were consistent despite multiple inflations and were also resilient to repeated inflations up to the rated burst pressure. Conclusions: These results demonstrate the potential of the system presented herein to be adapted for in situ, contactless pre-operative balloon assessment in clinical settings.

1. Introduction

Balloon aortic valvuloplasty (BAV) is a minimally invasive procedure used to treat severe, symptomatic aortic stenosis (AS), a condition where the aortic valve narrows due to calcifications, restricting blood flow and thus limiting organ oxygenation [1]. BAV in degenerative aortic stenosis was first described in 1986 by Cribier in three elderly patients [2]. In today’s modern surgery, BAV continues to serve an important role as a bridge to either surgical or transcatheter aortic valve implantation (TAVI) in hemodynamically unstable patients or in high-risk cases with anatomical features that require the native valve to be dilated [3].

Since Cribier’s first work almost forty years ago, BAV has clearly evolved in line with the current available technology. There is nowadays a wide array of commercially available angioplasty balloons that suit various applications and patient characteristics.

BAV balloon catheters are designed to inflate to a specific diameter at a given pressure to match the patient’s aortic valve dimensions; however, in most cases, manufacturers provide data of the balloon’s inflation diameter, with tolerances ranging from 1% to 20% [4]. This poses the challenge of having to perform pre-operative measurements to properly select the most suitable balloon size. Furthermore, the technique of balloon inflation is not well standardized across operators. The specific pressure, duration, and technique of balloon inflation can vary based on the operator’s experience and preference, with inflation performed manually in most cases without the aid of pressure measurements [5].

To perform a successful BAV procedure, it is important to achieve an adequate inflation of the selected balloon, making sure its size during inflation is reliably known to avoid it becoming under- or oversized with respect to the patent’s aortic annulus. An oversized balloon carries the possibility of aortic damage, while an undersized balloon could lead to a sub-optimal result [6]. Moreover, patients with aortic stenosis may exhibit a dynamic annulus where both the perimeter and the area of the aorta are largest, thus systolic measurements are conducted and used as a reference [7].

With the wide range of devices available for use, it is vital that the characteristics of the measurement equipment are studied to maximize the procedure’s efficacy, aiming to reduce, as much as possible, any possible complications. Additionally, given the advent of newer applications for balloon valvuloplasty (particularly in conjunction with TAVI in valve procedures), accurately determining the size of the balloon to be used for each patient becomes critical.

Current methods for matching balloon dimensions to a patient’s aortic valve are based on transthoracic echocardiography, transesophageal echocardiography and contrast-enhanced gated computed tomography (CT) [8]. Such methods require experienced echocardiographers or surgeons to determine the aortic annulus diameter for selecting the most suitable balloon size [9]. For instance, it is known that CT-derived measurements tend to be larger than those of 2D transthoracic echocardiography and transesophageal echocardiography, therefore it is key to combine data from both CT and echocardiography to ensure having more accurate annular dimensions.

In [9], BAV was used to measure the size of the aortic annulus before the implantation of a balloon-expandable transcatheter heart valve; the selection of the balloon dimensions was based on determining the free balloon diameter, which was manually measured using a calliper. In [10] the use of rigid rings (placed within the middle of the balloon) with predefined diameters was adopted to measure the distal and proximal balloon diameters. Both methods have the disadvantage of being contact-based measurements, which could compromise not only the accuracy of the measurements due to the contact pressure affecting the balloon diameter readings but also the sterility requirements. Alternatively, in [11], the use of an analytical model to estimate the size of the annular diameter derived from pressure data was proposed. Although this approach had the advantage of being contactless compared with previous studies, the balloon diameter was estimated using a mathematical model, rather than being measured.

In this paper, we present a bench-top non-contact experimental approach to measure the free balloon diameter using a bright-field microscopy-based machine vision system driven by autofocusing [12] and image stitching algorithms. The system was mounted on ROMI, a delta robotic system [13] used to achieve autonomous measurements. Our evaluation considers three balloon brands including TRUE Dilatation, Z-MED II and Edwards Lifesciences. Our experimental method was devised to enable the precise measurement of the balloon’s diameter at a range of inflation pressures corresponding to those parameters used by operators of BAV in a single center. This proposed proof-of-concept methodology provides an experimental and objective assessment of the balloon characteristics in a repeatable manner with the potential to be adapted for in situ use.

This paper is organized as follows: in Section 2 the materials and methods are presented, including a description of the experimental setup and the balloon’s selection. Section 3 and Section 4 outline the results and discussion of the proof-of-concept experiments conducted and Section 5 outlines the conclusions obtained in this study.

2. Materials and Methods

2.1. Balloon Selection

With a wide range of balloon technologies available for BAV, surgeons currently rely on manufacturers’ data to guide and select such devices.

We used the balloons available at the Sussex Cardiac Centre in Brighton normally used to perform daily BAV procedures and measured these in a laboratory environment at the University of Sussex. Our evaluation considers the three leading balloon brands and the most used diameters within our practice, including (a) TRUE Dilatation (considered as a balloon with improved performance), which has a vendor specified diameter tolerance of 1%; (b) Z-MED II, with an up to 10% tolerance reported in its manufacturer’s data sheet, and (c) Edwards Lifesciences, for which the vendor only specifies its nominal diameter.

The TRUE Dilatation balloon BAV catheter (Becton, Dickinson, Franklin Lakes, NJ, USA) is an over-the-wire catheter, with a noncompliant balloon composed of an opaque fibre-reinforced thermoplastic. The Z-MED II (B. Braun Medical, Bethlehem, PA, USA) and the Edwards Lifesciences balloons (Edwards Lifesciences, Irvine, CA, USA) are both over-the-wire catheters with a noncompliant balloon composed of a transparent thermoplastic elastomer.

2.2. Experimental Setup

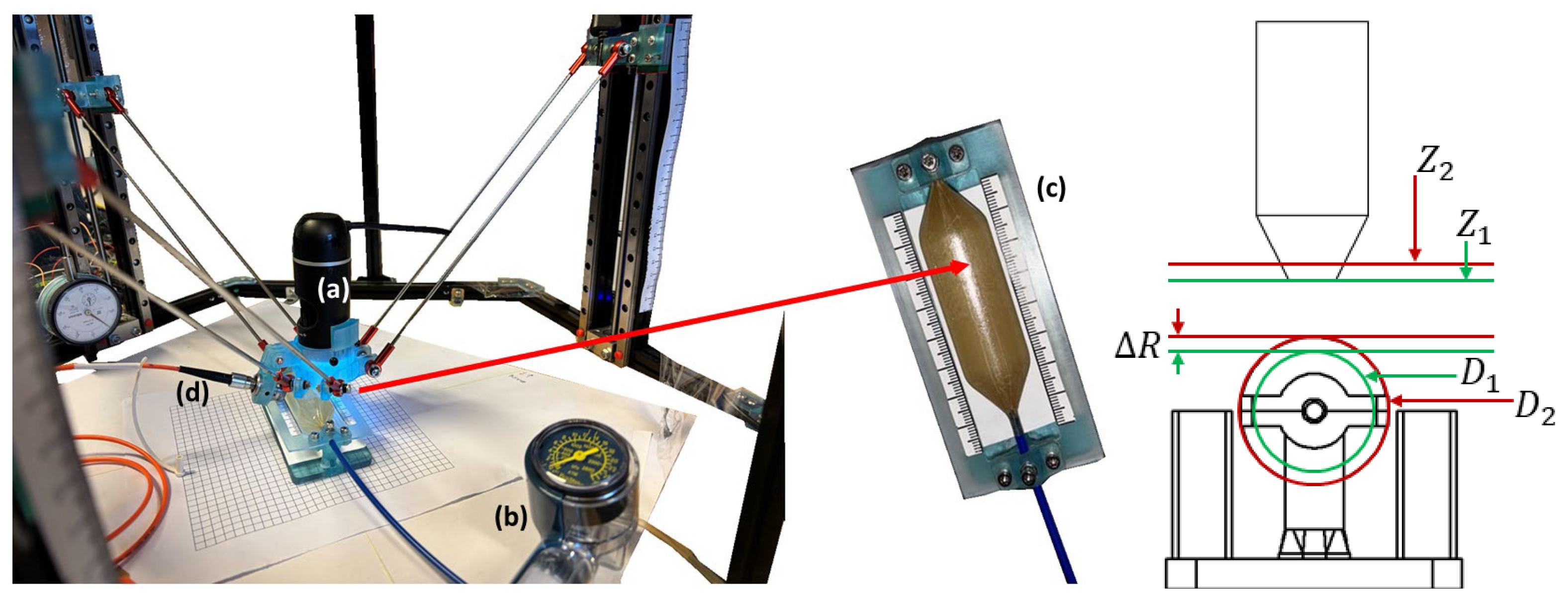
An experimental bench-top device was assembled, including a non-contact bright-field imaging system with the aim of performing pre-operative measurements of TAVI balloon diameters across a range of inflation pressures. Figure 1 shows the experimental setup, which consisted of (a) a bright-field microscopy-based machine vision system combined with image stitching and autofocusing algorithms, (b) a Boston scientific encore inflation device to determine the free balloon pressure, (c) a custom-made 3D printed universal mount, and (d) an auxiliary laser-based system for assisting the measurement of balloons made of transparent thermoplastic.

The imaging system was mounted in our custom-made three degrees-of-freedom, linear, delta robotic system (ROMI), which was previously reported on in [13]. The workspace of the ROMI robot was reported to have a pyramid shape volume with dimensions of ~114.2 mm × 114.2 mm × 110 mm and a depth of 130 mm, with a Z-axis single-step resolution of 1.32 μm and repeatability of ±0.02 μm. The ROMI system was adapted for this work to accurately measure BAV balloons at the nominal pressure followed by the maximum and minimum pressures specified by the manufacturer, and to autonomously provide the balloon diameters. The ROMI system was controlled via kinematic navigation.

The bright-field microscopy (Celestron LLC, Torrance, CA, USA) machine vision system was based on a five-element microscope objective lens with an effective focal length of 15.8 mm, image distortion of 0.10%, and variable magnification ranging from 20 to 200× (adjusted through a tube slider that changes the lens distance between the camera and the object). The CMOS camera had a five-megapixel resolution, with a pixel size of 1.75 µm (Figure 1a). Image stitching and autofocus were implemented by developing a custom-made GUI using National Instruments LabVIEW software (Version 2022 Q3) and executed through myRIO-1900 FPGA hardware (National Instruments, Austin, TX, USA).

2.3. Experimental Procedures

To experimentally assess the free balloon inflation diameter, we considered inflation parameters and procedures similar to those carried out during a typical surgery as follows: upon BAV deployment, once the balloon was positioned, rapid ventricular pacing was initiated and the balloon was rapidly inflated and deflated, usually with the balloon being inflated for three seconds followed by inflation and deflation not exceeding twenty seconds. This process was repeated up to five times per experiment.

For the selected balloons, the inflation rounds were conducted between the minimum pressure and the maximum pressure specified by the vendor. This was carried out using an Encore 26 inflation device (Boston Scientific, Marlborough, MA, USA) with a manufacturer-specified accuracy of ±3% (±0.78 atm) in the upper and lower quarter of the scale and ±2% (±0.52 atm) in the middle half of the scale.

The initial balloon diameter was measured by executing an automated robot navigation path to collect multiple fields-of-view across the balloon diameter. The acquired images were then stitched using the image stitching method described in Section 2.4, and the balloon diameter was then calculated using the embedded scale built in the custom 3D printed mount as shown in Figure 1c. The robotic system was then navigated to the topmost portion of the balloon’s curved surface which was set as the reference focal position. The balloon pressure was changed as described previously, resulting in a focal shift (ΔZ) observed through the visual feed from the bright-field microscopy system. The robotic system was then navigated within the Z axis to obtain a refocused image while collecting the actuator’s data to determine the focal shift, corresponding to the change in the balloon diameter (ΔD).

The right panel of Figure 1 shows the schematics of the geometric model used to convert the focal shift (ΔZ) to the diameter change (ΔD). The vertical displacement of the imaging system (∆Z) required to maintain focus on the balloon’s top surface was set to be equal to the change in the balloon’s radius (∆R), as shown in Equation (1):

$$∆Z=∆R$$

(1)

The proposed geometric model relied on the primary assumption that the balloon inflated symmetrically, meaning that its point of maximum height remained on the central vertical axis, which was set up directly beneath the imaging system. As the balloon is inflated, its radius increases uniformly. Consequently, the change in the vertical position of the balloon’s topmost surface, which is the focal plane, directly corresponds to the change in the balloon’s radius.

Since the change in diameter (∆D) was twice the change in the radius (D = 2 × ∆R), the conversion from the measured focal shift to the diameter change is given by Equation (2):

$$∆D=2·∆Z$$

(2)

To measure the vertical displacement, the imaging system was actuated using ROMI, which is driven by three stepper motors each one coupled to a leadscrew. When the motor rotated 1 step, the actual Z-axis displacement was 1.32 ± 0.02 µm. During the autofocusing routine, the custommade control software (LabVIEW 2022 Q3) counted the number of steps (N_steps) required to move the imaging system and refocused the image. The total vertical displacement (ΔZ) was then calculated using Equation (3).

$$\Delta Z=N\_steps\times 1.32 \mathsf{\mu }\mathrm{m}$$

(3)

This value was used in the geometric model to determine the change in the balloon diameter. A dedicated validation experiment of the geometric model is presented in Section 3.1.

The autofocusing method used to determine the optimum focal position for refocusing ROMI autonomously is described in Section 2.5. All the measurements were repeated five times and the results obtained were compared with those available from the manufacturer’s specifications.

2.4. Image Stitching Method

The robotic system was navigated across the balloon to provide a set of overlapping images with their respective spatial coordinates to form a mosaic. A total of 20 pictures, with an overlap of 80%, were considered. This high degree of overlap was essential, as some areas on the balloon’s surface lacked features which were required for image stitching. Thus, a high overlap ensured that, even if the image contained smooth, textureless regions, the stitching algorithm could still provide a reliable registration between the collected images. To calculate the precise relative positions between images, we employed a high precision registration engine integrating cubic B-spline interpolation and the least squares method [14]. Finally, image fusion was carried out through a weighted average method based on boundary distances. Figure 2 shows an example of the data collected before and after applying the stitching method. As expected, the balloon’s top portion remains defocused due to its curvature; however, this did not affect the initial balloon diameter measurement.

2.5. Passive Autofocus Strategy for TRUE Dilatation Balloons

To determine the optimum focal position for refocusing the robotic system autonomously, a passive autofocus strategy was implemented. This included a selection of algorithms that analyzed the phase and contrast from the image data obtained. This information was then used to provide a score related to the image focus. The passive autofocus was used in combination with the kinematic data of the robotic system to record the balloon diameter upon the change in pressure as described in Section 2.3.

Although several autofocus functions have been previously studied in the literature for a variety of samples imaged using bright-field microscopy (i.e., smears [15,16], molecular cytogenetic imaging [17], mycobacterium tuberculosis [18], and histology [19]), it is worth highlighting that each of these algorithms have not yet been evaluated with specific material characteristics such as those used for the manufacturing of BAV balloons.

In this work, we evaluated and selected the most suitable passive autofocusing function for each balloon. This was carried out by implementing a metric to assess the convergence coefficient of each algorithm. Fifteen algorithms were evaluated including Vollath’s F4, Volath’s F5, variance, normalized variance, entropy, variance of log histogram, energy of image Laplacian, tenengrad gradient, Brenner gradient, First-order Gaussian derivative, squared gradient, threshold absolute gradient, absolute tenengrad, image power and thresholder pixel count [15,16,17,18,19].

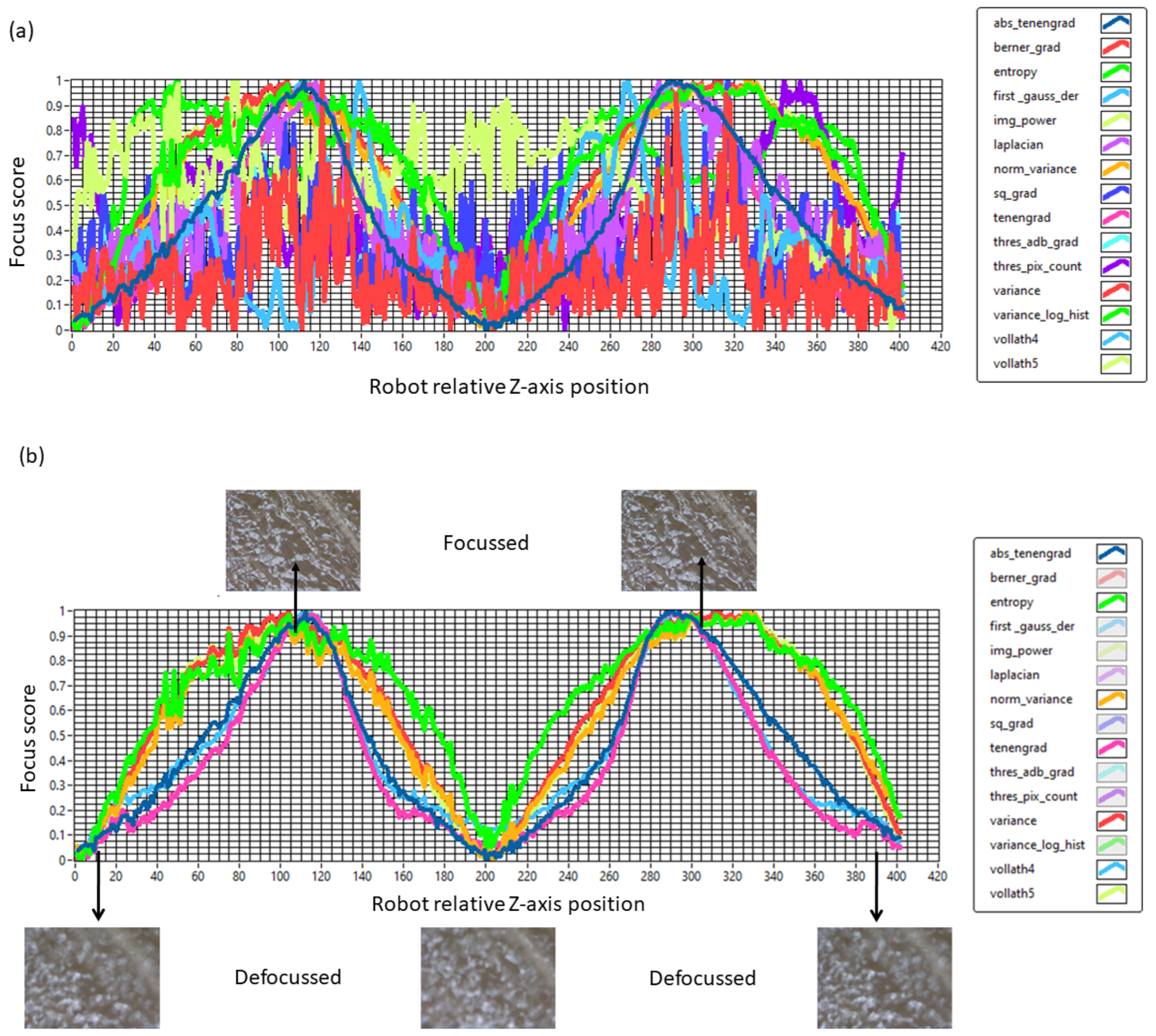
Figure 3a shows the results of the autofocusing algorithms evaluation using a TRUE Dilatation balloon including the focus score determined for each image and plotted as a function of the robotic system Z-axis relative position. It is worth pointing out that in Figure 3, the valleys represent the defocused images while the peaks represent the focal positions. Similarly, a sharp peak represents a single focal position value, whereas a wider/flatter peak contains a range of focal positions.

To quantitatively select the most suitable, autofocus evaluation function considering the TRUE Dilatation balloon, each algorithm convergence coefficient (k) was calculated using Equation (4):

$$k= {\displaystyle \frac{\left|y^{″}\right|}{{\left(1+{\left(y^{\prime }\right)}^2\right)}^{\frac{3}{2}}}}$$

(4)

where y is the quadratic function (y = ax² + bx + c) representing the obtained datapoints, x being the independent variable corresponding to the Z-axis position of the robotic system and k being the convergence coefficient (dependent variable).

The convergence coefficient defined by Equation (4) is a metric defined to obtain the sharpness of the peak or focal position. Using such metric, a large value indicates a desirable sharp peak, while small value is indicative of a wider/flatter peak, thus this metric was used to determine whether the focusing algorithm reached a unique and more robust solution vs. multiple solutions. Moreover, the slope of the curves generated while using the autofocusing algorithms provide information of convergence speed. Thus, the steeper the slope, the faster convergence that the algorithm will achieve. Therefore, a larger k value is desirable, as the larger the k value, the faster the algorithm converges at the peak [12] or focal position.

Table 1. Passive autofocus evaluation convergence ranking showing the top five performing algorithms.

Method	$\mathit{k}$	Rank
Vollath’s F4	$3.565\times {10}^{-5}$	1
Variance	$3.334\times {10}^{-5}$	2
Normalized variance	$3.277\times {10}^{-5}$	3
Entropy	$3.241\times {10}^{-5}$	4
Vollath’s F5	$3.166\times {10}^{-5}$	5

shows the results for the top five autofocus algorithms selection indicating that, for the TRUE Dilatation balloon, Vollrath’s F4 algorithm presents the highest convergence coefficient.

Following the results from Table 1 and Figure 3b, we selected Vollath’s F4 to perform autofocusing on the TRUE Dilatation balloon catheters. This algorithm analyzed the correlation between adjacent pixels to effectively capture the rough surface details of the balloon while also considering the high-frequency components contained within its structural details, making it well-suited for bright-field microscopy applications [19]. It is worth noticing that, for the TRUE Dilatation™ balloons, the autofocus algorithm performed a search over 984 µm in steps of 9.84 µm between image captures. In this part of the methodology, the robotic and machine vision system started from a defocused image (valley) and, upon Z-axis navigation, reached the focal position (peak). The process was repeated two times; therefore, the graphs presented have two peaks. Figure 3b shows a representative focus curve applied to the TRUE Dilatation balloon. The standard deviation (SD) of the resulting Z-axis peak positions from the three runs was calculated to be ±1.14 µm, representing the autofocus positional repeatability.

2.6. Passive Autofocus Strategy for Z-MED II and Edwards Lifesciences Balloons

A procedure similar to the previous one was applied to the Z-MED II and Edwards Lifesciences balloons with the aim of evaluating the most suitable autofocusing algorithm required for our measurements. When evaluating the 15 autofocusing algorithms with the Z-MED II and Edwards Lifesciences balloons, the results showed that none of the proposed autofocusing algorithms converged, as these balloons lacked identifiable features, as they were fabricated with a transparent thermoplastic. To address this challenge and provide the imaging system with the ability to identify between opaque and transparent materials, an auxiliary laser beam projection system was added to the same setup shown in Figure 1. This was performed with the aim of creating a reference pattern over the transparent surface of the balloon for the algorithm to have an identifiable feature.

Figure 4 shows the experimental setup combined with a laser beam projection system used for the identification of the balloon surface to help the autofocus algorithms to converge. The design employs the red emission provided by a FYLA Iceblink class 4 laser system (Paterna, Valencia, Spain). The broadband laser output was filtered using a 650/10 bandpass optical filter (Thorlabs, Newton, NJ, USA). To avoid saturating the imaging system camera, the laser output was attenuated using an ND variable filter (Thorlabs, Newton, NJ, USA, NDC-50C-4). The beam was then coupled into a Ø50 μm, 0.22 NA, Low OH, FC/PC-FC/PC Fibre Patch Cable (Thorlabs, Newton, NJ, USA). The light coming out from the multimode fibre was collimated and directed onto the balloon surface through a single aspheric lens element (CFC11P-A, Thorlabs, Newton, NJ, USA). The optical power was measured, using a thermal optical power sensor (S470C, Thorlabs, Newton, NJ, USA) connected to the power and energy meter interface (PM102, Thorlabs, Newton, NJ, USA). The obtained power at the sample was 0.25 mW.

The laser light interacting with the transparent balloons’ surfaces can be described by Snell’s law, where the reflection and refraction of light happen at the interface formed between the balloon’s material and the saline solution. In our experiments, the balloon materials’ transparency allowed the light to be transmitted, as is shown in Figure 4 (right insert) and given that the materials’ lack of imperfections, scattering was negligible, thus allowing us to have clear images of the laser beam projected against the surface of the transparent material.

The autofocusing algorithms were tested using the projection system and selected using Equation (4). Both the Edwards Lifesciences and Z-MED II balloons required a wider search over 1968 µm with a step size of 30.75 µm.

The absolute tenengrad autofocusing algorithm measures the image contrast based on the magnitude of the image gradients, with high sensitivity on the edge details such as those present within the laser projection. Unlike the squared-gradient methods, this algorithm uses absolute values, thus presenting the highest convergence coefficient for both the Edwards Lifesciences and the Z-MED II balloon catheters. Given this, we selected the absolute tenengrad autofocusing algorithm for use in the dimensional balloon tests.

2.7. Measurement Uncertainty Budget of the Experimental Setup

To quantify the system’s performance at a sub-millimeter scale, a measurement uncertainty budget was established following the principles of the Guide to the Expression of Uncertainty in Measurement (GUM) [20]. The main sources of uncertainty were first identified as follows: (a) the ROMI robot Z-axis repeatability, (b) the autofocus positional repeatability, (c) the image stitching error, and (d) the pressure gauge accuracy.

The GUM method was followed to estimate the uncertainties by calculating the standard uncertainty (u), the combined standard uncertainty ($u_c$), and the expanded (95% CI) uncertainty (U) using the following equation:

$${\mathrm{u}}_{\mathrm{c}}\left(∆\mathrm{D}\right)=\sqrt{{\mathrm{u}}_{\mathrm{z}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s}}^2+{\mathrm{u}}_{\mathrm{a}\mathrm{u}\mathrm{t}\mathrm{o}\mathrm{f}\mathrm{o}\mathrm{c}\mathrm{u}\mathrm{s}}^2+\dots }=3.24 \mathsf{\mu }\mathrm{m}$$

(5)

where each u component is used to represent every individual source of uncertainty as outlined above.

Table 2. Summary of the main sources of uncertainty present in our bench-top system, expressed in micrometers, including the combined standard uncertainty ($u_c$) and the expanded (95% CI) uncertainty (U). The expanded (95% CI) uncertainty ($u$) parameter validates the sub-millimeter accuracy achieved by the proposed robotic, non-contact optical approach.

Sources of Uncertainty	Standard Uncertainty (uc) in µm	Considerations to Determine Contribution of Each Uncertainty Source
ROMI Z-axis repeatability	±0.02	The Z-axis contributed with a positional uncertainty of ±0.02 µm [13]
Autofocus positional repeatability	±1.14	It was calculated by performing the autofocus routine repeatedly (n = 3) on the TRUE Dilatation™ balloon surface, as show in Figure 3b.
Image stitching error	±3.03	The registered standard deviation of 0.164 pixels for a representative image mosaic reported in [14] was used. We assumed an optical system calibration scale of 18.51 µm/pixel, which corresponded to a spatial uncertainty of ±0.164 pixels × 18.51 µm/pixel ≈ ±3.03 µm.
Pressure gauge accuracy	/	The Encore 26 inflation device has an accuracy specified by the manufacturer (see Section 2.3). However, as the measurements were carried out optically, the uncertainty contribution was already included in the autofocus positional repeatability [11].
Other effects	/	The digital microscopy system has an image distortion of 0.10%. This distortion was further reduced as the imaging was carried out at the central point of the field of view. Therefore, this effect was considered negligible.
$\mathrm{Combined} \mathrm{standard} \mathrm{uncertainty} (u_c$)	±3.24	Equation (5) was used to obtain the combined standard uncertainty.
$\mathrm{Expanded} (95\% \mathrm{CI}) \mathrm{uncertainty} (U$)	±6.47	The individual uncertainty components were combined using the root sum of squares (RSS) method to calculate the expanded (95% CI) standard uncertainty (U).

shows the main sources of uncertainty present in our bench-top system, expressed in micrometers, including the combined standard uncertainty ($u_c$) and the expanded (95% CI) uncertainty (U).

3. Results

The bench-top automated, non-contact optical workflow described in Section 2.2 was used to measure the diameter of aortic valvuloplasty balloons inflated using clinically relevant pressures. To ensure the results were equitable, a proof-of-concept experiment was performed to measure the balloon’s diameter at both room temperature (22 °C) and physiological temperature (using the saline solution at 37 °C). Section 3.4 presents an example of the results obtained, showing that the difference in diameter when comparing both scenarios was less than 1%; thus, the experiments presented in this section were conducted at room temperature.

Three BAV operators performed dummy inflations using a real-world technique with pressures routinely used within our center. This was carried out using the Encore 26, Boston Scientific percutaneous transluminal coronary angioplasty catheter inflator. The measurements were taken using a CMOS camera (FL3-U3-32S2C-CS, Teledyne FLIR, Arlington, VA, USA) to capture the inflation device dial. The recorded images were analyzed using image J software (National Institute of Health, Bethesda, MD, USA, version 1.54f). This ensured that operator-related variance did not influence the data collection; therefore, the final measured diameter was calculated using the acquired data.

3.1. Validation of the Geometric Model Presented in Section 2.3

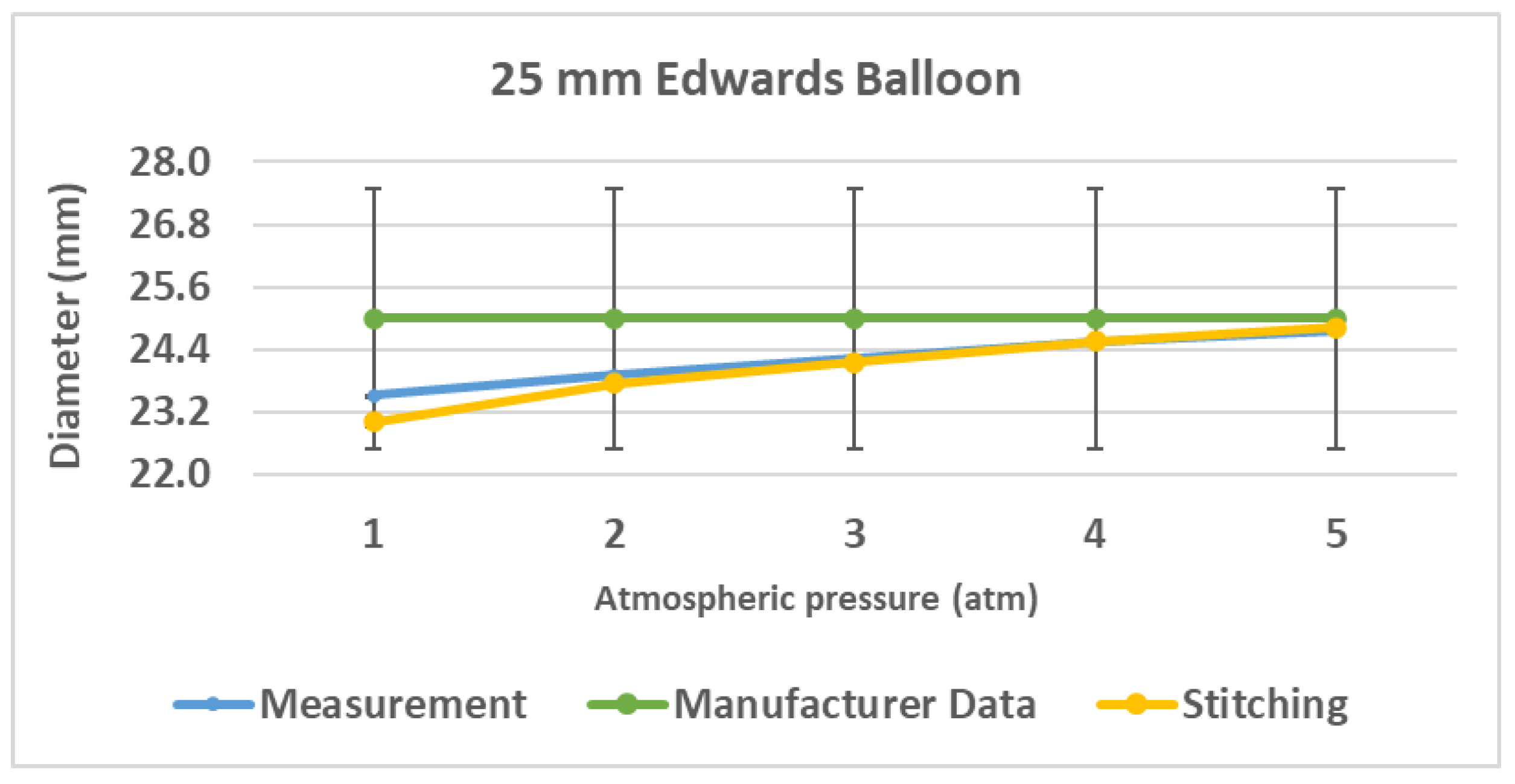
To empirically validate the geometric model presented in Section 2.3, a preliminary validation experiment was conducted using a 25 mm Edwards LifeSciences balloon.

The experiments were conducted considering the vendor-specified pressures ranging from 1 to 5 atm. The balloon’s diameter was measured independently using two methods: (1) the proposed focal-shift tracking method (referred to as ‘Measurement’) and (2) the full-width image stitching method [14], which served as the reference standard (‘stitching’).

Figure 5 shows the results from the empirical validation of the geometric method to measure the balloon’s diameter.

Results from the quantitative analysis of the data confirmed a strong agreement between both methods. The absolute difference between the mean diameters measured by each technique was calculated at each pressure. While the largest deviation of 0.50 mm occurred at 1 atm (a 2.17% relative difference), the agreement improved significantly as pressure increased. For the pressures ranging from 2 to 5 atm, the mean absolute difference was consistently low, ranging from 0.038 mm to 0.163 mm, representing a relative difference of less than 0.7%, thus considered to be within the experimental error.

To further assess the agreement from a statistical standpoint, a paired t-test was performed on the measurement data. The test confirmed that there were no statistically significant differences between both methods (p ≈ 0.221 > 0.05).

The quantitative analysis confirmed that the focal-shift approach provides a valid and accurate inference of the balloon’s diameter change, particularly after the initial unfolding stage.

3.2. Results from 22, 24, and 26 mm TRUE Dilatation Balloons

The experiments were carried out for the 22, 24, and 26 mm TRUE Dilatation balloons. The measurements were taken five times for each balloon to account for both the experimental error and to assess the balloon’s compliance at the same applied pressure. The results were compared to the provided manufacturer’s data. Figure 6 shows an example image obtained with the robotic non-contact optical system of the 26 mm TRUE Dilatation balloon inflated at a nominal pressure of 3 atm, measuring 26.07 ± 0.16 mm.

Figure 7 shows the pressure vs. diameter results comparing the robotic system measurements to the manufacturer’s data. The balloons were inflated from one to five atmospheres. The raw ballon inflation data can be found in the Supplementary Table S1: Balloon inflation raw data.

The results obtained from the 22 mm TRUE Dilatation balloon show a maximum diameter variation of up to +2.16% at 5 atm where the balloon over-inflates to +480 µm, which is outside the tolerance data provided by the manufacturer. Similarly, the 24 mm balloon presents an under-inflation diameter of −1.56% at 1 atmosphere when compared with the nominal diameter with a specified tolerance of 1%. However, the balloon is able to reach the nominal inflation diameter at 5 atmospheres with a small difference up to 70 µm. The 26 mm diameter balloon presented a maximum diameter deviation of 230 µm, corresponding to 0.9%, at five atmospheres, in comparison with the manufacturer-specified tolerance. This diameter variation was reduced to 0.26% at the nominal inflation pressure (i.e., 3 atm).

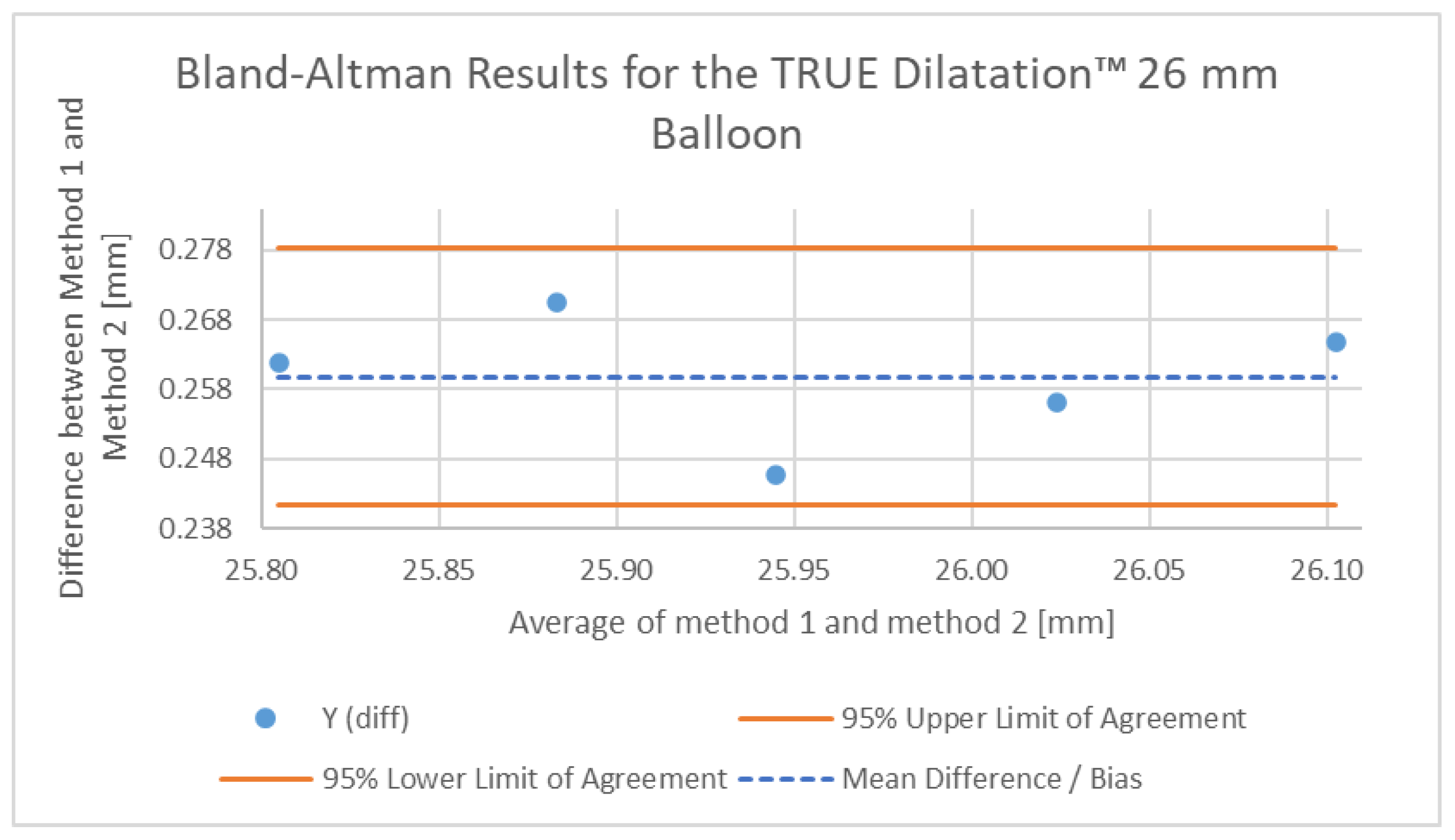
To further validate the accuracy of our non-contact optical method and quantify its systematic bias against an established technique, a Bland–Altman analysis was performed [21]. The resulting measurements for the 26 mm TRUE Dilatation™ balloon were compared against reference data from a published bench study reported in reference [10], which reported a contact-based methodology using calibrated rigid rings to measure balloon diameters.

The resulting Bland–Altman plot is shown in Figure 8. The analysis revealed a mean bias (average difference) of +0.259 mm, falling within the 95% limits of agreement ranging from 0.241 mm to 0.278 mm. This indicates that our non-contact method consistently measured the balloon diameter, being slightly larger than the measurements recorded using the rigid ring method reported in [10]. Such differences suggest a consistent and predictable difference between both measurement techniques.

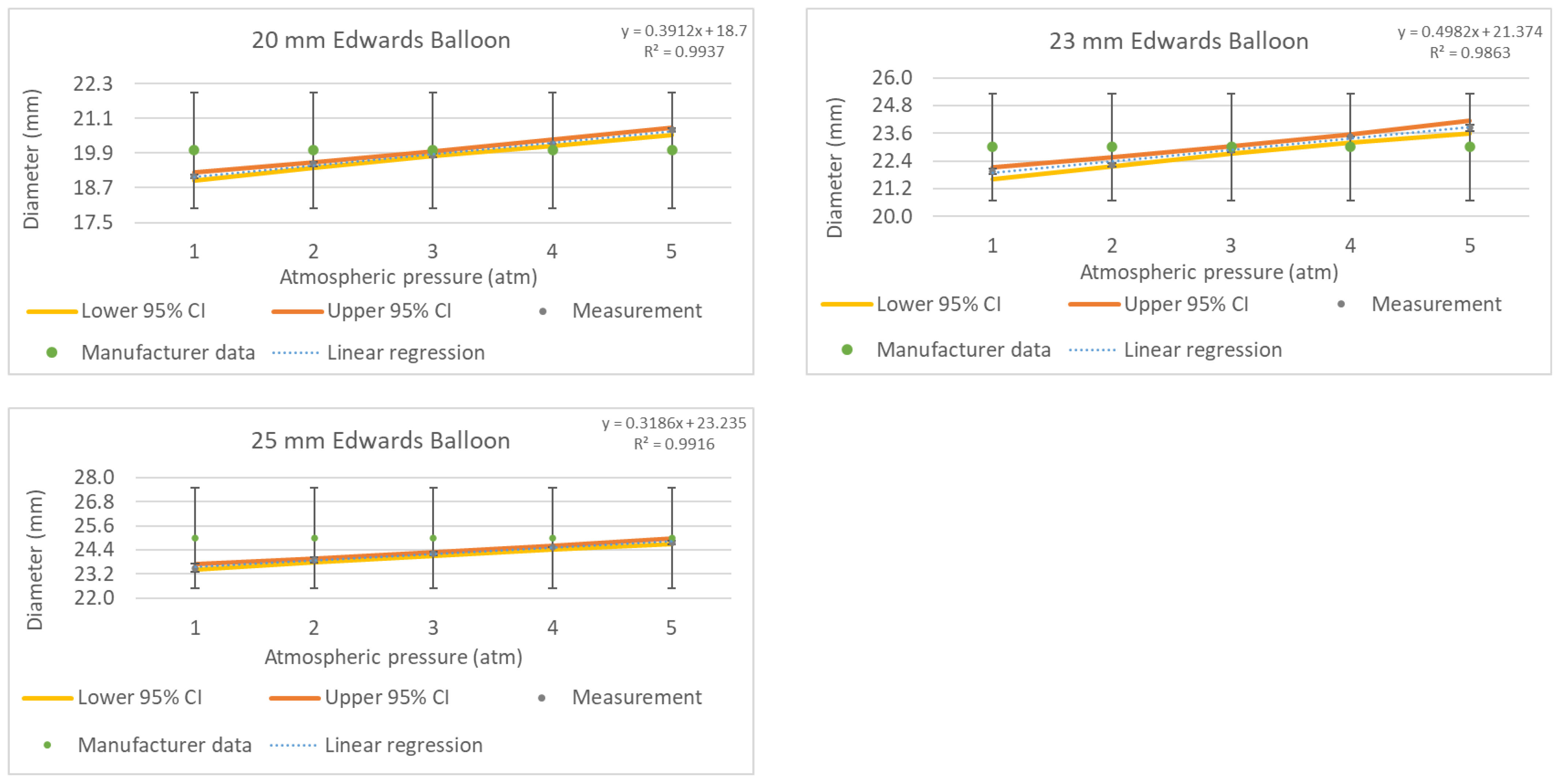
3.3. Results from 20, 23, and 25 mm Edwards Lifesciences Balloons

We measured three balloon sizes from Edwards Lifesciences with specified diameters of 20, 23, and 25 mm. Considering that these balloons are made of a transparent thermoplastic material, these measurements were taken using the auxiliary laser beam projection, as described in Section 2.6, to enable the autofocusing algorithms to converge and obtain the focused image of the balloon surface. Figure 9 shows an example image obtained with the robotic non-contact optical system using the 25 mm Edwards Lifesciences balloon inflated at a nominal pressure of 4 atm and measuring 24.55 ± 0.05 mm.

Figure 10 shows the pressure vs. diameter results obtained using the robotic system compared to the manufacturer’s data using the 20, 23, and 25 mm Edwards Lifesciences balloons inflated from one to five atmospheres. The raw ballon inflation data can be found in the Supplementary Table S1: Balloon inflation raw data.

The results obtained from the 20 mm Edwards Lifesciences balloon present a maximum diameter variation of up to +3.54% at 5 atm, exceeding the manufacturer-specified diameter by +710 µm. Given that there was no tolerance data specified by the vendor, pre-measuring the balloon and its deviation from nominal values could provide accurate guidance to surgeons on balloon selection.

Following the same trend, the 23 mm balloon presented an over-inflation diameter variation of +3.64% at 5 atmospheres, reaching an inflation diameter of 23.84 ± 0.13 mm. Finally, the measurements taken for the 25 mm Edwards Lifesciences balloon presented a maximum under-inflated diameter difference of −5.97% at 1 atm, which gradually was reduced to 0.91% at 5 atm. This balloon showed a diameter variation ranging from −1.5 mm to −230 µm when inflated between 1 and 5 atm, respectively.

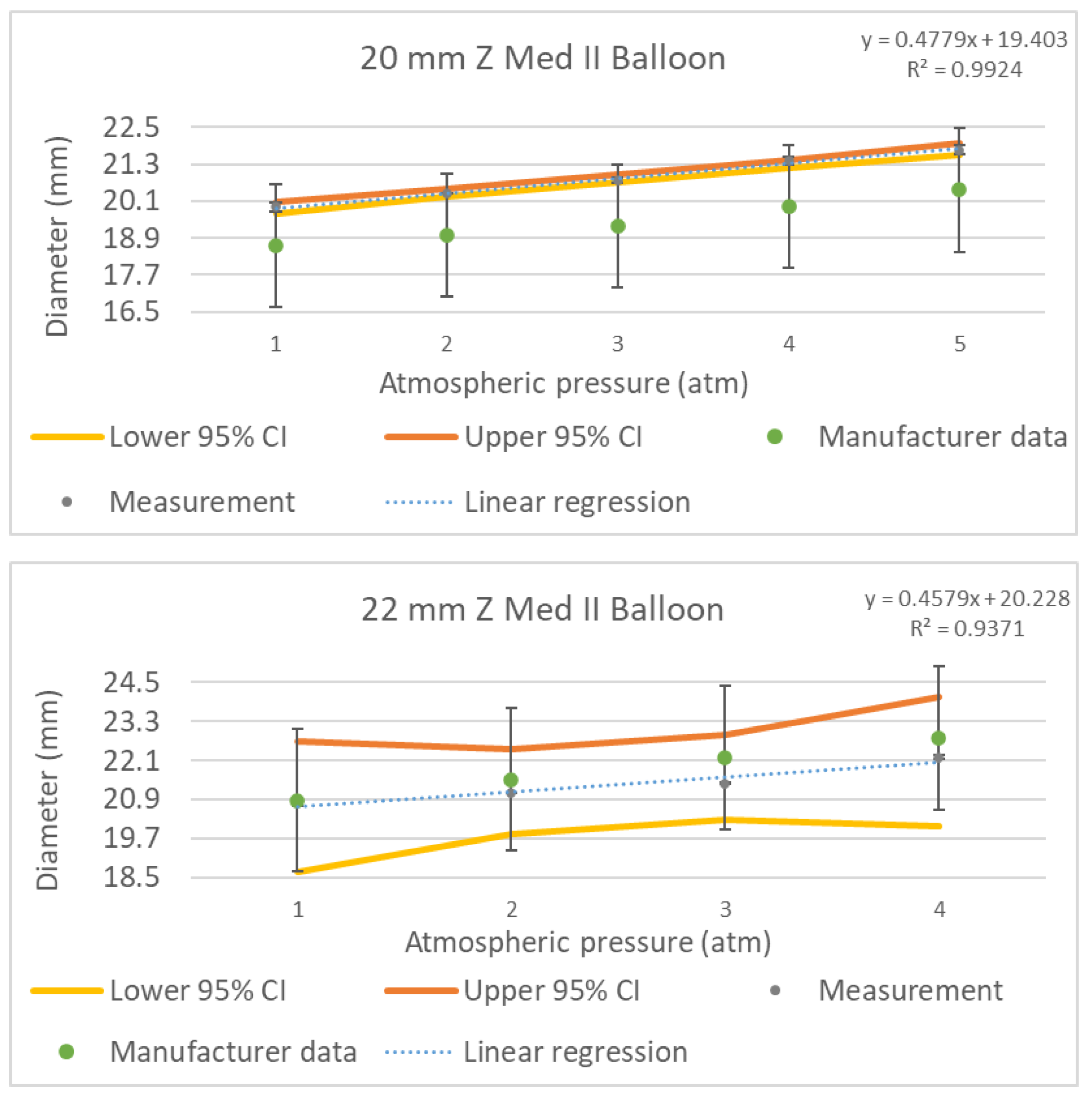
3.4. Results from 20 and 22 mm Z-MED II Balloons

Finally, in a similar way, we measured the 20 and 22 mm Z-MED II balloons. Given that these balloons were also fabricated using a transparent thermoplastic, the auxiliary laser beam projection described in Section 2.6 was also used. Figure 11 shows an example image obtained with the robotic, non-contact optical system of the 22 mm Z-MED II balloon inflated at a nominal pressure of 2 atm, measuring 21.1 ± 0.08 mm.

The manufacturer specification sheet outlines test measurement data taken for each balloon diameter applying the appropriate range of pressures [22]. The datasheet also specifies that the balloon can have a diameter variation of up to ±10% at the rated burst pressure. In our experiments we measured the devices at the rated burst pressure to validate the manufacturer’s specification and to assess the implications of a surgeon inflating the balloon to such pressures. Inflating the balloons to the rated burst pressure is required within our practice when using this balloon brand to reach the required diameter to match the patient’s aortic dimensions. Figure 12 shows the pressure vs. diameter calibration curves (grey points) of the 20 mm and 22 mm Z-MED II balloons obtained using our system, as well as the data points provided by the manufacturer (green points) for comparison purposes. The raw ballon inflation data can be found in the Supplementary Table S1: Balloon inflation raw data.

The results obtained from the 20 mm Z-MED II balloon presented a maximum diameter variation of up to +8.81% at 5 atm, exceeding the vendor-specified diameter by +1.76 mm. Although this value is in line with the manufacturer’s tolerated values, the nominal inflation pressure of the balloon still exceeded the value outlined by the manufacturer by 1.35 mm, thus making evident the benefit of measuring the balloons before a surgery. In contrast, the measured diameter of the 22 mm Z-MED II balloon was 22.2 ± 0.073 mm (4 atm), representing an under-inflation value of up to −585 µm at the rated burst pressure when compared with the diameter outlined in the manufacturer’s specifications. At the nominal inflation pressure of 2 atm, the balloon reached a final diameter of 21.1 ± 0.08 mm, with its diameter being under-inflated by −416 µm based on the manufacturer’s sizing chart.

Given the limited vendor information regarding the balloon materials (referred as thermoplastic non-compliant) for the three brands tested in this study, a proof-of-concept experiment was carried out to formally assess the validity of the free diameter measurement results obtained at room temperature (22 °C) and compared against physiological temperatures using saline solution at 37 °C. A paired t-test was performed using a 22 mm Z MED II balloon [23]. This balloon brand was chosen given that, from all the vendors, these showed the least satisfactory performance, and thus any change in their performance due to temperature was considered to be a good indicator of whether this should be further investigated with the other balloon brands.

Table 3. Example of 22 mm Z MED II balloon diameters obtained at both room temperature and physiological temperature. Positive percentage values represent over-inflation, and negative values represent under-inflation.

22 mm Z Med II
Pressure (atm)	Diameter [mm] with Fluid at 22 °C	Percentage Diameter Difference with Saline Solution at 37 °C
1.0	20.78 ± 0.85	−0.19%
2.0	21.10 ± 0.01	−0.5%
3.0	21.40 ± 0.03	+0.84%

shows the results of the experiments conducted using the 22 mm Z MED II balloon. The resulting variation in diameter when the experiments were conducted at room temperature (22 °C) vs. physiological temperatures (37 °C) resulted in a difference smaller than 1%.

The test yielded a p-value of 0.594. Since the p-value obtained was greater than the standard significance level of 0.05, we concluded that there were no statistically significant differences between both conditions, thus confirming that the balloon’s free diameter can be measured at room temperature.

3.5. Summary of Results

Table 4. Summary of the diameter variation results obtained experimentally when evaluating the TRUE Dilatation, Edwads Lifesciences, and Z-MED II balloons at 1 to 5 atm. The values under the pressure columns represent the average diameter variations with respect to the nominal balloon diameter in millimeters. The bold numbers are balloon diameters obtained at each balloon’s nominal pressure. The negative values represent the tested balloon being under-inflated while the positive values represent the tested balloon being over-inflated; both are expressed in millimeters.

Manufacturer	Nominal Diameter [mm]	Pressure [atm]
		1	2	3	4	5
TRUE Dilatation	22	+0.09	+0.16	+0.26	+0.36	+0.48
	24	−0.37	−0.30	−0.21	−0.11	+0.02
	26	−0.06	+0.02	+0.07	+0.15	+0.23
Edwards Lifesciences	20	−0.90	−0.47	−0.18	+0.22	+0.71
	23	−1.04	−0.77	−0.12	+0.44	+0.84
	25	−1.49	−1.10	−0.78	−0.45	−0.23
Z-MED II	20	−0.09	+0.34	+0.76	+1.41	+1.76
	22	−1.22	−0.90	−0.60	+0.21

summarizes the pressure results obtained experimentally when evaluating TRUE Dilatation, Edwads Lifesciences, and Z-MED II balloons at 1 to 5 atm. It shows the under- and over-inflation differences with respect to the nominal balloon diameters specified by the manufacturers. Positive values represent over-inflation, and negative values represent under-inflation. The bold figures are the measurements taken from the balloons at nominal pressure.

4. Discussion

Balloon catheters are used for standalone BAV procedures as well as to pre-dilate and/or post-dilate the aortic valve to facilitate the delivery and implantation of a new valve during TAVI procedures. Despite the number of balloon devices and manufacturers on the market, currently there have been no comparative studies that evaluate manufacturers’ balloon diameters experimentally nor has there been information about the characteristics of each balloon device. To maximize the safety and efficacy of these procedures, it is also important for the operators to have such information to ensure successful post-operative outcomes.

In BAV, it is often the case that the balloon is expanded more than once to achieve an adequate result. This requires that the balloon size, when inflated more than once at a given pressure, reaches the same diameter. In our experiments, all the balloons were able to satisfactorily inflate to approximately the same diameter after repeated inflations.

All the balloons (TRUE Dilatation, Edwards Lifesciences, and Z-MED II) evaluated in this study had linear behaviors, where the increase in their diameters seemed to be proportional to their intra-balloon pressures.

Overall, in our proof-of-concept experiments, the TRUE Dilatation balloons showed the smallest deviations of the three brands, having a linear increase in diameter with an average slope of 0.1. However, there were significant differences in the 22 and 24 mm balloons’ diameters, which exceeded the manufacturer tolerance specification of 1%.

The vendor of the Edwards Lifesciences balloons does not provide tolerance data; therefore, we were unable to compare the results obtained with the manufacturer-supplied data other than for its specified balloon size. These balloons performed well considering that their measured diameters were close to the specified dimensions at the given pressure (3 atm), with average differences in the range of 120 µm and a linear pressure to diameter having an average slope of 0.4.

The Z-MED II balloons had the least satisfactory performance, which was expected as the balloons’ manufacturer states a size variation of ±10% at the rated burst pressure, which was different for each size. This resulted in diameter variation differences ranging from an under-inflated diameter of −1.22 mm for the 22 mm balloon to an over-inflated diameter of +1.76 mm for the 20 mm balloon size.

Balloon sizing is important both to maximize the efficacy of procedures and to minimize potential complications, including an unsatisfactory prognosis [6]. Thus the ±1 to 2 mm sizing deviations observed in our bench-top study when compared with the data supplied by the manufacturers are highly relevant to the clinical context of TAVI. According to [24], procedural success is heavily dependent on achieving an optimal balloon inflation diameter matching the patient’s aortic valve annulus. While excessive oversizing of the balloons has been linked to the potential risk of annular damage, controlled oversizing has also been reported to reduce the prevalence of moderate-to-severe paravalvular leak. Therefore, by providing precise and data-supported balloon pressure versus diameter measurements to the operators, our automated bench-top robotic non-contact optical system could support the decision making of operators providing validated data and technology for the selection of the balloon size and therefore contribute to reduce procedural complications as well as allowing them to achieve improved patient outcomes.

Overall, the measurement results obtained in this study confirm that all the tested balloons performed close to their manufacturer’s specifications and within the reported tolerance ranges. However, each balloon had different inflation performances and thus tolerances of up to 10% justify the need for an automated, contactless, and standardized measurement methodology to determine each balloon’s inflation characteristics.

Contrasting our results with published contact-based methods for performing balloon diameter measurements, [10], we can validate that our results are in agreement with such works, demonstrating that our proposed method is suitable for performing automated measurements of surgical devices using our robotic non-contact optical approach.

Figure 13 summarizes the workflow for assessing BAV balloon diameters using the ROMI robot, the bright-field imaging system, the stitching and autofocusing algorithms, and the diameter computation pipelines. The system presented herein is a versatile system that can be potentially installed in the surgical room, with a low production cost as the system is based on off-the-shelf components. The time that it takes to deliver a measurement is less than four minutes per balloon, thus having the potential to contribute to decision making during the surgical workflow while complying with sterilization constraints due to the proposed robot’s non-contact optical approach.

Future work will focus on engineering a clinically viable prototype to be used in a clinical or operating room (OR) environment. A concrete translation plan with several critical modifications implemented in the proposed system would be required. Firstly, to ensure sterility, all non-sterile components, including the 3D printed mounts, would need to be machined using medical grade aluminum. The system, including the camera and laser, would need to be enclosed within a custom sterile drape. The efficacy of this draping solution would require formal bioburden validation. Secondly, the laser system could be substituted with a compact class I low-power device that would need to be assessed for its safety to comply with the OR laser safety regulations. Finally, the total workflow time for a single balloon measurement would need to be optimized to fit seamlessly into the fast-paced pre-procedural workflow of a catheterization procedure.

5. Conclusions

In this study, we have measured BAV balloons from three different vendors that we use in our daily surgical procedures at the Sussex Cardiac Centre. This proof-of-concept study was carried out using a robotic non-contact optical method to improve on the current existing methods when an operator needs to perform the procedure either manually or by relying on the vendor’s specifications. The device used in this work was based on a delta robotic (ROMI) system with an embedded bright-field microscopy machine vision system which included image stitching and autofocusing algorithms to accurately measure the initial balloon diameter at a submillimeter scale. To generate the pressure versus balloon diameter curves required by operators for the selection of the most suitable balloon size for each patient, an autofocusing algorithm was employed to measure changes of the free balloon diameter as a function of pressure. In those cases where the autofocusing algorithms failed to converge due to the balloons’ transparent materials, a laser projection system was used to enable the autofocusing algorithm to converge.

The experimental data shows that the TRUE Dilatation balloon presented the smallest deviations when compared with the manufacturer’s data, although the 22 and 24 mm balloons exceeded the 1% tolerance by +2.26% (over-inflation) and −1.56% (under-inflation), respectively. The Edwards Lifesciences and Z-MED II balloons presented inflation diameter variations ranging from −5.97% to + 8.81%, which led to a deviation of the specified balloon diameter of 1.76 mm. The standard error values obtained within our measurements revealed that the balloon diameters were consistent despite multiple inflations, suggesting that they were also resilient to repeated inflations up to the rated burst pressure.

The obtained results show a need for the presented system to be used in medical settings as an automated contactless pre-operative balloon characterization tool, providing operators with a standardized and objective methodology for balloon sizing in pre-operative planning. The system presented in this study has the potential to provide the basis for achieving standardized measurements when using noncompliant balloons for BAV procedures.

For the future deployment of the device presented herein in a clinical setting, a concrete translation plan that considers key critical modifications to ensure the sterility of the proposed equipment should be envisioned.