Influence of Exoskeleton Use on Cardiac Index
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants and Ethical Approval
- Trained professional welder
- Professional welding experience
- physically healthy
- musculoskeletal diseases
- cardiological diseases
- neurological diseases
- acute or chronic diseases
2.2. Experimental Design
2.3. Target Ratio
2.4. Equipment
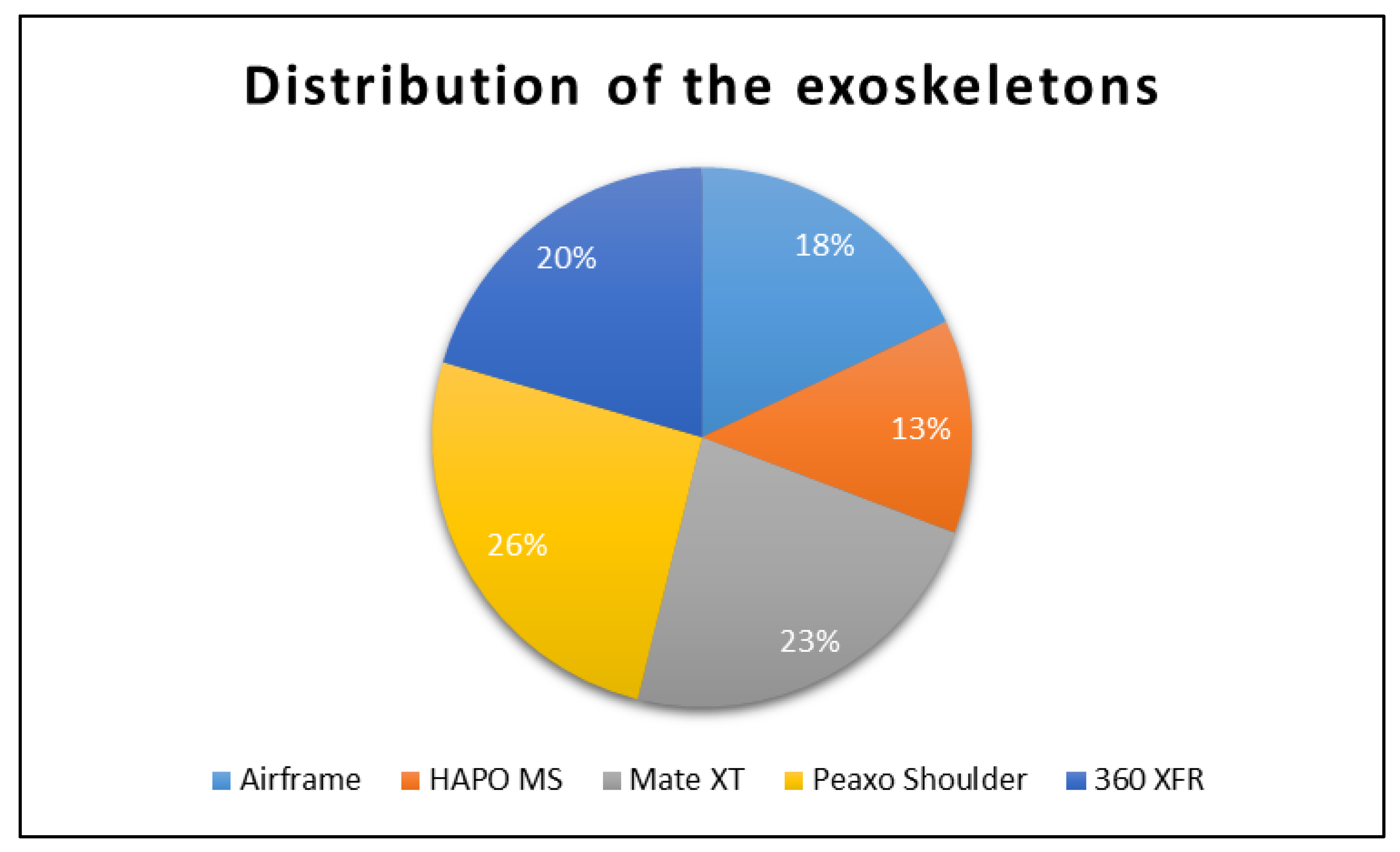
2.4.1. Exoskeletons
- Airframe®—Levitate Technologies, Inc., San Diego, CA, USA◦ Supporting force: 1.7 to 4.7 kg per arm
- HAPO MS—ErgoSanté, Anduze, France◦ Supporting force: up to 6 kg per arm
- Mate XT—Comau S.p.A., Grugliasco, Italy◦ Supporting force: 1.8 to 5.5 kg per arm
- Paexo Shoulder—Ottobock SE & Co. KGaA, Duderstadt, Germany◦ Supporting force: 1 to 4.5 kg per arm
- 360 XFR—Skel-Ex B.V., Rotterdam, The Netherlands◦ Supporting force: 1 to 4.9 kg per arm
2.4.2. Impedance Cardiography
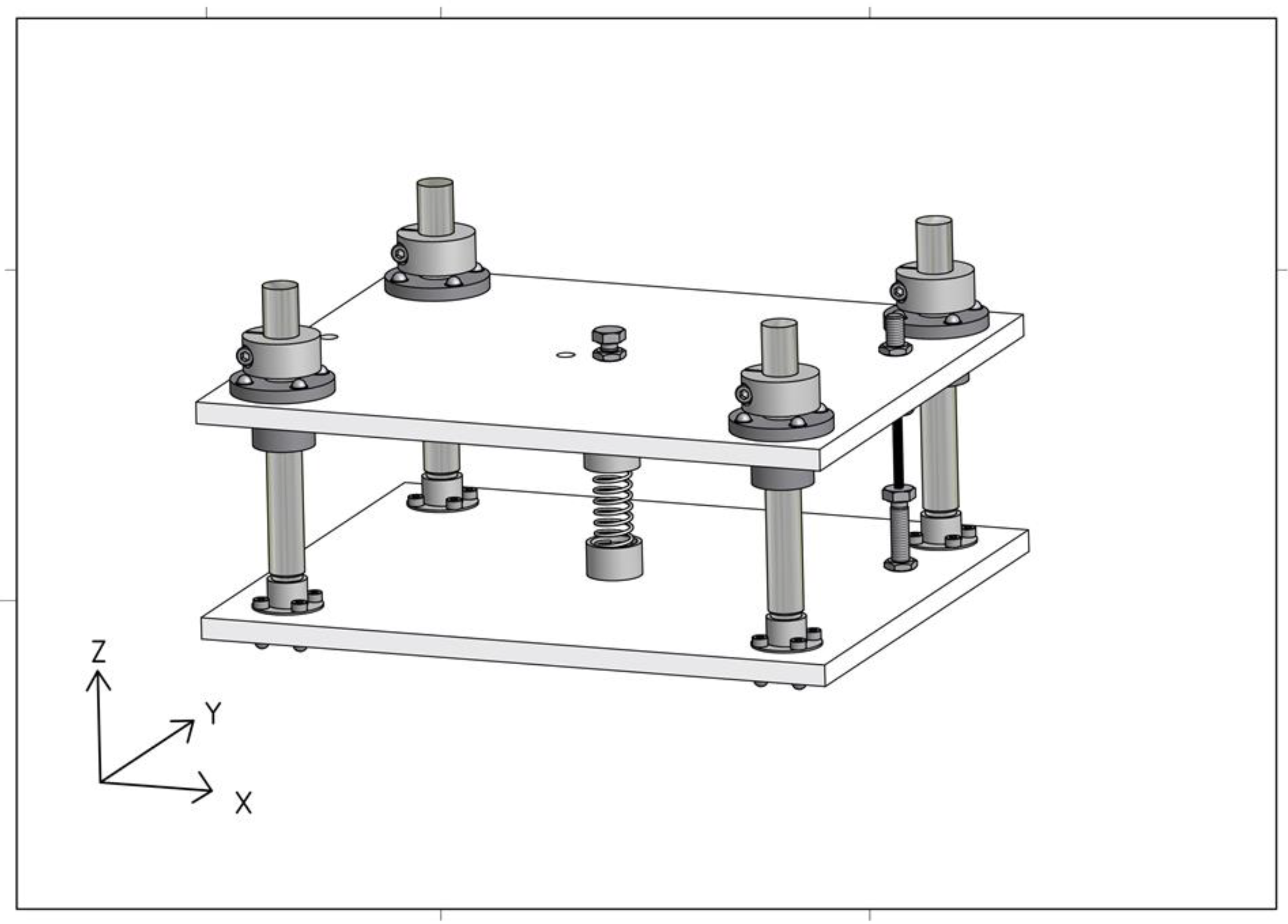
2.4.3. Grinding Simulator
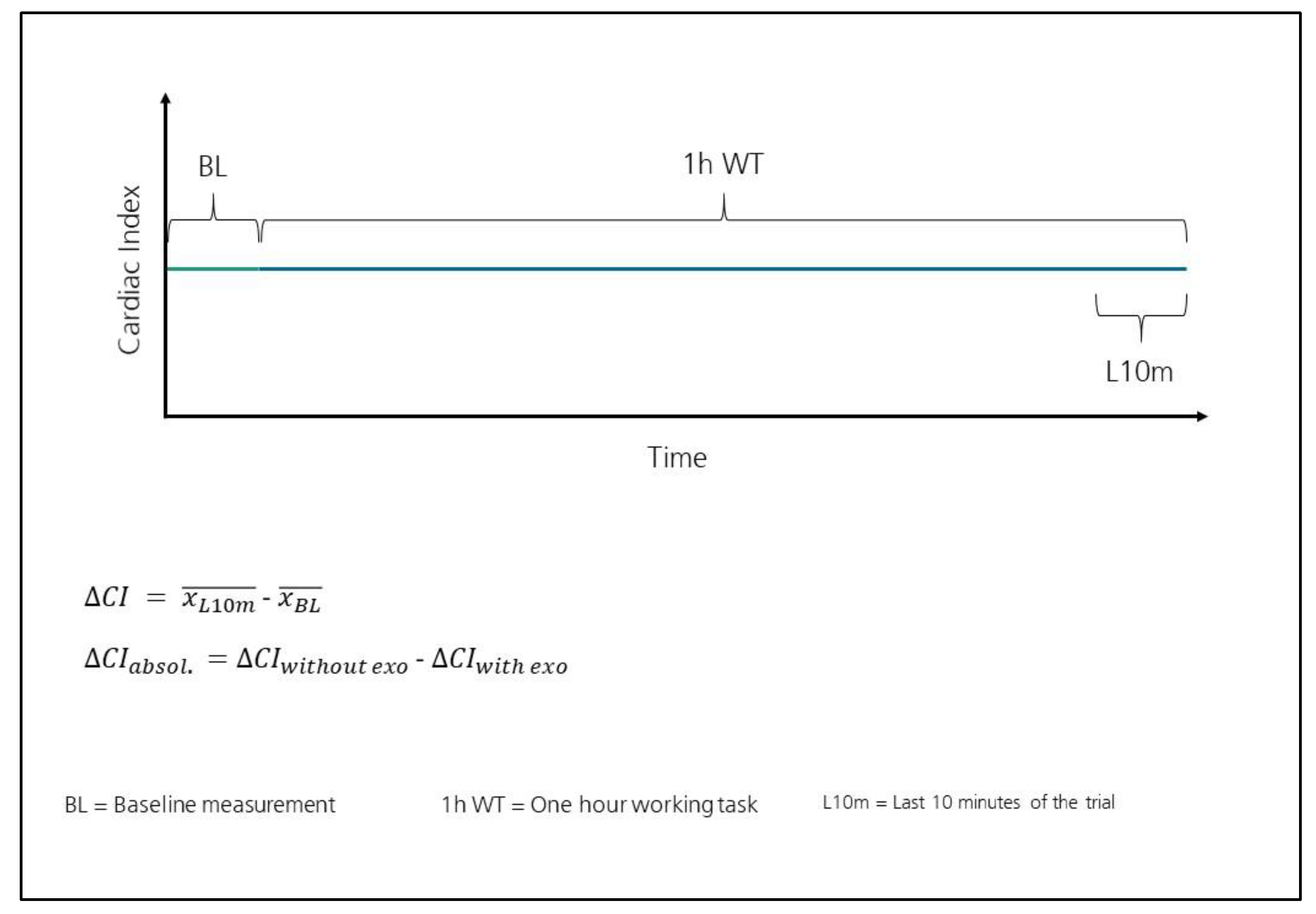
2.5. Data Analysis
3. Results
3.1. Distribution of the Two Samples and
3.2. Analysis of Variances of the Two Samples and
3.3. Analysis of Means of the Samples and
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| With Exoskeleton | Without Exoskeleton | ΔCIabsol. L/min/m2 | |||||
|---|---|---|---|---|---|---|---|
| ID | L/min/m2 | L/min/m2 | L/min/m2 | L/min/m2 | L/min/m2 | L/min/m2 | |
| 0301 | 3.628 | 3.308 | −0.320 | 3.779 | 4.116 | 0.337 | - |
| 0302 | 3.795 | 3.904 | 0.109 | 4.406 | 4.560 | 0.154 | - |
| 0303 | 3.153 | 3.105 | −0.048 | 3.420 | 3.458 | 0.038 | - |
| 0304 | 3.178 | 3.231 | 0.053 | 3.350 | 3.426 | 0.076 | - |
| 0306 | 3.832 | 3.473 | −0.359 | 3.694 | 3.832 | 0.137 | - |
| 0307 | 4.174 | 4.193 | 0.019 | 3.811 | 4.381 | 0.570 | - |
| 0309 | 2.608 | 2.742 | 0.135 | 3.031 | 3.389 | 0.358 | - |
| 0311 | 3.481 | 3.461 | −0.020 | 3.410 | 3.904 | 0.494 | - |
| 0312 | 2.918 | 2.912 | −0.006 | 2.889 | 2.978 | 0.089 | - |
| 0313 | 3.406 | 3.229 | −0.176 | 3.057 | 3.094 | 0.037 | - |
| 0314 | 3.022 | 2.861 | −0.161 | 2.700 | 2.782 | 0.082 | - |
| 0315 | 3.205 | 3.186 | −0.019 | 3.128 | 3.187 | 0.059 | - |
| 0316 | 4.086 | 4.392 | 0.306 | 4.714 | 5.141 | 0.427 | - |
| 0321 | 4.452 | 4.302 | −0.150 | 4.441 | 4.421 | −0.020 | - |
| 0322 | 3.280 | 2.924 | −0.356 | 2.317 | 2.756 | 0.440 | - |
| 0324 | 3.387 | 3.176 | −0.210 | 3.322 | 3.403 | 0.081 | - |
| 0325 | 3.277 | 3.243 | −0.034 | 2.953 | 3.142 | 0.190 | - |
| 0326 | 2.631 | 2.591 | −0.040 | 2.805 | 2.849 | 0.044 | - |
| 0327 | 4.554 | 3.742 | −0.812 | 3.571 | 4.385 | 0.814 | - |
| 0328 | 3.686 | 3.852 | 0.166 | 3.833 | 3.930 | 0.096 | - |
| 0329 | 3.811 | 3.697 | −0.113 | 3.700 | 4.652 | 0.952 | - |
| 0330 | 3.567 | 3.160 | −0.407 | 3.127 | 3.195 | 0.068 | - |
| 0331 | 3.910 | 3.706 | −0.204 | 3.321 | 3.554 | 0.233 | - |
| 0332 | 3.552 | 3.557 | 0.005 | 2.365 | 3.233 | 0.868 | - |
| 0333 | 3.339 | 3.330 | −0.009 | 3.038 | 3.226 | 0.189 | - |
| 0334 | 3.494 | 2.931 | −0.564 | 2.560 | 2.752 | 0.192 | - |
| 0335 | 2.553 | 2.445 | −0.108 | 2.729 | 2.738 | 0.009 | - |
| 0336 | 3.130 | 3.128 | −0.002 | 2.732 | 3.106 | 0.375 | - |
| 0337 | 3.132 | 2.978 | −0.153 | 3.036 | 3.007 | −0.029 | - |
| 0338 | 3.194 | 3.002 | −0.192 | 3.536 | 3.524 | −0.013 | - |
| 0339 | 3.438 | 3.305 | −0.132 | 3.213 | 3.548 | 0.335 | - |
| 0340 | 2.694 | 2.702 | 0.008 | 2.406 | 2.716 | 0.310 | - |
| 0341 | 3.846 | 3.752 | −0.094 | 3.500 | 3.826 | 0.326 | - |
| 0342 | 3.175 | 3.085 | −0.090 | 3.185 | 3.524 | 0.339 | - |
| 0343 | 2.854 | 2.812 | −0.042 | 2.993 | 3.248 | 0.255 | - |
| 0344 | 2.224 | 2.009 | −0.214 | 2.580 | 2.715 | 0.135 | - |
| 0345 | 3.473 | 3.456 | −0.017 | 3.264 | 3.449 | 0.185 | - |
| 0346 | 3.591 | 3.548 | −0.042 | 2.793 | 3.421 | 0.628 | - |
| 0347 | 2.769 | 2.776 | 0.007 | 2.664 | 2.760 | 0.096 | - |
| - | - | - | - | - | - | - | 0.365 |
References
- Lowe, B.D.; Billotte, W.G.; Peterson, D.R. ASTM F48 Formation and Standards for Industrial Exoskeletons and Exosuits. IISE Trans. Occup. Ergon. Hum. Factors 2019, 7, 3–4. [Google Scholar] [CrossRef] [PubMed]
- Bär, M.; Steinhilber, B.; Rieger, M.A.; Luger, T. The influence of using exoskeletons during occupational tasks on acute physical stress and strain compared to no exoskeleton—A systematic review and meta-analysis. Appl. Ergon. 2021, 94, 103385. [Google Scholar] [CrossRef]
- Bogue, R. Exoskeletons: A review of recent progress. Ind. Robot. 2022, 49, 813–818. [Google Scholar] [CrossRef]
- De Looze, M.P.; Bosch, T.; Krause, F.; Stadler, K.S.; O’Sullivan, L.W. Exoskeletons for industrial application and their potential effects on physical work load. Ergonomics 2016, 59, 671–681. [Google Scholar] [CrossRef] [PubMed]
- De Bock, S.; Ghillebert, J.; Govaerts, R.; Tassignon, B.; Rodriguez-Guerrero, C.; Crea, S.; Veneman, J.; Geeroms, J.; Meeusen, R.; De Pauw, K.; et al. Benchmarking occupational exoskeletons: An evidence mapping systematic review. Appl. Ergon. 2022, 98, 103582. [Google Scholar] [CrossRef] [PubMed]
- Del Ferraro, S.; Falcone, T.; Ranavolo, A.; Molinaro, V. The Effects of Upper-Body Exoskeletons on Human Metabolic Cost and Thermal Response during Work Tasks-A Systematic Review. Int. J. Environ. Res. Public Health 2020, 17, 7374. [Google Scholar] [CrossRef] [PubMed]
- Kermavnar, T.; de Vries, A.W.; de Looze, M.P.; O’Sullivan, L.W. Effects of industrial back-support exoskeletons on body loading and user experience: An updated systematic review. Ergonomics 2021, 64, 685–711. [Google Scholar] [CrossRef] [PubMed]
- Govaerts, R.; Tassignon, B.; Ghillebert, J.; Serrien, B.; De Bock, S.; Ampe, T.; El Makrini, I.; Vanderborght, B.; Meeusen, R.; De Pauw, K.; et al. Prevalence and incidence of work-related musculoskeletal disorders in secondary industries of 21st century Europe: A systematic review and meta-analysis. BMC Musculoskelet. Disord. 2021, 22, 751. [Google Scholar] [CrossRef] [PubMed]
- Bosch, T.; van Eck, J.; Knitel, K.; de Looze, M. The effects of a passive exoskeleton on muscle activity, discomfort and endurance time in forward bending work. Appl. Ergon. 2016, 54, 212–217. [Google Scholar] [CrossRef] [PubMed]
- Baltrusch, S.J.; van Dieën, J.H.; van Bennekom, C.A.M.; Houdijk, H. The effect of a passive trunk exoskeleton on functional performance in healthy individuals. Appl. Ergon. 2018, 72, 94–106. [Google Scholar] [CrossRef]
- Alemi, M.M.; Madinei, S.; Kim, S.; Srinivasan, D.; Nussbaum, M.A. Effects of Two Passive Back-Support Exoskeletons on Muscle Activity, Energy Expenditure, and Subjective Assessments During Repetitive Lifting. Hum. Factors 2020, 62, 458–474. [Google Scholar] [CrossRef] [PubMed]
- Madinei, S.; Alemi, M.M.; Kim, S.; Srinivasan, D.; Nussbaum, M.A. Biomechanical Evaluation of Passive Back-Support Exoskeletons in a Precision Manual Assembly Task: “Expected” Effects on Trunk Muscle Activity, Perceived Exertion, and Task Performance. Hum. Factors 2020, 62, 441–457. [Google Scholar] [CrossRef] [PubMed]
- Lotz, C.A.; Agnew, M.J.; Godwin, A.A.; Stevenson, J.M. The effect of an on-body personal lift assist device (PLAD) on fatigue during a repetitive lifting task. J. Electromyogr. Kinesiol. 2009, 19, 331–340. [Google Scholar] [CrossRef] [PubMed]
- Huysamen, K.; de Looze, M.; Bosch, T.; Ortiz, J.; Toxiri, S.; O’Sullivan, L.W. Assessment of an active industrial exoskeleton to aid dynamic lifting and lowering manual handling tasks. Appl. Ergon. 2018, 68, 125–131. [Google Scholar] [CrossRef] [PubMed]
- Alabdulkarim, S.; Nussbaum, M.A. Influences of different exoskeleton designs and tool mass on physical demands and performance in a simulated overhead drilling task. Appl. Ergon. 2019, 74, 55–66. [Google Scholar] [CrossRef] [PubMed]
- Alabdulkarim, S.; Farhan, A.M.; Ramadan, M.Z. Effects of a Wearable Carriage Aid on Whole-Body Physiological Measures and Balance. Appl. Sci. 2020, 10, 8076. [Google Scholar] [CrossRef]
- Weston, E.B.; Alizadeh, M.; Hani, H.; Knapik, G.G.; Souchereau, R.A.; Marras, W.S. A physiological and biomechanical investigation of three passive upper-extremity exoskeletons during simulated overhead work. Ergonomics 2022, 65, 105–117. [Google Scholar] [CrossRef] [PubMed]
- Erezuma, U.L.; Espin, A.; Torres-Unda, J.; Esain, I.; Irazusta, J.; Rodriguez-Larrad, A. Use of a passive lumbar back exoskeleton during a repetitive lifting task: Effects on physiologic parameters and intersubject variability. Int. J. Occup. Saf. Ergon. JOSE 2021, 1–8. [Google Scholar] [CrossRef]
- Knott, V.C. Evaluation von Exoskeletten zur Lastenhandhabung in der Logistik Mithilfe des Standardisierten Einsatzes der Spiroergometrie (Evaluation of Exoskeletons for Manual Load Handling in Logistics by Standardized Using of Cardiopulmonary Exercise Testing), 1st ed.; Verlag Dr. Hut: München, Germany, 2017. [Google Scholar]
- Kopp, V.; Holl, M.; Schalk, M.; Daub, U.; Bances, E.; García, B.; Schalk, I.; Siegert, J.; Schneider, U. Exoworkathlon: A prospective study approach for the evaluation of industrial exoskeletons. Wearable Technologies 2022, 3, E22. [Google Scholar] [CrossRef]
- Hollmann, W.; Strüder, H.K.; Predel, H.-G.; Tagarakis, C.V. Spiroergometrie: Kardiopulmonale Leistungsdiagnostik des Gesunden und Kranken; Schattauer: Stuttgart, Germany, 2006. [Google Scholar]
- Klinke, R. (Ed.) Lehrbuch der Physiologie: 55 Tabellen, 3rd ed.; Thieme: Stuttgart, Germany; New York, NY, USA, 2001. [Google Scholar]
- Stegemann, J. Leistungsphysiologie: Physiologische Grundlagen der Arbeit und des Sport; 20 Tabellen, 3rd ed.; Thieme: Stuttgart, Germany, 1984. [Google Scholar]
- Kroidl, R.; Schwarz, S.; Lehnigk, B.; Fritsch, J. (Eds.) Kursbuch Spiroergometrie: Technik und Befundung Verständlich Gemacht, 3rd ed.; Thieme: Stuttgart, Germany, 2014. [Google Scholar]
- Schwarz, S.; Lehnigk, B.; Schwittai, W. (Eds.) Lungenfunktionsdiagnostik und Spiroergometrie, 1st ed.; Thieme: Stuttgart, Germany, 2017. [Google Scholar]
- Bachl, N. Molekulare Sport- und Leistungsphysiologie: Molekulare, Zellbiologische und Genetische Aspekte der Körperlichen Leistungsfähigkeit; Springer: Vienna, Austria, 2017. [Google Scholar]
- Lorne, E.; Mahjoub, Y.; Diouf, M.; Sleghem, J.; Buchalet, C.; Guinot, P.-G.; Petiot, S.; Kessavane, A.; Dehedin, B.; Dupont, H. Accuracy of impedance cardiography for evaluating trends in cardiac output: A comparison with oesophageal Doppler. Br. J. Anaesth. 2014, 113, 596–602. [Google Scholar] [CrossRef]
- Scherhag, A.; Kaden, J.J.; Kentschke, E.; Sueselbeck, T.; Borggrefe, M. Comparison of impedance cardiography and thermodilution-derived measurements of stroke volume and cardiac output at rest and during exercise testing. Cardiovasc. Drugs Ther. 2005, 19, 141–147. [Google Scholar] [CrossRef] [PubMed]
- Yung, G.L.; Fedullo, P.F.; Kinninger, K.; Johnson, W.; Channick, R.N. Comparison of impedance cardiography to direct Fick and thermodilution cardiac output determination in pulmonary arterial hypertension. Congest. Heart Fail. 2004, 10, 7–10. [Google Scholar] [CrossRef] [PubMed]
- Rasch, D.; Guiard, V. The robustness of parametric statistical methods. Psychol. Sci. 2004, 46, 175–208. [Google Scholar]
- Gangestad, S.W.; Thornhill, R. The analysis of fluctuating asymmetry redux: The robustness of parametric statistics. Anim. Behav. 1998, 55, 497–501. [Google Scholar] [CrossRef] [PubMed]
- Schmalz, T.; Colienne, A.; Bywater, E.; Fritzsche, L.; Gärtner, C.; Bellmann, M.; Reimer, S.; Ernst, M. A Passive Back-Support Exoskeleton for Manual Materials Handling: Reduction of Low Back Loading and Metabolic Effort during Repetitive Lifting. IISE Trans. Occup. Ergon. Hum. Factors 2022, 10, 7–20. [Google Scholar] [CrossRef]




| Subject ID | BMI | Age |
|---|---|---|
| 0305 | 48 | 20 |
| 0308 | 36 | 20 |
| 0323 | 34 | 17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schalk, M.; Schalk, I.; Bauernhansl, T.; Siegert, J.; Schneider, U. Influence of Exoskeleton Use on Cardiac Index. Hearts 2022, 3, 117-128. https://doi.org/10.3390/hearts3040014
Schalk M, Schalk I, Bauernhansl T, Siegert J, Schneider U. Influence of Exoskeleton Use on Cardiac Index. Hearts. 2022; 3(4):117-128. https://doi.org/10.3390/hearts3040014
Chicago/Turabian StyleSchalk, Marco, Ines Schalk, Thomas Bauernhansl, Jörg Siegert, and Urs Schneider. 2022. "Influence of Exoskeleton Use on Cardiac Index" Hearts 3, no. 4: 117-128. https://doi.org/10.3390/hearts3040014
APA StyleSchalk, M., Schalk, I., Bauernhansl, T., Siegert, J., & Schneider, U. (2022). Influence of Exoskeleton Use on Cardiac Index. Hearts, 3(4), 117-128. https://doi.org/10.3390/hearts3040014






