Hyperfine Coupling Constants of Photoinduced Axial Symmetry NV Centers in a 6H Silicon Carbide: DFT and High-Field ENDOR Spectroscopy Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample
2.2. Experimental Approaches
2.3. Computational Method
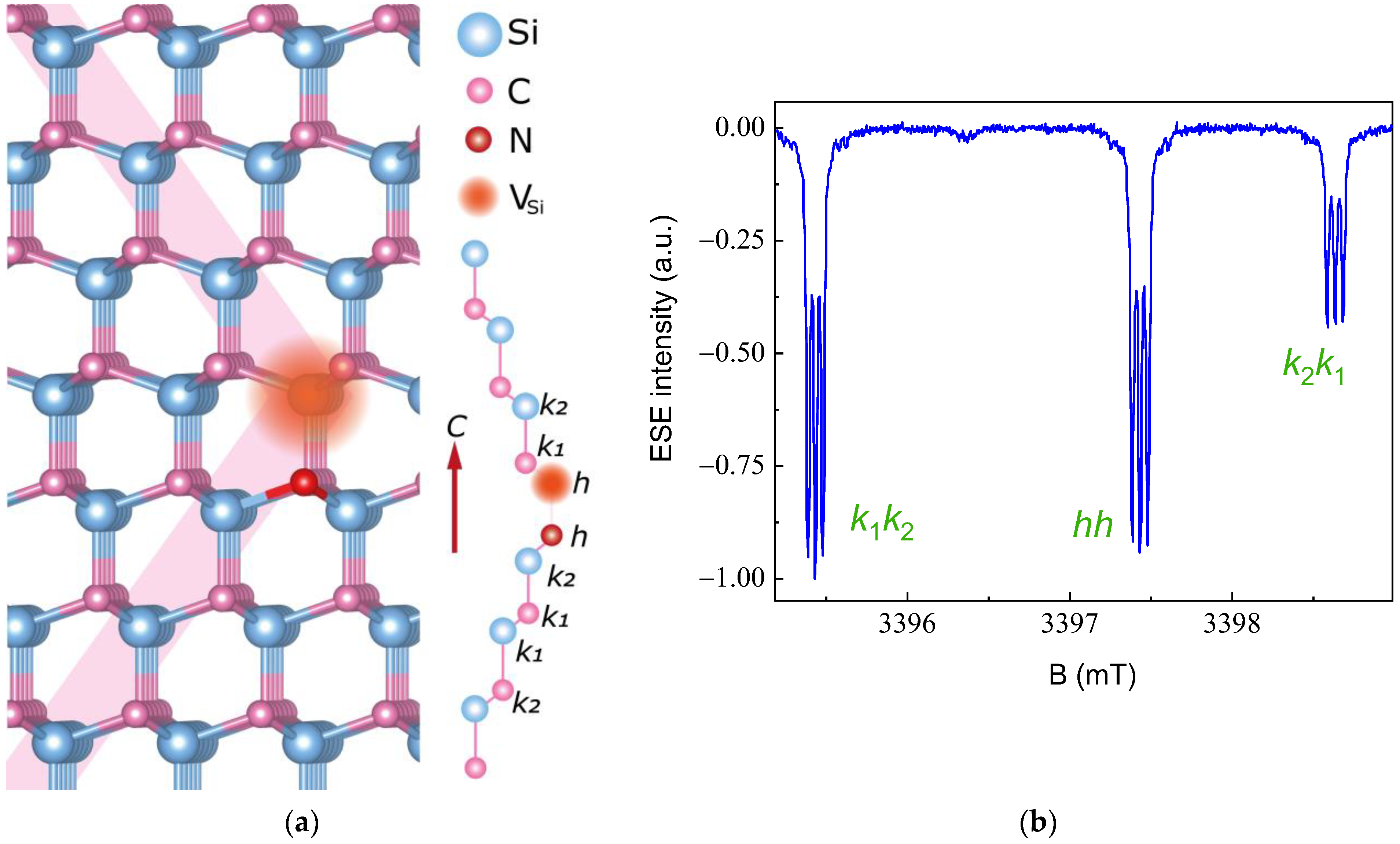
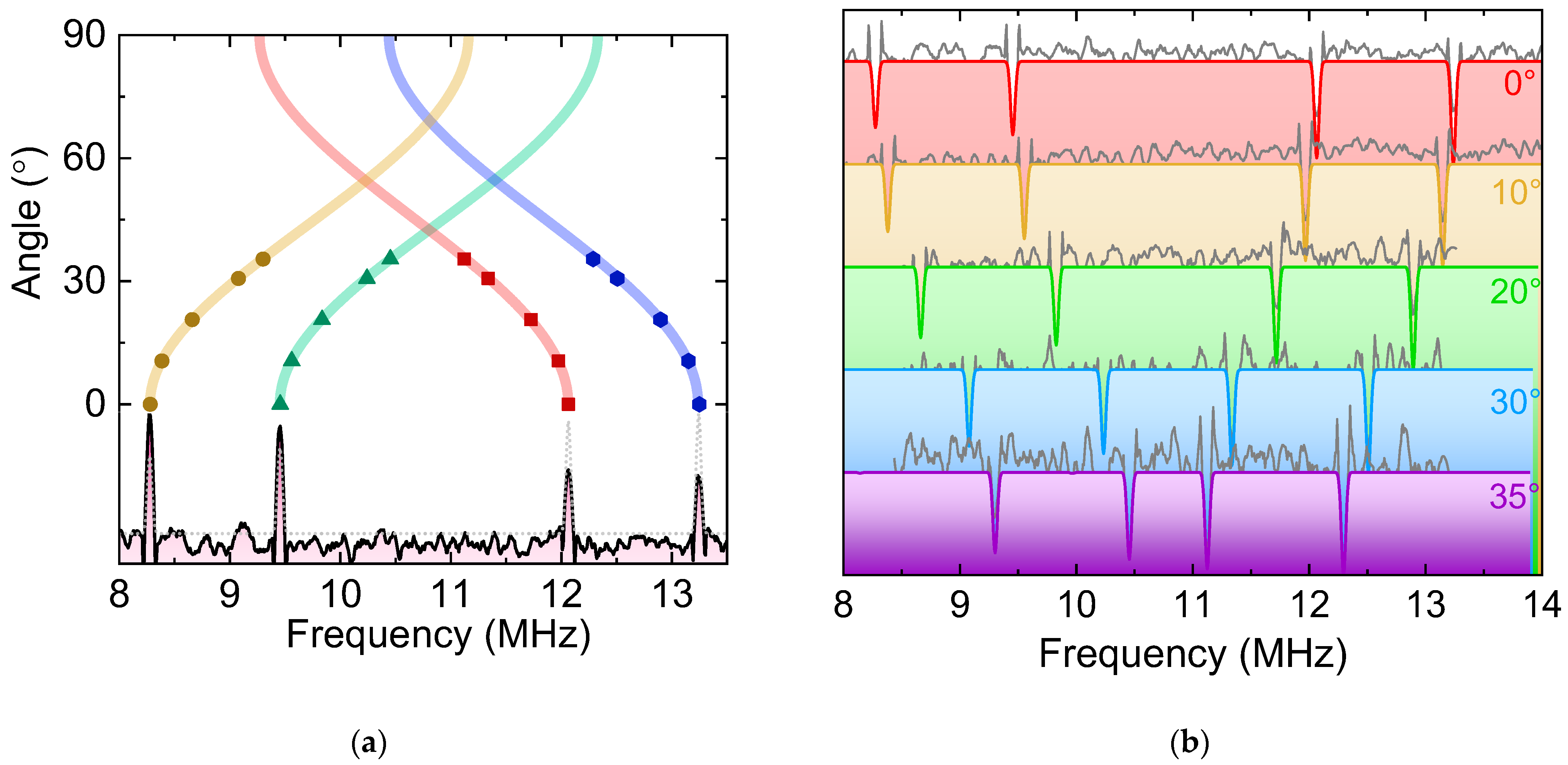
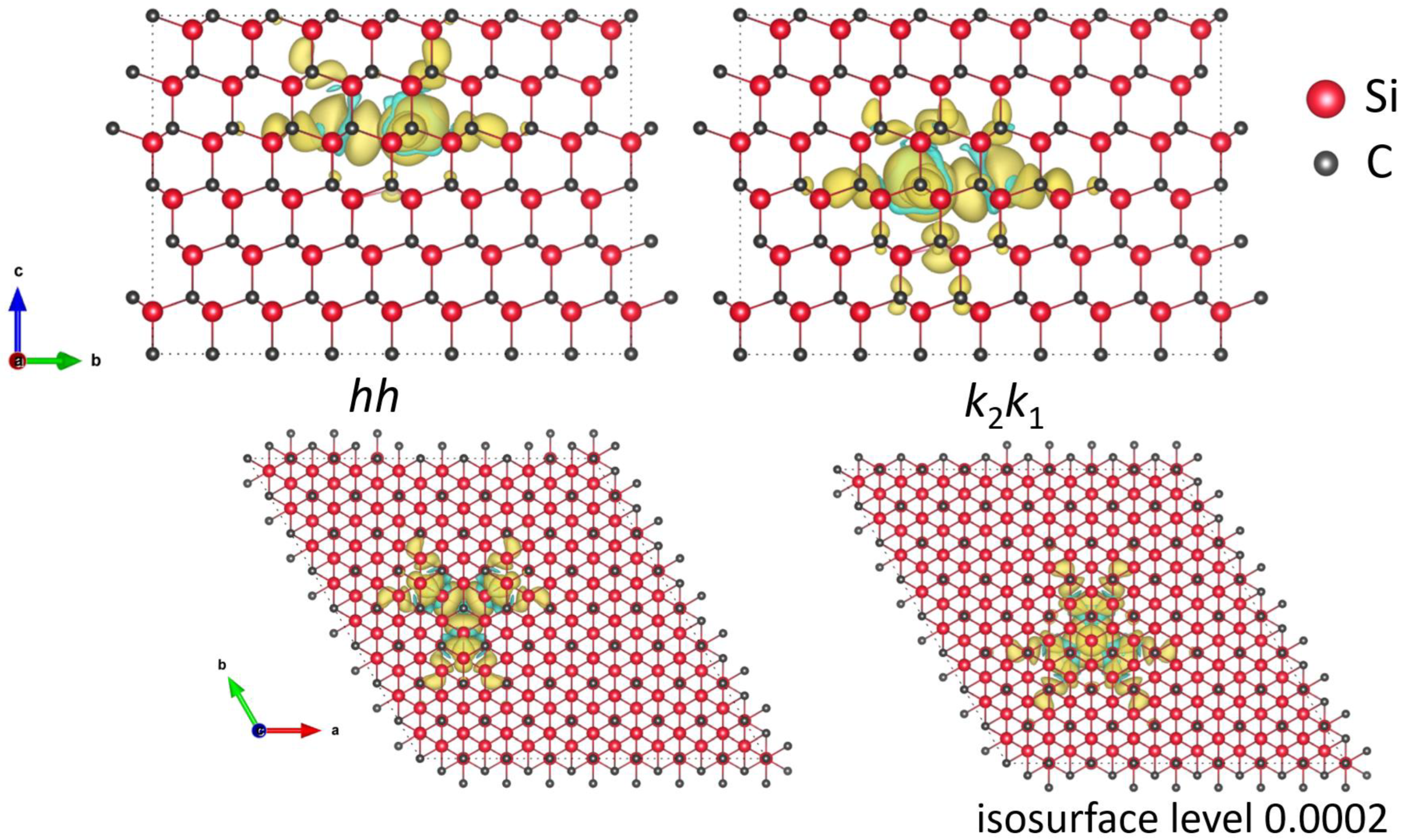
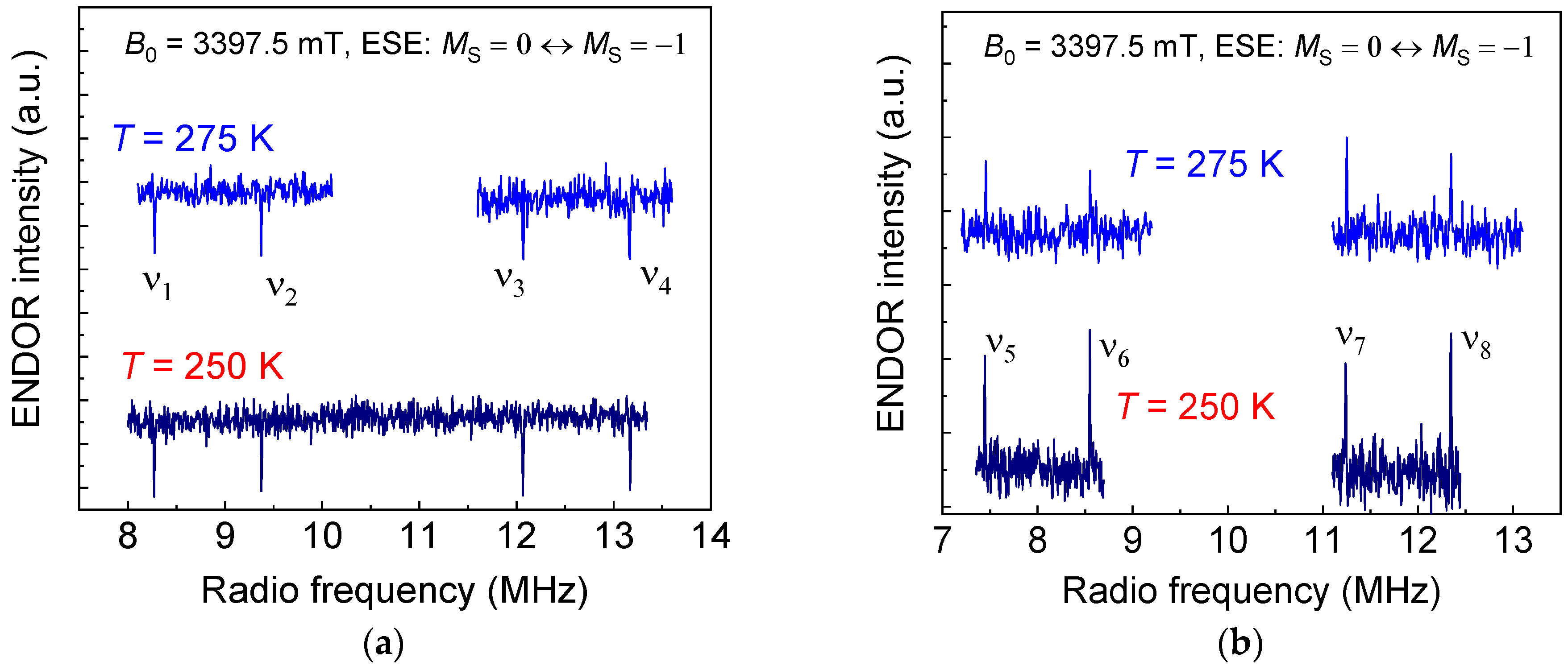
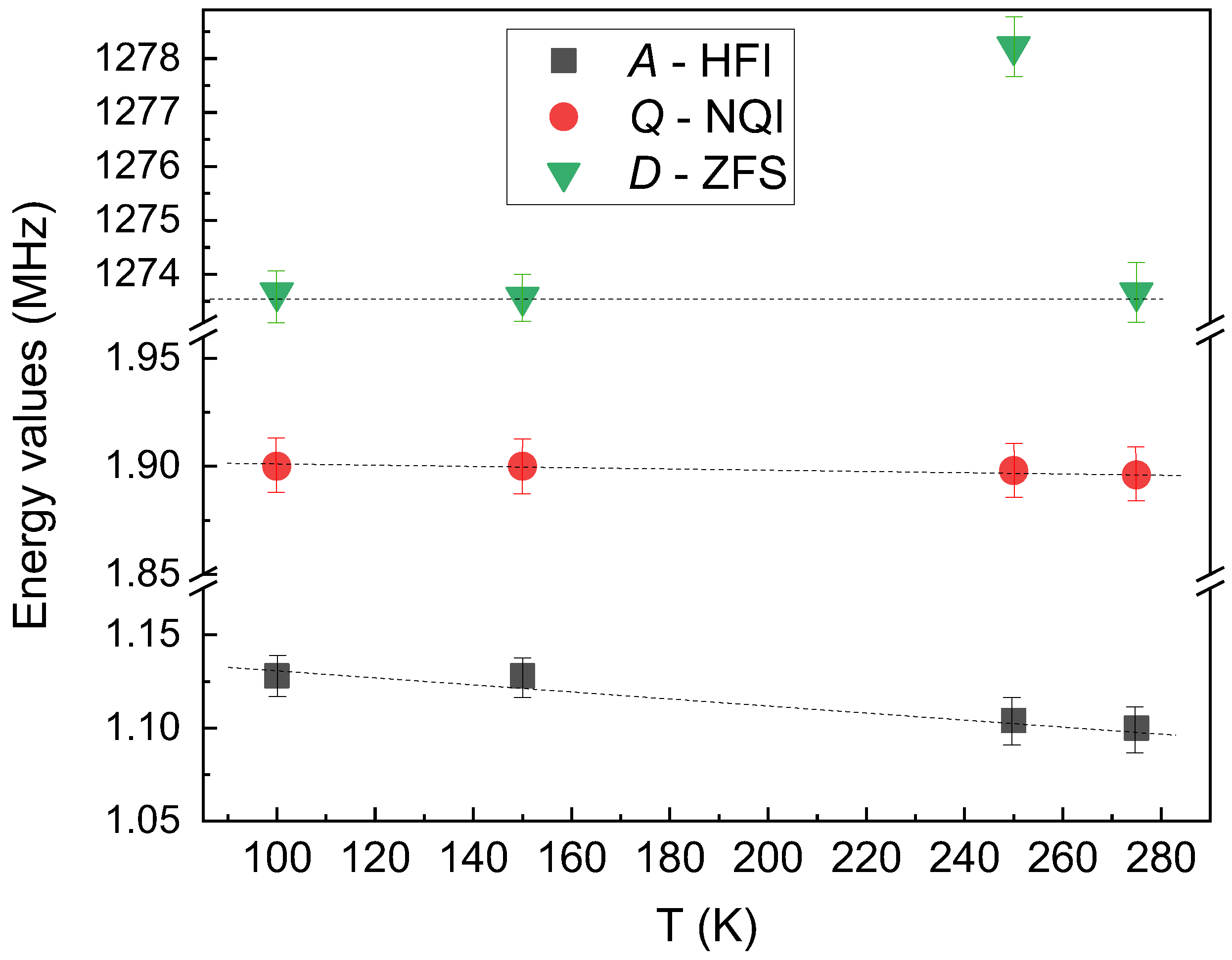
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EPR | Electron paramagnetic resonance |
| MW | Microwave |
| RF | Radiofrequency |
| NV | Nitrogen vacancy |
| ESE | Electron spin echo |
| DFT | Density functional theory |
| ZFS | Zero-field splitting |
| ENDOR | Electron nuclear double resonance |
References
- Heremans, F.J.; Yale, C.G.; Awschalom, D.D. Control of Spin Defects in Wide-Bandgap Semiconductors for Quantum Technologies. IEEE Access 2016, 104, 2009–2023. [Google Scholar] [CrossRef]
- Atatüre, M.; Englund, D.; Vamivakas, N.; Lee, S.; Wrachtrup, J. Material platforms for spin-based photonic quantum technologies. Nat. Rev. Mater. 2018, 3, 38–51. [Google Scholar] [CrossRef]
- Capan, I. Defects in Silicon Carbide as Quantum Qubits: Recent Advances in Defect Engineering. Appl. Sci. 2025, 15, 5606. [Google Scholar] [CrossRef]
- Pezzagna, S.; Meijer, J. Quantum computer based on color centers in diamond. Appl. Phys. Rev. 2021, 8, 011308. [Google Scholar] [CrossRef]
- Chou, Y.; Huang, S.Y.; Goan, H.S. Optimal control of fast and high-fidelity quantum gates with electron and nuclear spins of a nitrogen-vacancy center in diamond. Phys. Rev. A 2015, 91, 052315. [Google Scholar] [CrossRef]
- Castelletto, S.; Boretti, A. Silicon carbide color centers for quantum applications. Phys. Photonics 2020, 2, 022001. [Google Scholar] [CrossRef]
- Singh, H.; Anisimov, A.N.; Breev, I.D.; Baranov, P.G.; Suter, D. Optical spin initialization of spin-3/2 silicon vacancy centers in 6H–SiC at room temperature. Phys. Rev. B 2021, 103, 104103. [Google Scholar] [CrossRef]
- Csóré, A.; Von Bardeleben, H.J.; Cantin, J.L.; Gali, A. Characterization and formation of NV centers in 3 C, 4 H, and 6 H SiC: An ab initio study. Phys. Rev. B 2017, 96, 085204. [Google Scholar] [CrossRef]
- Castelletto, S.; Peruzzo, A.; Bonato, C.; Johnson, B.C.; Radulaski, M.; Ou, H.; Kaiser, F.; Wrachtrup, J. Silicon carbide photonics bridging quantum technology. ACS Photonics 2022, 9, 1434–1457. [Google Scholar] [CrossRef]
- Capan, I. Electrically active defects in 3C, 4H, and 6H silicon carbide polytypes: A review. Crystals 2025, 15, 255. [Google Scholar] [CrossRef]
- Khazen, K.; Von Bardeleben, H.J.; Zargaleh, S.A.; Cantin, J.L.; Zhao, M.; Gao, W.; Biktagirov, T.; Gerstmann, U. High-resolution resonant excitation of NV centers in 6 H-SiC: A matrix for quantum technology applications. Phys. Rev. B 2019, 100, 205202. [Google Scholar] [CrossRef]
- Shafizadeh, D.; Davidsson, J.; Ohshima, T.; Abrikosov, I.A.; Son, N.T.; Ivanov, I.G. Selection rules in the excitation of the divacancy and the nitrogen-vacancy pair in 4 H-and 6 H-SiC. Phys. Rev. B 2024, 109, 235203. [Google Scholar] [CrossRef]
- Cheng, G.D.; Wan, Y.P.; Yan, S.Y. Optical and spin coherence properties of NV center in diamond and 3C-SiC. Comput. Mater. Sci. 2018, 154, 60–64. [Google Scholar] [CrossRef]
- Pfaff, W.; Taminiau, T.H.; Robledo, L.; Bernien, H.; Markham, M.; Twitchen, D.J.; Hanson, R. Demonstration of entanglement-by-measurement of solid-state qubits. Nat. Phys. 2013, 9, 29–33. [Google Scholar] [CrossRef]
- Dehollain, J.P.; Simmons, S.; Muhonen, J.T.; Kalra, R.; Laucht, A.; Hudson, F.; Itoh, K.M.; Jamieson, D.N.; McCallum, J.C.; Dzurak, A.S.; et al. Bell’s inequality violation with spins in silicon. Nat. Nanotechnol. 2016, 11, 242–246. [Google Scholar] [CrossRef] [PubMed]
- Kalra, R.; Laucht, A.; Hill, C.D.; Morello, A. Robust two-qubit gates for donors in silicon controlled by hyperfine interactions. Phys. Rev. X 2014, 4, 021044. [Google Scholar] [CrossRef]
- Saeedi, K.; Simmons, S.; Salvail, J.Z.; Dluhy, P.; Riemann, H.; Abrosimov, N.V.; Becker, P.; Pohl, H.; Morton, J.J.L.; Thewalt, M.L.W. Room-Temperature Quantum Bit Storage Exceeding 39 Minutes Using Ionized Donors in Silicon-28. Science 2013, 342, 830–833. [Google Scholar] [CrossRef]
- Latypova, L.; Murzakhanov, F.; Mamin, G.; Sadovnikova, M.; von Bardeleben, H.J.; Rau, J.V.; Gafurov, M. Exploring High-Spin Color Centers in Wide Band Gap Semiconductors SiC: A Comprehensive Magnetic Resonance Investigation (EPR and ENDOR Analysis). Molecules 2024, 29, 3033. [Google Scholar] [CrossRef]
- Doherty, M.W.; Manson, N.B.; Delaney, P.; Jelezko, F.; Wrachtrup, J.; Hollenberg, L.C. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. [Google Scholar] [CrossRef]
- Murzakhanov, F.F.; Sadovnikova, M.A.; Mamin, G.V.; Nagalyuk, S.S.; von Bardeleben, H.J.; Schmidt, W.G.; Biktagirov, T.; Gerstmann, U.; Soltamov, V.A. 14N Hyperfine and nuclear interactions of axial and basal NV centers in 4H-SiC: A high frequency (94 GHz) ENDOR study. J. Appl. Phys. 2023, 134, 123906. [Google Scholar] [CrossRef]
- Latypova, L.R.; Gracheva, I.N.; Shurtakova, D.V.; Murzakhanov, F.F.; Sadovnikova, M.A.; Mamin, G.V.; Gafurov, M.R. Electron–Nuclear Interactions of NV Defects in an Isotopically Purified 6 H-28SiC Crystal. J. Phys. Chem. C 2024, 128, 18559–18565. [Google Scholar] [CrossRef]
- Jarmola, A.; Fescenko, I.; Acosta, V.M.; Doherty, M.W.; Fatemi, F.K.; Ivanov, T.; Budker, D.; Malinovsky, V.S. Robust optical readout and characterization of nuclear spin transitions in nitrogen-vacancy ensembles in diamond. Phys. Rev. Res. 2020, 2, 023094. [Google Scholar] [CrossRef]
- Xu, S.; Liu, M.; Xie, T.; Zhao, Z.; Shi, Q.; Yu, P.; Duan, C.; Shi, F.; Du, J. High-precision measurements and first-principles explanation of the temperature-dependent C 13 and N 14 hyperfine interactions of single NV− centers in diamond at room temperature. Phys. Rev. B 2023, 107, L140101. [Google Scholar] [CrossRef]
- Soshenko, V.V.; Vorobyov, V.V.; Bolshedvorskii, S.V.; Rubinas, O.; Cojocaru, I.; Kudlatsky, B.; Zeleneev, A.I.; Bolshedvorskii1, S.V.; Sorokin, V.N.; Smolyaninov, A.N.; et al. Temperature drift rate for nuclear terms of the NV-center ground-state Hamiltonian. Phys. Rev. B 2020, 102, 125133. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Stoll, S.; Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef]
- von Bardeleben, H.J.; Cantin, J.L.; Csóré, A.; Gali, A.; Rauls, E.; Gerstman, U. NV centers in 3C, 4H, and 6H silicon carbide: A variable platform for solid-state qubits and nanosensors. Phys. Rev. B 2016, 94, 121202. [Google Scholar] [CrossRef]
- Gracheva, I.N.; Murzakhanov, F.F.; Mamin, G.V.; Sadovnikova, M.A.; Gabbasov, B.F.; Mokhov, E.N.; Gafurov, M.R. Symmetry of the hyperfine and quadrupole interactions of boron vacancies in a hexagonal boron nitride. J. Phys. Chem. C 2023, 127, 3634–3639. [Google Scholar] [CrossRef]
- Bradley, C.E.; Randall, J.; Abobeih, M.H.; Berrevoets, R.C.; Degen, M.J.; Bakker, M.A.; Markham, M.; Twitchen, D. J.; Taminiau, T.H. A ten-qubit solid-state spin register with quantum memory up to one minute. Phys. Rev. X 2019, 9, 031045. [Google Scholar] [CrossRef]
- Joas, T.; Ferlemann, F.; Sailer, R.; Vetter, P.J.; Zhang, J.; Said, R.S.; Teraji, T.; Onoda, S.; Calarco, T.; Genov, G.; et al. High-Fidelity Electron Spin Gates for Scaling Diamond Quantum Registers. Phys. Rev. X 2025, 15, 021069. [Google Scholar] [CrossRef]
- Doherty, M.W.; Dolde, F.; Fedder, H.; Jelezko, F.; Wrachtrup, J.; Manson, N.B.; Hollenberg, L.C.L. Theory of the Ground-State Spin of the NV- Center in Diamond. Phys. Rev. B 2012, 85, 205203. [Google Scholar] [CrossRef]
- Murzakhanov, F.F.; Yavkin, B.V.; Mamin, G.V.; Orlinskii, S.B.; Von Bardeleben, H.J.; Biktagirov, T.; Gerstmann, U.; Soltamov, V.A. Hyperfine and nuclear quadrupole splitting of the NV− ground state in 4 H-SiC. Phys. Rev. B 2021, 103, 245203. [Google Scholar] [CrossRef]
- Disselhorst, J.A.; Vandermeer, H.; Poluektov, O.G.; Schmidt, J. A pulsed EPR and ENDOR spectrometer operating at 95 GHz. J. Magn. Reson. Ser. A 1995, 115, 183–188. [Google Scholar] [CrossRef]
- Jiang, Z.; Cai, H.; Cernansky, R.; Liu, X.; Gao, W. Quantum sensing of radio-frequency signal with NV centers in SiC. Sci. Adv. 2023, 9, eadg2080. [Google Scholar] [CrossRef]
- Khazen, K.; von Bardeleben, H.J. NV-centers in SiC: A solution for quantum computing technology? Front. Quantum Sci. Technol. 2023, 2, 1115039. [Google Scholar] [CrossRef]
- Gottscholl, A.; Diez, M.; Soltamov, V.; Kasper, C.; Krauße, D.; Sperlich, A.; Kianinia, M.; Bradac, C.; Aharonovich, I.; Dyakonov, V. Spin defects in hBN as promising temperature, pressure and magnetic field quantum sensors. Nat. Commun. 2021, 12, 4480. [Google Scholar] [CrossRef] [PubMed]
- Moreva, E.; Bernardi, E.; Traina, P.; Sosso, A.; Tchernij, S.D.; Forneris, J.; Picollo, F.; Brida, G.; Pastuović, Ž.; Degiovanni, I.P.; et al. Practical applications of quantum sensing: A simple method to enhance the sensitivity of nitrogen-vacancy-based temperature sensors. Phys. Rev. Appl. 2020, 13, 054057. [Google Scholar] [CrossRef]
- Acosta, V.M.; Jarmola, A.; Zipp, L.J.; Ledbetter, M.P.; Bauch, E.; Budker, D. Broadband magnetometry by infrared-absorption detection of diamond NV centers and associated temperature dependence. In Proceedings of the Advances in Photonics of Quantum Computing, Memory, and Communication IV SPIE, San Francisco, CA, USA, 22–27 January 2011; Volume 7948, pp. 145–153. [Google Scholar] [CrossRef]
- Acosta, V.M.; Bauch, E.; Ledbetter, M.P.; Waxman, A.; Bouchard, L.S.; Budker, D. Temperature dependence of the nitrogen-vacancy magnetic resonance in diamond. Phys. Rev. Lett. 2010, 104, 070801. [Google Scholar] [CrossRef]
- Barson, M.S.J.; Reddy, P.; Yang, S.; Manson, N.B.; Wrachtrup, J.; Doherty, M.W. Temperature dependence of the C 13 hyperfine structure of the negatively charged nitrogen-vacancy center in diamond. Phys. Rev. B 2019, 99, 094101. [Google Scholar] [CrossRef]
- Doherty, M.W.; Acosta, V.M.; Jarmola, A.; Barson, M.S.; Manson, N.B.; Budker, D.; Hollenberg, L.C. Temperature shifts of the resonances of the NV− center in diamond. Phys. Rev. B 2014, 90, 041201. [Google Scholar] [CrossRef]
- Barson, M.S.; Peddibhotla, P.; Ovartchaiyapong, P.; Ganesan, K.; Taylor, R.L.; Gebert, M.; Mielens, Z.; Koslowski, B.; Simpson, D.A.; McGuinness, L.P.; et al. Nanomechanical sensing using spins in diamond. Nano Lett. 2017, 17, 1496–1503. [Google Scholar] [CrossRef] [PubMed]
- Neumeier, J.J.; Shvyd’ko, Y.V.; Haskel, D. Thermal expansion of 4H and 6H SiC from 5 K to 340 K. J. Phys. Chem. Solids 2024, 187, 111860. [Google Scholar] [CrossRef]

| NVhh | A-Tensor Values (MHz) | Cq (MHz) |
|---|---|---|
| Experiment | aiso = −1.175; b ≤ 0.02 | 2.523 |
| Theory | aiso = −1.140; b = 0.088 | 2.6194 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ermakova, Y.; Dmitrieva, E.; Gracheva, I.; Shurtakova, D.; Sadovnikova, M.; Murzakhanov, F.; Mamin, G.; Nagalyuk, S.; Mokhov, E.; Gafurov, M. Hyperfine Coupling Constants of Photoinduced Axial Symmetry NV Centers in a 6H Silicon Carbide: DFT and High-Field ENDOR Spectroscopy Study. Appl. Nano 2025, 6, 23. https://doi.org/10.3390/applnano6040023
Ermakova Y, Dmitrieva E, Gracheva I, Shurtakova D, Sadovnikova M, Murzakhanov F, Mamin G, Nagalyuk S, Mokhov E, Gafurov M. Hyperfine Coupling Constants of Photoinduced Axial Symmetry NV Centers in a 6H Silicon Carbide: DFT and High-Field ENDOR Spectroscopy Study. Applied Nano. 2025; 6(4):23. https://doi.org/10.3390/applnano6040023
Chicago/Turabian StyleErmakova, Yuliya, Ekaterina Dmitrieva, Irina Gracheva, Darya Shurtakova, Margarita Sadovnikova, Fadis Murzakhanov, Georgy Mamin, Sergey Nagalyuk, Evgeny Mokhov, and Marat Gafurov. 2025. "Hyperfine Coupling Constants of Photoinduced Axial Symmetry NV Centers in a 6H Silicon Carbide: DFT and High-Field ENDOR Spectroscopy Study" Applied Nano 6, no. 4: 23. https://doi.org/10.3390/applnano6040023
APA StyleErmakova, Y., Dmitrieva, E., Gracheva, I., Shurtakova, D., Sadovnikova, M., Murzakhanov, F., Mamin, G., Nagalyuk, S., Mokhov, E., & Gafurov, M. (2025). Hyperfine Coupling Constants of Photoinduced Axial Symmetry NV Centers in a 6H Silicon Carbide: DFT and High-Field ENDOR Spectroscopy Study. Applied Nano, 6(4), 23. https://doi.org/10.3390/applnano6040023







