Theory for Electrochemical Heat Sources and Exothermic Explosions: The Akbari–Ganji Method
Abstract
:1. Introduction
2. Mathematical Formulation and Analysis of the Problems
3. New Analytical Expression of the Temperature Distribution Using the Akbari–Ganji Method
4. Previous Analytical Results
5. Discussion
Numerical Simulation
6. Limiting Case
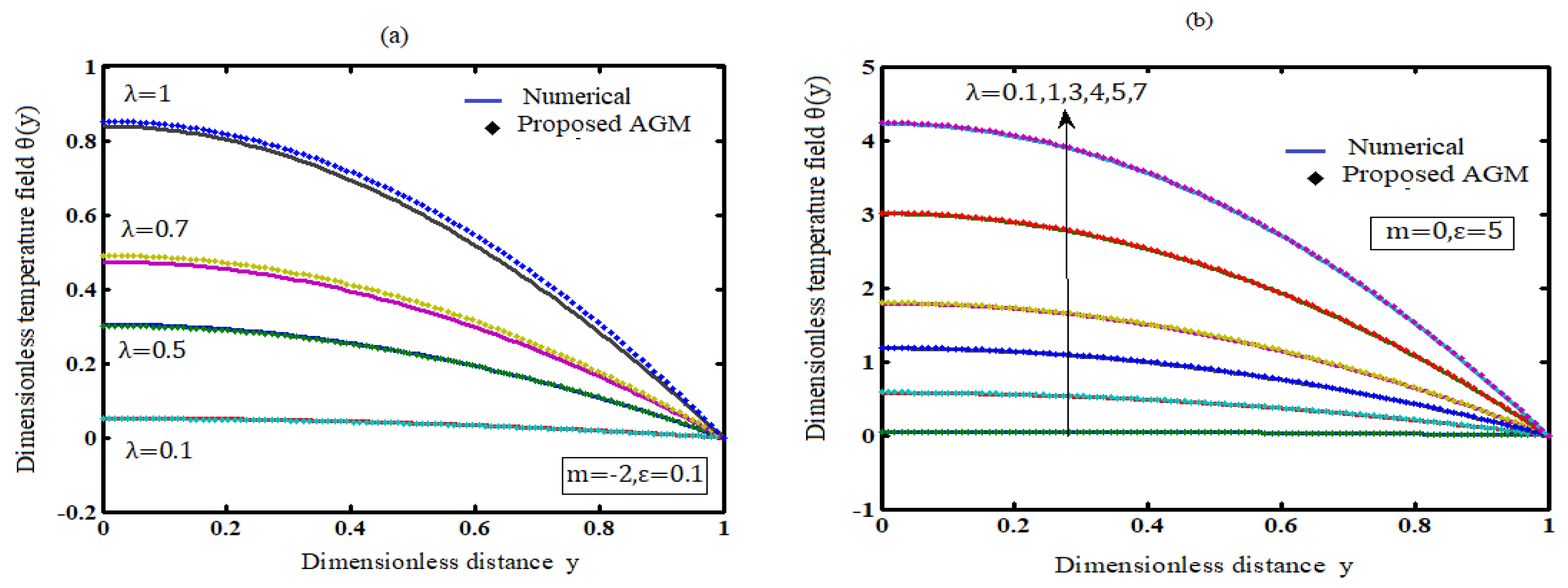
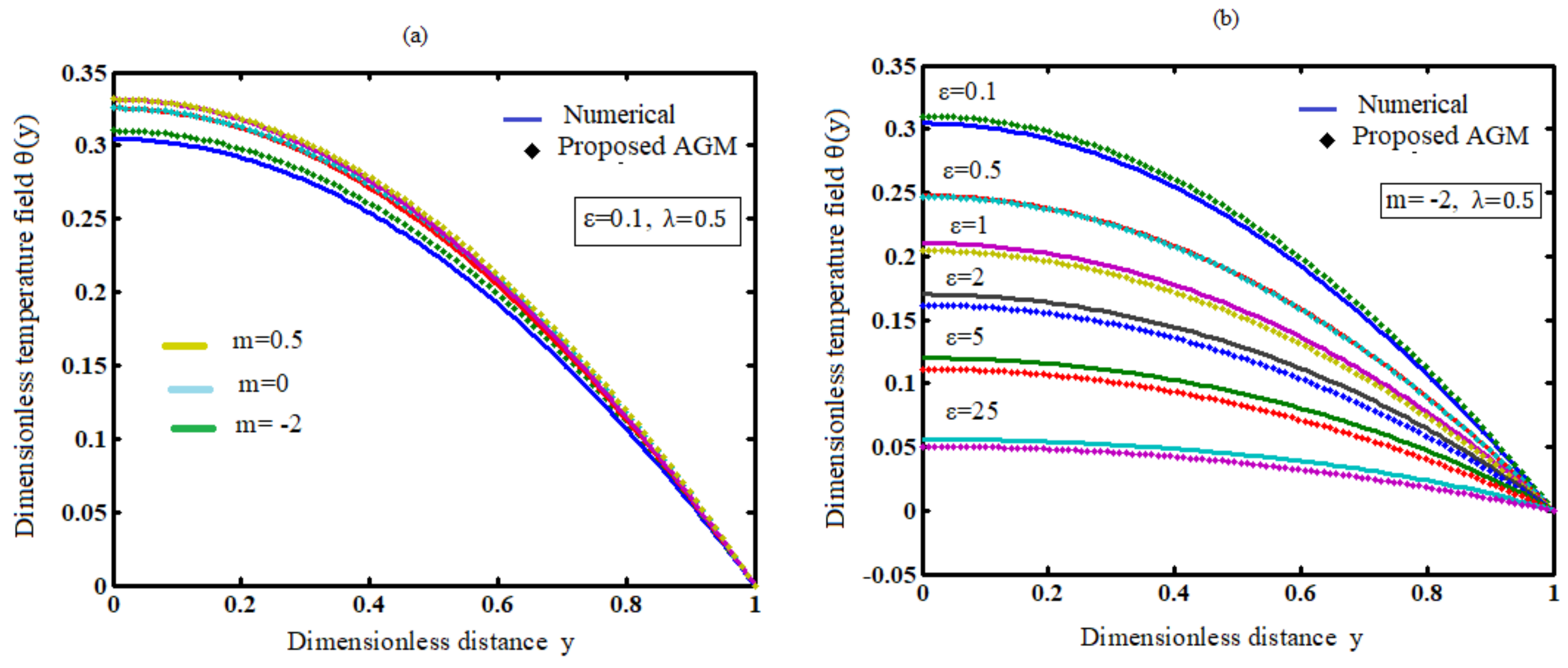
7. Influence of the Parameters on Temperature
7.1. Influence of the Frank-Kamenetskii Parameter on Temperature
7.2. Influence of the Numerical Exponent (m) on Temperature
7.3. Influence of the Activation Energy Parameter (ε) on Temperature
7.4. Extension of the Theoretical Model for Cylindrical and Spherical Geometries
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| Slab half width | ||
| Rate constant | None | |
| Initial concentration of the reactant species | ||
| Activation energy | ||
| Planck’s number | ||
| Thermal conductivity of the material | ||
| Boltzmann’s constant | ||
| Heat of reaction | ||
| Universal gas constant | ||
| Absolute temperature | ||
| Wall temperature | ||
| Vibration frequency | ||
| Dimensionless distance | None | |
| Distance measured in the normal direction in the plate | m | |
| Dimensionless temperature field | None | |
| Frank-Kamenetskii parameter | None | |
| Activation energy parameter | None | |
| m | The numerical exponent, such that m = −2, 0, 1/2 represent the numerical exponent for sensitised, Arrhenius, and bimolecular kinetics respectively. | None |
Appendix A. Basic Concept of the Akbari–Ganji Method
References
- Hatchard, T.D.; MacNeil, D.D.; Basu, A.; Dahn, J.R. Thermal model of cylindrical and prismatic lithium-ion cells. J. Electrochem. Soc. 2001, 148, A755–A761. [Google Scholar] [CrossRef]
- Kim, G.H.; Pesaran, A.; Spotnitz, R. A three-dimensional thermal abuse model for lithium-ion cells. J. Power Sources 2007, 170, 476–489. [Google Scholar] [CrossRef]
- Peng, P.; Sun, Y.; Jiang, F. Thermal analyses of LiCoO2 lithium-ion battery during oven tests. Heat Mass Transf. 2014, 50, 1405–1416. [Google Scholar] [CrossRef]
- Peng, P.; Sun, Y.; Jiang, F. Numerical simulations and thermal behavior analysis for oven thermal abusing of LiCoO2 lithium-ion battery. CIESC J. 2014, 65, 647–657. [Google Scholar]
- Chiu, K.C.; Lin, C.H.; Yeh, S.F.; Lin, Y.H.; Chen, K.C. An electrochemical modeling of lithium-ion battery nail penetration. J. Power Sources 2014, 251, 254–263. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Sun, J. Catastrophe analysis of cylindrical lithium ion battery. Nonlinear Dyn. 2010, 61, 763–772. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal runaway caused fire and explosion of lithium ion battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Lisbona, D.; Snee, T. A review of hazards associated with lithium and lithium-ion batteries. Process. Saf. Environ. Prot. 2011, 89, 434–442. [Google Scholar] [CrossRef]
- Ziebert, C.; Melcher, A.; Lei, B.; Zhao, W.; Rohde, M.; Seifert, H.J. Chapter Six—Electrochemical–Thermal Characterization and Thermal Modeling for Batteries. In Emerging Nanotechnologies in Rechargeable Energy Storage Systems; Micro and Nano Technologies: Karlsruhe Institute of Technology, Institute of Applied Materials—Applied Materials Physics: Eggenstein-Leopoldshafen, Germany, 2017; pp. 195–229. [Google Scholar]
- Guo, G.; Long, B.; Cheng, B.; Zhou, S.; Cao, B. Three-dimensional thermal finite element modeling of lithium-ion battery in thermal abuse application. J. Power Sources 2010, 195, 2393–2398. [Google Scholar] [CrossRef]
- Frank-Kamenetskii, D.A. Diffusion and Heat Transfer in Chemical Kinetics; Plenum Press: New York, NY, USA, 1969. [Google Scholar]
- Boddington, T.; Gray, P.; Robinson, C. Thermal explosions and the disappearance of criticality at small activation energies: Exact results for the slab. Proc. R. Soc. Lond. 1979, 368, 441–461. [Google Scholar]
- Boddington, T.; Feng, C.G.; Gray, P. Thermal explosions, criticality and the disappearance of criticality in systems with distributed temperatures. I. arbitrary biot number and general reaction rate laws. Proc. R. Soc. Lond 1983, 390, 247–264. [Google Scholar]
- Boddington, T.; Gray, P.; Wake, G.C. Theory of thermal explosions with simultaneous parallel reactions. I. foundations and the one-dimensional case. Proc. R. Soc. Lond. 1984, 393, 85–100. [Google Scholar]
- Graham-Eagle, J.G.; Wake, G.C. Theory of thermal explosions with simultaneous parallel reactions. II. The two- and three-dimensional cases and the variational method. Proc. R. Soc. Lond. A 1820, 401, 195–202. [Google Scholar]
- Balakrishnan, E.; Swift, A.; Wake, G.C. Critical values for some nonclass A geometries in thermal ignition theory. Math. Comput. Model. 1996, 24, 1–10. [Google Scholar] [CrossRef]
- Makinde, O.D. Exothermic explosions in a slab: A case study of series summation technique. Int. Commun. Heat Mass Transf. 2004, 31, 1227–1231. [Google Scholar] [CrossRef]
- Ananthaswamy, V.; Subha, M. Analytical expressions for exothermic explosions in a slab. Int. J. Res. Granthaalayah 2014, 1, 22–33. [Google Scholar] [CrossRef]
- Er-Riani, M.; Chetehouna, K. On the critical behaviour of exothermic explosions in class A geometries. Math. Probl. Eng. 2011, 2011, 536056. [Google Scholar] [CrossRef]
- Heydari, H.; Avazzadeh, Z.; Cattan, C. Taylor’s series expansion method for nonlinear variable-order fractional 2D optimal control problems. Alex. Eng. J. 2020, 59, 4737–4743. [Google Scholar] [CrossRef]
- He, J.H. Taylor series solution for a third order boundary value problem arising in Architectural Engineering. Ain Shams Eng. J. 2022, 11, 1411–1414. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. A reliable modification of Adomian decomposition method. Appl. Math. Comput. 1999, 102, 77–86. [Google Scholar] [CrossRef]
- Abukhaled, M. Variational iteration method for nonlinear singular two-point boundary value problems arising in human physiology. J. Math. 2013, 2013, 720134. [Google Scholar] [CrossRef]
- Dharmalingam, M.; Veeramuni, M. Akbari-Ganji’s method (AGM) for solving non-linear reaction—Diffusion equation in the electroactive polymer film. J. Electroanal. Chem. 2019, 844, 1–5. [Google Scholar] [CrossRef]
- Meresht, N.B.; Ganji, D.D. Solving nonlinear differential equation arising in dynamical systems by AGM. Int. J. Appl. Comput. Math. 2017, 3, 1507–1523. [Google Scholar] [CrossRef]

| Num. | AGM Equation (12) This Work | HAM [18] | PM [17] | Error % AGM Equation (12) This Work | Error % HAM [18] | Error % PM [17] | |
|---|---|---|---|---|---|---|---|
| 0 | 0.0517 | 0.0517 | 0.0517 | 0.0516 | 0.0000 | 0.0000 | 0.1934 |
| 0.2 | 0.0496 | 0.0496 | 0.0496 | 0.0495 | 0.0000 | 0.0000 | 0.2016 |
| 0.4 | 0.0432 | 0.0436 | 0.0434 | 0.0433 | 0.9259 | 0.0230 | 0.4629 |
| 0.6 | 0.0327 | 0.0324 | 0.0330 | 0.0329 | 0.9174 | 0.0303 | 0.6116 |
| 0.8 | 0.0179 | 0.0180 | 0.0185 | 0.0185 | 0.5586 | 3.3519 | 3.3519 |
| 1 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Average error (%) | 0.3493 | 0.5675 | 0.8036 | ||||
| Num. | AGM Equation (12) This Work | HAM [18] | PM [17] | Error % AGM Equation (12) This Work | Error % HAM [18] | Error % PM [17] | |
|---|---|---|---|---|---|---|---|
| 0 | 0.3045 | 0.3201 | 0.2951 | 0.2823 | 4.8133 | 3.0870 | 7.2906 |
| 0.2 | 0.2916 | 0.3001 | 0.2829 | 0.2707 | 2.8000 | 2.9835 | 7.1673 |
| 0.4 | 0.2532 | 0.2548 | 0.2466 | 0.2363 | 0.6319 | 2.5671 | 6.6745 |
| 0.6 | 0.1899 | 0.1893 | 0.1869 | 0.1792 | 0.3159 | 1.5798 | 5.6334 |
| 0.8 | 0.1031 | 0.1030 | 0.1041 | 0.1002 | 0.0970 | 0.9699 | 2.8128 |
| 1 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Average error (%) | 1.4430 | 1.8645 | 4.9298 | ||||
| Num. | AGM Equation (12) This Work | HAM [18] | PM [17] | Error % AGM Equation (12) This Work | Error % HAM [18] | Error % PM [17] | |
|---|---|---|---|---|---|---|---|
| 0 | 0.0522 | 0.0523 | 0.0521 | 0.0522 | 0.1916 | 0.1916 | 0.0000 |
| 0.2 | 0.0501 | 0.0501 | 0.0500 | 0.0501 | 0.0000 | 0.1996 | 0.0000 |
| 0.4 | 0.0436 | 0.0437 | 0.0437 | 0.0438 | 0.2294 | 0.2294 | 0.4587 |
| 0.6 | 0.0329 | 0.0331 | 0.0332 | 0.0333 | 0.6079 | 0.9118 | 1.2158 |
| 0.8 | 0.0180 | 0.0181 | 0.0188 | 0.0187 | 0.5555 | 4.4444 | 3.8889 |
| 1 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Average error (%) | 0.2641 | 0.9961 | 0.9272 | ||||
| Num. | AGM Equation (12) This Work | HAM [18] | PM [17] | Error % AGM Equation (12) | Error % HAM [18] | Error % PM [17] | |
|---|---|---|---|---|---|---|---|
| 0 | 0.3255 | 0.3208 | 0.3192 | 0.3172 | 1.4439 | 1.9355 | 2.5499 |
| 0.2 | 0.3116 | 0.3077 | 0.3059 | 0.3040 | 1.2516 | 1.8292 | 2.4390 |
| 0.4 | 0.2701 | 0.2684 | 0.2662 | 0.2646 | 0.6294 | 1.4439 | 2.0363 |
| 0.6 | 0.2021 | 0.2030 | 0.2011 | 0.1994 | 0.4433 | 0.4948 | 1.3360 |
| 0.8 | 0.1093 | 0.1113 | 0.1117 | 0.1110 | 1.8230 | 2.1958 | 1.5553 |
| 1 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Average error (%) | 0.9319 | 1.3163 | 1.6527 | ||||
| Exact Solution Equation (15) | AGM Equation (12) | Error % | Exact Solution Equation (15) | AGM Equation (12) | Error % | Exact Solution Equation (15) | AGM Equation (12) | Error % | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0522 | 0.0527 | 0.9578 | 0.1733 | 0.1795 | 3.5776 | 0.3290 | 0.3474 | 5.5927 |
| 0.2 | 0.0501 | 0.0505 | 0.7984 | 0.1661 | 0.1689 | 1.6857 | 0.3148 | 0.3246 | 3.1131 |
| 0.4 | 0.0436 | 0.0439 | 0.6881 | 0.1443 | 0.1440 | 0.2079 | 0.2728 | 0.2768 | 1.4663 |
| 0.6 | 0.0329 | 0.0330 | 0.3039 | 0.1085 | 0.1087 | 0.1843 | 0.2040 | 0.2060 | 0.9804 |
| 0.8 | 0.0180 | 0.0180 | 0.0000 | 0.0590 | 0.0590 | 0.0000 | 0.1102 | 0.1102 | 0.0000 |
| 1 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Average error (%) | 0.4580 | Average error (%) | 0.9426 | Average error (%) | 1.8587 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vanaja, R.; Jeyabarathi, P.; Rajendran, L.; Lyons, M.E.G. Theory for Electrochemical Heat Sources and Exothermic Explosions: The Akbari–Ganji Method. Electrochem 2023, 4, 424-434. https://doi.org/10.3390/electrochem4030027
Vanaja R, Jeyabarathi P, Rajendran L, Lyons MEG. Theory for Electrochemical Heat Sources and Exothermic Explosions: The Akbari–Ganji Method. Electrochem. 2023; 4(3):424-434. https://doi.org/10.3390/electrochem4030027
Chicago/Turabian StyleVanaja, Ramalingam, Ponraj Jeyabarathi, Lakshmanan Rajendran, and Michael Edward Gerard Lyons. 2023. "Theory for Electrochemical Heat Sources and Exothermic Explosions: The Akbari–Ganji Method" Electrochem 4, no. 3: 424-434. https://doi.org/10.3390/electrochem4030027
APA StyleVanaja, R., Jeyabarathi, P., Rajendran, L., & Lyons, M. E. G. (2023). Theory for Electrochemical Heat Sources and Exothermic Explosions: The Akbari–Ganji Method. Electrochem, 4(3), 424-434. https://doi.org/10.3390/electrochem4030027







