Research on Monitoring and Intelligent Identification of Typical Defects in Small and Medium-Sized Bridges Based on Ultra-Weak FBG Sensing Array
Abstract
1. Introduction
2. Principles of FBG Array Sensing and Machine Learning
2.1. Principle of FBG Array Sensing
2.2. Principles of Machine Learning
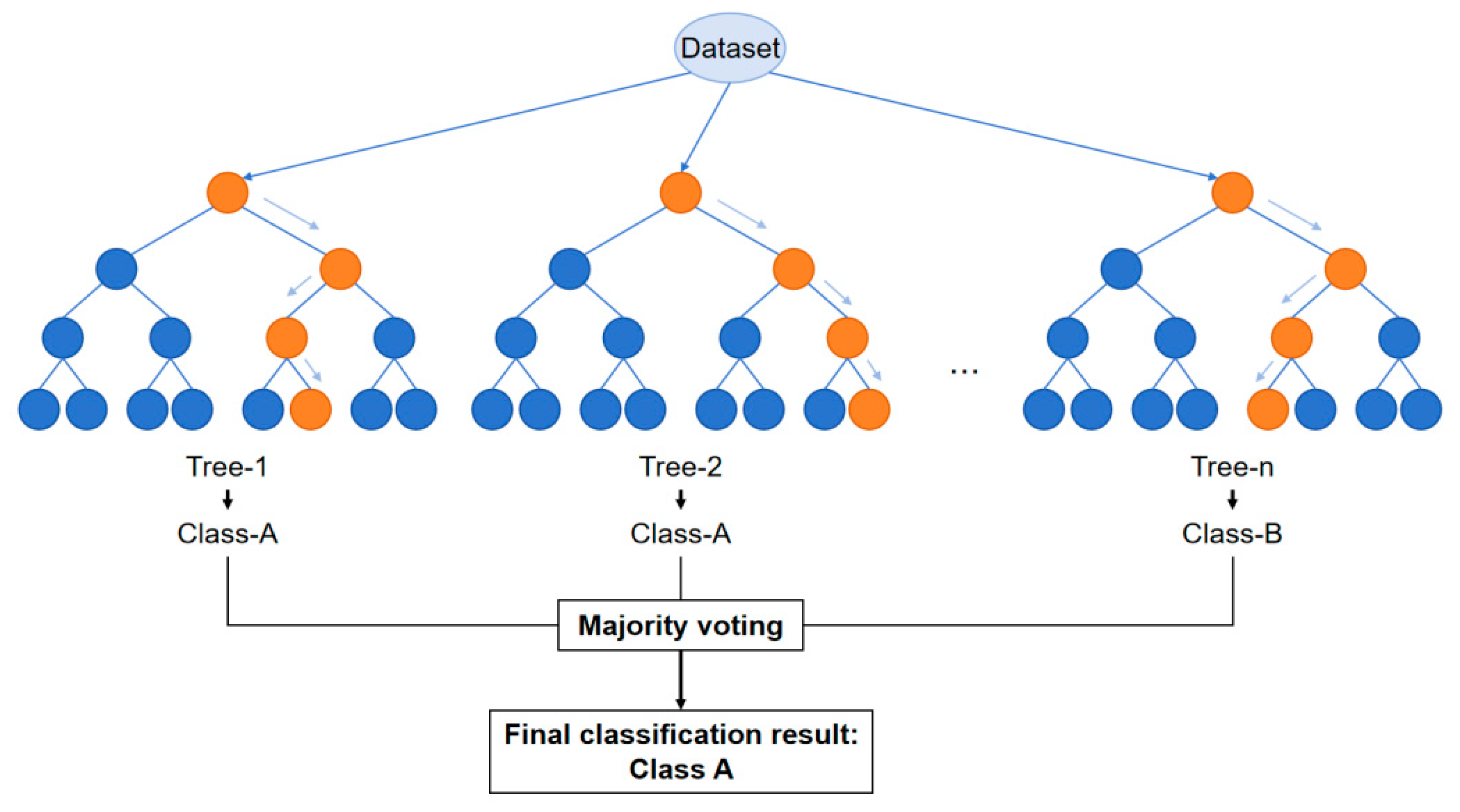
2.2.1. Random Forest
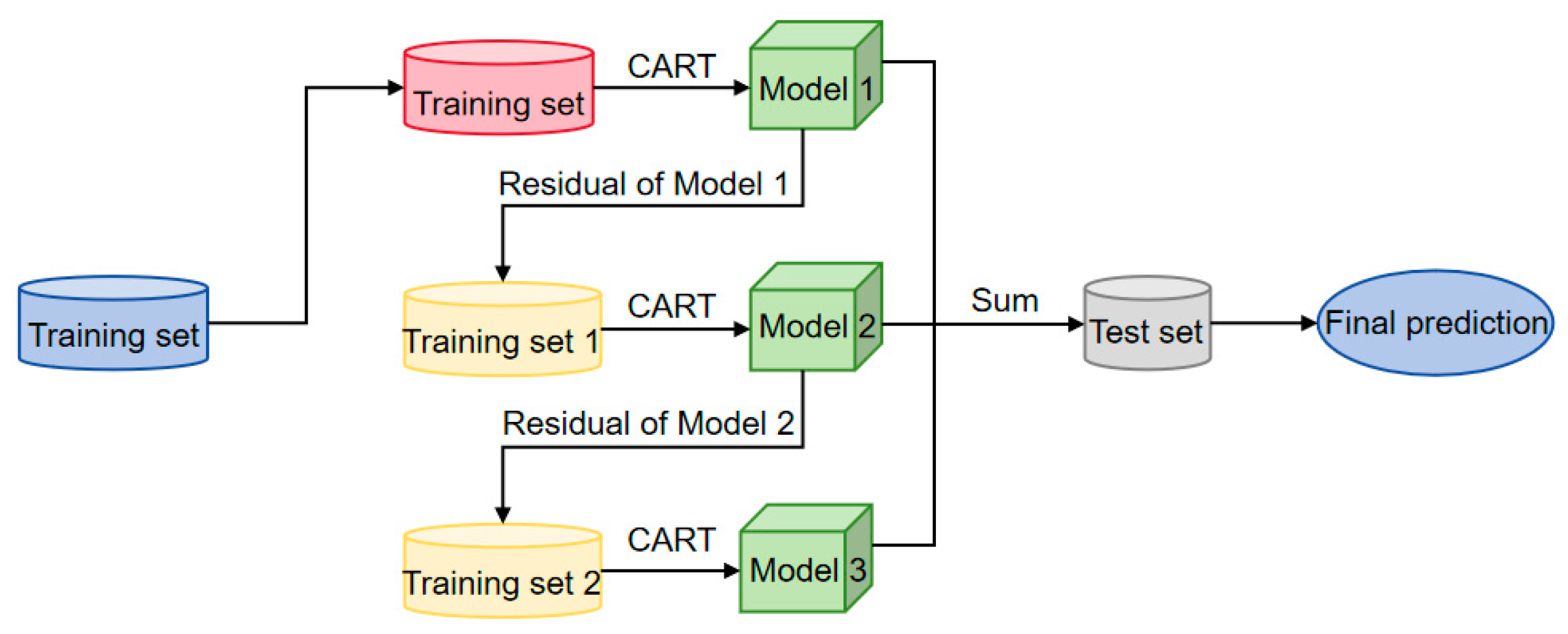
2.2.2. XGBoost
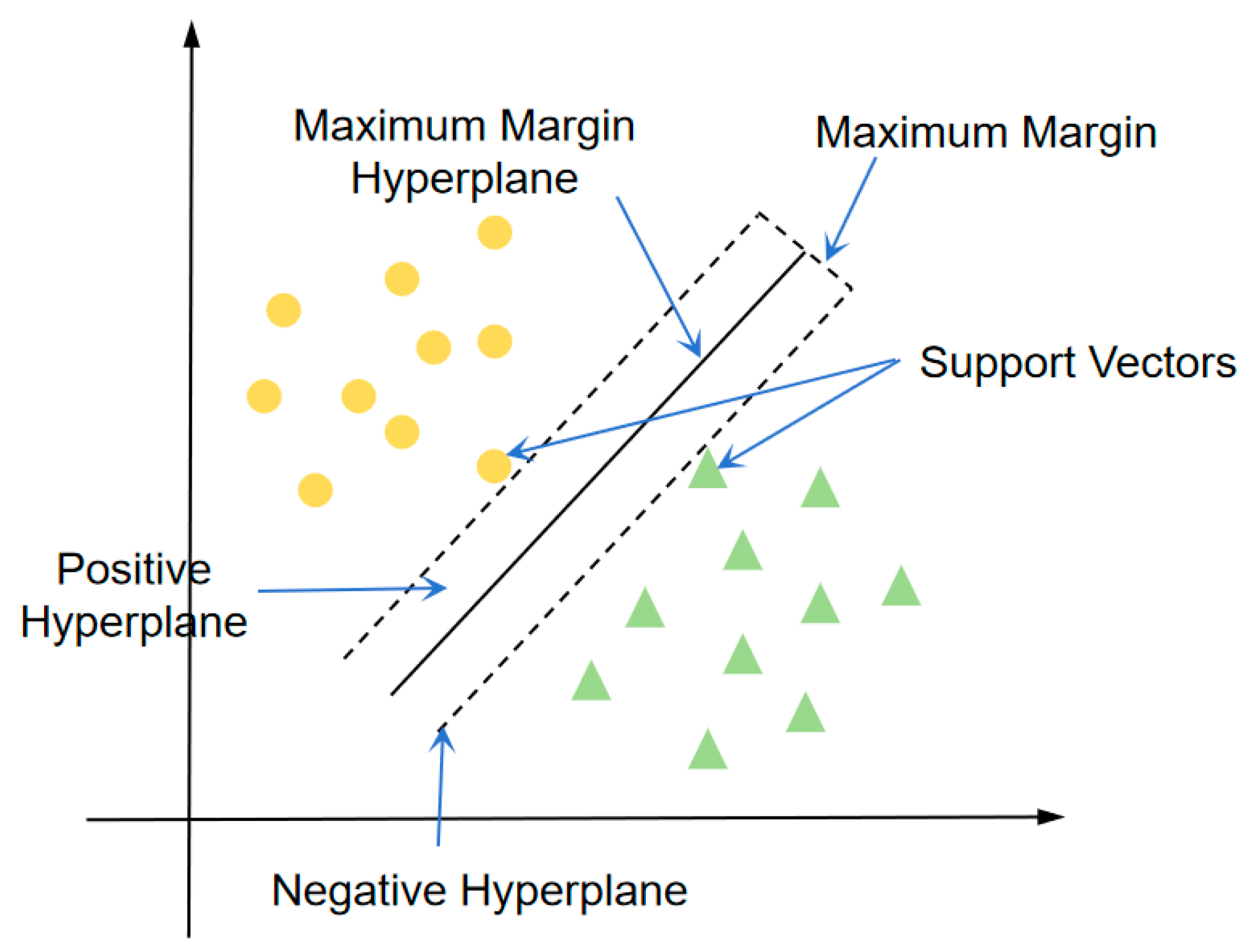
2.2.3. Support Vector Machine
3. Damage Simulation Experiment and Feature Extraction
3.1. Damage Simulation Experiment
3.1.1. Optical Fiber Cable Layout Scheme
3.1.2. Experimental Conditions
3.1.3. Damage Simulation Methods
3.2. Feature Extraction and Label Assignment
3.2.1. Feature Selection for Single-Slab Loading Identification
3.2.2. Feature Extraction for Eccentric Loading Identification
3.2.3. Feature Extraction for Bearing Detachment Identification
3.2.4. Feature Extraction for Weight-Level Identification
4. Model Construction and Evaluation
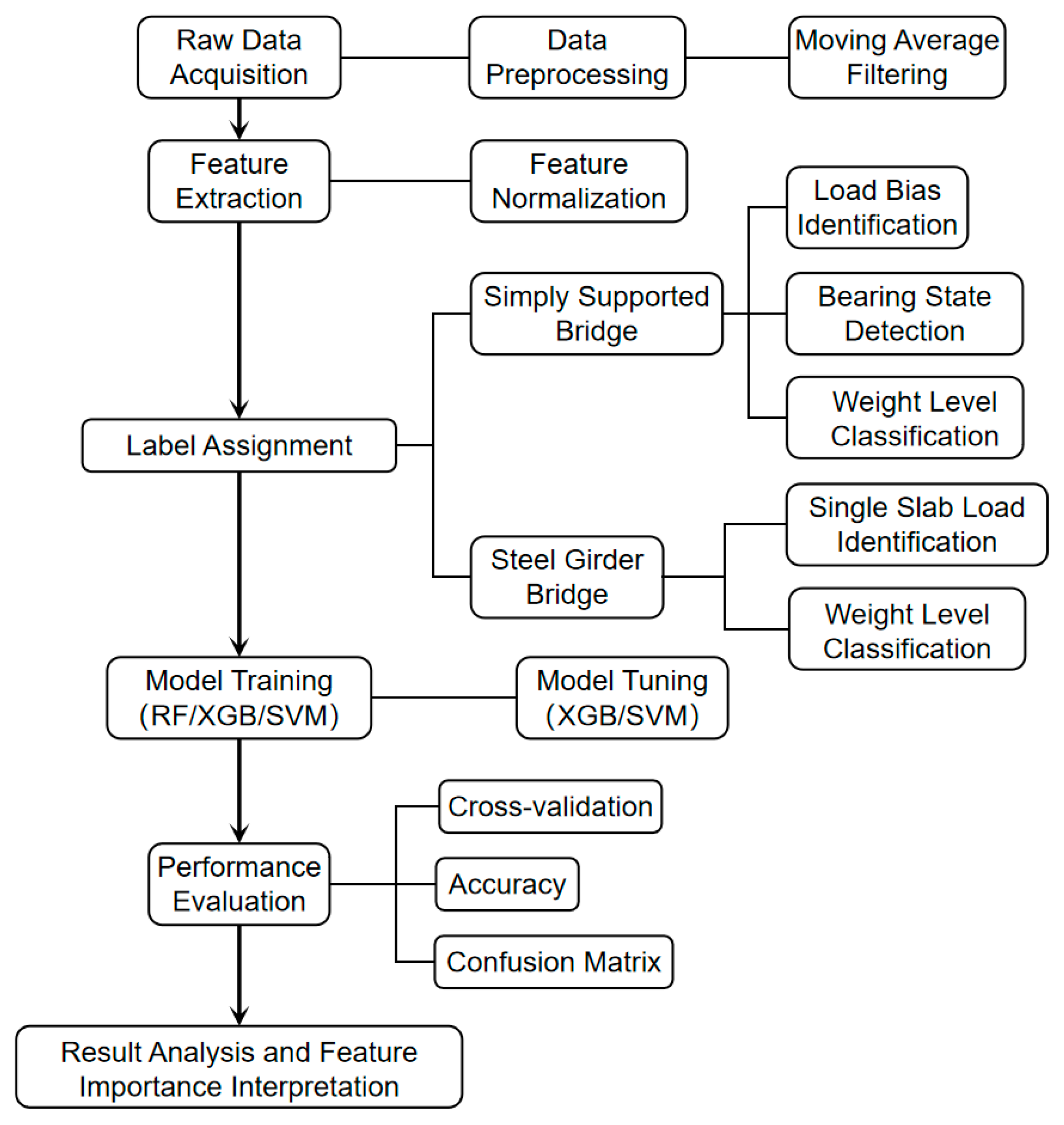
4.1. Modeling Process
4.2. Comparative Analysis of Models
4.3. Evaluation Metrics and Performance Analysis
4.3.1. Single-Slab Load Identification
4.3.2. Eccentric Load Identification
4.3.3. Bearing Detachment Identification
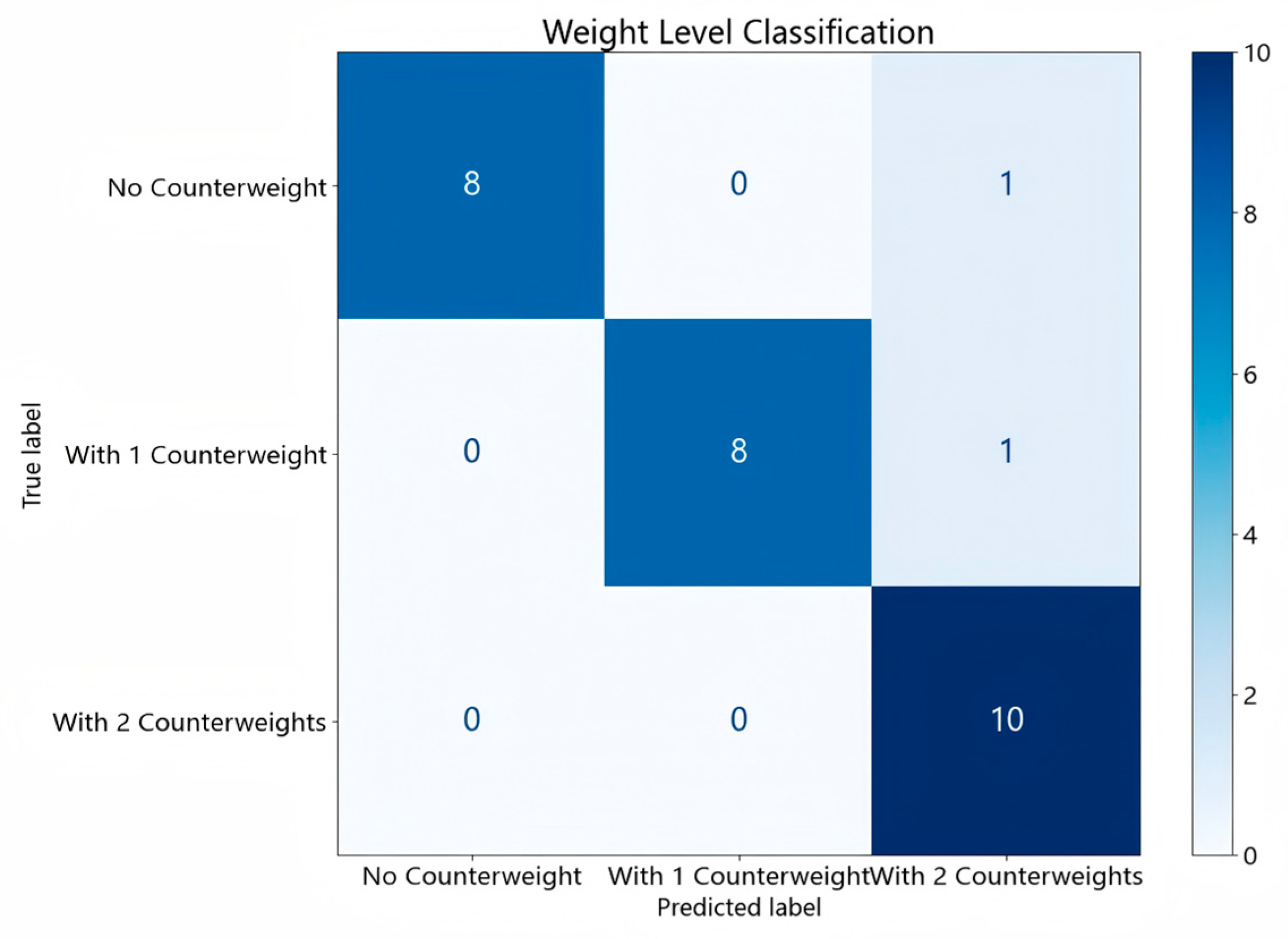
4.3.4. Weight-Level Identification
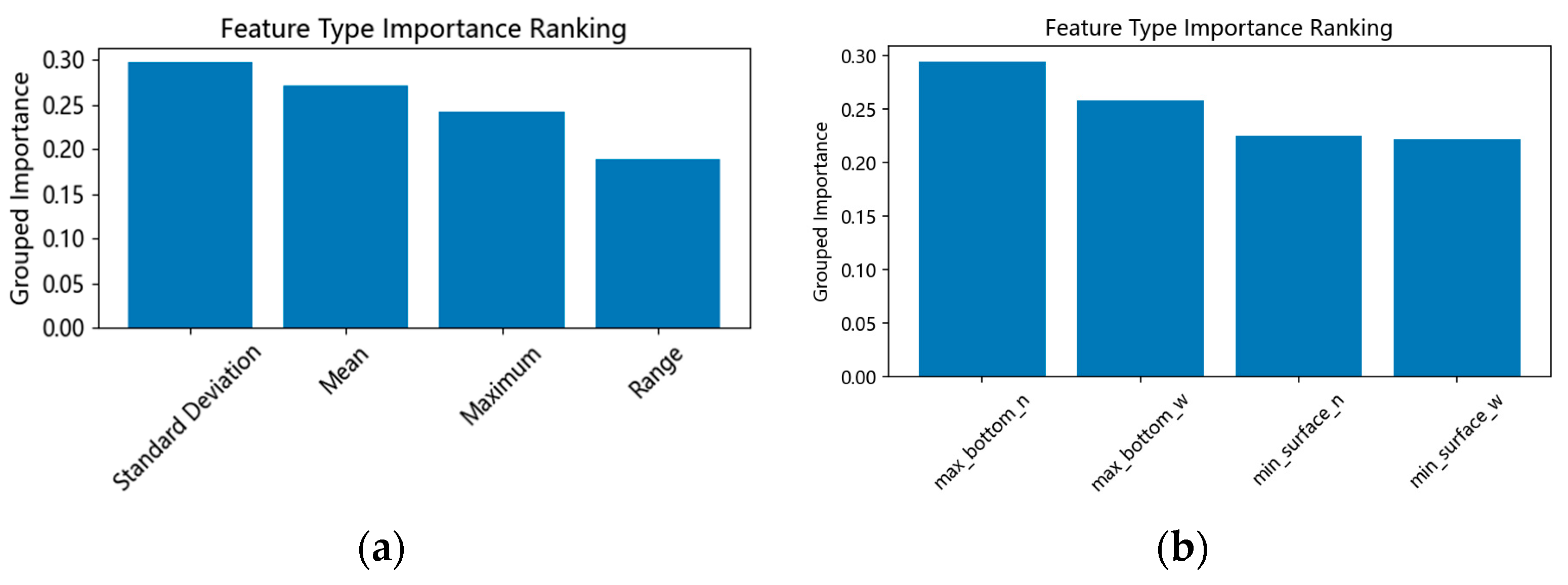
4.4. Key Feature Analysis and Interpretation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UWFBG | Ultra-weak Fiber Bragg Grating |
| FBG | Fiber Bragg Grating |
| CNNs | Convolutional Neural Networks |
| YOLO | You Only Look Once |
| RF | Random Forest |
| XGBoost | extreme Gradient Boosting |
| SVM | Support Vector Machine |
| TDM | Time Division Multiplexing |
| WDM | Wavelength division multiplexing |
| GBDT | Gradient Boosted Decision Trees |
References
- Wu, H.J.; Chen, H.W.; Qu, H.R. A Preliminary Study on the Differences in Health Monitoring between Medium and Small Span Concrete Beam Bridges and Long Span Bridges. J. China Foreign Highw. 2021, 41, 157–163. [Google Scholar]
- Yi, T.H.; Zheng, X.; Yang, D.H.; Li, H. Lightweight Design Method for Structural Health Monitoring System of Short-and Medium-Span Bridges. J. Vib. Eng. 2023, 36, 458–466. [Google Scholar]
- Zhang, X.; Pan, L.; Fan, F.; Lin, H. Design and Application of Health Monitoring System for Small and Medium Span Bridges. Guangdong Highw. Commun. 2022, 48, 54–59. [Google Scholar]
- Wu, K.J. Research on Bridge Monitoring Based on Distributed Brillouin Optical Fiber Sensing. Master’s Thesis, Harbin University of Science and Technology, Harbin, China, 2020. [Google Scholar]
- Wei, Y.; Lu, H.P.; Liu, X.M.; Duan, M.M.; Li, G. Monitoring Technology of Continuous Girder Bridge Based on Long-Gauge Fiber Bragg Grating Sensors. J. Railw. Sci. Eng. 2017, 14, 2231–2238. [Google Scholar]
- Yue, L.; Wang, Q.; Liu, F.; Nan, Q.; He, G.; Li, S. Research on Distributed Strain Monitoring of a Bridge Based on a Strained Optical Cable with Weak Fiber Bragg Grating Array. Opt. Express 2024, 32, 11693–11714. [Google Scholar] [CrossRef] [PubMed]
- Nan, Q.; Lin, X.; Yue, L.; Liu, F.; Li, S.; Li, K.; Liang, X.; Li, Y. Experimental Research on Strain Distribution Measurement of PC Beams Based on Weak Grating Array Sensing Technology. Opt. Express 2024, 32, 33641–33655. [Google Scholar] [CrossRef]
- Gui, X.; Li, Z.Y.; Wang, H.H.; Wang, L.; Guo, H. Review of Distributed Optical Fiber Sensing Technology and Application Based on Large-Scale Grating Array Fiber. J. Appl. Sci. 2021, 39, 747–776. [Google Scholar]
- Cao, J.X. Bridge Structure Deformation Monitoring Method Based on Ultra-Weak Fiber Bragg Grating Array and Its Application. World Bridges 2025, 53, 102–107. [Google Scholar]
- Gan, W.B.; Jiang, R.; Li, C.L.; Yang, M. Continuous Grating Array Sensing Technology and Its Applications. Laser Optoeletron. Prog. 2021, 58, 95–103. [Google Scholar]
- Nan, Q.M.; Li, S.; Yue, L.N. A Novel Strain Sensor Based on Ultra-Weak FBG Sensing Array and Its Performance Test. In Proceedings of the Optical Fiber Sensors, Hamamatsu-shi, Japan, 20–24 November 2023; p. 4. [Google Scholar]
- Dong, Z.Q.; Liu, F.; Jiang, Z.Z. Literature Review of Application of Artificial Intelligence on Bridge Health Monitoring. Shanxi Sci. Technol. Transp. 2024, 4, 108–112. [Google Scholar]
- Ye, Z.J.; Huang, Z.X.; Tao, Y.R.; Dong, G.; Xu, H. Research on Highway Bridge Disease Detection Based on Artificial Intelligence Technology. Transp. Bus. China 2024, 16, 138–140. [Google Scholar]
- Li, G.; Zhao, X.; Du, K.; Ru, F.; Zhang, Y. Recognition and Evaluation of Bridge Cracks with Modified Active Contour Model and Greedy Search-Based Support Vector Machine. Autom. Constr. 2017, 78, 51–61. [Google Scholar] [CrossRef]
- German, S.; Brilakis, I.; DesRoches, R. Rapid Entropy-Based Detection and Properties Measurement of Concrete Spalling with Machine Vision for Post-Earthquake Safety Assessments. Adv. Eng. Inform. 2012, 26, 846–858. [Google Scholar] [CrossRef]
- Mundt, M.; Majumder, S.; Murali, S.; Panetsos, P.; Ramesh, V. Meta-Learning Convolutional Neural Architectures for Multi-Target Concrete Defect Classification with the COncrete DEfect BRidge IMage Dataset. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Prasanna, P.; Dana, K.J.; Gucunski, N.; Basily, B.B.; La, H.M.; Lim, R.S.; Parvardeh, H. Automated Crack Detection on Concrete Bridges. IEEE Trans. Autom. Sci. Eng. 2016, 13, 591–599. [Google Scholar] [CrossRef]
- Qi, S.; Jiang, S.; Zhang, Z. MA Mask R-CNN: MPR and AFPN Based Mask R-CNN. In Proceedings of the ICPCSEE 2021 (7th International Conference of Pioneering Computer Scientists, Engineers and Educators), Taiyuan, China, 17–20 September 2021; p. 4. [Google Scholar]
- Chen, J.; Chen, X.D.; Zhao, H.; Ji, H.; Chen, R.; Yao, K.; Zhao, R. Experimental Research and Application of Non-Destructive Detecting Techniques for Concrete-Filled Steel Tubes Based on Infrared Thermal Imaging and Ultrasonic Method. J. Build. Struct. 2021, 42 (Suppl. S2), 444–453. [Google Scholar]
- Chen, H.; Qin, Y.; Chen, J.; Yao, K.; Li, W.; Tian, Y. Experimental Research on the Non-Destructive Detecting Technique on Concrete-Filled Steel Tube Based on Infrared Thermal Imaging Method and Ultrasonic Method. Build. Struct. 2020, 50 (Suppl. S1), 890–895. [Google Scholar]
- Cheng, D.Q.; Zhuang, D.W. Research on Non-Destructive Testing of Concrete Structure Defects Based on Electromagnetic Technology. Block-Brick-Tile 2025, 2, 125–128. [Google Scholar]
- Jiang, X.S.; Li, M.; Ren, L.; Lu, L. Application of Fiber Bragg Grating Sensor in Monitoring Concrete Deformations and Cracks. Constr. Technol. 2013, 42, 52–54. [Google Scholar]
- Jian, Z.; Songrong, Q.; Can, T. Automated Bridge Surface Crack Detection and Segmentation Using Computer Vision-Based Deep Learning Model. Eng. Appl. Artif. Intell. 2022, 115, 105225. [Google Scholar] [CrossRef]
- Flah, M.; Suleiman, R.A.; Nehdi, L.M. Classification and Quantification of Cracks in Concrete Structures Using Deep Learning Image-Based Techniques. Cem. Concr. Compos. 2020, 114, 103781. [Google Scholar] [CrossRef]
- Wu, W.W. Research on Automated Point Cloud Segmentation and Intelligent Recognition of Surface Defects of Small and Medium-Span Bridges Based on Unmanned Aerial Vehicles. Master’s Thesis, Southeast University, Nanjing, China, 2023. [Google Scholar]
- Li, F. Intelligent Recognition of Bridge Structural Cracks Based on Unmanned Aerial Vehicles and Deep Learning. Master’s Thesis, Hunan University, Changsha, China, 2021. [Google Scholar]
- Wang, J.Q. Research on Distributed Temperature Sensing Technology Based on Densely Spaced Grating Array Fiber. Ph.D. Thesis, Wuhan University of Technology, Wuhan, China, 2022. [Google Scholar]
- Rao, Y.-J. In-fibre Bragg grating sensors. Meas. Sci. Technol. 1997, 8, 355. [Google Scholar] [CrossRef]
- Ho, T.K.; IEEE (Institute of Electrical and Electronics Engineers). Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 278–282. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. arXiv 2016, arXiv:1603.02754. [Google Scholar] [CrossRef]
- Sun, A.; Lim, E.-P.; Ng, W.-K. Web Classification Using Support Vector Machine. In Proceedings of the Web Information and Data Management Conference, Singapore, 4–8 November 2002; Nanyang Technological University: Singapore, 2002. [Google Scholar]
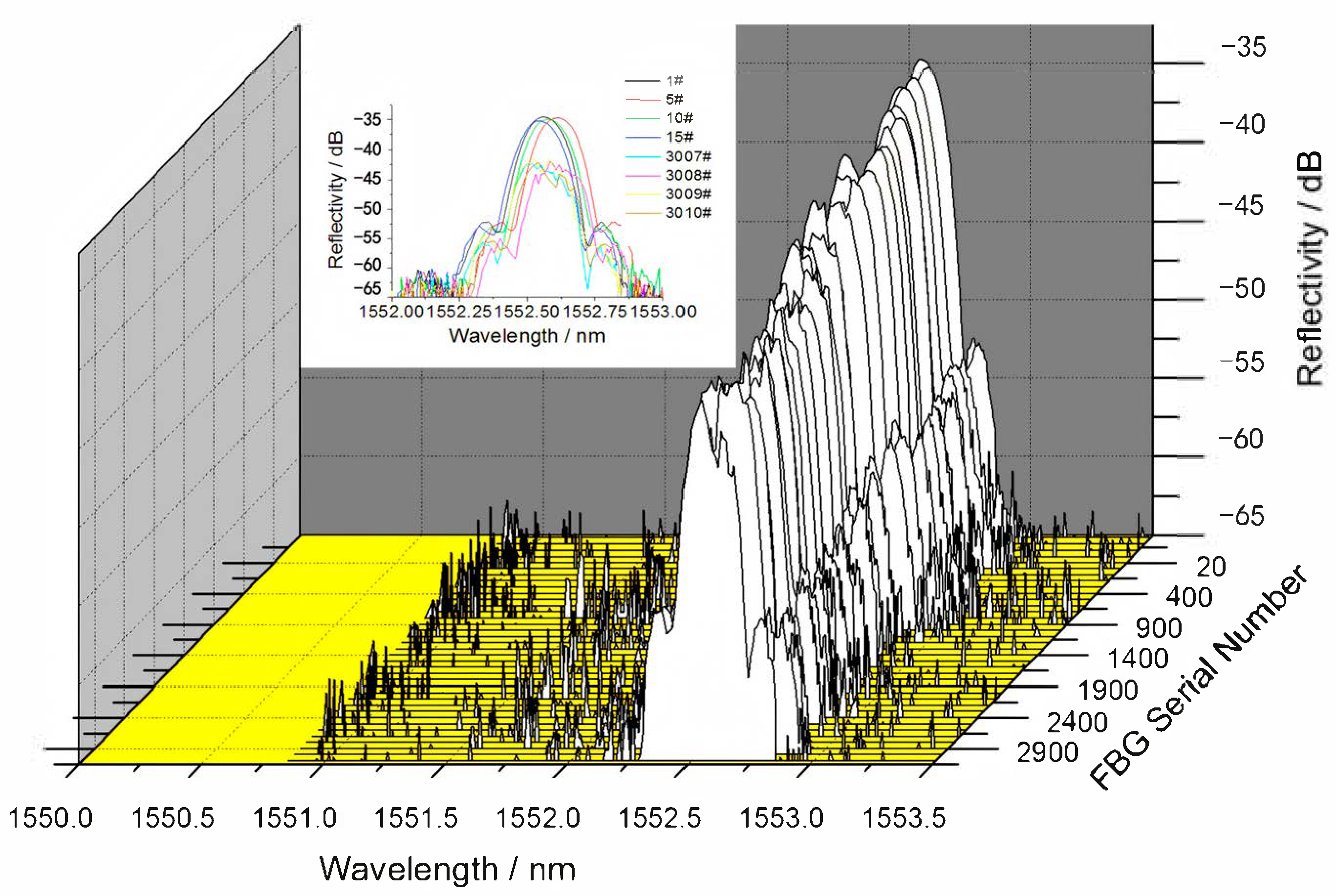











| Type | Sensitivity | Number of Nodes | Bandwidth | System Complexity |
|---|---|---|---|---|
| Brillouin | Moderate | Continuously distributed; up to tens of thousands of points | Narrowband; slow dynamic response | Complex system |
| Rayleigh | Relatively high | Continuously distributed; up to tens of thousands of points | Broadband; suitable for dynamic events | Complex system |
| Conventional FBG | High | Dozens to just over one hundred, constrained by spectral bandwidth | Moderate | Moderate system |
| UWFBG | High | Continuously distributed; up to tens of thousands of points | Relatively wide | Relatively complex system |
| Bridge Types | Defect Condition | Driving Conditions | Data Quantity | |
|---|---|---|---|---|
| Simply supported bridge | Two-slab Travel | One forklift traveling in the outer lane (No counterweight\Counterweight 1\Counterweights 2) | No counterweight: 7 Counterweight 1: 10 Counterweights 2: 10 | |
| Single-slab Travel | One forklift traveling in the inner lane (No counterweight\Counterweight 1\Counterweights 2) | No counterweight: 10 Counterweight 1: 10 Counterweights 2: 10 | ||
| Mid-joint Travel | One forklift crossing slab joints (No counterweight\Counterweight 1\Counterweights 2) | No counterweight: 10 Counterweight 1: 9 Counterweights 2: 10 | ||
| Steel girder bridge | Eccentric Loading | One forklift traveling in the middle lane (No counterweight\Counterweight 1\Counterweights 2) | No counterweight: 6 Counterweight 1: 8 Counterweights 2: 9 | |
| One forklift traveling in the inner lane (No counterweight\Counterweight 1\Counterweights 2) | No counterweight: 5 Counterweight 1: 9 Counterweights 2: 10 | |||
| One forklift traveling in the outer lane (No counterweight\Counterweight 1\Counterweights 2) | No counterweight: 8 Counterweight 1: 7 Counterweights 2: 9 | |||
| Bearing Detachment | One forklift traveling in the outer lane (No counterweight) | 5 | ||
| Bearing Detachment at Pier 7 | One forklift traveling in the outer lane (No counterweight\Counterweight 1\Counterweights 2) | No counterweight: 5 Counterweight 1: 5 Counterweights 2: 5 | ||
| Steel Girder Bridge | Simply Supported Bridge | ||||
|---|---|---|---|---|---|
| Eccentric Loading Identification | Bearing Detachment Identification | Weight-Level Identification | Single-Slab Load Identification | Weight-Level Identification | |
| RF | 0.9205 | 0.9679 | 0.9372 | 0.8333 | 1.0000 |
| XGBoost | 0.9051 | 0.9513 | 0.9218 | 0.8333 | 0.9833 |
| SVM | 0.9205 | 0.9833 | 0.9051 | 0.8500 | 1.0000 |
| Precision | Recall | F1-Score | Support | |
|---|---|---|---|---|
| Two-slab Travel | 1.00 | 1.00 | 1.00 | 8 |
| Single-slab Travel | 1.00 | 1.00 | 1.00 | 9 |
| Mid-joint Travel | 1.00 | 1.00 | 1.00 | 9 |
| Accuracy | 1.00 | 26 |
| F1-Score (XGBoost) | F1-Score (SVM) | Support | |
|---|---|---|---|
| Two-slab Travel | 0.94 | 0.78 | 8 |
| Single-slab Travel | 0.89 | 0.82 | 9 |
| Mid-joint Travel | 0.82 | 0.94 | 9 |
| Accuracy | 0.88 | 0.85 | 26 |
| Precision | Recall | F1-Score | Support | |
|---|---|---|---|---|
| Normal Load | 0.75 | 0.86 | 0.80 | 7 |
| Internal Eccentric Load | 0.75 | 0.86 | 0.80 | 7 |
| External Eccentric Load | 0.92 | 0.79 | 0.85 | 14 |
| Accuracy | 0.82 | 28 |
| F1-Score (XGBoost) | F1-Score (SVM) | Support | |
|---|---|---|---|
| Normal Load | 0.80 | 0.80 | 7 |
| Internal Eccentric Load | 0.75 | 0.80 | 7 |
| External Eccentric Load | 0.80 | 0.85 | 14 |
| Accuracy | 0.79 | 0.82 | 28 |
| Precision | Recall | F1-Score | Support | |
|---|---|---|---|---|
| Bearing Intact | 0.96 | 1.00 | 0.98 | 23 |
| Bearing Detached | 1.00 | 0.80 | 0.89 | 5 |
| Accuracy | 0.96 | 28 |
| F1-Score (XGBoost) | F1-Score (SVM) | Support | |
|---|---|---|---|
| Bearing Intact | 0.96 | 0.98 | 23 |
| Bearing Detached | 0.75 | 0.89 | 5 |
| Accuracy | 0.93 | 0.96 | 28 |
| Precision | Recall | F1-Score | Support | |
|---|---|---|---|---|
| No counterweight | 1.00 | 1.00 | 1.00 | 6 |
| With 1 Counterweight | 1.00 | 1.00 | 1.00 | 13 |
| With 2 Counterweights | 1.00 | 1.00 | 1.00 | 7 |
| Accuracy | 1.00 | 26 |
| Precision | Recall | F1-Score | Support | |
|---|---|---|---|---|
| No counterweight | 1.00 | 0.89 | 0.94 | 9 |
| With 1 Counterweight | 1.00 | 0.89 | 0.94 | 9 |
| With 2 Counterweights | 0.83 | 1.00 | 0.91 | 10 |
| Accuracy | 0.93 | 28 |
| F1-Score (XGBoost) | F1-Score (SVM) | Support | |
|---|---|---|---|
| No counterweight | 0.88 | 0.94 | 9 |
| With 1 Counterweight | 0.84 | 0.84 | 9 |
| With 2 Counterweights | 0.95 | 0.90 | 10 |
| Accuracy | 0.89 | 0.89 | 28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Zhang, Y.; Kang, Y.; Li, S.; Nan, Q.; Yue, L.; Yang, Y.; Zhou, M. Research on Monitoring and Intelligent Identification of Typical Defects in Small and Medium-Sized Bridges Based on Ultra-Weak FBG Sensing Array. Optics 2025, 6, 43. https://doi.org/10.3390/opt6030043
Lin X, Zhang Y, Kang Y, Li S, Nan Q, Yue L, Yang Y, Zhou M. Research on Monitoring and Intelligent Identification of Typical Defects in Small and Medium-Sized Bridges Based on Ultra-Weak FBG Sensing Array. Optics. 2025; 6(3):43. https://doi.org/10.3390/opt6030043
Chicago/Turabian StyleLin, Xinyan, Yichan Zhang, Yinglong Kang, Sheng Li, Qiuming Nan, Lina Yue, Yan Yang, and Min Zhou. 2025. "Research on Monitoring and Intelligent Identification of Typical Defects in Small and Medium-Sized Bridges Based on Ultra-Weak FBG Sensing Array" Optics 6, no. 3: 43. https://doi.org/10.3390/opt6030043
APA StyleLin, X., Zhang, Y., Kang, Y., Li, S., Nan, Q., Yue, L., Yang, Y., & Zhou, M. (2025). Research on Monitoring and Intelligent Identification of Typical Defects in Small and Medium-Sized Bridges Based on Ultra-Weak FBG Sensing Array. Optics, 6(3), 43. https://doi.org/10.3390/opt6030043





