Abstract
Optical frequency domain reflectometry (OFDR) is one of the key diagnostic tools for fiber optic components and circuits built on them. A low signal-to-noise ratio, resulting from the low intensity of backscattered signals, prevents the correct quantitative description of the medium parameters. Known methods of signal denoising, such as empirical mode decomposition, frequency filtering, and activation function dynamic averaging, make the signal smoother but introduce errors into its dynamic characteristics, changing the intensity of reflection peaks and distorting the backscattering level. We propose a method to reduce OFDR trace noise using elliptical arc fitting (EAF). The obtained results indicate that this algorithm efficiently processes both areas with and without contrasting back reflections, with zero distortion of Fresnel reflection peaks, and with zero attenuation error in regions without Fresnel reflections. At the same time, other methods distort reflection peaks by 14.2–42.6% and shift the correct level of Rayleigh scattering by 27.2–67.3%. Further work will be aimed at increasing the accuracy of the method and testing it with other types of data.
1. Introduction
Photonic integrated circuits and fiber optics, as well as other integrated optical components, are used in a variety of optoelectronic instruments in the field of telecommunications, fiber optic sensors, and various other areas of science and technology [1,2,3]. Ensuring compliance with the fundamental structural optical and geometrical parameters of these components, as well as the assemblies interconnected via optical fibers, is essential for the high-performance operation and stable functioning of optoelectronic systems [4,5]. Diagnostics of these components and related circuits are typically performed using optical frequency domain reflectometry (OFDR) techniques, which offer high spatial resolution and relatively extended sensing lengths [6,7,8]. These systems use continuous radiation to probe the waveguide, which is swept in wavelength over time according to a linear function. This approach enables high spatial resolution and significant dynamic range [9,10]. The most significant parameters of the OFDR traces include the attenuation coefficient of the optical signal and the intensity of back reflection peaks. However, there are several challenges associated with the detection and processing of backscattered data, as these data are often noisy, and not all variations in backscatter components are informative. It is therefore appropriate to exclude some of these variations from traces if possible.
An example of such uninformative data is represented by the pseudorandom interference patterns created by reflections from adjacent clusters of silicon oxide and germanium molecules at different locations along the fiber optic line. Various techniques are employed in different types of optical reflectometry to eliminate noise and other artifacts: from conventional frequency filters and approximations of the trace using various functions to empirical and variational mode decompositions. When processing frequency domain traces, the main issue is that averaging, which is required to filter out noise components from regions without contrasting backscattered light, results in signal distortion in other sections of the fiber optic line, where reflective events occur.
Any optical reflectometer or distributed fiber optic sensor faces the task of recording ultra-weak backscattering [11,12,13]. The noise of photodetectors, sometimes comparable in intensity to the useful signal, begins to play a decisive role when it is necessary to record backscattered signals from sections of the optical fiber remote from the laser [14,15,16]. It is especially important to maintain the correct signal-to-noise ratio in the case of recording an even weaker signal than that in Rayleigh scattering—as seen in spontaneous or stimulated Brillouin scattering [14,17,18], in particular, if optical fibers with high losses are studied [19]. Since the backscattered signal in this case has the spectral form of a Lorentzian function, the corresponding approximating methods are used to obtain the correct frequency shift [20,21]. The Rayleigh scattering spectra are determined by spatial patterns determined by conglomerates of silica and germanium oxides molecules in the fiber core and cannot be approximated by any known functions in the frequency domain, so the main work with data in systems of this type is performed in the spatial domain. Thus, a moving average and a moving differential, which provide integration and differentiation, respectively, in a window sliding in space can be successfully applied [22,23,24]. These approaches can increase the signal-to-noise ratio but distort the events on the trace. Given these facts, the challenge of creating an approximation method that works in the spatial domain and does not distort the signal is especially attractive.
The goal of this study is to test simple data processing algorithms and evaluate the efficiency and quality of the backscatter signal processing achieved through OFDR.
2. Experimental Setup and Basic Signal Processing
In order to obtain backscattering data, the setup shown in Figure 1 was constructed. The core principle of this setup involves sweeping the laser source’s wavelength over a wide range while simultaneously recording the interference pattern between reference and scattered signals. By analyzing this spectral data through Fourier transformation, spatial information about changes in the refractive index or strain within the fiber can be extracted with high resolution.
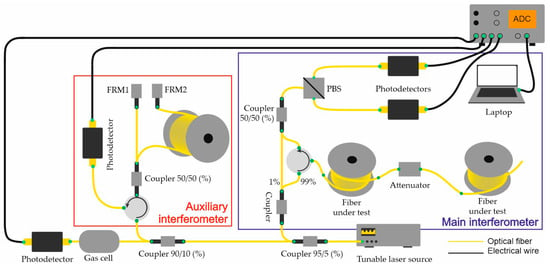
Figure 1.
The experimental setup.
Since the laser source is nonlinearly frequency-tuned, an auxiliary interferometer must be included in the system. The data obtained by such an interferometer are used to resample the main data, which compensates for the nonlinearity of laser sweeping.
In this experiment, the continuous and highly coherent radiation from a tunable laser source (Santec TSL-570-P-480640-P-F-AP-00-1 with 50 kHz linewidth, Santec, Fukuoka, Japan) was split into three independent paths. One of these paths was the main interferometer, consisting of a three-port fiber circulator and optical power couplers (all passive optical components in this setup were manufactured by AFR, Zhuhai, China). The other two paths were reference channels, each containing different components: one included two Faraday mirror assemblies (AFW FOFM-15-L-1-2, AFW Technologies, Ltd., Hallam, Victoria, Australia), with a delay line in one arm (single-mode SMF28 fiber, Corning Inc., Corning, NY, USA), while the other contained a wavelength reference (acetylene gas cell, 50 mTorr, HCN, Wavelength References, Corvallis, OR, USA) as a wavelength monitor. All radiation from these paths was detected using Femto photodetectors (HCA-S-200M, FEMTO Messtechnik GmbH, Berlin, Germany). The radiation was split again into two paths before reaching the photodiodes in the main interferometer using a polarization splitter, allowing for the monitoring of polarization changes along the line. An SMF28 optical fiber with two reflection events was also used as the test line. In order to observe significant optical losses in the trace, an optical power attenuator was incorporated into the line. The maximum possible sweeping range of the laser source was 150 nm. Variation in this parameter allows for the flexible control of not only the measurement time but also the spatial resolution. In these experiments, we used a tuning range of 40 nm. This allowed us to obtain a spatial resolution of about 20 μm. The attenuator was selected such that the signal reduction in the raw trace would be 2 dB. This value was monitored by measuring the accumulation of the signal along the length of the trace over 3500 data points. The system was calibrated using a variable attenuator and an OBR4600 reference reflector by Luna Inc., Roanoke, VA, USA.
Since the signal from the main interferometer was captured by two photodetectors, which are responsible for recording the signal in two polarization states, the resulting signal was generated by applying a vector summation, as is commonly performed in such cases [25,26]. An example of the trace without any further processing is presented in Figure 2a.
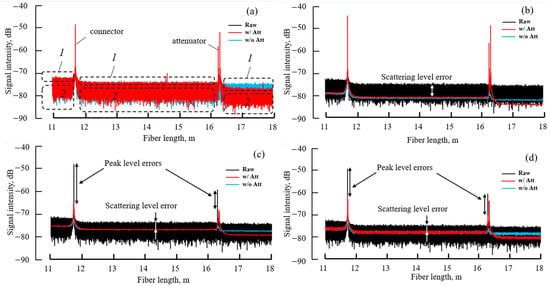
Figure 2.
Frequency domain traces before processing (a); the result of the AFDA processing of traces (b); the result of the frequency filtering processing of traces (c); the result of processing traces using empirical mode decomposition and their reverse reconstruction using selected modes (d). Raw data—black; processed data obtained without the attenuator—blue; processed data obtained with the attenuator—red.
In this figure, as well as the subsequent ones, the trace without the attenuator is shown in blue and that with the attenuator in red. Within the areas of the traces associated with backscattering, there are points with varying scattering intensities that can be identified. Those with higher intensities, representing region 1, produce data with a greater signal-to-noise ratio, which can ideally be approximated using a linear function. These points will be described by a straight line, where the angle of the slope of the line with respect to the x-axis will represent the attenuation coefficient for the optical signal within the fiber. Other points (region 2) exhibit a lower signal-to-noise ratio due to their random nature and are therefore not suitable for further processing. Thus, the desired signal processing should lead not only to the preservation of Fresnel reflection peaks but also to the signal replacement with an envelope in region 1.
To summarize, to evaluate the processing efficiency, we will use the following four parameters:
- Distortion of Fresnel reflection peaks.
- Attenuation coefficient on a non-reflecting event.
- Signal dispersion on a monotonous segment.
- Displacement of the Rayleigh scattering region after processing.
The first parameter shows how much the Fresnel reflection peak height has been distorted after processing by one method or another. This parameter is very important for monitoring back reflections in various circuits, including integrated optical chips. The second parameter characterizes how much the attenuation coefficient of the optical signal has changed in a particular location of the line. This characteristic is important for almost all the samples under study. The third parameter is signal dispersion. We believe that this can be a good quantitative measure for the statistical evaluation of the data under study. The fourth parameter characterizes how much the Rayleigh scattering level has shifted after processing by one algorithm or another. If such a shift is minimal, then the determination of other parameters that are calculated relative to its level becomes more accurate.
Before applying the method that we developed for processing frequency domain traces, we evaluated the suitability of several existing techniques for this purpose. These included frequency filtering [27] and empirical mode decomposition [28,29], as well as the activation function dynamic averaging (AFDA) method [30].
Digital frequency filtering [27,31,32,33,34] is a well-described technique in the scientific and educational literature. The cutoff frequency of Matlab’s highpass IIR filter (MathWorks, Inc., Natick, MA, USA) was chosen as one order of magnitude higher than the beat frequency of the farthest reflection in the line, and the attenuation in the suppression band was chosen as equal to 60 dB, based on the ADC bit depth of 16 bits. Methods such as empirical mode decomposition and the AFDA method require a brief description to understand their fundamental principles.
2.1. Empirical Mode Decomposition
Empirical mode decomposition (EMD), also known as the Huang–Hilbert Transform [29], is a sophisticated method for analyzing nonlinear and nonstationary signals. The basic idea of this method is to decompose a complex signal into a series of simple oscillating components called Intrinsic Mode Functions (IMFs). These components are signals, each with their own frequency and amplitude characteristics. An analysis can be performed on both natural data and man-made signals, which include OFDR traces. They are obtained by jointly processing the data from the main and auxiliary interferometers in OFDR after applying the equal frequency resampling method, as described in [35], or the zero-crossing method, as described in [36], and the subsequent fast Fourier transform of the discrete signal. Next, the empirical mode decomposition method comes into play, which can be represented as the following stages:
- After the Fourier transform was performed in the previous stage, all local maxima and minima of the original OFDR trace are searched for.
- Using the found extrema, the upper envelope (by connecting the maxima of the smooth curve) and the lower envelope (by connecting the minimum values) are constructed.
- The average value is calculated by averaging the values of the upper and lower envelopes at each point of the signal.
- Then the difference between the original signal and the average value is calculated, and this way, the first IMF is obtained. This process is repeated recursively until one of the two process termination conditions occurs:
- -
- The residual component becomes practically constant or a monotonic function.
- -
- The number of extracted IMFs reaches a predetermined maximum.
Since each individual mode can contain different percentages of noise and useful signals, only those that will increase the signal-to-noise ratio of the resulting trace are used for the further composition (reconstruction) of the signal. An example of selecting the exact IMFs for reconstructing a filtered signal is described by us in [28].
2.2. The AFDA Method
This algorithm involves a window of width , which is centered on the point being processed (). During each iteration, the window is shifted by one point to the right so that the signal strength values within the window are averaged. In order to process all data points, it is necessary to calculate the average of signal strength values at the left and right edges of the original data set. These values can be obtained by either averaging the noise level or using the modal value. Additionally, the size of the window can be adjusted based on the signal magnitude or its derivative at the right edge of the window. This will minimize the averaging of signals that are identified as useful and reduce the resulting distortion. However, all of these approaches, when used together, still differ slightly from the threshold algorithm and can cause distortions in the processed data [31]. Therefore, it is advisable to supplement the set of techniques described based on moving averages with an activation function (this term is borrowed from the fields of neural networks and artificial intelligence). For instance, the linear unit function of Gaussian error is suitable for this purpose, supplemented with an exponent and forming a sigmoidal curve that tends towards specified limits at both the left and right boundaries:
If
else
where erf—Gaussian error function; —maximum window size.
Therefore, the relationship between the size of the smoothing window and the strength of the signal at the processed point becomes nonlinear, as shown in Figure 3.
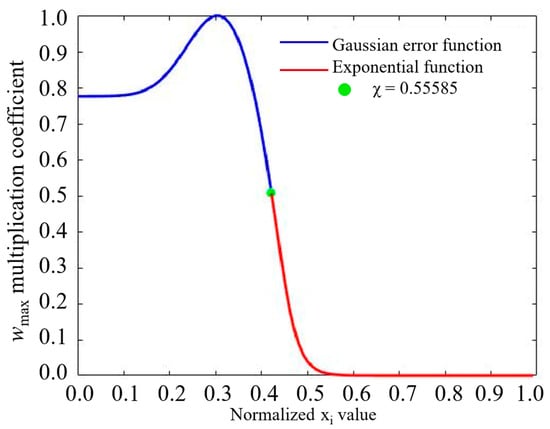
Figure 3.
The activation function combining the Gaussian error linear unit function and the exponential one to suppress the distortions and nonlinearly vary the averaging window size in signal denoising techniques. Adopted from [30].
The experiments showed that this allows one to eliminate distortion and improve the accuracy of the noise reduction method. This algorithm, based on the moving average and augmented by an activation function, has been described in more detail in [30].
In the case study described here, the points to the left and right of the original data were filled with the average value of the noise signal level. To suppress noise, the AFDA algorithm mentioned above with = 1000 was used.
From Figure 2a–d, which also show the original trace without an attenuator in black for clarity, it can be observed that frequency filtering and empirical mode decomposition, followed by the reverse composition of modes back into the original, reduced the noise component of the backscatter in some way. However, at the same time, they significantly reduced the intensity of retro-reflection peaks.
The AFDA dynamic filter also produces a similar effect, although it may be possible to fine-tune its parameters. Additionally, the regions responsible for backscatter decreased in the processed data set and are located at a much lower level on the trace compared to region 1.
Since information about back reflection intensity and backscattering levels is crucial for several studies, these techniques must be excluded from the data processing pipeline. The following section of this article describes an alternative approach that avoids these limitations. We will analyze its efficacy and compare it quantitatively with the aforementioned methods.
2.3. Elliptical Arc Fitting (EAF) Method
Our approach involves associating each point on the graph with a specific segment of a curve, where the values of the function are determined only by the value at the starting point and are independent of the values at nearby points, which can vary significantly. This eliminates the need for averaging and avoids associated problems. We then discard all points below the resulting curves, resulting in the desired envelope.
A half-circle (with the starting point as its top edge) could serve as the shape for the curve segment. However, since the scales along each axis are unrelated to one another, it is more appropriate to use a half-ellipse.
Next, there is no need to modify the signal in any way within the area of Fresnel reflection. We propose using a criterion based on the k-nearest neighbor principle for this purpose: if there are a large number of original graph points (greater than a certain threshold value C) in the vicinity of a given point, we will consider that point to be part of a “stochastic” region free from Fresnel reflections and thus construct an elliptical arc for that point, whereas if there are fewer neighbors in the point vicinity, we will not construct an arc.
The only remaining task is to determine the vicinity in which we will calculate the number of other points in the graph. In fact, we already possess this information—it is the portion of the plane enclosed by the ellipse itself. Figure 4 illustrates the principle of the proposed method.
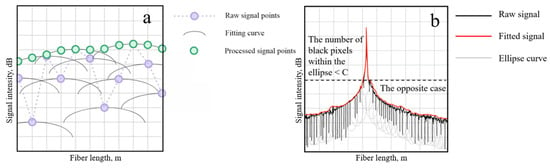
Figure 4.
The principle of the proposed method: (a) building a fitted curve; (b) the resulting fitted signal.
For the algorithm to work correctly, it is important to choose the right parameters—the two semi-axes of the ellipse and the threshold C. If the values of the semi-axes are low or C is too high, a good envelope will not be obtained, and if the values of the semi-axes are too high or C is too low, the signal will be strongly distorted (including the Fresnel reflection region).
To specify the size of ellipse semi-axes and the value of the threshold, a brief evaluation of the trace signal dispersion in a monotonous area was performed. First, it is necessary to determine the size of the desired ellipse’s axes. In order to conduct this, the threshold value is set to zero, and fitting is performed on a monotonous segment of the trace. The resulting trace is then analyzed. Figure 5 shows the dependence of signal dispersion on the size of the horizontal semi-axis.
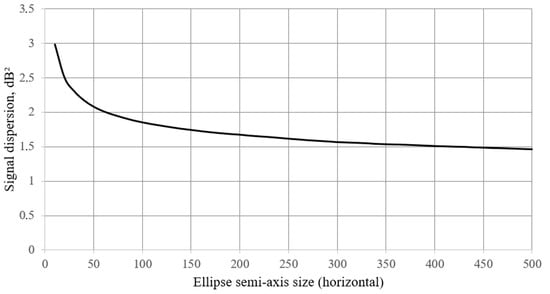
Figure 5.
Signal deviation after adjusting ellipse semi-axis (horizontal) size with threshold C = 0. Horizontal axis is given in samples.
It can be seen from this figure that after the semi-axis reaches 400 samples, the decrease in dispersion is insignificant. At the same time, further increasing the size would significantly reduce the spatial resolution and increase processing time. Thus, the optimal value of the horizontal semi-axis is 400. The dependence of the dispersion on the ellipse vertical semi-axis size is of a similar nature and gives an optimal semi-axis value of 10 samples.
The next step is to select a threshold value for a given ellipse size. Since the maximum number of points falling into an ellipse of a given radius is known from the previous step, the values for the threshold are sorted in the range from zero to the maximum. After that, the dependence of the signal dispersion on the threshold value is calculated. The resulting dependency can be seen in Figure 6.
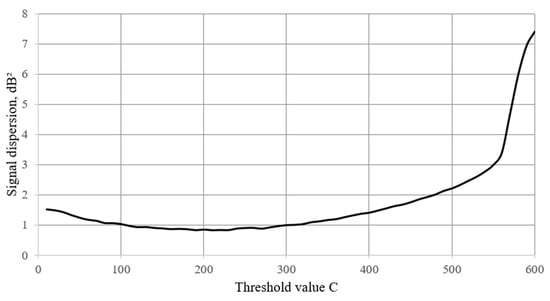
Figure 6.
Signal dispersion after adjusting threshold C with semi-axis size set to 400/10 (horizontal/vertical). Horizontal axis is given in samples.
From Figure 6, it is clear that the dispersion of the processed signal decreases with C until the point when the threshold value becomes too high, and thus there are fewer points for which the condition is fulfilled. Eventually, the algorithm stops working altogether, which leads to a sharp rise in dispersion.
From Figure 5 and Figure 6, it is possible to determine the optimal values of parameters to further process the whole trace. In this case, it is 400 for the horizontal axis, 10 for the vertical axis, and 200 for threshold C.
The algorithm for processing a frequency domain trace can be described as follows:
- The source data is digitized into an array of real variables P with a bit depth corresponding to the bit depth of the analog-to-digital converter (in this study, 16 bits).
- A two-dimensional array of coordinates is created from the trace, with one cell in the array corresponding to a single point in the trace. One cell of the array contains two values (abscissa, ordinate—[i, P]).
- A procedure is applied to each coordinate in the array that counts the number of other points in the array within a specified radius of the current coordinate. This procedure uses a formula to determine whether a point is within the specified radius of another point and increments a counter variable M for each such point. The condition for the points to fall into the specified area is determined using the following formula:
If M > C, the intensity values in the trace, P, are replaced with values determined by an elliptical arc, which is defined parametrically using the following equations:
If M ≤ C, no replacement action will be taken on the elements within this window. Specifically, the elements in the trace whose intensity value is greater than will not be replaced either.
- 4.
- When all the elements within the scan window have been updated, it advances one position to the right (in the direction of incrementing the element number), until the end of the array is reached.
A flowchart describing the EAF algorithm can be seen in Figure 7.
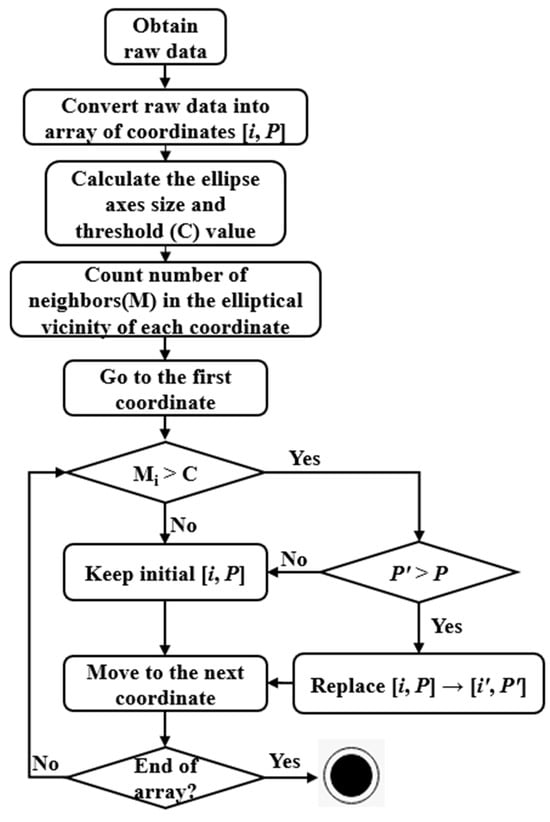
Figure 7.
A flowchart of the EAF algorithm.
One of the key tasks for the presented algorithm is to speed up the calculation process. The transition to a one-dimensional problem allowed us to significantly reduce the calculation time, but the algorithm can still be optimized. A classic example of such optimization can be seen in the fast version of the discrete Fourier transform. Another important task is to adapt the algorithm for use in hardware calculations. In addition, further work can be directed to intelligent signal decimation—this becomes especially relevant when the task is to visualize data, in which case a large number of points is not required.
3. Results and Discussion
3.1. Main Results
Figure 8 shows the traces processed using the proposed method. Zone F1 depicts the part of the trace that contains the first reflecting event, zone R1 represents a monotonous but noisy section of the trace, and zone F2 represents a section containing a connector or attenuator. Zone R2 contains information on Rayleigh scattering after the connector or attenuator. The two parts of the trace are illustrated in a separate, enlarged drawing for ease of understanding.
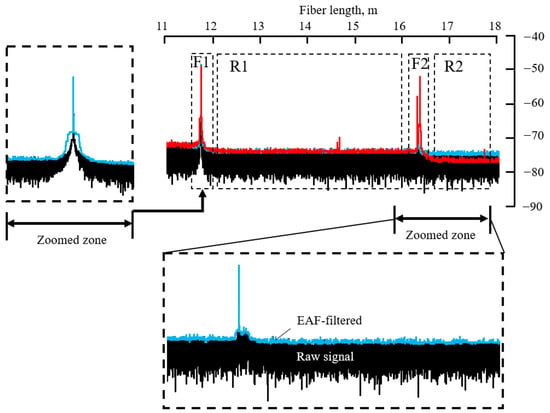
Figure 8.
Results of EAF algorithm. Raw data—black; processed data obtained without attenuator—blue; processed data obtained with attenuator—red.
Despite the visualization of data at various scales, the figures do not provide a visual assessment of the quantitative characteristics of the presented algorithm or a comparison with the effectiveness of methods described previously. Therefore, the main parameters are summarized in Table 1. The first column of the table describes the values being studied. The second column provides a characterization of the value for the AFDA method. The third column describes values for frequency filtering (FF). The fourth column represents values for empirical mode decomposition (EMD). The fifth column shows values for the method presented in this paper (EAF). The sixth column gives information about the parameters of the original raw signal.

Table 1.
The results of processing optical frequency domain traces by various methods.
Further, we will examine the criteria used to conduct a quantitative comparison of the methods, which are described in the following order: from the top row of Table 1 to the bottom.
The first row contains a parameter that describes the change in the intensity of the reflected peak caused by processing. As noted above, this is one of the key parameters that must be assessed, as metrological applications of optical frequency domain reflectometry typically involve analyzing reflected signals in various structures, such as integrated optical circuits, where information on reflecting events must be acquired with high accuracy.
3.2. The EAF Method Compared to the Other Ones
3.2.1. Distortion of Fresnel Reflection Peaks
The primary criterion is to maintain the intensity of reflecting events after digital signal processing. To evaluate this parameter, we computed the percentage difference in peak intensity at the position of the F1 peak compared to the intensity of the processed peak after using various techniques. The calculations showed that all methods other than those presented in this paper distorted the dynamic characteristics of the signal, including the reflection peaks. Frequency filtering caused the most significant negative changes to the signal, with a peak intensity change of 53.8%. Empirical mode decomposition was slightly less destructive, with a change in peak intensity of 42.6%. This is due to the fact that both methods involve filtering frequencies or modes, which contribute not only to noise but also to useful signal components, making it difficult to separate them. The AFDA method induced the least distortion to the data, with a change in peak height of 14.2%. Although it is known that this method leads to the most severe dynamic distortions, it still performed well in this evaluation. This is due to the fact that in the AFDA algorithm, the amount of dynamic distortion is determined by the intensity of the signal—the higher it is, the less distortion. Therefore, intense peaks are only slightly distorted. For the method proposed in this paper, the intensity difference is 0%, as mentioned above. This is because the algorithm leaves unchanged those parts that contain sharp changes in the refractive index.
The parameter discussed in this section is crucial when joining integrated optical components and optical fibers as well as assembling optoelectronic circuits from individual optical fibers and fiber optic elements with their welded or detachable connections.
If we consider the reflection peak distortion without taking into account the EAF method (which does not distort the data), then the AFDA method has the lowest distortion with a peak intensity change of 14.2%. If we consider the characteristic reflection at the junction between the optical fiber and channel waveguide on a lithium niobate substrate, which has a reflection coefficient of −90 dB, this is equivalent to 12.8 dB. The value of the reflection coefficient is underestimated by approximately 20-fold when controlling the coupling between fiber optic and integrated optical elements, for example, in interferometric sensors. This may be the cause of the appearance of parasitic interference. Therefore, in order to visualize and control the peak intensity of the Fresnel reflection, we propose using either the original signal or the signal processed using the EAF method. However, when the goal is to estimate the height of the peak relative to the Rayleigh scattering level, this method is the only solution out of those considered in this paper.
3.2.2. The Attenuation Coefficient on a Non-Reflecting Event
The second row of the table presents the parameter that characterizes the optical signal’s attenuation coefficient. Assuming that the attenuation caused by the attenuator is a measurable, instrumentally recorded phenomenon, and the attenuation in a single-mode fiber over several meters of length is negligible, we took the average values of the R2 traces obtained with and without an attenuator and then calculated the difference between these two averages. Thus, considering the statistics of several thousand data points from the original signal, we derived the reference value for the attenuation coefficient induced by the attenuator: 2.0 dB.
As expected, the AFDA method demonstrated the poorest result here, showing an optical signal with an attenuation coefficient of 4.4 dB. Such a high level of distortion in the attenuation coefficient during data processing using this method is caused by, as mentioned in the previous paragraph, the dynamic distortion for low-intensity signals, including all backscattered data. This leads to a situation where the low-intensity signal is shifted downward after averaging by a value that is strongly correlated with its initial intensity.
For two signals (with and without an attenuator), the initial intensities naturally differed, and therefore they shifted relative to each other after processing, significantly affecting the attenuation coefficient.
The method proposed in this study produced a much more precise result. Using the EAF method, the attenuation coefficient of an optical signal was measured to be 2.4 dB, although there is still a noticeable difference in the estimated attenuation coefficients. We attribute this to the following factors: first, the number of data points for averaging is limited; second, the raw signal in the trace with an attenuator contains a larger number of low-SNR points compared to the same raw signal without an attenuator. This affects the average value used to calculate the reference signal. The frequency filtering and empirical mode decomposition methods demonstrated attenuation coefficients that are close to the expected values of 2.0 dB and 2.1 dB, respectively. These results can be attributed to the strengths of these techniques.
3.2.3. Signal Dispersion on a Monotonous Segment
The third row of the table presents the value that characterizes the measure of random value variance (due to randomness in the scattering process), namely, the intensity of the signal in the R1 region of the trace.
In the signal under study, we are primarily concerned with the component that is significantly influenced by the waveguide properties of the medium and unaffected by random processes. Therefore, when evaluating this parameter, we will assume that high dispersion in a monotonic section of the trace is an undesirable outcome.
As expected, the original signal has the highest variability, with unfiltered high-frequency components contributing a variance of 60 dB2. However, empirical mode decomposition followed by signal reconstruction slightly reduced the variability, resulting in a variance of 2.0 dB2.
These results are not particularly impressive, likely due to the inappropriate choice of modes for signal reconstruction. The EAF method proposed in this study showed better results, with a variance of 0.9 dB2. The best results were achieved by the AFDA and frequency filtering techniques, demonstrating variance values of approximately 0.12 dB2. At present, signal dispersion is not utilized in the analysis of frequency domain traces, according to our knowledge, so it is not yet possible to determine which values are considered critical and which are within acceptable limits. Nevertheless, we deem it advisable at this time to accumulate statistical data and apply methods that produce an output signal with minimal variability.
3.2.4. Displacement of Rayleigh Scattering Region After Processing
The next significant parameter for comparison was the difference in the maximum values of the monotonic portion of the R1 trace for the untreated and treated traces, expressed as a percentage. As previously mentioned in previous sections of this paper, when evaluating the level of Rayleigh scattering within monotonic portions of a trace, it is necessary to rely on points with high signal-to-noise ratios. This parameter indicates how much the trace level has shifted in relation to the desired level, i.e., in relation to points with a high SNR after signal processing. A lower value of this parameter is preferable for the subsequent estimation of the intensity of Fresnel reflection peaks in relation to the Rayleigh scattering level.
The AFDA method, frequency filtering algorithm, and empirical mode decomposition yielded the following results: 67.3%, 36.2%, and 27.2%, respectively. Considering that these percentages were already calculated using logarithmic units, it is possible to imagine the severity of these distortions. Therefore, all of the methods under consideration, except for EAF, produce an error that significantly alters the Rayleigh scattering level and, consequently, the intensity of Fresnel reflection peaks calculated based on it, which is unacceptably inaccurate.
Thus, the proposed elliptical arc fitting method demonstrated superiority in two important aspects required for estimating the level of back reflections. Firstly, it does not alter the magnitude of the reflection peak and the Rayleigh scattering level relative to which this magnitude is determined.
The negative aspects of the method are as follows: Firstly, there is a slight broadening of peaks (see Figure 5), which is caused by triggering the threshold algorithm (at level C). However, the top of the peak remains unaltered, and it is easy to determine its exact spatial coordinates. Additionally, this method did not perfectly eliminate noise from the trace, and in some cases, it distorts the attenuation coefficients of the optical signal. This issue requires further investigation using verified attenuators, which we will address in future research.
It is important to remember that phantom peaks in backscatter data are quite common in both commercial distributed fiber optic sensor systems and laboratory research setups. Their nature can be different: they can be either repeated reflections from contrast events on the trace due to the physics of the process or bursts caused by incorrect digitization or data processing (usually delta functions). In both cases, it is necessary to take all measures to eliminate these interferences—be it hardware approaches or modified algorithms, since the presented method is not intended for these purposes. EAF will treat these bursts as real events, so it is better to eliminate such interferences before applying the presented algorithm. Thus, combining the EAF method and ghost peak removal approaches may be a further important task.
It should be noted that the presented method should be applied only to the amplitude part of the spectrum. In addition, it is necessary to save the unprocessed version of the data for the correct formation of the sensor signal. In this case, the use of the method will not negatively affect the quality of the signal phase extraction or the operation of noise suppression methods.
4. Conclusions and Future Works
In this paper, we present a novel method for processing OFDR traces that focuses on the accurate visualization of reflection peaks and the calculation of their actual intensities in relation to the Rayleigh scattering level. Experiments indicate that the method successfully copes with this task, maintaining the correct Rayleigh scattering level and actual values of Fresnel reflection peaks, as well as successfully filtering out samples with low signal-to-noise ratios. However, several significant drawbacks need to be addressed in future work. These include small spatial distortions in the signal that occur during reflective events. Although these distortions do not affect the accuracy of locating these events, as the tops of the peaks are still visualized correctly, further work is required to address these issues. However, other reflective events may occur near these peaks and fall within the area of the broadened peak, potentially leading to loss. It is also essential to conduct additional studies using reliable attenuators in order to refine the attenuation coefficients for the optical signal generated after processing using the proposed method.
This technique may also be useful in the study of fiber Bragg grating spectra [37,38,39]. In addition, there are still quite a few interesting problems related to signal processing in distributed sensing. Thus, in distributed sensors based on Raman scattering, the intensities of the Stokes and anti-Stokes components of the signal are recorded, which in some cases can also be noisy [38,39]. In its current form, the proposed method, applied to data of this kind, will give some error in determining the fiber temperature, mainly towards an increase. Therefore, as possible works aimed at applying the method we presented in this area, we can highlight the choice of such an approximating function that would provide the correct signal level on the reflector.
Author Contributions
A.K.: writing, data processing, and coding; D.K.: setup arrangement, experiment, data processing, and coding; A.T.: data processing and coding; T.A.: writing and experiment; K.L.: writing and setup arrangement; M.B.: setup arrangement and experiment; Y.K.: project supervision, writing, setup arrangement, and experiment; F.B.: writing and proof-reading. All authors have read and agreed to the published version of the manuscript.
Funding
The work in Section 2, Section 2.2, Section 2.3, Section 3, and Section 4 was performed as a part of the State Assignment No. 124020600009-2, and Section 1 and Section 2.1 were supported by the Russian Science Foundation, project No. 23-79-10059, URL: https://rscf.ru/project/23-79-10059/ (accessed on 20 May 2025).
Data Availability Statement
The experimental data presented in this study are available upon reasonable request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sosunov, A.V.; Petukhov, I.V.; Kichigin, V.I.; Ponomarev, R.S.; Mololkin, A.A.; Kuneva, M. The Impact of Various Factors on the Surface of X-Cut Lithium Niobate and Properties of Proton-Exchanged Waveguides. Ferroelectrics 2024, 618, 1300–1312. [Google Scholar] [CrossRef]
- Petrov, A.; Golovchenko, A.; Bisyarin, M.; Ushakov, N.; Kotov, O. Intermodal Fiber Interferometer with Spectral Interrogation and Fourier Analysis of Output Signals for Sensor Application. Photonics 2024, 11, 423. [Google Scholar] [CrossRef]
- Yang, C.; Wang, Z.; Xiao, K.; Ushakov, N.; Kumar, S.; Li, X.; Min, R. Portable Optical Fiber Biosensors Integrated with Smartphone: Technologies, Applications, and Challenges. Biomed. Opt. Express 2024, 15, 1630. [Google Scholar] [CrossRef]
- Zhirnov, A.A.; Choban, T.V.; Stepanov, K.V.; Koshelev, K.I.; Chernutsky, A.O.; Pnev, A.B.; Karasik, V.E. Distributed Acoustic Sensor Using a Double Sagnac Interferometer Based on Wavelength Division Multiplexing. Sensors 2022, 22, 2772. [Google Scholar] [CrossRef] [PubMed]
- Moskalev, D.; Voblikov, E.; Kozlov, A.; Salgaeva, U.; Maximenko, V.; Krishtop, V. Model of Anisotropic Ring Resonator Based on Coupled Mode Theory. Opt. Contin. 2025, 4, 210. [Google Scholar] [CrossRef]
- Lobach, I.A.; Fotiadi, A.A.; Yatseev, V.A.; Konstantinov, Y.A.; Barkov, F.L.; Claude, D.; Kambur, D.A.; Belokrylov, M.E.; Turov, A.T.; Korobko, D.A. Newest Methods and Approaches to Enhance the Performance of Optical Frequency-Domain Reflectometers. Sensors 2024, 24, 5432. [Google Scholar] [CrossRef]
- Krivosheina, D.A.; Tkachenko, A.Y.; Lobach, I.A.; Kablukov, S.I. Coherent Optical Frequency Reflectometer Based on a Self-Sweeping Fiber Laser for Distributed Measurements. Bull. Lebedev Phys. Inst. 2023, 50 (Suppl. S3), S305–S313. [Google Scholar] [CrossRef]
- Liang, C.; Bai, Q.; Wang, Y.; Gao, Y.; Zhang, H.; Jin, B. Spatial Resolution Enhancement in OFDR Using Margenau Hill Spectrogram. J. Light. Technol. 2024, 42, 3399–3408. [Google Scholar] [CrossRef]
- Ogu, R.; Tanimura, D.; Zhang, C.; Ito, F.; Yoshimura, Y.; Aoshika, H.; Imai, M. Long Range Static and Dynamic Strain Measurement by Using Phase-Noise-Compensated OFDR. J. Light. Technol. 2024, 42, 6240–6245. [Google Scholar] [CrossRef]
- Guo, Z.; Yan, J.; Han, G.; Yu, Y.; Greenwood, D.; Marco, J. High-Resolution Φ-OFDR Using Phase Unwrap and Nonlinearity Suppression. J. Light. Technol. 2023, 41, 2885–2891. [Google Scholar] [CrossRef]
- Wosniok, A.; Krebber, K. Distributed Fiber Optic Radiation Sensors. Saf. Nucl. Waste Dispos. 2021, 1, 15–16. [Google Scholar] [CrossRef]
- Poorghasem, S.; Shah, H.A.; Meng, W.; Bao, Y. Measuring Early-Age Shrinkage of Concrete Incorporating Shrinkage Reducing Admixtures Using Distributed Fiber Optic Sensors. Measurement 2025, 246, 116763. [Google Scholar] [CrossRef]
- Tan, X.; Poorghasem, S.; Huang, Y.; Feng, X.; Bao, Y. Monitoring of Pipelines Subjected to Interactive Bending and Dent Using Distributed Fiber Optic Sensors. Autom. Constr. 2024, 160, 105306. [Google Scholar] [CrossRef]
- Balbier, C.; Bucks, S.; Scurti, F.; Lee, S. High-Temperature Fiber Optic Sensor Performance for Heat Pipe Instrumentation. IEEE Sens. J. 2025, 25, 17117–17127. [Google Scholar] [CrossRef]
- Romanet, M.; Rochat, É.; Beugnot, J.-C.; Phan Huy, K. Extended-Range and Faster Photon-Counting Brillouin Optical Time Domain Reflectometer. Optica 2025, 12, 564. [Google Scholar] [CrossRef]
- Wang, H.; Fratta, D. Fiber Optic Monitoring in Mines. In Proceedings of the 58th U.S. Rock Mechanics/Geomechanics Symposium, Golden, CO, USA, 23–26 June 2024; ARMA: Golden, CO, USA, 2024; p. D021S012R001. [Google Scholar] [CrossRef]
- Hong, C.; Xu, C.; Chen, W.; Liu, J.; Tan, J. Monitoring Excavation-Induced Deformation of a Secant Pile Wall Using Distributed Fiber Optic Sensors. Sensors 2025, 25, 254. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Zhou, J.; Sun, C.; Zhang, X.; Ansari, F. Theoretical and Experimental Investigations into Crack Detection with BOTDR-Distributed Fiber Optic Sensors. J. Eng. Mech. 2013, 139, 1797–1807. [Google Scholar] [CrossRef]
- Bogachkov, I.V.; Gorlov, N.I. Experimental Investigations into Characteristics of Mandelshtam–Brillouin Scattering in Single-Mode Optical Fiber of Various Types. Instrum. Exp. Tech. 2023, 66, 775–781. [Google Scholar] [CrossRef]
- Li, C.; Li, Y. Fitting of Brillouin Spectrum Based on LabVIEW. In Proceedings of the 5th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing China, 24 September 2009; IEEE: Beijing, China, 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Lourakis, M.L.A.; Argyros, A.A. Is Levenberg-Marquardt the Most Efficient Optimization Algorithm for Implementing Bundle Adjustment? In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05) Volume 1, Online, 17–21 October 2005; IEEE: Beijing, China, 2005; Volume 2, pp. 1526–1531. [Google Scholar] [CrossRef]
- Zhu, X.; Zhao, S.; Li, X.; Zhang, R.; Kong, M. Optimization of the Moving Averaging–Moving Differential Algorithm for Φ-OTDR. Appl. Opt. 2022, 61, 5633. [Google Scholar] [CrossRef]
- Jabidin, H.Z.; Ibrahim, S.A.; Kalilur Raheem, M.M.; Mansoor, A.; Zan, M.S.D.; Bakar, A.A.A.; Abdul-Rashid, H.A. Analysis of Combined Moving-Average Moving-Differential Algorithms to Enhance SNR in Distributed Optical Fiber Acoustic Sensors. Results Eng. 2025, 26, 105268. [Google Scholar] [CrossRef]
- Kwon, Y.-S.; Naeem, K.; Jeon, M.Y.; Kwon, I. Effect of Parameters in Moving Average Method for Event Detection Enhancement Using Phase Sensitive OTDR. In Proceedings of the 25th Optical Fiber Sensors Conference (OFS), Jeju, Republic of Korea, 28 April 2017. [Google Scholar] [CrossRef]
- Chen, D.; Liu, Q.; He, Z. Phase-Detection Distributed Fiber-Optic Vibration Sensor without Fading-Noise Based on Time-Gated Digital OFDR. Opt. Express 2017, 25, 8315. [Google Scholar] [CrossRef]
- Fu, C.; Li, P.; Sui, R.; Peng, Z.; Zhong, H.; Yin, X.; Wang, Y. High-Spatial-Resolution OFDR Distributed Temperature Sensor Based on Step-by-Step and Image Wavelet Denoising Methods. Sensors 2022, 22, 9972. [Google Scholar] [CrossRef] [PubMed]
- Alsahlanee, A.T. Convergence Rate for Low-Pass Infinite Impulse Response Digital Filter. J. Phys. Conf. Ser. 2021, 1963, 012103. [Google Scholar] [CrossRef]
- Belokrylov, M.E.; Kambur, D.A.; Konstantinov, Y.A.; Claude, D.; Barkov, F.L. An Optical Frequency Domain Reflectometer’s (OFDR) Performance Improvement via Empirical Mode Decomposition (EMD) and Frequency Filtration for Smart Sensing. Sensors 2024, 24, 1253. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Turov, A.T.; Barkov, F.L.; Konstantinov, Y.A.; Korobko, D.A.; Lopez-Mercado, C.A.; Fotiadi, A.A. Activation Function Dynamic Averaging as a Technique for Nonlinear 2D Data Denoising in Distributed Acoustic Sensors. Algorithms 2023, 16, 440. [Google Scholar] [CrossRef]
- Goswami, O.P.; Shukla, A.; Kumar, M.; Bhargava, A. Optimal Design of Digital Low-Pass Filters Using Multiverse Optimization. J. Electr. Eng. 2024, 75, 253–257. [Google Scholar] [CrossRef]
- Turulin, I.I.; Mogheer, H.S. Method and Algorithm for Synthesis of Controlled Digital Low-Pass Butterworth Filters on the Example of A 4th Order Filter. In Proceedings of the International Ural Conference on Electrical Power Engineering (UralCon), Magnitogorsk, Russia, 23–25 September 2022; IEEE: Magnitogorsk, Russia, 2022; pp. 336–340. [Google Scholar] [CrossRef]
- Singh, D.S.; Kumar, M. Design and Implementation of Third Order Low Pass Digital FIR Filter Using Pipelining Retiming Technique. IJEAT 2021, 10, 178–184. [Google Scholar] [CrossRef]
- Darak, S.J.; Prasad, V.A.; Lai, E.M.-K. Efficient Implementation of Reconfigurable Warped Digital Filters with Variable Low-Pass, High-Pass, Bandpass, and Bandstop Responses. IEEE Trans. VLSI Syst. 2013, 21, 1165–1169. [Google Scholar] [CrossRef]
- Guo, Z.; Han, G.; Yan, J.; Greenwood, D.; Marco, J.; Yu, Y. Ultimate Spatial Resolution Realisation in Optical Frequency Domain Reflectometry with Equal Frequency Resampling. Sensors 2021, 21, 4632. [Google Scholar] [CrossRef]
- Zhao, S.; Cui, J.; Tan, J. Nonlinearity Correction in OFDR System Using a Zero-Crossing Detection-Based Clock and Self-Reference. Sensors 2019, 19, 3660. [Google Scholar] [CrossRef]
- Sakhabutdinov, A.J.; Morozov, O.G.; Ivanov, A.A.; Misbakhov, R.S. Multiple Frequencies Analysis in FBG Based Instantaneous Frequency Measurements. In Proceedings of the 2018 Systems of Signals Generating and Processing in the Field of on Board Communications, Moscow, Russia, 20–21 March 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Bazzo, J.P.; Pipa, D.R.; Martelli, C.; Vagner Da Silva, E.; Cardozo Da Silva, J.C. Improving Spatial Resolution of Raman DTS Using Total Variation Deconvolution. IEEE Sens. J. 2016, 16, 4425–4430. [Google Scholar] [CrossRef]
- Rosolem, J.B.; Bassan, F.R.; De Freitas, D.E.; Salgado, F.C. Raman DTS Based on OTDR Improved by Using Gain-Controlled EDFA and Pre-Shaped Simplex Code. IEEE Sens. J. 2017, 17, 3346–3353. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).