Automatic Focusing of Off-Axis Digital Holographic Microscopy by Combining the Discrete Cosine Transform Sparse Dictionary with the Edge Preservation Index
Abstract
1. Introduction
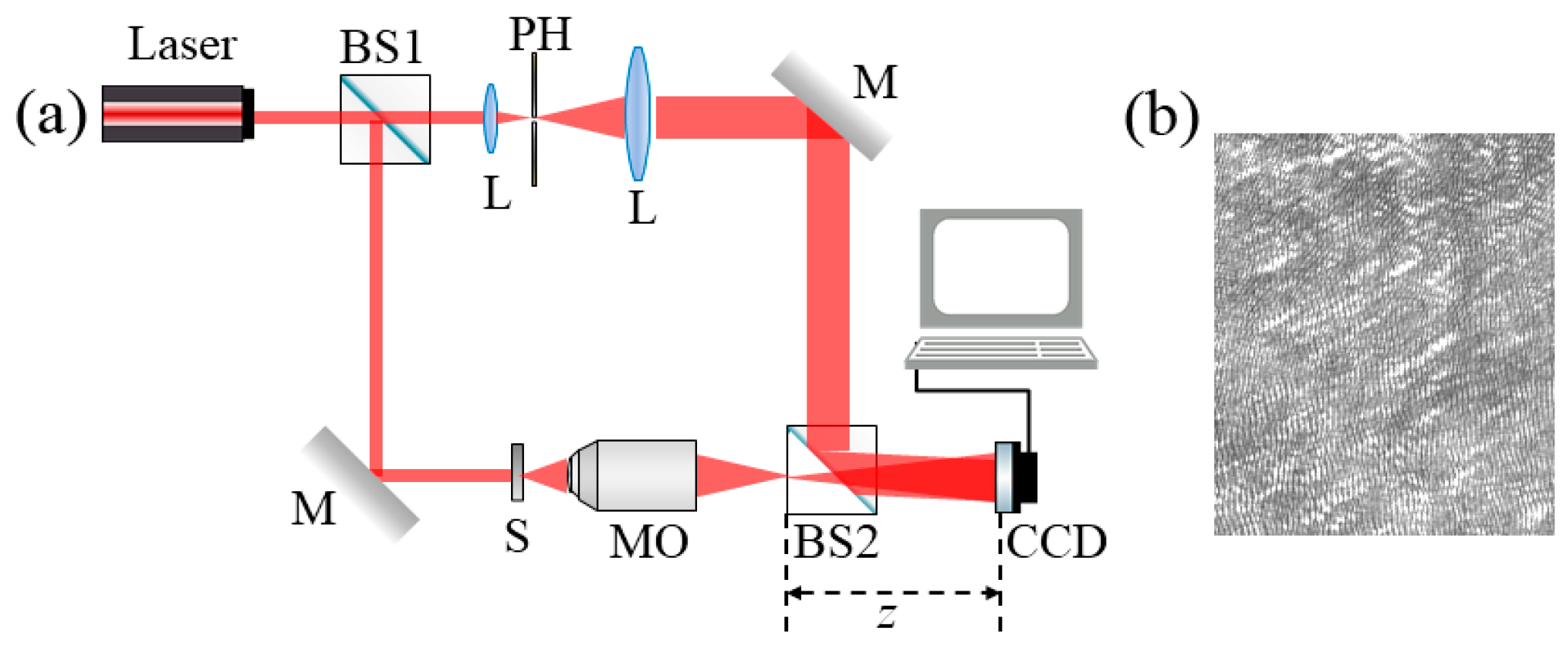
2. Off-Axis Digital Fresnel Hologram Reconstruction
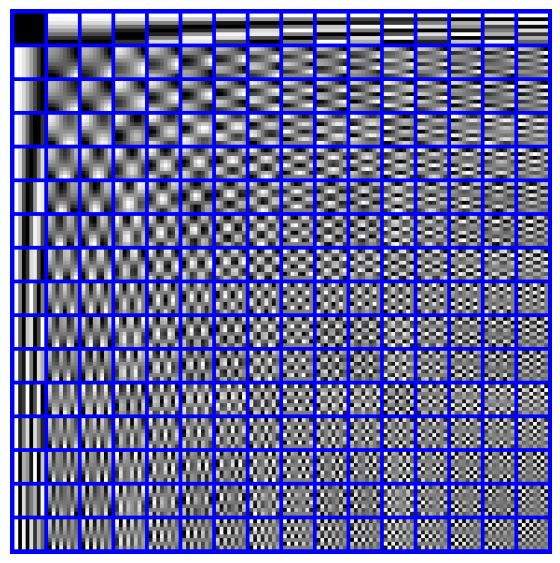
3. Basic Principle and Process of Denoising Image Through the DCT Dictionary
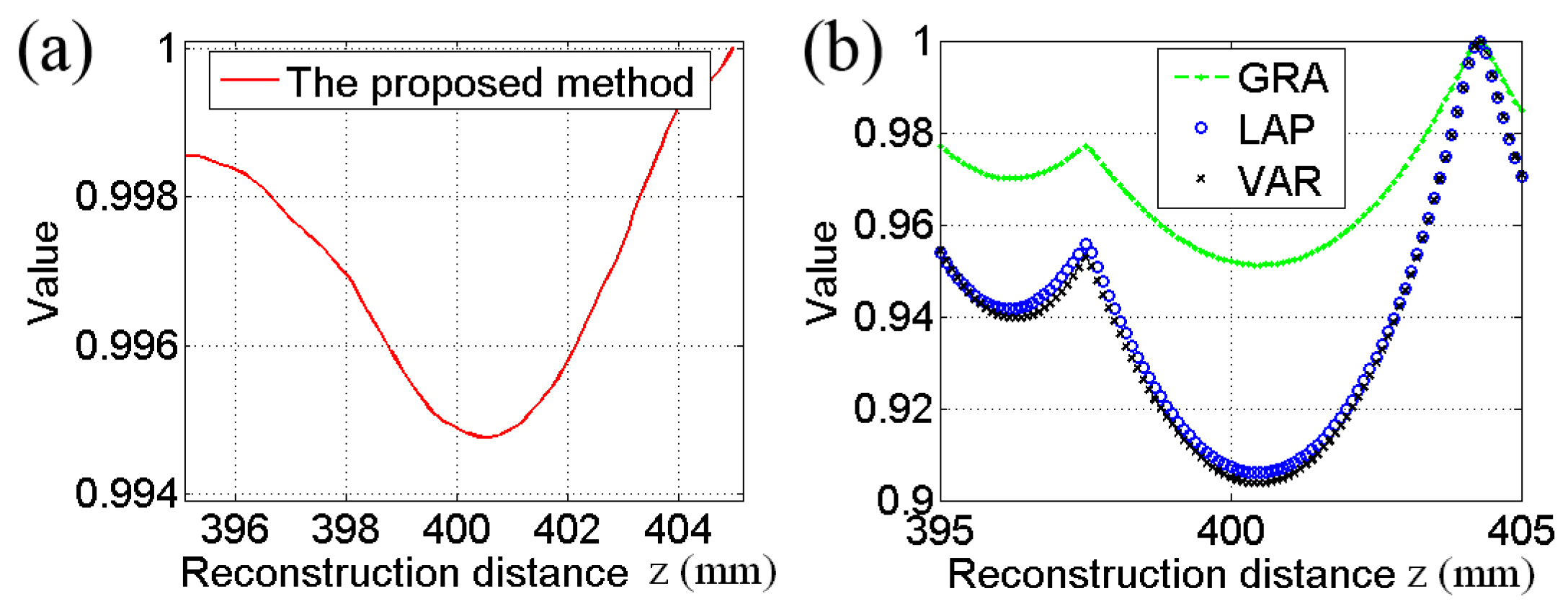
4. Focus Evaluation Function: The Edge Preservation Index
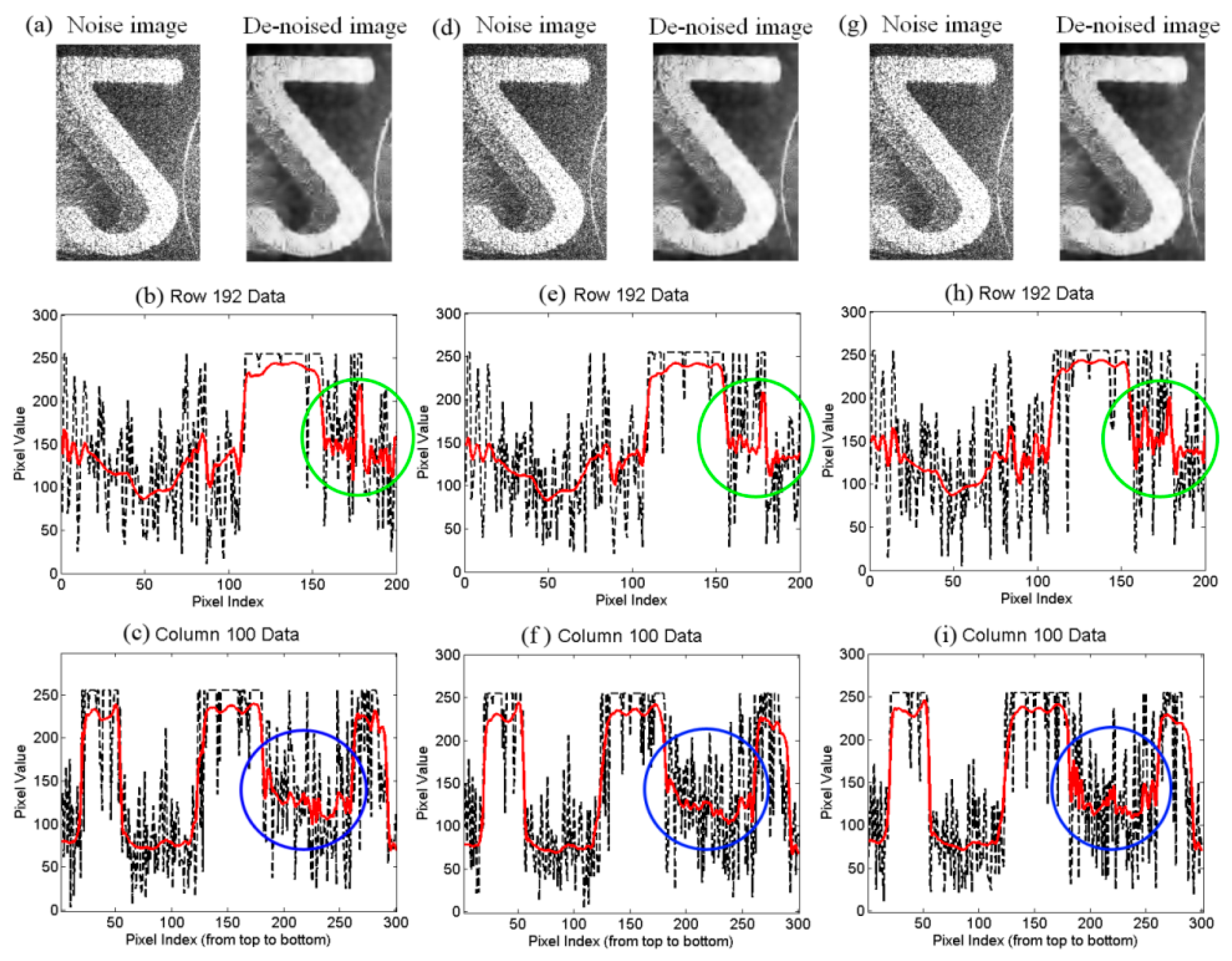
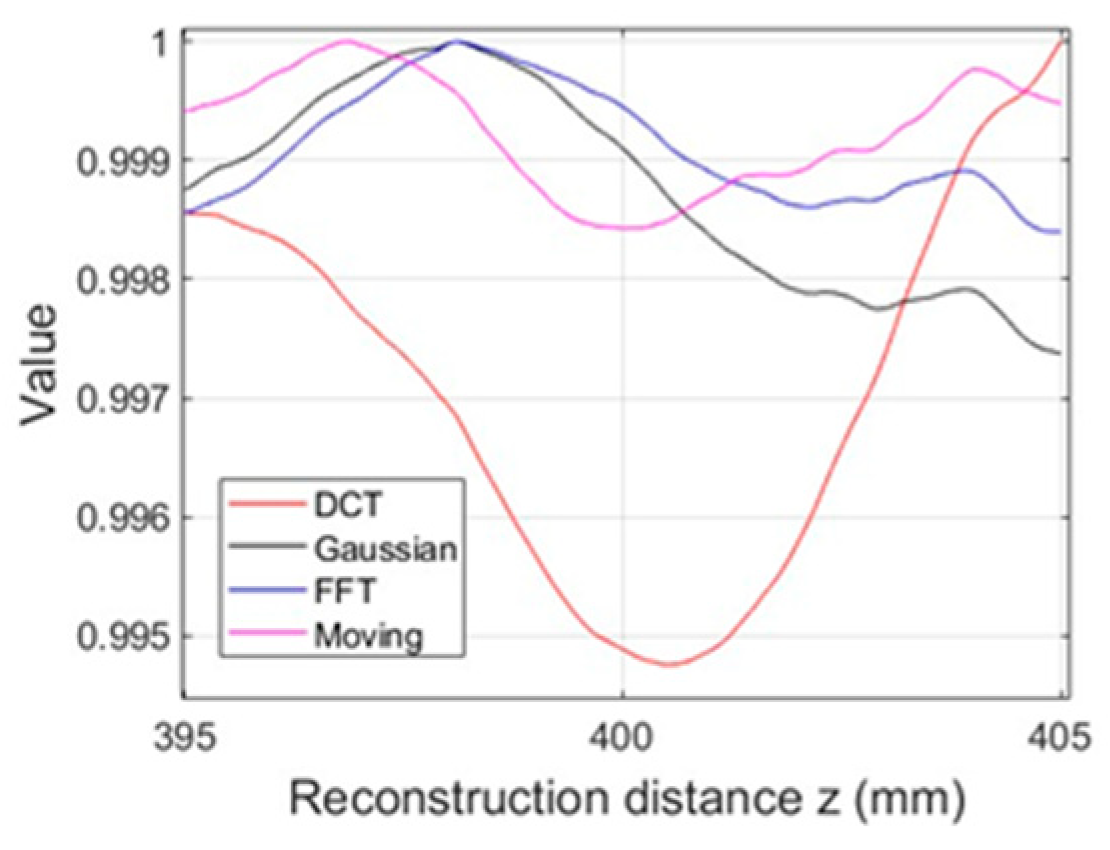
5. Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anand, V.; Tahara, T.; Lee, W.M. Advanced optical holographic imaging technologies. Appl. Phys. B 2022, 128, 198. [Google Scholar] [CrossRef]
- Li, S.; Kner, P.A. Optimizing self-interference digital holography for single-molecule localization. Opt. Express 2023, 31, 29352–29367. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Dai, S.; Ma, C.; Xi, T.; Di, J.; Zhao, J. A review of common-path off-axis digital holography: Towards high stable optical instrument manufacturing. Light Adv. Manuf. 2021, 2, 333–349. [Google Scholar] [CrossRef]
- Ghosh, A.; Noble, J.; Sebastian, A.; Das, S.; Liu, Z. Digital holography for non-invasive quantitative imaging of two-dimensional materials. J. Appl. Phys. 2020, 127, 084901. [Google Scholar] [CrossRef]
- Huang, J.; Cai, W.; Wu, Y.; Wu, X. Recent advances and applications of digital holography in multiphase reactive/nonreactive flows: A review. Meas. Sci. Technol. 2021, 33, 022001. [Google Scholar] [CrossRef]
- Li, T.; Wu, Y.; Wu, X. Morphology and position measurement of irregular opaque particle with digital holography of side scattering. Powder Technol. 2021, 394, 384–393. [Google Scholar] [CrossRef]
- Di, J.; Song, Y.; Xi, T.; Zhang, J.; Li, Y.; Ma, C.; Wang, K.; Zhao, J. Dual-wavelength common-path digital holographic microscopy for quantitative phase imaging of biological cells. Opt. Eng. 2017, 56, 111712. [Google Scholar] [CrossRef]
- Huang, J.; Li, S.; Zi, Y.; Qian, Y.; Cai, W.; Aldén, M.; Li, Z. Clustering-based particle detection method for digital holography to detect the three-dimensional location and in-plane size of particles. Meas. Sci. Technol. 2021, 32, 055205. [Google Scholar] [CrossRef]
- Trusiak, M.; Picazo-Bueno, J.A.; Zdankowski, P.; Micó, V. DarkFocus: Numerical autofocusing in digital in-line holographic microscopy using variance of computational dark-field gradient. Opt. Laser Eng. 2020, 134, 106195. [Google Scholar] [CrossRef]
- Tang, M.; Liu, C.; Wang, X.P. Autofocusing and image fusion for multi-focus plankton imaging by digital holographic microscopy. Appl. Opt. 2020, 59, 333–345. [Google Scholar] [CrossRef]
- Wen, Y.; Wang, H.; Anand, A.; Qu, W.; Cheng, H.; Dong, Z.; Wu, Y. A fast autofocus method based on virtual differential optical path in digital holography: Theory and applications. Opt. Laser Eng. 2019, 121, 133–142. [Google Scholar] [CrossRef]
- Ou, H.; Wu, Y.; Lam, E.Y.; Wang, B.Z. New autofocus and reconstruction method based on a connected domain. Opt. Lett. 2018, 43, 2201–2203. [Google Scholar] [CrossRef] [PubMed]
- Memmolo, P.; Paturzo, M.; Javidi, B.; Netti, P.A.; Ferraro, P. Refocusing criterion via sparsity measurements in digital holography. Opt. Lett. 2014, 39, 4719–4722. [Google Scholar] [CrossRef] [PubMed]
- Langehanenberg, P.; Kemper, B.; Dirksen, D.; Von Bally, G. Autofocusing in digital holographic phase contrast microscopy on pure phase objects for live cell imaging. Appl. Opt. 2008, 47, D176–D182. [Google Scholar] [CrossRef]
- Long, J.; Yan, H.; Li, K.; Zhang, Y.; Pan, S.; Cai, P. Autofocusing by phase difference in reflective digital holography. Appl. Opt. 2022, 61, 2284–2292. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, H.; Wu, Y.; Tamamitsu, M.; Ozcan, A. Edge sparsity criterion for robust holographic autofocusing. Opt. Lett. 2017, 42, 3824–3827. [Google Scholar] [CrossRef]
- Fatih Toy, M.; Kühn, J.; Richard, S.; Parent, J.; Egli, M.; Depeursinge, C. Accelerated autofocusing of off-axis holograms using critical sampling. Opt. Lett. 2012, 37, 5094–5096. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Z.; Jin, S.; Cao, L. Hough transform-based multi-object autofocusing compressive holography. Appl. Opt. 2023, 62, D23–D30. [Google Scholar] [CrossRef]
- Ghosh, A.; Kulkarni, R.; Mondal, P.K. Autofocusing in digital holography using eigenvalues. Appl. Opt. 2021, 60, 1031–1040. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Z.; Jin, S.; Cao, L. Autofocusing of in-line holography based on compressive sensing. Opt. Laser Eng. 2021, 146, 106678. [Google Scholar] [CrossRef]
- Ren, Z.; Xu, Z.; Lam, E.Y. Learning-based nonparametric autofocusing for digital holography. Optica 2018, 5, 337–344. [Google Scholar] [CrossRef]
- Lin, W.; Chen, L.; Chen, Y.; Cai, W.; Hu, Y.; Wen, K. Single-shot speckle reduction by elimination of redundant speckle patterns in digital holography. Appl. Opt. 2020, 59, 5066–5072. [Google Scholar] [CrossRef]
- Bianco, V.; Memmolo, P.; Leo, M.; Montresor, S.; Distante, C.; Paturzo, M.; Picart, P.; Javidi, B.; Ferraro, P. Strategies for reducing speckle noise in digital holography. Light Sci. Appl. 2018, 7, 48. [Google Scholar] [CrossRef] [PubMed]
- Bianco, V.; Memmolo, P.; Paturzo, M.; Finizio, A.; Javidi, B.; Ferraro, P. Quasi noise-free digital holography. Light Sci. Appl. 2016, 5, e16142. [Google Scholar] [CrossRef] [PubMed]
- Hincapie, D.; Herrera-Ramírez, J.; Garcia-Sucerquia, J. Single-shot speckle reduction in numerical reconstruction of digitally recorded holograms. Opt. Lett. 2015, 40, 1623–1626. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, D.G.A. Improving the intensity-contrast image of a noisy digital hologram by convolution of Chebyshev type 2 and elliptic filters. Appl. Opt. 2021, 60, 3823–3829. [Google Scholar] [CrossRef]
- Chen, K.; Chen, L.; Xiao, J.; Li, J.; Hu, Y.; Wen, K. Reduction of speckle noise in digital holography using a neighborhood filter based on multiple sub-reconstructed images. Opt. Express 2022, 30, 9222–9232. [Google Scholar] [CrossRef]
- Montrésor, S.; Memmolo, P.; Bianco, V.; Ferraro, P.; Picart, P. Comparative study of multi-look processing for phase map de-noising in digital Fresnel holographic interferometry. J. Opt. Soc. Am. A 2019, 36, A59–A66. [Google Scholar] [CrossRef]
- Fang, Q.; Xia, H.; Song, Q.; Zhang, M.; Guo, R.; Montresor, S.; Picart, P. Speckle denoising based on deep learning via a conditional generative adversarial network in digital holographic interferometry. Opt. Express 2022, 30, 20666–20683. [Google Scholar] [CrossRef]
- Yan, K.; Chang, L.; Andrianakis, M.; Tornari, V.; Yu, Y. Deep learning-based wrapped phase denoising method for application in digital holographic speckle pattern interferometry. Appl. Sci. 2020, 10, 4044. [Google Scholar] [CrossRef]
- Montresor, S.; Tahon, M.; Laurent, A.; Picart, P. Computational de-noising based on deep learning for phase data in digital holographic interferometry. APL Photonics 2020, 5, 030802. [Google Scholar] [CrossRef]
- Zeng, T.; Zhu, Y.; Lam, E.Y. Deep learning for digital holography: A review. Opt. Express 2021, 29, 40572–40593. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Jia, S.; Zhou, X.; Zhang, H.; Wang, L.; Li, G.; Wang, Z. Digital holographic microscopy phase noise reduction based on an over-complete chunked discrete cosine transform sparse dictionary. Opt. Laser Eng. 2023, 166, 107571. [Google Scholar] [CrossRef]
- Picazo-Bueno, J.A.; Trusiak, M.; Micó, V. Single-shot slightly off-axis digital holographic microscopy with add-on module based on beamsplitter cube. Opt. Express 2019, 27, 5655–5669. [Google Scholar] [CrossRef]
- Reddy, B.L.; Ramachandran, P.; Nelleri, A. Optimal Fresnelet sparsification for compressive complex wave retrieval from an off-axis digital Fresnel hologram. Opt. Eng. 2021, 60, 073102. [Google Scholar] [CrossRef]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef]
- Waske, B.; Braun, M.; Menz, G. A segment-based speckle filter using multisensoral remote sensing imagery. IEEE Geosci. Remote Sens. Lett. 2007, 4, 231–235. [Google Scholar] [CrossRef]
- Ri, S.; Takimoto, T.; Xia, P.; Wang, Q.; Tsuda, H.; Ogihara, S. Accurate phase analysis of interferometric fringes by the spatiotemporal phase-shifting method. J. Opt. 2020, 22, 105703. [Google Scholar] [CrossRef]
- Soncco, D.C.; Barbanson, C.; Nikolova, M.; Almansa, A.; Ferrec, Y. Fast and accurate multiplicative decomposition forfringe removal in interferometric images. IEEE Trans. Comput. Imaging 2017, 3, 187–201. [Google Scholar] [CrossRef]
- Galaktionov, I.; Sheldakova, J.; Toporovsky, V.; Kudryashov, A. Modified fizeau interferometer with the polynomial and FFT smoothing algorithm. Proc. SPIE 2022, 12223, 6. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Qiu, P.; Zhang, Y. Automatic Focusing of Off-Axis Digital Holographic Microscopy by Combining the Discrete Cosine Transform Sparse Dictionary with the Edge Preservation Index. Optics 2025, 6, 17. https://doi.org/10.3390/opt6020017
Liu Z, Qiu P, Zhang Y. Automatic Focusing of Off-Axis Digital Holographic Microscopy by Combining the Discrete Cosine Transform Sparse Dictionary with the Edge Preservation Index. Optics. 2025; 6(2):17. https://doi.org/10.3390/opt6020017
Chicago/Turabian StyleLiu, Zhaoliang, Peizhen Qiu, and Yupei Zhang. 2025. "Automatic Focusing of Off-Axis Digital Holographic Microscopy by Combining the Discrete Cosine Transform Sparse Dictionary with the Edge Preservation Index" Optics 6, no. 2: 17. https://doi.org/10.3390/opt6020017
APA StyleLiu, Z., Qiu, P., & Zhang, Y. (2025). Automatic Focusing of Off-Axis Digital Holographic Microscopy by Combining the Discrete Cosine Transform Sparse Dictionary with the Edge Preservation Index. Optics, 6(2), 17. https://doi.org/10.3390/opt6020017





