Theoretical Model of Curved Liquid Surface in the Microholes for Molding Microlenses
Abstract
1. Introduction
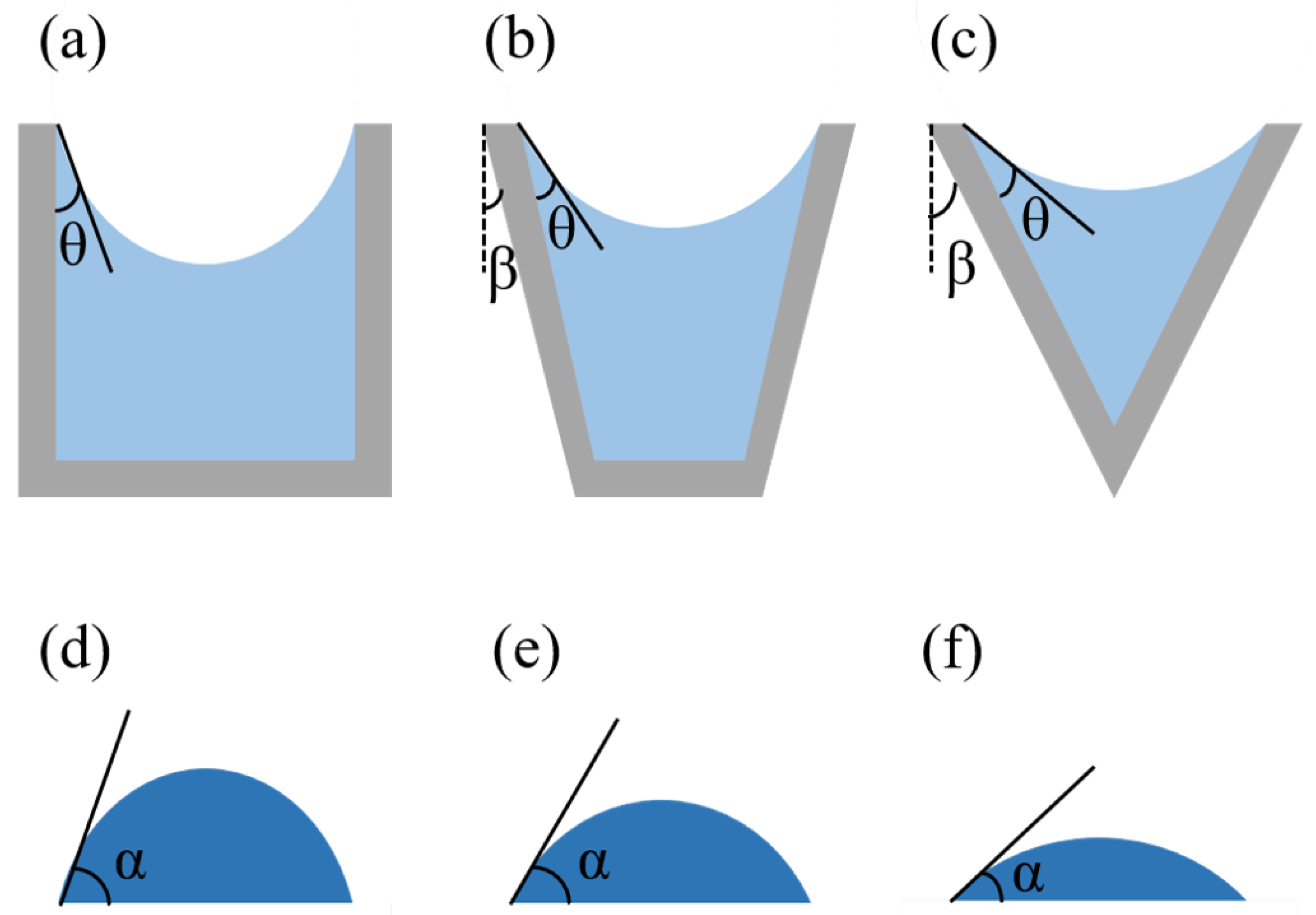
2. Design of Microlens in the Pre-Defined Microholes
3. Models for the Formation of the Microlens Mold
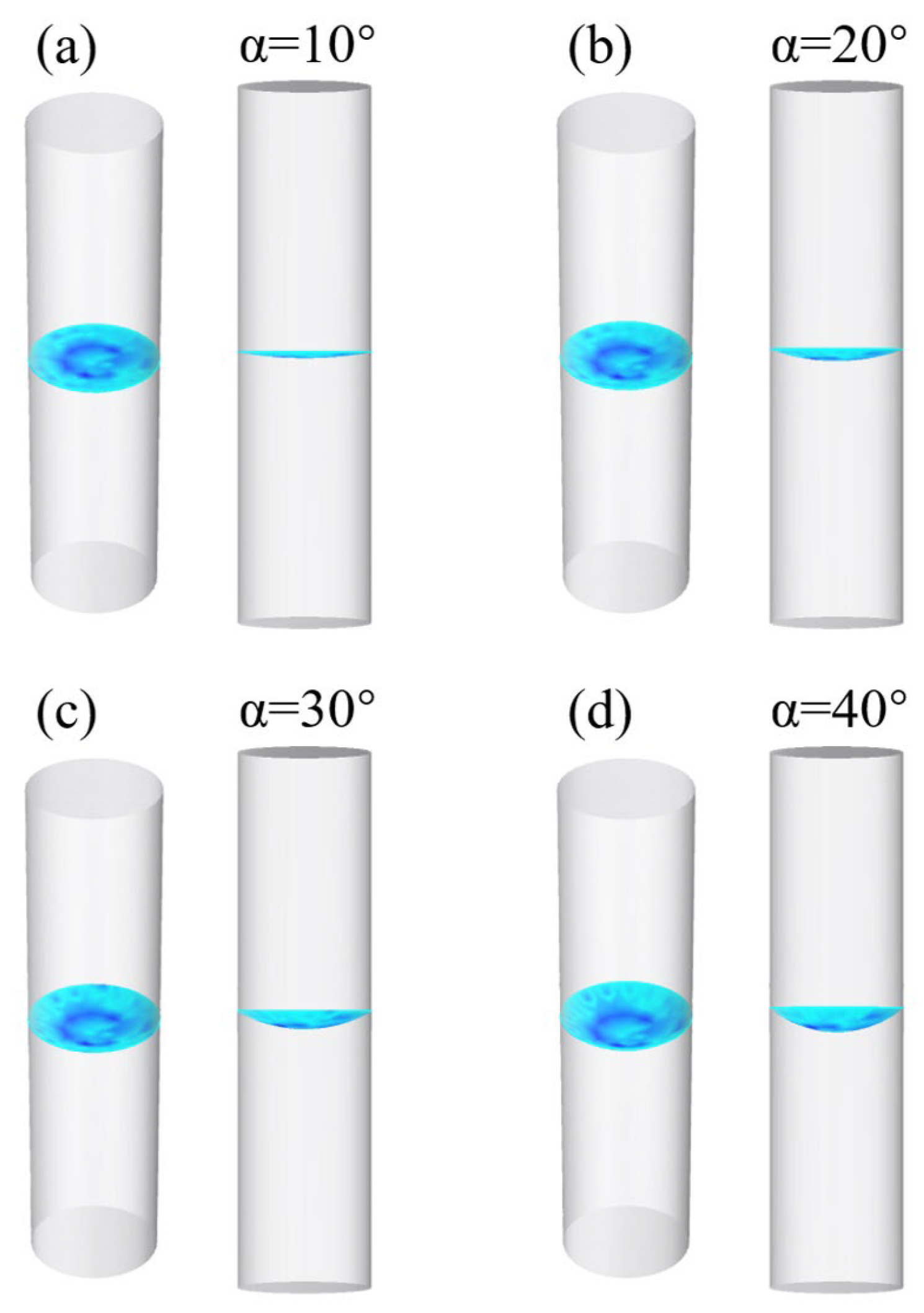
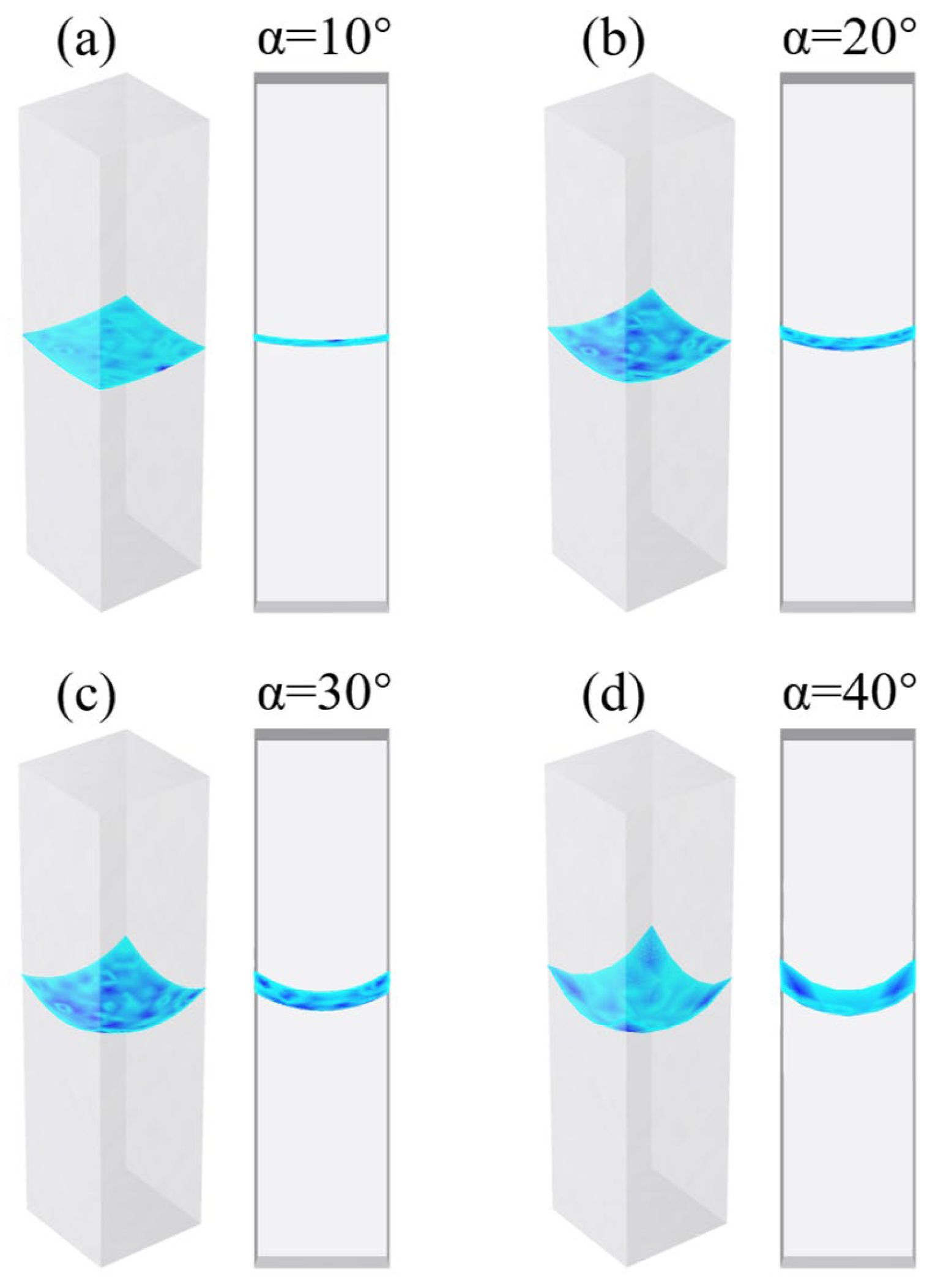
3.1. Numerical Model Based on Finite–Difference Time–Domain (FDTD) Method
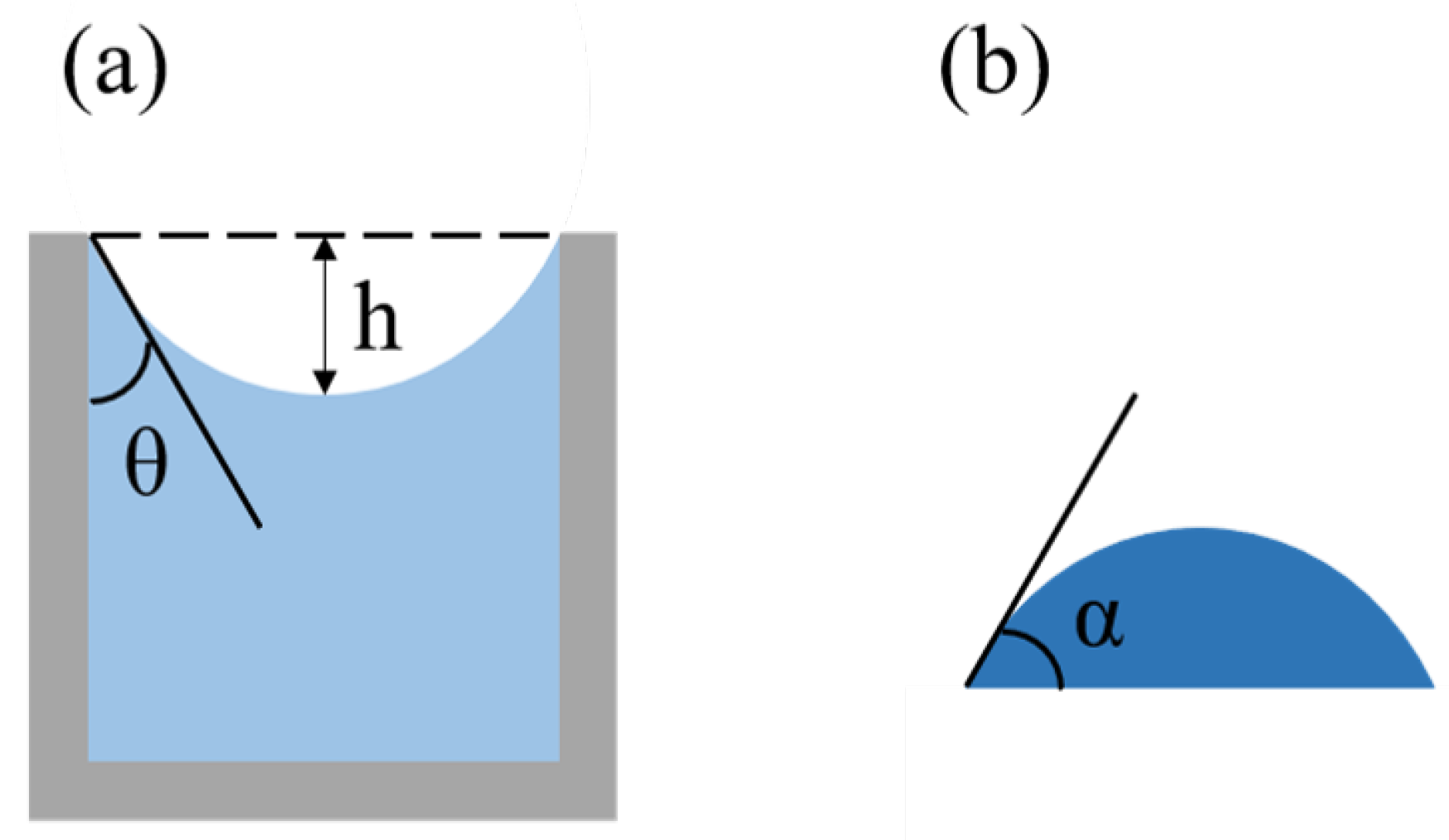
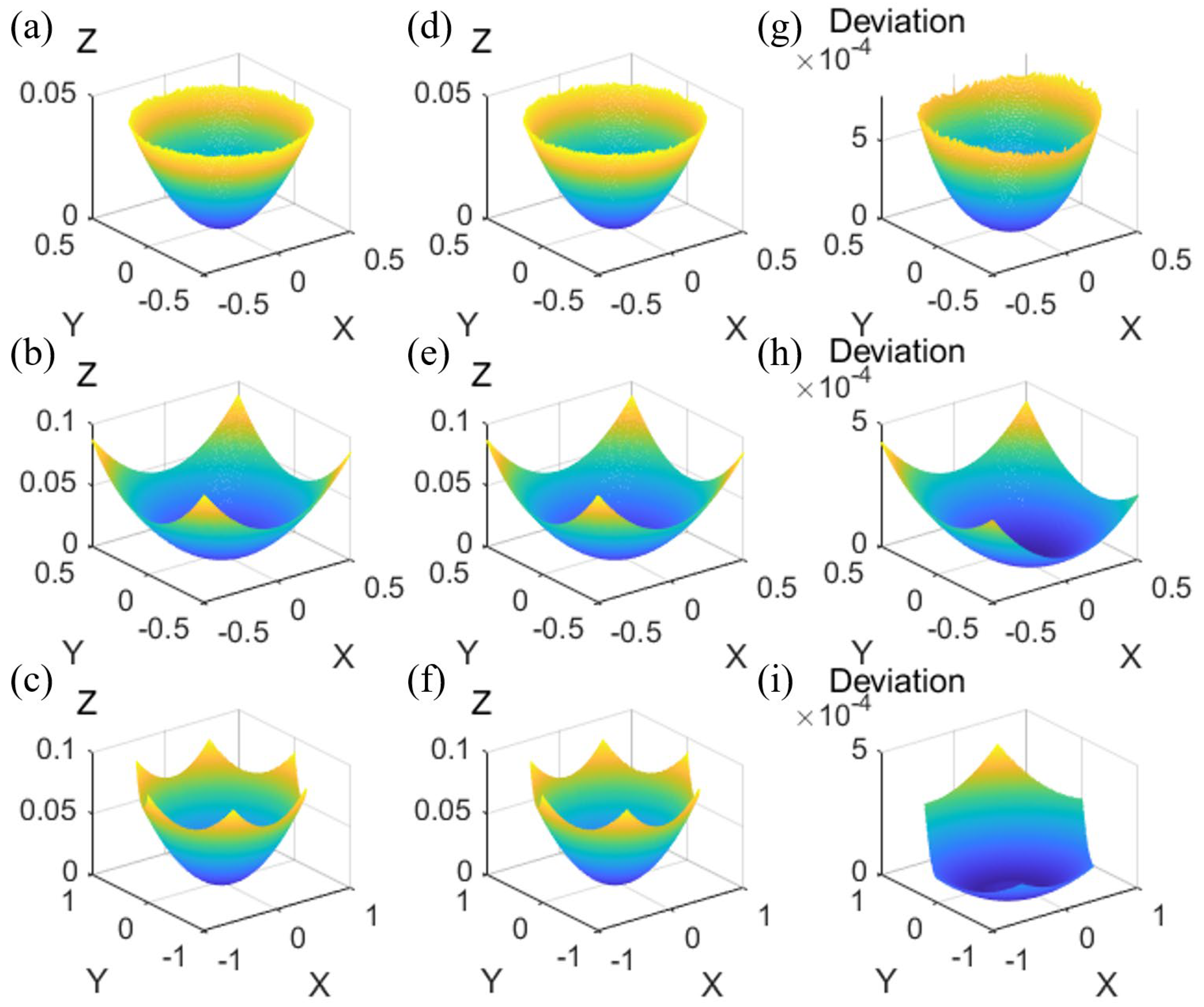
3.2. Theoretical Model Based on Mathematical Derivation
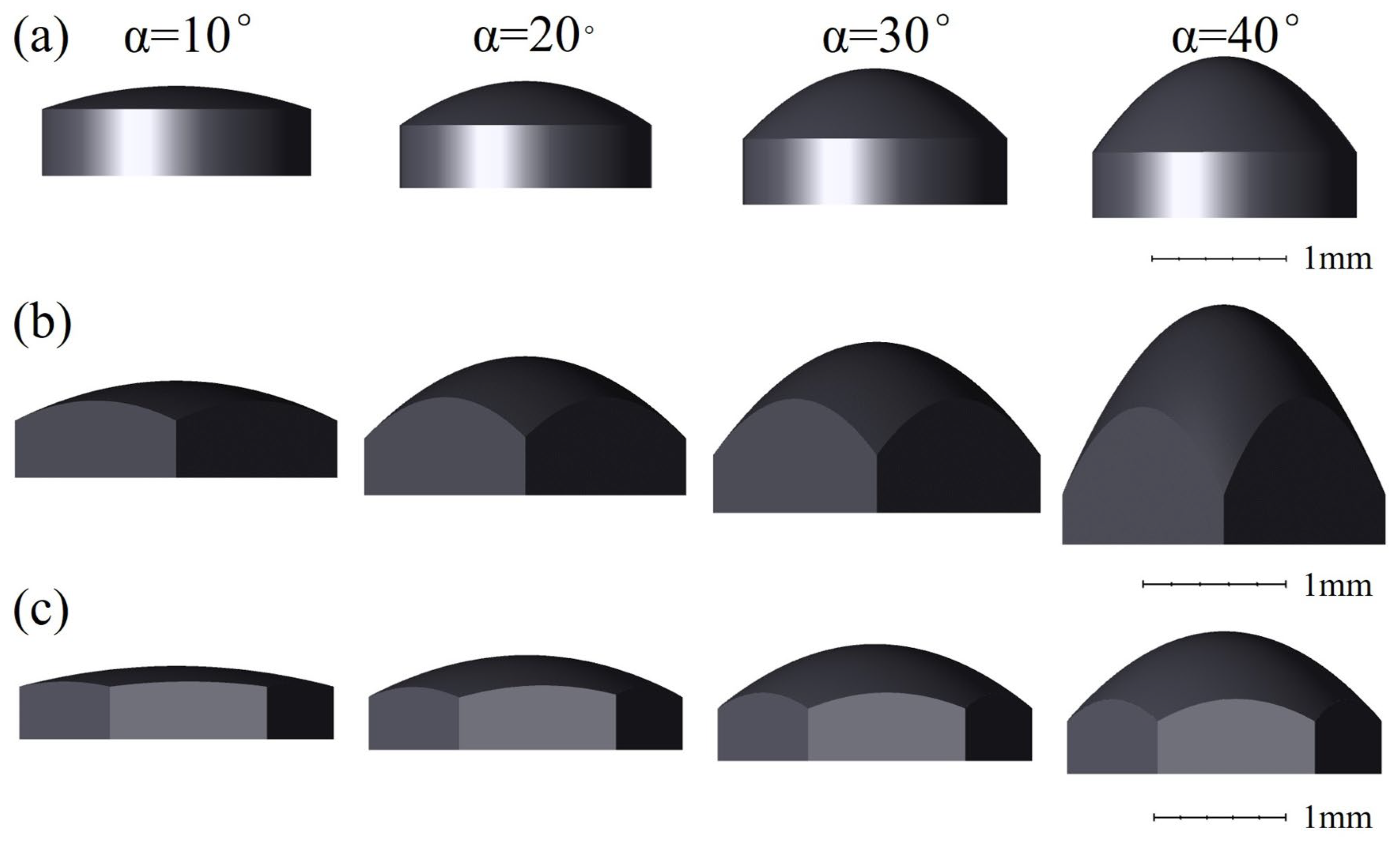
4. Profile of Microlens
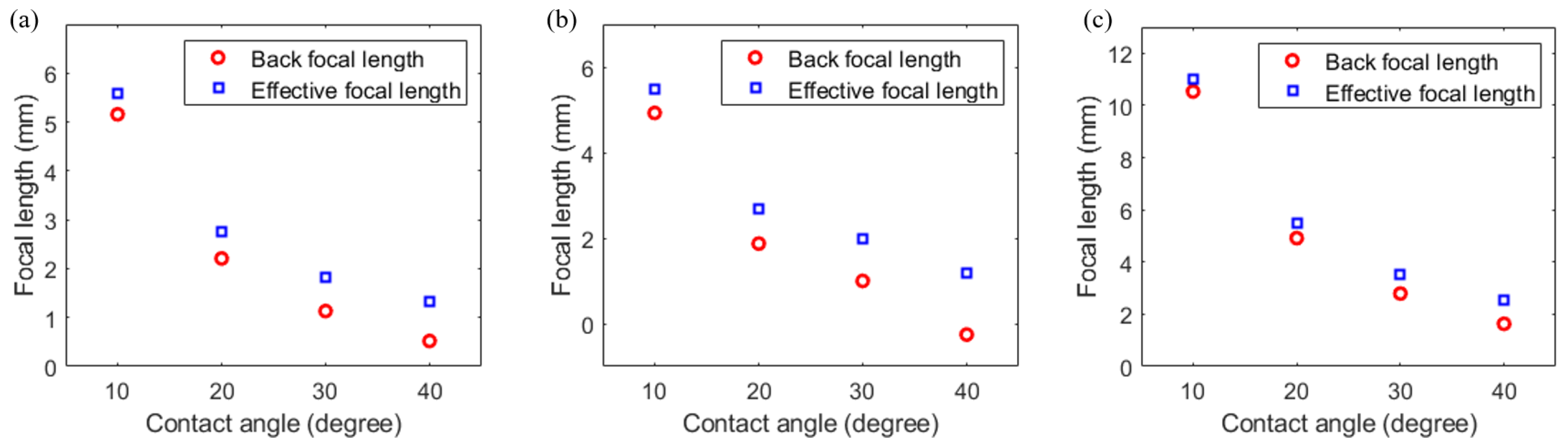
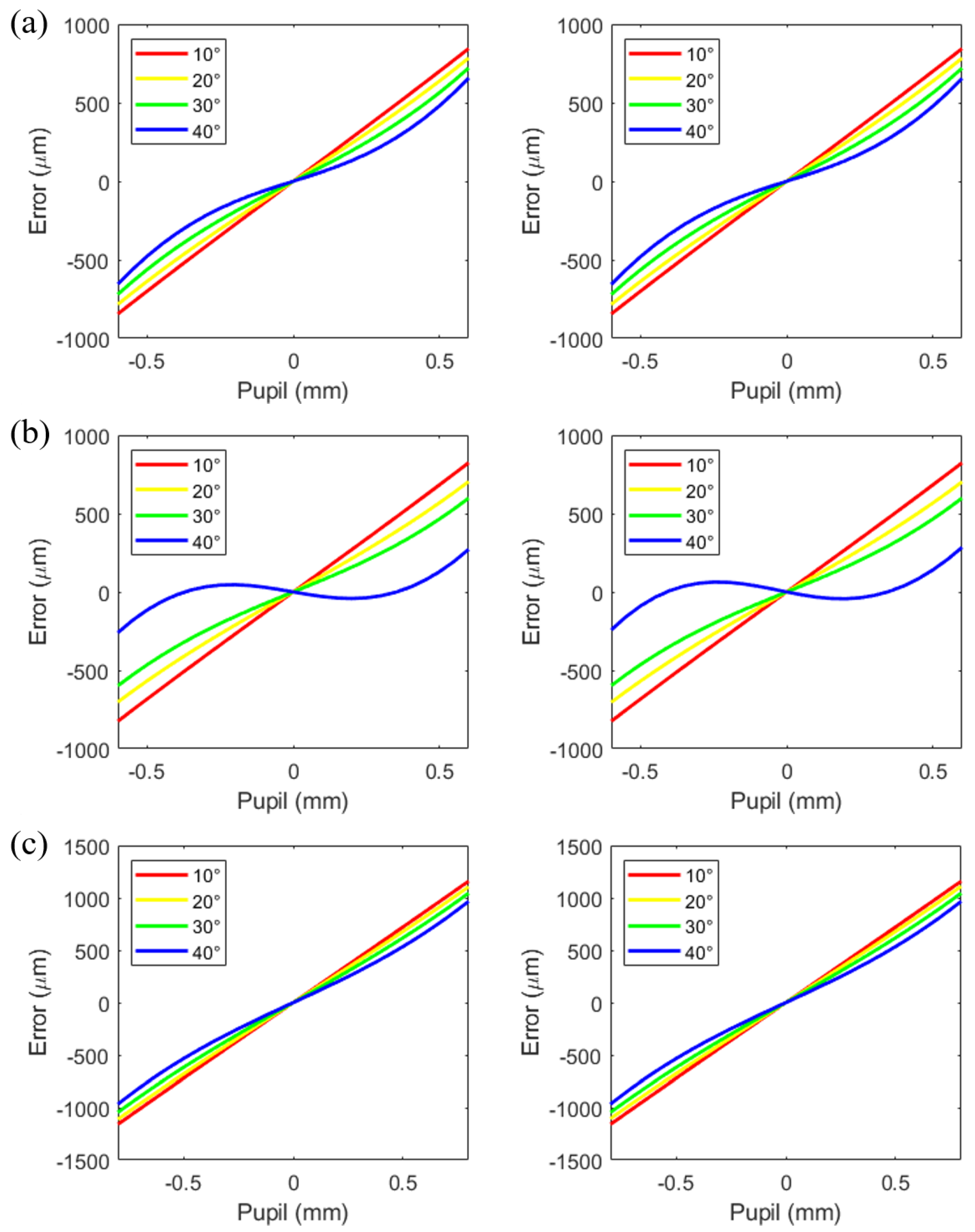
5. Optical Characteristics of the Microlens
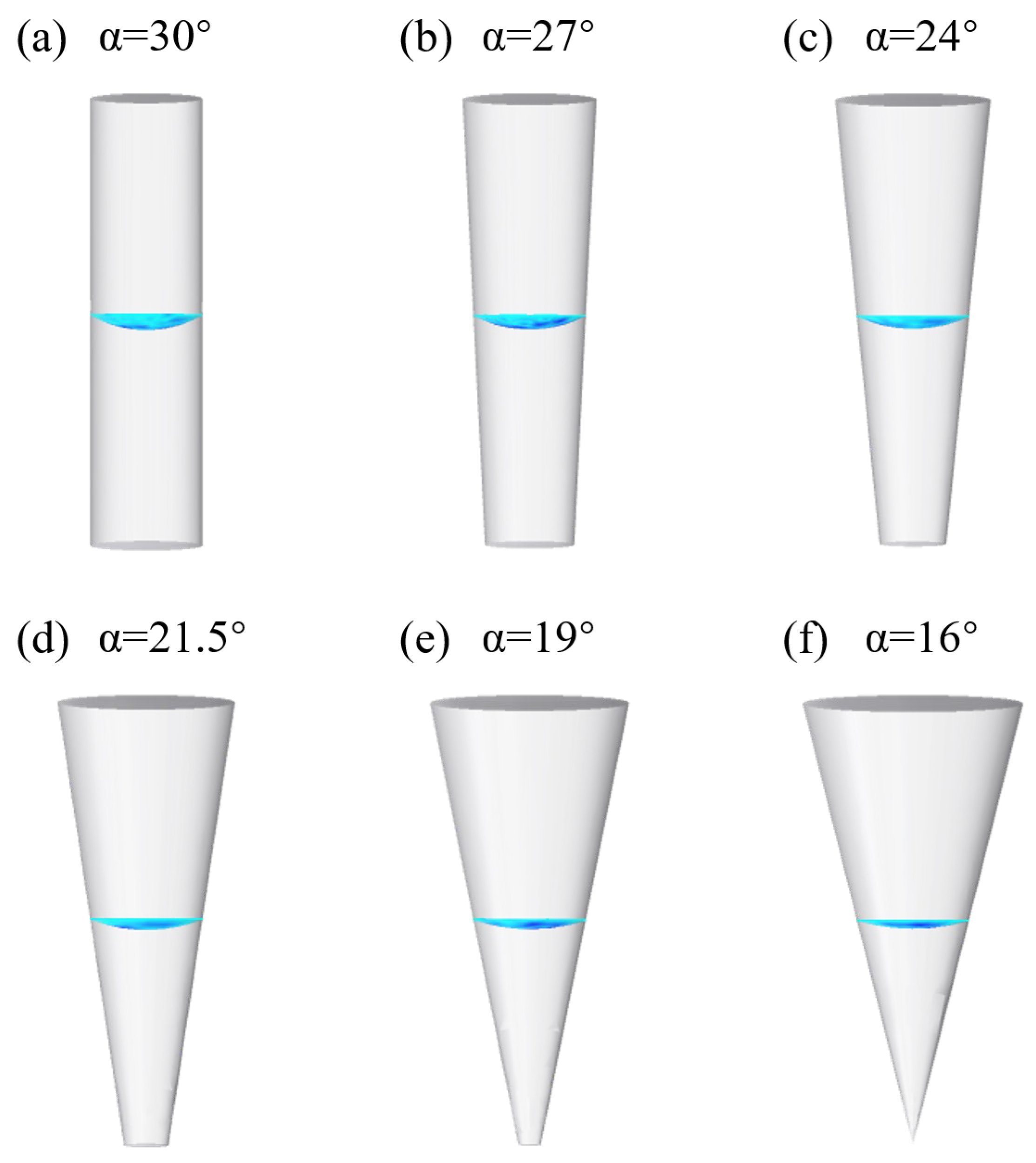
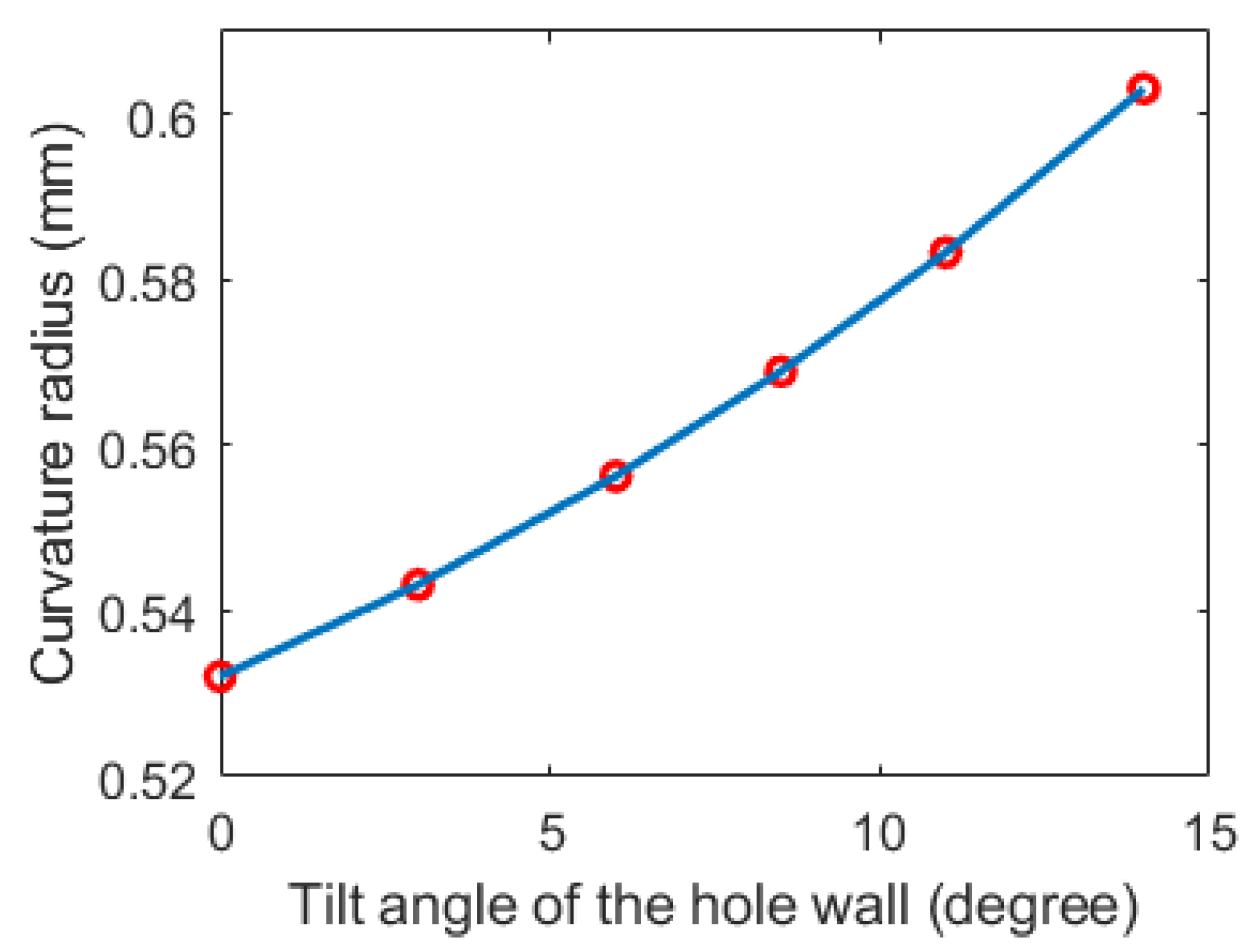
6. Microlenses Based on Microfluidic Flip-Flop Molds with Inclined Wall Holes
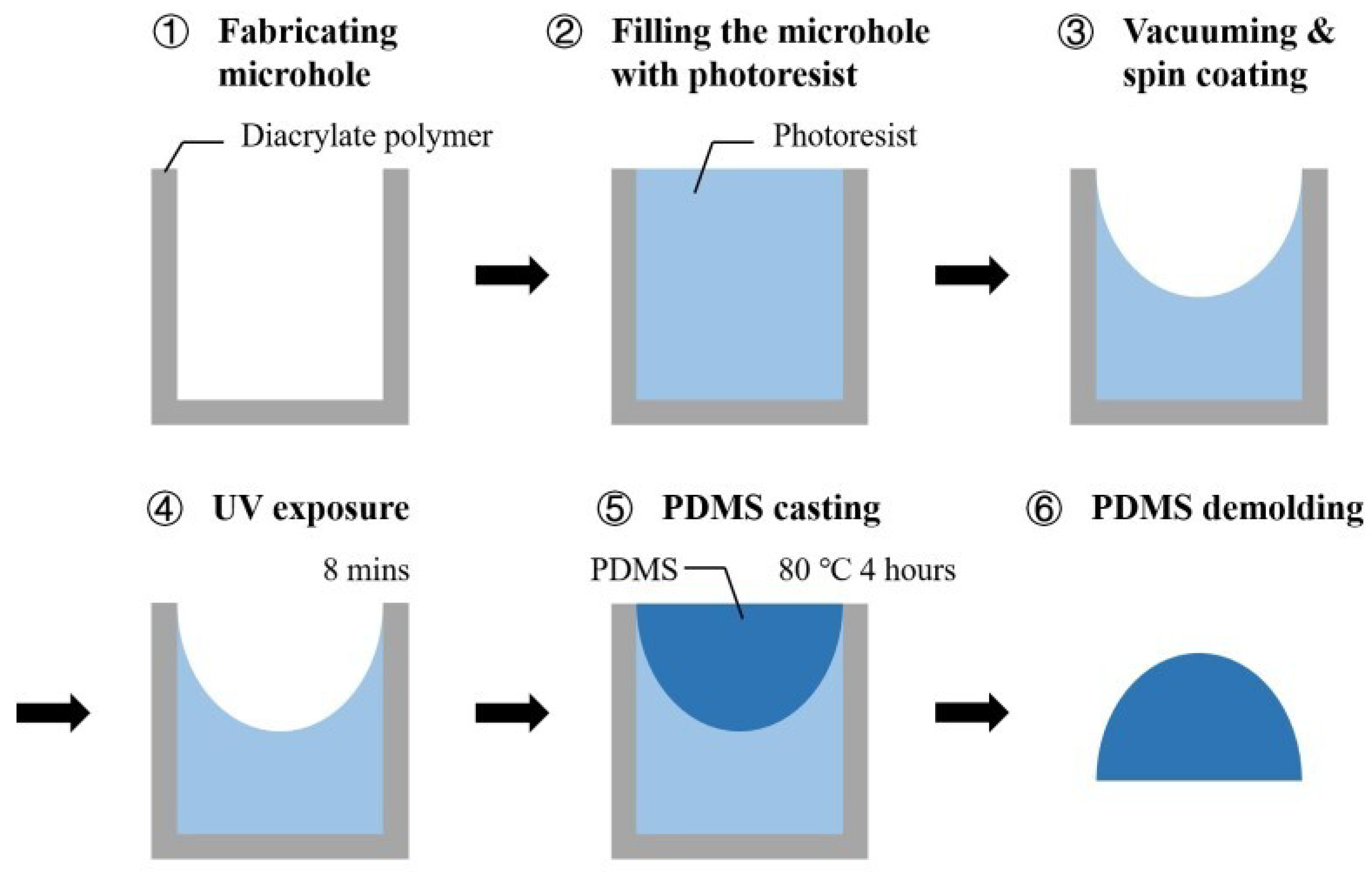
7. Schemes for Microlens Fabrication
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, J.L.; Zhang, J.; Shan, X.N.; Zhang, Y.W.; Peng, H.Y.; Qin, L.; Tan, Y.N.; Wang, L.J. Conversion of a Gaussian-distributed circular beam to a flat-top-distributed square beam in laser shock processing based on a micro-lens array structure. Optik 2023, 274, 170525. [Google Scholar] [CrossRef]
- Gradkowski, K.; Morrissey, P.E.; Brien, P. Packaging of micro-lens arrays to photonic integrated circuits using beam shape evaluation. J. Phys. Photonics 2024, 6, 035022. [Google Scholar]
- Garza-Rivera, A.; Gómez-Correa, J.E.; Renero-Carrillo, F.J.; Trevino, J.P.; Coello, V. Gabor superlens with variable focus. Chin. Opt. Lett. 2020, 18, 122201. [Google Scholar]
- Wang, W.W.; Chen, G.X.; Weng, Y.L.; Weng, X.Y.; Zhou, X.T.; Wu, C.X.; Guo, T.L.; Yan, Q.; Lin, Z.X.; Zhang, Y.G. Large-scale microlens arrays on flexible substrate with improved numerical aperture for curved integral imaging 3D display. Sci. Rep. 2020, 10, 11741. [Google Scholar]
- Choi, I.S.; Park, S.; Jeon, S.; Kwon, Y.W.; Park, R.; Taylor, R.A.; Kyhm, K.; Hong, S.W. Strain-tunable optical microlens arrays with deformable wrinkles for spatially coordinated image projection on a security substrate. Microsyst. Nanoeng. 2022, 8, 98. [Google Scholar]
- Liu, Z.H.; Hu, G.W.; Ye, H.P.; Wei, M.Y.; Guo, Z.H.; Chen, K.X.; Liu, C.; Tang, B.; Zhou, G.F. Mold-free self-assembled scalable microlens arrays with ultrasmooth surface and record-high resolution. Light Sci. Appl. 2023, 12, 143. [Google Scholar] [CrossRef]
- Xu, C.; Guan, X.; Abbasi, S.A.; Xia, N.; Ngai, T.; Zhang, L.; Ho, H.P.; Ng, S.H.C.; Yuan, W. Liquid-shaped microlens for scalable production of ultrahigh-resolution optical coherence tomography microendoscope. Commun. Eng. 2024, 3, 1. [Google Scholar] [CrossRef]
- Ahn, K.H.; Park, E.S.; Nam, S.M. Usefulness of a 1064 nm Microlens Array-type, Picosecond-dominant Laser for Pigmented Scars with Improvement of Vancouver Scar Scale. Med. Lasers 2019, 8, 19. [Google Scholar]
- Choi, J.; Duc, T.M.; Kim, H.; Hwang, J.K.; Kang, H.W. Diffractive micro-lens array (DLA) for uniform and selective picosecond laser treatment. Biomed. Opt. Express 2023, 14, 1992. [Google Scholar]
- Liang, X.X.; Yan, M.M.; Xu, Y.Z.; Zhang, T.C.; Zhang, D.N.; Zhang, C.R.; Wang, B.; Yi, F.T.; Liu, J. The fabrication of microlens array in PMMA material with the assistant of nickel pillars by LIGA technology and thermal reflow method. Microsyst. Technol. 2023, 29, 763. [Google Scholar]
- Yong, Y.Q.; Chen, S.; Chen, H.; Ge, H.X.; Hao, Z.B. A Rapid Fabrication Method of Large-Area MLAs with Variable Curvature for Retroreflectors Based on Thermal Reflow. Micromachines 2024, 15, 816. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Dong, X.S.; Wang, X.F.; Xiao, J.F.; Sun, Q.Q.; Shen, L.F.; Lan, J.; Shen, Z.F.; Xu, J.F.; Du, Y.Q.Y. Fabrication of Large-Area Silicon Spherical Microlens Arrays by Thermal Reflow and ICP Etching. Micromachines 2024, 15, 460. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.H.; Wu, Y.L.; Chen, L.; Bakhtiyari, A.N.; Yu, W.H.; Qi, D.F.; Zheng, H.Y. Spatial light assisted femtosecond laser direct writing of a bionic superhydrophobic Fresnel microlens arrays. Opt. Laser Technol. 2024, 180, 111451. [Google Scholar]
- Deng, H.T.; Qi, D.F.; Wang, X.M.; Liu, Y.H.; Shangguan, S.Y.; Zhang, J.G.; Shen, X.; Liu, X.Y.; Wang, J.; Zheng, H.Y. Femtosecond laser writing of infrared microlens arrays on chalcogenide glass. Opt. Laser Technol. 2023, 159, 108953. [Google Scholar]
- Huang, L.; Hong, Z.H.; Chen, Q.D.; Zhang, Y.L.; Zhao, S.Q.; Dong, Y.J.; Liu, Y.Q.; Liu, H. Imaging/nonimaging microoptical elements and stereoscopic systems based on femtosecond laser direct writing. Light Adv. Manuf. 2023, 4, 543. [Google Scholar]
- Wang, H.; Zhang, W.; Ladika, D.; Yu, H.; Gailevičius, D.; Wang, H.; Pan, C.; Nair, P.N.S.; Ke, Y.; Mori, T.; et al. Two-Photon Polymerization Lithography for Optics and Photonics: Fundamentals, Materials, Technologies, and Applications. Adv. Funct. Mater. 2023, 33, 2214211. [Google Scholar]
- Wang, Z.H.; Wu, Y.L.; Yu, W.H.; Qi, D.F.; Bakhtiyari, A.N.; Zheng, H.Y. Investigation into fabrication and optical characteristics of tunable optofluidic microlenses using two-photon polymerization. Opt. Express 2024, 32, 7448. [Google Scholar]
- Dirdal, C.A.; Jensen, G.U.; Angelskår, H.; Thrane, P.C.V.; Gjessing, J.; Ordnung, D.A. Towards high-throughput large-area metalens fabrication using UV-nanoimprint lithography and Bosch deep reactive ion etching. Opt. Express 2020, 28, 15542. [Google Scholar]
- Zheng, J.X.; Tian, K.S.; Qi, J.Y.; Guo, M.R.; Liu, X.Q. Advances in fabrication of micro-optical components by femtosecond laser with etching technology. Opt. Laser Technol. 2023, 167, 109793. [Google Scholar]
- Aderneuer, T.; Fernández, O.; Ferrini, R. Two-photon grayscale lithography for free-form micro-optical arrays. Opt. Express 2021, 29, 39511. [Google Scholar]
- Lamprecht, B.; Ulm, A.; Lichtenegger, P.; Leiner, C.; Nemitz, W.; Sommer, C. Origination of free-form micro-optical elements using one- and two-photon grayscale laser lithography. Appl. Opt. 2022, 61, 1863. [Google Scholar] [CrossRef] [PubMed]
- Garcia, I.S.; Ferreira, C.; Santos, J.D.; Martins, M.; Dias, R.A.; Aguiam, D.E. Fabrication of a MEMS Micromirror Based on Bulk Silicon Micromachining Combined with Grayscale Lithography. J. Microelectromech. Syst. 2020, 29, 734. [Google Scholar] [CrossRef]
- Chen, P.C.; Chang, Y.P.; Zhang, R.H.; Wu, C.C.; Tang, G.R. Microfabricated microfluidic platforms for creating microlens array. Opt. Express 2017, 25, 16101. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Dai, B.; Huang, Y.; Wang, H.; Yang, Z.; Wang, K.; Zhuang, S.; Zhang, D.W. Fabrication of polymer microlens array with controllable focal length by modifying surface wettability. Opt. Express 2018, 26, 4172. [Google Scholar] [CrossRef]
- Liu, C.; Wang, D.; Wang, Q.; Xing, Y. Multifunctional optofluidic lens with beam steering. Opt. Express 2020, 28, 7734. [Google Scholar] [CrossRef]
- Long, Y.; Song, Z.Y.; Pan, M.L.; Tao, C.X.; Hong, R.J.; Dai, B.; Zhang, D.W. Fabrication of uniform-aperture multi-focus microlens array by curving microfluid in the microholes with inclined walls. Opt. Express 2021, 29, 12763. [Google Scholar] [CrossRef]
- Bogdanowicz, R.; Jönsson-Niedziółka, M.; Vereshchagina, E.; Dettlaff, A.; Boonkaew, S.; Pierpaoli, M.; Wittendorp, P.; Jain, S.; Tyholdt, F.; Thomas, J.; et al. Microfluidic devices for photo-and spectroelectrochemical applications. Curr. Opin. Electrochem. 2022, 36, 101138. [Google Scholar] [CrossRef]
- Golozar, M.; Chu, W.K.; Casto, L.D.; McCauley, J.; Butterworth, A.L.; Mathies, R.A. Fabrication of high-quality glass microfluidic devices for bioanalytical and space flight applications. MethodsX 2020, 7, 101043. [Google Scholar] [CrossRef]
- Dai, B.; Zhang, L.; Zhao, C.L.; Bachman, H.; Becker, R.; Mai, J.; Jiao, Z.; Li, W.; Zheng, L.L.; Wan, X.J.; et al. Biomimetic apposition compound eye fabricated using microfluidic-assisted 3D printing. Nat. Commun. 2021, 12, 6458. [Google Scholar] [CrossRef]
- Xu, Z.H.; Zhou, J.Y.; Wang, B.; Meng, Z.M. Design of Refractive/Diffractive Hybrid Projection Lens for DMD-Based Maskless Lithography. Optics 2021, 2, 103–112. [Google Scholar] [CrossRef]
- Xu, M.; Li, J.; Chang, X.Y.; Chen, C.F.; Lu, H.B.; Wang, Z. Self-assembled microlens array with controllable curvatures for integral imaging 3D display. Opt. Lasers Eng. 2024, 180, 108322. [Google Scholar] [CrossRef]
- Gerlach, F.; Hussong, J.; Roisman, I.V.; Tropea, C. Capillary rivulet rise in real-world corners. Colloids Surf. A Physicochem. Eng. Asp. 2020, 592, 124530. [Google Scholar] [CrossRef]
- Li, C.X.; Dai, H.Y.; Gao, C.; Jiang, L. Bioinspired inner microstructured tube controlled capillary rise. Appl. Biol. Sci. 2019, 116, 12704. [Google Scholar] [CrossRef]
- Zuo, Z.W.; Wang, J.F.; Huo, Y.P.; Wang, D.B.; Ji, H.B. Experimental simulation of capillary effect on rough flat surfaces. Particuology 2022, 60, 115. [Google Scholar] [CrossRef]
- Abadi, G.B.; Bahrami, M. The effect of surface roughness on capillary rise in micro-grooves. Sci. Rep. 2022, 12, 14867. [Google Scholar]
- Chen, S.T.; Duan, L.; Li, Y.; Ding, F.L.; Liu, J.T.; Li, W. Capillary Phenomena Between Plates from Statics to Dynamics Under Microgravity. Microgravity Sci. Technol. 2022, 34, 70. [Google Scholar]
- Li, W.; Wu, D.; Li, Y.; Chen, S.Y.; Ding, F.L.; Kang, Q.; Chen, S.T. Static profiles of capillary surfaces in the annular space between two coaxial cones under microgravity. Acta Mech. Sin. 2024, 40, 123218. [Google Scholar]
- Son, S.Y.; Chen, L.; Kang, Q.J.; Derome, D.; Carmeliet, J. Contact Angle Effects on Pore and Corner Arc Menisci in Polygonal Capillary Tubes Studied with the Pseudopotential Multiphase Lattice Boltzmann Model. Computation 2016, 4, 12. [Google Scholar] [CrossRef]
- Mohseni, K. Surface Tension Capillarity and Contact Angle. In Encyclopedia of Microfluidics and Nanofluidics; Li, D., Ed.; Springer: Boston, MA, USA, 2008; pp. 1949–1956. [Google Scholar]
- Liou, W.W.; Peng, Y.Q.; Parker, P.E. Analytical modeling of capillary flow in tubes of nonuniform cross section. J. Colloid Interface Sci. 2009, 333, 389–399. [Google Scholar] [CrossRef]
- Vermolen, F.; Gharasoo, M.G.; Zitha, P.L.J.; Bruining, J. Numerical Solutions of Some Diffuse Interface Problems: The Cahn-Hilliard Equation and the Model of Thomas and Windle. Int. J. Multiscale Comput. Eng. 2009, 7, 523–543. [Google Scholar] [CrossRef]
- Athukorallage, B.; Iyer, R. On a two-point boundary value problem for the 2-D Navier-Stokes equations arising from capillary effect. Math. Model. Nat. Phenom. 2020, 15, 17. [Google Scholar]
- Wu, P.K.; Zhang, H.; Nikolov, A.; Wasan, D. Rise of the main meniscus in rectangular capillaries: Experiments and modeling. J. Colloid Interface Sci. 2016, 461, 195. [Google Scholar] [PubMed]
- Durán-Ramírez, V.M.; Muñoz-Maciel, J.; Casillas-Rodríguez, F.J.; Mora-Gonzalez, M.; Peña-Lecona, F.G. Exact Equations for the Back and Effective Focal Lengths of a Plano-Concave Thick Lens. Optics 2024, 5, 452–464. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Long, Y.; Zhang, X.; Wei, L.; Dai, B.; Zhang, D. Theoretical Model of Curved Liquid Surface in the Microholes for Molding Microlenses. Optics 2025, 6, 13. https://doi.org/10.3390/opt6020013
Shi Y, Long Y, Zhang X, Wei L, Dai B, Zhang D. Theoretical Model of Curved Liquid Surface in the Microholes for Molding Microlenses. Optics. 2025; 6(2):13. https://doi.org/10.3390/opt6020013
Chicago/Turabian StyleShi, Yuyang, Yan Long, Xuhui Zhang, Li Wei, Bo Dai, and Dawei Zhang. 2025. "Theoretical Model of Curved Liquid Surface in the Microholes for Molding Microlenses" Optics 6, no. 2: 13. https://doi.org/10.3390/opt6020013
APA StyleShi, Y., Long, Y., Zhang, X., Wei, L., Dai, B., & Zhang, D. (2025). Theoretical Model of Curved Liquid Surface in the Microholes for Molding Microlenses. Optics, 6(2), 13. https://doi.org/10.3390/opt6020013





