Acetone Absorption Cross-Section in the Near-Infrared of the Methyl Stretch Overtone and Application for Analysis of Human Breath
Abstract
1. Introduction
2. Theoretical Basis
2.1. Description of Spectral Measurement with CRDS
2.2. Retrieving Concentrations from Absorption Measurements: Analysis of a Gas Mixture
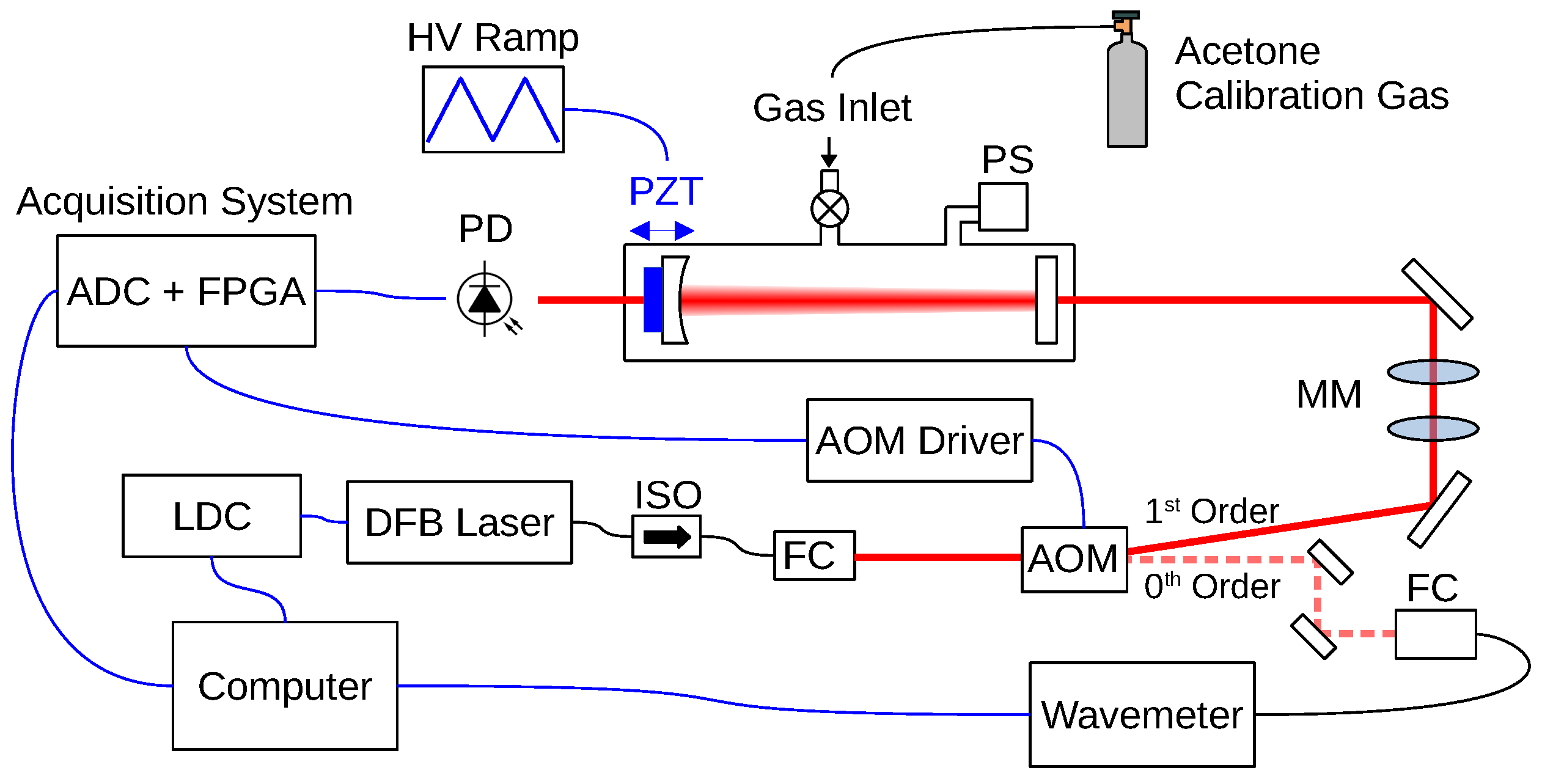
3. Experimental Setup and Methods
3.1. Experimental Apparatus
3.2. Scan of the Wavelength
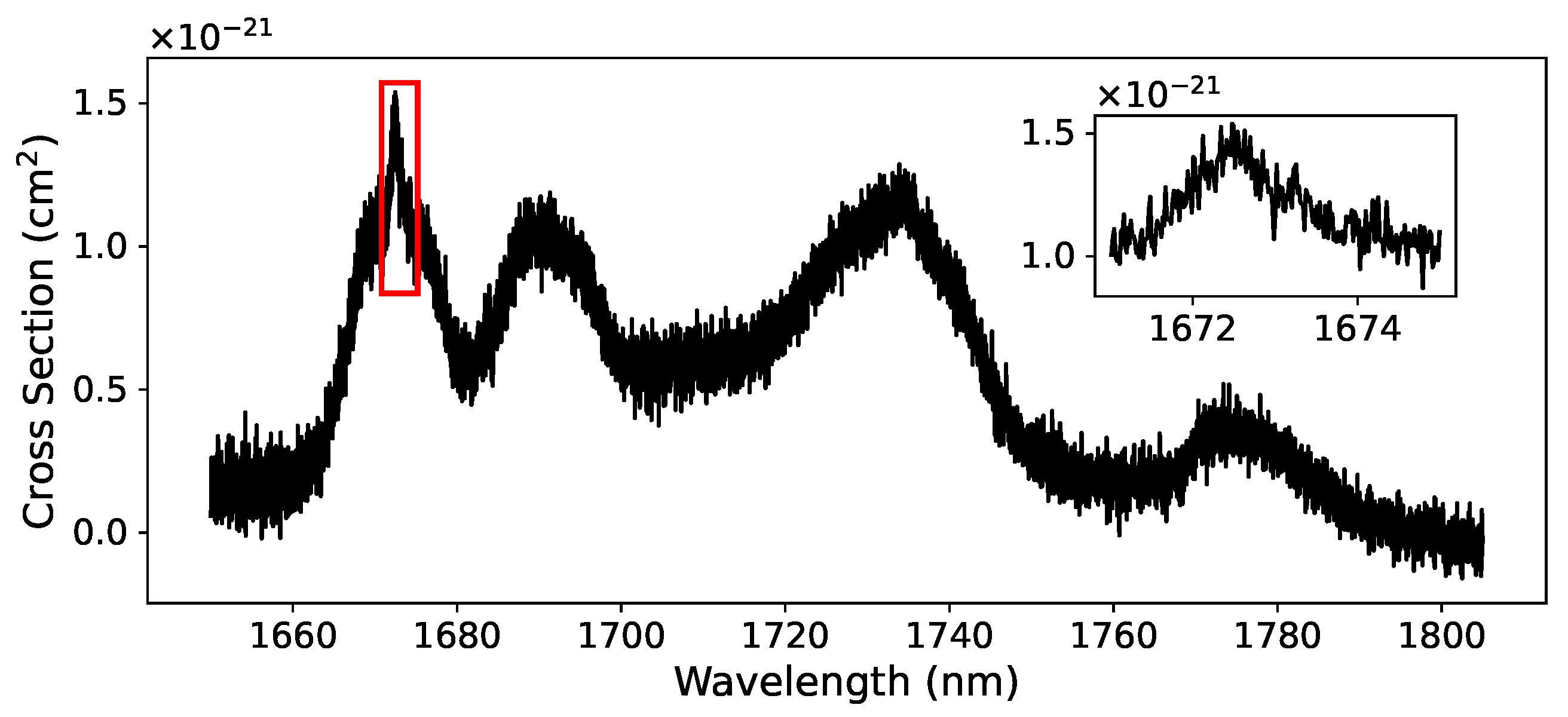
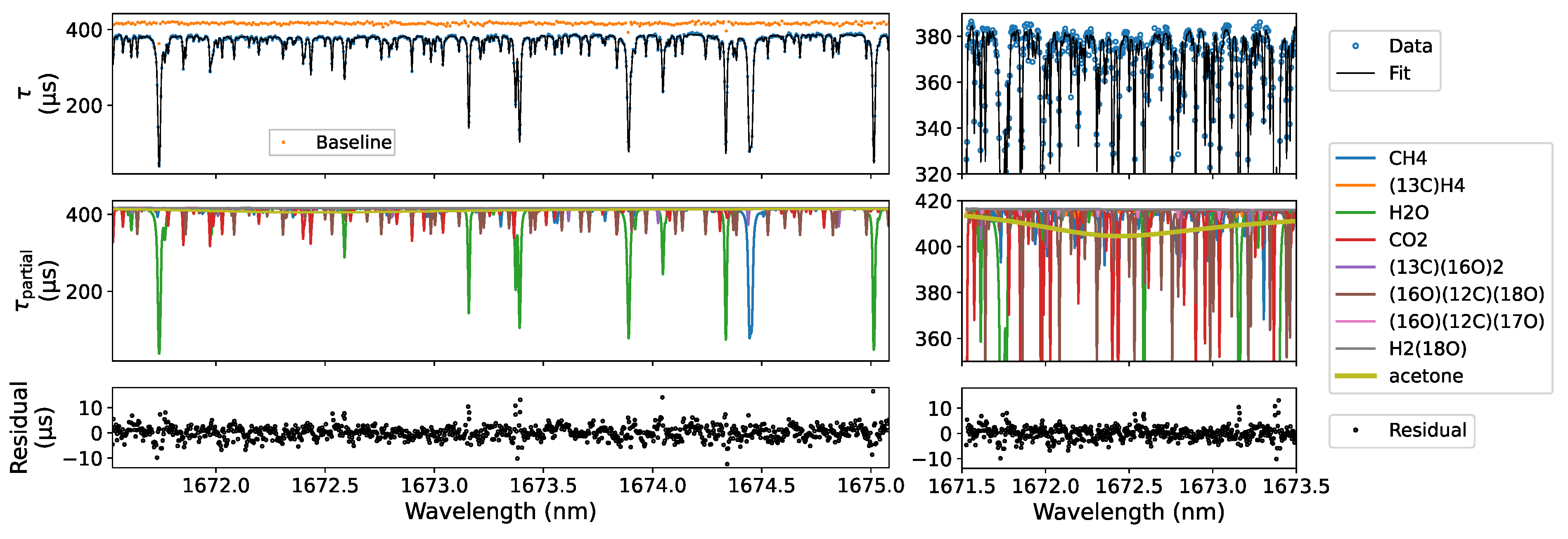
3.3. Acetone NIR Absorption Characterization
4. Results
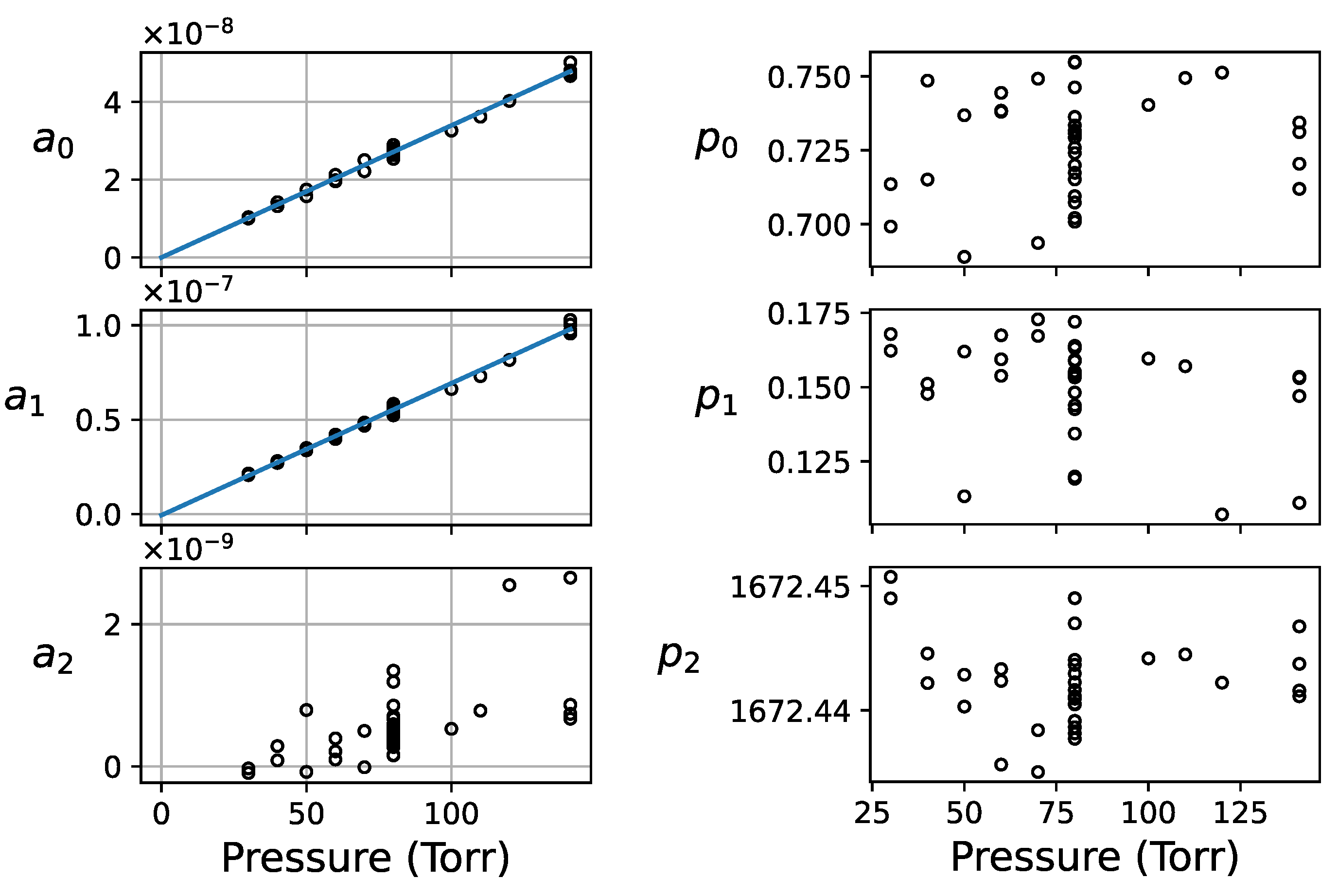
4.1. Pressure Dependence of the NIR Acetone Absorption
Absorption Linearity in the Range of 30–500 Torr
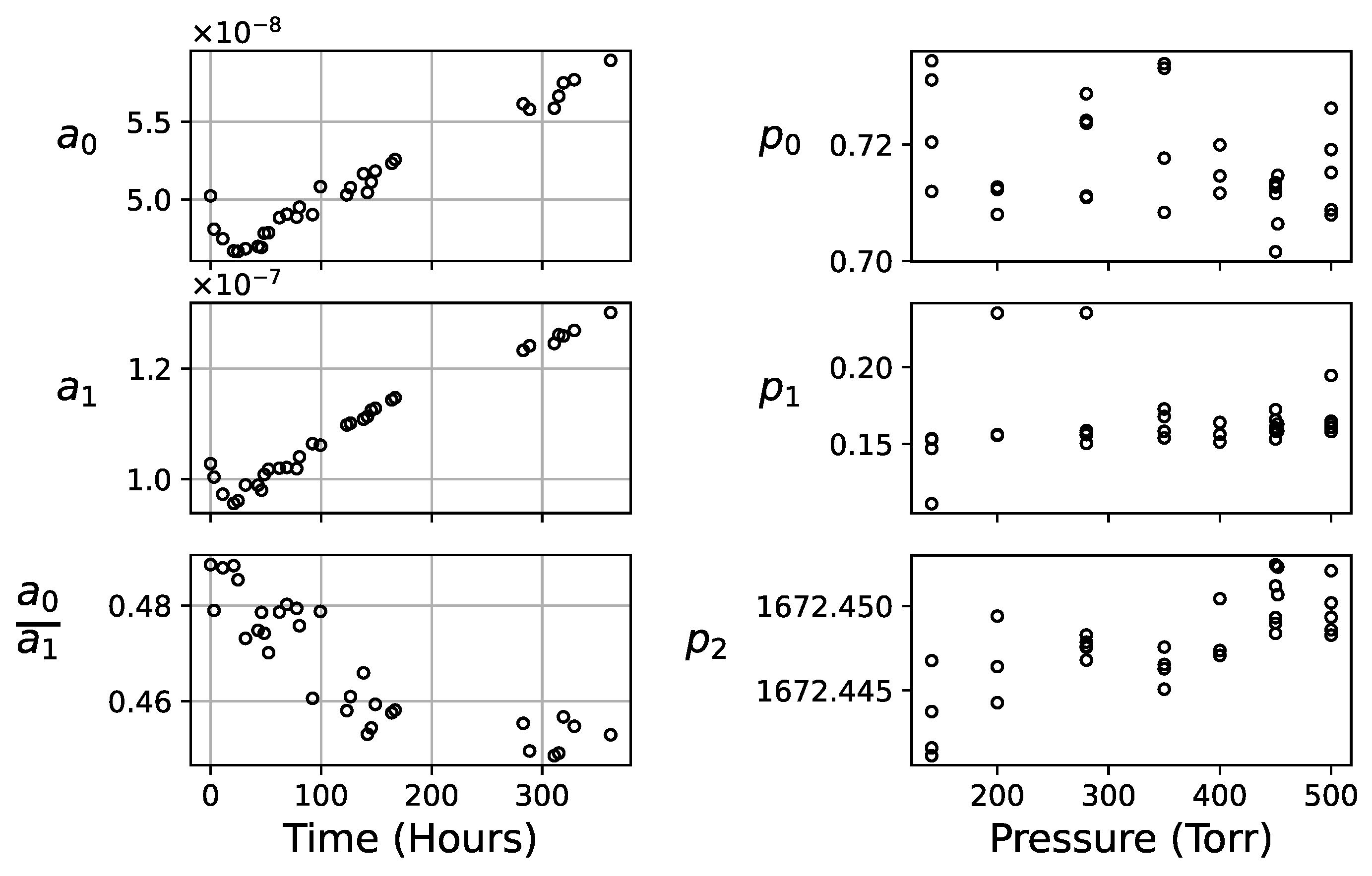
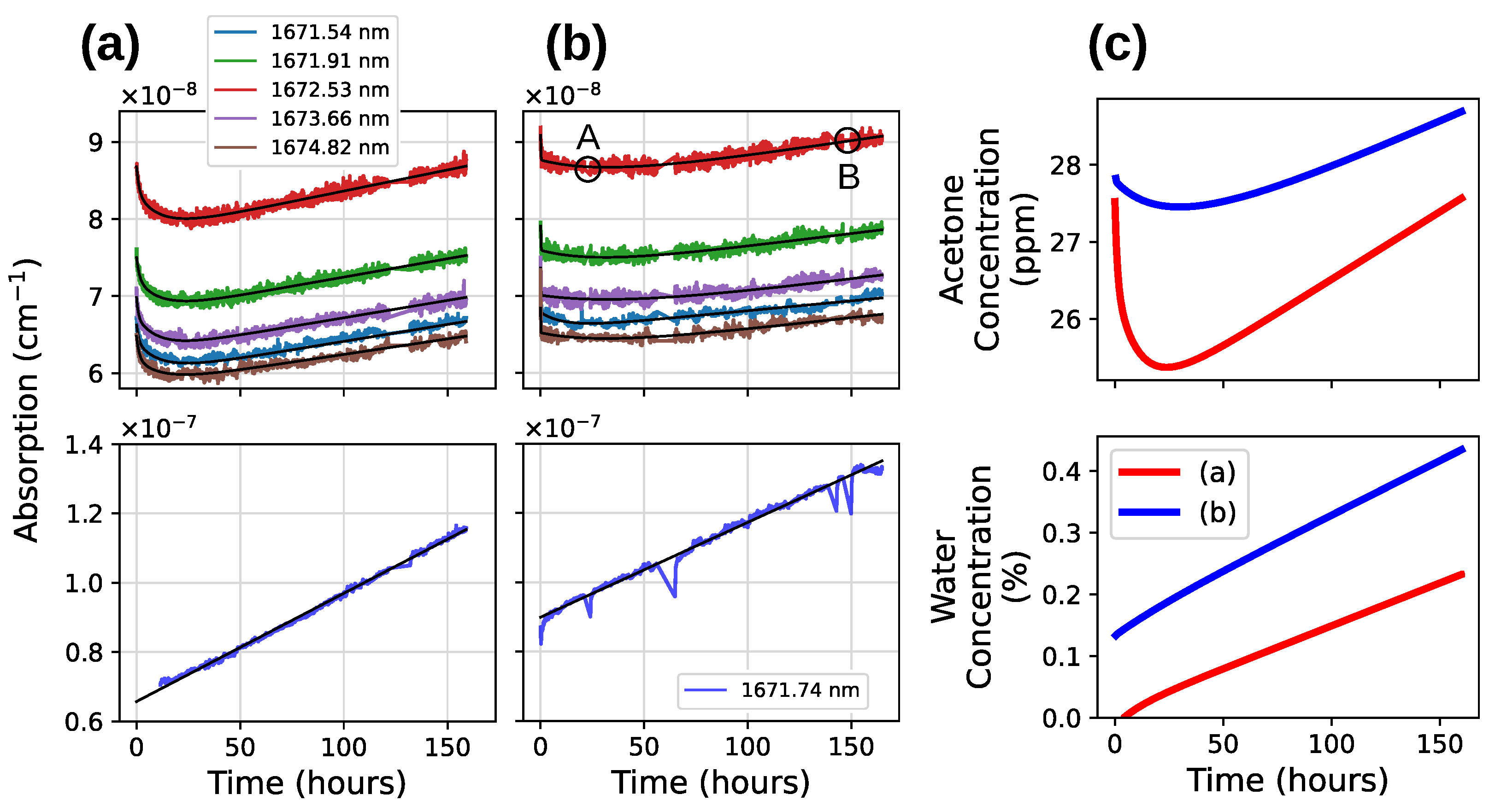
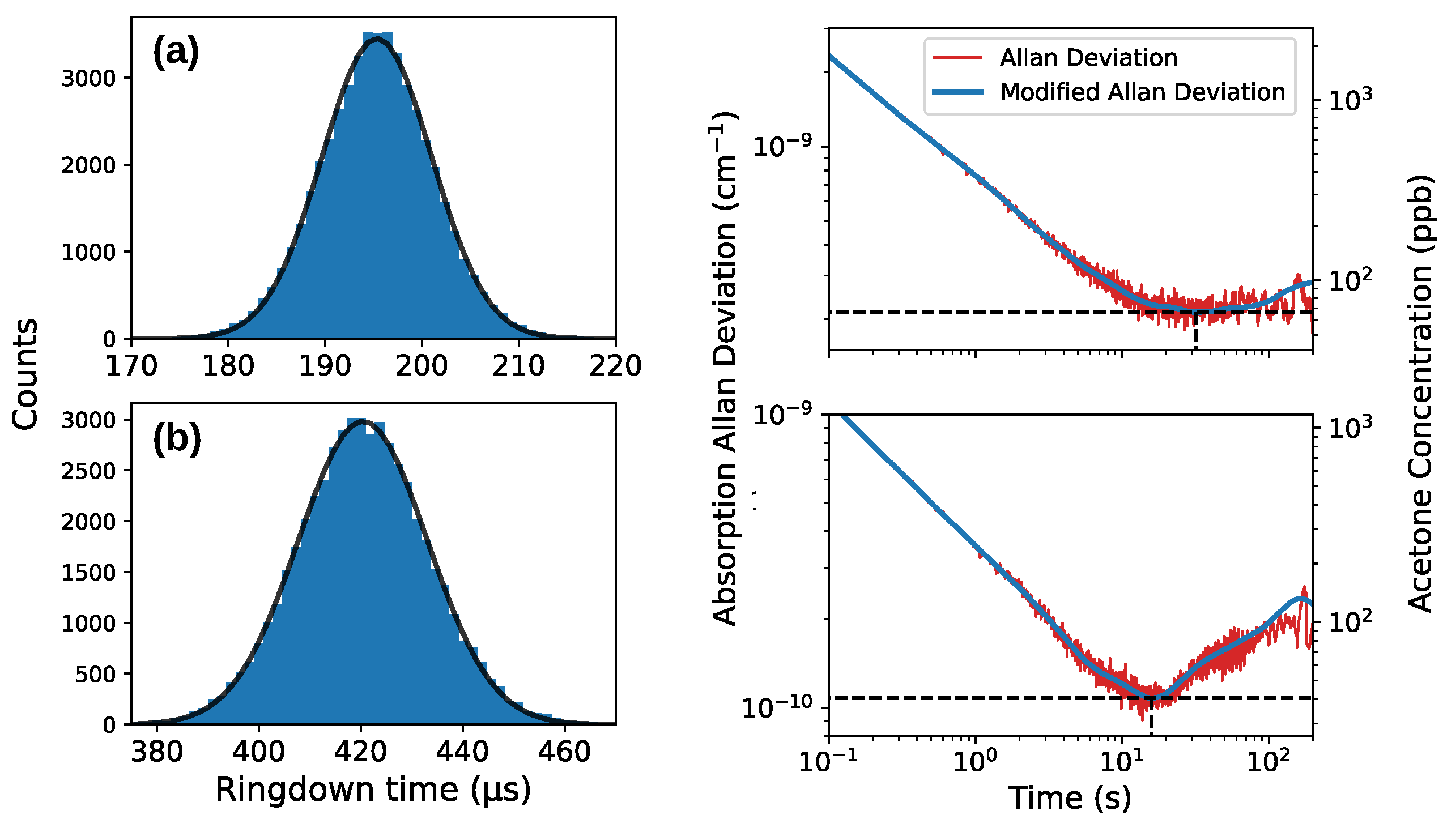
4.2. Drift of the Acetone Absorption
4.3. Determination of Model Coefficients
| Coefficient | Value | Uncertainty | Unit |
|---|---|---|---|
| 0.002 | nm | ||
| 0.002 | unitless | ||
| nm |
4.4. Measurements with Diluted Breath Samples and Breath Dilution Procedure
4.5. Detection Limit
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Wavelength Measurement
Interferometric Wavemeter
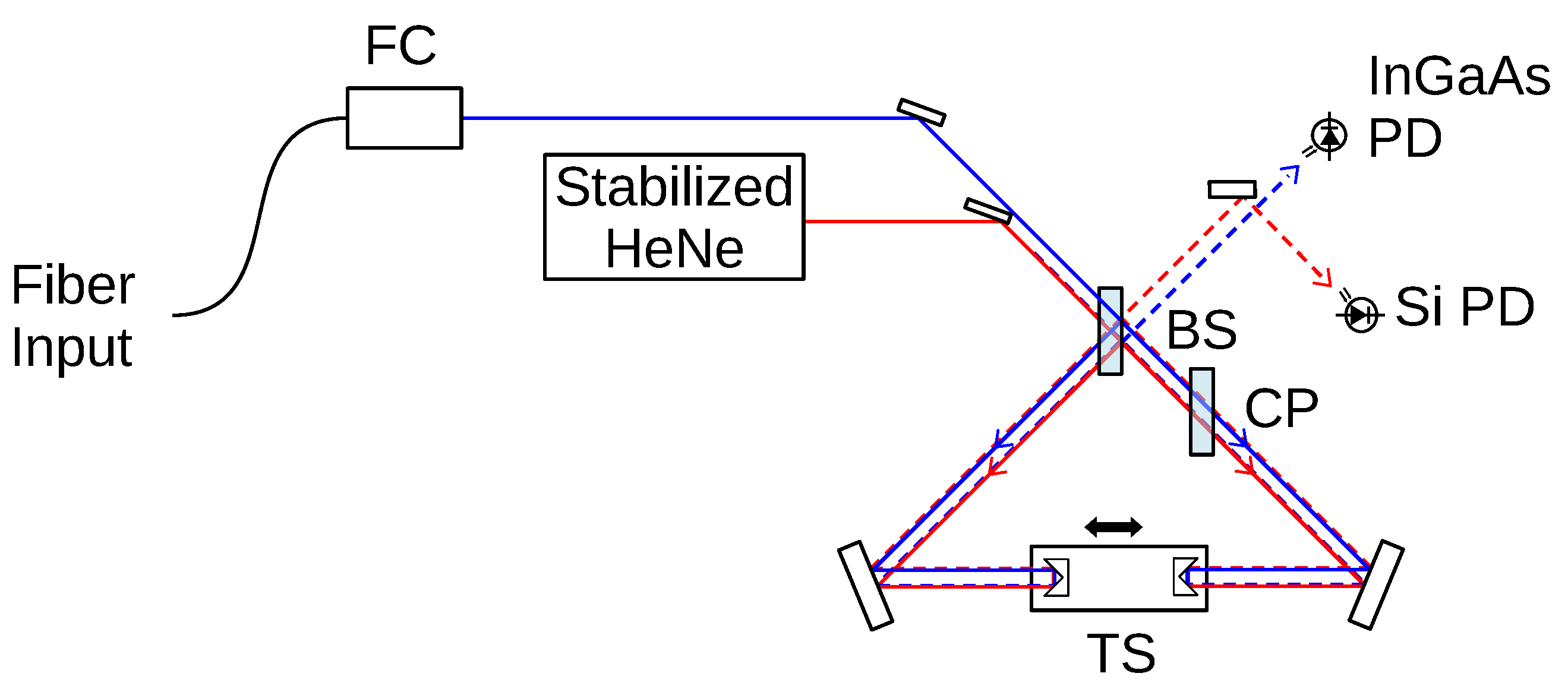
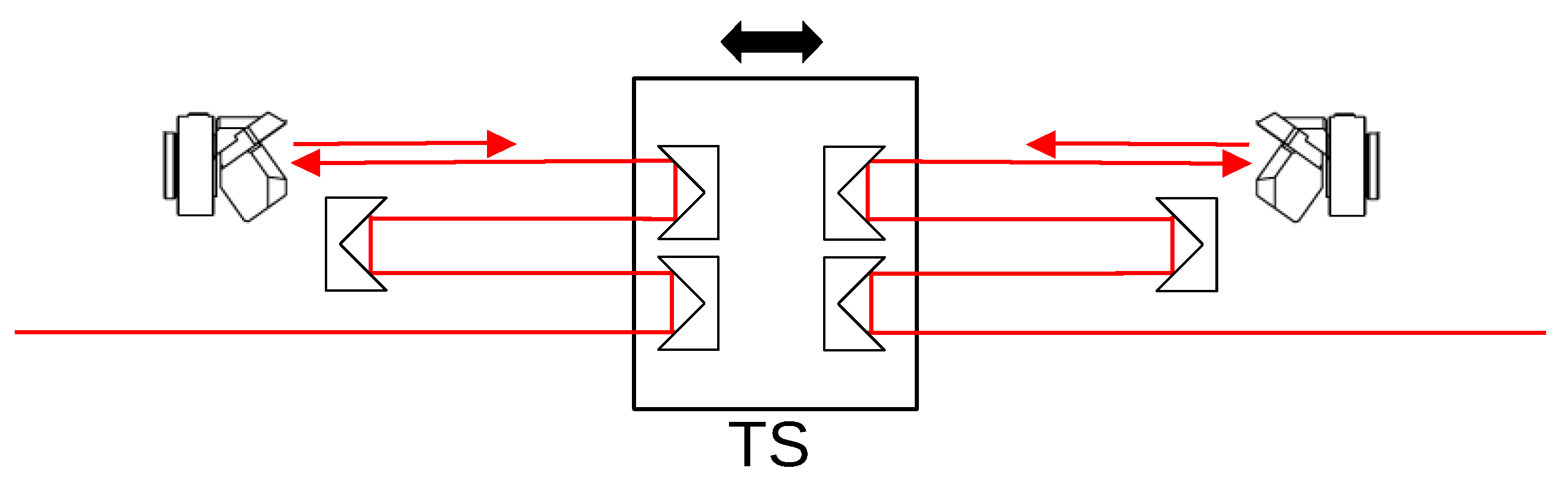
Appendix B. Choice of Weighting Function
Appendix C. Simulation of Fitting Procedure
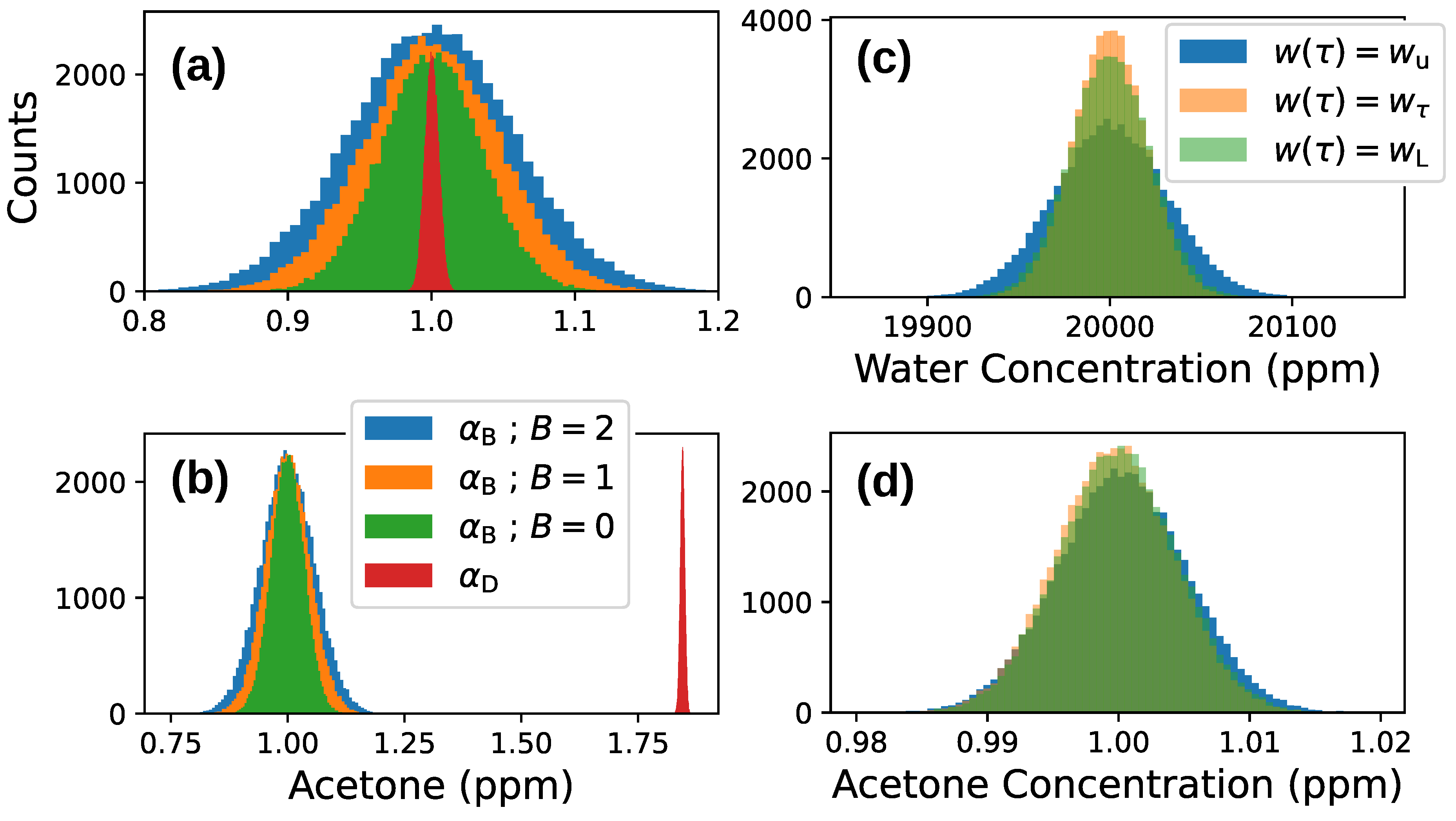
| Species | Relative Error | Concentration |
|---|---|---|
| (ppm) | ||
| CH4 | 0.26% | 2 |
| 13CH4 | 21% | 0.02246 |
| H2O * | 0.10% | 23,000 |
| CO2 | 0.33% | 32,000 |
| 13CO2 | 1.2% | 359.36 |
| CO(18O) | 0.32% | 128.32 |
| CO(17O) | 7.9% | 24.0 |
| H2(18O) | 9.6% | 46.0 |
| Acetone * | 0.45% | 1.0 |
| Model | Acetone Relative Error |
|---|---|
| 0.45% | |
| 3.3% | |
| 4.6% | |
| 5.5% |
| Weight Function | CH4 | H2O | CO2 | CO(18O) | Acetone |
|---|---|---|---|---|---|
| 2.006 | 20,051.7 | 32,080.3 | 128.7 | 1.0860 | |
| (Unweighted) | 4.5% | 2.6% | 5.5% | 5.4% | 7.6% |
| 1.999 | 19,953.1 | 31,955.6 | 128.0 | 0.9125 | |
| 4.4% | 1.7% | 5.4% | 5.3% | 8.3% | |
| 2.002 | 19,991.2 | 32,005.1 | 128.3 | 0.9987 | |
| 4.4% | 1.8% | 5.4% | 5.3% | 7.6% | |
| 2.002 | 19,996.5 | 32,012.5 | 128.4 | 1.0087 | |
| 4.5% | 1.9% | 5.4% | 5.3% | 7.5% | |
| Exact | 2.0 | 20,000.0 | 32,000.0 | 128.32 | 1.0 |
References
- Wang, Z.; Wang, C. Is breath acetone a biomarker of diabetes? A historical review on breath acetone measurements. J. Breath Res. 2013, 7, 037109. [Google Scholar] [CrossRef]
- Marcondes-Braga, F.G.; Gioli-Pereira, L.; Bernardez-Pereira, S.; Batista, G.L.; Mangini, S.; Issa, V.S.; Fernandes, F.; Bocchi, E.A.; Ayub-Ferreira, S.M.; Mansur, A.J.; et al. Exhaled breath acetone for predicting cardiac and overall mortality in chronic heart failure patients. ESC Heart Fail. 2020, 7, 1744–1752. [Google Scholar] [CrossRef]
- Marcondes-Braga, F.G.; Gutz, I.G.R.; Batista, G.L.; Saldiva, P.H.N.; Ayub-Ferreira, S.M.; Issa, V.S.; Mangini, S.; Bocchi, E.A.; Bacal, F. Exhaled acetone as a new biomaker of heart failure severity. Chest 2012, 142, 457–466. [Google Scholar] [CrossRef]
- Owen, O.E.; Trapp, V.E.; Skutches, C.L.; Mozzoli, M.A.; Hoeldtke, R.D.; Boden, G.; Reichard, G.A., Jr. Acetone Metabolism During Diabetic Ketoacidosis. Diabetes 1982, 31, 242–248. [Google Scholar] [CrossRef]
- Stafstrom, C.E.; Rho, J.M. Epilepsy and the Ketogenic Diet; Springer Science and Business Media: New York, NY, USA, 2004. [Google Scholar]
- Singh, H.B.; O’Hara, D.; Herlth, D.; Sachse, W.; Blake, D.R.; Bradshaw, J.D.; Kanakidou, M.; Crutzen, P.J. Acetone in the atmosphere: Distribution, sources, and sinks. J. Geophys. Res. Atmos. 1994, 99, 1805–1819. [Google Scholar] [CrossRef]
- Schade, G.W.; Goldstein, A.H. Seasonal measurements of acetone and methanol: Abundances and implications for atmospheric budgets. Glob. Biogeochem. Cycles 2006, 20, GB1011. [Google Scholar] [CrossRef]
- Snyder, L.E.; Lovas, F.J.; Mehringer, D.M.; Miao, N.Y.; Kuan, Y.J.; Hollis, J.M.; Jewell, P.R. Confirmation of Interstellar Acetone. Astrophys. J. 2002, 578, 245. [Google Scholar] [CrossRef]
- Lykke, J.M.; Coutens, A.; Jørgensen, J.K.; van der Wiel, M.H.D.; Garrod, R.T.; Müller, H.S.P.; Bjerkeli, P.; Bourke, T.L.; Calcutt, H.; Drozdovskaya, M.N.; et al. The ALMA-PILS survey: First detections of ethylene oxide, acetone and propanal toward the low-mass protostar IRAS 16293-2422. Astron. Astrophys. 2017, 597, A53. [Google Scholar] [CrossRef]
- Kosterev, A.A.; Malinovsky, A.L.; Tittel, F.K.; Gmachl, C.; Capasso, F.; Sivco, D.L.; Baillargeon, J.N.; Hutchinson, A.L.; Cho, A.Y. Cavity ringdown spectroscopic detection of nitric oxide with a continuous-wave quantum-cascade laser. Appl. Opt. 2001, 40, 5522–5529. [Google Scholar] [CrossRef]
- Manne, J.; Sukhorukov, O.; Jäger, W.; Tulip, J. Pulsed quantum cascade laser-based cavity ring-down spectroscopy for ammonia detection in breath. Appl. Opt. 2006, 45, 9230–9237. [Google Scholar] [CrossRef]
- Wang, C.; Surampudi, A.B. An acetone breath analyzer using cavity ringdown spectroscopy: An initial test with human subjects under various situations. Meas. Sci. Technol. 2008, 19, 105604. [Google Scholar] [CrossRef]
- Ghorbani, R.; Schmidt, F.M. ICL-based TDLAS sensor for real-time breath gas analysis of carbon monoxide isotopes. Opt. Express 2017, 25, 12743–12752. [Google Scholar] [CrossRef]
- Philippe, L.C.; Hanson, R.K. Laser diode wavelength-modulation spectroscopy for simultaneous measurement of temperature, pressure, and velocity in shock-heated oxygen flows. Appl. Opt. 1993, 32, 6090–6103. [Google Scholar] [CrossRef]
- Xia, J.; Zhu, F.; Kolomenskii, A.A.; Bounds, J.; Zhang, S.; Amani, M.; Fernyhough, L.J.; Schuessler, H.A. Sensitive acetone detection with a mid-IR interband cascade laser and wavelength modulation spectroscopy. OSA Contin. 2019, 2, 640–654. [Google Scholar] [CrossRef]
- Thorpe, M.J.; Balslev-Clausen, D.; Kirchner, M.S.; Ye, J. Cavity-enhanced optical frequency comb spectroscopy: Application to human breath analysis. Opt. Express 2008, 16, 2387–2397. [Google Scholar] [CrossRef]
- Wang, C.; Sahay, P. Breath Analysis Using Laser Spectroscopic Techniques: Breath Biomarkers, Spectral Fingerprints, and Detection Limits. Sensors 2009, 9, 8230–8262. [Google Scholar] [CrossRef]
- Stacewicz, T.; Bielecki, Z.; Wojtas, J.; Magryta, P.; Mikolajczyk, J.; Szabra, D. Detection of disease markers in human breath with laser absorption spectroscopy. Opto-Electron. Rev. 2016, 24, 82–94. [Google Scholar] [CrossRef]
- Xia, J.; Zhu, F.; Bounds, J.; Aluauee, E.; Kolomenskii, A.; Dong, Q.; He, J.; Meadows, C.; Zhang, S.; Schuessler, H. Spectroscopic trace gas detection in air-based gas mixtures: Some methods and applications for breath analysis and environmental monitoring. J. Appl. Phys. 2022, 131, 220901. [Google Scholar] [CrossRef]
- Pangerl, J.; Moser, E.; Müller, M.; Weigl, S.; Jobst, S.; Rück, T.; Bierl, R.; Matysik, F.M. A sub-ppbv-level Acetone and Ethanol Quantum Cascade Laser Based Photoacoustic Sensor—Characterization and Multi-Component Spectra Recording in Synthetic Breath. Photoacoustics 2023, 30, 100473. [Google Scholar] [CrossRef]
- Szabó, A.; Ruzsanyi, V.; Unterkofler, K.; Mohácsi, A.; Tuboly, E.; Boros, M.; Szabó, G.; Hinterhuber, H.; Amann, A. Exhaled methane concentration profiles during exercise on an ergometer. J. Breath Res. 2015, 9, 016009. [Google Scholar] [CrossRef]
- Wang, C.; Mbi, A. A new acetone detection device using cavity ringdown spectroscopy at 266 nm: Evaluation of the instrument performance using acetone sample solutions. Meas. Sci. Technol. 2007, 18, 2731. [Google Scholar] [CrossRef]
- Cias, P.; Wang, C.; Dibble, T.S. Absorption Cross-Sections of the C—H Overtone of Volatile Organic Compounds: 2 Methyl-1,3-Butadiene (Isoprene), 1,3-Butadiene, and 2,3-Dimethyl-1,3-Butadiene. Appl. Spectrosc. 2007, 61, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Harrison, J.J.; Humpage, N.; Allen, N.D.; Waterfall, A.M.; Bernath, P.F.; Remedios, J.J. Mid-infrared absorption cross sections for acetone (propanone). J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 457–464. [Google Scholar] [CrossRef]
- Sharpe, S.W.; Johnson, T.J.; Sams, R.L.; Chu, P.M.; Rhoderick, G.C.; Johnson, P.A. Gas-Phase Databases for Quantitative Infrared Spectroscopy. Appl. Spectrosc. 2004, 58, 1452–1461. [Google Scholar] [CrossRef] [PubMed]
- Johnson, T.J.; Hughey, K.D.; Blake, T.A.; Sharpe, S.W.; Myers, T.L.; Sams, R.L. Confirmation of PNNL Quantitative Infrared Cross-Sections for Isobutane. J. Phys. Chem. A 2021, 125, 3793–3801. [Google Scholar] [CrossRef] [PubMed]
- Romanini, D.; Kachanov, A.; Sadeghi, N.; Stoeckel, F. CW cavity ring down spectroscopy. Chem. Phys. Lett. 1997, 264, 316–322. [Google Scholar] [CrossRef]
- Zalicki, P.; Zare, R.N. Cavity ring-down spectroscopy for quantitative absorption measurements. J. Chem. Phys. 1995, 102, 2708–2717. [Google Scholar] [CrossRef]
- Karman, T.; Gordon, I.E.; van der Avoird, A.; Baranov, Y.I.; Boulet, C.; Drouin, B.J.; Groenenboom, G.C.; Gustafsson, M.; Hartmann, J.M.; Kurucz, R.L.; et al. Update of the HITRAN collision-induced absorption section. Icarus 2019, 328, 160–175. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hargreaves, E.R.; Hashemi, R.; Karlovets, E.V.; Skinner, F.M.; Conway, E.K.; Hill, C.; Kochanov, R.V.; Tan, Y.; et al. The HITRAN2020 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- Laane, J. Chapter Optimal Signal Processing in Cavity Ring-Down Spectroscopy. In Frontiers of Molecular Spectroscopy, 1st ed.; Laane, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Istratov, A.A.; Vyvenko, O.F. Exponential analysis in physical phenomena. Rev. Sci. Instruments 1999, 70, 1233–1257. [Google Scholar] [CrossRef]
- Wang, C.; Scherrer, S.T.; Hossain, D. Measurements of Cavity Ringdown Spectroscopy of Acetone in the Ultraviolet and Near-Infrared Spectral Regions: Potential for Development of a Breath Analyzer. Appl. Spectrosc. 2004, 58, 784–791. [Google Scholar] [CrossRef] [PubMed]
- Kochanov, R.; Gordon, I.; Rothman, L.; Wcisło, P.; Hill, C.; Wilzewski, J. HITRAN Application Programming Interface (HAPI): A comprehensive approach to working with spectroscopic data. J. Quant. Spectrosc. Radiat. Transf. 2016, 177, 15–30. [Google Scholar] [CrossRef]
- Huang, H.; Lehmann, K.K. Long-term stability in continuous wave cavity ringdown spectroscopy experiments. Appl. Opt. 2010, 49, 1378–1387. [Google Scholar] [CrossRef] [PubMed]
- Sandorfy, C. Overtones and Combination Tones: Application to the Study of Molecular Associations. In Infrared and Raman Spectroscopy of Biological Molecules; Theophanides, T.M., Ed.; Springer: Dordrecht, The Netherlands, 1979; pp. 305–318. [Google Scholar]
- Weyer, L.; Lo, S.C. Spectra–Structure Correlations in the Near-Infrared. In Handbook of Vibrational Spectroscopy; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Harrison, J.J.; Allen, N.D.; Bernath, P.F. Infrared absorption cross sections for acetone (propanone) in the 3µm region. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 53–58. [Google Scholar] [CrossRef]
- Henry, B.R. The local mode model and overtone spectra: A probe of molecular structure and conformation. Accounts Chem. Res. 1987, 20, 429–435. [Google Scholar] [CrossRef]
- Peale, R.E.; Muravjov, A.V.; Fredricksen, C.J.; Boreman, G.D.; Saxena, H.; Braunstein, G.; Vaks, V.L.; Maslovsky, A.V.; Nikifirov, S.D. Spectral signatures of acetone vapor from ultraviolet to millimeter wavelengths. Int. J. High Speed Electron. Syst. 2008, 18, 627–637. [Google Scholar] [CrossRef]
- Hanazaki, I.; Baba, M.; Nagashima, U. Orientational site splitting of methyl C-H overtones in acetone and acetaldehyde. J. Phys. Chem. 1985, 89, 5637–5645. [Google Scholar] [CrossRef]
- Penndorf, R. Tables of the Refractive Index for Standard Air and the Rayleigh Scattering Coefficient for the Spectral Region between 0.2 and 20.0 μ and Their Application to Atmospheric Optics. J. Opt. Soc. Am. 1957, 47, 176–182. [Google Scholar] [CrossRef]
- Levine, I. Quantum Chemistry; Pearson Advanced Chemistry Series; Pearson: London, UK, 2014; p. 73. [Google Scholar]
- Denzer, W.; Hancock, G.; Islam, M.; Langley, C.E.; Peverall, R.; Ritchie, G.A.D.; Taylor, D. Trace species detection in the near infrared using Fourier transform broadband cavity enhanced absorption spectroscopy: Initial studies on potential breath analytes. Analyst 2011, 136, 801–806. [Google Scholar] [CrossRef]
- Mahdi, T.; Ahmad, A.; Nasef, M.M.; Ripin, A. State-of-the-Art Technologies for Separation of Azeotropic Mixtures. Sep. Purif. Rev. 2015, 44, 308–330. [Google Scholar] [CrossRef]
- Duan, S.X.; Jayne, J.T.; Davidovits, P.; Worsnop, D.R.; Zahniser, M.S.; Kolb, C.E. Uptake of gas-phase acetone by water surfaces. J. Phys. Chem. 1993, 97, 2284–2288. [Google Scholar] [CrossRef]
- Chen, J.; Hsiung, G.; Hsu, Y.; Chang, S.; Chen, C.; Lee, W.; Ku, J.; Chan, C.; Joung, L.; Chou, W. Water adsorption–desorption on aluminum surface. Appl. Surf. Sci. 2001, 169–170, 679–684. [Google Scholar] [CrossRef]
- Coutinho, K.; Saavedra, N.; Canuto, S. Theoretical analysis of the hydrogen bond interaction between acetone and water. J. Mol. Struct. 1999, 466, 69–75. [Google Scholar] [CrossRef]
- Max, J.J.; Chapados, C. Infrared spectroscopy of acetone–water liquid mixtures. I. Factor analysis. J. Chem. Phys. 2003, 119, 5632–5643. [Google Scholar] [CrossRef]
- Max, J.J.; Chapados, C. Infrared spectroscopy of acetone–water liquid mixtures. II. Molecular model. J. Chem. Phys. 2004, 120, 6625–6641. [Google Scholar] [CrossRef]
- Li, G.; Liu, Y.; Jiao, Y.; Zhang, Z.; Wu, Y.; Zhang, X.; Zhao, H.; Li, J.; Song, Y.; Li, Q.; et al. Mid-infrared acetone sensor for exhaled gas using FWA-LSSVM and empirical mode decomposition algorithm. Measurement 2023, 213, 112716. [Google Scholar] [CrossRef]
- Bastide, G.M.G.B.H.; Remund, A.L.; Oosthuizen, D.N.; Derron, N.; Gerber, P.A.; Weber, I.C. Handheld device quantifies breath acetone for real-life metabolic health monitoring. Sens. Diagn. 2023, 2, 918–928. [Google Scholar] [CrossRef]
- Kwaśny, M.; Bombalska, A. Optical Methods of Methane Detection. Sensors 2023, 23, 2834. [Google Scholar] [CrossRef]
- Shao, L.; Mei, J.; Chen, J.; Tan, T.; Wang, G.; Liu, K.; Gao, X. Simultaneous Sensitive Determination of δ13C, δ18O, and δ17O in Human Breath CO2 Based on ICL Direct Absorption Spectroscopy. Sensors 2022, 22, 1527. [Google Scholar] [CrossRef]
- Bakkaloglu, S.; Lowry, D.; Fisher, R.E.; Menoud, M.; Lanoisellé, M.; Chen, H.; Röckmann, T.; Nisbet, E.G. Stable isotopic signatures of methane from waste sources through atmospheric measurements. Atmos. Environ. 2022, 276, 119021. [Google Scholar] [CrossRef]
- Demtröder, W. Spectroscopic Instrumentation. In Laser Spectroscopy: Vol. 1 Basic Principles; Springer: Berlin/Heidelberg, Germany, 2008; pp. 99–233. [Google Scholar] [CrossRef]
- van Zee, R.D.; Hodges, J.T.; Looney, J.P. Pulsed, single-mode cavity ringdown spectroscopy. Appl. Opt. 1999, 38, 3951–3960. [Google Scholar] [CrossRef] [PubMed]

| Gas | Pre-Dil. | Post-Dil. | Expected | Deviation |
|---|---|---|---|---|
| Species | (ppm) | (ppm) | (%) | |
| CH4 | 7.34 | 6.74 | 6.32 | 6.57% |
| 0.092 | 0.088 | 0.080 | 11.6% | |
| H2O | 21,730 | 20,940 | 18,740 | 11.7% |
| CO2 | 31,400 | 28,600 | 27,000 | 5.8% |
| 344 | 300 | 296 | 2.7% | |
| 128.0 | 119.5 | 110.3 | 8.27% | |
| 24 | 24 | 21 | 17% | |
| 32 | 36 | 28 | 29% | |
| Acetone | 0.34 | 2.31 | 2.29 | 0.74% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bounds, J.; Aluauee, E.; Kolomenskii, A.; Schuessler, H. Acetone Absorption Cross-Section in the Near-Infrared of the Methyl Stretch Overtone and Application for Analysis of Human Breath. Optics 2025, 6, 9. https://doi.org/10.3390/opt6010009
Bounds J, Aluauee E, Kolomenskii A, Schuessler H. Acetone Absorption Cross-Section in the Near-Infrared of the Methyl Stretch Overtone and Application for Analysis of Human Breath. Optics. 2025; 6(1):9. https://doi.org/10.3390/opt6010009
Chicago/Turabian StyleBounds, James, Eshtar Aluauee, Alexandre Kolomenskii, and Hans Schuessler. 2025. "Acetone Absorption Cross-Section in the Near-Infrared of the Methyl Stretch Overtone and Application for Analysis of Human Breath" Optics 6, no. 1: 9. https://doi.org/10.3390/opt6010009
APA StyleBounds, J., Aluauee, E., Kolomenskii, A., & Schuessler, H. (2025). Acetone Absorption Cross-Section in the Near-Infrared of the Methyl Stretch Overtone and Application for Analysis of Human Breath. Optics, 6(1), 9. https://doi.org/10.3390/opt6010009






