The Triplet–Triplet Annihilation Efficiency of Some 9,10-Substituted Diphenyl Anthracene Variants—A Decisive Analysis from Kinetic Rate Constants
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Substituted DPA Structures and Basic Photophysical Characterization
3.1.1. Molecular Structures
3.1.2. Basic Absorption and Emission Properties
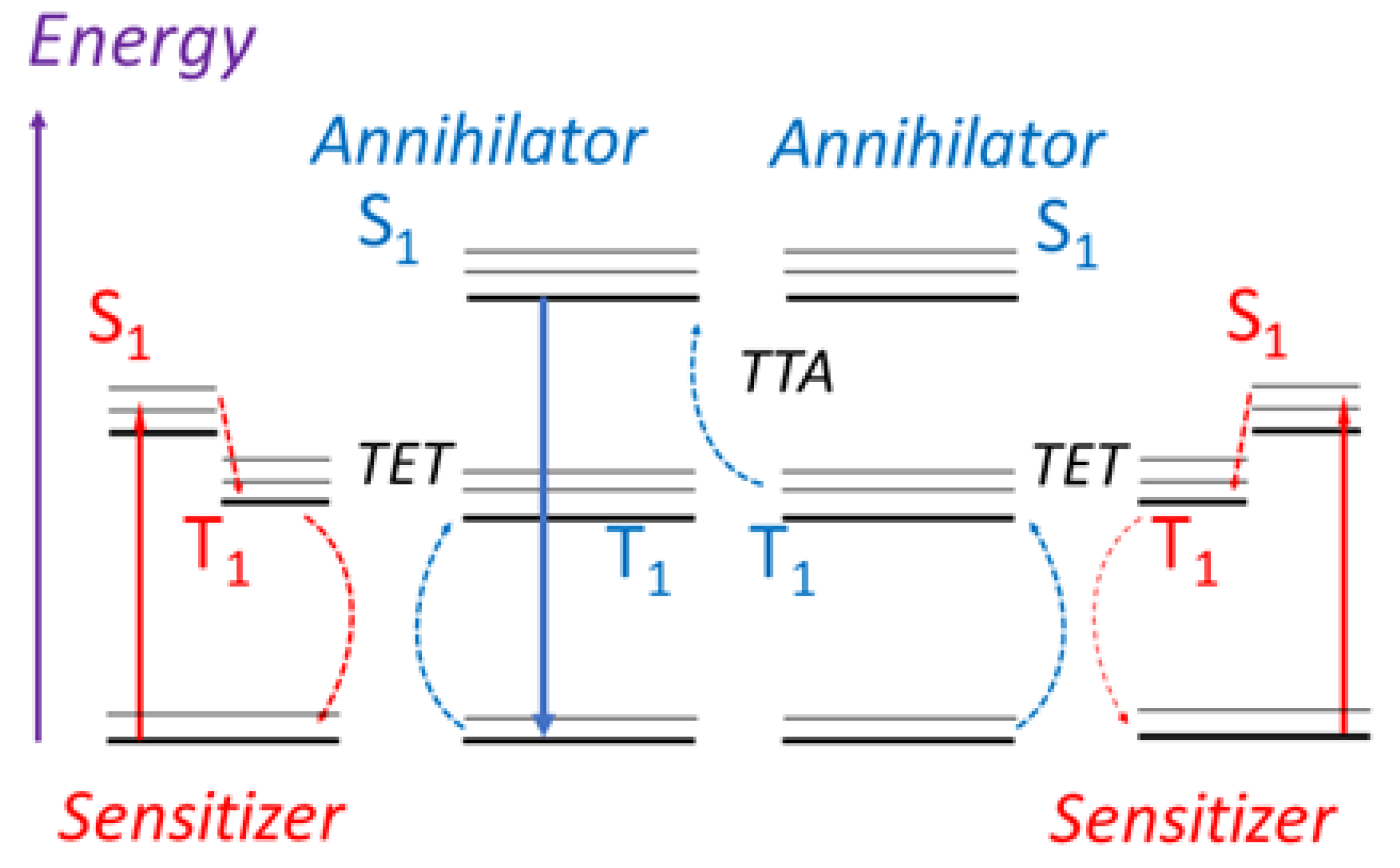
3.2. Delayed Fluorescence
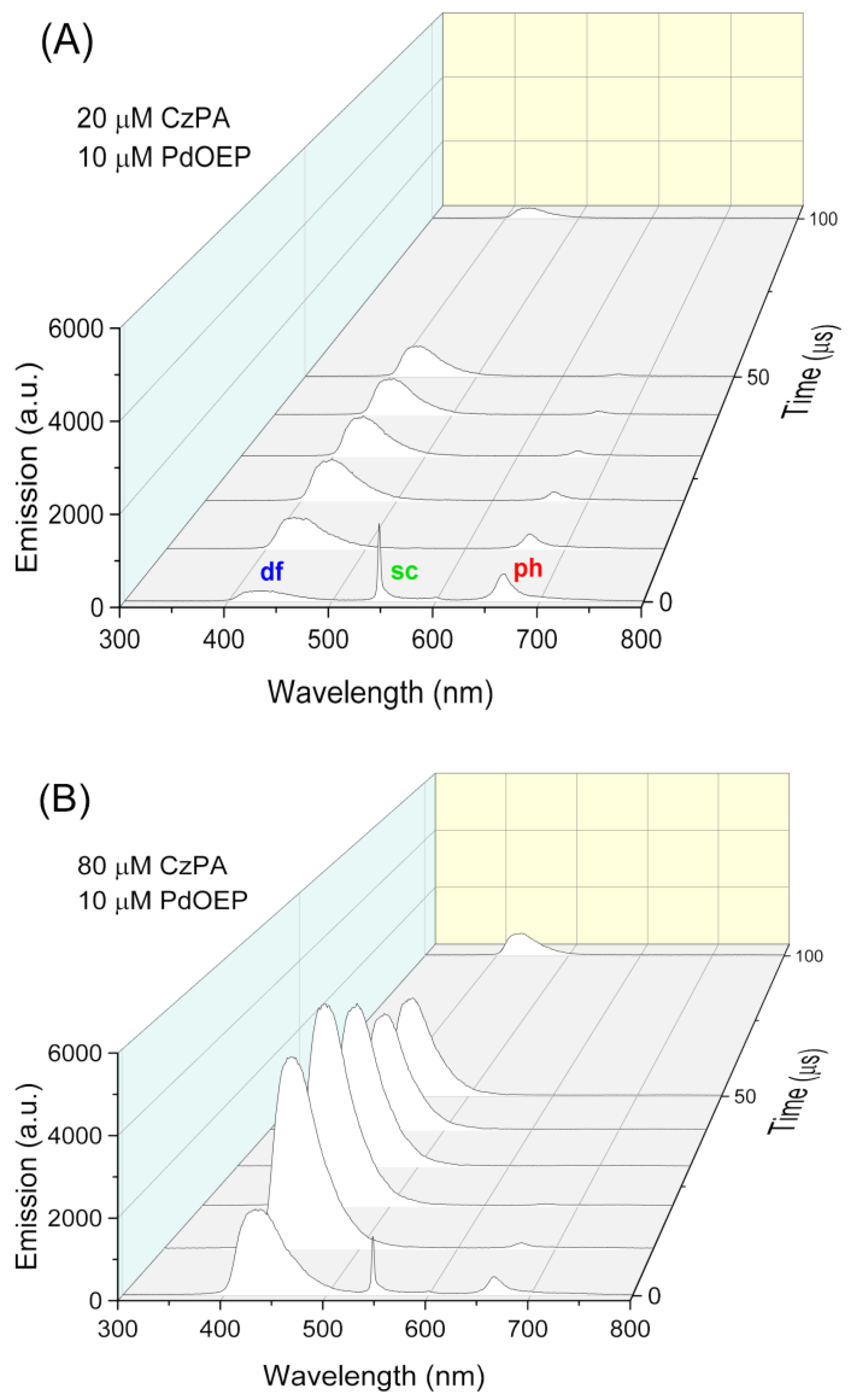
3.2.1. Time-Gated Measurements of Delayed Fluorescence
3.2.2. Quantifying the Triplet Energy Transfer Rate, kTET
3.2.3. Quantifying the TTA Rate and the Natural Quenching of the Annihilator
3.2.4. The Overall Efficiency of the TET and TTA Processes
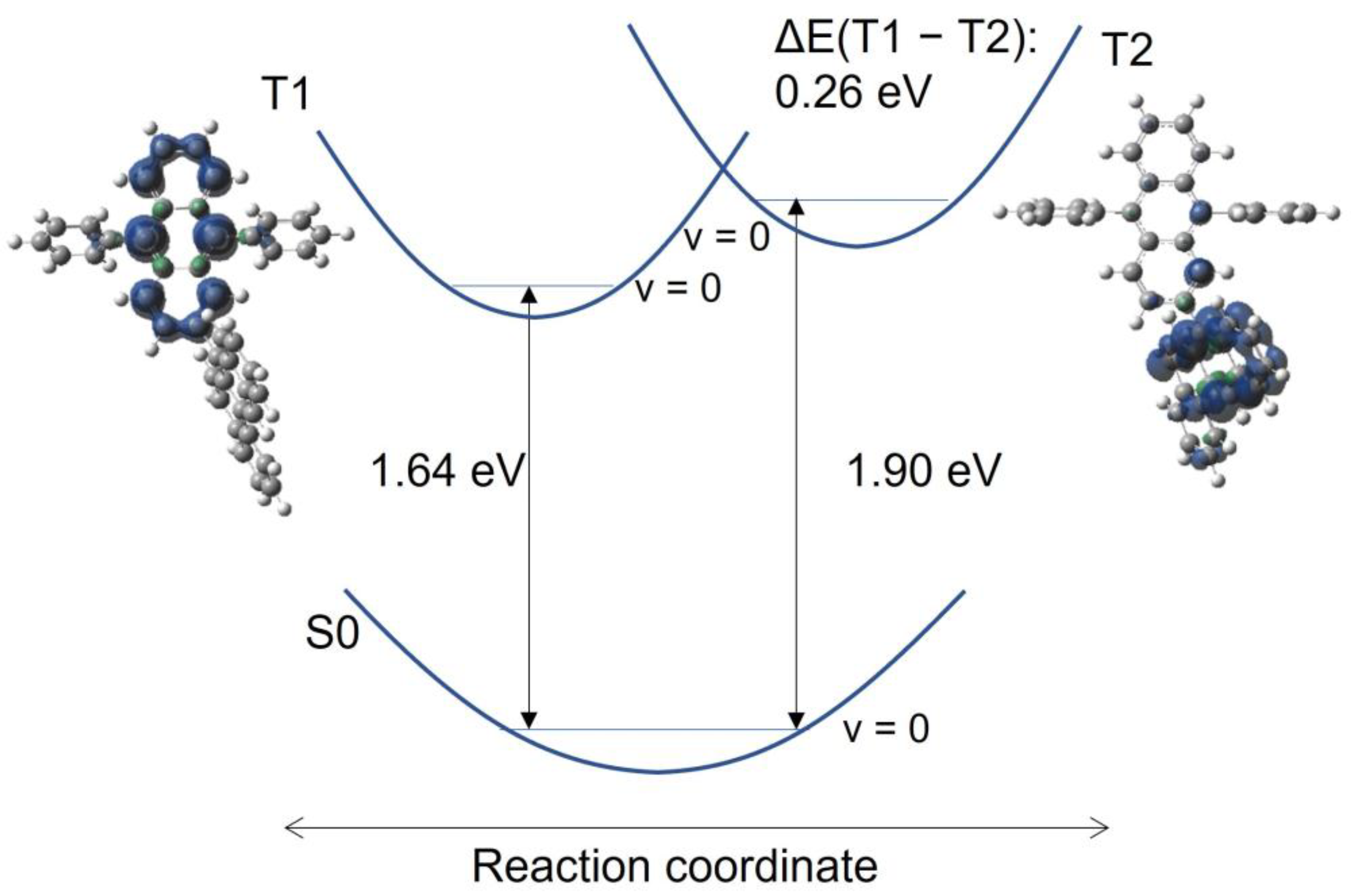
3.3. Quantum Chemical Calculations of the Triplet Levels and Molecular Orbitals
4. Discussions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Parker, C.A.; Hatchard, C.G. Delayed Fluorescence from Solutions of Anthracene and Phenantracene. Proc. R. Soc. Lond. Ser. A 1962, 269, 574–584. [Google Scholar]
- Gray, V.; Dreos, A.; Erhart, P.; Albinsson, B.; Moth-Poulsen, K.; Abrahamsson, M. Loss channels in triplet-triplet annihilation photon upconversion: Importance of annihilator single and triplet surface shapes. Phys. Chem. Chem. Phys. 2017, 19, 10931–10939. [Google Scholar] [CrossRef] [PubMed]
- Nishimura, N.; Gray, V.; Allardice, J.R.; Zhang, Z.; Pershin, A.; Beljonne, D.; Rao, A. Photon Upconversion from Near-Infrared to Blue Light with TIPS-Anthracene as an Efficient Triplet-Triplet Annihilator. ACS Mater. Lett. 2019, 1, 660–664. [Google Scholar] [CrossRef]
- Olesund, A.; Gray, V.; Mårtensson, J.; Albinsson, B. Diphenylanthracene Dimers for Triplet-Triplet Annihilation Photon Upconversion: Mechanistic Insights for Intramolecular Pathways and the Importance of Molecular Geometry. J. Am. Chem. Soc. 2021, 143, 5745–5754. [Google Scholar] [CrossRef]
- Bjelland, M.V.; Nakashima, H.; Hashimoto, N.; Seo, S.; Melø, T.B.; Lindgren, M. Non-approximative Kinetics of Triplet-Triplet Annihilation at Room Temperature: Solvent Effects on Delayed Fluorescence. ChemPhotoChem 2023, 7, e202300064. [Google Scholar] [CrossRef]
- Gray, V.; Moth-Poulsen, K.; Albinsson, B.; Abrahamsson, M. Towards efficient solit-state triplet-triplet annihilation based photon upconversion: Supramolecular, macromolecular and self-assembled systems. Coord. Chem. Rev. 2019, 123, 20181–20187. [Google Scholar]
- Gao, G.; Prasad, S.K.K.; Zhang, B.; Dvorak, M.; Tayebjee, M.J.Y.; McCamey, D.R.; Schmidt, T.W.; Smith, T.; Wong, W.W.H. Intramolecular versus Intermolecular Triplet Fusion in Multichromophoric Photochemical Upconversion. J. Phys. Chem. C 2019, 123, 20181–20187. [Google Scholar] [CrossRef]
- Dzebo, D.; Börjesson, K.; Gray, V.; Moth-Poulsen, K.; Albinsson, B. Intramolecular Triplet-Triplet Annihilation Upconversion in 9,10-Diphenylanthracene Oligomers and Dendrimers. J. Phys. Chem. C 2016, 120, 23397–23406. [Google Scholar] [CrossRef]
- He, G.; Churchill, E.M.; Parenti, K.R.; Zhang, J.; Narayanan, P.; Namata, F.; Malkoch, M.; Congreve, D.N.; Cacciuto, A.; Sfeir, M.Y.; et al. Promoting multiexciton interactions in singlet fission and triplet fusion upconversion dendrimers. Nat. Commun. 2023, 14, 6080. [Google Scholar] [CrossRef] [PubMed]
- Niihori, N.; Kosaka, T.; Negishi, Y. Triplet-triplet annihilation-based photon upconversion using nanoparticles and nanoclusters. Mater. Horiz. 2024, 11, 2304. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Yu, T.; Chen, J.; Hu, R.; Yang, G.; Zeng, Y.; Li, Y. Recent advances of triplet-triplet annihilation upconversion in photochemical transformations. Curr. Opin. Green Sustain. Chem. 2023, 43, 100841. [Google Scholar] [CrossRef]
- Fukagawa, H.; Shimizu, T.; Ohbe, N.; Tokito, S.; Tokumaru, K.; Fujikake, H. Anthracene derivatives as efficient emitting hosts for blue organic light-emitting diodes utilizing triplet–triplet annihilation. Org. Electron. 2012, 13, 1197–1203. [Google Scholar] [CrossRef]
- Zhang, Y.; Lee, J.; Forreste, S.R. Tenfold increase in the lifetime of blue phosphorescent organic light-emitting diodes. Nat. Commun. 2014, 5, 5008. [Google Scholar] [CrossRef] [PubMed]
- Miyashita, T.; Jaimes, P.; Mardini, A.; Fumanal, M.; Lee Tang, M. High-Level Reverse Intersystem Crossing and Molecular Rigidity Improve Spin Statistics for Triplet-Triplet Annihilation Upconversion. J. Phys. Chem. Lett. 2023, 14, 6119–6126. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Zhou, M.; Wie, Y.; Zhou, X.; Liu, S.; Zhang, S.; Zhang, B. Solvent effects on the triplet-triplet annihilation upconversion of diiodo-Bodipy and perylene. Phys. Chem. Chem. Phys. 2017, 19, 1516–1525. [Google Scholar] [CrossRef]
- Kawakami, S.; Nakashima, H.; Kojima, K.; Nomura, R.; Ohsawa, N.; Inventors; Semiconductor Energy Laboratory Co., Ltd. Anthracene Derivative, Material or Light Emitting Element, Light Emitting Element, Light Emitting Device, and Electronic Appliance. US Patent US 7,879,464, 1 February 2011. [Google Scholar]
- Suzuki, H.; Seo, S.; Kawakami, S.; Suzuki, S.; Inventors; Semiconductor Energy Laboratory Co., Ltd. Dibenzo[c,g]carbazole Compound, Light-Emitting Element, Light-Emitting Device, Display Device, Lighting Device and Electronic Device. US Patent US 8,986,857, 24 March 2015. [Google Scholar]
- Kadoma, H.; Seo, S.; Suzuki, H.; Hashimoto, N.; Suzuki, T.; Inventors; Semiconductor Energy Laboratory Co., Ltd. Organic Compound, Light-Emitting Device, Light-Emitting Apparatus, Electronic Apparatus, and Lighting Apparatus. US Patent Application Publication US 2021/0119133, 22 April 2021. [Google Scholar]
- Gao, W.; Herron, N.; Inventors; LG Chem, Ltd., Assignee. Electroactive Materials. US Patent US 11,114,621, 7 September 2021. [Google Scholar]
- Rurack, K.; Spieles, M. Fluorescence Quantum Yields of a Series of Red and Near-Infrared Dyes Emitting at 600–1000 nm. Anal. Chem. 2011, 83, 1232–1242. [Google Scholar] [CrossRef] [PubMed]
- Marta, P.; Fausto, O.; Fausto, E.; Pier, L.G. New molecular pairs for low power non-coherent triplet–triplet annihilation based upconversion: Dependence on the triplet energies of sensitizer and emitter. J. Lumin. 2013, 135, 265–270. [Google Scholar] [CrossRef]
- Hageberg, I.U.; Arja, K.; Vindstad, B.E.; Bergvoll, J.K.; Gederaas, O.A.; Melø, T.-B.; Nilsson, K.P.R.; Lindgren, M. Photophysics of Glycosylated Ring-Fused Chlorin Complexes and Their Photosensitizing Effects on Cancer Cells. ChemPhotoChem 2023, 7, e202300028. Available online: https://chemistry-europe.onlinelibrary.wiley.com/doi/full/10.1002/cptc.202300028 (accessed on 6 March 2025). [CrossRef]
- Cheng, Y.Y.; Khoury, T.; Clady, R.G.C.R.; Tayebjee, M.J.Y.; Ekins-Daukes, N.J.; Crossley, M.J.; Schmidt, T.W. On the efficiency limit of triplet–triplet annihilation for photochemical upconversion. Phys. Chem. Chem. Phys. 2010, 12, 66–71. [Google Scholar] [CrossRef]
- Schultze, T.F.; Schmidt, T.W. Photochemical upconversion: Present status and prospects for its application to solar energy conversion. Energy Environ. Sci. 2015, 8, 103–125. [Google Scholar] [CrossRef]
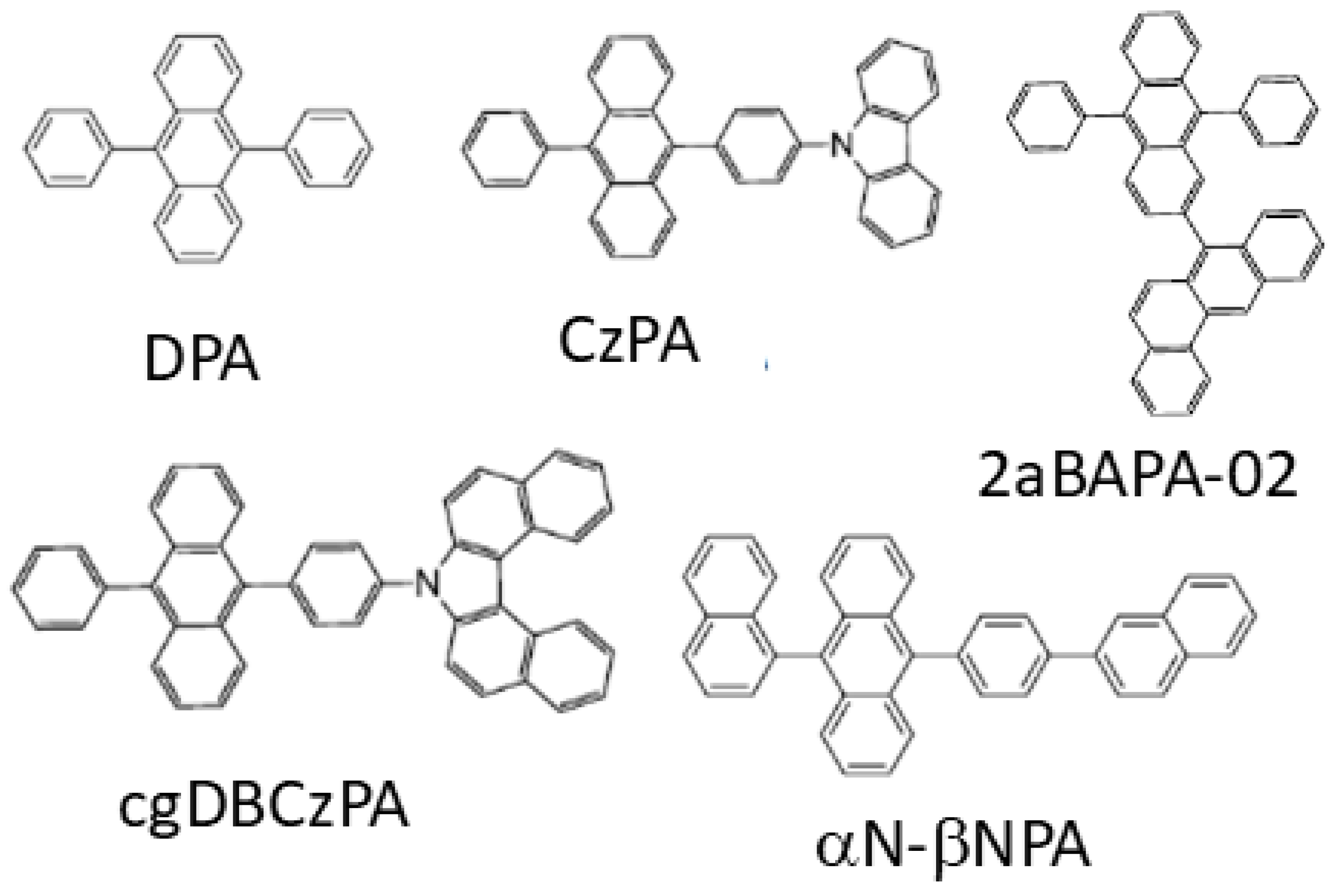
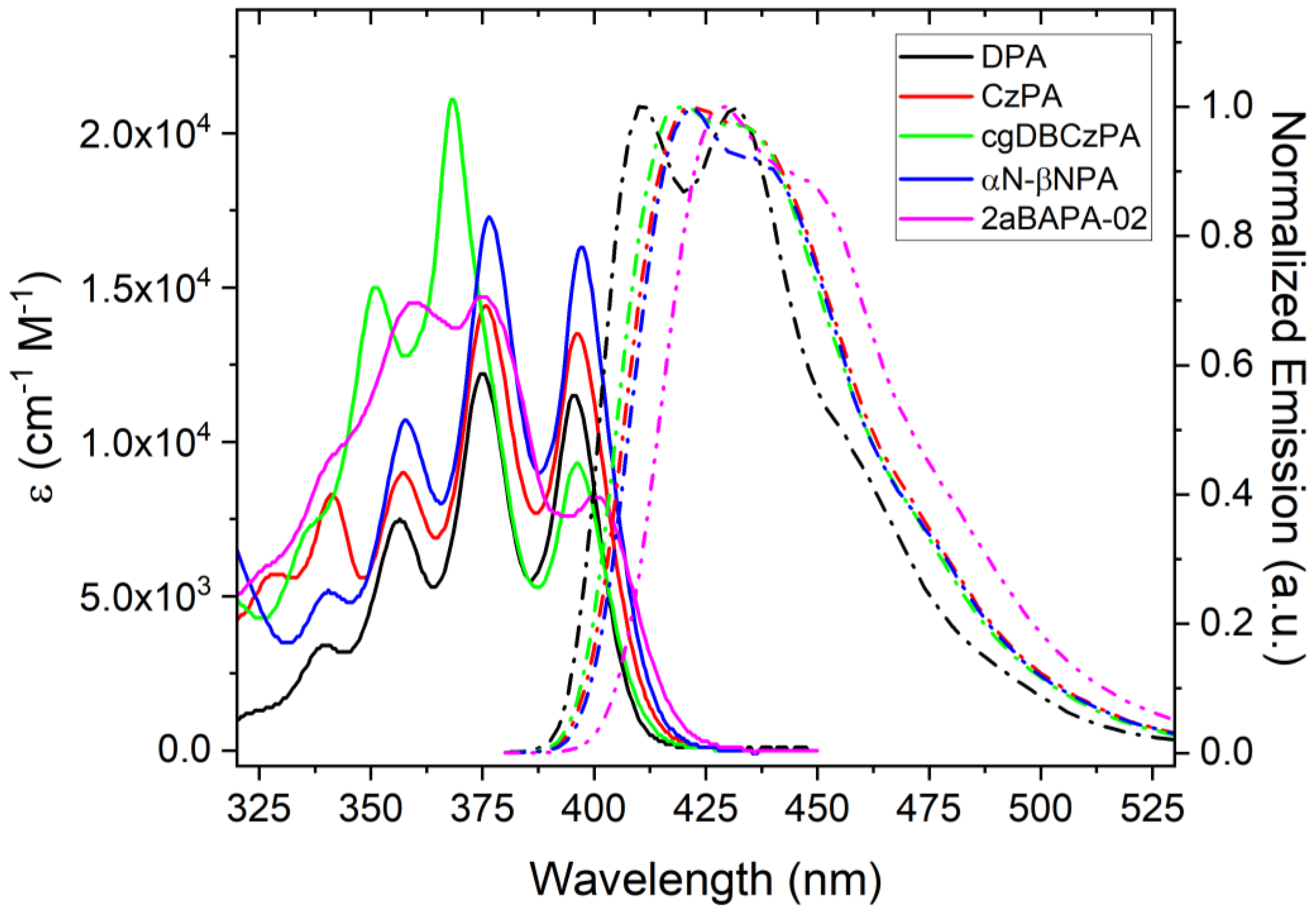

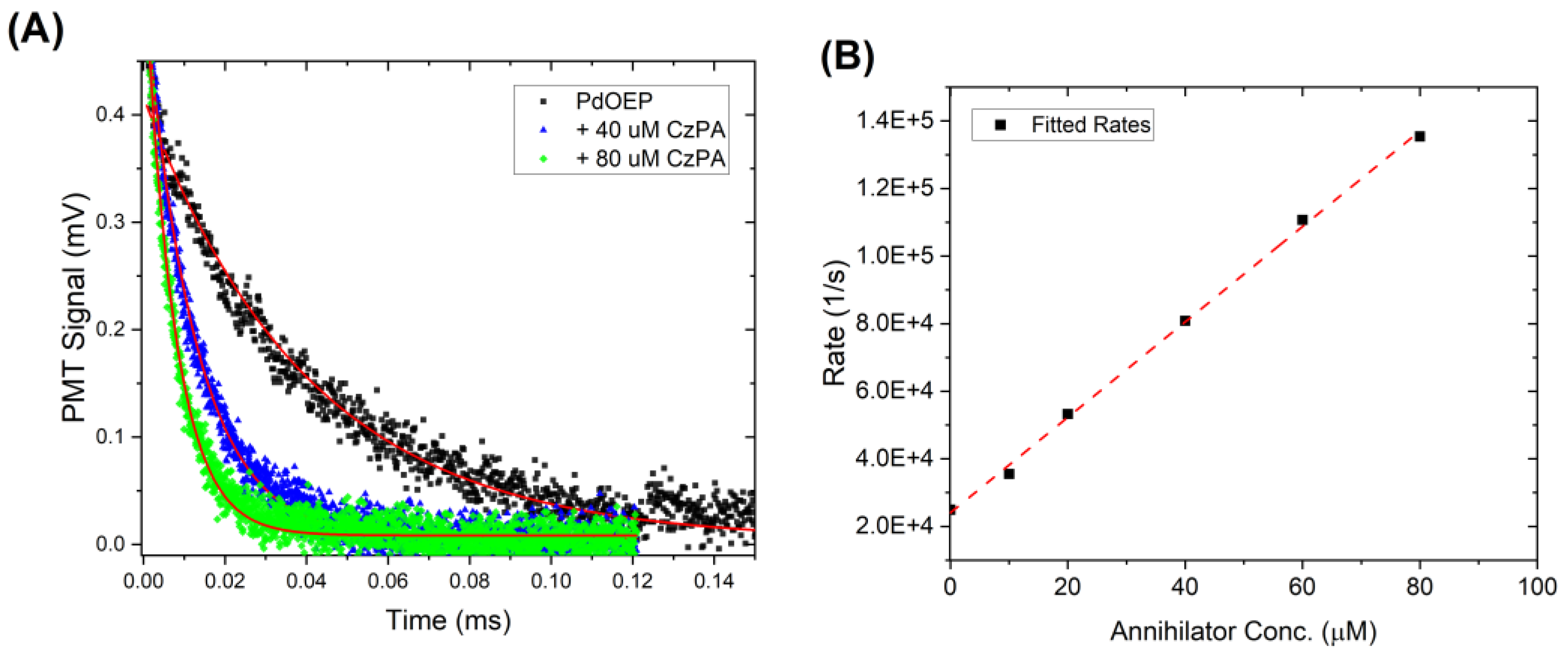
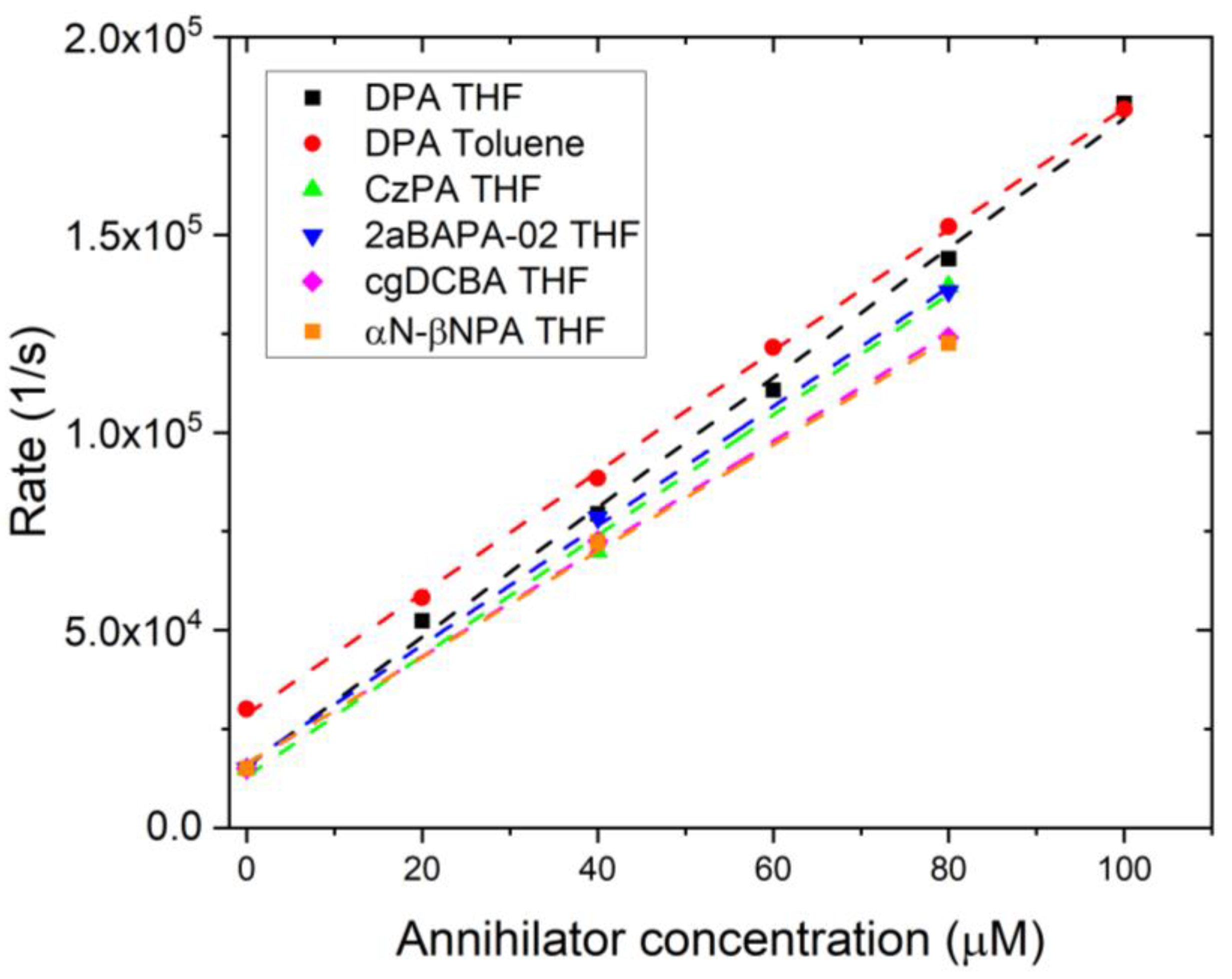
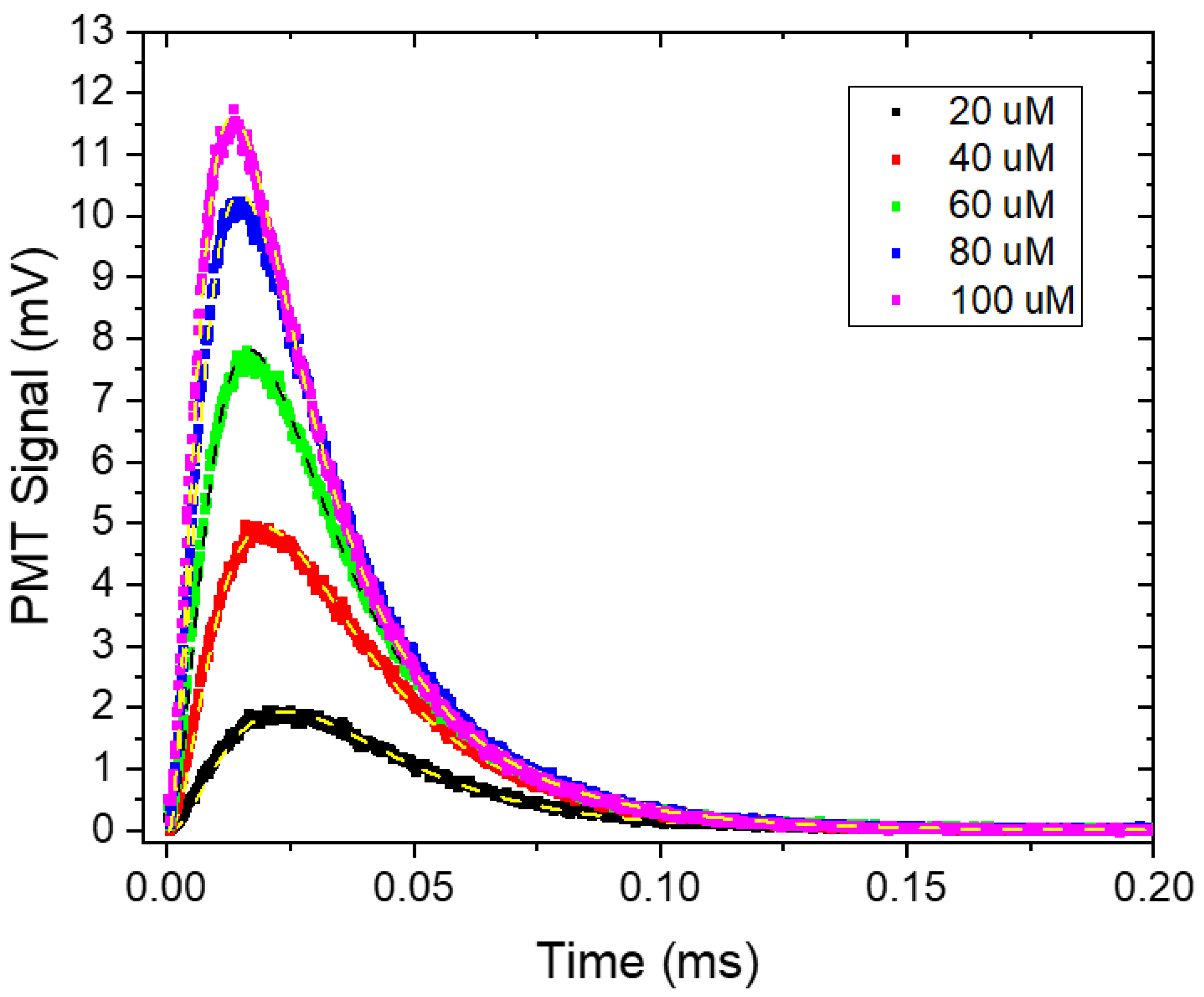
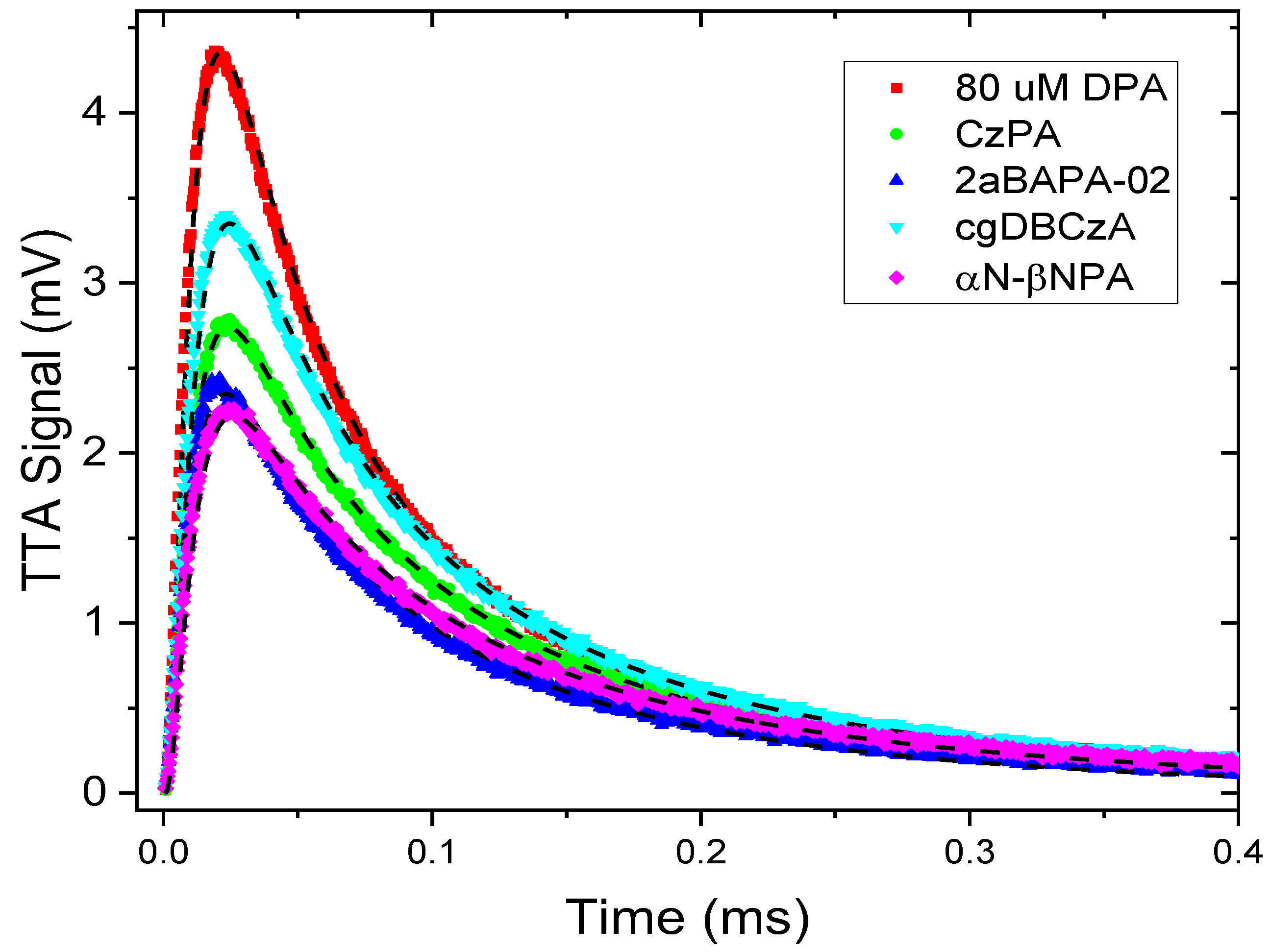
| Compound | 1 Decay Time (ns) | 2 QY (Toluene) | 2 QY (THF) |
|---|---|---|---|
| DPA | 6.62 ± 0.034 | 0.93 ± 0.054 | 0.94 ± 0.06 |
| CzPA | 5.07 ± 0.026 | 0.89 ± 0.051 | 0.96 ± 0.13 |
| cgDBCzPA | 4.77 ± 0.029 | 0.84 ± 0.059 | 0.83 ± 0.11 |
| 2aBAPA-02 | 6.92 ± 0.033 | 0.71 ± 0.042 | 0.78 ± 0.06 |
| αN-βNPA | 3.67 ± 0.027 | 0.73 ± 0.043 | 0.75± 0.07 |
| Compound | 1 kTET (109 s−1M−1) | k3A (s−1) | 2 K·kTTA (s−1) |
|---|---|---|---|
| DPA | 1.53 ± 0.016 | 16,000 ± 3100 | 12,000 ± 1900 |
| CzPA | 1.28 ± 0.060 | 16,400 ± 1000 | 13,200 ± 2500 |
| cgDBCzPA | 1.44 ± 0.047 | 26,300 ± 2800 | 11,900 ± 3900 |
| 2aBAPA-02 | 1.47 ± 0.060 | 12,400 ± 1000 | 12,400 ± 1500 |
| αN-βNPA | 1.39 ± 0.095 | 17,100 ± 3500 | 6110 ± 840 |
| Compound | 1 kTET (109 s−1M−1) | k3A (s−1) | 2 K·kTTA (s−1) |
|---|---|---|---|
| DPA | 1.64 ± 0.043 | 1240 ± 330 | 6110 ± 170 |
| CzPA | 1.52 ± 0.087 | 1450 ± 2.8 | 3320 ± 470 |
| cgDBCzPA | 1.36 ± 0.043 | 1380 ± 290 | 4250 ±410 |
| 2aBAPA-02 | 1.51 ± 0.045 | 1730 ± 130 | 3720 ± 420 |
| αN-βNPA | 1.34 ± 0.051 | 1590 ± 520 | 3400 ± 310 |
| Compound | ΦTET | ΦTTA | ΦTET·ΦTTA |
|---|---|---|---|
| DPA | 0.776 ± 0.023 | 0.300 ± 0.025 | 0.233 ± 0.021 |
| CzPA | 0.743 ± 0.025 | 0.308 ± 0.013 | 0.229 ± 0.013 |
| cgDBCzPA | 0.765 ± 0.009 | 0.238 ± 0.024 | 0.182 ± 0.020 |
| 2aBAPA-02 | 0.769 ± 0.024 | 0.333 ± 0.011 | 0.256± 0.012 |
| αN-βNPA | 0.759 ± 0.009 | 0.208 ± 0.026 | 0.158± 0.021 |
| Compound | ΦTET | ΦTTA | ΦTET·ΦTTA |
|---|---|---|---|
| DPA | 0.896 ± 0.008 | 0.454 ± 0.011 | 0.407 ± 0.011 |
| CzPA | 0.888 ± 0.008 | 0.410 ± 0.005 | 0.364 ± 0.006 |
| cgDBCzPA | 0.877 ± 0.009 | 0.430 ± 0.013 | 0.377 ± 0.012 |
| 2aBAPA-02 | 0.888 ± 0.008 | 0.406 ± 0.007 | 0.360± 0.007 |
| αN-βNPA | 0.875 ± 0.009 | 0.405 ± 0.025 | 0.354± 0.022 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lindgren, M.; Bjelland, V.M.; Melø, T.-B.; McCracken, C.; Seo, S.; Nakashima, H. The Triplet–Triplet Annihilation Efficiency of Some 9,10-Substituted Diphenyl Anthracene Variants—A Decisive Analysis from Kinetic Rate Constants. Optics 2025, 6, 8. https://doi.org/10.3390/opt6010008
Lindgren M, Bjelland VM, Melø T-B, McCracken C, Seo S, Nakashima H. The Triplet–Triplet Annihilation Efficiency of Some 9,10-Substituted Diphenyl Anthracene Variants—A Decisive Analysis from Kinetic Rate Constants. Optics. 2025; 6(1):8. https://doi.org/10.3390/opt6010008
Chicago/Turabian StyleLindgren, Mikael, Victoria M. Bjelland, Thor-Bernt Melø, Callum McCracken, Satoshi Seo, and Harue Nakashima. 2025. "The Triplet–Triplet Annihilation Efficiency of Some 9,10-Substituted Diphenyl Anthracene Variants—A Decisive Analysis from Kinetic Rate Constants" Optics 6, no. 1: 8. https://doi.org/10.3390/opt6010008
APA StyleLindgren, M., Bjelland, V. M., Melø, T.-B., McCracken, C., Seo, S., & Nakashima, H. (2025). The Triplet–Triplet Annihilation Efficiency of Some 9,10-Substituted Diphenyl Anthracene Variants—A Decisive Analysis from Kinetic Rate Constants. Optics, 6(1), 8. https://doi.org/10.3390/opt6010008







