Resolution Improvement for Coherent Illumination Microscopy via Incident Light Phase Modulation
Abstract
1. Introduction
2. Theoretical Analysis and Simulation Model
2.1. Theoretical Analysis
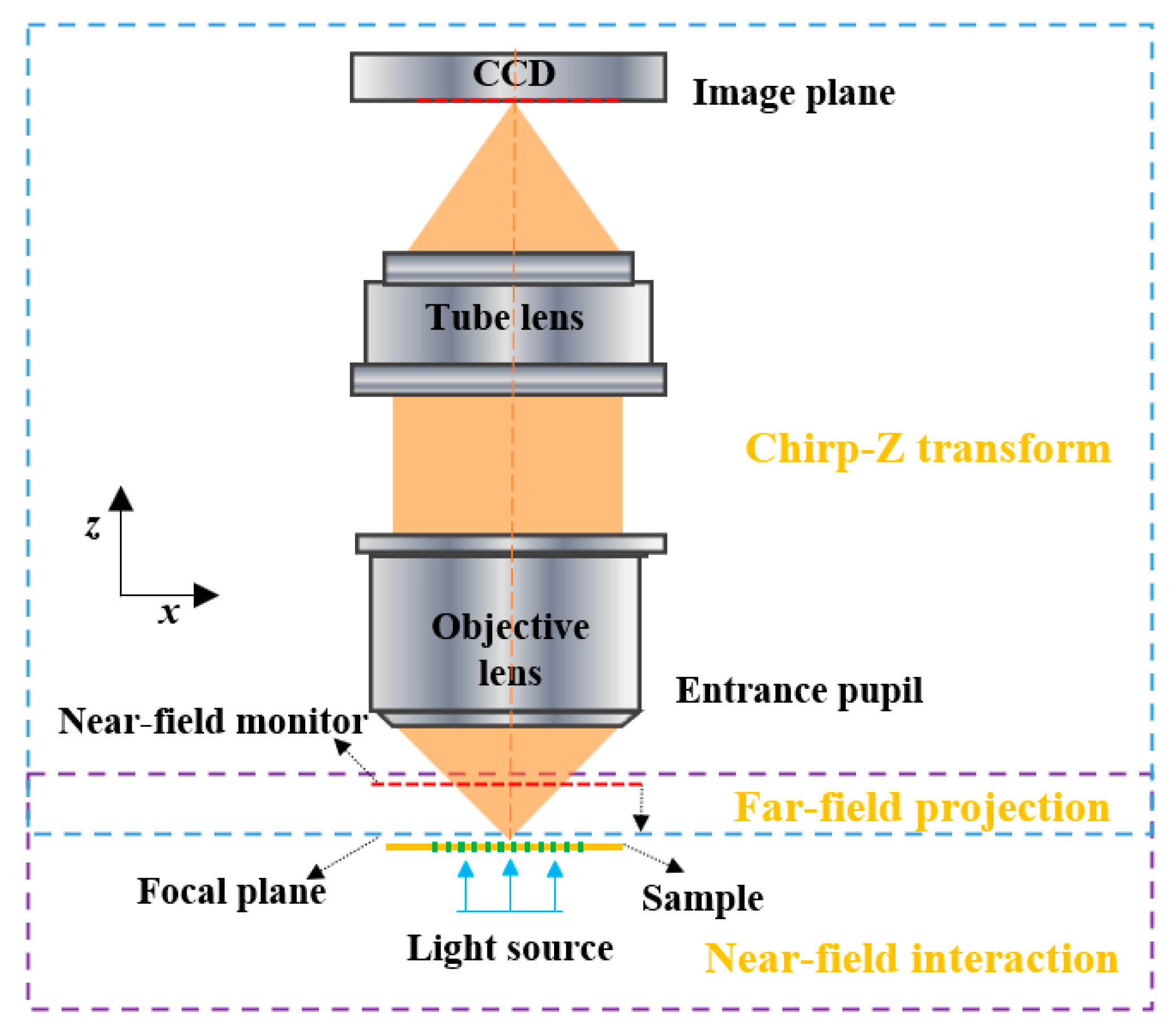
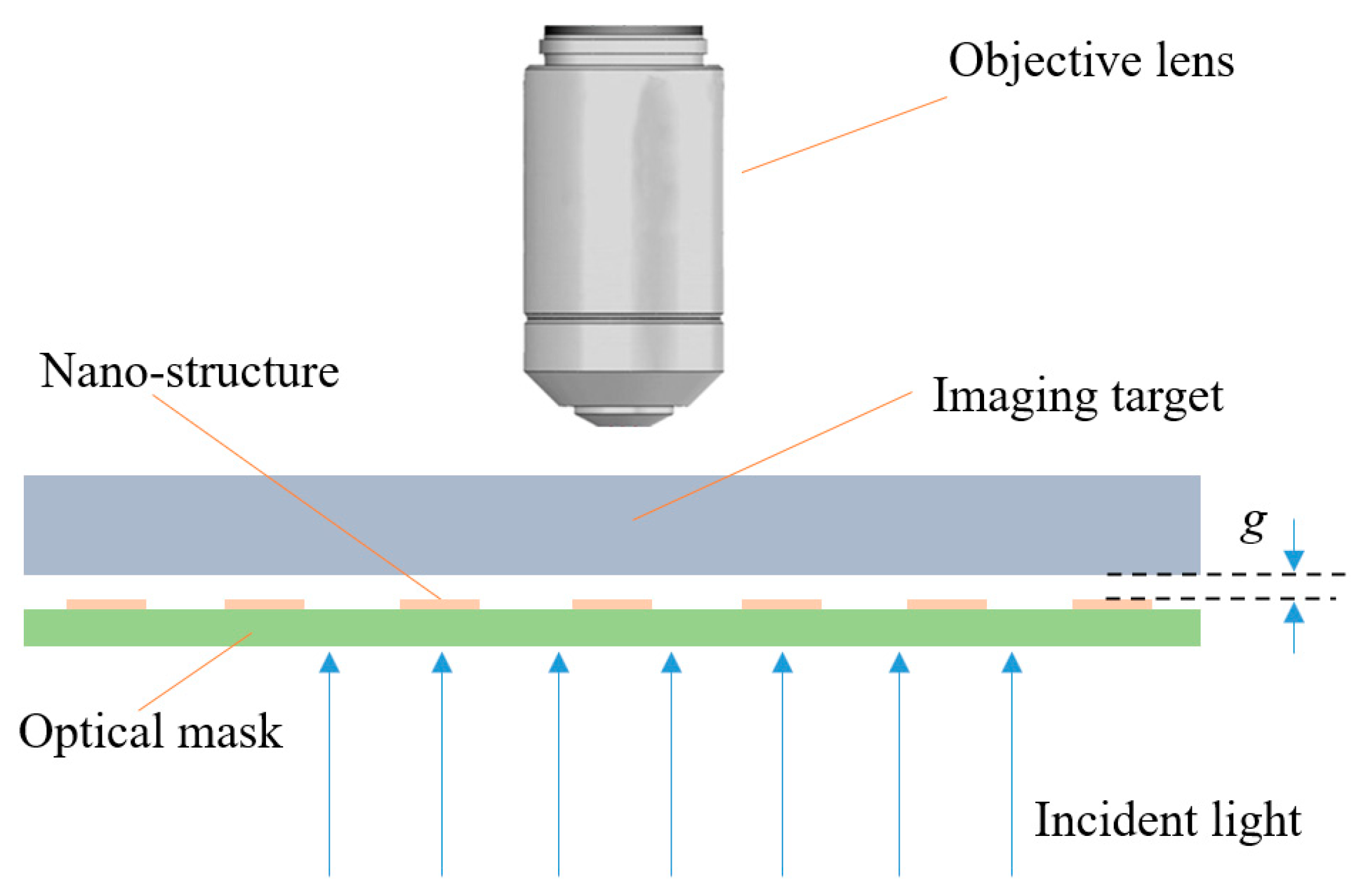
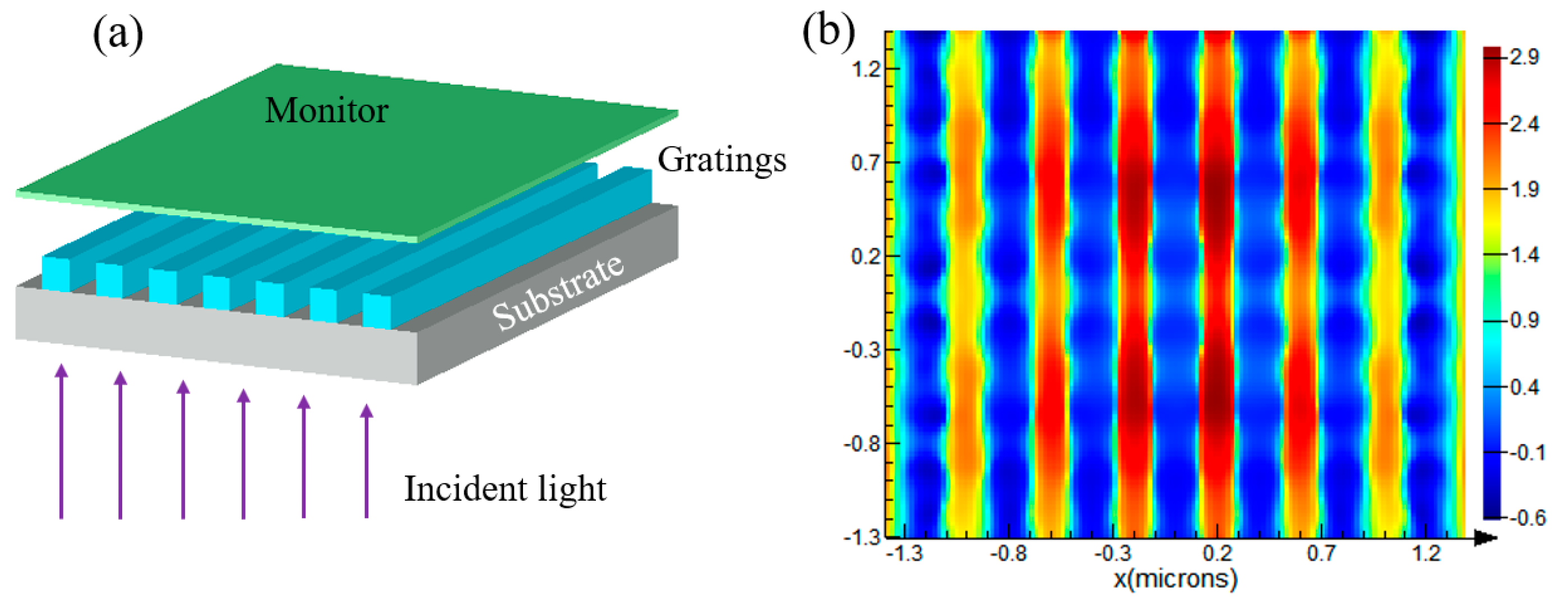
2.2. Simulation Model
3. Results and Discussion
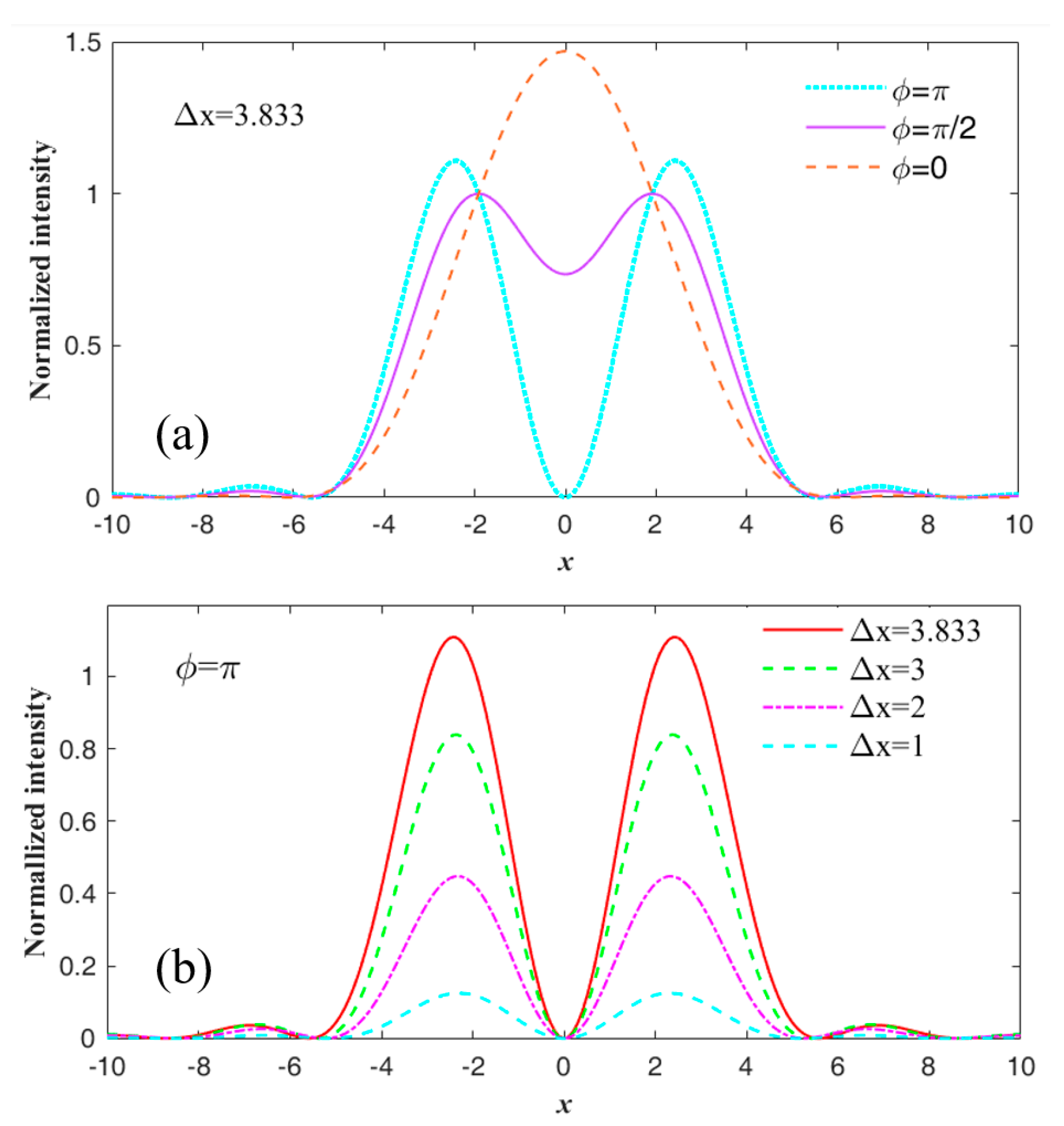
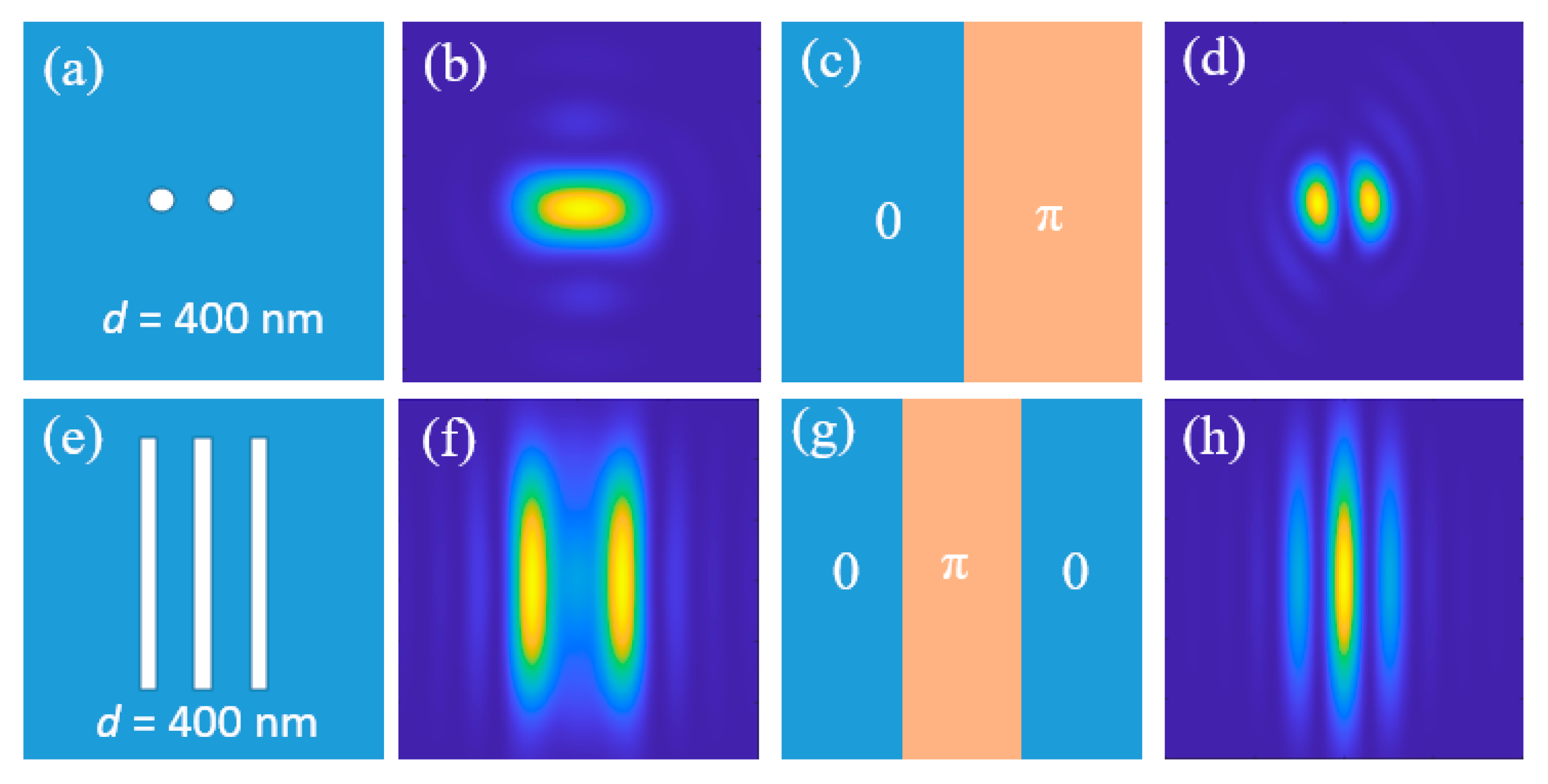
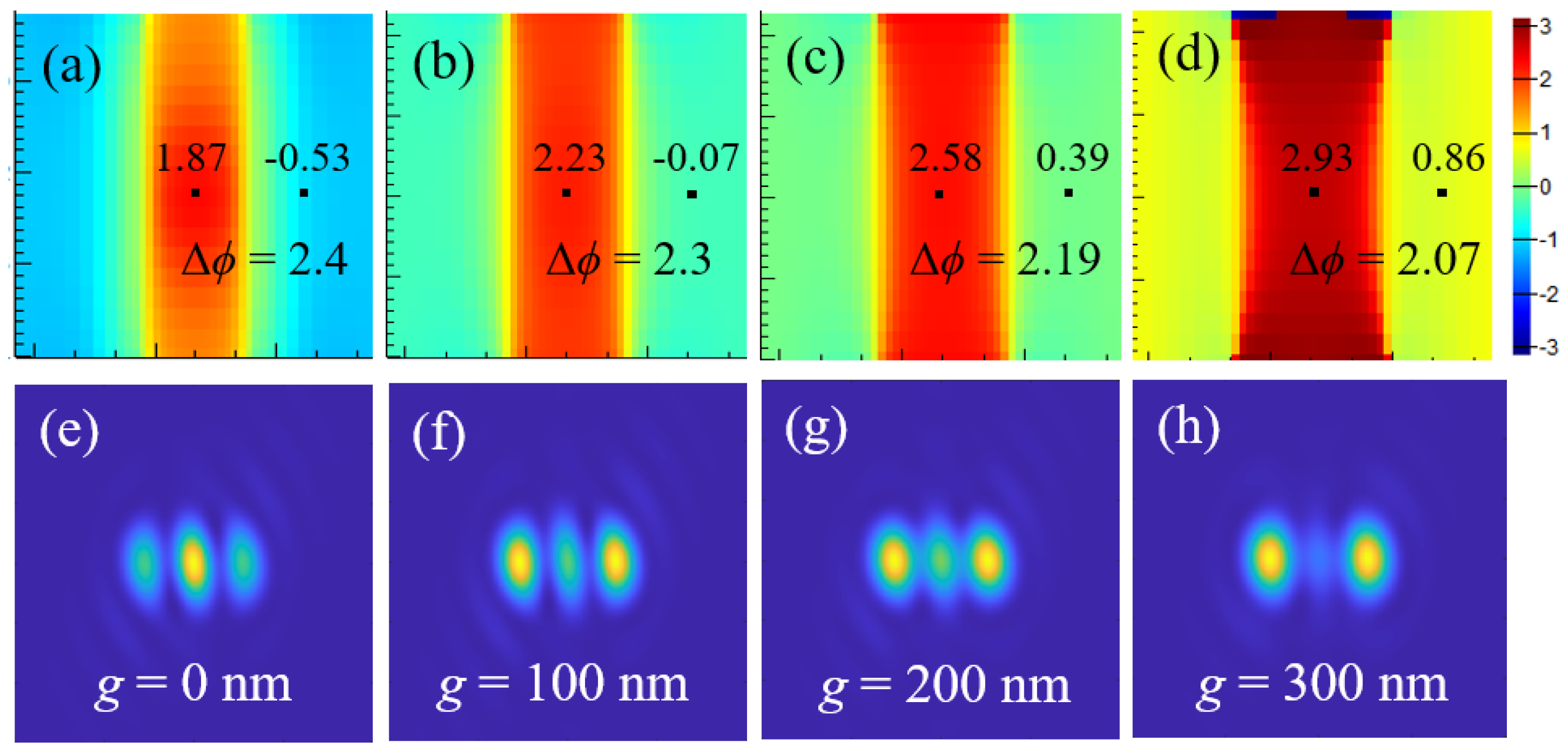
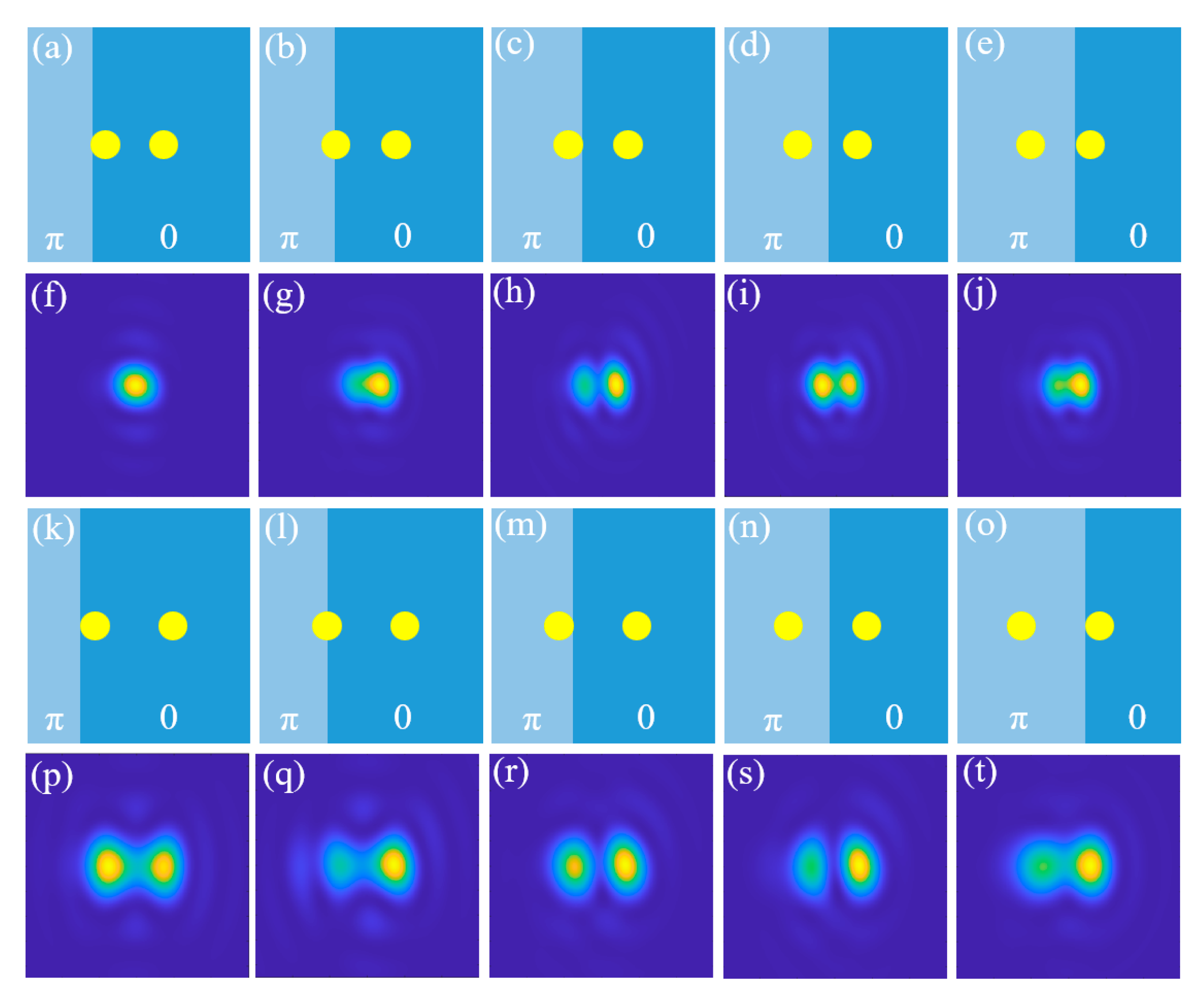
3.1. Influence of Optical Phase on the Diffraction Limit
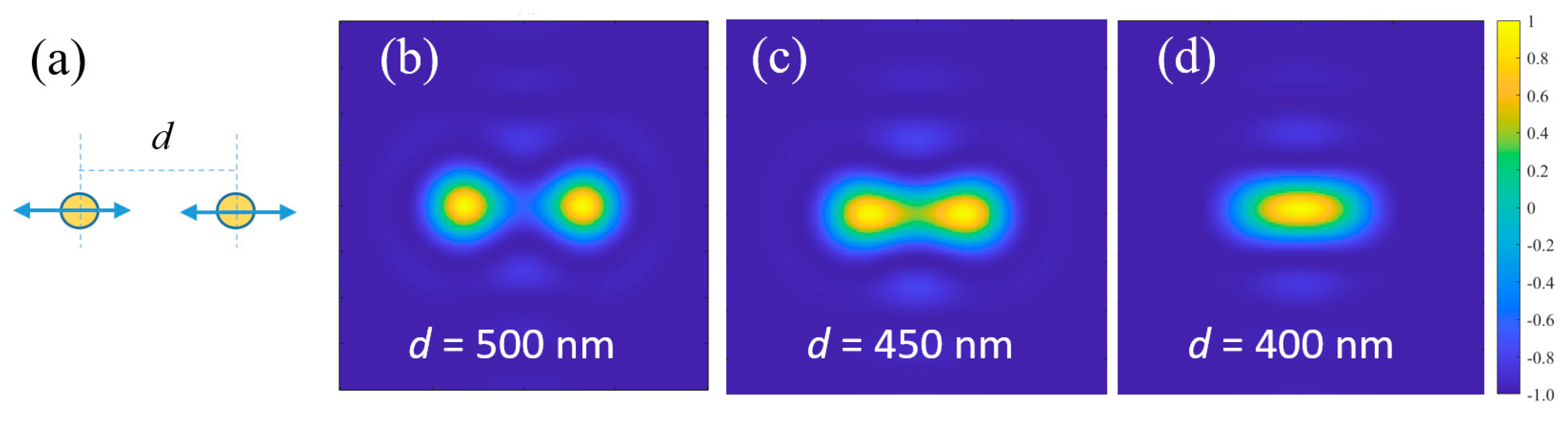
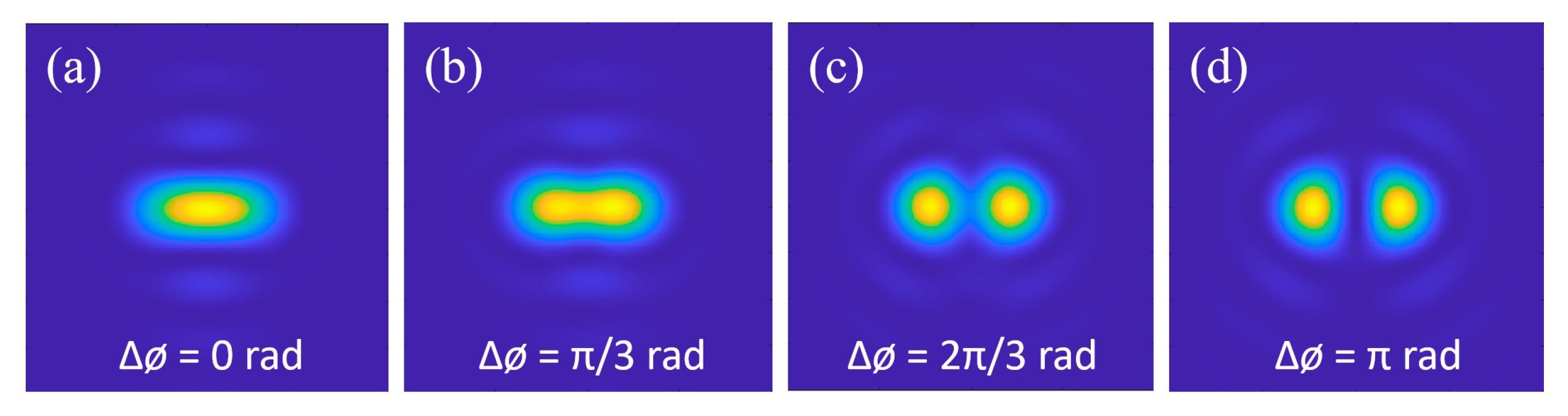
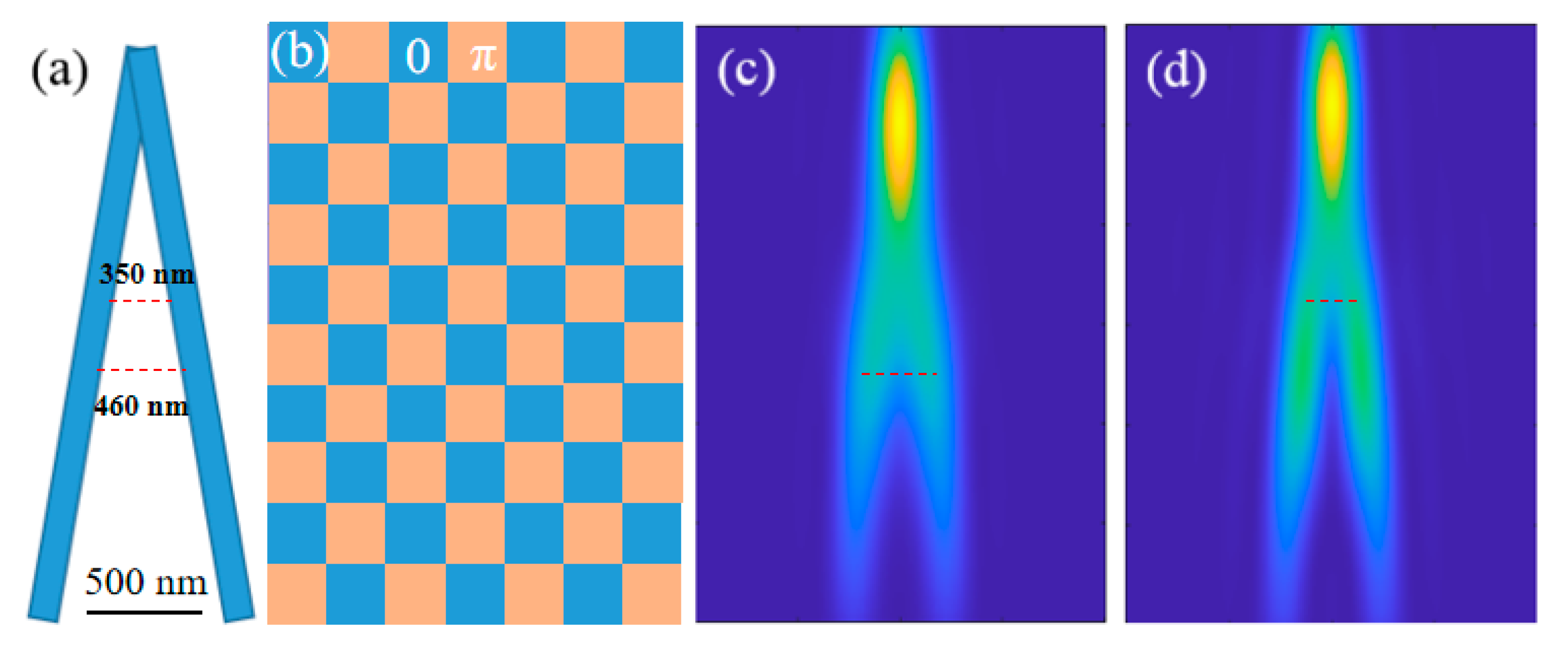
3.2. Super-Resolution Imaging System Based on Phase Modulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, D.R. Progresses in implementation of STED microscopy. Meas. Sci. Technol. 2023, 34, 102002. [Google Scholar] [CrossRef]
- Li, C.; Liu, S.; Wang, W.; Liu, W.; Liu, X. Recent research on stimulated emission depletion microscopy for reducing photobleaching. J. Microsc. 2018, 271, 4–16. [Google Scholar] [CrossRef] [PubMed]
- Leung, B.; Chou, K. Review of super-resolution fluorescence microscopy for biology. Appl. Spectrosc. 2011, 65, 967–980. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Tehrani, K.; Kner, P. Multicolor 3D super-resolution imaging by quantum dot stochastic optical reconstruction microscopy. ACS Nano 2015, 9, 2917–2925. [Google Scholar] [CrossRef] [PubMed]
- Haji, B.; Beheiry, M.E.; Dahan, M. PSF engineering in multifocus microscopy for increased depth volumetric imaging. Biomed. Opt. Express 2016, 7, 726. [Google Scholar] [CrossRef] [PubMed]
- Izeddin, I.; Beheiry, M.E.; Andilla, J.; Ciepielewski, D.; Darzacq, X.; Dahan, M. PSF shaping using adaptive optics for three-dimensional single-molecule super-resolution imaging and tracking. Opt. Express 2012, 20, 4957–4967. [Google Scholar] [CrossRef] [PubMed]
- Gustafsson, M. Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy. J. Microsc. 2000, 198, 82–87. [Google Scholar] [CrossRef] [PubMed]
- Shao, L.; Kner, P.; Rego, E.; Gustafsson, M. Super-resolution 3D microscopy of live whole cells using structured illumination. Nat. Methods 2011, 8, 1044–1046. [Google Scholar] [CrossRef] [PubMed]
- Rogers, E.; Lindberg, J.; ROY, T.; Savo, S.; Chad, J.; Dennis, M.; Zhwludev, N. A super-oscillatory lens optical microscope for subwavelength imaging. Nat. Mater. 2012, 11, 432–435. [Google Scholar] [CrossRef] [PubMed]
- Qin, F.; Huang, K.; Wu, J.; Jiao, J.; Luo, X.; Qiu, C.; Hong, M. Shaping a subwavelength needle with ultra-long focal length by focusing azimuthally polarized light. Sci. Rep. 2015, 5, 09977. [Google Scholar] [CrossRef] [PubMed]
- Willig, K.; Rizzoli, S.; Westphal, V.; Jahn, R.; Hell, S. STED microscopy reveals that synaptotagmin remains clustered after synaptic vesicle exocytosis. Nature 2006, 440, 935–939. [Google Scholar] [CrossRef] [PubMed]
- Ash, E.A.; Nicholls, G. Super-resolution aperture sanning microscope. Nature 1972, 237, 510–512. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Guo, W.; Li, L.; Luk’yanchuk, B.; Khan, A.; Chen, Z.; Hong, M. Optical virtual imaging at 50 nm lateral resolution with a white-light nanoscope. Nat. Commun. 2011, 2, 218. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Deng, Y.; Zhou, W.; Yu, M.; Urbach, H.P.; Wu, Y. Effects of whispering gallery mode in microsphere super-resolution imaging. Appl. Phys. B 2017, 123, 236. [Google Scholar] [CrossRef]
- Yang, H.; Moullan, N.; Auwerx, J.; Gijs, M.A.M. Super-resolution biological microscopy using virtual imaging by a microsphere nanoscope. Small 2014, 10, 1712–1718. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Durant, S.; Lee, H.; Pikus, Y.; Fang, N.; Xiong, Y.; Sun, C.; Zhang, X. Far-Field optical superlens. Nano Lett. 2007, 7, 403–408. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Kuang, C.; Hao, X.; Pang, C.; Xu, P.; Li, H.; Yu, C.; Xu, Y.; Nan, D. Fluorescent nanowire ring illumination for wide-field far-field subdiffraction imaging. Phys. Rev. Lett. 2017, 118, 076101. [Google Scholar] [CrossRef] [PubMed]
- Hao, X.; Liu, X.; Kuang, C.; Li, Y.; Ku, Y.; Zhang, H.; Li, H.; Tong, L. Far-field super-resolution imaging using near-field illumination by micro-fiber. Appl. Phys. Lett. 2013, 102, 013104. [Google Scholar] [CrossRef]
- Ling, J.; Wang, Y.; Liu, X.; Wang, X. Resolution improvement of dark-field microscopy via micro-particle near-field illumination. Opt. Lett. 2021, 46, 1265–1268. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, J.; Li, Y.; Guo, J.; Liu, X.; Wang, X. Resolution Improvement for Coherent Illumination Microscopy via Incident Light Phase Modulation. Optics 2024, 5, 406-415. https://doi.org/10.3390/opt5040030
Ling J, Li Y, Guo J, Liu X, Wang X. Resolution Improvement for Coherent Illumination Microscopy via Incident Light Phase Modulation. Optics. 2024; 5(4):406-415. https://doi.org/10.3390/opt5040030
Chicago/Turabian StyleLing, Jinzhong, Yangyang Li, Jinkun Guo, Xin Liu, and Xiaorui Wang. 2024. "Resolution Improvement for Coherent Illumination Microscopy via Incident Light Phase Modulation" Optics 5, no. 4: 406-415. https://doi.org/10.3390/opt5040030
APA StyleLing, J., Li, Y., Guo, J., Liu, X., & Wang, X. (2024). Resolution Improvement for Coherent Illumination Microscopy via Incident Light Phase Modulation. Optics, 5(4), 406-415. https://doi.org/10.3390/opt5040030





