Subsurface Spectroscopy in Heterogeneous Materials Using Self-Healing Laser Beams
Abstract
1. Introduction
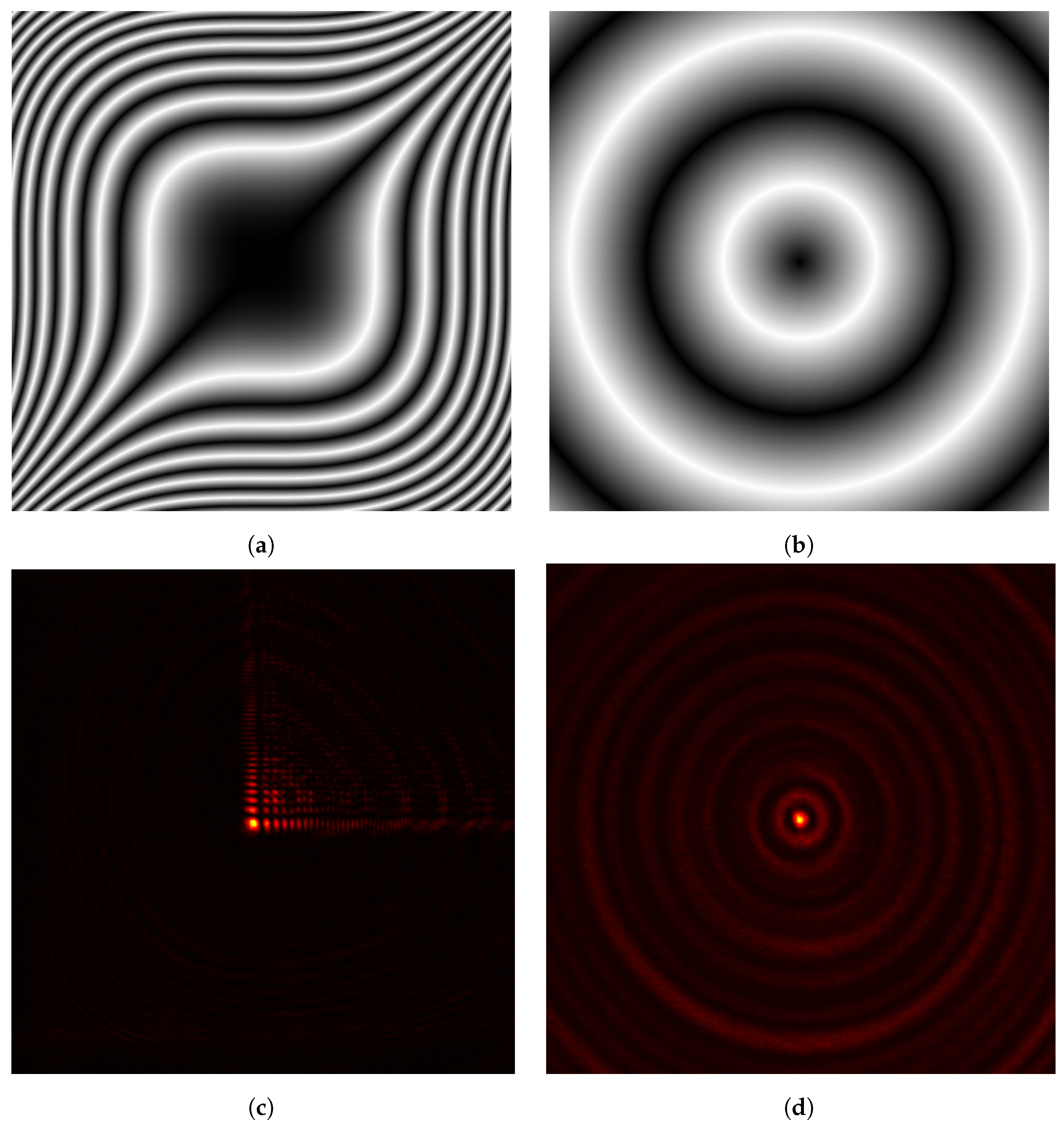
2. Method
2.1. Samples
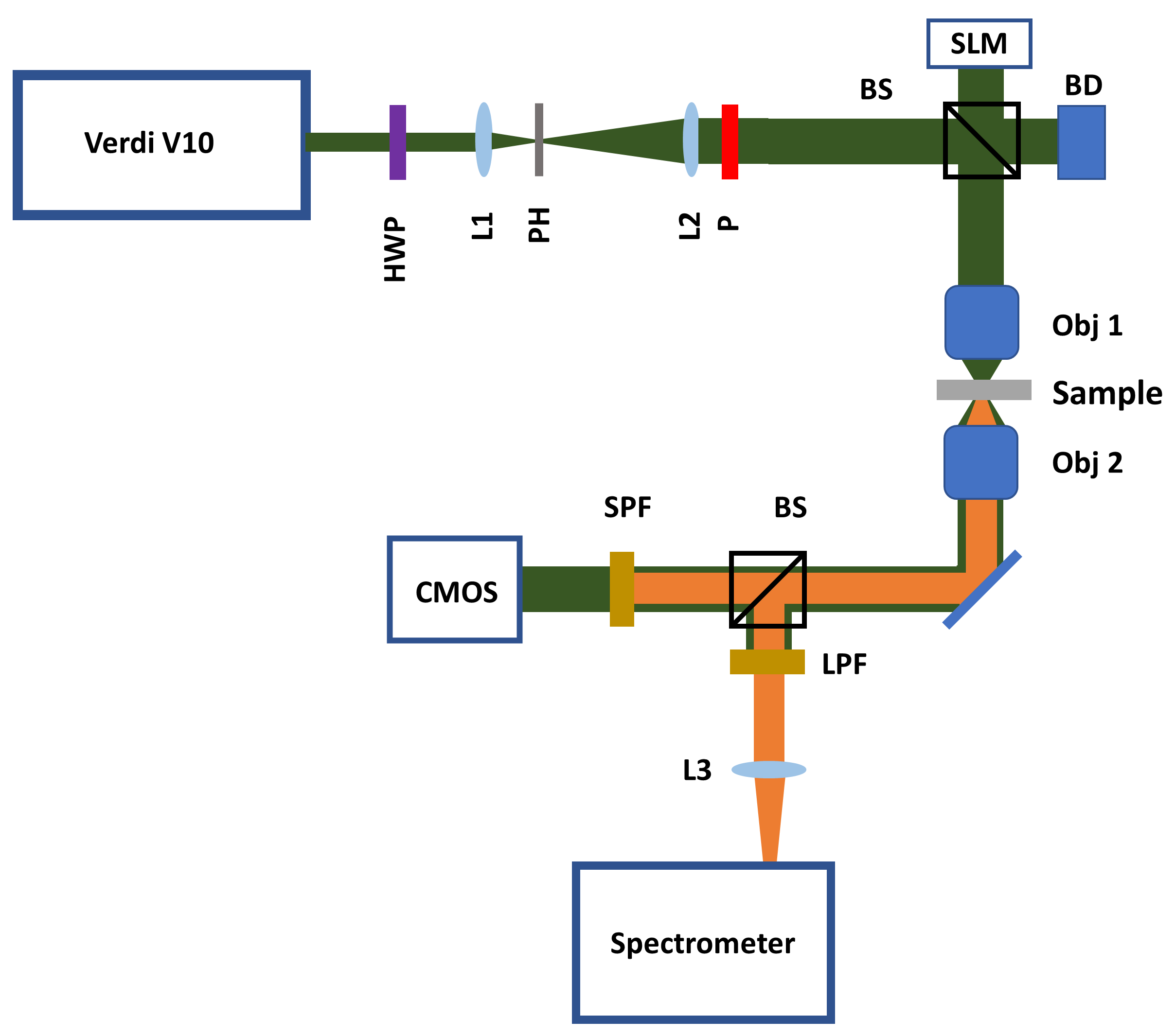
2.2. Experimental Setup
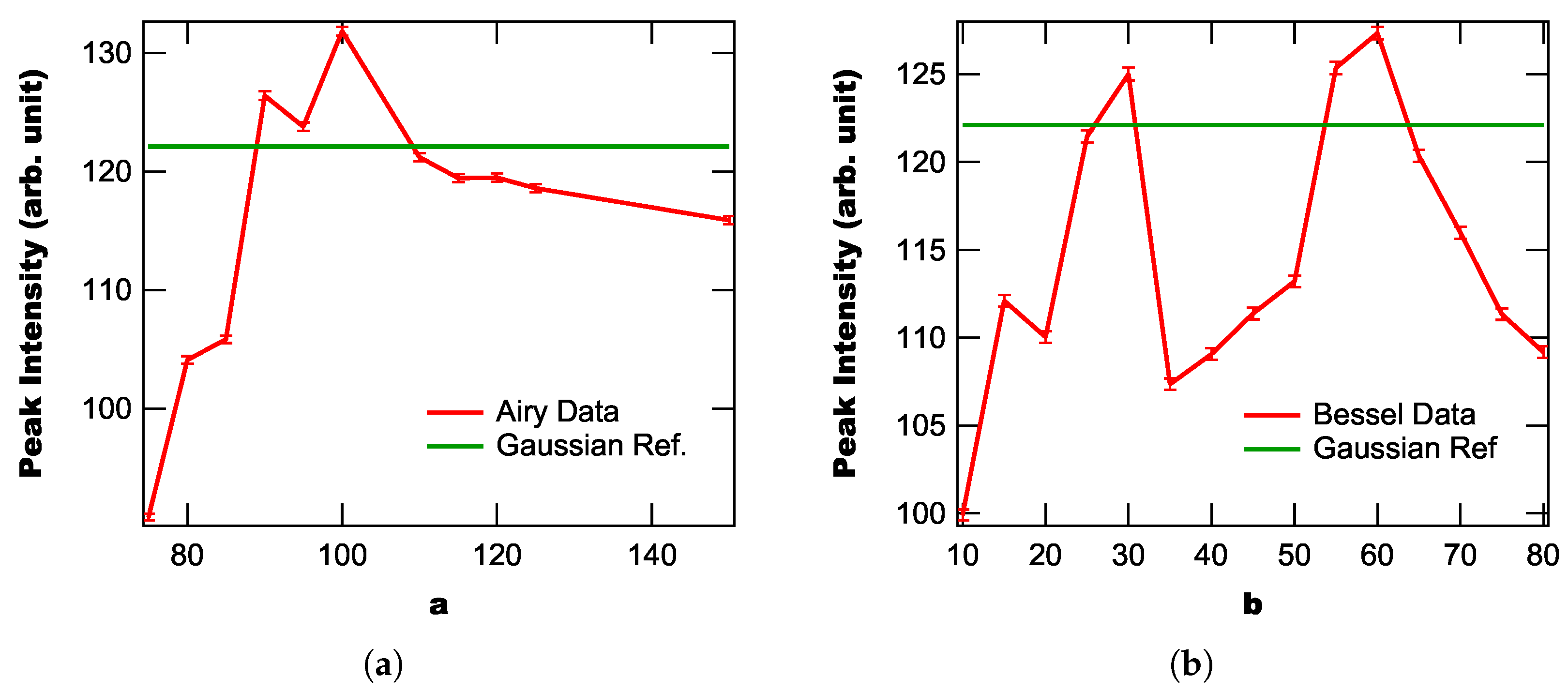
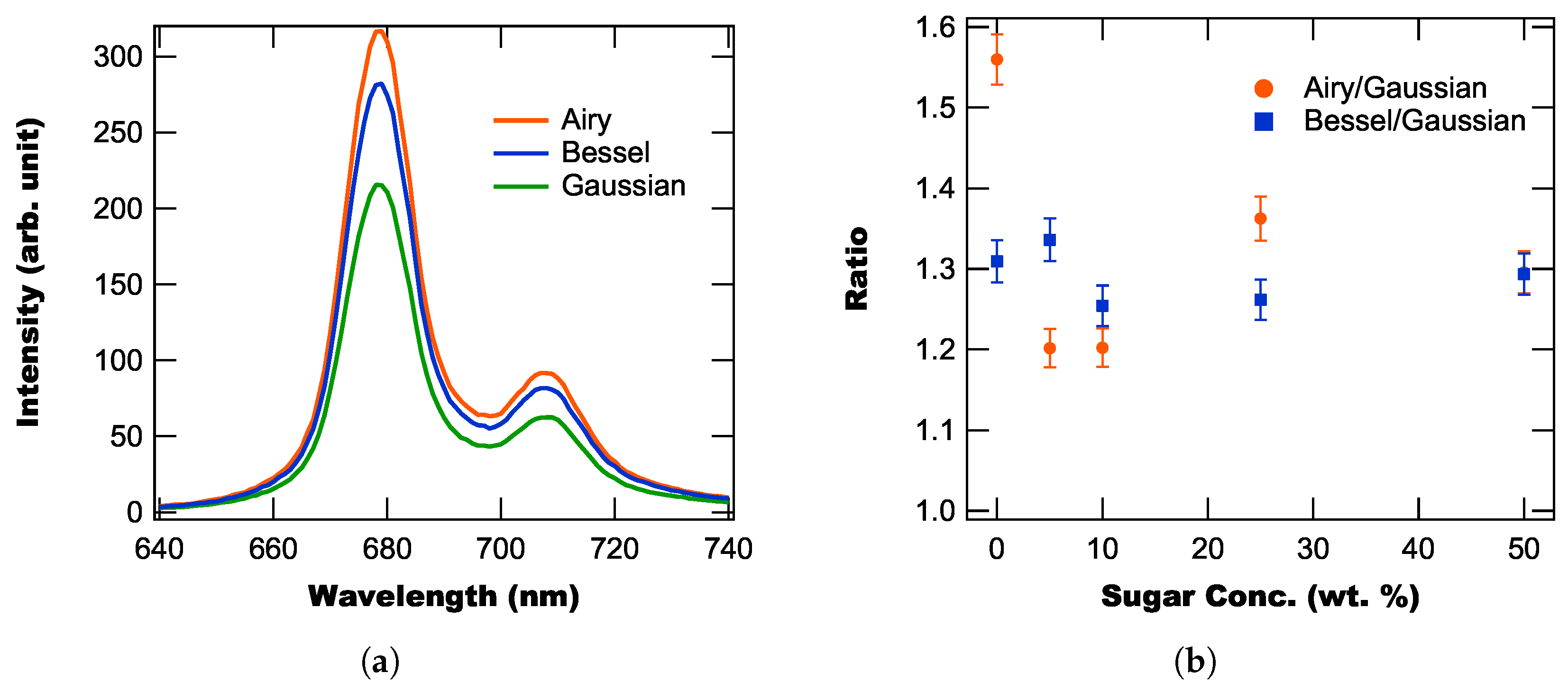
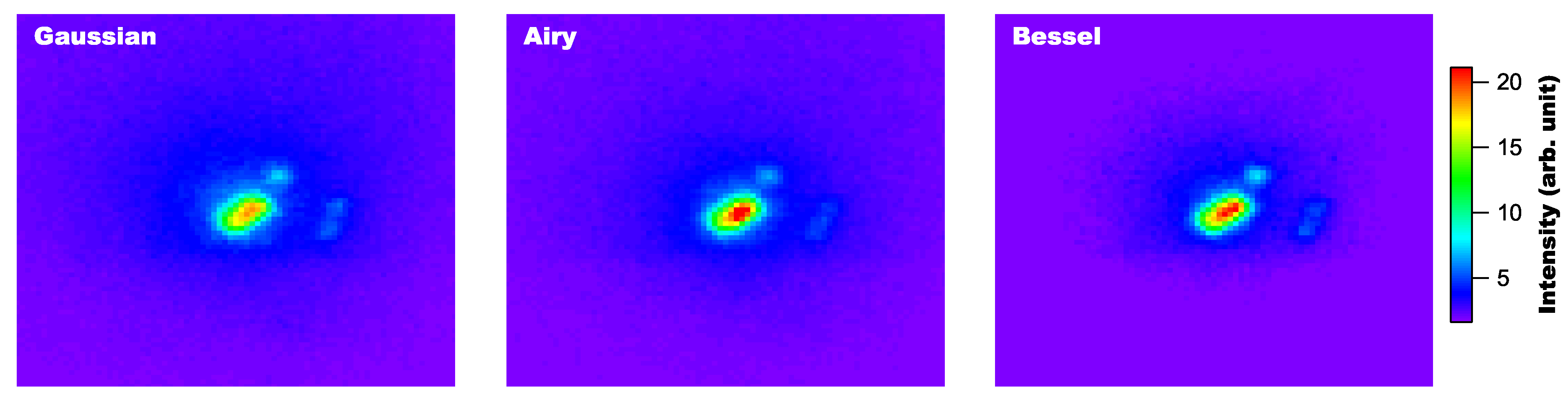
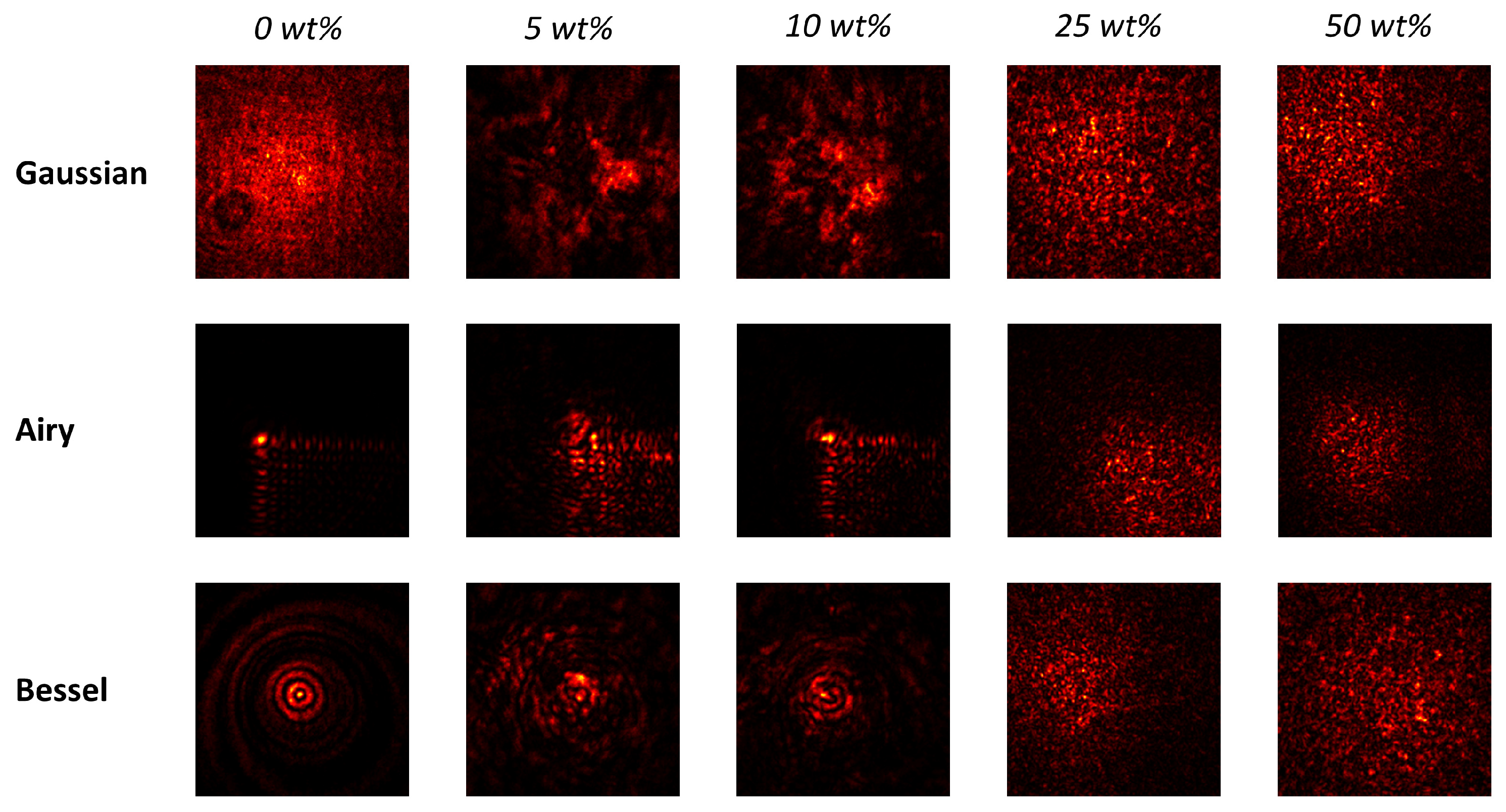
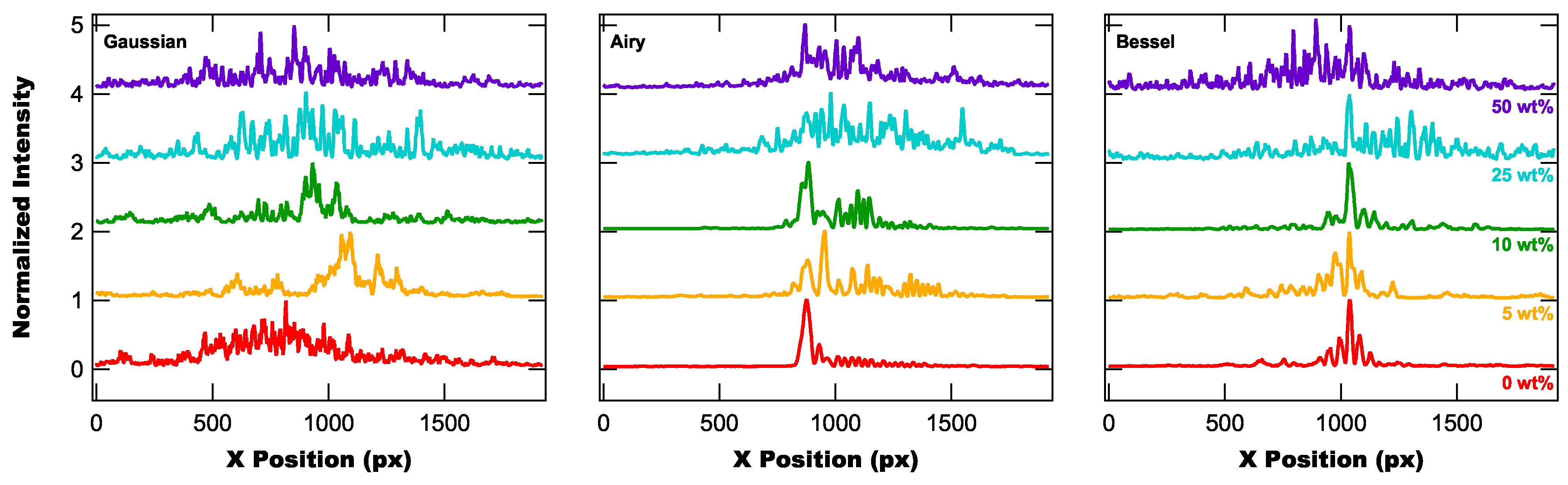
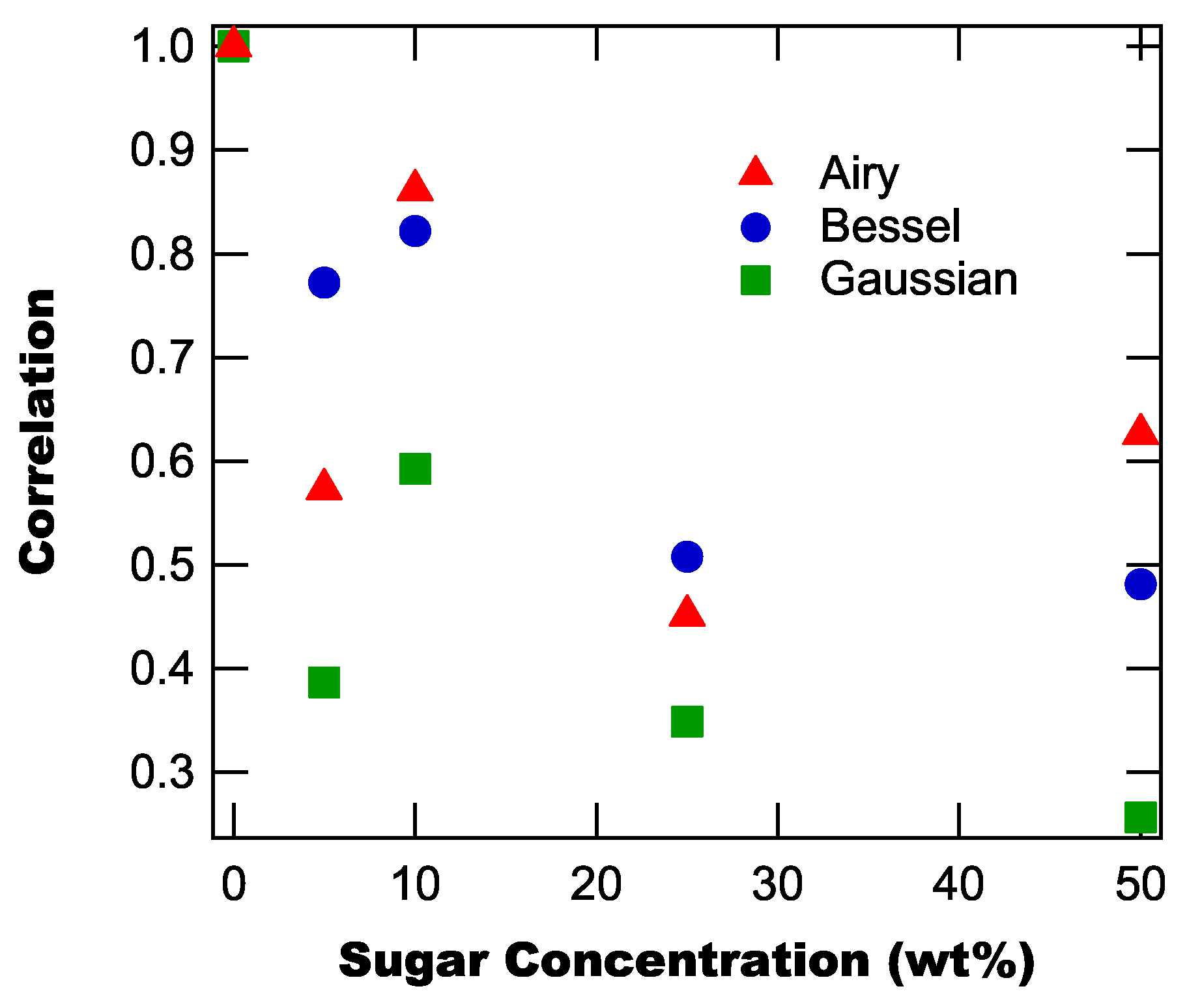
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anderson, B.R.; Gese, N.; Eilers, H. Monitoring Sub-surface Chemical Reactions in Heterogeneous Materials Using Wavefront-shaping-assisted Bidirectional Focusing. Opt. Lett. 2022, 47, 2036–2039. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.R.; Gese, N.; Eilers, H. Spectroscopic properties of Eu:Y(acac)3(DPEPO) and characterization of its photo- and thermal- degradation. J. Lumin. 2022, 251, 119183. [Google Scholar] [CrossRef]
- Anderson, B.R.; Gese, N.J.; Eilers, H. Subsurface spectroscopy of heterogeneous materials using optical wavefront shaping. AIP Conf. Proc. 2023, 2844, 260001. [Google Scholar] [CrossRef]
- Anderson, B.R.; Gese, N.; Eilers, H. Subsurface Spectroscopy of Thermal Degradation Inside an Inert PBX Simulant Using Feedback-assisted Wavefront Shaping. Appl. Spectrosc. 2024, in press. [Google Scholar]
- Vellekoop, I. Feedback-based Wavefront Shaping. Opt. Express 2015, 23, 12190–12206. [Google Scholar] [CrossRef]
- Moore, D.S. Probing Dynamic Processes in Explosives and Propellants—Science Issues. AIP Conf. Proc. 2018, 1979, 100028. [Google Scholar] [CrossRef]
- Shen, Y.; Pidishety, S.; Nape, I.; Dudley, A. Self-healing of structured light: A review. J. Opt. 2022, 24, 103001. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, X.; Goutsoulas, M.; Li, D.; Yang, X.; Yin, S.; Xu, J.; Christodoulides, D.N.; Efremidis, N.K.; Chen, Z. Robust propagation of pin-like optical beam through atmospheric turbulence. APL Photonics 2019, 4, 076103. [Google Scholar] [CrossRef]
- Vetter, C.; Steinkopf, R.; Bergner, K.; Ornigotti, M.; Nolte, S.; Gross, H.; Szameit, A. Realization of Free-Space Long-Distance Self-Healing Bessel Beams. Laser Photonics Rev. 2019, 13, 1900103. [Google Scholar] [CrossRef]
- Li, S.; Wang, J. Adaptive free-space optical communications through turbulence using self-healing Bessel beams. Sci. Rep. 2017, 7, 43233. [Google Scholar] [CrossRef]
- Birch, P.; Ituen, I.; Young, R.; Chatwin, C. Long-distance Bessel beam propagation through Kolmogorov turbulence. J. Opt. Soc. Am. A 2015, 32, 2066. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Zhang, W.; Wang, L.; Li, W.; Gong, L.; Cheng, W.; Chen, H.; Gruska, J. Propagation and self-healing properties of Bessel–Gaussian beam carrying orbital angular momentum in an underwater environment. Sci. Rep. 2019, 9, 2019. [Google Scholar] [CrossRef] [PubMed]
- Morgan, K.S.; Miller, J.K.; Li, W.; Li, Y.; Johnson, E.G. Higher order bessel beams integrated in time (HOBBIT) for free space underwater sensing and communication. In OCEANS 2017—Anchorage; IEEE: New York, NY, USA, 2017; pp. 1–4. [Google Scholar]
- Vettenburg, T.; Dalgarno, H.I.C.; Nylk, J.; Coll-Lladó, C.; Ferrier, D.E.K.; Čižmár, T.; Gunn-Moore, F.J.; Dholakia, K. Light-sheet microscopy using an Airy beam. Nat. Methods 2014, 11, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Bando, K.; Yabuuchi, S.; Li, M.; Kubo, T.; Oketani, R.; Smith, N.I.; Fujita, K. Bessel-beam illumination Raman microscopy. Biomed. Opt. Express 2022, 13, 3161. [Google Scholar] [CrossRef] [PubMed]
- Garces-Chavez, V.; McGloin, D.; Melville, H.; Sibbett, W.; Dholakia, K. Simultaneous micromanipulation in multiple planes using a self-reconstructing light beam. Nature 2002, 419, 145–147. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Ren, Y.X.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical trapping with structured light: A review. Adv. Photonics 2021, 3, 034001. [Google Scholar] [CrossRef]
- Otte, E.; Denz, C. Optical trapping gets structure: Structured light for advanced optical manipulation. Appl. Phys. Rev. 2020, 7. [Google Scholar] [CrossRef]
- Lib, O.; Bromberg, Y. Spatially entangled Airy photons. Opt. Lett. 2020, 45, 1399. [Google Scholar] [CrossRef]
- Baghdasaryan, B.; Steinlechner, F.; Fritzsche, S. Characterization of opening angle correlations of a biphoton state decomposed in Bessel modes. Phys. Rev. A 2020, 101, 043844. [Google Scholar] [CrossRef]
- Forbes, A.; Nape, I. Quantum mechanics with patterns of light: Progress in high dimensional and multidimensional entanglement with structured light. AVS Quantum Sci. 2019, 1, 011701. [Google Scholar] [CrossRef]
- Matsumoto, N.; Ando, T.; Inoue, T.; Ohtake, Y.; Fukuchi, N.; Hara, T. Generation of high-quality higher-order Laguerre–Gaussian beams using liquid-crystal-on-silicon spatial light modulators. J. Opt. Soc. Am. A 2008, 25, 1642. [Google Scholar] [CrossRef] [PubMed]
- Yan, M.; Ma, L. Generation of Higher-Order Hermite–Gaussian Modes via Cascaded Phase-Only Spatial Light Modulators. Mathematics 2022, 10, 1631. [Google Scholar] [CrossRef]
- Conry Young, J.P.; Dix, S. Generation of Generalized–Gauss Laser Beams via a Spatial Light Modulator. J. Ark. Acad. Sci. 2018, 72, 14–18. [Google Scholar] [CrossRef]
- Sundin, E.M.; Navarro, G.; Li, C. Modulated high-order Hermite–Gaussian beams with uniform intensity distribution. Opt. Commun. 2024, 554, 130217. [Google Scholar] [CrossRef]
- Conti, C.; Botteon, A.; Colombo, C.; Pinna, D.; Realini, M.; Matousek, P. Advances in Raman spectroscopy for the non-destructive subsurface analysis of artworks: Micro-SORS. J. Cult. Herit. 2020, 43, 319–328. [Google Scholar] [CrossRef]
- Mosca, S.; Conti, C.; Stone, N.; Matousek, P. Spatially offset Raman spectroscopy. Nat. Rev. Methods Prim. 2021, 1, 21. [Google Scholar] [CrossRef]
- Matousek, P.; Stone, N. Development of deep subsurface Raman spectroscopy for medical diagnosis and disease monitoring. Chem. Soc. Rev. 2016, 45, 1794–1802. [Google Scholar] [CrossRef] [PubMed]
- Mosca, S.; Dey, P.; Salimi, M.; Gardner, B.; Palombo, F.; Stone, N.; Matousek, P. Spatially Offset Raman Spectroscopy—How Deep? Anal. Chem. 2021, 93, 6755–6762. [Google Scholar] [CrossRef]
- Matousek, P. Inverse Spatially Offset Raman Spectroscopy for Deep Noninvasive Probing of Turbid Media. Appl. Spectrosc. 2006, 60, 1341–1347. [Google Scholar] [CrossRef]
- Mustafa, H.A.; Akkus, O. Comparison of diffuse versus inverse spatially-offset Raman spectroscopy modalities for analyte detection through barriers. Vib. Spectrosc. 2021, 113, 103228. [Google Scholar] [CrossRef]
- Khan, K.M.; Dutta, S.B.; Krishna, H.; Majumder, S.K. Inverse SORS for detecting a low Raman-active turbid sample placed inside a highly Raman-active diffusely scattering matrix—A feasibility study. J. Biophotonics 2016, 9, 879–887. [Google Scholar] [CrossRef] [PubMed]
- Khan, K.M.; Dutta, S.B.; Kumar, N.; Dalal, A.; Srivastava, A.; Krishna, H.; Majumder, S.K. Inverse spatially-offset Raman spectroscopy using optical fibers: An axicon lens-free approach. J. Biophotonics 2019, 12, e201900140. [Google Scholar] [CrossRef] [PubMed]
- Siviloglou, G.A.; Christodoulides, D.N. Accelerating finite energy Airy beams. Opt. Lett. 2007, 32, 979. [Google Scholar] [CrossRef] [PubMed]
- Chattrapiban, N.; Rogers, E.A.; Cofield, D.; Hill, W.T.; Roy, R. Generation of nondiffracting Bessel beams by use of a spatial light modulator. Opt. Lett. 2003, 28, 2183–2185. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anderson, B.R.; Gese, N.; Eilers, H. Subsurface Spectroscopy in Heterogeneous Materials Using Self-Healing Laser Beams. Optics 2024, 5, 310-318. https://doi.org/10.3390/opt5020022
Anderson BR, Gese N, Eilers H. Subsurface Spectroscopy in Heterogeneous Materials Using Self-Healing Laser Beams. Optics. 2024; 5(2):310-318. https://doi.org/10.3390/opt5020022
Chicago/Turabian StyleAnderson, Benjamin R., Natalie Gese, and Hergen Eilers. 2024. "Subsurface Spectroscopy in Heterogeneous Materials Using Self-Healing Laser Beams" Optics 5, no. 2: 310-318. https://doi.org/10.3390/opt5020022
APA StyleAnderson, B. R., Gese, N., & Eilers, H. (2024). Subsurface Spectroscopy in Heterogeneous Materials Using Self-Healing Laser Beams. Optics, 5(2), 310-318. https://doi.org/10.3390/opt5020022




