Transition of Orbital Electrons by Electromagnetic Waves

Abstract

An electromagnetic (EM) wave is a form of continuous energy, of which both the frequency and the amplitude are parts, as shown in a recent report. All the facts relating to the photoelectric effect are explained by the new modified EM wave concept. Since the photon concept is not able to explain the intensity effect and the ejection direction clearly, it cannot be used to explain nonlinear optical phenomena clearly. The current understanding of the interaction process between orbital electrons and light may not be realistic. In this work, the electron transition process is explained with the new modified EM wave concept. The orbital electrons of a material rotate circularly by the sinusoidal fields of the EM waves. In this way, the electrons absorb light energy as rotational kinetic energy. During the first rotational cycle, the electrons with large enough radii face different potential barriers in neighboring orbits. Consequently, the electrons’ speed is obstructed, and the electrons move behind their natural places (phase); in other words, the electrons cannot follow the required phase of EM waves. Thus, sufficient energetic electrons are scattered from their orbit. The high-intensity EM waves reach the inner orbits of the targeted atom and transit electrons from different orbits. The light can regenerate through processes with different frequencies. The frequency of the regenerated light can be higher than that of primary light, depending on the energy (frequency and amplitude) of the primary light. The results of previous reports match the prediction of the new concept of EM waves. The new wave concept may be able to explain all photonic behaviors of light clearly.

1. Introduction

The electron transition, orbit-to-orbit and orbit-to-vacuum, of a material occur through different forces. The most notable cause of electron transition is light–electron interaction, which is an important task in the science, engineering and technology sectors. After the discovery of the photoelectric effect [1], the classical EM wave concept failed to explain it. Subsequently, Albert Einstein [2] introduced the quantum (photon) concept of light through the explanation of the photoelectric effect in 1905. Einstein explained Lenard’s experimental results [3] of the photoelectric effect. Furthermore, Einstein considered that light is discrete by parts, as in Max Plank [4]’s consideration. The photon contains momentum and it collides with the electrons of photocell materials. As a result, the electrons are ejected. Millikan was dissatisfied [5] with the explanation of the photoelectric effect by the photon concept from 1905 to 1915. Einstein himself was unhappy with the quantum concept. Stephen Hawking [6] wrote in his book that “Einstein refused to believe in the reality of quantum mechanics, despite the important role he had played in its development”. Subsequently, Millikan determined Plank’s constant [7] according to the photon concept in 1916.

The photon concept was not able to explain interference, polarization, etc., during its initial period. De Broglie [8] proposed that photon moves as a wave in 1923. Since then, the photon concept has been known as the duality concept. In some approaches, light is considered a wave, and in others, it is a particle, which is not suitable logic scientifically. If the photon moves as a wave, Einstein’s explanation of the photoelectric effect must be revised. The duality as well as photon concept may not match well with some results of experiments [9,10,11,12,13,14]. Braunstein et al. [9] observed photo-ionization cross-sections of CH₄ and reported that the agreement between calculated and measured photoelectron-asymmetry parameters is unsatisfactory. E. T. Jaynes [12] commented in his research paper that the quantum concept is a mathematical logic only, noting that “This is the grounds for our suggestion that present quantum mechanics is only an empty mathematical shell in which a future physical theory may, perhaps, be built”. Pathria [13] noted the Fowler plot, in which the photoelectrons are ejected by light energy lower than the work function of the palladium element. They thought that ejection had occurred for light and thermal energies, but this was not true. Muhibbullah et al. [14] showed that the total energy of the photon and heat is lower than the work function. Furthermore, the photon concept cannot explain the ejection direction of photoelectrons because their energy equation (E = hν) is not related to the vector. The energy equation of the photon concept has some further limitations. The energy of low-frequency EM waves, such as short-waves, medium-waves, long-waves, etc., is not measurable by the energy equation, even though these EM waves have the same nature as light. The photon theory is not capable of interpreting the (continuous light) solar spectrum. It cannot explain amplitude modulation, because the photons travel as waves but have no amplitude, as stated by De-Broglie [8]. Two other ambiguities in the photon concept are given in detail in the next Section 1.1 and Section 1.2.

1.1. Speed of Electron after Collision with Multiple Photons

Harmonic generation is a nonlinear optical phenomenon in which n numbers of photons with the same frequency interact coherently with a nonlinear material and generate a new photon with n times more energy than the primary photon. In this process, several coherent photons are required to collide with an orbital electron at a moment. The energy conservation of the nth harmonic generation can be written as

$$nh\nu =h\nu ’ (\mathrm{J}),$$

(1)

where nν = ν′, n = 1, 2, 3, etc., and ν and ν′ are the frequencies of the primary and secondary light, respectively. The momentum conservation of the single photon and an electron can be written as

$$\frac{h\nu }{C}=m^{*}{\upsilon }_1 ({\mathrm{kgms}}^{-1}),$$

(2)

where m* is the effective mass of the orbital electrons and ${\upsilon }_1$ is the velocity of the electron. For the nth harmonic generation, the momentum conservative equation should be

$$\frac{nh\nu }{C}=m^{*}{\upsilon }_2 ({\mathrm{kgms}}^{-1}),$$

(3)

where ${\upsilon }_2$ is the velocity of the electron in cases of n number coherent photons interacting with an electron. From Equations (2) and (3), we can write the following equation:

$$n{\upsilon }_1={\upsilon }_2 ({\mathrm{ms}}^{-1}).$$

(4)

The velocity of the affected electron should be increased for higher photon energy, as in Equation (2). If the velocity of the electron is high enough through the collision of the high-energy photon, then the mass of the electron can be considered relativistic. Consequently, Equation (2), which describes the velocity of the electron, can be written as

$${\upsilon }_3=\frac{h\nu }{\sqrt{m_{\mathrm{o}}^2{C}^2+\frac{h^2{\nu }^2}{C^2}}} ({\mathrm{ms}}^{-1}),$$

(5)

where m_o is the rest mass of the electron. For cases in which n number of coherent photons interacts with a single electron, then the electron velocity should be increased and Equation (5) can be written as

$${\upsilon }_4=\frac{nh\nu }{\sqrt{m_{\mathrm{o}}^2{C}^2+\frac{h^2{\nu }^2}{C^2}}} ({\mathrm{ms}}^{-1}).$$

(6)

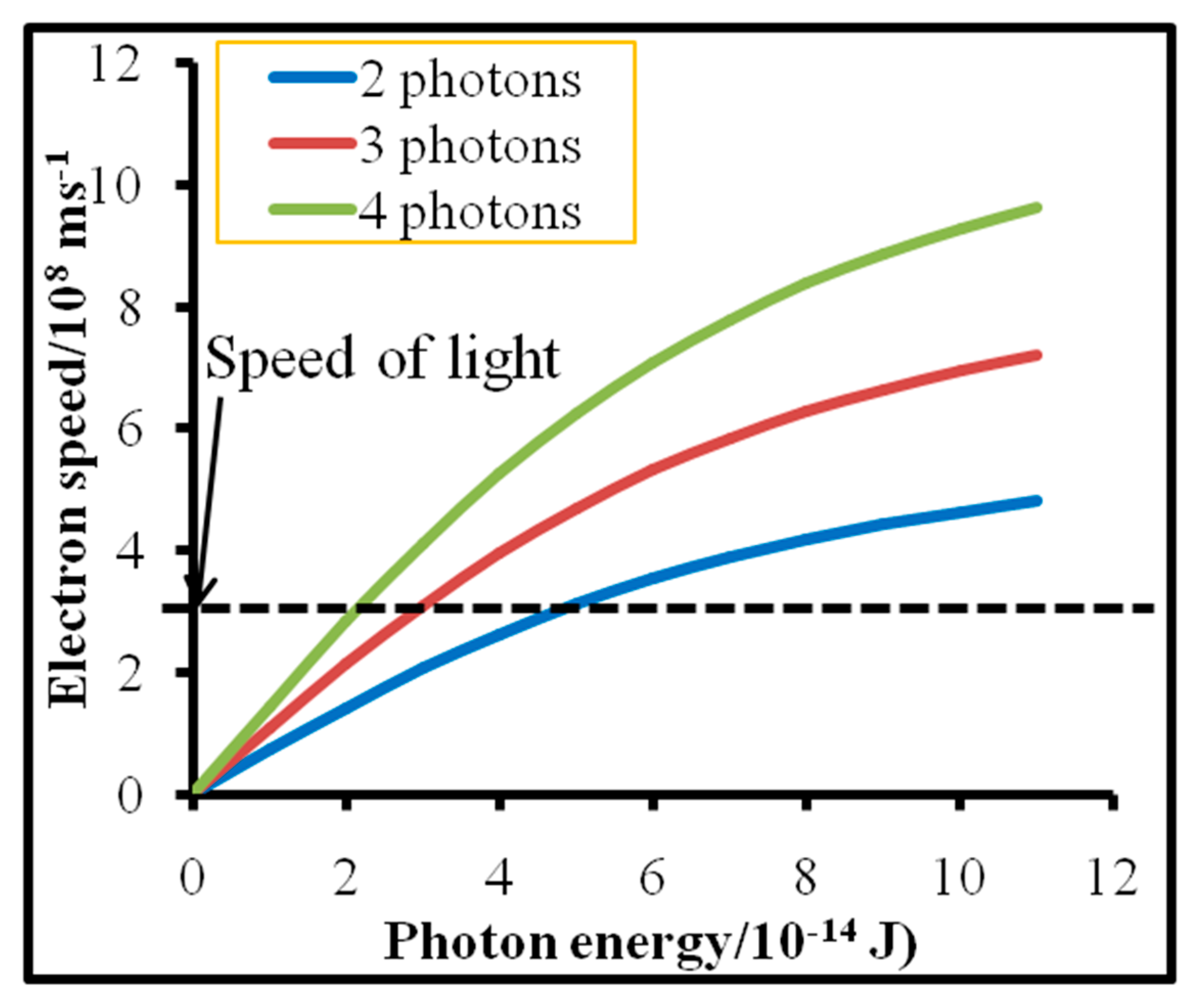
Equation (6) indicates that the electron velocity can be equal to the speed of light for a collision with multiple coherent photons. To plot the photon energy versus the electron velocity, we consider the values of the parameters of Equation (6) as h = 6.626 × 10⁻³⁴ Js, C = 2.998 × 10⁸ ms⁻¹ and, for convenience, m* = m_o = 9.1094 × 10⁻³¹ kg. The graph of the electron velocity is shown in Figure 1. The value of the photon energy hν is taken randomly with a suitable interval. Figure 1 reveals that the electron speed is equal to the light velocity for gamma rays with energies of 0.55 × 10⁻¹⁴ J, 1.0 × 10⁻¹⁴ J and 2.4 × 10⁻¹⁴ J (wavelengths 36.12, 19.87 and 8.28 pm, respectively) for interactions with 2, 3 and 4 coherent photons, respectively. The speed of the electrons has to be faster than light when the photons’ energies are greater than 0.55 × 10⁻¹⁴ J, 1.0 × 10⁻¹⁴ J and 2.4 × 10⁻¹⁴ J for interactions with 2, 3 and 4 coherent photons, respectively. The gamma rays of this range and the values higher than the energy of the range are available (0.15 pm to 3.434 pm; energy 1.325 × 10⁻¹² J to 5.788 × 10⁻¹⁴ J) [15]. According to the photon concept, multiple coherent photons are able to collide with an electron in a linear path, at which point Equation (6) is true. According to the theory of relativity, the speed of electrons should not equal or exceed the speed of light. This was the case here. Therefore, there is a problem in either the theory of relativity or the photon concept (or both). If the problem is in the photon concept, then the explanation of photonic phenomena, including the generation process of the laser-induced breakdown spectrum and the anti-Stoke spectrum, is not reliable.

1.2. Momentum Conservation of Multiple Photons with an Electron

Photons collide with electrons of high energy and remove them from the orbits to generate the laser-induced spectrum and the anti-Stoke spectrum. We wish to be clear about the momentum conservation in this case. Equation (4) indicates that the n number of coherent photons increases the velocity of an electron n times more. That is, if two photons hit one electron coherently, then the electron obtains a velocity that is twice as great as in the collision of a single photon. In this way, the primary coherent photons together transit an electron with more energy from an orbit and, as a result, light is produced with increased (for instance, double) frequency in the case of the second harmonic generation. However, the explanation for the momentum conservation of the photon concept is not practical, as in, for example, Newton’s cradle experiment. Ball I and ball II (or more) of Newton’s cradle move slightly away from ball III (standing ball) and hit ball III together at speed (Figure 2a). Next, front ball III moves away from the other end at the same speed along the direction of ball I, as shown in Figure 2 (videos of Newton’s cradle are available on YouTube). Ball I is stopped after hitting, and ball II moves ahead, together with ball III (Figure 2b) without changing its velocity. Here, the conservation law of momentum is obeyed. Balls I and II do not stop, and ball III does not move at double speed. The photon has momentum and obeys the conservative law, as in Einstein’s explanation. Therefore, in the case of harmonic generation, when two coherent photons hit an electron together, one photon should be absorbed by the electron and the other photon should move forward with its velocity, such as ball II in Figure 2b, and the momentum of the moving electron should be equal to the momentum of the absorbed photon. Since another photon should not be absorbed and should move ahead with its velocity, the electron should not gain more energy than that gained by a single photon interaction. Usually, the energy of a laser photon is lower than the energy of inner orbital electrons due to its low frequency, according to the photon concept. Therefore, large numbers of coherent photons from a focused laser are not able to remove an electron of high vacuum energy from the inner (e.g., K) shell according to the conservative momentum laws, since these multiple coherent photons do not act as a high-energy single photon. The focused laser is able to remove orbital electrons whose energy is equal to the energy (hν) of a laser photon only. The remaining photons pass through the target material. Consequently, the focused laser is not able to build the laser-induced and anti-Stoke spectra, according to the photon concept. This means that photon theory is not able to explain electron transition or light regeneration with higher frequencies (including harmonic) than the frequency of primary light.

The above facts may cast doubt on the duality (photon) concept. For these reasons, nonlinear optical phenomena may not be clearly explained by the concept, especially in cases in which the frequency of the regenerated light is greater than the frequency of the source light, such as the generation of the laser-induced breakdown spectrum [16,17,18,19,20,21,22,23] and anti-Stoke scattering spectrum [24,25,26,27]. The logic of the interaction process between orbital electrons and light may not be reliable. An alternative concept may solve the problem with better logic.

A group of researchers [28] proposed a modified EM wave concept in 2017. In the modified EM wave concept, both the frequency and the amplitude are parts of the wave’s energy. Recently, Muhibbullah et al. [14,28,29] explained the photoelectric effect using the modified EM wave concept in 2019. They observed that, at a constant frequency, the value of the stopping potential is increased a notable amount (twice) for increased intensity. The experimental results matched the predictions of the modified EM-wave concept. Furthermore, Muhibbullah et al. [14] explained the exceptional part of the Fowler plot by using the modified EM wave concept. They showed that the total value of the thermal (k_BT) and photon (hν) energies (4.709 eV) is smaller than the work function (ϕ = 4.97 eV) of the palladium; therefore, their explanation [13] using the photon concept was unconvincing. The researchers [14] clarified that the ejection occurred through sufficient intensive light energy to be greater than the work function of the photocell material. In addition, Muhibbullah et al. found the direction of the ejected photoelectrons [30], which also matches the prediction of the modified EM wave theory. Therefore, the new modified EM wave concept may offer a better explanation of the orbital electron transition process. The concept may help develop the recent applications of EM waves [31,32]. In the present work, we explain the electron transition process of orbital electrons in view of the modified EM wave concept theoretically, and a simulated work is presented.

According to the propagating EM wave theory [33], the electric field, magnetic field, and propagating direction are orthogonal to each other. According to the modified EM wave concept, the phase difference between the electric and magnetic fields is 90 degrees [34]. Under the influence of light, the electrons in a material rotate circularly through the electric and magnetic fields of the EM waves. If the rotated electron meets an obstacle (or faces changing potential) in its path, then the electron fails to obey the phase of the light and is bound to scatter.

2. Basic Principle

In this work, the transition of orbital electrons is explained by light in view of the modified EM wave concept. Usually, high-frequency EM waves (X-rays, gamma rays, etc.) are able to transmit electrons from inner orbits; however, sufficiently intensive low-frequency (e.g., focused-laser) EM waves also have this ability. The light–electron interaction mechanism of the modified EM wave concept is different from the interaction mechanism of the photon concept. Therefore, the result of the light–electron interaction in the EM wave concept is different, especially when the frequency of the regenerated light is greater than the frequency of the source light. Consequently, we focus on this type of regenerated light (laser-induced spectrum [15,16,17,18,19,20,21,22] and the anti-Stoke spectrum [23,24,25,26], including harmonic generation). We describe the light–electron interaction mechanism, the energy balancing and the frequency of the regenerated light in this section.

The interaction of electrons with EM waves, in which electrons are situated in the homogeneous potential of the conduction bands of photocell materials, is discussed elsewhere [14,29,30,34,35]. Here, we discuss a light–electron interaction in which the electrons are situated in a constant potential, but the region of the potential is an atomic orbit. 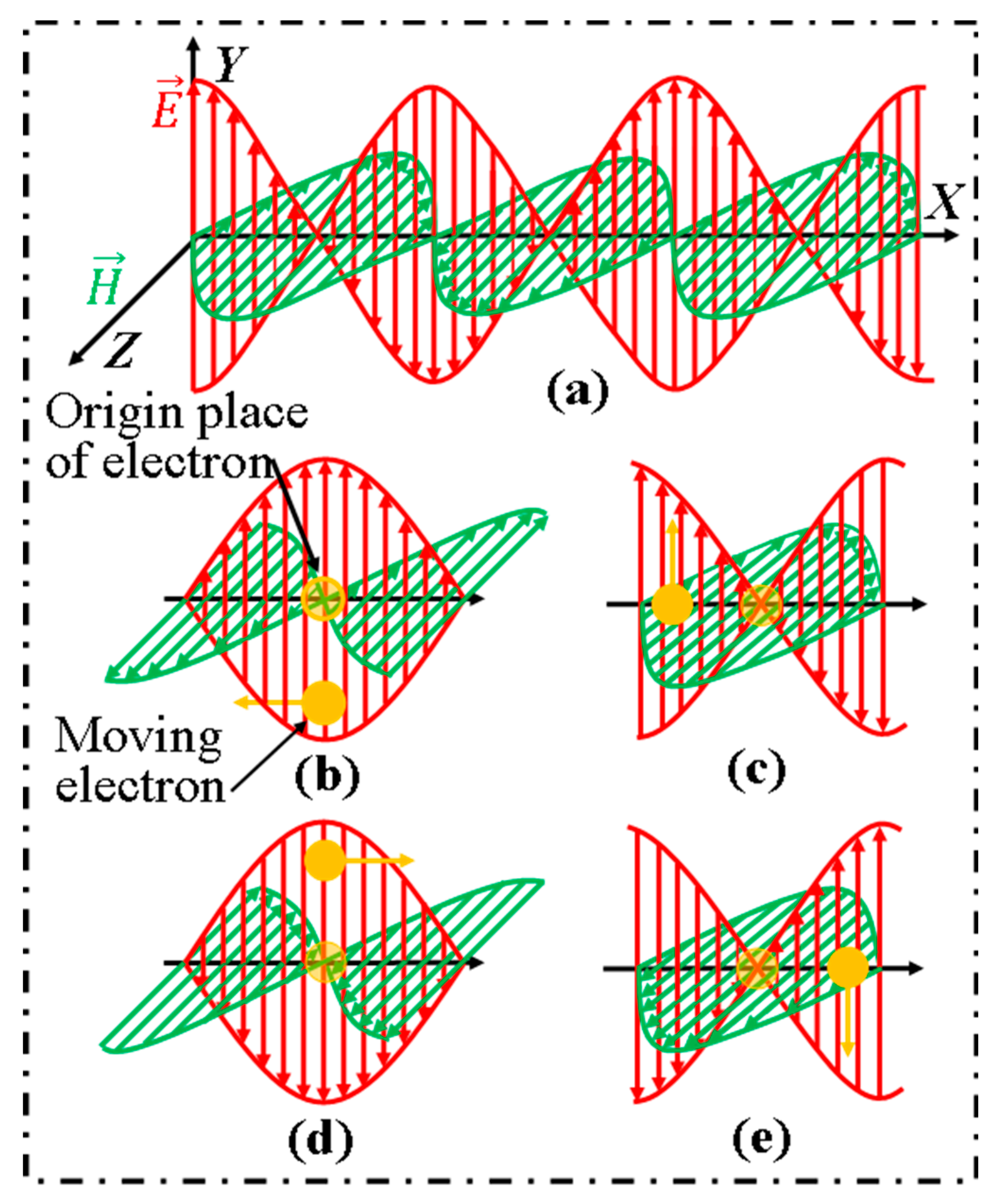Let us consider a coordinate in which the resulting electric field (E) of a monochromatic EM wave lies along the Y axis, the resulting magnetic field (H) lies along the Z axis, and the EM wave propagates along the X axis (Figure 3a). Additionally, let us consider that an electron in an atomic orbit is immersed in the EM wave. Consequently, the electric force acts on the electron along the Y axis, and the magnetic field applies a force along the X axis according to the Lorentz force; therefore, the electron obtains motion on the xy plane. Since the electric field and magnetic field are sinusoidal, both the values of the displacements (x and y) of the electron must be sinusoidal. According to one report [34], the electric field is the driver, and the EM wave source forms a sinusoidal electric field continuously. The EM waves contain a phase difference of 90 degrees between the electric and magnetic fields [34]. In this situation, the electron obtains a circular motion clockwise, as shown in Figure 3b–e. The electric and magnetic fields force the electron continuously, after which the electron obtains a (circularly moving) position, called an “abode” [14,29,30]. This means that the abode is a position in the EM waves in which free electrons are bound to occupy the position by the electric and magnetic forces. The abode does not travel with the EM waves; it rotates only in the EM fields. The abode is a phase of circular motion of the electron.

When the electric field is maximal with a positive value, at that moment, the abode with the electron is situated at the maximum displacement on the negative side of the Y axis for the negative charge of the electron, as shown in Figure 3b. At this point, the absolute magnetic field is zero, but the change rate of the magnetic field is maximal [34] with a positive value, after which the electron obtains a magnetic force along the negative direction of the X axis. After a moment, the electron obtains an increased magnetic field, after which the direction of the velocity of the electron is bent toward the Y axis, according to Fleming’s right-hand-triangle rule for the initial velocity. When the magnetic field is maximal, the electron is situated on the negative side of its original point, with maximum displacement on the X axis (with y = 0), as shown in Figure 3c. Subsequently, the value of the magnetic field starts to decrease (the electric field starts to increase), and the electron remains on the arc of the circular path. The electron reaches the positive side of the Y axis with a maximum value when the electric field reaches its maximum value, as shown in Figure 3d. When the magnetic field reaches its maximum, the electron reaches the front of its original position with maximum displacement. In this way, the abode with electrons moves circularly and clockwise through the sinusoidal EM fields. 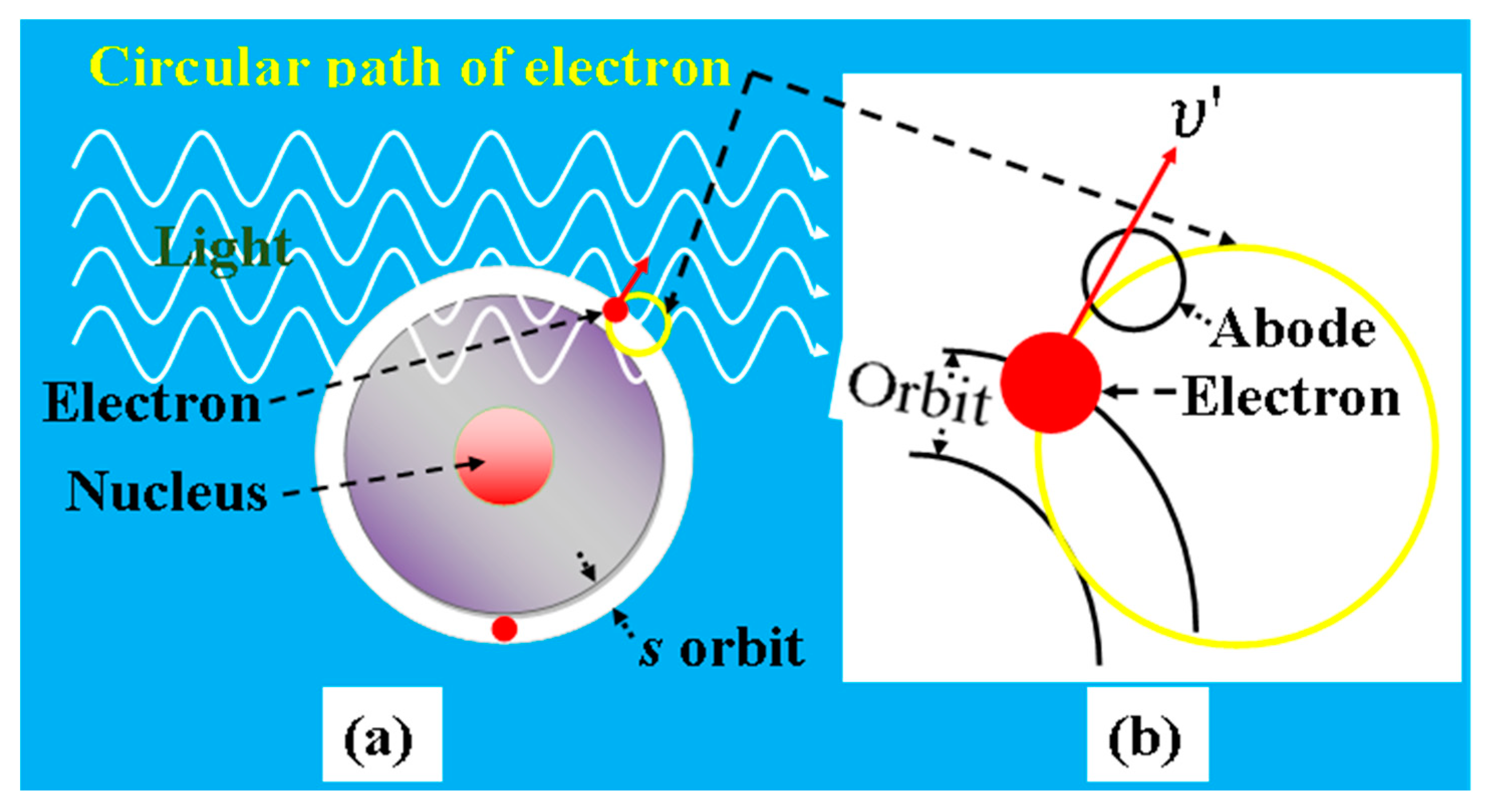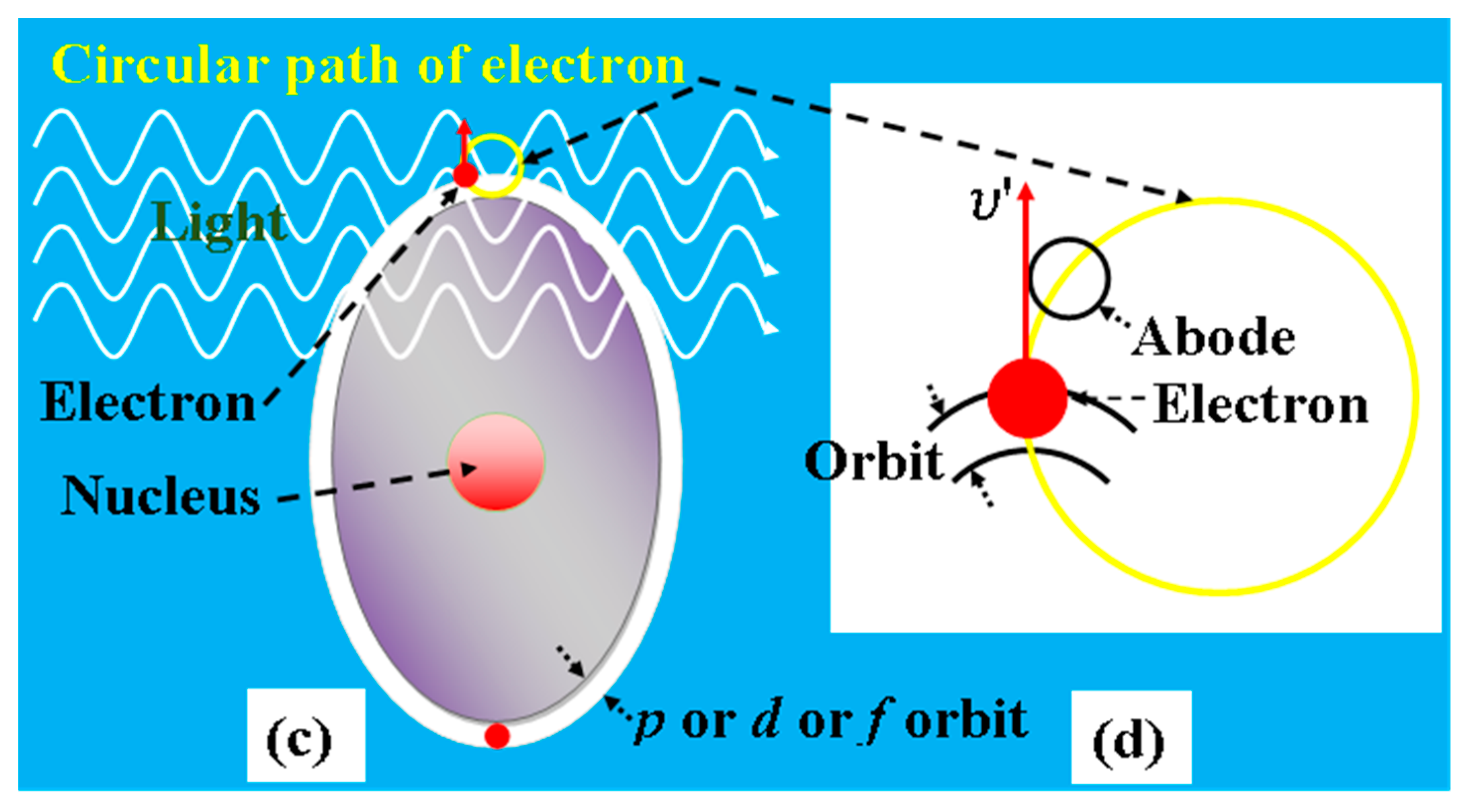The mass of the electron may affect little to reach the maximum value of its velocity (v) initially. At the initial moment of rotation, the radius starts to increase from zero. Therefore, the electron can easily follow the phase due to its small radius. The radius increases gradually and reaches the final position of the abode within a short time. In the atomic orbit, the electrons travel in a homogeneous but spherically shaped potential in the absence of an EM wave. Since no work is undertaken for this movement, the electrons easily undergo circular motion after obtaining oscillating EM fields in the case of electron movement in a homogeneous potential. If the radius of the electrons is large enough, in this case, the velocity of the electrons is obstructed by the spherical potential wall of the atomic orbit (Figure 4a) and the non-spherical potential wall of the atomic orbit (Figure 4c), but the abode is moved with the subsequent phase of EM radiation (Figure 4b,d, respectively). Thus, the abode moves ahead from the electrons, and, next, the moving electrons move out from the back side of the abodes. Subsequently, a phase difference occurs between the abode and the electrons. Thus, the electrons fail to obtain the force from the EM fields, and the electrons are scattered from the orbit along their instant linear momentum, as shown in Figure 4. The scattered electrons may face the effect of another potentiality from the neighboring orbit of an atom after scattering. However, the scattering ability and direction depend on the resultant forces of the EM radiation and orbits. Sufficiently intensive EM waves with any frequency can transit electrons from their orbits, depending on the orbital energies. For cases of higher frequency of EM waves such as X-rays or gamma rays, the energy of the rotational electrons is very high (see Equation (8)), and, therefore, the scattering of the electrons is larger. However, a minimum intensity is needed for scattering because the rotational electrons have to move to the different potential regions to create the transition situation. Alternatively, this may occur through a phonon vibration. If the atoms of the target material face phonon vibration, the whole structure of the orbits vibrates with the atoms. In this case, the facing of the changing potential of the rotational electrons is not similar to the absence of phonon energy. The phase of light does not vibrate with the phonon vibration; therefore, the electrons are scattered earlier or later than in the phonon-free situation, depending on the instant phase of the light. In the case of spinning motion, the spins of a couple of electrons in an orbit are opposite, according to Pauli’s exclusion principle. In a wave front as well as in the phase of an EM wave, the coupled electrons may try to align in the same direction of spin through the actions of EM fields. This alignment may create a force because the new alignment hampers their natural spinning rotation (unpublished; a presentation in a seminar [35]). This force may also help scatter the electron from orbit. It is possible that not all couples obtain the same phase of the EM waves at a moment due to their random positions in an atom, but some couples of electrons may obtain the same phase of light and create scattering situations.

The EM wave has continuous energy and moves electrons of the target material circularly. The radius of the circle depends on the values of the electric and magnetic fields because the static and varying electric field and the varying magnetic field apply force on electrons proportionally. The electrons absorb the energy of the EM waves by getting rotation and achieving rotational kinetic energy up to a limit for a certain light intensity. If the wave front of an EM wave falls on a material, then all the electrons of the first layer are able to absorb a certain limit of energy of the EM fields with a maximum radius. The remaining EM wave energy (with the same frequency but relatively less intensity) moves to the second layer and is then absorbed, and so on. Consequently, the radius of the electrons of the later layer is smaller than that of the previous layer. The intense laser ray contains huge energy and may able to reach the bottom orbit of all the atoms of the target material, depending on the energy of the focused laser.

According to the modified EM wave concept, the energy flux density equation is frequency-dependent. For a numerical description of energy conservation, let us consider a wave front of monochromatic light with frequency f falling on a material. The average energy density of the incident light can be written [28] as

$$E=\frac{1}{2}\pi f\epsilon \mu S{E}_{\mathrm{m}}{H}_{\mathrm{m}} ({\mathrm{Jm}}^{-2}),$$

(7)

where ε is the electric permittivity and µ is the magnetic permeability of the medium (target material), S is an irradiated area, and E_m and H_m are the maximum electric and magnetic fields of the light, respectively. The light energy is continuous; consequently, the numbers of electrons per unit area (N) of the first layer of the material are rotated together by its electric and magnetic fields. The rotated electrons absorb light as kinetic energy. For an intensity of light, the radius (r) of the circular motion of the electrons is constant. The kinetic energy of the rotational electrons can be written as

$$E=\frac{1}{2}Nm{\omega }^2{r}^2=2Nm{\pi }^2{f}^2{r}^2 ({\mathrm{Jm}}^{-2}),$$

(8)

where m is the mass of the electrons outside the atoms. If we ignore the lost portion of light energy (reflection and other), the kinetic energy of the electrons should be equal to the light energy. In this case, the radius of the circular motion can be written from Equations (7) and (8) as

$$r=\sqrt{\frac{\mu \epsilon S}{4Nm\pi f}{E}_{\mathrm{m}}{H}_{\mathrm{m}}} (\mathrm{m}).$$

(9)

If the areal density of the electrons of the first layer is insufficient (say N′) to absorb the total light energy, then the partial absorbed energy (E′) per unit area can be:

$$E^{\prime }=2N^{\prime }m{\pi }^2{f}^2{r}^2 ({\mathrm{Jm}}^{-2}).$$

(10)

The intensity of the light should be reduced after passing the first layer without changing its primary frequency; subsequently, the radii (say r₁ > r₂ > … > r_n) of the electrons should gradually decrease in each layer. Let us consider that the n layers of the electrons absorb the total light energy. The total absorbed energy E per unit area can be written as

$$E=2m{\pi }^2{f}^2\left(N_1{r}_1^2+N_2{r}_2^2+ \dots \dots .+N_{\mathrm{n}}{r}_n^2\right) ({\mathrm{Jm}}^{-2})$$

(11)

where N₁, N₂, …N_n are the areal densities of the electrons for different layers (1st, 2nd, …, nth). The focused laser contains high-intensity EM fields. Therefore, it may be possible to transmit electrons from the last (nth) layer of the target material with sufficient intensive light. In other words, a lower frequency but very high intensity of light can remove electrons from the deepest (K) shells. The higher frequency of light can be generated through intensive light at lower frequencies. The formation of plasma is possible and, in this way, the laser-induced spectrum can be generated. In a similar way, the anti-Stoke spectrum can also be generated. The addition of phonon energy is not mandatory to generate the anti-Stoke spectrum according to the modified EM wave theory.

To observe the speed of scattered electrons, let us consider a monochromatic EM wave with total energy (E) which falls on a material surface with value S (m²). Some part of the energy is absorbed by converting the kinetic energy (E_k) of the electrons of the material, and other parts are wasted (E_w) as heat energy and in other ways. The total energy of the surface area can be written as

$$E=E_{\mathrm{w}}+E_{\mathrm{k}} (\mathrm{J})$$

(12)

If the lost part is very small (or we take it to be zero, E_w = 0, for convenience) then all EM wave energy is converted as the kinetic energy of the electrons as

$$E=E_{\mathrm{ki}}=\frac{1}{2}N{m}^{*}{\upsilon }^2 (\mathrm{J})$$

(13)

Here, m* is the mass of an electron in the material, N (saying) is the number of rotated electrons of the region S, and $\upsilon$ is the velocity of the electrons in the material. If a moving electron (with kinetic energy $\frac{1}{2}{m}^{*}{\upsilon }^2$) is able to eject from the orbit, then the electron loses little energy as work function (W_o). The velocity of the outgoing electron is reduced (say ${\upsilon }_{\mathrm{o}}$, after scattering) by the energy loss, and the energy equation can be written as

$$E=\frac{1}{2}Nm{\upsilon }_{\mathrm{o}}^2+N{W}_{\mathrm{o}} (\mathrm{J})$$

(14)

Here, the electron is out of the potential region (or material), and the mass of it is m. For relativistic mass, the above equation can be written as

$$E=\frac{Nm{\upsilon }_{\mathrm{o}}^2}{2\sqrt{1-\frac{{\upsilon }_{\mathrm{o}}^2}{{\mathrm{C}}^2}}}+N{W}_{\mathrm{o}} (\mathrm{J})$$

(15)

or $\frac{N{m}_{\mathrm{o}}C{\upsilon }_{\mathrm{o}}^2}{\sqrt{C^2-{\upsilon }_{\mathrm{o}}^2}}=2\left(E-N{W}_{\mathrm{o}}\right)$

Here, the electron rest mass is m_o (9.1 × 10⁻³¹ kg), and the speed of light is C (2.998 × 10⁸ ms⁻¹). To avoid complexity, let A = Nm_oC, and B = (E − NW_o). We obtain

$$A^2{\upsilon }_{\mathrm{o}}^4+4B^2{\upsilon }_{\mathrm{o}}^2-4B^2{C}^2=0$$

or ${\upsilon }_{\mathrm{o}}^2=\frac{-4B^2\pm \sqrt{16B^4+16A^2{B}^2{C}^2}}{2A^2}$

since ${\upsilon }_{\mathrm{o}}=\frac{\sqrt{-4B^2-\sqrt{16B^4+16A^2{B}^2{C}^2}}}{\sqrt{2}A}$ is not realistic.

Thus, ${\upsilon }_{\mathrm{o}}=\frac{\sqrt{-4B^2+\sqrt{16B^4+16A^2{B}^2{C}^2}}}{\sqrt{2}A}$

Then, the speed of the scattered electron should be written as

$${\upsilon }_{\mathrm{o}}=\frac{\sqrt{2B\left(\sqrt{B^2+C^2{A}^2}-B\right)}}{A}$$

(16)

The speed of scattered electrons can be found using the above equation. The electrons eject straight from the arc of the circular path as shown in the Figure 4.

3. Results and Discussion

The radius of the rotation of the electrons depends on the value of the electric and magnetic fields as well as the light intensity. According to Equation (9), the radius of the circular motion is proportional to the square root value of the electric and magnetic field intensities. A graph was plotted for the radius versus the electric and magnetic fields, which is shown in Figure 5. For the simulation, we consider the value of $\sqrt{\frac{\mu \epsilon S}{4Nm\pi f}}$ as 1 (arbitrary unit) to avoid complexity, and we can assume that all these parameters are constants. Figure 5 shows that the radius of the rotational motion increases nonlinearly with the electric and magnetic fields. An experimental report [30] shows that the radius of the circular motion increases with light intensity. The nature of the intensity versus radius is similar to Figure 5; that means the results in Figure 5 are in agreement with the report. The electric and magnetic fields are parts of the energy of the EM waves, along with their frequencies, according to the modified EM wave concept. The increased intensity increases the radius as well as the absorbed energy of the electrons, which increases the stopping potential of the photoelectron; the prediction matches the results of a photoelectric effect experiment [29]. The photon concept [14] cannot explain the intensity effect clearly. If the areal density of the electrons of the first layer is not sufficiently large to absorb the total light energy, then the radius of the circular motion is constant, with a maximum value up to a limit of areal density (N_c) for a light intensity, as shown in Figure 6. In this case, the absorbed energy is proportional to the areal densities of the electrons. To plot the graph, the value of 2mπ²f² is kept constant. After exceeding the critical limit of the areal density, the electrons absorb the total light energy and, subsequently, the radius starts to decrease for monochromatic light, as predicted by Equation (10).

The intensity (energy) of the light should be reduced after passing the first layer, after which the radii (say r₁, r₂, …, r_n) of the electrons should become gradually smaller in each layer for a constant frequency. Subsequently, the energy of the light is chronologically reduced to the later layer. However, sufficiently intensive focused lasers may remove electrons from the K shell, as we mentioned previously. As a result, light is generated with high frequency, although the frequency of the primary light (laser) is smaller. In the laser-induced [16,17,18,19,20,21,22,23] spectrum, there are many regenerated lights in which the frequency of the regenerated light is greater than the primary light. According to the photon concept, the explanation of regenerated light with higher frequency (higher than the source light) is possible only when the target material is gone in plasma state; the exception is for the case of harmonic generation. There are few experiments in which the sample is immersed in water; in that case, the temperature should be up to 100 degrees Celsius. In this temperature, the sample may not go to plasma state, but light is regenerated with higher frequency (400 nm wavelength) [21]. The light source is a Q-switched Nd:YAG laser, with a repetition rate of 10 Hz and pulse width of 10 ns. Second harmonic generated (532 nm wavelength) light is used. The frequency of the regenerated light is also not harmonic. According to the modified EM wave concept, the spectrum can be generated by a focused laser without the formation of a plasma state. Similarly, the anti-Stoke [24,25,26,27] spectrum can also be generated by intense laser irradiation. If the intensity of the focused laser is very high, then the orbital electrons cannot return to the orbits for absorbing energy as kinetic form; in this situation, the target material moves into the plasma state. A low frequency is not a barrier to building the plasma state in the concept of modified EM waves. If the target materials are formed as plasma states, the range of the laser-induced frequency should increase.

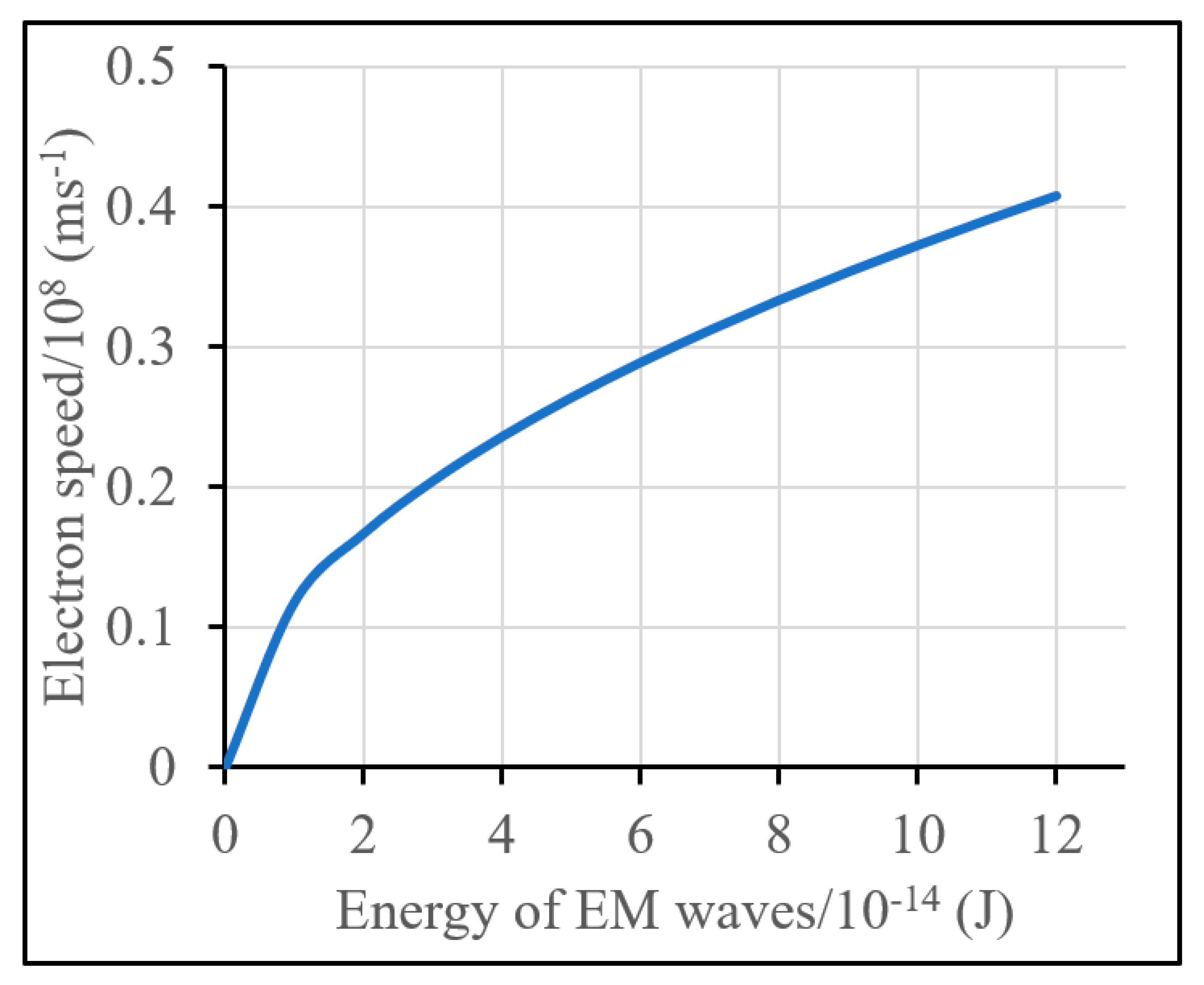
To plot the speed of scattered electrons versus energy of the EM waves, it would be better if we obtained the experimental values of a few parameters. Now, the values of the parameters are unavailable. We have taken the values from the previous report of photoelectric effect in this work. This is better than the random choice. In the report, the electrons number of the irradiated area (3.96 × 10⁻⁴ m²) was 157 (=N), and the work-function was W_o = 1.04 × 10⁻¹⁹ J (0.649 eV). The EM wave energy range was the range of visible light [30]. We have plotted the energy of the EM waves (range 0 to 12 × 10⁻¹⁴ J) versus the speed of scattered electrons using Equation (16). The electron starts to eject after absorbing the energy more than the total work-function NW_o (1.633 × 10⁻¹⁷ J). Figure 7 shows that the speed of the scattered electrons is less than the speed of light for the energy range. However, the speed may exceed the light speed for an ultra higher energy of the EM waves. The comparison of the photon concept and modified EM wave concept is difficult because the measurement processes of energy of the photon and modified EM wave concepts are different. One is discrete, and the other is continuous. Showing the energies of the concepts is not possible on a scale. To observe the present work at a glance, a comparison of the photon and modified EM wave concepts is given in

Table 1. A comparison between the photon and EM wave concepts.

Items	Photon Concept	Modified EM Wave Concept
Application area	It can explain all photonic behavior of light, and the concept can explain classical phenomena of light moderately.	It can explain all classical behavior of light clearly, and the concept can explain all facts of the photoelectric effect clearly as well. It is expected that other modern phenomena can be explained by the concept.
Light-electron interaction process	In this process, the photon collides mechanically with electrons.	In this process, the electric and magnetic fields of EM waves force on electrons.
Scattering direction	Cannot determine.	Can determine.
Intensity effect	Cannot explain.	Can explain.
Light regeneration	Cannot explain the regeneration of light of higher frequency without formation of plasma state.	Can explain the light regeneration of any frequency including harmonic generation and anti-Stoke generation with and without formation of plasma state.

.

The light is continuous energy, and its value depends on both the frequency and the amplitude of the electric and magnetic fields; therefore, it can produce light with any frequency. In conclusion, we can say that the frequency of secondary light (including harmonic) can be higher with any value than the frequency of primary light when light is considered as EM waves.

4. Conclusions

The new, modified EM wave concept predicts that the frequency of regenerated light can be smaller, equal to or greater than the frequency of the source light. We explained the electron transition process in view of the modified EM wave concept. Under light, the electrons in a material rotate circularly through the electric and magnetic fields of the EM waves for a 90-degree phase difference. The rotational electron enters different potential regions and meets an obstacle during potential change. At this point, the electrons’ speed becomes slower, after which the electrons fail to follow the phase of the light and are bound to scatter. High-intensity EM waves of a low frequency are able to reach the inner orbit of the atom and transit electrons to regenerate EM waves of a high frequency. Since the light intensity is part of energy, as is the frequency of the light, the rotated electrons absorb energy from the light continuously rather than discretely. Therefore, the frequency of secondary light can be higher (including harmonic) than the frequency of primary light. The experimental results of the laser-induced and anti-Stoke spectra must match with the prediction of the new concept of modified EM waves. The application of light may be increased for the new concept of modified EM waves. Other photonic behaviors of light, such as the Compton effect, will be explained by using the EM wave concept in the near future.