Recent Progress in Short and Mid-Infrared Single-Photon Generation: A Review
Abstract
1. Introduction
2. Probabilistic Sources
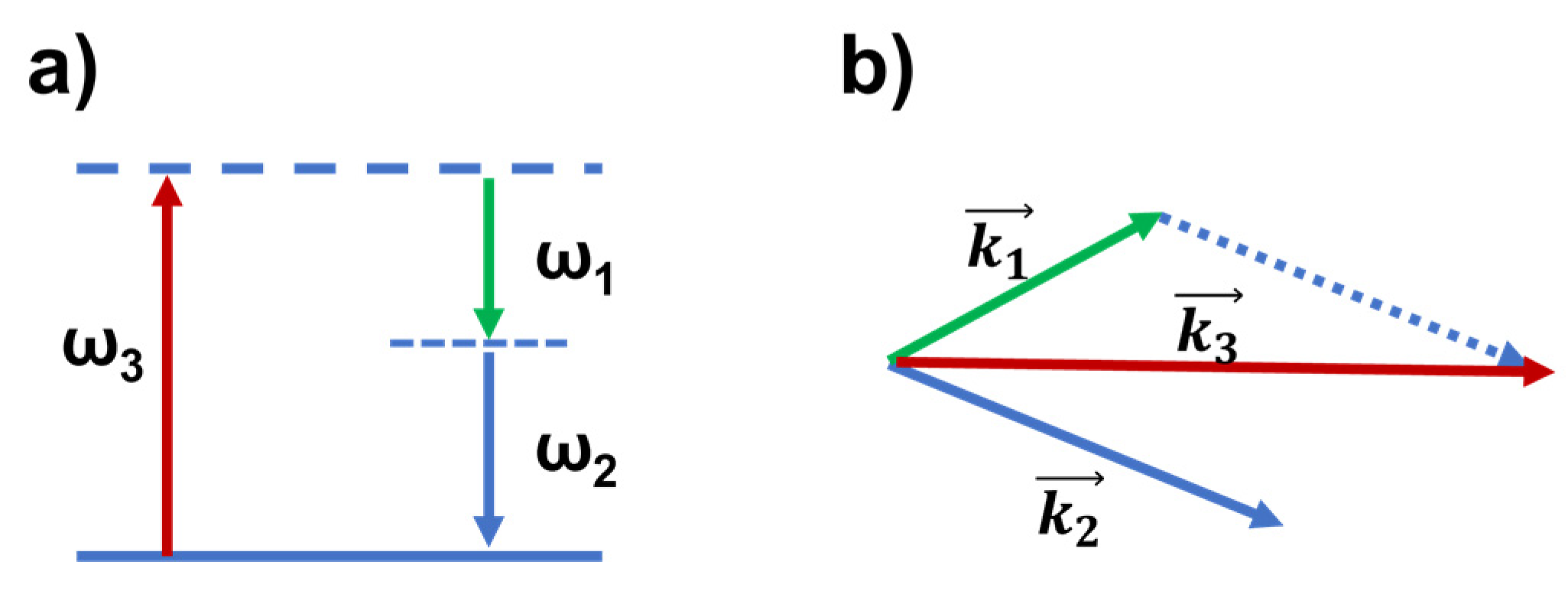
2.1. Parametric Downconversion
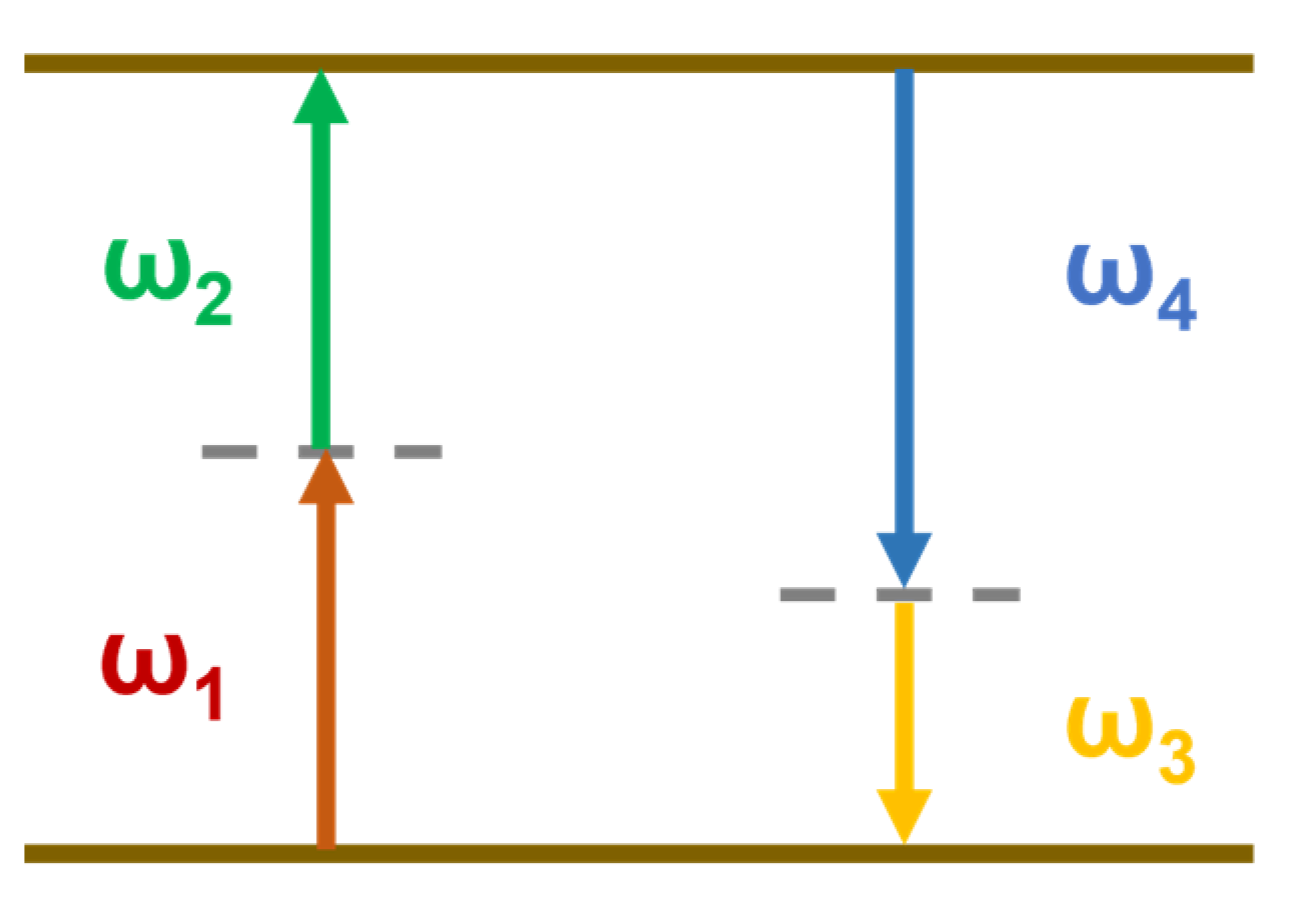
2.2. Four Wave Mixing
3. Characterization of the Source
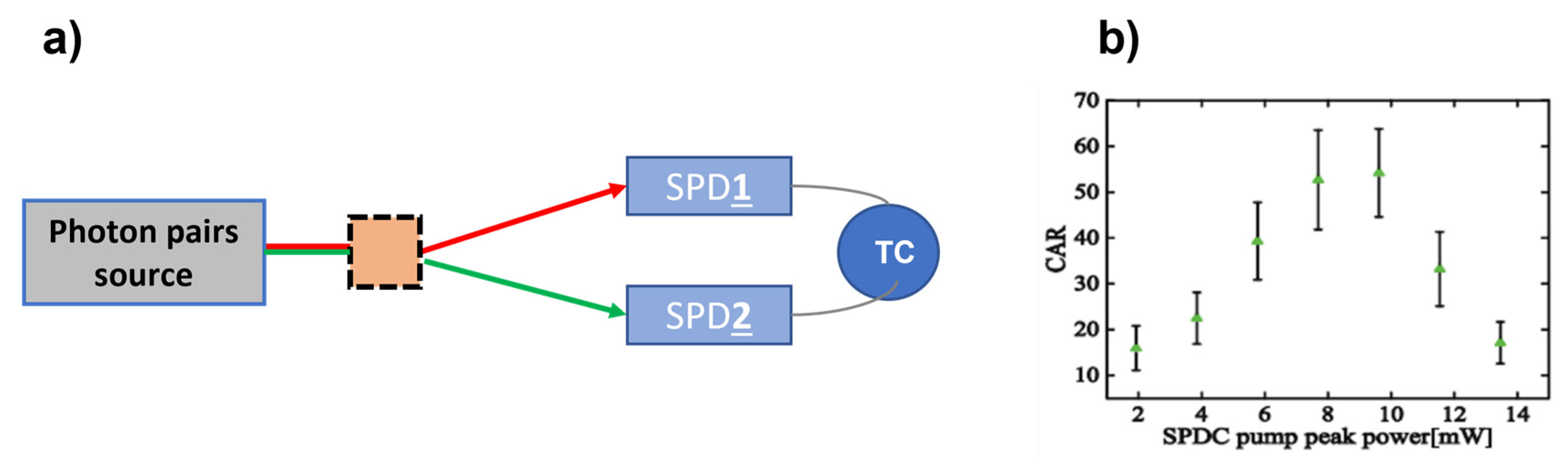
3.1. Coincidence Measurements and CAR
3.2. Purity and Second Order Correlation Function
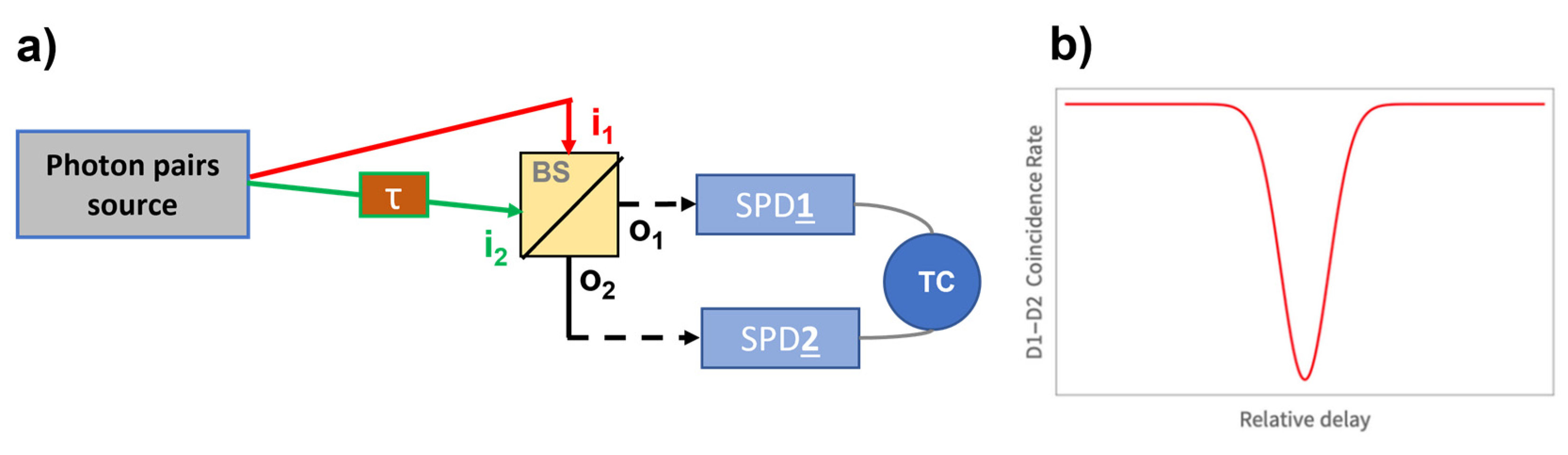
3.3. Indistinguishability with HOM Interference
4. SPDC in the MIR
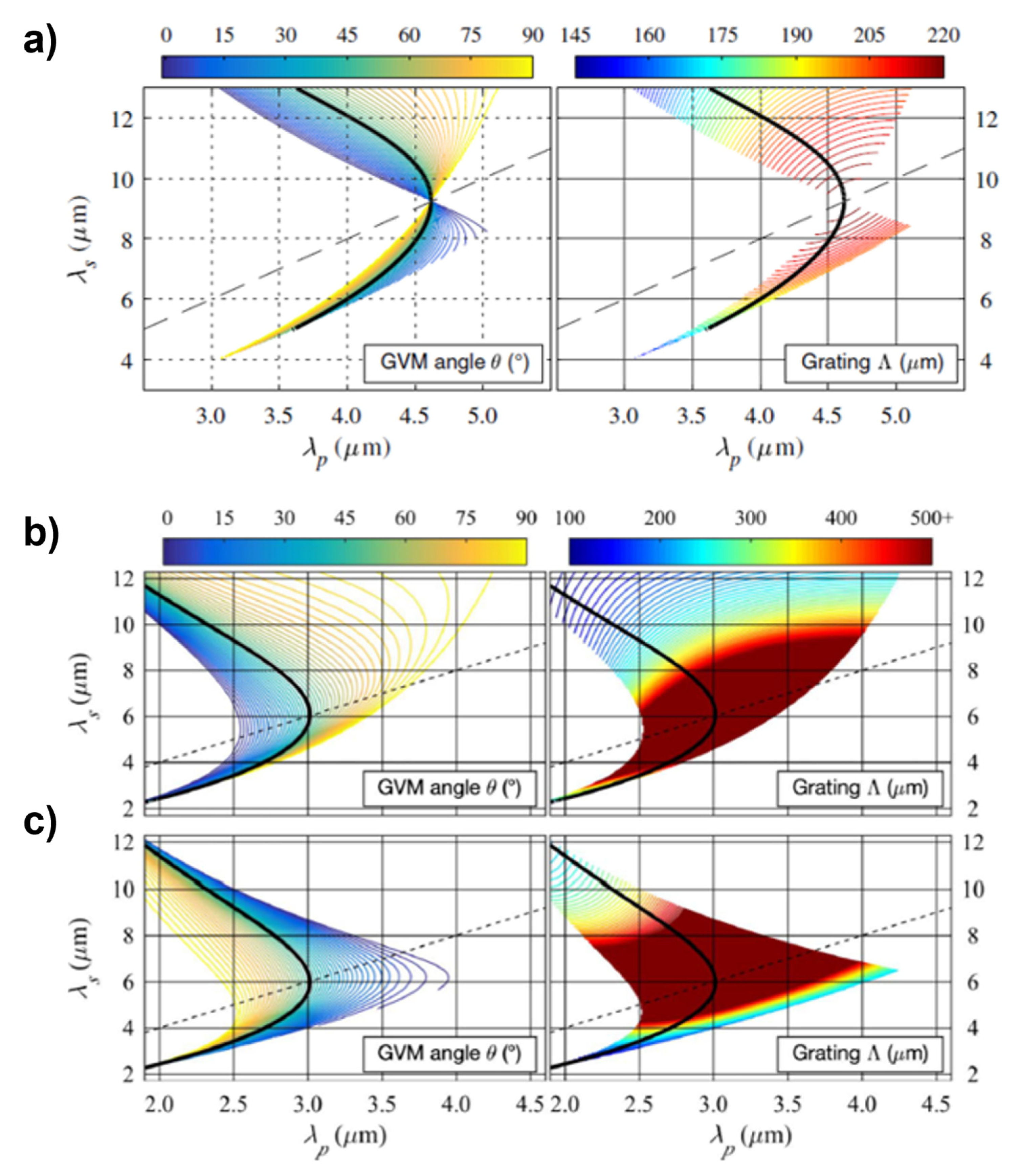
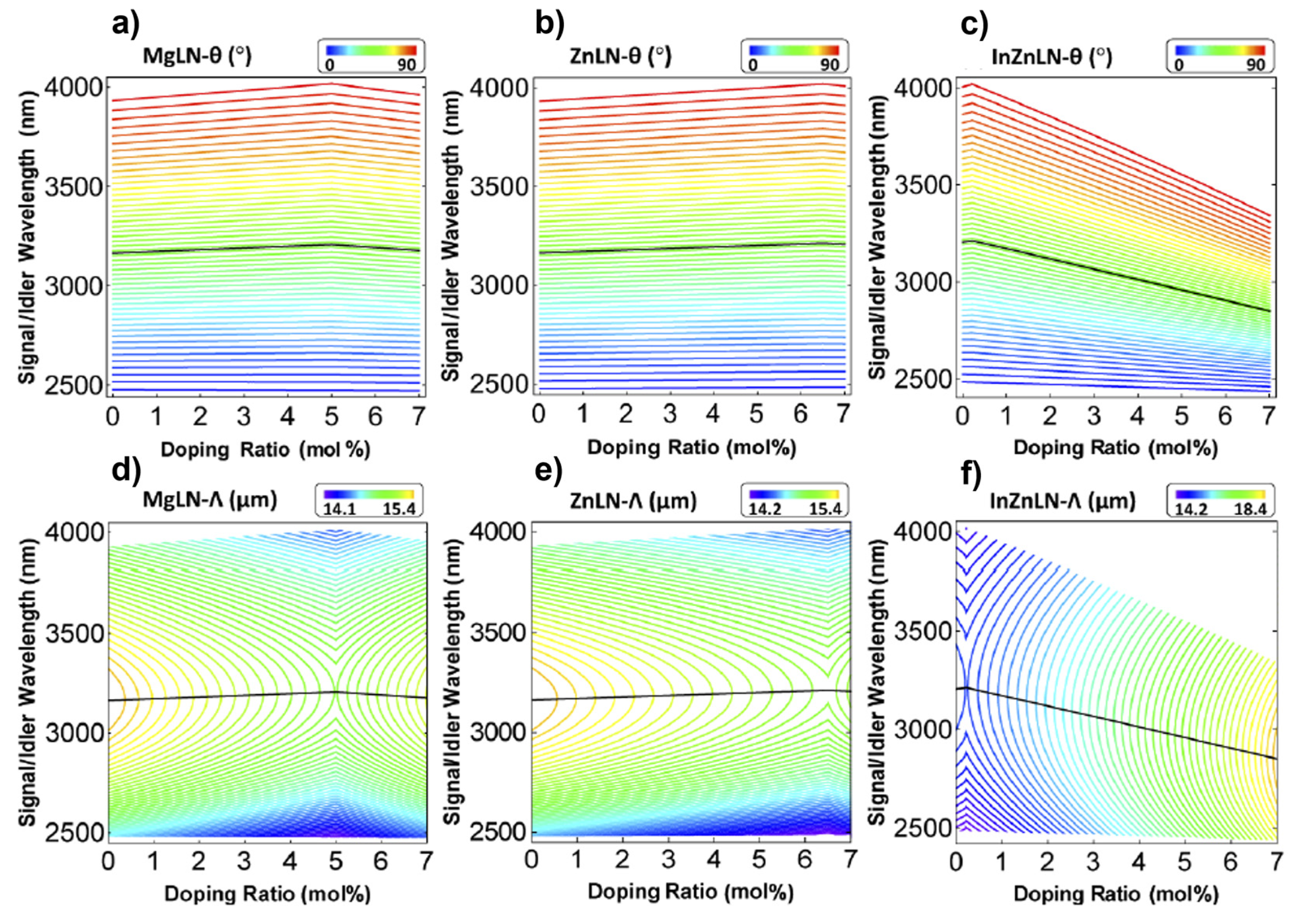
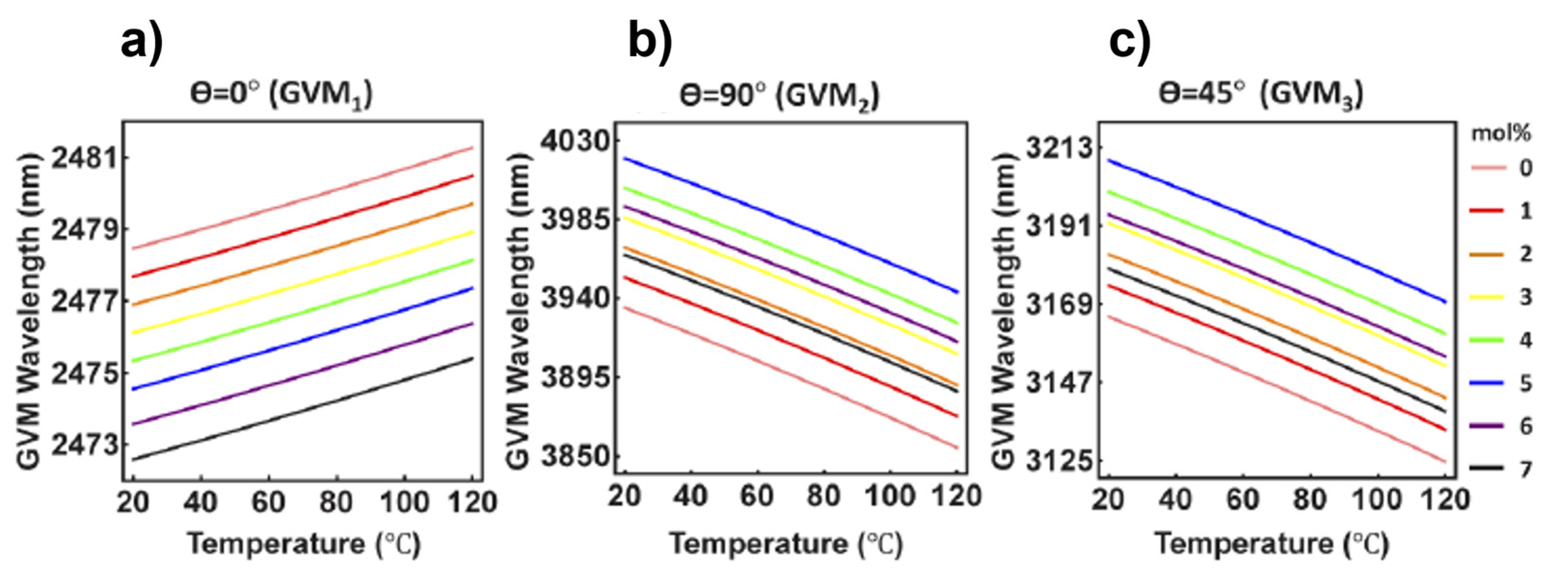
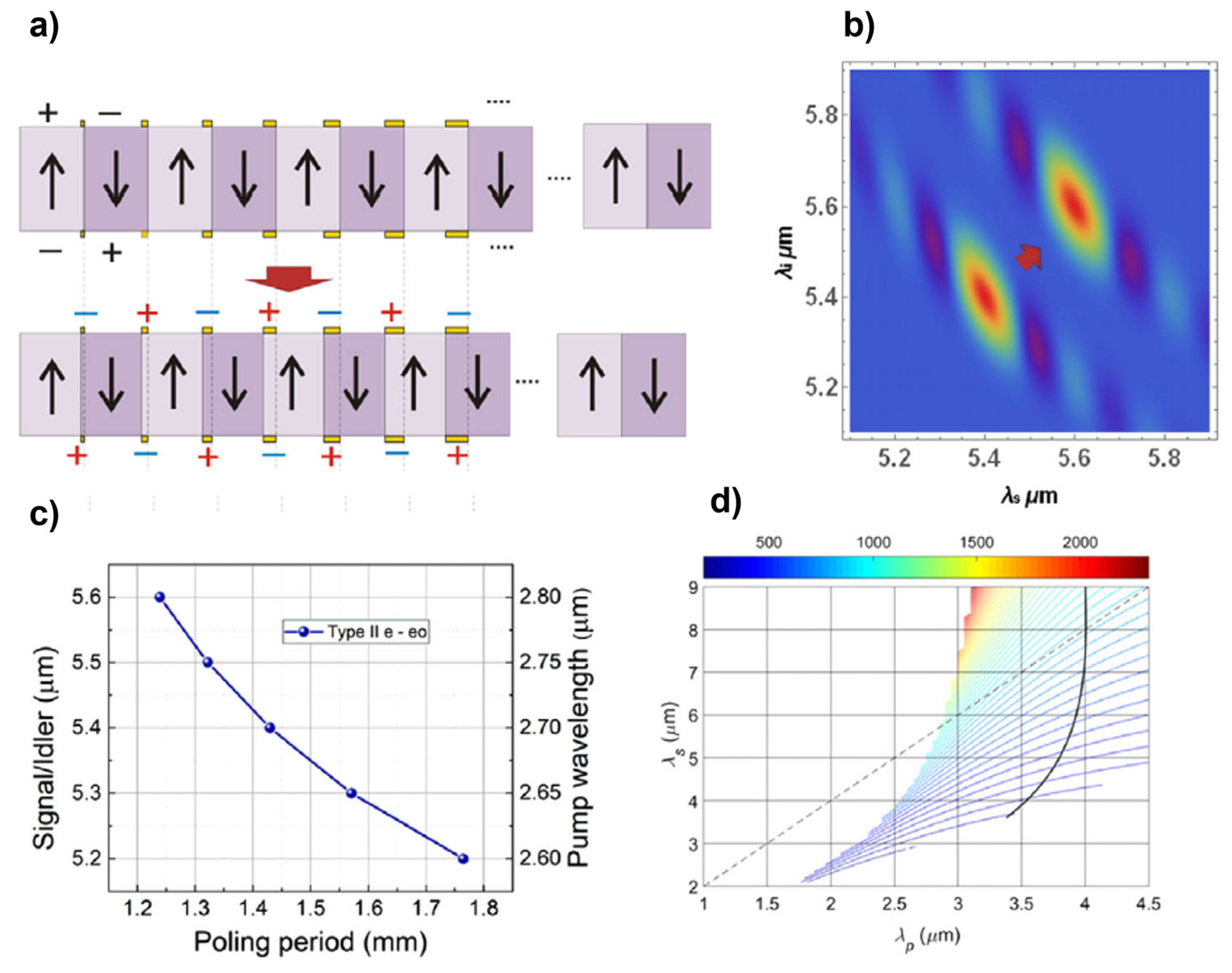
4.1. Numerical Study
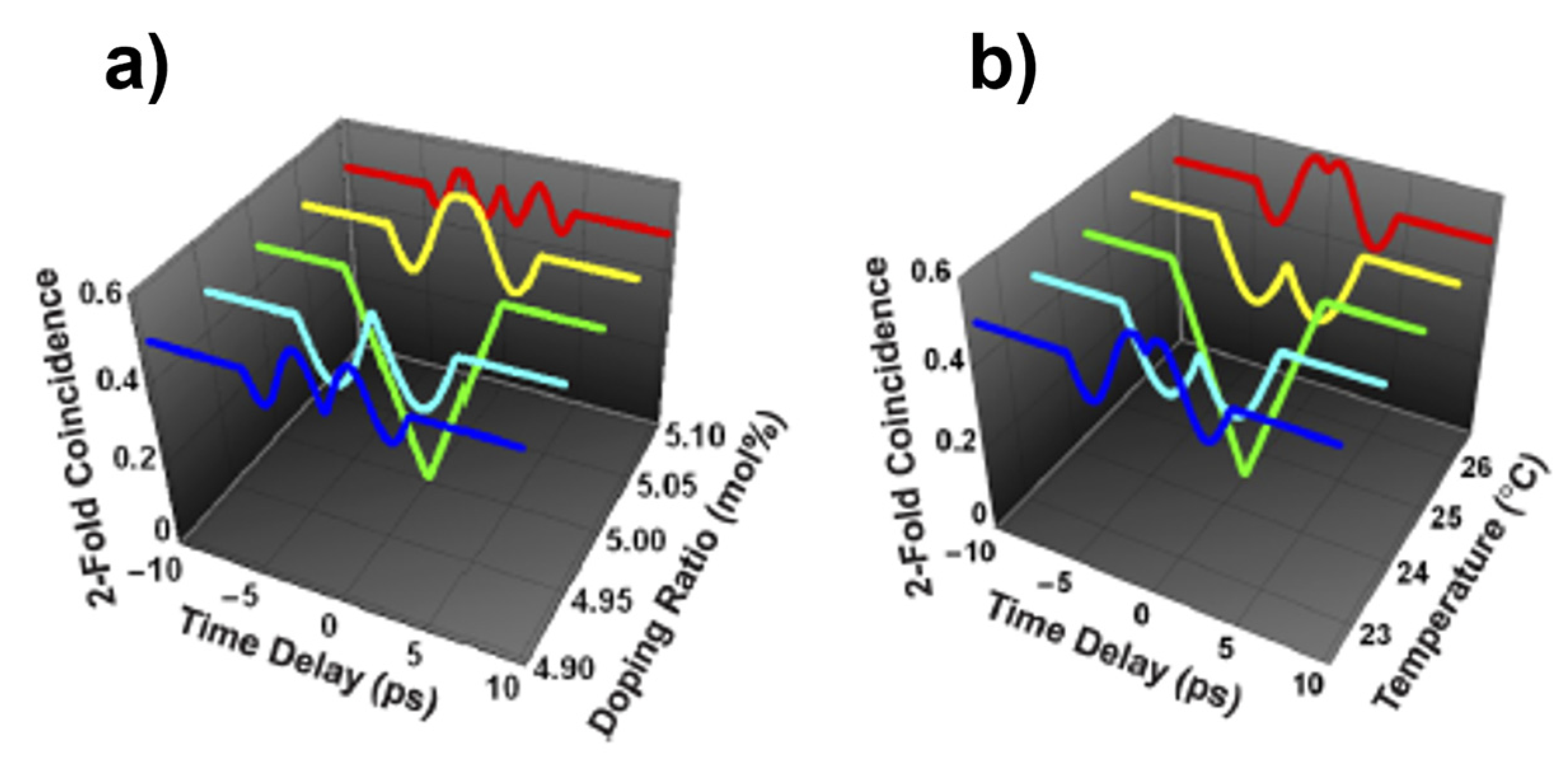
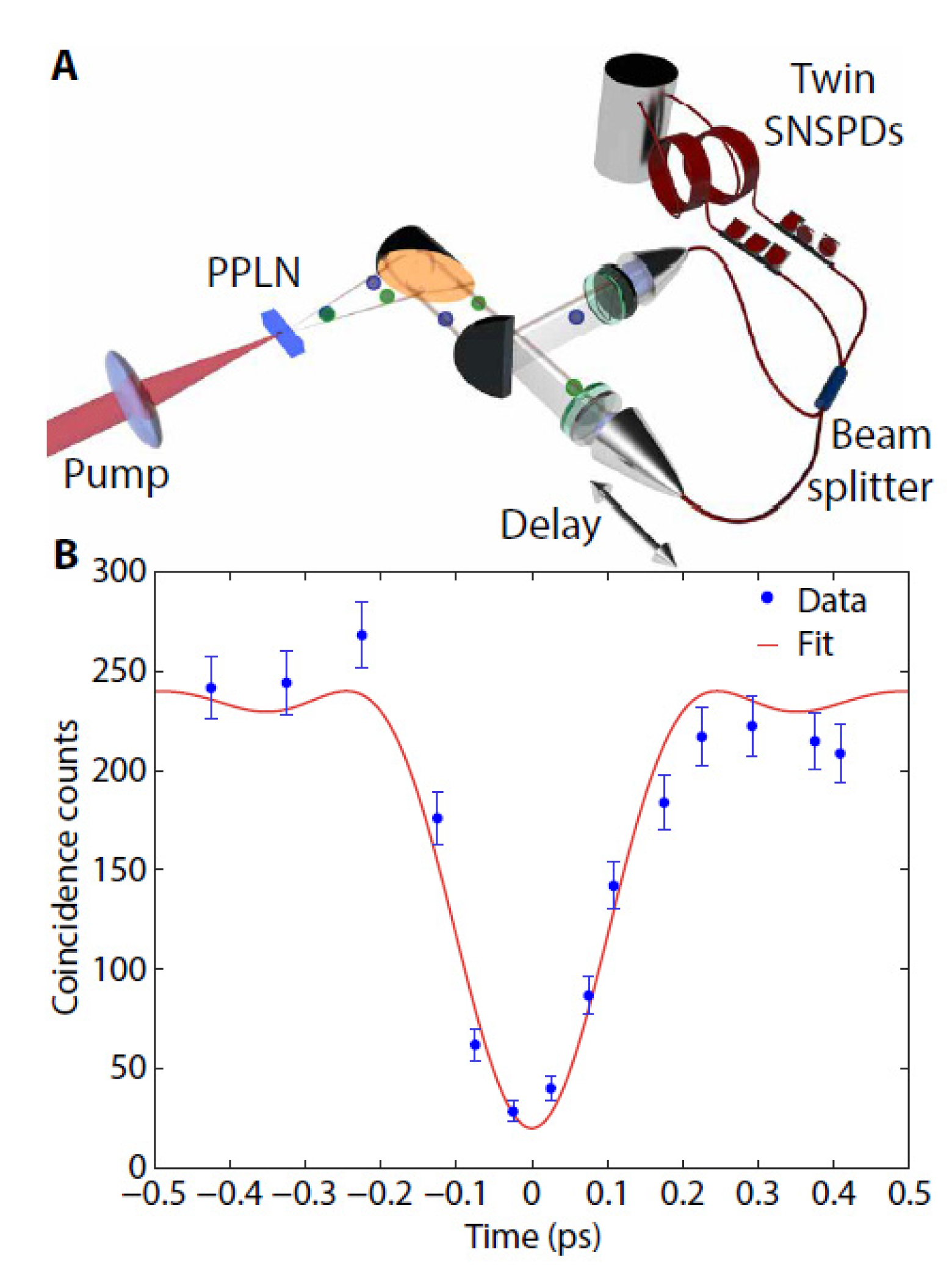
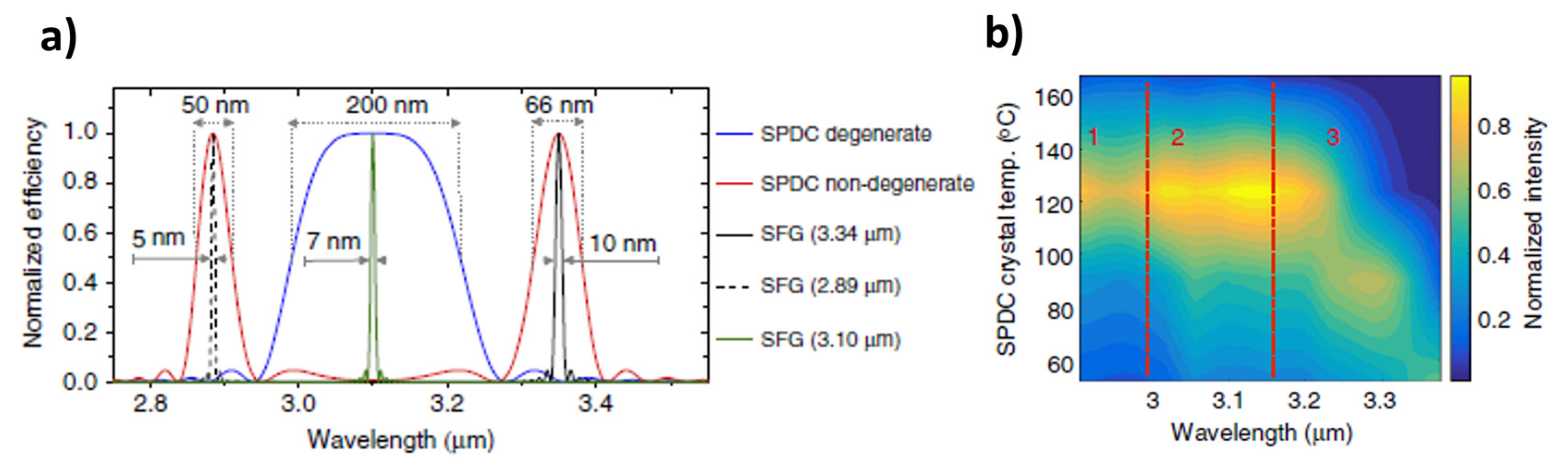
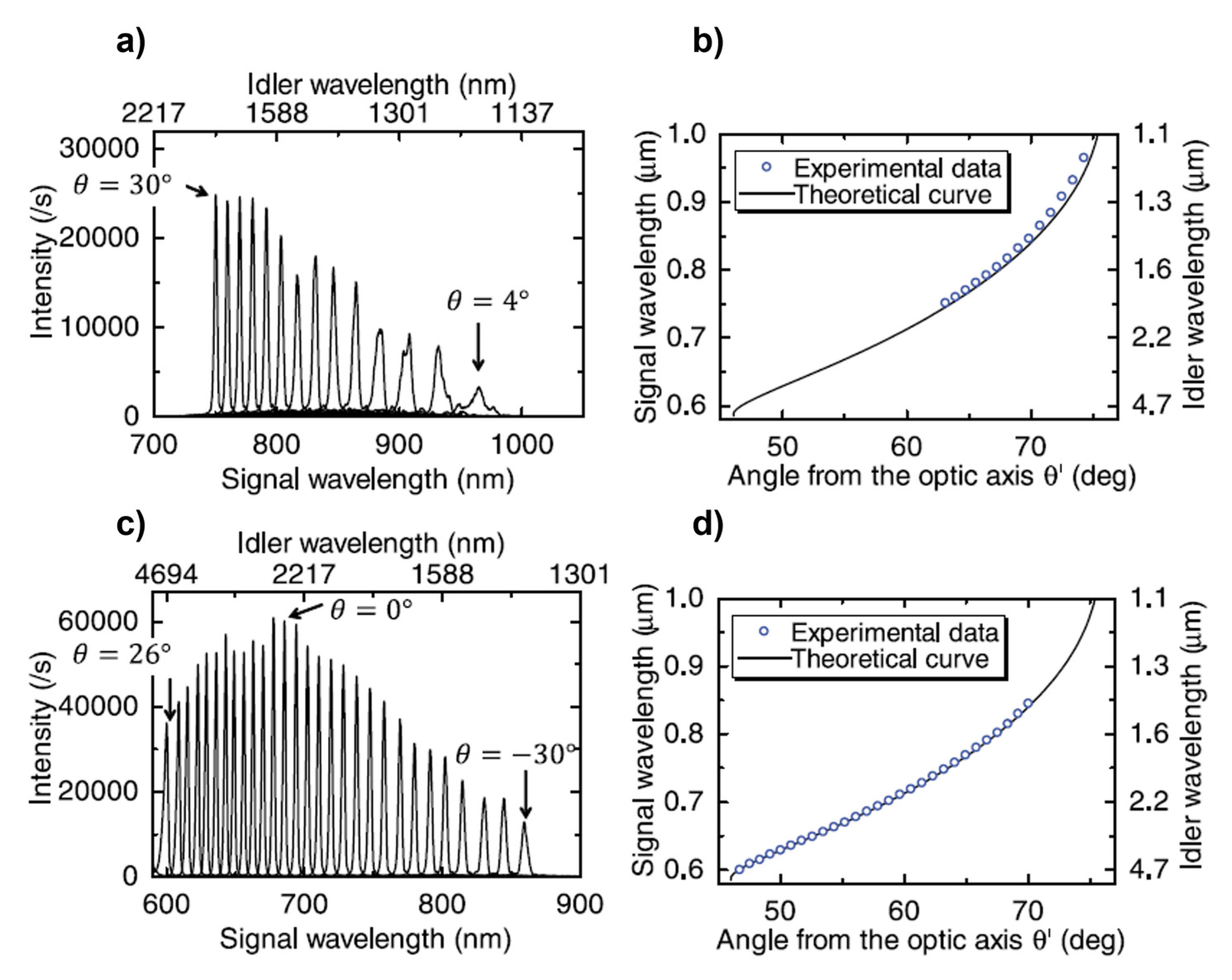
4.2. Experimental Results
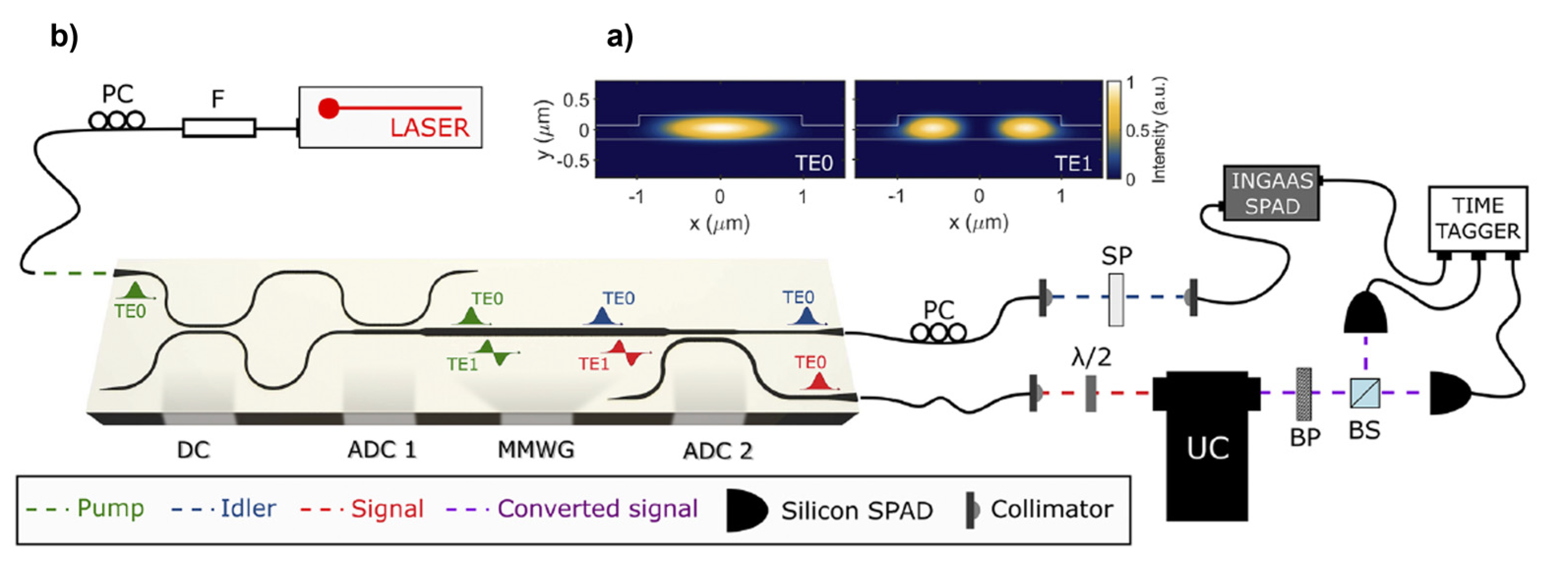
5. FWM in MIR
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moreau, P.A.; Sabines-Chesterking, J.; Whittaker, R.; Joshi, S.K.; Birchall, P.M.; McMillan, A.; Matthews, J.C. Demonstrating an absolute quantum advantage in direct absorption measurement. Sci. Rep. 2017, 7, 6256. [Google Scholar] [CrossRef]
- Slussarenko, S.; Weston, M.M.; Chrzanowski, H.M.; Shalm, L.K.; Verma, V.B.; Nam, S.W.; Pryde, G.J. Unconditional violation of the shot-noise limit in photonic quantum metrology. Nat. Photonics 2017, 11, 700–703. [Google Scholar] [CrossRef]
- Gilaberte Basset, M.; Setzpfandt, F.; Steinlechner, F.; Beckert, E.; Pertsch, T.; Gräfe, M. Perspectives for applications of quantum imaging. Laser Photonics Rev. 2019, 13, 1900097. [Google Scholar] [CrossRef]
- Kuo, P.S.; Gerrits, T.; Verma, V.B.; Nam, S.W. Spectral correlation and interference in non-degenerate photon pairs at telecom wavelengths. Opt. Lett. 2016, 41, 5074–5077. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 10–12 December 1984; pp. 175–179. [Google Scholar]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef] [PubMed]
- Giustina, M.; Versteegh, M.A.; Wengerowsky, S.; Handsteiner, J.; Hochrainer, A.; Phelan, K.; Steinlechner, F.; Kofler, J.; Larsson, J.-Å.; Abellán, C.; et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Phys. Rev. Lett. 2015, 115, 250401. [Google Scholar] [CrossRef] [PubMed]
- Pironio, S.; Acín, A.; Massar, S.; de La Giroday, A.B.; Matsukevich, D.N.; Maunz, P.; Olmschenk, S.; Hayes, D.; Luo, L.; Manning, T.A. Random numbers certified by Bell’s theorem. Nature 2010, 464, 1021–1024. [Google Scholar] [CrossRef] [PubMed]
- Okano, M.; Okamoto, R.; Tanaka, A.; Subashchandran, S.; Takeuchi, S. Generation of broadband spontaneous parametric fluorescence using multiple bulk nonlinear crystals. Opt. Express 2012, 20, 13977–13987. [Google Scholar] [CrossRef]
- Jabir, M.V.; Samanta, G.K. Robust, high brightness, degenerate entangled photon source at room temperature. Sci. Rep. 2017, 7, 12613. [Google Scholar] [CrossRef]
- Niizeki, K.; Ikeda, K.; Zheng, M.; Xie, X.; Okamura, K.; Takei, N.; Namekata, N.; Inoue, S.; Kosaka, H.; Horikiri, T. Ultrabright narrow-band telecom two-photon source for long-distance quantum communication. Appl. Phys. Express 2018, 11, 042801. [Google Scholar] [CrossRef]
- El Shamy, R.S.; Khalil, D.; Swillam, M.A. Mid infrared optical gas sensor using plasmonic Mach-Zehnder interferometer. Sci. Rep. 2020, 10, 1293. [Google Scholar] [CrossRef]
- Chen, K.; Liu, S.; Zhang, B.; Gong, Z.; Chen, Y.; Zhang, M.; Deng, H.; Guo, M.; Ma, F.; Zhu, F.; et al. Highly sensitive photoacoustic multi-gas analyzer combined with mid-infrared broadband source and near-infrared laser. Opt. Lasers Eng. 2020, 124, 105844. [Google Scholar] [CrossRef]
- Wang, Q.; Hao, L.; Zhang, Y.; Xu, L.; Yang, C.; Yang, X.; Zhao, Y. Super-resolving quantum lidar: Entangled coherent-state sources with binary-outcome photon counting measurement suffice to beat the shot-noise limit. Opt. Express 2016, 24, 5045–5056. [Google Scholar] [CrossRef] [PubMed]
- Tittl, A.; Michel, A.K.U.; Schäferling, M.; Yin, X.; Gholipour, B.; Cui, L.; Wuttig, M.; Taubner, T.; Neubrech, F.; Giessen, H. A switchable mid-infrared plasmonic perfect absorber with multispectral thermal imaging capability. Adv. Mater. 2015, 27, 4597–4603. [Google Scholar] [CrossRef]
- Fernandez, D.C.; Bhargava, R.; Hewitt, S.M.; Levin, I.W. Infrared spectroscopic imaging for histopathologic recognition. Nat. Biotechnol. 2005, 23, 469–474. [Google Scholar] [CrossRef] [PubMed]
- Amrania, H.; Antonacci, G.; Chan, C.H.; Drummond, L.; Otto, W.R.; Wright, N.A.; Phillips, C. Digistain: A digital staining instrument for histopathology. Opt. Express 2012, 20, 7290–7299. [Google Scholar] [CrossRef] [PubMed]
- Ravaro, M.; Locatelli, M.; Pugliese, E.; Di Leo, I.; de Cumis, M.S.; d’Amato, F.; Poggi, P.; Consolino, L.; Meucci, R.; Ferraro, P.; et al. Mid-infrared digital holography and holographic interferometry with a tunable quantum cascade laser. Opt. Lett. 2014, 39, 4843–4846. [Google Scholar] [CrossRef] [PubMed]
- Aellen, T.; Giovannini, M.; Faist, J.; von der Weid, J.P. Feasibility study of free-space quantum key distribution in the mid-infrared. Quantum Inf. Comput. 2008, 8, 1–11. [Google Scholar]
- Bellei, F.; Cartwright, A.P.; McCaughan, A.N.; Dane, A.E.; Najafi, F.; Zhao, Q.; Berggren, K.K. Free-space-coupled superconducting nanowire single-photon detectors for infrared optical communications. Opt. Express 2016, 24, 3248–3257. [Google Scholar] [CrossRef]
- Salisbury, J.W.; D’Aria, D.M. Emissivity of terrestrial materials in the 8–14 μm atmospheric window. Remote Sens. Environ. 1992, 42, 83–106. [Google Scholar] [CrossRef]
- Colvero, C.P.; Cordeiro, M.C.R.; De Faria, G.V.; Von der Weid, J.P. Experimental comparison between far-and near-infrared wavelengths in free-space optical systems. Microw. Opt. Technol. Lett. 2005, 46, 319–323. [Google Scholar] [CrossRef]
- Manor, H.; Arnon, S. Performance of an optical wireless communication system as a function of wavelength. Appl. Opt. 2003, 42, 4285–4294. [Google Scholar] [CrossRef]
- Soref, R. Enabling 2 μm communications. Nat. Photonics 2015, 9, 358–359. [Google Scholar] [CrossRef]
- Dello Russo, S.; Elefante, A.; Dequal, D.; Pallotti, D.K.; Santamaria Amato, L.; Sgobba, F.; Siciliani de Cumis, M. Advances in Mid-Infrared Single-Photon Detection. Photonics 2022, 9, 470. [Google Scholar] [CrossRef]
- Meyer-Scott, E.; Silberhorn, C.; Migdall, A. Single-photon sources: Approaching the ideal through multiplexing. Rev. Sci. Instrum. 2020, 91, 041101. [Google Scholar] [CrossRef]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145. [Google Scholar] [CrossRef]
- Grangier, P.; Sanders, B.; Vuckovic, J. Focus on single photons on demand. New J. Phys. 2004, 6, E04. [Google Scholar] [CrossRef]
- Senellart, P.; Solomon, G.; White, A. High-performance semiconductor quantum-dot single-photon sources. Nat. Nanotechnol. 2017, 12, 1026–1039. [Google Scholar] [CrossRef]
- Shalm, L.K.; Meyer-Scott, E.; Christensen, B.G.; Bierhorst, P.; Wayne, M.A.; Stevens, M.J.; Gerrits, T.; Glancy, S.; Hamel, D.R.; Allman, M.S.; et al. Strong loophole-free test of local realism. Phys. Rev. Lett. 2015, 115, 250402. [Google Scholar] [CrossRef]
- Ono, T.; Okamoto, R.; Takeuchi, S. An entanglement-enhanced microscope. Nat. Commun. 2013, 4, 2426. [Google Scholar] [CrossRef]
- Christ, A.; Silberhorn, C. Limits on the deterministic creation of pure single-photon states using parametric down-conversion. Phys. Rev. A 2012, 85, 023829. [Google Scholar] [CrossRef]
- Couteau, C. Spontaneous parametric down-conversion. Contemp. Phys. 2018, 59, 291–304. [Google Scholar] [CrossRef]
- Sharping, J.E.; Lee, K.F.; Foster, M.A.; Turner, A.C.; Schmidt, B.S.; Lipson, M.; Gaeta, A.L.; Kumar, P. Generation of correlated photons in nanoscale silicon waveguides. Opt. Express 2006, 14, 12388–12393. [Google Scholar] [CrossRef] [PubMed]
- Ballato, J.; Hawkins, T.; Foy, P.; Stolen, R.; Kokuoz, B.; Ellison, M.; McMillen, C.; Reppert, J.; Rao, A.M.; Daw, M.; et al. Silicon optical fiber. Opt. Express 2008, 16, 18675–18683. [Google Scholar] [CrossRef] [PubMed]
- Chunnilall, C.J.; Degiovanni, I.P.; Kück, S.; Müller, I.; Sinclair, A.G. Metrology of single-photon sources and detectors: A review. Opt. Eng. 2014, 53, 081910. [Google Scholar] [CrossRef]
- Mäntynen, H.; Anttu, N.; Sun, Z.; Lipsanen, H. Single-photon sources with quantum dots in III–V nanowires. Nanophotonics 2019, 8, 747–769. [Google Scholar] [CrossRef]
- Sua, Y.M.; Fan, H.; Shahverdi, A.; Chen, J.Y.; Huang, Y.P. Direct generation and detection of quantum correlated photons with 3.2 um wavelength spacing. Sci. Rep. 2017, 7, 17494. [Google Scholar] [CrossRef]
- Prabhakar, S.; Shields, T.; Dada, A.C.; Ebrahim, M.; Taylor, G.G.; Morozov, D.; Erotokritou, K.; Miki, S.; Yabuno, M.; Terai, H.; et al. Two-photon quantum interference and entanglement at 2.1 μm. Sci. Adv. 2020, 6, eaay5195. [Google Scholar] [CrossRef]
- Osorio, C.I.; Sangouard, N.; Thew, R.T. On the purity and indistinguishability of down-converted photons. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 055501. [Google Scholar] [CrossRef]
- Hong, C.K.; Ou, Z.Y.; Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 1987, 59, 2044. [Google Scholar] [CrossRef]
- Brańczyk, A.M. Hong-ou-mandel interference. arXiv 2017, arXiv:1711.00080. [Google Scholar]
- Karan, S.; Aarav, S.; Bharadhwaj, H.; Taneja, L.; De, A.; Kulkarni, G.; Meher, N.; Jha, A.K. Phase matching in β-barium borate crystals for spontaneous parametric down-conversion. J. Opt. 2020, 22, 083501. [Google Scholar] [CrossRef]
- Holló, C.T.; Sarkadi, T.; Galambos, M.; Bíró, D.; Barócsi, A.; Koppa, P.; Erdei, G. Compact, single-mode fiber-coupled, correlated photon pair source based on type-I beta-barium borate crystal. Opt. Eng. 2022, 61, 025101. [Google Scholar] [CrossRef]
- Bajaj, A.; Khanna, A.; Chen, B.; Longstaffe, J.G.; Zwanziger, U.W.; Zwanziger, J.W.; Gómez, Y.; González, F. Structural investigation of bismuth borate glasses and crystalline phases. J. Non-Cryst. Solids 2009, 355, 45–53. [Google Scholar] [CrossRef]
- Rangarajan, R.; Goggin, M.; Kwiat, P. Optimizing type-I polarization-entangled photons. Opt. Express 2009, 17, 18920–18933. [Google Scholar] [CrossRef] [PubMed]
- Fujii, G.; Namekata, N.; Motoya, M.; Kurimura, S.; Inoue, S. Bright narrowband source of photon pairs at optical telecommunication wavelengths using a type-II periodically poled lithium niobate waveguide. Opt. Express 2007, 15, 12769–12776. [Google Scholar] [CrossRef]
- Kumar, R.; Yadav, V.K.; Ghosh, J. Postselection-free, hyperentangled photon pairs in a periodically poled lithium-niobate ridge waveguide. Phys. Rev. A 2020, 102, 033722. [Google Scholar] [CrossRef]
- Zhao, J.; Ma, C.; Rüsing, M.; Mookherjea, S. High quality entangled photon pair generation in periodically poled thin-film lithium niobate waveguides. Phys. Rev. Lett. 2020, 124, 163603. [Google Scholar] [CrossRef] [PubMed]
- Takesue, H.; Inoue, K.; Tadanaga, O.; Nishida, Y.; Asobe, M. Generation of pulsed polarization-entangled photon pairs in a 1.55-µm band with a periodically poled lithium niobate waveguide and an orthogonal polarization delay circuit. Opt. Lett. 2005, 30, 293–295. [Google Scholar] [CrossRef]
- Shi, B.S.; Tomita, A. Highly efficient generation of pulsed photon pairs with bulk periodically poled potassium titanyl phosphate. JOSA B 2004, 21, 2081–2084. [Google Scholar] [CrossRef]
- McCracken, R.A.; Graffitti, F.; Fedrizzi, A. Numerical investigation of mid-infrared single-photon generation. JOSA B 2018, 35, C38–C48. [Google Scholar] [CrossRef]
- Kumar, R.; Ghosh, J. Joint spectral amplitude analysis of SPDC photon pairs in a multimode ppLN ridge waveguide. arXiv 2019, arXiv:1906.10344. [Google Scholar]
- Ghosh, G.; Endo, M.; Iwasaki, T. Temperature-dependent Sellmeier coefficients and chromatic dispersions for some optical fiber glasses. J. Light. Technol. 1994, 12, 1338–1342. [Google Scholar] [CrossRef]
- Ghosh, G. Sellmeier coefficients and dispersion of thermo-optic coefficients for some optical glasses. Appl. Opt. 1997, 36, 1540–1546. [Google Scholar] [CrossRef]
- Brańczyk, A.M.; Fedrizzi, A.; Stace, T.M.; Ralph, T.C.; White, A.G. Engineered optical nonlinearity for quantum light sources. Opt. Express 2011, 19, 55–65. [Google Scholar] [CrossRef] [PubMed]
- Wei, B.; Cai, W.H.; Ding, C.; Deng, G.W.; Shimizu, R.; Zhou, Q.; Jin, R.B. Mid-infrared spectrally-uncorrelated biphotons generation from doped PPLN: A theoretical investigation. Opt. Express 2021, 29, 256–271. [Google Scholar] [CrossRef]
- Kundys, D.; Graffitti, F.; McCracken, R.A.; Fedrizzi, A.; Kundys, B. Numerical Study of Reconfigurable Mid-IR Single Photon Sources Based on Functional Ferroelectrics. Adv. Quantum Technol. 2020, 3, 1900092. [Google Scholar] [CrossRef]
- Mancinelli, M.; Trenti, A.; Piccione, S.; Fontana, G.; Dam, J.S.; Tidemand-Lichtenberg, P.; Pedersen, C.; Pavesi, L. Mid-infrared coincidence measurements on twin photons at room temperature. Nat. Commun. 2017, 8, 15184. [Google Scholar] [CrossRef]
- Arahata, M.; Mukai, Y.; Cao, B.; Tashima, T.; Okamoto, R.; Takeuchi, S. Wavelength variable generation and detection of photon pairs in visible and mid-infrared regions via spontaneous parametric downconversion. JOSA B 2021, 38, 1934–1941. [Google Scholar] [CrossRef]
- Fukuda, H.; Yamada, K.; Shoji, T.; Takahashi, M.; Tsuchizawa, T.; Watanabe, T.; Takahashi, J.-I.; Itabashi, S.I. Four-wave mixing in silicon wire waveguides. Opt. Express 2005, 13, 4629–4637. [Google Scholar] [CrossRef] [PubMed]
- Soref, R. The past, present, and future of silicon photonics. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 1678–1687. [Google Scholar] [CrossRef]
- Guo, K.; Christensen, E.N.; Christensen, J.B.; Koefoed, J.G.; Bacco, D.; Ding, Y.; Ou, H.; Rottwitt, K. High coincidence-to-accidental ratio continuous-wave photon-pair generation in a grating-coupled silicon strip waveguide. Appl. Phys. Express 2017, 10, 062801. [Google Scholar] [CrossRef]
- Shi, X.; Guo, K.; Christensen, J.B.; Castaneda, M.A.U.; Liu, X.; Ou, H.; Rottwitt, K. Multichannel photon-pair generation with strong and uniform spectral correlation in a silicon microring resonator. Phys. Rev. Appl. 2019, 12, 034053. [Google Scholar] [CrossRef]
- Tsang, H.K.; Wong, C.S.; Liang, T.K.; Day, I.E.; Roberts, S.W.; Harpin, A.; Drake, J.F.; Asghari, M. Optical dispersion, two-photon absorption and self-phase modulation in silicon waveguides at 1.5 μ m wavelength. Appl. Phys. Lett. 2002, 80, 416–418. [Google Scholar] [CrossRef]
- Tzintzarov, G.N.; Ildefonso, A.; Teng, J.W.; Frounchi, M.; Djikeng, A.; Iyengar, P.; Goley, P.S.; Khachatrian, A.; Hales, J.; Bahr, R.; et al. Optical single-event transients induced in integrated silicon-photonic waveguides by two-photon absorption. IEEE Trans. Nucl. Sci. 2021, 68, 785–792. [Google Scholar] [CrossRef]
- Monat, C.; Ebnali-Heidari, M.; Grillet, C.; Corcoran, B.; Eggleton, B.J.; White, T.P.; O’Faolain, L.; Li, J.; Krauss, T.F. Four-wave mixing in slow light engineered silicon photonic crystal waveguides. Opt. Express 2010, 18, 22915–22927. [Google Scholar] [CrossRef]
- Liu, X.; Osgood, R.M.; Vlasov, Y.A.; Green, W.M. Mid-infrared optical parametric amplifier using silicon nanophotonic waveguides. Nat. Photonics 2010, 4, 557–560. [Google Scholar] [CrossRef]
- Jalali, B. Nonlinear optics in the mid-infrared. Nat. Photonics 2010, 4, 506–508. [Google Scholar] [CrossRef]
- Hagan, D.E.; Knights, A.P. Mechanisms for optical loss in SOI waveguides for mid-infrared wavelengths around 2 μm. J. Opt. 2016, 19, 025801. [Google Scholar] [CrossRef]
- Grillot, F.; Vivien, L.; Laval, S.; Pascal, D.; Cassan, E. Size influence on the propagation loss induced by sidewall roughness in ultrasmall SOI waveguides. IEEE Photonics Technol. Lett. 2004, 16, 1661–1663. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Rosenfeld, L.M.; Sulway, D.A.; Sinclair, G.F.; Anant, V.; Thompson, M.G.; Rarity, J.G.; Silverstone, J.W. Mid-infrared quantum optics in silicon. Opt. Express 2020, 28, 37092–37102. [Google Scholar] [CrossRef]
- Signorini, S.; Sanna, M.; Piccione, S.; Ghulinyan, M.; Tidemand-Lichtenberg, P.; Pedersen, C.; Pavesi, L. A silicon source of heralded single photons at 2 μm. APL Photonics 2021, 6, 126103. [Google Scholar] [CrossRef]
- Signorini, S.; Mancinelli, M.; Borghi, M.; Bernard, M.; Ghulinyan, M.; Pucker, G.; Pavesi, L. Intermodal four-wave mixing in silicon waveguides. Photonics Res. 2018, 6, 805–814. [Google Scholar] [CrossRef]
- Foster, M.A.; Turner, A.C.; Sharping, J.E.; Schmidt, B.S.; Lipson, M.; Gaeta, A.L. Broad-band optical parametric gain on a silicon photonic chip. Nature 2006, 441, 960–963. [Google Scholar] [CrossRef]
- Guo, K.; Lin, L.; Christensen, J.B.; Christensen, E.N.; Shi, X.; Ding, Y.; Rottwitt, K.; Ou, H. Broadband wavelength conversion in a silicon vertical-dual-slot waveguide. Opt. Express 2017, 25, 32964–32971. [Google Scholar] [CrossRef]
- Essiambre, R.J.; Mestre, M.A.; Ryf, R.; Gnauck, A.H.; Tkach, R.W.; Chraplyvy, A.R.; Sun, Y.; Jiang, X.; Lingle, R. Experimental investigation of inter-modal four-wave mixing in few-mode fibers. IEEE Photonics Technol. Lett. 2013, 25, 539–542. [Google Scholar] [CrossRef]
- Corrielli, G.; Crespi, A.; Osellame, R. Femtosecond laser micromachining for integrated quantum photonics. Nanophotonics 2021, 10, 3789–3812. [Google Scholar] [CrossRef]
- Liu, S.; Zheng, Y.; Fang, Z.; Ye, X.; Cheng, Y.; Chen, X. Effective four-wave mixing in the lithium niobate on insulator microdisk by cascading quadratic processes. Opt. Lett. 2019, 44, 1456–1459. [Google Scholar] [CrossRef]
- Shi, X.; Fan, W.; Lu, Y.; Hansen, A.K.; Chi, M.; Yi, A.; Ou, X.; Rottwitt, K.; Ou, H. Polarization and spatial mode dependent four-wave mixing in a 4H-silicon carbide microring resonator. APL Photonics 2021, 6, 076106. [Google Scholar] [CrossRef]
- Jung, H.; Tang, H.X. Aluminum nitride as nonlinear optical material for on-chip frequency comb generation and frequency conversion. Nanophotonics 2016, 5, 263–271. [Google Scholar] [CrossRef]
- Guidry, M.A.; Lukin, D.M.; Yang, K.Y.; Trivedi, R.; Vučković, J. Quantum optics of soliton microcombs. Nat. Photonics 2022, 16, 52–58. [Google Scholar] [CrossRef]




| Process | Material | λ (nm) | Generation Probability (W−2) | CAR Max | Heralded gh2(0) | Conversion Efficiency | HOM Visibility | Ref |
|---|---|---|---|---|---|---|---|---|
| SPDC | PPNL | 2890 3340 | X | 15.7 ± 0.4 | X | −110 dB | X | [59] |
| SPDC | MgO-PPLN | 780 3950 | X | 54 ± 7 | 0.08 ± 0.015 | −87 dB | X | [38] |
| SPDC | MgO-PPLN | 2090 | X | 180 ± 50 | X | X | 88.1% | [39] |
| Intra-modal SFWM | SOI | ~2071 | 0.28 | 25.7 ± 1.1 | X | X | 0.993 ± 0.017 | [73] |
| Inter-modal SFWM | SOI | 1259.7 2015.2 | 0.70 ± 0.10 | 40.4 ± 0.9 | 0.23 ± 0.08 | X | X | [74] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elefante, A.; Dello Russo, S.; Sgobba, F.; Santamaria Amato, L.; Pallotti, D.K.; Dequal, D.; Siciliani de Cumis, M. Recent Progress in Short and Mid-Infrared Single-Photon Generation: A Review. Optics 2023, 4, 13-38. https://doi.org/10.3390/opt4010003
Elefante A, Dello Russo S, Sgobba F, Santamaria Amato L, Pallotti DK, Dequal D, Siciliani de Cumis M. Recent Progress in Short and Mid-Infrared Single-Photon Generation: A Review. Optics. 2023; 4(1):13-38. https://doi.org/10.3390/opt4010003
Chicago/Turabian StyleElefante, Arianna, Stefano Dello Russo, Fabrizio Sgobba, Luigi Santamaria Amato, Deborah Katia Pallotti, Daniele Dequal, and Mario Siciliani de Cumis. 2023. "Recent Progress in Short and Mid-Infrared Single-Photon Generation: A Review" Optics 4, no. 1: 13-38. https://doi.org/10.3390/opt4010003
APA StyleElefante, A., Dello Russo, S., Sgobba, F., Santamaria Amato, L., Pallotti, D. K., Dequal, D., & Siciliani de Cumis, M. (2023). Recent Progress in Short and Mid-Infrared Single-Photon Generation: A Review. Optics, 4(1), 13-38. https://doi.org/10.3390/opt4010003









