Near-Field Behaviors of Internal Energy Flows of Free-Space Electromagnetic Waves Induced by Electric Point Dipoles

Abstract

Both orbital and spin energy fluxes constitute the internal flows decomposed from a Poynting vector. For generic electromagnetic waves propagating through source-free media, these energy fluxes are quadratic in field variables so that their properties are not easily predictable. Notwithstanding, their near-field behaviors play important roles in nanoscale photonics. For time-oscillatory fields, we found two hitherto-overlooked distinctions between the two internal flows. The first is an unequal level between them because the vorticity of an orbital energy flux plays a role comparable to a spin energy flux itself. The second is regarding the electric-magnetic dual symmetry in handling the two internal flows, whence the reactive helicity plays a role as important as the electromagnetic helicity. By helicity conservation, an inter-electric-magnetic transport is possible for the spin angular momentum density, while the electric and magnetic constituents of orbital energy fluxes admit only respective intra-electric and intra-magnetic transports. We have tested the validities of all these claims by exemplarily taking the electromagnetic fields induced by an electric point dipole, either a linear or a circular one. We have thus made new contributions not only in deriving explicit forms of the internal energy flows but also in revealing the magnetic activities hidden under the electromagnetic waves induced by electric point dipoles.

1. Introduction

Nanoscale optics offers ever-growing scientific curiosities [1,2,3], while benefiting from modern nano-fabrication technology [4]. We find the importance of the near field behaviors in connection with diverse electric effects, magnetic effects, and magneto-electric coupling effects [5,6,7]. For instance, near-field electrospinning (NFES) is a key fabrication technique for optical fibers. For a proper operation of an NFES device, a crucial role is played by the (mostly static) electric field, not in the far field but in the near field in and around an exquisitely shaped three-dimensional (3D) spinneret [8]. Such precise controls of electrostatic forces should be compatible with the desired flow characteristics of polymers. Magnetic-field assisted NFES is also employed for producing highly aligned nanofibers.

Laser cooling and atomic nanofabrication (ANF) require precise information on various near-field behaviors of optical fields [6]. Far-field behaviors can be roughly examined by ray-optics techniques, whereas near-field behaviors should be investigated via wave physics that accounts for various coherent interferences. For instance, standing waves generated from two counter-propagating optical waves with orthogonal polarizations offer a one-dimensional (1D) potential gradient which serves as an immaterial light mask for achieving the desired ANF [6]. In other words, a spatially inhomogeneous polarization gradient is established on subwavelength scales by judiciously adjusting the near-field features of applied light fields [6].

Recently, metamaterials and/or meta-surfaces receive increasing attention thanks to diverse electromagnetic (EM) and magneto-electric functionalities that are made possible by various nano-scale fabrications [5,7]. In this respect, one conceives various geometries for unit-cell meta-atoms ranging from twisted (helical) Omega particles (finite-wire-and-loops), split-ring resonators (SRRs), etc. Of course, suitable two-dimensional (2D) and/or 3D arrangements are necessary for the meta-atoms, say, as in graded-phase surfaces. By suitably selecting geometries and materials for those meta-atoms, desired cross-coupling effects can thus be realized. For instance, a magneto-optical Kerr effect (MOKE) [7] is employed for inducing cross-phase modulation (XPM) involving interferences. In this connection, interferences between the transverse-electric (TE) and transverse-magnetic (TM) modes accompany MOKEs to some degrees.

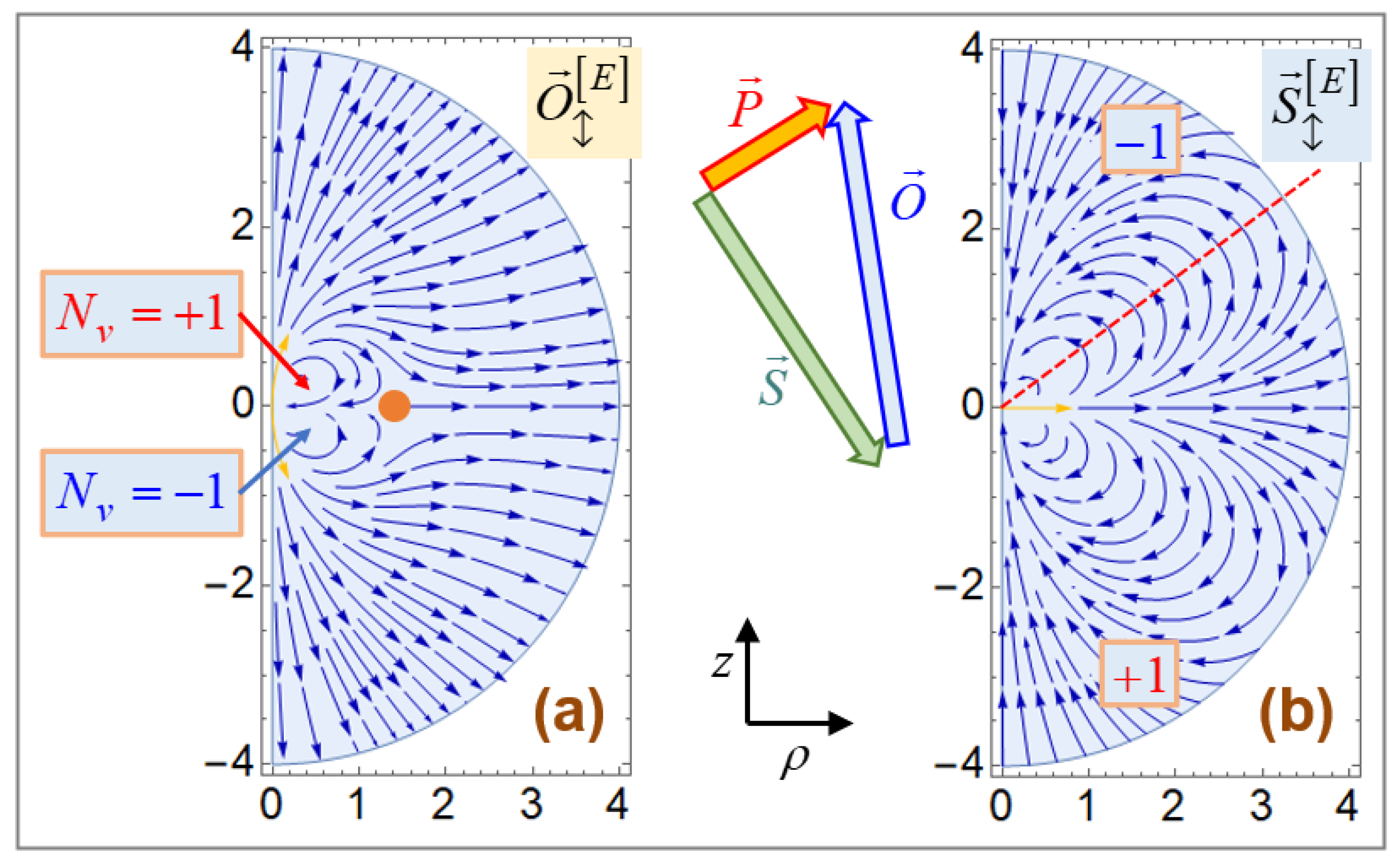
Meanwhile, a precise near-field mode structure of EM waves underlies a perfect spatial mode matching for atom-field coupling that is often assumed in quantum electrodynamics (QED) [7]. In the quantum regime, the ever-present mode mismatching noise should be taken into consideration. The electric-magnetic dual symmetry (or democracy) is exploited in formulating key EM parameters as illustrated by Figure 1a [3,9,10,11,12,13,14,15]. As an example, the Green-dyadic formulation [5] is made according to the electric-magnetic dual symmetry. In this connection, the interplay between optical fields and atomic processes becomes more sophisticated when optical vortices are involved in an either cylindrical or spherical configuration. Here, the spins of electrons are allowed to get into interactions with the spins of photons (EM waves) so that the near-field behaviors of the EM wave around electrons are essential [7].

Let us turn our attention from electrostatics and/or magnetostatics to more electromagnetic waves. On nanoscales, the near-field behaviors become important, for instance, around emitters and nanostructures [16,17,18]. such as nanoscale gratings [19]. Here, EM waves play crucial roles in a generation, transport, switching [20], and detection [21]. Suppose that $\left\{\overrightarrow{E},\overrightarrow{H}\right\}$ are electric and magnetic field vectors as solutions to the Maxwell equations over a source-free (i.e., with neither electric charges nor electric currents) medium [22]. These field vectors are assumed smooth (viz., continuously differentiable with respect to space) except at the origin, where a light source is located. In addition, we assume our media to be both loss-free and frequency-dispersion-free throughout this study [9]. It is then relatively easy to find EM waves propagating at least for simple geometries and for time-oscillatory fields [10,23].

Although EM waves are normally solutions to the linear Maxwell equations, the key parameters of interests to us are mostly bilinear or quadratic in the field variables [9,24,25]. One such quadratic parameter is the ‘spin angular-momentum (SAM) density’ (‘SAM density’ for short): the electric portion ${\overrightarrow{M}}^{\left[E\right]}\equiv \mathrm{Im}\left({\overrightarrow{E}}^{*}\times \overrightarrow{E}\right)$ and the magnetic portion ${\overrightarrow{M}}^{\left[H\right]}\equiv \mathrm{Im}\left({\overrightarrow{H}}^{*}\times \overrightarrow{H}\right)$. Here, the superscript ‘$*$’ denotes a complex conjugate, while $\left\{\mathrm{Re},\mathrm{Im}\right\}$ stands respectively for the real and imaginary parts.

In antenna theory [5,26,27], one could associate ‘active’ and ‘reactive’ respectively with ‘radiating’ and ‘non-radiative’. In this connection, the ‘reactive near field’ is defined as that region immediately surrounding the antenna wherein the reactive field predominates. In between this reactive near field and the ‘(Fraunhofer) far field’ lies the ‘radiating near field’, being alternatively called either the ‘(Fresnel) intermediate field’ or the ‘transition field’. In comparison, this ‘reactive near field’ is alternatively called either the ‘nearest part of the near field’ or the ‘non-radiative near field. In the case of a Mie scattering of a dielectric sphere, the electromagnetic helicity being active, especially in the near field arises from interactions among multiple scattered waves even if an external incident wave is linearly polarized [28]. As regards EM waves, both EM and reactive helicity parameters make one of the key characteristics in addition to the omni-important Poynting vector [6,18,29]. Although the far-field behaviors are crucial to antennas considered as detectors and many applications [5], the near-field behaviors play important roles in properly designing antennas as electro-optic (EO) energy-conversion devices [27].

Whenever a vectorial parameter such as the Poynting vector exhibits a vortex, it is highly likely that its anti-vortex coexists such that the net vorticity vanishes over the whole space [18,29]. In addition, it is highly probable that such a vortical feature can be found in the near field of an EM source. Resultantly, those near-field vortices in the Poynting vector are largely accompanied by the local energy backflows, although the Poynting vector itself stays forward-directed in the far field. Take note that a single plane wave does not normally carry any vortical feature. We learn from various wave configurations that vortical features are associated with interferences among multiple waves [6,10,19,24,30,31], for instance, non-paraxial counter-propagating waves [18], or the total wave consisting of an incident wave and a scattered wave in Mie scatterings [28].

When a magneto-optical (MO) material, say, a plasmonic scatterer [5,22], with a certain magnetic susceptibility is passively immersed in an EM field, a static magnetization proportional to ${\overrightarrow{E}}^{*}\times \overrightarrow{E}$ is induced on that material by the EM field [13,19,20,32,33]. This inverse Faraday effect is distinct from the ‘direct’ Faraday effect, where a magnetic field serves as an excitation agent [34]. The conservation law $\nabla ·{\overrightarrow{M}}^{\left[E\right]}+\nabla ·{\overrightarrow{M}}^{\left[H\right]}=0$ of the total SAM density is nothing but the helicity conservation law for time-oscillatory fields [30]. Figure 1a illustrates this conservation law. Notwithstanding, it has been seldom recognized that $\nabla ·{\overrightarrow{M}}^{\left[E\right]}=-\nabla ·{\overrightarrow{M}}^{\left[H\right]}\ne 0$, thus meaning either source or sink for $\left\{{\overrightarrow{M}}^{\left[E\right]},{\overrightarrow{M}}^{\left[H\right]}\right\}$. We can hence measure one of these two divergences to get the other divergence. Furthermore, it is well-founded that $\nabla ·{\overrightarrow{M}}^{\left[H\right]}=-\nabla ·{\overrightarrow{M}}^{\left[E\right]}=2\mathrm{Re}\left(\overrightarrow{E}·{\overrightarrow{H}}^{*}\right)$ [3,11,22].

The parameter $K^{(\Leftarrow )}\equiv \mathrm{Re}\left(\overrightarrow{E}·{\overrightarrow{H}}^{*}\right)$ is called the ‘reactive helicity’, while the well-known ‘electromagnetic (EM) helicity’ is defined by $K^{(\Rightarrow )}\equiv \mathrm{Im}\left(\overrightarrow{E}·{\overrightarrow{H}}^{*}\right)$ [14]. Meanwhile, $K^{(\Rightarrow )}$ is sometimes called the ‘chirality’ [2,18], whereas $K^{(\Leftarrow )}$ is variously called: a ‘reactive helicity density’, a ‘real helicity’, or a ‘magnetoelectric (ME) energy’ [12,13]. This pair $\left\{K^{(\Rightarrow )},K^{(\Leftarrow )}\right\}$ of helicities has its counterpart pair of a Poynting vector $\overrightarrow{P}\equiv \mathrm{Re}\left(\overrightarrow{E}\times {\overrightarrow{H}}^{*}\right)$ and a reactive Poynting vector ${\overrightarrow{P}}^{(\Leftarrow )}\equiv \mathrm{Im}\left(\overrightarrow{E}\times {\overrightarrow{H}}^{*}\right)$. In this aspect, evanescent waves and light scatterings of nanoparticles are worked out in [12,13,14]. From perspectives of experimental measurements, $\left\{K^{(\Rightarrow )},K^{(\Leftarrow )}\right\}$ turn out stronger respectively in the far and near fields [12]. Henceforth, both $\left\{K^{(\Rightarrow )},K^{(\Leftarrow )}\right\}$ are collectively called field helicities.

We have checked the validities of all these claims by taking as examples the EM field induced by an electric point dipole, either a linear or a circular one. Primary (self-illuminating) point dipoles serve as suitable models not only for emitters [5,18,22,35,36] but also for atomic physics [6]. In this respect, we are not dealing with secondary dipoles, namely, either electric or magnetic dipole moments induced on nano-objects or nanostructures by incident illuminations [12,14,19,22,30]. Because of the interaction between the incident and scattered EM fields, passive dipoles (for instance, particle-induced dipoles [30]) lead usually to nonzero helicities except under special conditions. In comparison, our EM field arising from a sole primary linear dipole possesses no field helicity, while a sole primary circular dipole gives rise to nonzero field helicity. The reason for our choice of dipole-induced EM fields is that the divergence-free conditions $\nabla ·{\overrightarrow{M}}^{\left[E\right]}=\nabla ·{\overrightarrow{M}}^{\left[H\right]}=0$ are separately satisfied for the EM field induced by a linear dipole, whereas the sum $\nabla ·{\overrightarrow{M}}^{\left[E\right]}+\nabla ·{\overrightarrow{M}}^{\left[H\right]}=0$ is satisfied for the EM field induced by a circular dipole.

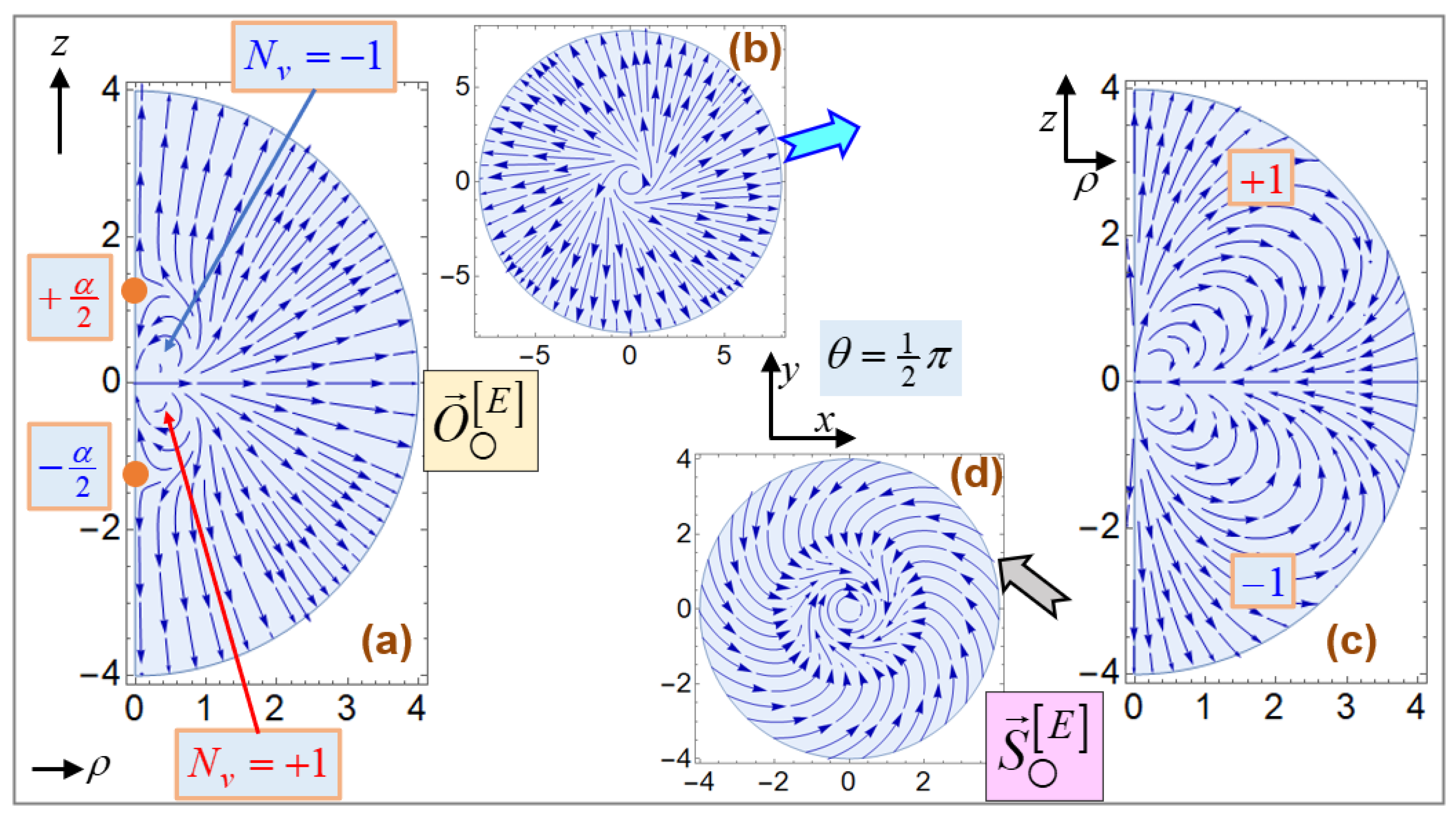
Panels (c) and (d) of Figure 1 illustrate this distinction. Our EM fields induced by point dipoles are spherically propagating so that the relevant formulas are rather complicated in comparison to the EM fields describable in the Cartesian and cylindrical systems. The pair $\left\{{\overrightarrow{M}}^{\left[E\right]},{\overrightarrow{M}}^{\left[H\right]}\right\}$ signifies a state of polarization of an EM field [15,18,37,38]. Panels (c) and (d) of Figure 1 display the zones of near-circular polarizations respectively for a linear dipole and a circular dipole. Roughly speaking, both zones of near-circular polarizations are located around the vertical axis. Notwithstanding, there is a significant distinction between the respective spatial regions where near-circular polarizations are achieved: 2D and pencil-hull-shaped on panel (c) [18] versus 3D and cone-shaped on panel (d) [10,14,15,25,37,38,39].

In this connection, we have analytically found the surface of near-circular polarizations in the case of the EM field induced by a linear electric point dipole [40]. Although this study is a follow-up of [40] for a linear dipole with respect to polarization properties, expanded studies are performed here on a circular dipole and the internal flows for both types of dipoles.

Both spin and orbital energy fluxes as internal energy flows of a Poynting vector have been investigated for various EM fields. Unfortunately, such internal flows have not been seriously investigated for the EM field induced by electric point dipoles. For instance, we found backward flows in the internal energy fluxes [18,25,37,41]. In addition, we discovered characters relevant both to cylindrical vector beams [19,32,35,36,42], to focused beams of finite size [10,15,23,43], and to pulsed focusing [18]. It is well-known that the pair $\left\{{\overrightarrow{M}}^{\left[E\right]},{\overrightarrow{M}}^{\left[H\right]}\right\}$ are the helicity fluxes, while being related to the spin energy fluxes [12]. In comparison, the orbital energy flux has no such underlying parameters.

This study is structured in the following way. Section 2 presents generic formulas for key parameters. Section 3 provides a set of essential properties for the EM fields induced by electric point dipoles. Section 4 and Section 5 provide numerically evaluated properties of the EM fields induced respectively by a linear dipole and by a circular dipole. Section 6 provides discussions followed by a conclusion. We have prepared Sections S1–S6 of Supplementary Materials (‘Supplementary Materials’ for short) roughly in parallel to the developments made by this main text. A good starting point is Section S1 of Supplementary Materials, where fluid-dynamical analogies are drawn [44]. Complementary Supplementary Materials are also provided by our previous works on vortex flows [44], EM fields induced by a linear electric point dipole [40], and a Mie scattering [28].

2. Analysis of Internal Energy Fluxes

Figure 1b depicts usual coordinate systems, where the field (or observation) point is located at $\overrightarrow{r}\equiv r{\widehat{e}}_r$. Notice the difference that $\left\{\rho ,r\right\}$ denote, respectively, the cylinder- and sphere-radial coordinates [1]. The polar angle is restricted to $0\le \theta \le \pi$, while $0\le \varphi <2\pi$. Let $\left\{t,\omega \right\}$ be frequency and time with $\omega ,t>0$ for time-harmonic monochromatic fields. The vacuum wave number $k\equiv \omega /c$ is defined with $c$ as the light speed in vacuum. To save notations, spatial coordinates are redefined by the substitutions $k\overrightarrow{r}\to \overrightarrow{r}$, according to which $k\nabla \to \nabla$. Since $k$ is $2\pi$ times the inverse wavelength of an EM field, our near field is henceforth characterized by the dimensionless range on the order of $r=1$. In the case of radio waves, a typical wavelength measures ten meters or so, thereby corresponding to fourteen megahertz [2]. A similar set of formulations is employed in [40].

With $i\times i\equiv -1$, the dimensional temporal factor $\exp \left(-i\omega t\right)$ becomes a dimensionless $\exp \left(-it\right)$ [6]. For the sake of simplicity, we take the medium to be a loss-free dielectric with constant $\left\{\epsilon ,\mu \right\}$ being an electric permittivity and a magnetic permeability. When $\left\{\epsilon ,\mu \right\}$ are properly absorbed into $\overrightarrow{E}$ and $\overrightarrow{H}$, we make the replacements: $\sqrt{\epsilon }\overrightarrow{E}\to \overrightarrow{E}$ and $\sqrt{\mu }\overrightarrow{H}\to \overrightarrow{H}$. Meanwhile, we do not need to take both electric displacement and magnetic induction into consideration since we are dealing with free space. Resultantly, both dimensionless field variables $\left\{\overrightarrow{E},\overrightarrow{H}\right\}$ become comparable on the same level of dimensions [1,3,18]. It is exciting to see in [2] where one maintains this source-free condition over the tiny volume of radius $100nm$ around a source.

The dimensionless Maxwell equations are thus reformulated into the set: the Ampère–Maxwell law $\nabla \times \overrightarrow{H}=-i\overrightarrow{E}$, and the Faraday–Lenz law $\nabla \times \overrightarrow{E}=i\overrightarrow{H}$ alongside two Gauss laws $\nabla ·\overrightarrow{E}=0$ and $\nabla ·\overrightarrow{H}=0$ for a source-free EM field. The Poynting vector $\overrightarrow{P}$ is decomposable through $\overrightarrow{P}=\overrightarrow{O}+\overrightarrow{S}$ into two constituents [9,10,18,23,24,37,41].

$$\begin{array}{l}{I}^{\left[avg\right]}\equiv \frac{1}{2}\left({\left|\overrightarrow{E}\right|}^2+{\left|\overrightarrow{H}\right|}^2\right),\begin{array}{c}\end{array}{I}^{\Leftarrow }\equiv \frac{1}{2}\left({\left|\overrightarrow{H}\right|}^2-{\left|\overrightarrow{E}\right|}^2\right)\\ \overrightarrow{P}\equiv \mathrm{Re}\left({\overrightarrow{E}}^{*}\times \overrightarrow{H}\right)={\overrightarrow{O}}^{\left[avg\right]}+{\overrightarrow{S}}^{\left[avg\right]}={\overrightarrow{O}}^{\left[E\right]}+{\overrightarrow{S}}^{\left[E\right]}={\overrightarrow{O}}^{\left[H\right]}+{\overrightarrow{S}}^{\left[H\right]}\\ \{\begin{array}{l}{\overrightarrow{P}}^{\left[E\right]}\equiv \mathrm{Im}\left[{\overrightarrow{E}}^{*}\times \left(\nabla \times \overrightarrow{E}\right)\right]\\ {\overrightarrow{P}}^{\left[H\right]}\equiv \mathrm{Im}\left[{\overrightarrow{H}}^{*}\times \left(\nabla \times \overrightarrow{H}\right)\right]\end{array}\Rightarrow \overrightarrow{P}\equiv {\overrightarrow{P}}^{\left[avg\right]}={\overrightarrow{P}}^{\left[E\right]}={\overrightarrow{P}}^{\left[H\right]}\\ {\overrightarrow{P}}^{\Leftarrow }\equiv \mathrm{Im}\left(\overrightarrow{E}\times {\overrightarrow{H}}^{*}\right)\end{array}$$

(1)

The superscripts ‘$\left[E\right],\left[H\right],\left[avg\right]$’ stand respectively for ‘electric’, ‘magnetic’ and ‘average’. We have formed an average Poynting vector ${\overrightarrow{P}}^{\left[avg\right]}$ as the average of ${\overrightarrow{P}}^{\left[E\right]}\equiv \mathrm{Im}\left[{\overrightarrow{E}}^{*}\times \left(\nabla \times \overrightarrow{E}\right)\right]$ and ${\overrightarrow{P}}^{\left[H\right]}\equiv \mathrm{Im}\left[{\overrightarrow{H}}^{*}\times \left(\nabla \times \overrightarrow{H}\right)\right]$ according to the electric-magnetic dual symmetry. The equalities $\overrightarrow{P}\equiv {\overrightarrow{P}}^{\left[avg\right]}={\overrightarrow{P}}^{\left[E\right]}={\overrightarrow{P}}^{\left[H\right]}$ in Equation (1) can be easily proved via the Maxwell equations. Besides, $I^{\left[avg\right]}\equiv \frac{1}{2}\left({\left|\overrightarrow{E}\right|}^2+{\left|\overrightarrow{H}\right|}^2\right)$ is the average field intensity, while $I^{\Leftarrow }\equiv \frac{1}{2}\left({\left|\overrightarrow{H}\right|}^2-{\left|\overrightarrow{E}\right|}^2\right)$ is the average reactive field intensity. It is also well-studied that the pair $\left\{I^{\left[avg\right]},{\overrightarrow{P}}^{\left[avg\right]}\right\}$ in Equation (1) constitutes the energy conservation law when both pairs are relaxed to be transient. Hence, $\overrightarrow{P}\equiv {\overrightarrow{P}}^{\left[avg\right]}$ is the ‘total energy flux’. After time averaging, the conservation law is reduced just to $\nabla ·{\overrightarrow{P}}^{\left[avg\right]}=0$ under the double constraints $\nabla ·\overrightarrow{E}=\nabla ·\overrightarrow{H}=0$ [2,9,11,12,14,23,24,25,30,32].

By the afore-mentioned electric-magnetic dual symmetry, an ‘orbital energy flux’ $\overrightarrow{O}$ and a ‘spin energy flux’ $\overrightarrow{S}$ are expressible as follows for time-oscillatory fields.

$$\{\begin{array}{l}{\overrightarrow{O}}^{\left[f\right]}\equiv \mathrm{Im}\left[{\overrightarrow{f}}^{*}·(\nabla )\overrightarrow{f}\right]\\ {\overrightarrow{S}}^{\left[f\right]}\equiv -\mathrm{Im}\left[\left({\overrightarrow{f}}^{*}·\nabla \right)\overrightarrow{f}\right]\end{array},\begin{array}{c}\end{array}\{\begin{array}{l}{\overrightarrow{O}}^{\left[avg\right]}\equiv \frac{1}{2}\left({\overrightarrow{O}}^{\left[E\right]}+{\overrightarrow{O}}^{\left[H\right]}\right)\\ {\overrightarrow{S}}^{\left[avg\right]}\equiv \frac{1}{2}\left({\overrightarrow{S}}^{\left[E\right]}+{\overrightarrow{S}}^{\left[H\right]}\right)\end{array}$$

(2)

Both $\left\{{\overrightarrow{O}}^{\left[f\right]},{\overrightarrow{S}}^{\left[f\right]}\right\}$ constitute the internal energy flow, [9,10,12,15,16,17,18,24,32,37,38,41,42]. For simplicity, we omitted a factor of half ($1/2$) arising from taking time averages of $\left\{{\overrightarrow{P}}^{\left[f\right]},{\overrightarrow{O}}^{\left[f\right]},{\overrightarrow{S}}^{\left[f\right]}\right\}$.

For EM waves propagating through a source-free medium, we can easily reach the following by consulting the two spin energy fluxes (namely, the Belinfante spin momentum [12]) ${\overrightarrow{S}}^{\left[f\right]}$ in Equation (2) [18,32,37,38].

$$\begin{array}{l}{\overrightarrow{M}}^{\left[f\right]}\equiv \mathrm{Im}\left({\overrightarrow{f}}^{*}\times \overrightarrow{f}\right),\begin{array}{c}\end{array}{\overrightarrow{S}}^{\left[f\right]}=\nabla \times \left(\frac{1}{2}{\overrightarrow{M}}^{\left[f\right]}\right)\\ {\overrightarrow{M}}^{\left[avg\right]}\equiv \frac{1}{2}\left({\overrightarrow{M}}^{\left[E\right]}+{\overrightarrow{M}}^{\left[H\right]}\right)\\ \nabla ·{\overrightarrow{M}}^{\left[E\right]}=-\nabla ·{\overrightarrow{M}}^{\left[H\right]}\ne 0\Rightarrow \nabla ·{\overrightarrow{M}}^{\left[avg\right]}=0\end{array}$$

(3)

Henceforth, ${\overrightarrow{M}}^{\left[f\right]}$ is called a ‘SAM density’, although we find alternative names: a ‘field-polarization ellipticity’ [3], a ‘spin density’ [23], a ‘chirality flux’ [11], or just a SAM [3]. The right of Figure 1a illustrates an inter-electric-magnetic conversion of $\overrightarrow{M}$, where the sources respectively for ${\overrightarrow{M}}^{\left[f\right]}$ cancel each other [1]. In other words, ${\overrightarrow{M}}^{\left[f\right]}$ is not solenoidal, but its average ${\overrightarrow{M}}^{\left[avg\right]}$ is solenoidal. This conversion in $\overrightarrow{M}$ expressed in Equation (3) is different from the spin-to-orbital conversions between $\left\{{\overrightarrow{O}}^{\left[f\right]},{\overrightarrow{S}}^{\left[f\right]}\right\}$ [10,43]. See Section S2 of Supplementary Materials. For more details. When electron spins are involved, the illustration in Figure 1 would become much more complicated.

In contrast to ${\overrightarrow{S}}^{\left[f\right]}=\nabla \times \left(\frac{1}{2}{\overrightarrow{M}}^{\left[f\right]}\right)$ in Equation (3), the orbital energy flux ${\overrightarrow{O}}^{\left[f\right]}$ is not a vorticity of another vector. Notwithstanding, $\nabla ·{\overrightarrow{O}}^{\left[f\right]}=0$ by the energy conservation for time-oscillatory fields, since $\nabla ·\overrightarrow{P}=\nabla ·{\overrightarrow{S}}^{\left[f\right]}=0$ [12]. Consequently, there is no inter-electric-magnetic conversion between $\left\{{\overrightarrow{O}}^{\left[E\right]},{\overrightarrow{O}}^{\left[H\right]}\right\}$ as illustrated on the left of Figure 1a. We found diverse optical vortices and singularities not only with the Poynting vector but also with its associated internal energy fluxes $\left\{{\overrightarrow{O}}^{\left[f\right]},{\overrightarrow{S}}^{\left[f\right]}\right\}$ [10,18,24,25,37].

Consider a complex vector $\overrightarrow{E}·{\overrightarrow{H}}^{*}\equiv K^{(\Leftarrow )}+i{K}^{(\Rightarrow )}$ [10,12,13,17,24,28]. Complementing Equation (3), we have the following formal set.

$$\begin{array}{l}\overrightarrow{E}·{\overrightarrow{H}}^{*}\equiv K^{(\Leftarrow )}+i{K}^{(\Rightarrow )}\Rightarrow \\ \{\begin{array}{l}{K}^{(\Leftarrow )}\equiv \mathrm{Re}\left(\overrightarrow{E}·{\overrightarrow{H}}^{*}\right)=\nabla ·\left(\frac{1}{2}{\overrightarrow{M}}^{\left[H\right]}\right)=-\nabla ·\left(\frac{1}{2}{\overrightarrow{M}}^{\left[E\right]}\right)\\ K^{(\Rightarrow )}\equiv \mathrm{Im}\left(\overrightarrow{E}·{\overrightarrow{H}}^{*}\right)=\frac{1}{2}\mathrm{Re}\left[{\overrightarrow{E}}^{*}·\left(\nabla \times \overrightarrow{E}\right)+{\overrightarrow{H}}^{*}·\left(\nabla \times \overrightarrow{H}\right)\right]\end{array}\end{array}$$

(4)

As with $\left\{I^{\left[avg\right]},{\overrightarrow{P}}^{\left[avg\right]}\right\}$ in Equation (1), the pair $\left\{K^{(\Rightarrow )},{\overrightarrow{M}}^{\left[avg\right]}\right\}$ in Equation (4) constitutes the helicity conservation law, which can be understood when both parameters are relaxed to be time-transient [11,12,14,25,30]. Hence, ${\overrightarrow{M}}^{\left[avg\right]}$ is the total helicity flux. After time averaging, the helicity conservation law is reduced just to $\nabla ·{\overrightarrow{M}}^{\left[avg\right]}=0$, namely, the average spin AM density vanishes.

The most interesting result is that $K^{(\Leftarrow )}=\nabla ·\left(\frac{1}{2}{\overrightarrow{M}}^{\left[H\right]}\right)$ in view of the divergences in Equation (3), where $K^{(\Leftarrow )}$ serves as a source or a sink for the SAM density ${\overrightarrow{M}}^{\left[f\right]}$. For this reason, $K^{(\Leftarrow )}$ is called a ‘magnetoelectric (ME) energy density’ [13] or a ‘ME helicity density’. From a physical viewpoint, $K^{(\Leftarrow )}$ designates how large the inter-electric-magnetic transport between $\left\{{\overrightarrow{M}}^{\left[E\right]},{\overrightarrow{M}}^{\left[H\right]}\right\}$. Notice that $K^{(\Leftarrow )}$ serves as a polarization current because $K^{(\Leftarrow )}$ is related to $\left\{{\overrightarrow{M}}^{\left[E\right]},{\overrightarrow{M}}^{\left[H\right]}\right\}$, each of which is linked in turn to the electric polarization and magnetic polarization. We will discuss in full detail the issue of polarizations in the upcoming Figures 3 and 6.

Both helicity parameters $\left\{K^{(\Leftarrow )},K^{(\Rightarrow )}\right\}$ in this study arise only from electromagnetic effects, but not from magneto-electric (M-E) effects. In this connection, any M-E effects alluded to in this study refer to the property of either foreign objects or other structures that might be immersed in the electromagnetic waves [5]. Such M-E effects of a foreign object have been thoroughly treated by [12,14].

Therefore, the SAM densities are interchangeable across their electric and magnetic sub-constituents. We call this phenomenon an ‘inter-electric-magnetic’ transport. In comparison, $\nabla ·{\overrightarrow{O}}^{\left[E\right]}=\nabla ·{\overrightarrow{O}}^{\left[H\right]}=0$, whence both electric and magnetic portions of the orbital energy flux do not communicate with each other. We call this phenomenon an ‘intra-electric-magnetic’ transport. We stress that the spin energy fluxes are still experiencing no inter-electric-magnetic transport since $\nabla ·{\overrightarrow{S}}^{\left[E\right]}=\nabla ·{\overrightarrow{S}}^{\left[H\right]}=0$. We have illustrated both distinguishing properties in Figure 1a.

Because of what we call the ‘magnetization current’ $2{\overrightarrow{S}}^{\left[f\right]}=\nabla \times {\overrightarrow{M}}^{\left[f\right]}$ in Equation (3), $2{\overrightarrow{S}}^{\left[f\right]}$ is a vorticity of ${\overrightarrow{M}}^{\left[f\right]}$ [9,44]. We reserve the terms ‘SAM’ for $\overrightarrow{r}\times {\overrightarrow{S}}^{\left[f\right]}$ that is the angular momentum of the spin part of a linear momentum. Meanwhile, we reach from $2{\overrightarrow{S}}^{\left[f\right]}=\nabla \times {\overrightarrow{M}}^{\left[f\right]}$ in Equation (3) a generic identity $2\nabla \times {\overrightarrow{S}}^{\left[f\right]}=\nabla \left(\nabla ·{\overrightarrow{M}}^{\left[f\right]}\right)-{\nabla }^2{\overrightarrow{M}}^{\left[f\right]}$. Therefore, the vorticity $\nabla \times {\overrightarrow{S}}^{\left[f\right]}$ is affected not only by the diffusion through the vector Laplacian ${\nabla }^2{\overrightarrow{M}}^{\left[f\right]}$ but also by the gradient $\nabla \left(\nabla ·{\overrightarrow{M}}^{\left[f\right]}\right)$. On the electric-magnetic dual symmetry, we have $\nabla ·{\overrightarrow{M}}^{\left[avg\right]}=0$ in Equation (3) so that $2\nabla \times {\overrightarrow{S}}^{\left[avg\right]}=-{\nabla }^2{\overrightarrow{M}}^{\left[avg\right]}$ for the average parameters.

We learn from Equation (3) that ${\overrightarrow{O}}^{\left[f\right]}$ lies more on the level of ${\overrightarrow{M}}^{\left[f\right]}$, although $\left\{{\overrightarrow{O}}^{\left[E\right]},{\overrightarrow{O}}^{\left[H\right]}\right\}$ are officially on the level of ${\overrightarrow{S}}^{\left[f\right]}$ according to the decomposition rule $\overrightarrow{P}={\overrightarrow{O}}^{\left[f\right]}+{\overrightarrow{S}}^{\left[f\right]}$ presented in Equation (1). From a physical viewpoint, the vorticity $\nabla \times {\overrightarrow{O}}^{\left[f\right]}$ of an orbital energy flux plays a role comparable to a spin energy flux ${\overrightarrow{S}}^{\left[f\right]}$ itself, while an orbital energy flux ${\overrightarrow{O}}^{\left[f\right]}$ acts similar to a SAM density ${\overrightarrow{M}}^{\left[f\right]}$. Put differently, ${\overrightarrow{O}}^{\left[f\right]}$ cannot be expressed as a vorticity of some vector, in contrast to $2{\overrightarrow{S}}^{\left[f\right]}=\nabla \times {\overrightarrow{M}}^{\left[f\right]}$ in Equation (3) [15,18,37,38]. We find no explicit statement on this unequal level between $\left\{{\overrightarrow{O}}^{\left[f\right]},{\overrightarrow{S}}^{\left[f\right]}\right\}$ in the literature to the best of our knowledge

We can find a simple case with $\nabla ·{\overrightarrow{M}}^{\left[f\right]}=0$ in Equation (3) for the EM field that comes with a (plasmonic) evanescent wave established across a planar interface. Since this example is of the mainstay of this study, we placed details in Section S3.4 of Supplementary Materials. See also [1,3,9,10,12,15,23,24,37,41]. Closely related to the divergence-full $\nabla ·{\overrightarrow{M}}^{\left[f\right]}\ne 0$ are non-planar and non-2D effects due to height fluctuations or slight curvatures of nominally 2D materials [18,37]. For instance, artificially sculptured thin films or nanostructures with designed structural chirality are intended to generate a nonzero $\nabla ·{\overrightarrow{M}}^{\left[f\right]}$ [2]. Of course, curvature effects accompanying sharp nanotips are particularly significant in altering the Poynting-vector flows [1,43].

3. Key Field Parameters Induced by Point Dipoles

For concreteness, we consider two types of electric point dipoles: (i) a linear dipole ${\widehat{p}}_{\updownarrow }$ aligned along the vertical $z$-axis as shown in Figure 1c, and (ii) a circular dipole ${\widehat{p}}_{○}\equiv \frac{1}{\sqrt{2}}\left({\widehat{e}}_x+\alpha i{\widehat{e}}_y\right)$ lying on the horizontal $xy$-plane as sketched in Figure 1d. In brief,

$$\{\begin{array}{l}{\widehat{p}}_{\updownarrow }\equiv \alpha {\widehat{e}}_z:\begin{array}{c}\end{array}{\overrightarrow{N}}_{\updownarrow }=\overrightarrow{0}\\ {\widehat{p}}_{○}\equiv \frac{1}{\sqrt{2}}\left({\widehat{e}}_x+\alpha i{\widehat{e}}_y\right)=\frac{1}{\sqrt{2}}{e}^{\alpha i\varphi }\left({\widehat{e}}_{\rho }+\alpha i{\widehat{e}}_{\varphi }\right):\begin{array}{c}\end{array}{\overrightarrow{N}}_{○}=\alpha {\widehat{e}}_z\end{array}$$

(5)

Here, $\alpha =\pm 1$ is the spin index, and the unit basis vectors are $\left\{{\widehat{e}}_x,{\widehat{e}}_y,{\widehat{e}}_z\right\}$ and the likes. Moreover, the normalization is made such that $\left|\widehat{p}\right|=1$ for both types of dipoles [37], where the dipole moment $\widehat{p}$ is one of $\left\{{\widehat{p}}_{\updownarrow },{\widehat{p}}_{○}\right\}$ provided in Equation (5). The superscript ‘$\updownarrow$’ stands for ‘vertical linear’, while ‘$○$’ stands for ‘planar circular’. The vectorial intrinsic property of a dipole is characterized by a dipole-polarization ellipticity $\overrightarrow{N}\equiv \mathrm{Im}\left({\widehat{p}}^{*}\times \widehat{p}\right)$ that characterizes the collective electric currents within a dipole. Hence, $\left|\overrightarrow{N}\right|\le 1$. Let us reiterate that we are not dealing with the intrinsic spins of electrons. Starting with a vector potential $\overrightarrow{A}\equiv -i{r}^{-1}{e}^{ir}\widehat{p}$, we obtain $\overrightarrow{H}=\nabla \times \overrightarrow{A}$ and $\overrightarrow{E}=i\nabla \times \overrightarrow{H}$ in sequel. An equivalent way of evaluating $\left\{\overrightarrow{E},\overrightarrow{H}\right\}$ is detailed in Section S3 of Supplementary Materials [2,3,9,10,12,15,22,23,25,38,39,45]. For reference, we find $\widehat{p}·{\widehat{m}}^{*}\equiv K_{\left[pm\right]}^{(\Leftarrow )}+i{K}_{\left[pm\right]}^{(\Rightarrow )}$ in the case with the co-existence of an electric dipole $\widehat{p}$ and magnetic dipole $\widehat{m}$ (being not considered in this study) for polarizable particles [12,14,22,30].

Let us list below the EM field induced by a linear dipole along with key field parameters.

$$\begin{array}{l}\{\begin{array}{l}{\overrightarrow{H}}_{\updownarrow }=-\alpha \frac{e^{ir}}{r}\left(1+\frac{i}{r}\right)\sin \theta {\widehat{e}}_{\varphi }\\ {\overrightarrow{E}}_{\updownarrow }=\frac{\alpha e^{ir}}{r}\left[\left(\frac{1}{r}-i\right)\frac{2\cos \theta }{r}{\widehat{e}}_r-\left(1+\frac{i}{r}-\frac{1}{r^2}\right)\sin \theta {\widehat{e}}_{\theta }\right]\end{array}\\ {\overrightarrow{P}}_{\updownarrow }=\frac{{\sin }^2\theta }{r^2}{\widehat{e}}_r,\begin{array}{c}\end{array}{\overrightarrow{P}}_{\updownarrow }^{\Leftarrow }=\frac{{\sin }^2\theta }{r^5}{\widehat{e}}_r-\left(1+\frac{1}{r^2}\right)\frac{\sin \left(2\theta \right)}{r^3}{\widehat{e}}_{\theta }\\ \{\begin{array}{l}{M}_{\updownarrow ,\varphi }^{\left[E\right]}=-\frac{2\sin \left(2\theta \right)}{r^3}\equiv -\frac{4\rho z}{r^5}\\ {\overrightarrow{S}}_{\updownarrow }^{\left[E\right]}=-\frac{1+3\cos \left(2\theta \right)}{r^4}{\widehat{e}}_r-\frac{2\sin \left(2\theta \right)}{r^4}{\widehat{e}}_{\theta }\end{array}\end{array}$$

(6)

Our ${\overrightarrow{M}}_{\updownarrow }^{\left[E\right]}$ in Equation (6) is identical (after frame changes) to that presented by [23] that is expressed in the Cartesian coordinates. There are several zero values: ${\overrightarrow{M}}_{\updownarrow }^{\left[H\right]}={\overrightarrow{S}}_{\updownarrow }^{\left[H\right]}=\overrightarrow{0}$ [15] and $K_{\updownarrow }^{(\Rightarrow )}=K_{\updownarrow }^{(\Leftarrow )}=0$, thereby standing for no interaction between $\left\{{\overrightarrow{E}}_{\updownarrow },{\overrightarrow{H}}_{\updownarrow }\right\}$. The field variables in Equation (6) are akin to those of cylindrical paraxial beams [30,43]. The magnitude ratio $\left|{\overrightarrow{P}}_{\updownarrow }/{\overrightarrow{P}}_{\updownarrow }^{\Leftarrow }\right|$ is rather cumbersome so we take $\left|{\overrightarrow{P}}_{\updownarrow ,r}/{\overrightarrow{P}}_{\updownarrow ,r}^{\Leftarrow }\right|=r^3$ only in the radial direction.

Likewise, the EM field induced by a circular dipole is given below along with all the attendant key field parameters [6,28].

$$\begin{array}{l}\{\begin{array}{l}{\overrightarrow{H}}_{○}=\frac{1}{r}\left(1+\frac{i}{r}\right)\frac{e^{i\left(r+\alpha \varphi \right)}}{\sqrt{2}}\left(-\alpha i{\widehat{e}}_{\theta }+\cos \theta {\widehat{e}}_{\varphi }\right)\\ {\overrightarrow{E}}_{○}=\frac{e^{i\left(r+\alpha \varphi \right)}}{r\sqrt{2}}\left[\frac{1}{r}\left(\frac{1}{r}-i\right)2\sin \theta {\widehat{e}}_r+\left(1+\frac{i}{r}-\frac{1}{r^2}\right)\left(\cos \theta {\widehat{e}}_{\theta }+\alpha i{\widehat{e}}_{\varphi }\right)\right]\end{array}\\ K_{○}^{(\Rightarrow )}=\alpha \frac{\cos \theta }{r^2},\begin{array}{c}\end{array}{K}_{○}^{(\Leftarrow )}=-\frac{\alpha \cos \theta }{r^5}\\ \{\begin{array}{l}{\overrightarrow{P}}_{○}=\frac{1+{\cos }^2\theta }{2r^2}{\widehat{e}}_r+\alpha \frac{\sin \theta }{r^3}\left(1+\frac{1}{r^2}\right){\widehat{e}}_{\varphi }\\ {\overrightarrow{P}}_{○}^{\Leftarrow }=\frac{{\cos }^2\theta +1}{2r^5}{\widehat{e}}_r+\frac{\cos \theta \sin \theta }{r^3}\left(1+\frac{1}{r^2}\right){\widehat{e}}_{\theta }\end{array}\\ \{\begin{array}{l}{\overrightarrow{M}}_{○}^{\left[E\right]}=\frac{1}{r^2}\left[\alpha \left(1-\frac{1}{r^2}+\frac{1}{r^4}\right)\cos \theta {\widehat{e}}_r+\alpha \frac{2\sin \theta }{r^4}{\widehat{e}}_{\theta }+\frac{\sin \left(2\theta \right)}{r}{\widehat{e}}_{\varphi }\right]\\ {\overrightarrow{M}}_{○}^{\left[H\right]}=\alpha \frac{\cos \theta }{r^2}\left(1+\frac{1}{r^2}\right){\widehat{e}}_r\end{array}\\ \{\begin{array}{l}{\overrightarrow{S}}_{○}^{\left[E\right]}=\frac{1+3\cos \left(2\theta \right)}{2r^4}{\widehat{e}}_r+\frac{\sin \left(2\theta \right)}{r^4}{\widehat{e}}_{\theta }+\alpha \frac{\sin \theta }{2r^3}\left(1-\frac{1}{r^2}-\frac{9}{r^4}\right){\widehat{e}}_{\varphi }\\ {\overrightarrow{S}}_{○}^{\left[H\right]}=\alpha \frac{\sin \theta }{2r^3}\left(1+\frac{1}{r^2}\right){\widehat{e}}_{\varphi }\end{array}\end{array}$$

(7)

Considering the helicities in Equation (4), $K_{○}^{(\Rightarrow )}\ne 0\ne K_{○}^{(\Leftarrow )}$ stands for nonzero interactions between $\left\{{\overrightarrow{E}}_{○},{\overrightarrow{H}}_{○}\right\}$. Moreover, it is exciting to confirm that $\left\{K_{○}^{(\Rightarrow )},K_{○}^{(\Leftarrow )}\right\}$ are more active respectively in the far and near fields because of the respective proportionality relations $\left|K_{○}^{(\Rightarrow )}\right|\propto r^{-2}$ and $\left|K_{○}^{(\Leftarrow )}\right|\propto r^{-5}$. This distinction in the response regions will be useful for ‘spatial-zone discriminatory enantiomeric separation’ [12,14]. The ratio $\left|K_{○}^{(\Rightarrow )}/K_{○}^{(\Leftarrow )}\right|=r^3$ is written solely in terms of the sphere-radial distance in our case. Consequently, this ratio $\left|K_{○}^{(\Rightarrow )}/K_{○}^{(\Leftarrow )}\right|=r^3$ is clearer than the analytical formula given by Equation (21) of [12] for the evanescent waves, where this ratio is expressed in terms of the incidence angle (through the wave numbers denoting propagations along a boundary and cross-boundary decay). As a polarization current according to Equation (4), $K_{○}^{(\Leftarrow )}=-\alpha r^{-5}\cos \theta$ grows in magnitude to infinity as $r\to 0$, while it vanishes along the horizon at $\theta =\frac{1}{2}\pi$.

As in the case with a linear dipole, the magnitude ratio $\left|{\overrightarrow{P}}_{○}/{\overrightarrow{P}}_{○}^{\Leftarrow }\right|$ is rather cumbersome so that we take $\left|{\overrightarrow{P}}_{○,r}/{\overrightarrow{P}}_{○,r}^{\Leftarrow }\right|=r^3$ only in the radial direction. Hence, we have a neat pair $\left|K^{(\Rightarrow )}/K^{(\Leftarrow )}\right|=\left|{\overrightarrow{P}}_{○,r}/{\overrightarrow{P}}_{○,r}^{\Leftarrow }\right|=r^3$ for the EM and reactive parameters. Hence, this pair of ratios corroborates the importance of the reactive parameters in the near field. In other words, $\nabla ·{\overrightarrow{M}}^{\left[f\right]}$ bears truly a near-field character [9,12,13], as will be shown on the forthcoming Figure 6d. In comparison, $\left|{\overrightarrow{P}}_{○,r}/{\overrightarrow{P}}_{○,r}^{\Leftarrow }\right|\propto r^3$ is partially exhibited by Equation (32) of [12]. However, we cannot easily come up with $\left|I_{○}^{\left[avg\right]}/I_{○}^{\Leftarrow }\right|\propto r^3$ for the energy ratio.

The common propagator $\exp \left[i\left(r-t\right)\right]$ in both Equations (6) and (7) confirms that induced waves are propagating outwardly in the sphere-radial direction, thus being quite distinct from the well-studied cylindrical waves. Of course, dipoles in circular arrays get harder to deal with due to the $\varphi$- dependence [2,19,25,32,35,36,39,42,45]. Meanwhile, the radial component of the magnetic field vanishes at least for the EM field induced either by a linear dipole or by a circular dipole.

Our solutions in Equations (6) and (7) hold true throughout the loss-free dielectric except right on the origin so that $\nabla ·\overrightarrow{H}=\nabla ·\overrightarrow{E}=0$ are easily verifiable for $\left\{\overrightarrow{E},\overrightarrow{H}\right\}$ in Equations (6) and (7). Besides, we can easily evaluate the field intensities $\left\{{\left|\overrightarrow{H}\right|}^2,{\left|\overrightarrow{E}\right|}^2\right\}$ as provided respectively in Sections S4 and S5 of Supplementary Materials. All the field parameters presented in Equations (6) and (7) enjoy (azimuthally) rotational symmetry, i.e., $\varphi$-independence except for the field variables $\left\{\overrightarrow{E},\overrightarrow{H}\right\}$. Moreover, one often-overlooked point in literature is the usefulness of the electric-field gradient tensor $\nabla \overrightarrow{E}$ [41]. The derivations of Equations (1)–(7) are presented in Sections S3 and S4 of Supplementary Materials in view of tensor analysis. From the perspective of continuum mechanics, it is also shown that both orbital and spin energy fluxes possess not only shear but also twist characters [1,9,10,13,18,19,24,25]. In this respect, the axial-vector (or pseudo-vector) theorem is particularly useful in understanding the vortex feature of the spin energy flux as explained not only in Section S1 of Supplementary Materials but also by [44] and [31].

We have derived the analytic formulas for both ${\overrightarrow{S}}_{\updownarrow }^{\left[f\right]}$ of Equation (6) and ${\overrightarrow{S}}_{○}^{\left[f\right]}$ of Equation (7) for the first time as far as we are aware [32]. The respective derivations of $\overrightarrow{S}$ are most easily made through ${\overrightarrow{S}}^{\left[f\right]}=\nabla \times \left(\frac{1}{2}{\overrightarrow{M}}^{\left[f\right]}\right)$ of Equation (3) from a SAM density ${\overrightarrow{M}}^{\left[f\right]}\equiv \mathrm{Im}\left({\overrightarrow{f}}^{*}\times \overrightarrow{f}\right)$ with $\overrightarrow{f}$ being one of $\left\{\overrightarrow{E},\overrightarrow{H}\right\}$ provided by Equations (6) and (7). We find from ${\overrightarrow{O}}^{\left[f\right]}={\overrightarrow{P}}^{\left[f\right]}-{\overrightarrow{S}}^{\left[f\right]}$ that $\left|{\overrightarrow{S}}_{\updownarrow }^{\left[avg\right]}\right|/\left|{\overrightarrow{O}}_{\updownarrow }^{\left[avg\right]}\right|\to r^{-2}$ as $r\to \infty$ in the far field in Equation (6), Likewise, $\left|{\overrightarrow{S}}_{○}^{\left[avg\right]}\right|/\left|{\overrightarrow{O}}_{○}^{\left[avg\right]}\right|\to r^{-1}$ in the far field in Equation (7). Therefore, the orbital energy flux is dominant over the spin energy flux in the far field. Consequently, it is no surprise that long-distance free-space optical communication is exclusively concerned with the orbital angular momentum.

For easy interpretation of forthcoming numerical results, we define the normalized parameters $\left\{K^{(\Rightarrow )},K^{(\Leftarrow )},\overrightarrow{P},{\overrightarrow{O}}^{\left[f\right]},{\overrightarrow{S}}^{\left[f\right]},{\overrightarrow{M}}^{\left[f\right]}\right\}$ as follows in correspondence to Equations (1)–(4) [1,2,3,9,15,24,25,35].

$$\begin{array}{l}{K}^{(\Rightarrow )}\equiv \frac{K^{(\Rightarrow )}}{I^{\left[avg\right]}},K^{(\Leftarrow )}\equiv \frac{K^{(\Leftarrow )}}{I^{\left[avg\right]}},\overrightarrow{P}\equiv \frac{\overrightarrow{P}}{I^{\left[avg\right]}}\\ {\overrightarrow{O}}^{\left[f\right]}\equiv \frac{{\overrightarrow{O}}^{\left[f\right]}}{{\left|\overrightarrow{f}\right|}^2},{\overrightarrow{S}}^{\left[f\right]}\equiv \frac{{\overrightarrow{S}}^{\left[f\right]}}{{\left|\overrightarrow{f}\right|}^2},{\overrightarrow{M}}^{\left[f\right]}\equiv \frac{{\overrightarrow{M}}^{\left[f\right]}}{{\left|\overrightarrow{f}\right|}^2}\end{array}$$

(8)

Here, $\overrightarrow{f}$ is one of $\left\{\overrightarrow{E},\overrightarrow{H}\right\}$. Note additionally that both $\left\{K^{(\Rightarrow )},K^{(\Leftarrow )},\overrightarrow{P}\right\}$ are formed by dividing through $I^{\left[avg\right]}$ because both parameters automatically incorporate the electric-magnetic dual symmetry. Meanwhile, $K^{(\Rightarrow )}$ is alternatively called a ‘helicity parameter’ [14]. We let a near-unity value of $\left|K^{(\Rightarrow )}\right|$ refer to ‘superchiral’ [11,14], of which we gave a detailed account in the case with a Mie scattering [28]. By construction, the script parameters in Equation (8) are bounded in magnitudes by unity with the help of the Cauchy-Schwarz inequality. Especially, $\overrightarrow{P}\equiv \overrightarrow{P}/I^{\left[avg\right]}$ stands for the ‘energy-flux velocity’ (or the ‘total energy-flux velocity’ in full), which should remain subluminal, namely, $\left|\overrightarrow{P}\right|\le 1$ [3,25].

Based on Equations (6) and (7), let us compare the divergence-free $\nabla ·{\overrightarrow{M}}_{\updownarrow }^{\left[E\right]}=0$ for the linear-dipole-induced field and $\nabla ·{\overrightarrow{M}}_{○}^{\left[E\right]}=2\alpha r^{-5}\cos \theta$ for the circular-dipole-induced field. This distinction is illustrated in panels (b) and (c) of Figure 1. By comparing $\left\{{\overrightarrow{N}}_{\updownarrow }=\overrightarrow{0},{\overrightarrow{N}}_{○}=\alpha {\widehat{e}}_z\right\}$ in Equation (5) with $\left\{\nabla ·{\overrightarrow{M}}_{\updownarrow }^{\left[E\right]}=0,\nabla ·{\overrightarrow{M}}_{○}^{\left[E\right]}\ne 0\right\}$, the EM field induced by a linear dipole is free of a source in a SAM density, whereas the EM field induced by a circular dipole is laden with a source in a SAM density. There is thus a generation of a SAM density from a nonexistent dipole-polarization ellipticity ${\overrightarrow{N}}_{\updownarrow }=\overrightarrow{0}$ for a linear dipole. In comparison, a sort of transfer takes place from a nonzero ${\overrightarrow{N}}_{○}=\alpha {\widehat{e}}_z$ into a SAM density $\left|{\overrightarrow{M}}_{○}^{\left[f\right]}\right|$ for a circular dipole. Recall in Equation (5) that a circular dipole is a linear combination of two linear dipoles with an in-quadrature phase delay. Such a distinction in either generation or transfer of SAM densities is linked to either generation or transfer of the EM and reactive helicities in the case with a Mie scattering [28].

Near-field numerical computations have been developed to address nanoscale photonics [1,2,5,37,41]. Here, the Maxwell equations are solved to provide the spatial distributions of $\left\{\overrightarrow{E},\overrightarrow{H}\right\}$, whence we can compute not only the reactive helicity but also other field parameters. By taking numerical divergence, we can thus evaluate $K^{(\Leftarrow )}=-\nabla ·\left(\frac{1}{2}{\overrightarrow{M}}^{\left[E\right]}\right)$. An electric field can also be evaluated from the measurement data on its magnitude and phase [22,43].

Other key field parameters are also evaluated from measurements on external agents that are immersed in the EM field under consideration. In this regard, both $\overrightarrow{O}$ and $\overrightarrow{S}$ can be deduced by measuring forces and/or toques exerted on immersed nano-objects [6,12,13,14]. Since ${\overrightarrow{O}}^{\left[f\right]}={\overrightarrow{P}}^{\left[f\right]}-{\overrightarrow{S}}^{\left[f\right]}$, two of $\left\{{\overrightarrow{P}}^{\left[f\right]},{\overrightarrow{O}}^{\left[f\right]},{\overrightarrow{S}}^{\left[f\right]}\right\}$ are required to determine the third. In particular, ${\overrightarrow{S}}^{\left[E\right]}=\nabla \times \left(\frac{1}{2}{\overrightarrow{M}}^{\left[E\right]}\right)$ as the curl of the SAM density of the electric field constitutes a non-conservative contribution to the scattering force on an immersed nano-object. The absorptive and/or polarizable properties of those immersed nano-objects help us to come up with both EM and reactive helicities [10,12,13,14,15,16,17,19,21,23,32,37,38,39,41]. Another method is to measure the field intensity along two orthogonal directions [4,6].

Conversely, $K^{(\Leftarrow )}=\nabla ·\left(\frac{1}{2}{\overrightarrow{M}}^{\left[H\right]}\right)=-\nabla ·\left(\frac{1}{2}{\overrightarrow{M}}^{\left[E\right]}\right)$ would help us map the electric and magnetic fields whenever the EM field under consideration is induced by the simultaneous presence of an electric dipole and a magnetic dipole. The conservation law $\nabla ·{\overrightarrow{M}}^{\left[avg\right]}=0$ in Equation (3) complements the fact that rotating the transverse coordinates induces opposite phase shifts in the right- and left-hand circularly polarized waves propagating along a certain axis. This relation $\nabla ·{\overrightarrow{M}}^{\left[E\right]}=-\nabla ·{\overrightarrow{M}}^{\left[H\right]}$ of Equation (3) is related to but not equal to the ‘dual-antisymmetric’ relation presented in [10]. One reason for this discrepancy in the term ‘dual-antisymmetric’ lies in the fact that $\nabla ·{\overrightarrow{M}}^{\left[E\right]}+\nabla ·{\overrightarrow{M}}^{\left[H\right]}=0$ does not always mean ${\overrightarrow{M}}^{\left[E\right]}+{\overrightarrow{M}}^{\left[H\right]}=0$.

Let us tell what we have achieved in this study. Although various formulas presented in Section 2 have already been scattered in the references mentioned there, we have made clearer the relationships among them as illustrated in Figure 1a. The actual formulas presented in Equations (6) and (7) have been analytically derived for the first time in this study in the two special cases of electric point dipoles. Especially, the explicit forms of the pairs of the internal energy flow, $\left\{{\overrightarrow{S}}_{\updownarrow }^{\left[E\right]},{\overrightarrow{O}}_{\updownarrow }^{\left[E\right]}\right\}$ and $\left\{{\overrightarrow{S}}_{○}^{\left[E\right]},{\overrightarrow{O}}_{○}^{\left[E\right]},{\overrightarrow{S}}_{○}^{\left[H\right]},{\overrightarrow{O}}_{○}^{\left[H\right]}\right\}$, have never been published anywhere. The following Section 4 and Section 5 show numerical behaviors in appropriate coordinate frames respectively for the linear and circular electric point dipoles.

4. Numerical Evaluations of Electromagnetic Fields for a Linear Dipole

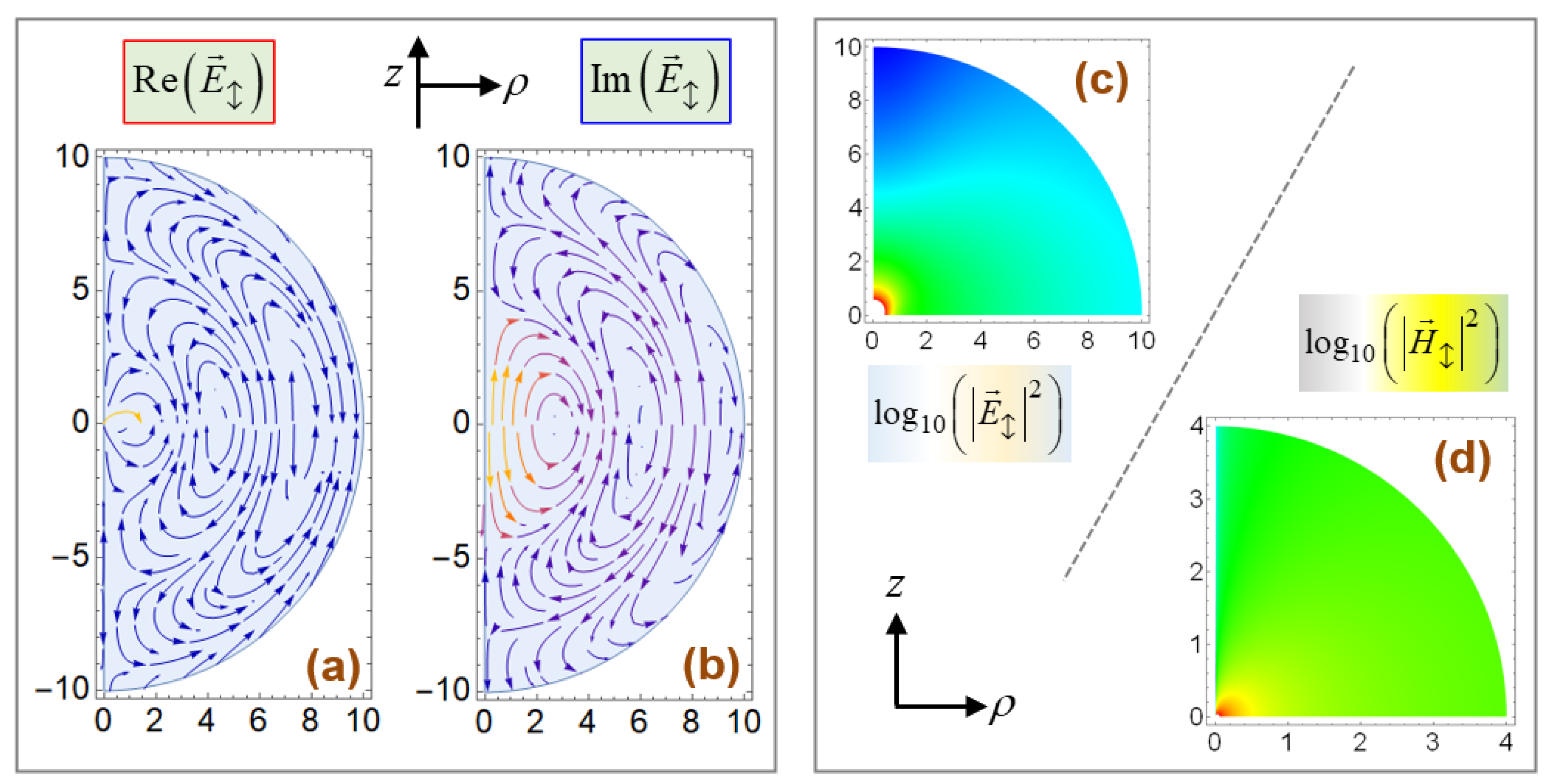
Figure 2 displays the induced fields ${\overrightarrow{E}}_{\updownarrow }$ and the field intensities for a linear dipole [10,18,22,24,32], where EM fields themselves exhibit vortices and singularities. It is noted in Figure 2c that a dark region prevails in the vertical direction [5]. Since the SAM density ${\overrightarrow{M}}^{\left[f\right]}\equiv \mathrm{Im}\left({\overrightarrow{f}}^{*}\times \overrightarrow{f}\right)$ can alternatively be cast into ${\overrightarrow{M}}^{\left[f\right]}=2\mathrm{Re}\left(\overrightarrow{f}\right)\times \mathrm{Im}\left(\overrightarrow{f}\right)$, Figure 2a,b help to guess at ${\overrightarrow{M}}^{\left[E\right]}$. We present these textbook matters in Figure 2 to help explain what we have newly found in the forthcoming Figure 3 and Figure 4. We have placed additional figures in Section S4 of Supplementary Materials. Throughout this study, we set $\alpha =+1$ except when otherwise stated. We find diverse vortical features of field variables as presented in Supplementary Materials of [28], where a Mie scattering is examined.

Figure 3 displays further characters for the EM field induced by a linear dipole. The purely sphere-radial streamlines of ${\overrightarrow{P}}_{\updownarrow }$ is not presented here. Figure 3a displays the magnitude $\left|{\overrightarrow{P}}_{\updownarrow }\right|$ of the normalized Poynting vector. In all directions except along the linear-dipolar axis, we find that $\left|{\overrightarrow{P}}_{\updownarrow }\right|\to 1$ in the far-field limit. As expected, subluminal energy velocity prevails over the whole space [10,25]. Figure 3b shows the relative intensity ratio $E_{\theta }^r\equiv {\left({\left|E_r\right|}^2+{\left|E_{\theta }\right|}^2\right)}^{-1}\left({\left|E_r\right|}^2-{\left|E_{\theta }\right|}^2\right)$. It turns out that Figure 3a,b are complementary to each other [30]. The difference ${\left|{\overrightarrow{E}}_{\updownarrow }\right|}^2-{\left|{\overrightarrow{H}}_{\updownarrow }\right|}^2$ in the field intensities is proportional to the reactive energy [12] as shown by Figure S2 of Section S4 of Supplementary Materials.

Figure 3. (a) The streamlines formed by ${\overrightarrow{P}}_{\updownarrow }\equiv {\overrightarrow{P}}_{\updownarrow }/I_{\updownarrow }^{\left[avg\right]}$ for a linear dipole. (b) The relative intensity ratio $E_{\theta }^r\equiv {\left({\left|E_r\right|}^2+{\left|E_{\theta }\right|}^2\right)}^{-1}\left({\left|E_r\right|}^2-{\left|E_{\theta }\right|}^2\right)$. (c) The azimuthal component $M_{\updownarrow ,\varphi }^{\left[E\right]}$ of the per-electric-field-intensity vector ${\overrightarrow{M}}_{\updownarrow }^{\left[E\right]}$. (d) Near-circular polarization states with $0.99\le \left|M_{\updownarrow ,\varphi }\right|\le 1$. All plots are made over $r\le 10$ for illustrating the spherical domains on a certain meridional $z\rho$ -plane.

Figure 3. (a) The streamlines formed by ${\overrightarrow{P}}_{\updownarrow }\equiv {\overrightarrow{P}}_{\updownarrow }/I_{\updownarrow }^{\left[avg\right]}$ for a linear dipole. (b) The relative intensity ratio $E_{\theta }^r\equiv {\left({\left|E_r\right|}^2+{\left|E_{\theta }\right|}^2\right)}^{-1}\left({\left|E_r\right|}^2-{\left|E_{\theta }\right|}^2\right)$. (c) The azimuthal component $M_{\updownarrow ,\varphi }^{\left[E\right]}$ of the per-electric-field-intensity vector ${\overrightarrow{M}}_{\updownarrow }^{\left[E\right]}$. (d) Near-circular polarization states with $0.99\le \left|M_{\updownarrow ,\varphi }\right|\le 1$. All plots are made over $r\le 10$ for illustrating the spherical domains on a certain meridional $z\rho$ -plane.

Meanwhile, the per-electric-field-intensity vector ${\overrightarrow{M}}_{\updownarrow }^{\left[E\right]}$ in Equation (8) becomes a scalar $M_{\updownarrow ,\varphi }^{\left[E\right]}\equiv {\left|{\overrightarrow{E}}_{\updownarrow }\right|}^{-2}{M}_{\updownarrow ,\varphi }^{\left[E\right]}$ by use of a sole nonzero component according to Equation (6). It turns out that $M_{\updownarrow ,\varphi }^{\left[E\right]}=2{\left|\overrightarrow{E}\right|}^{-2}\mathrm{Im}\left(E_z^{*}{E}_{\rho }\right)$ so that it is a ratio between two Stokes parameters [14] or the degree of circular polarization (DoCP) [3,9,10,11,15,18,23,24,37,38]. We rediscover from Equation (6) that the transverse component $M_{\updownarrow ,\varphi }^{\left[E\right]}$ does not depend on the spin index $\alpha =\pm 1$. Figure 3c displays this DoCP over a certain meridional $z\rho$-plane, thus being negative and positive respectively over the northern and southern hemispheres. We have recovered hence a half-twist or a four-lobe pattern in the polar direction [15,23,37,38]. In addition, $\left|M_{\updownarrow ,\varphi }^{\left[E\right]}\right|$ exhibits larger values along the linear-dipolar axis as is $\left|{\overrightarrow{P}}_{\updownarrow }\right|$ on panel (b). Other pairs of electric-field components can be taken in forming proper DOCPs depending on specific wave configurations [14,19].

Based on Figure 3c, we have drawn Figure 3d with a cut-off on $\left|M_{\updownarrow ,\varphi }^{\left[E\right]}\right|$ by enforcing $M_{\updownarrow ,\varphi }^{\left[E\right]}=0$ if $\left|M_{\updownarrow ,\varphi }^{\left[E\right]}\right|<0.99$. Resultantly, the blue curve on the northern hemisphere indicates the approximate locations of $\left|M_{\updownarrow ,\varphi }^{\left[E\right]}\right|\to 1$, albeit a perfect circular polarization exists nowhere. The desirability of a perfect circular polarization of an EM field can be found in [12] as regards zero back-scattering. Because of the rotational symmetry, the pair of curves in Figure 3d implies respectively pencil-hull-like tapered cylindrical surfaces as summarily depicted in Figure 1c [1,5,14,35,37]. In this respect, Figure 3d shows that $M_{\updownarrow ,\varphi }^{\left[E\right]}=0$ on the horizontal plane in confirmation of Equation (6). That is why the blue and red strips are drawn in Figure 3d such that they run short of neither the origin nor the horizontal plane. These fading portions are called here ‘tapered surfaces’, over which ${\overrightarrow{M}}_{\updownarrow }^{\left[E\right]}\ne \overrightarrow{0}$ are being slowly established for the EM field although ${\overrightarrow{N}}_{\updownarrow }=\overrightarrow{0}$ for a linear dipole as listed in Equation (5) [32].

Figure 4 displays the streamlines formed by $\left\{{\overrightarrow{O}}_{\updownarrow }^{\left[E\right]},{\overrightarrow{S}}_{\updownarrow }^{\left[E\right]}\right\}$. Notice that the absence of the azimuthal component $S_{\updownarrow ,\varphi }^{\left[E\right]}=0$ in Equation (6) does not affect these streamlines on the meridional $z\rho$-plane. In Figure 4a, the orbital energy flux exhibits vortices in the near field close to the origin. We indicated in Figure 4a the ‘circular saddle’ (because of the rotational symmetry) by the solid dot in the vermillion color. By ${\overrightarrow{O}}_{\updownarrow }^{\left[E\right]}={\overrightarrow{P}}_{\updownarrow }^{\left[E\right]}-{\overrightarrow{S}}_{\updownarrow }^{\left[E\right]}$ with ${\overrightarrow{S}}_{\updownarrow }^{\left[E\right]}$ in Equation (6), this saddle circle has the sphere-radius of $r=\sqrt{2}$. Inside this circular off-axis saddle, we find nested closed loops of streamlines around the vertical axis. Following the counter-rotational skyrmions of [18], we can thus assign (non-rigorous) vorticity numbers $N_v=\pm 1$ to the 3D toroidal vortices in Figure 4a: $N_v=+1$ for the upper clockwise rotation, and $N_v=-1$ for the lower counterclockwise rotation for ${\overrightarrow{O}}_{\updownarrow }^{\left[E\right]}$. In Figure 4b, the vorticity numbers are interchanged for ${\overrightarrow{S}}_{\updownarrow }^{\left[E\right]}$, while the respective vortices seem to occupy the lower and upper hemispheres.

Figure 4. The streamlines formed by the internal flows over any meridional $z\rho$-plane for a linear dipole: (a) the orbital energy flux ${\overrightarrow{O}}_{\updownarrow }^{\left[E\right]}$, and (b) the spin energy flux ${\overrightarrow{S}}_{\updownarrow }^{\left[E\right]}$.

Figure 4. The streamlines formed by the internal flows over any meridional $z\rho$-plane for a linear dipole: (a) the orbital energy flux ${\overrightarrow{O}}_{\updownarrow }^{\left[E\right]}$, and (b) the spin energy flux ${\overrightarrow{S}}_{\updownarrow }^{\left[E\right]}$.

Outside these two loop saddles, the streamlines of ${\overrightarrow{O}}_{\updownarrow }^{\left[E\right]}$ are open to infinity [10,18,24,41,42,43]. The trajectories of the spin energy flux ${\overrightarrow{S}}_{\updownarrow }^{\left[E\right]}$ shown in Figure 4b are self-similar because the polar-angle dependence is separable from the sphere-radial dependence as seen from Equation (6). See Section S6 of Supplementary Materials for the derivation of such trajectories in the case of the EM field induced by a circularly polarized electric point dipole, because both dipoles lead to analogous trajectories.

In each of Figure 4a,b, a vortex-antivortex pair is made up of one vortex from the northern hemisphere and another antivortex from the southern hemisphere [18]. Moreover, the net EM helicity disappears, i.e., $K_{\updownarrow }^{(\Rightarrow )}=0$ in Equation (6) in correspondence to the source property ${\overrightarrow{N}}_{\updownarrow }=\overrightarrow{0}$ stated in Equation (5) [2]. Concerning the vorticity of an orbital energy flux, we find that $\nabla \times {\overrightarrow{O}}^{\left[f\right]}=2\mathrm{Re}\left(\nabla \overrightarrow{f}\right)\times \mathrm{Im}\left(\nabla \overrightarrow{f}\right)$ as proved in Section S2 of Supplementary Materials. This formula states that the vorticity in ${\overrightarrow{O}}^{\left[f\right]}$ is linked to the field gradients, according to which experiments can be set up. As sketched in the center of Figure 4, both magnitudes $\left\{\left|{\overrightarrow{O}}_{\updownarrow }^{\left[E\right]}\right|,\left|{\overrightarrow{S}}_{\updownarrow }^{\left[E\right]}\right|\right\}$ exceed $\left|{\overrightarrow{P}}_{\updownarrow }\right|$ over most spaces. Hence, the ambiguity in determining reverse internal flows as mentioned in [37] is now resolved by comparing the two panels in Figure 4. When focusing on the radial distributions, the spin energy flux is stronger in the near field and the intermediate (Fresnel) field, while the orbital energy flux is stronger in the far field [6,12,19,26,27].

Let us return to the needle-shaped level curves in Figure 3d, where higher values of the DoCP $\left|M_{\updownarrow ,\varphi }^{\left[E\right]}\right|$ are achieved. Due to the rotational symmetry around the vertical $z$-axis, this pair of curves corresponds to 2D surfaces. We can hence alternatively give the name ‘hollow needles’ to these pencil-hull-like tapered cylindrical surfaces displayed in Figure 1c and Figure 3d. Along such optical needles, a uniform conversion takes place from the orbital energy flux to the spin energy flux from an input position (corresponding to the far field in this study) toward a focal point (corresponding to the dipole position at the origin in this study) [6,10,30,32,39,43]. An analytical formula for this pair of cylindrical surfaces is derived in [40], where detailed discussions are offered in both Figure 2 and Figure 3. In contrast, Figure 4 on the internal energy flows has never been so far presented.

In this connection, consider a geometrically needle-shaped plasmonic nanoantenna, upon which light is illuminated along the axis [1]. When the electric-field polarization lies on the cross-sectional plane of that needle, this transverse field component is found to get converted into the longitudinal component along the needle axis as the light propagates along the axis [4,31]. In the meantime, the spin-to-orbital conversion in this study is caused by the spatially diverging area of the spherical EM waves induced by a linear dipole. Therefore, our EM field is a sort of ‘reverse focused’ (alternatively, either scattered or defocused wave), as marked by the downward arrow in Figure 3c. In addition, a focused beam normally experiences either circular-to-linear or linear-to-circular conversion in the field polarization [1,10,15,23,35,37,38,46]. In comparison, our EM field emanating from the linear dipole experiences a linear-to-circular conversion as it is further radiated into the far field as seen in Figure 3c,d. Taken, together, internal energy flows in Figure 4 are better understood with the help of the optical needles in Figure 3.

5. Numerical Evaluations of Electromagnetic Fields for a Circular Dipole

Figures S3–S5 provided in Section S6 of Supplementary Materials presents a set of streamlines formed by $\mathrm{Re}\left({\overrightarrow{E}}_{○}\right)$ and $\mathrm{Im}\left({\overrightarrow{E}}_{○}\right)$ both on meridional $z\rho$-planes and on the horizontal $xy$-planes. Although we find complicated structures such as saddles, stagnation points, and singularities in 3D spaces, they are not fundamentally distinct from those displayed in Figure 2a,b for a linear dipole [11,18]. By evaluating $\nabla {\overrightarrow{E}}_{○}$, we have learned that both symmetric and skew-symmetric parts of ${\overrightarrow{E}}_{○}$ are nonzero, thus indicating both shear and spin (twist) in the electric field [44], as explained in more detail by Section S1 of Supplementary Materials. As displayed in Figure S6 in Section S6 of Supplementary Materials, the field intensities $\left\{{\left|{\overrightarrow{E}}_{○}\right|}^2,{\left|{\overrightarrow{H}}_{○}\right|}^2\right\}$ exhibit spatial distributions largely close to $\left\{{\left|{\overrightarrow{E}}_{\updownarrow }\right|}^2,{\left|{\overrightarrow{H}}_{\updownarrow }\right|}^2\right\}$ shown in Figure 2 in the sense that both pairs decrease approximately with increasing sphere-radial distance. The difference ${\left|{\overrightarrow{E}}_{○}\right|}^2-{\left|{\overrightarrow{H}}_{○}\right|}^2$ in the field intensities is proportional to the reactive energy [12].

Figure 5 displays various characters for the EM field induced by a circular dipole. Figure 5a shows the per-mean-field-intensity field helicity $K_{○}^{(\Rightarrow )}\equiv K_{○}^{(\Rightarrow )}/I_{○}^{\left[EH\right]}$ plotted on the northern hemisphere, with $K_{○}^{(\Rightarrow )}$ given in Equation (7). Take note that $K_{○}^{(\Rightarrow )}$ undergoes a sign reversal across the horizontal plane, while its magnitude remains bounded by unity [19]. Although the circular dipole is endowed with a unity dipole-polarization ellipticity $\left|{\overrightarrow{N}}_{○}\right|=1$ right on the horizontal plane according to Equation (5), Figure 5a confirms that the EM helicity increases approximately upwardly in the vertical direction. We find on Figure 5b that $\left|{\overrightarrow{P}}_{○}\right|$ is weaker in the near field, while it approaches unity (i.e., remaining in a luminal speed) in the far field as on Figure 3a [19].

The streamlines formed by ${\overrightarrow{P}}_{○}$ over the meridional $z\rho$-plane is pointing in the pure sphere-radial direction as for a linear dipole (hence not shown here). One might ascribe such a simple picture to the missing polar component, i.e., $P_{○,\varphi }=0$ in Equation (7). This simple picture turns out correct only on the meridional $z\rho$-plane with $\varphi =0$ due to the nonzero azimuthal component, viz., $P_{○,\varphi }\ne 0$. See Figure S7 of Section S6 in Supplementary Materials for several plots on other meridional $z\rho$-planes with varying $\varphi$. We find that even $P_{○,r}<0$ over some portion of space, thus denoting sphere-radially backward flows [18,25,37,41].

Figure 5c shows the resulting spiral streamlines of ${\overrightarrow{P}}_{○}$ on the horizontal plane in case with $\alpha =+1$, thus displaying counterclockwise (CCW) circulations. With $\alpha =-1$, clockwise (CW) rotations accompany the spiral flows. Figure 5d displays helical trajectories traversed by the Poynting vector. Analytic formulas of these trajectories are derived in Section S6 of Supplementary Materials. They are constructed by combining a sphere-radial trajectory on a meridional $r\theta$-plane analogous to Figure 3a and a spiral trajectory of Figure 5c on a latitudinal $xy$-plane [10,17,24,43].

Figure 5e–g illustrates the polar-angle dependences of key properties provided by Equations (6) and (7) by fixing the radial coordinates at suitable values. In Figure 5e, the magnitude of $\left|{\overrightarrow{P}}_{\updownarrow }\right|$ on the blue dotted curve for a linear dipole exhibits the famous dependence on ${\sin }^2\theta$, whereas the magnitude of $\left|{\overrightarrow{P}}_{○}\right|$ on the red solid curve for a circular dipole exhibits the equally famous dependence on $1+{\cos }^2\theta$. Figure 5f shows the angle dependences of the corresponding electric-field intensities $\left\{{\left|{\overrightarrow{E}}_{\updownarrow }\right|}^2,{\left|{\overrightarrow{E}}_{○}\right|}^2\right\}$. Roughly speaking, the curves in Figure 5e,f are complementary.

In comparison, Figure 5g shows $K_{○}^{(\Rightarrow )}\propto \cos \theta$, which are not familiar to a general readership. Hence, the reactive helicity $K_{○}^{(\Leftarrow )}\propto \left(-\cos \theta \right)$ is lop-sided (namely, being positive for all $\theta$) in the southern hemisphere as a source of $\nabla ·\left(\frac{1}{2}{\overrightarrow{M}}^{\left[H\right]}\right)=K^{(\Leftarrow )}$ according to Equation (4).

When compared to the sole nonzero component $M_{\updownarrow ,\varphi }^{\left[E\right]}$ in Equation (6) [40], its counterpart ${\overrightarrow{M}}_{○}^{\left[E\right]}$ given in Equation (7) has all three nonzero components. Therefore, the per-electric-field-intensity ${\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\equiv {\left|{\overrightarrow{E}}_{○}\right|}^{-2}{\overrightarrow{M}}_{○}^{\left[E\right]}$ defined in Equation (8) is inadequate for characterizing a unique electric degree of circular polarization (DoCP) [9,32,37]. Figure 6a displays $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|$ on a meridional $\rho z$-plane, thereby being a sort of counterpart of the pair of panels (c) and (d) of Figure 3. Obviously, $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|$ is symmetrical across the horizontal plane. Take note of Figure 6a that $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|$ exhibits larger values along the vertical axis perpendicular to the circular-dipole plane. Based on Figure 6a, Figure 6b is drawn by imposing a cut-off on $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|$ such that $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|=0$ is forcefully assigned if $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|<0.99$. Resultantly, the red zones on both hemispheres indicate the approximate locations of $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|\to 1$, although a state of perfect circular polarization is not accessible over the whole space.

Figure 6. (a) The magnitude $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|$ of the EM field induced by a circular dipole on any meridional $\rho z$-plane. (b) Near-circular polarization states defined by the narrow range such that $0.99\le \left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|\le 1$ with the schematic figure on the left denotes the 3D volumetric filled funnel and spout region near the origin. (c) The normalized magnetic-field polarization ellipticity ${\overrightarrow{\mathcal{M}}}_{○}^{\left[H\right]}\equiv {\left|{\overrightarrow{H}}_{○}\right|}^{-2}{\overrightarrow{M}}_{○}^{\left[H\right]}$, where the red and blue colors denote the regions respectively for $0.99<{\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[H\right]}\right|}^{-2}\le 1$ and $0\le {\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[H\right]}\right|}^{-2}<0.99$. (d) The normalized reactive helicity $K_{○}^{(\Leftarrow )}$.

Figure 6. (a) The magnitude $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|$ of the EM field induced by a circular dipole on any meridional $\rho z$-plane. (b) Near-circular polarization states defined by the narrow range such that $0.99\le \left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|\le 1$ with the schematic figure on the left denotes the 3D volumetric filled funnel and spout region near the origin. (c) The normalized magnetic-field polarization ellipticity ${\overrightarrow{\mathcal{M}}}_{○}^{\left[H\right]}\equiv {\left|{\overrightarrow{H}}_{○}\right|}^{-2}{\overrightarrow{M}}_{○}^{\left[H\right]}$, where the red and blue colors denote the regions respectively for $0.99<{\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[H\right]}\right|}^{-2}\le 1$ and $0\le {\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[H\right]}\right|}^{-2}<0.99$. (d) The normalized reactive helicity $K_{○}^{(\Leftarrow )}$.

Because of the rotational symmetry, the pair of red zones in Figure 6b implies respectively funnel-like tapered filled cones in a 3D space as schematically depicted on the left of Figure 6b. In this small cartoon, the ‘spout’ dangling at the bottom of a cone corresponds to such a 3D tapered portion. With both hemispheres on the meridional plane taken together, the zones with $0.99\le \left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|\le 1$ comprise a double-conical volumetric structure with a central connecting spout [25]. For a circular dipole, the filled-cone-shaped funnel displayed in Figure 1d and Figure 6b is a loose form of a reverse focused or defocused wave [4,38]. Considering the proportionality relations $M_{\updownarrow ,\varphi }^{\left[E\right]},M_{○,\varphi }^{\left[E\right]}\propto \sin \left(2\theta \right)$ given in Equations (6) and (7), the normalized field-ellipticity parameter $M_{\updownarrow ,\varphi }^{\left[E\right]}$ presented in Figure 3c,d is analogous to $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|$ on Figure 6 [42].

According to ${\overrightarrow{\mathcal{M}}}^{\left[f\right]}\equiv {\left|\overrightarrow{f}\right|}^{-2}{\overrightarrow{M}}^{\left[f\right]}$ in Equation (8), the magnetic ${\overrightarrow{\mathcal{M}}}_{○}^{\left[H\right]}\equiv {\left|\overrightarrow{H}\right|}^{-2}{\overrightarrow{M}}_{○}^{\left[H\right]}$ is easily formed as a counterpart of the electric ${\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\equiv {\left|\overrightarrow{E}\right|}^{-2}{\overrightarrow{M}}_{○}^{\left[E\right]}$ [14]. From $\left\{{\overrightarrow{H}}_{○},{\overrightarrow{M}}_{○}^{\left[H\right]}\right\}$ of Equation (8), we have thus arrived at the following neat formula.

$${\overrightarrow{\mathcal{M}}}_{○}^{\left[H\right]}\equiv \frac{{\overrightarrow{M}}_{○}^{\left[H\right]}}{{\left|\overrightarrow{H}\right|}^2}\equiv \frac{\mathrm{Im}\left({\overrightarrow{H}}^{*}\times \overrightarrow{H}\right)}{{\left|\overrightarrow{H}\right|}^2}=\alpha \frac{2\cos \theta }{1+{\cos }^2\theta }{\widehat{e}}_r$$

(9)

The scalar parameter $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[H\right]}\right|$ is the ‘magnetic DoCP’, which is obviously bounded by unity such that $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[H\right]}\right|\le 1$ [19]. We found that $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[H\right]}\right|$ is continuously decreasing from the axial direction toward the horizontal direction. We have plotted instead in Figure 6c the cut-off values such that $0.99\le \left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[H\right]}\right|\le 1$, which turns out to occupy an analogous region as the electric DoCP shown in Figure 6b. The ‘subluminality factor’ in [25] with $\cos \theta$ as an axicon angle corresponds exactly to $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[H\right]}\right|$ in Equation (9), thus being equal to the relative energy velocity $P_z$ in terms of our notation in Equation (8).

One minor distinction in Figure 6 is that the zone with $0.99\le \left|{\overrightarrow{M}}_{○}^{\left[H\right]}\right|\le 1$ on Figure 6c does not exhibit a spout portion unlike $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[E\right]}\right|$ in Figure 6b. See the dotted black circle around the coordinate origin in Figure 6c. The reason is that we are dealing with an electric (not magnetic) circular dipole. Therefore,$\left|M_{○,z}^{\left[E\right]}\right|>\left|M_{○,z}^{\left[H\right]}\right|$ or $\left|M_{○,z}^{\left[E\right]}\right|<\left|M_{○,z}^{\left[H\right]}\right|$ along the vertical axis depending on the radial ranges (namely, near or far field) [32]. We find in Figure 6a that $\left|{\overrightarrow{M}}_{○}^{\left[E\right]}\right|$ undergoes a spreading along the vertical axis, which stands in stark contrast to an almost perfect sphere-radial spreading as expected from Figure 5b by $\left|{\overrightarrow{P}}_{○}\right|\equiv \left|{\overrightarrow{P}}_{○}/I_{○}^{\left[avg\right]}\right|$ [10,15,37,38,39]. Figure 6d shows the normalized reactive helicity ${\mathcal{K}}_{○}^{(\Leftarrow )}\equiv {\left(I^{\left[avg\right]}\right)}^{-1}\mathrm{Re}\left(\overrightarrow{E}·{\overrightarrow{H}}^{*}\right)$, which turns out strong only in the near field. In comparison, ${\mathcal{K}}_{○}^{(\Rightarrow )}$ on Figure 5a is varied mostly with respect to the polar angle $\theta$, while being largely indifferent to the radial distance.

Figure 7 displays the streamlines formed by the electric portions $\left\{{\overrightarrow{O}}_{○}^{\left[E\right]},{\overrightarrow{S}}_{○}^{\left[E\right]}\right\}$ of both orbital and energy fluxes on the meridional $z\rho$-planes. In comparison to Equation (6), we find in Equation (7) that the streamlines formed by ${\overrightarrow{S}}_{○}^{\left[E\right]}$ for a circular dipole on a meridional plane are identical to those formed by ${\overrightarrow{S}}_{\updownarrow }^{\left[E\right]}$ for a linear dipole. It is because the meridional components $\left\{S_{\updownarrow ,r}^{\left[E\right]},S_{\updownarrow ,\theta }^{\left[E\right]}\right\}$ in Equation (6) is exactly $-2$ times (hence being in a reverse direction) their respective counterparts $\left\{S_{○,r}^{\left[E\right]},S_{○,\theta }^{\left[E\right]}\right\}$ in Equation (7). However, the streamlines formed respectively by $\left\{{\overrightarrow{O}}_{\updownarrow }^{\left[E\right]},{\overrightarrow{O}}_{○}^{\left[E\right]}\right\}$ are appreciably different since the radial components of the Poynting vectors $\left\{P_{\updownarrow ,r},P_{○,r}\right\}$ are quite different from each other. For the streamlines in Figure 7a for ${\overrightarrow{O}}_{○}^{\left[E\right]}$, we placed a pair of on-axis saddle points on the vertical axis as marked by the vermillion-color dots. We find from Equation (7) that these saddles are located at $r=\pm \sqrt{2}$ [41]. The streamlines in Figure 7c for ${\overrightarrow{S}}_{○}^{\left[E\right]}$ appear analogous to those of ${\overrightarrow{S}}_{\updownarrow }^{\left[E\right]}$ shown in Figure 4b, except for the afore-mentioned sign reversals.

Figure 7. The streamlines formed by the internal flows over a meridional $z\rho$-plane with $\varphi =0$ for a circular dipole: (a) for the electric-portion orbital energy flux ${\overrightarrow{O}}_{○}^{\left[E\right]}$, and (c) for the electric-portion spin energy flux ${\overrightarrow{S}}_{○}^{\left[E\right]}$. Both plotted over the horizontal $xy$-planes at $\theta =\frac{1}{2}\pi$: (b) for the electric-portion orbital energy flux ${\overrightarrow{O}}_{○}^{\left[E\right]}$, and (d) for the electric-portion spin energy flux ${\overrightarrow{S}}_{○}^{\left[E\right]}$.

Figure 7. The streamlines formed by the internal flows over a meridional $z\rho$-plane with $\varphi =0$ for a circular dipole: (a) for the electric-portion orbital energy flux ${\overrightarrow{O}}_{○}^{\left[E\right]}$, and (c) for the electric-portion spin energy flux ${\overrightarrow{S}}_{○}^{\left[E\right]}$. Both plotted over the horizontal $xy$-planes at $\theta =\frac{1}{2}\pi$: (b) for the electric-portion orbital energy flux ${\overrightarrow{O}}_{○}^{\left[E\right]}$, and (d) for the electric-portion spin energy flux ${\overrightarrow{S}}_{○}^{\left[E\right]}$.

We indicate on Figure 7a two saddles with $K_{○}^{(\Rightarrow )}=\pm 1/2$ of opposite EM helicities for $\alpha =\pm 1$ according to $K_{○}^{(\Rightarrow )}=\alpha r^{-2}\cos \theta$ as given by Equation (8) [18]. This behavior stands in stark contrast to the single circular saddle lying on the horizontal plane of Figure 4a for ${\overrightarrow{O}}_{\updownarrow }^{\left[E\right]}$ together with $K_{\updownarrow }^{(\Rightarrow )}=0$ over the whole space. In addition, we find in Figure 7a a pair of loop vortices of ${\overrightarrow{O}}_{○}^{\left[E\right]}$ near the origin. As we have assigned (non-rigorous) vorticity numbers on Figure 4a, we can assign the vorticity number $N_v=\pm 1$ to the 3D toroidal vortices on Figure 7a: $N_v=\pm 1$ for the lower clockwise rotation, and $N_v=-1$ for the upper counterclockwise rotation for ${\overrightarrow{O}}_{○}^{\left[E\right]}$ [18]. Likewise, in Figure 7b, the vorticity numbers are interchanged for ${\overrightarrow{S}}_{○}^{\left[E\right]}$, while the respective vortices seem to occupy the upper and lower hemi-spheres.

Therefore,${\overrightarrow{O}}_{○}^{\left[E\right]}$ reveals its backflow accompanying vortices, while the Poynting vector ${\overrightarrow{P}}_{○}$ displayed in Figure 5d is still forwardly directed even in this zone [10,18,24,42]. Another difference is that backflows in a generic Poynting vector are likely to take place in the regions of low $I^{\left[avg\right]}$ (lying in the far field in our case) [29], whereas backflows in the internal energy fluxes $\left\{{\overrightarrow{O}}_{○}^{\left[f\right]},{\overrightarrow{S}}_{○}^{\left[f\right]}\right\}$ are more likely to take place in the regions of high $I^{\left[avg\right]}$ (lying in the near field in our case) [18].

Figure 7b,d display the streamlines formed respectively by $\left\{{\overrightarrow{O}}_{○}^{\left[E\right]},{\overrightarrow{S}}_{○}^{\left[E\right]}\right\}$ over the horizon, whence we can confirm a rotational symmetry. It is worthwhile noting near the center of Figure 7d that the spiral streamlines reverse their rotational directions from CCW to CW. We can find the radial location of this azimuthal-flow reversal by setting $S_{○,\varphi }^{\left[E\right]}=0$ in Equation (7) [24]. Reversals in the rotational flows take place also in toroidal light pulses (TLPs) [18]. Rotational fluid flows exhibit analogous rotational reverse flows as well [44].

As for Figure 4, Figure 7 helps us in estimating the relative magnitudes among $\left\{{\overrightarrow{P}}_{○},{\overrightarrow{O}}_{○}^{\left[E\right]},{\overrightarrow{S}}_{○}^{\left[E\right]}\right\}$ and any reverse backward flows [18,37]. According to Equation (7), $S_{○,\rho }^{\left[E\right]}=-r^{-4}\ne 0$ on the horizon in the sphere-radial direction as $r\to 0$. Hence, there is a radial suction of the spin energy flux in Figure 7d near the origin which is compensated by the meridional supply in correspondence to the divergence-free condition $\nabla ·{\overrightarrow{S}}_{○}^{\left[E\right]}=0$. Notwithstanding, $\left|S_{○,\rho }^{\left[E\right]}/S_{○,\theta }^{\left[E\right]}\right|\to 0$ due to much stronger azimuthal rotation near the origin, whence the streamlines look oriented purely in the azimuthal direction. The reversal in the spiral directions by ${\overrightarrow{S}}_{○}^{\left[E\right]}$ shown on the horizon of Figure 7d starkly contrasts with the uniform spiral direction exhibited by ${\overrightarrow{O}}_{○}^{\left[E\right]}$ in Figure 7b. Since $S_{○,\varphi }^{\left[E\right]}\ne P_{○,\varphi }$ according to Equation (7), $O_{○,\varphi }^{\left[E\right]}\ne 0$ so that the electric-portion orbital energy flux is not purely sphere-radial as seen in Figure 7a. We prepared further plots of ${\overrightarrow{S}}_{○}^{\left[E\right]}$ on the latitudinal planes with varying vertical locations in Figure S9 of Section S6 in Supplementary Materials, where superluminal speeds are featured by both ${\overrightarrow{O}}_{○}^{\left[E\right]}\equiv {\left|\overrightarrow{E}\right|}^{-2}{\overrightarrow{O}}_{○}^{\left[E\right]}$ and ${\overrightarrow{S}}_{○}^{\left[E\right]}\equiv {\left|\overrightarrow{E}\right|}^{-2}{\overrightarrow{S}}_{○}^{\left[E\right]}$ [12,25]. In brief, the EM field induced by an electric point dipole of circular polarization encompasses both TE and TM modes.

6. Discussion

Most key parameters considered so far are quadratic in the field variables [9,24,25] so that their behaviors are unpredictable until we evaluate the actual participating terms for a specific wave configuration such as given in Equation (6) or (7). Since we are in this study mainly concerned with the energy fluxes as linear momenta, a fundamental discussion is briefly made on angular momentum in Sections S1, S2, and S5 of Supplementary Materials [3,9,15,16,19,24,45].

Suppose that two or four linearly polarized plane waves of equal intensities collide (namely, cross-propagate) at a single point. In such multiple-wave collisions, there arises a nonzero spin energy flux with an attendant near-field vortex feature owing to the non-parallelism and non-zero phase difference(s) among the colliding plane waves [13,19,24,25,45]. In this connection, consider a uniform circular array on a plane consisting of electric point linear dipoles [45]. In this case, the combined EM field should exhibit $\nabla ·{\overrightarrow{M}}^{\left[E\right]}=-\nabla ·{\overrightarrow{M}}^{\left[H\right]}\ne 0$ although all those linear dipoles are oriented normally to the same plane. It is because of the interference among the EM fields induced by multiple linear dipoles in the presence of phase differences among them [6,10,19,24,30,31]. Of course, an array of in-plane linear dipoles (either radially or azimuthally polarized) endows a combined induced EM field with $\nabla ·{\overrightarrow{M}}^{\left[E\right]}=-\nabla ·{\overrightarrow{M}}^{\left[H\right]}\ne 0$. See the near-field behaviors for such arrays consisting of finite-number linear dipoles [40].

When an electric point dipole is placed over a planar wall as either in practice or in the Sommerfeld problem, there would arise diverse contents of a SAM density [1,2,5,6,10,19,22,31]. In these cases, finding internal energy fluxes will be challenging from the perspective of numerical computations. Even for such a complicated finite space bounded by solid curved boundaries, the average SAM density is never generated because $\nabla ·{\overrightarrow{M}}^{\left[avg\right]}=0$, if the medium is free of electric charges and currents [1]. Meanwhile, we also find $M_r^{\left[E\right]}\ne 0$ for the EM field is induced by a uniform circular antenna array (UCAA) [5,45]. In this case, the induced EM field is also likely to exhibit the exchange $\nabla ·{\overrightarrow{M}}^{\left[E\right]}=-\nabla ·{\overrightarrow{M}}^{\left[H\right]}\ne 0$ of Equation (3). Arrayed Rayleigh scatters are working in an analogous fashion to give rise to a near-vertical emission upon excitation [19].

The zones of near-circular polarization displayed in Figure 6 for a circular dipole are much more voluminous than the thin surfaces in Figure 3c,d obtained for a linear dipole. This is indeed a manifestation of the difference between the 3D (more precisely speaking, $2\frac{1}{2}$-D) field induced by a circular dipole and the 2D field induced by a linear dipole. In this aspect, the single nonzero ${\mathcal{M}}_{\updownarrow ,\varphi }^{\left[E\right]}\equiv {\left|{\overrightarrow{E}}_{\updownarrow }\right|}^{-2}{M}_{\updownarrow ,\varphi }^{\left[E\right]}$ in Equation (6) is a proper indicator of the degree of circular polarization (DoCP) [1]. In comparison, we have taken a pseudo-DoCP $\left|{\overrightarrow{\mathcal{M}}}_{○}^{\left[f\right]}\right|$ as shown on Figure 6 [11,15,18,22,25,38]. Therefore, the Stokes parameters are gravely insufficient in properly addressing the state of polarization, partly because our spherical waves defy a certain easy-to-define plane. In this respect, generic 3D EM fields as presented in Equation (7) require, say, the 3D polarization algebra based on the nine Gell-Mann matrices [15,37,39]. Detection of DoCPs becomes also easier for planar sensing surfaces [21].

We learn that difficulties in assessing DoCP are largely linked to those 3D characters that have been circumvented by paraxial approximations [15,18,19,25,30]. For this reason, spin properties passing through planar metasurfaces lend themselves to relatively easier evaluations of key parameters [11,21,45,46]. In comparison, the EM field induced by a single point dipole is hardly paraxial as shown in Figure 2, Figure 3, Figure 5, and Figure 6. Metasurfaces with slight nonplanar defects (artificial or unwanted) would lead to an electric-portion SAM density ${\overrightarrow{M}}^{\left[E\right]}$ being fully 3D for which $\nabla ·{\overrightarrow{M}}^{\left[E\right]}\ne 0$ is expected in general. Metasurfaces of geometrical planarity but of compositional in-plane anisotropy are also likely to exhibit $\nabla ·{\overrightarrow{M}}^{\left[E\right]}\ne 0$.

With respect to $\nabla ·{\overrightarrow{M}}^{\left[E\right]}=-\nabla ·{\overrightarrow{M}}^{\left[H\right]}\ne 0$ in Equation (3), what we call an ‘implicit transport’ between $\left\{{\overrightarrow{S}}_{○}^{\left[E\right]},{\overrightarrow{S}}_{○}^{\left[H\right]}\right\}$ has been stated as a difference between two diffusions of polarization probabilities in Equation (3.52) of [24]. In comparison, we were able to analytically evaluate an ‘explicit diffusion’ ${\nabla }^2{\overrightarrow{S}}_{○}^{\left[E\right]}$ based on Equation (7), as presented in Section S5 of Supplementary Materials. Consequently, it turns out that there is a sole nonzero component ${\widehat{e}}_{\varphi }·\left({\nabla }^2{\overrightarrow{S}}_{○}^{\left[E\right]}\right)$ in the azimuthal direction. What is more interesting is the existence of an inversion with ${\widehat{e}}_{\varphi }·\left({\nabla }^2{\overrightarrow{S}}_{○}^{\left[E\right]}\right)=0$ at $r=\sqrt{12}\approx 3.464$, which is approximately twice the flow-reversal location at $r\approx 1.882$ for $S_{○,\varphi }=0$ as mentioned in Figure 7d. See Sections S1, S2, and S5 of Supplementary Materials for relevant formulas.

It will be worthwhile examining $\nabla ·{\overrightarrow{M}}^{\left[E\right]}=-\nabla ·{\overrightarrow{M}}^{\left[H\right]}$ for either twisted (helical) Omega particle or split-ring resonator (SRR) [5,7]. Here, an electrically responsive material, say, a noble metal, causes a magnetic character according to the Faraday–Lenz law $\nabla \times \overrightarrow{E}=i\overrightarrow{H}$. In other words, a geometric loop in the unit cell of a metamaterial leads to a loop current that constitutes in turn a magnetic effect. We illustrated such a loop current in the case of a Mie scattering off a dielectric sphere [28]. Therefore, even dielectric structures turn out to contain seeds for possible magneto-electric interactions [28]. If either twisted Omega particle or SRR was made of magneto-optical materials, the resulting equality $\nabla ·{\overrightarrow{M}}^{\left[E\right]}=-\nabla ·{\overrightarrow{M}}^{\left[H\right]}$ would get more interesting. Here, a near-field analysis over the volume encompassing a unit cell will be mandatory.

Lastly, we admit that the entire analysis presented in this study should be significantly altered to cope with transient electromagnetic waves including optical pulses [18,25]. In the future, we hope to perform analytical studies on the internal flows in the near field in the case with other types of dipoles: electric, magnetic, toroidal dipoles; and multipoles and combinations among them (Huygens dipoles and Janus dipoles) [18,22,31,39,44].

7. Conclusions

We have examined the properties of the orbital and spin energy fluxes as decomposed constituents of a Poynting vector for electromagnetic waves propagating through source-free homogeneous media. We thus found that the spin angular momentum density undergoes inter-electric-magnetic transport due to nonzero reactive helicity. As a way of confirming the validity of those generic findings, we have worked out various key parameters for the electromagnetic fields induced either by a linear dipole or by a circular dipole. In addition to presenting explicit formulas for the internal flows, our central contribution is to identify a distinctive difference between the two types of electromagnetic fields: the linear-dipole-induced field carries only intra-electric-magnetic transports, but the circular-dipole-induced field admits an inter-electric-magnetic transport. Indeed, the magnetic activities are hidden under the electromagnetic waves induced by electric point dipoles.

We have examined the whole-field characteristics of the electromagnetic fields as regards the states of polarization and the trajectories traversed by the internal energy fluxes. In this way, we have illustrated that optical vortices and singularities manifest themselves in different fashions depending on the two- and three-dimensional natures of electromagnetic fields. Last but not the least, the electromagnetic helicity and reactive helicity turn out to be stronger respectively in the far and near fields.