Ultra-Low Power All-Optically Tuned Hybrid Graphene Ultra Silicon-Rich Nitride Ring Resonator-Based Add-Drop Filter for DWDM Systems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Athermality and Polarization Sensitivity
2.2. Optical Properties of Graphene
2.3. Nonlinear Effects Induced Refractive Index Change
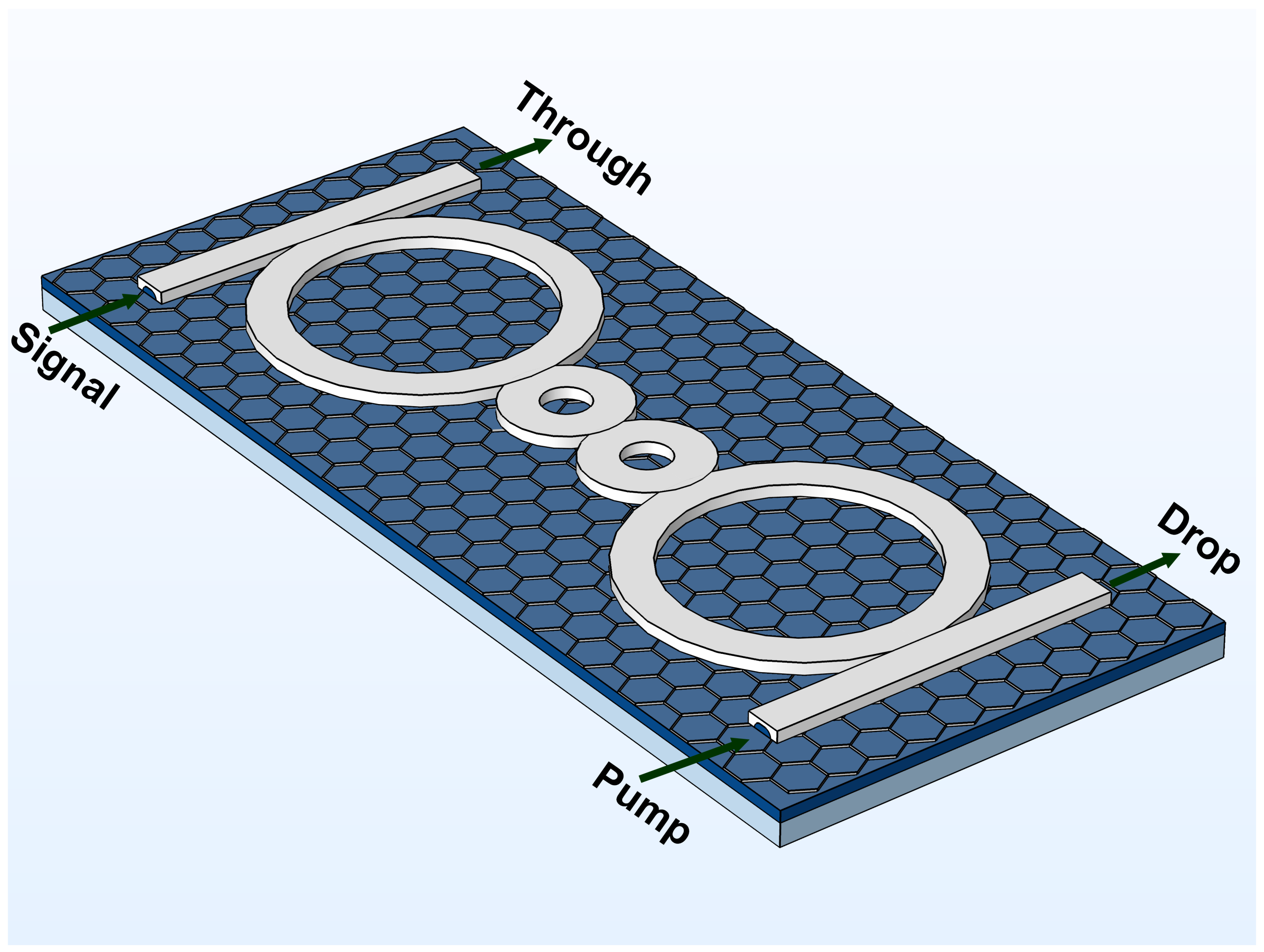
2.4. Methodology
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Abbreviations and Nomenclature
| TE | Tranverse Electric |
| TM | Transverse Magnetic |
| DWDM | Dense Wavelength Division Multiplexing |
| CMOS | Complementary metal-oxide-semiconductor |
| IoT | Internet of Things |
| Si | Silicon |
| Silicon-Rich Nitride | |
| or URSRN | Ultra Silicon-Rich Nitride |
| TPA | Two-Photon Absorption |
| FCA | Free Carrier Absorption |
| PIC | Photonic-Integrated Circuits |
| C | Graphene |
| Silicon Oxide | |
| Titanium Oxide | |
| CTE | Coefficient of Thermal Expansion |
References
- Karimi, R.; Koohi, S.; Tinati, M.; Hessabi, S. A thermally-resilient all-optical network-on-chip. Microelectron. Reliab. 2019, 99, 74–86. [Google Scholar] [CrossRef]
- Vale, V.; Almeida, R.C., Jr. Power, routing, Modulation Level and Spectrum Assignment in all-optical and elastic networks. Opt. Switch. Netw. 2019, 32, 14–24. [Google Scholar] [CrossRef]
- Rani, A.; Bhamrah, M.S.; Dewra, S. Performance evaluation of the dense wavelength division multiplexing system using reconfigurable optical add/drop multiplexer based on digital switches. Opt. Quantum Electron. 2020, 52, 480. [Google Scholar] [CrossRef]
- Dai, T.; Shen, A.; Wang, G.; Wang, Y.; Li, Y.; Jiang, X.; Yang, J. Bandwidth and wavelength tunable optical passband filter based on silicon multiple microring resonators. Opt. Lett. 2016, 41, 4807–4810. [Google Scholar] [CrossRef]
- Vey Van, K.A. Optical Microring Resonators: Theory, Techniques, and Applications; CRC Press: Boca Raton, FL, USA; Taylor et Francis Group: Abingdon, UK, 2018; p. 250. [Google Scholar] [CrossRef]
- Thomson, D.; Zilkie, A.; Bowers, J.E.; Komljenovic, T.; Reed, G.T.; Vivien, L.; Marris-Morini, D.; Cassan, E.; Virot, L.; Fédéli, J.M.; et al. Roadmap on silicon photonics. J. Opt. 2016, 18, 073003. [Google Scholar] [CrossRef]
- Hill, P.; Klitis, C.; Guilhabert, B.; Sorel, M.; Gu, E.; Dawson, M.D.; Strain, M.J. All-optical tuning of a diamond micro-disk resonator on silicon. Photonics Res. 2019, 8, 318–324. [Google Scholar] [CrossRef]
- Ooi, K.J.; Leong, P.C.; Ang, L.K.; Tan, D.T. All-optical control on a graphene-on-silicon waveguide modulator. Sci. Rep. 2017, 7, 12748. [Google Scholar] [CrossRef]
- Bahadori, M.; Nikdast, M.; Rumley, S.; Dai, L.Y.; Janosik, N.; Van Vaerenbergh, T.; Gazman, A.; Cheng, Q.; Polster, R.; Bergman, K. Design Space Exploration of Microring Resonators in Silicon Photonic Interconnects: Impact of the Ring Curvature. J. Light. Technol. 2018, 36, 2767–2782. [Google Scholar] [CrossRef]
- Manganelli, C.L.; Pintus, P.; Gambini, F.; Fowler, D.; Fournier, M.; Faralli, S.; Kopp, C.; Oton, C.J. Large-FSR Thermally Tunable Double-Ring Filters for WDM Applications in Silicon Photonics. IEEE Photonics J. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Ahmed, A.N.R.; Shi, S.; Zablocki, M.; Yao, P.; Prather, D.W. Tunable hybrid silicon nitride and thin-film lithium niobate electro-optic microresonator. Opt. Lett. 2019, 44, 618–621. [Google Scholar] [CrossRef]
- Dubray, O.; Abraham, A.; Hassan, K.; Olivier, S.; Marris-Morini, D.; Vivien, L.; O’Connor, I.; Menezo, S. Electro-Optical Ring Modulator: An Ultracompact Model for the Comparison and Optimization of p-n, p-i-n, and Capacitive Junction. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 89–98. [Google Scholar] [CrossRef]
- Li, S.; Chen, W.; Wang, P.; Fu, Q.; Zhang, J.; Zhang, B.; Dai, T.; Wang, Y.; Yang, J. Bandwidth-tunable optical passband filter based on graphene-silicon waveguide. Opt. Commun. 2018, 426, 206–211. [Google Scholar] [CrossRef]
- Han, H.; Xiang, B. Simulation and analysis of electro-optic tunable microring resonators in silicon thin film on lithium niobate. Sci. Rep. 2019, 9, 6302. [Google Scholar] [CrossRef]
- Ahmed, N.; Nelan, S.; Shi, S.; Yao, P.; Mercante, A.; Prather, D. Sub-volt electro-optical modulator on thin-film lithium niobate and silicon nitride hybrid platform. Opt. Lett. 2020, 45, 1112–1115. [Google Scholar] [CrossRef]
- Chen, M.; Liu, L.; Xu, L.; Ye, M.; Jin, X.; Yu, Z. On-Chip all-optical tunable filter with high tuning efficiency. IEEE Photonics J. 2020, 12, 1–10. [Google Scholar] [CrossRef]
- Wang, J.; Fan, L.; Varghese, L.T.; Shen, H.; Xuan, Y.; Niu, B.; Qi, M. A theoretical model for an optical diode built with nonlinear silicon microrings. J. Light. Technol. 2013, 31, 313–321. [Google Scholar] [CrossRef]
- Meng, Y.; Lu, R.; Shen, Y.; Liu, Y.; Gong, M. Ultracompact graphene-assisted ring resonator optical router. Opt. Commun. 2017, 405, 73–79. [Google Scholar] [CrossRef]
- Tu, Z.; Chen, D.; Hu, H.; Gao, S.; Guan, X. Characterization and Optimal Design of Silicon-Rich Nitride Nonlinear Waveguides for 2 μm Wavelength Band. Appl. Sci. 2020, 10, 8087. [Google Scholar] [CrossRef]
- Choi, J.W.; Sohn, B.U.; Chen, G.F.; Ng, D.K.; Tan, D.T. Correlated photon pair generation in ultra-silicon-rich nitride waveguide. Opt. Commun. 2020, 463, 125351. [Google Scholar] [CrossRef]
- Tan, D.T.H.; Ng, D.K.T.; Choi, J.W.; Sahin, E.; Sohn, B.U.; Chen, G.F.R.; Xing, P.; Gao, H.; Cao, Y. Nonlinear optics in ultra-silicon-rich nitride devices: Recent developments and future outlook. Adv. Phys. X 2021, 6, 1905544. [Google Scholar] [CrossRef]
- Wang, T.; Ng, D.K.; Ng, S.K.; Toh, Y.T.; Chee, A.K.; Chen, G.F.; Wang, Q.; Tan, D.T. Supercontinuum generation in bandgap engineered, back-end CMOS compatible silicon rich nitride waveguides. Laser Photonics Rev. 2015, 9, 498–506. [Google Scholar] [CrossRef]
- Choi, J.W.; Chen, G.F.; Ng, D.; Ooi, K.J.; Tan, D.T. Wideband nonlinear spectral broadening in ultra-short ultra-silicon rich nitride waveguides. Sci. Rep. 2016, 6, 27120. [Google Scholar] [CrossRef]
- Sahin, E.; Ooi, K.J.; Chen, G.; Ng, D.K.; Png, C.; Tan, D.T. Enhanced optical nonlinearities in CMOS-compatible ultra-silicon-rich nitride photonic crystal waveguides. Appl. Phys. Lett. 2017, 111, 121104. [Google Scholar] [CrossRef]
- Ooi, K.; Ng, D.; Wang, T.; Chee, A.; Ng, S.; Wang, Q.; Ang, L.; Agarwal, A.; Kimerling, L.; Tan, D. Pushing the limits of CMOS optical parametric amplifiers with USRN: Si7N3 above the two-photon absorption edge. Nat. Commun. 2017, 8, 13878. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Si, J.; Yu, X.; Deng, X. Optical spatial differentiator based on subwavelength high-contrast gratings. Appl. Phys. Lett. 2018, 112, 181102. [Google Scholar] [CrossRef]
- Krückel, C.J.; Fülöp, A.; Klintberg, T.; Bengtsson, J.; Andrekson, P.A.; Víctor Torres-Company. Linear and nonlinear characterization of low-stress high-confinement silicon-rich nitride waveguides. Opt. Express 2015, 23, 25827–25837. [Google Scholar] [CrossRef]
- Vorobev, A.S.; Bianco, G.V.; Bruno, G.; D’Orazio, A.; O’Faolain, L.; Grande, M. Tuning of Graphene-Based Optical Devices Operating in the Near-Infrared. Appl. Sci. 2021, 11, 8367. [Google Scholar] [CrossRef]
- Ataloglou, V.G.; Christopoulos, T.; Kriezis, E.E. Nonlinear coupled-mode-theory framework for graphene-induced saturable absorption in nanophotonic resonant structures. Phys. Rev. A 2018, 97, 063836. [Google Scholar] [CrossRef]
- Conteduca, D.; Dell’Olio, F.; Ciminelli, C.; Armenise, M. Resonant graphene-based tunable optical delay line. IEEE Photonics J. 2015, 7, 1–9. [Google Scholar] [CrossRef]
- Demongodin, P.; El Dirani, H.; Lhuillier, J.; Crochemore, R.; Kemiche, M.; Wood, T.; Callard, S.; Rojo-Romeo, P.; Sciancalepore, C.; Grillet, C.; et al. Ultrafast saturable absorption dynamics in hybrid graphene/Si3N4 waveguides. APL Photonics 2019, 4, 076102. [Google Scholar] [CrossRef]
- Namnabat, S.; Kim, K.J.; Jones, A.; Himmelhuber, R.; DeRose, C.T.; Trotter, D.C.; Starbuck, A.L.; Pomerene, A.; Lentine, A.L.; Norwood, R.A. Athermal silicon optical add-drop multiplexers based on thermo-optic coefficient tuning of sol-gel material. Opt. Express 2017, 25, 21471–21482. [Google Scholar] [CrossRef]
- Venghaus, H. Wavelength Filters in Fibre Optics; Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Deng, G.; Zhao, T.; Yin, Z.; Yang, J. Bandpass filter based on comb shaped graphene nanoribbons. OSA Contin. 2019, 2, 2614–2622. [Google Scholar] [CrossRef]
- Čtyrokỳ, J.; Petráček, J.; Kwiecien, P.; Richter, I.; Kuzmiak, V. Graphene on an optical waveguide: Comparison of simulation approaches. Opt. Quantum Electron. 2020, 52, 149. [Google Scholar] [CrossRef]
- Wang, Y.; Lei, L.; Zang, J.; Dong, W.; Zhang, X.; Xu, P. High Efficiency Electro-Optic Modulation in a Graphene Silicon Hybrid Tapered Microring Resonator. IEEE Access 2021, 9, 87869–87876. [Google Scholar] [CrossRef]
- Liu, L.; Liao, S.; Xue, W.; Yue, J. Tunable all-optical microwave filter with high tuning efficiency. Opt. Express 2020, 28, 6918–6928. [Google Scholar] [CrossRef]
- Abdullah, F.; Alani, F.; Yaqoub, Y.; Hamdan, M.; Brady, M.K.; Cronin, J.J.J.; Cardona, M.M.; Bravo, J.J.; Caruana, A.; Casidy, R.; et al. Research Proposal Example. Int. Educ. Stud. 2010, 6, 86–95. [Google Scholar] [CrossRef]
- Long, Y.; Wang, J. All-optical tuning of a nonlinear silicon microring assisted microwave photonic filter: Theory and experiment. Opt. Express 2015, 23, 17758–17771. [Google Scholar] [CrossRef]
- G.694.1 (02/2012); Spectral Grids for WDM Applications: DWDM Frequency Grid. ITU-T: Geneva, Switzerland, 2012; pp. 1–16. Available online: https://www.itu.int/rec/T-REC-G.694.1-202010-I (accessed on 27 June 2022).
- Dell’Olio, F.; Conteduca, D.; Brunetti, G.; Armenise, M.N.; Ciminelli, C. Novel CMOS-Compatible Athermal and Polarization-Insensitive Ring Resonator as Photonic Notch Filter. IEEE Photonics J. 2018, 10, 1–11. [Google Scholar] [CrossRef]
- Liu, L.; Yang, Y.; Li, Z.; Jin, X.; Mo, W.; Liu, X. Low power consumption and continuously tunable all-optical microwave filter based on an opto-mechanical microring resonator. Opt. Express 2017, 25, 960–971. [Google Scholar] [CrossRef] [PubMed]













| at 1.55 m m/W ] | [eV] | |
|---|---|---|
| Si [27] | ≈4 | 1.12 |
| [27] | ≈0.24 | ≈5 |
| [21] | 28 | 2.1 |
| Graphene [8,28] | – | 0 |
| Mode | (m) | pol (%) | (m) | ||
|---|---|---|---|---|---|
| TE | 2.4755 | 1.58315 | 3.8025 | 95 | 0.345 |
| TM | 2.4753 | 1.58315 | 3.7937 | 93 | 0.324 |
| Parameter | Value (nm) | Description |
|---|---|---|
| Width | 600 | Width of the waveguide |
| 269 | Maximum height of the upper cladding | |
| 161 | Minimum height of the upper cladding | |
| 300 | Height of the under cladding | |
| w | 200 | Width of the core |
| H | 100 | Height of the core |
| h | 50 | Height of the slab |
| 8 | Thickness of the graphene layer |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rukerandanga, F.; Musyoki, S.; Ataro, E. Ultra-Low Power All-Optically Tuned Hybrid Graphene Ultra Silicon-Rich Nitride Ring Resonator-Based Add-Drop Filter for DWDM Systems. Optics 2022, 3, 287-303. https://doi.org/10.3390/opt3030027
Rukerandanga F, Musyoki S, Ataro E. Ultra-Low Power All-Optically Tuned Hybrid Graphene Ultra Silicon-Rich Nitride Ring Resonator-Based Add-Drop Filter for DWDM Systems. Optics. 2022; 3(3):287-303. https://doi.org/10.3390/opt3030027
Chicago/Turabian StyleRukerandanga, Filston, Stephen Musyoki, and Edwin Ataro. 2022. "Ultra-Low Power All-Optically Tuned Hybrid Graphene Ultra Silicon-Rich Nitride Ring Resonator-Based Add-Drop Filter for DWDM Systems" Optics 3, no. 3: 287-303. https://doi.org/10.3390/opt3030027
APA StyleRukerandanga, F., Musyoki, S., & Ataro, E. (2022). Ultra-Low Power All-Optically Tuned Hybrid Graphene Ultra Silicon-Rich Nitride Ring Resonator-Based Add-Drop Filter for DWDM Systems. Optics, 3(3), 287-303. https://doi.org/10.3390/opt3030027






