A Theoretical Description of Node-Aligned Resonant Waveguide Gratings

Abstract

Waveguide gratings are used for applications such as guided-mode resonance filters and fiber-to-chip couplers. A waveguide grating typically consists of a stack of a single-mode slab waveguide and a grating. The filling factor of the grating with respect to the mode intensity profile can be altered via changing the waveguide’s refractive index. As a result, the propagation length of the mode is slightly sensitive to refractive index changes. Here, we theoretically investigate whether this sensitivity can be increased by using alternative waveguide grating geometries. Using rigorous coupled-wave analysis (RCWA), the filling factors of the modes of waveguide gratings supporting more than one mode are simulated. It is observed that both long propagation lengths and large sensitivities with respect to refractive index changes can be achieved by using the intensity nodes of higher-order modes.

1. Introduction

Passive and low-loss planar optical waveguides can transport light over large areas [1,2,3,4]. When they are combined with optical elements such as diffraction gratings (termed waveguide gratings), they can be used for applications such as optical filters [5,6,7,8,9,10] and sensors [11,12,13,14,15,16,17] via exploiting guided mode resonances. Commonly, only the spectral positions of resonance are sensitive to refractive index changes, while the corresponding propagation length $L_{prop}$ remains almost constant. This circumstance indicates the necessity of spectrometers for such devices based on waveguide gratings. With a large sensitivity of $L_{prop}$, small refractive index changes could be directly translated into a spatial variation in the outcoupled guided light. This can be detected by an array of simple broadband photodetectors.

Beyond passive refractive index sensors, a large sensitivity would allow for electrical control of $L_{prop}$, which opens up new possibilities such as active beam deflectors or modulators. To meet the requirement of long propagation lengths, it is desirable to use fast and loss-free effects such as the electro-optic Pockels or Kerr effect. However, those effects enable small refractive index tuning in the order of $\Delta n\approx {10}^{-4}\dots {10}^{-3}$ [18,19,20] only, which requires large sensitivities of $L_{prop}$. Thus, it is of no surprise that reports about electrooptic detuning of waveguide gratings can only rarely be found in the literature to date and rather show the control of the spectral positions of resonances than the control of the propagation length [21,22].

In fact, there is a way to overcome these limits. It has been shown that intensity nodes of TE modes (s-polarized modes with a transversal electric field node) can be used to maximize the propagation length [23,24,25] by placing a lossy, diffractive, or scattering structure at the node position. This way, spectrally narrow resonances can also be obtained [26]. Conceptually, it has been estimated that such node modes should provide high sensitivities, as a slight shift of the node position largely affects the propagation length [27]. However, this concept has not been discussed in the scientific literature yet.

Here, we explicitly and exemplarily show that the node of the $T{E}_1$ mode in planar waveguide gratings allows obtaining long propagation lengths of more than ${10}^5\lambda$ and large sensitivities in the order of $L_{prop}\left(n\right)/L_{prop}\left(n+\Delta n\right)\approx 1.5\times {10}^6$ for $\Delta n=1\times {10}^{-4}$.

2. Results and Discussion

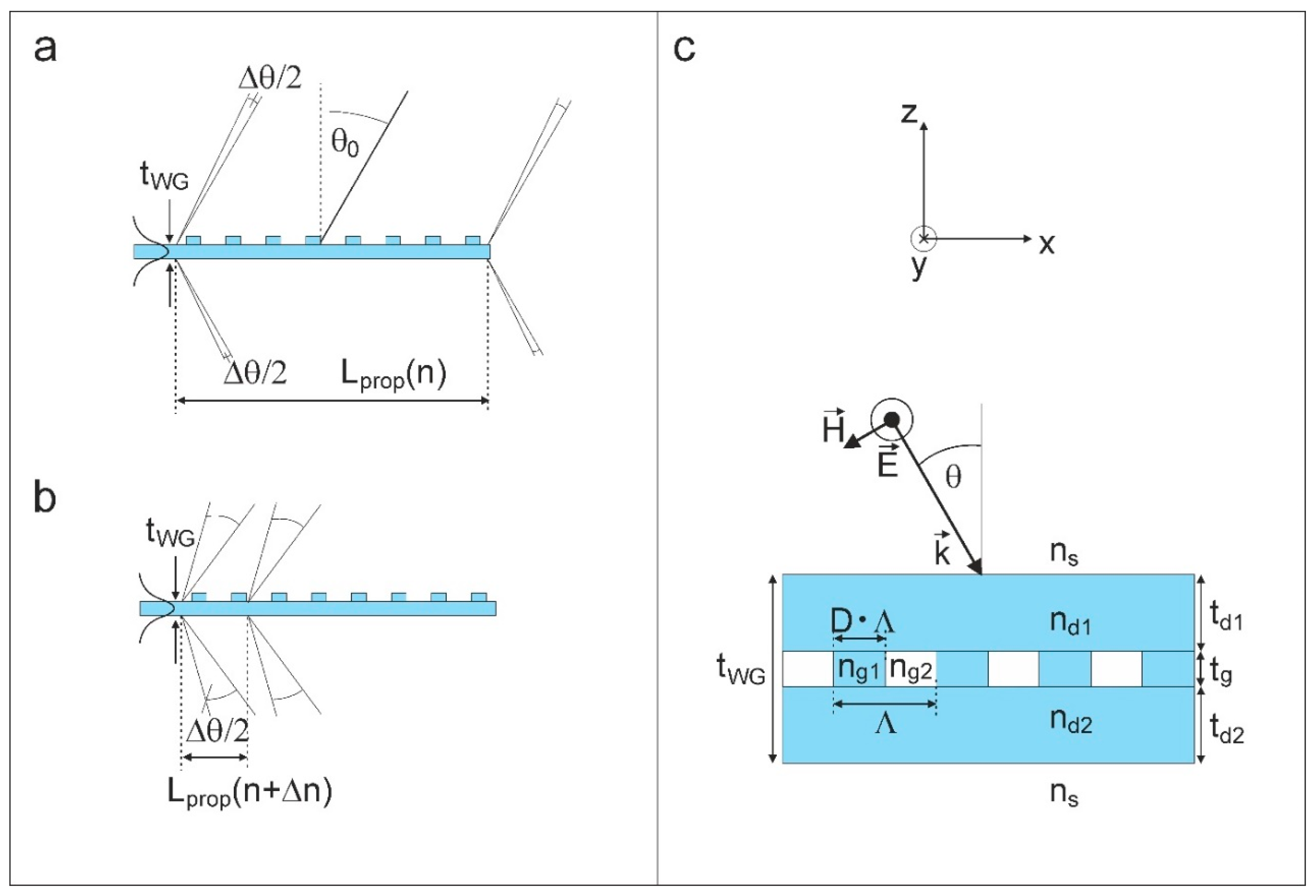
2.1. Definition of Geometry and Symmetry Parameters

A visualization of the sensitivity of the propagation length with respect to refractive index changes is shown in Figure 1a,b. Light propagates through a waveguide grating mode in the positive x-direction. Due to the interaction with the grating, light is emitted into free space with a propagation length $L_{prop}$ under a mean angle ${\theta }_0$ and with an angular divergence of $\Delta \theta$. Without a change in the refractive index, the propagation length is large, and $\Delta \theta$ is small. When a refractive index change $\Delta n$ is introduced, the propagation length is much shorter, and $\Delta \theta$ is larger. Detailed equations on these relations are provided later in this text.

Figure 1. (a) A waveguide grating with an eigenmode of large propagation length $L_{prop}$ and, thus, a small angular divergence $\Delta \theta$. ${\theta }_0$ is the mean angle under which light is emitted; (b) a shorter propagation length $L_{prop}$ and larger $\Delta \theta$ under refractive index tuning ($n\to n+\Delta n$ ); (c) the definition of the geometry parameters of the proposed waveguide grating. TE-polarized light is considered. Further details are provided in the text.

To present a strategy for how a large sensitivity of the propagation length can be achieved, we used the geometry of a waveguide grating, which is defined by the parameters in Figure 1c. It consists of an infinitely extended rectangular grating of period Λ, refractive indices $n_{g1}$ and $n_{g2}$, and a duty cycle $D$. Two dielectric layers of thicknesses $t_{d1}$ and $t_{d2}$, as well as refractive indices $n_{d1}$ and $n_{d2}$, surround the grating. For all simulations in this research, we considered s-polarized plane-wave incidence (TE) in the x–z plane, with a lateral momentum $k_{x,0}$.

To provide a measure of symmetry for both the waveguide grating’s refractive indices and thicknesses, we defined the symmetry parameters as

$${\chi }_{gp}=1-\frac{\left|t_{d1}-t_{d2}\right|}{t_{d1}+t_{d2}}$$

and

$${\chi }_n=\frac{n_{d1}}{n_{d2}},$$

where “gp” represents the grating position, and “n” represents the refractive index profile. Values of ${\chi }_{gp}=1.0$ and ${\chi }_n=1.0$ indicate a fully symmetric waveguide grating.

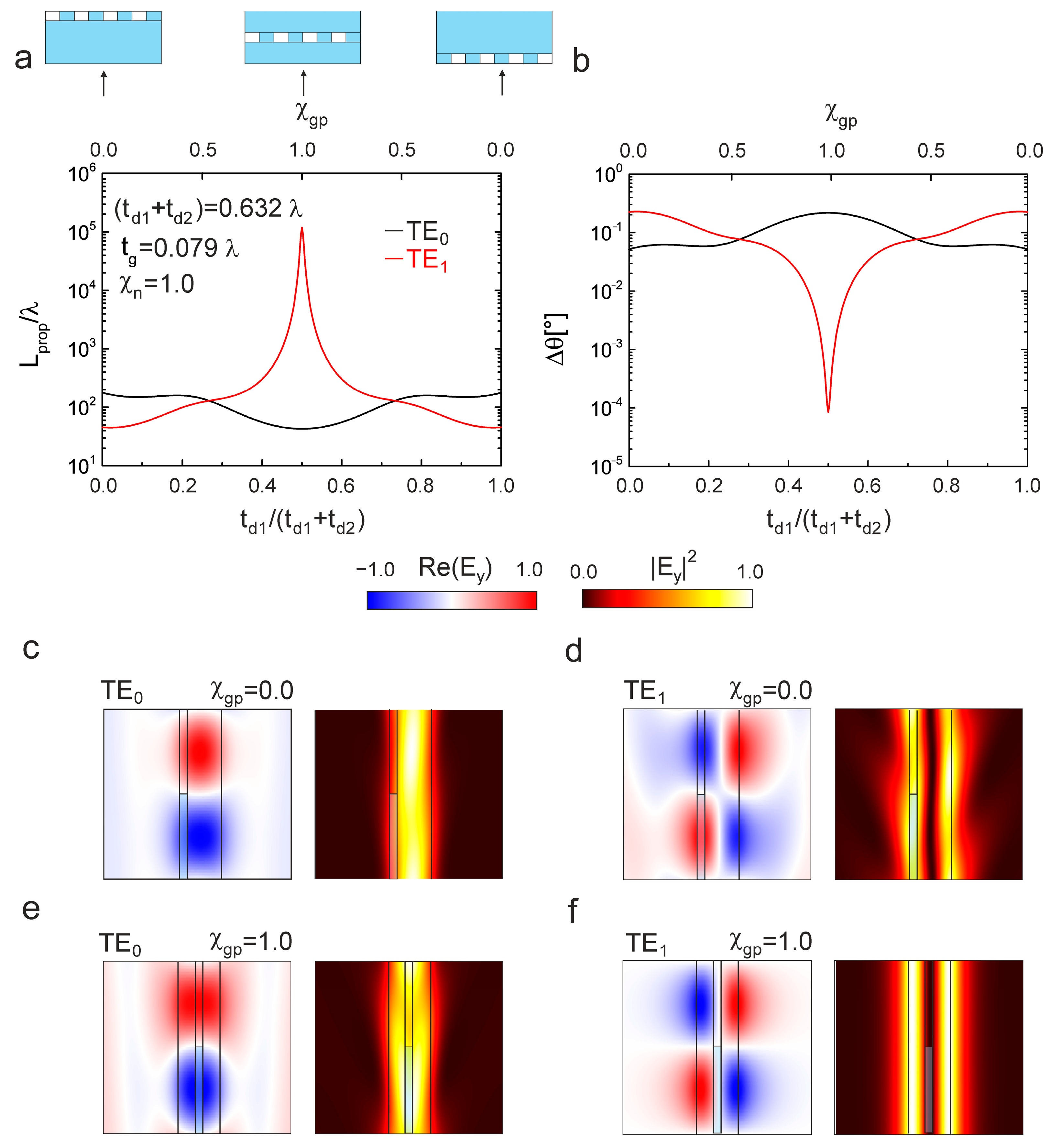
2.2. Geometry with $n_{g1}=n_{g2}$

To introduce some measures of interest and explain the role of the ${TE}_k$ mode, as well as the role of symmetry, we defined a waveguide grating with the parameters $t_d=0.632 \lambda$, $t_g=0.079 \lambda$, $n_s=1.0$, $n_{d1}=n_{d2}=1.5$ (${\chi }_n=1.0$), and $n_{g1}=n_{g2}=1.275$, and compared the cases of ${\chi }_{gp}=0.0$ (Figure 2a,b) and ${\chi }_{gp}=1.0$ (Figure 2c,d). As it is known from the literature, such a waveguide grating exhibits eigenmodes (${TE}_k$) that can be found for distinct real-valued lateral momenta $k_{x,0,k}=k_0 n_{eff,TE,k}$, whereby $n_{eff,TE,k}$ is the effective refractive index of an eigenmode. The index $k$ counts the number of nodes of the electric field distribution $Re(E_y)$ attributed to an eigenmode. Thus, the ${TE}_0$ has no nodes of $Re(E_y)$, while the ${TE}_1$ mode exhibits exactly one node of $Re(E_y)$. This node causes an interesting behavior of the filling factor of the grating layer

$$FF=\frac{{{\displaystyle \int }}_{z_g}^{z_g+t_g}{\left|E_y\right|}^{2}dz}{{{\displaystyle \int }}_{-\infty }^{\infty }{\left|E_y\right|}^{2}dz},$$

where $z_g$ and $z_g+t_g$ define the first and second interface of the grating layer with respect to $z$. While relatively large values of $FF$ between 0.033 and 0.129 occur for all asymmetric cases as well as for the ${TE}_0$ mode at ${\chi }_{gp}=1.0$, we observe a substantially lower value of $FF=0.002$ for the ${TE}_1$ mode when ${\chi }_{gp}=1.0$.

Figure 2. The distributions of the normalized electric field $Re\left(E_y\right)$ and normalized intensity $I\propto {\left|E_y\right|}^2$ as well as filling factors ($FF$) of two exemplary waveguide grating geometries with $t_{d1}+t_{d2}=0.632 \lambda$, $t_g=0.079 \lambda$, $n_s=1.0$, $n_{d1}=n_{d2}=1.5$ (${\chi }_n=1.0$) and $n_{g1}=n_{g2}=1.275$: (a) TE₀ mode at ${\chi }_{gp}=0$; (b) TE₁ mode at ${\chi }_{gp}=0.0$; (c) TE₁ mode at ${\chi }_{gp}=1.0$; (d) TE₁ mode at ${\chi }_{gp}=1.0$.

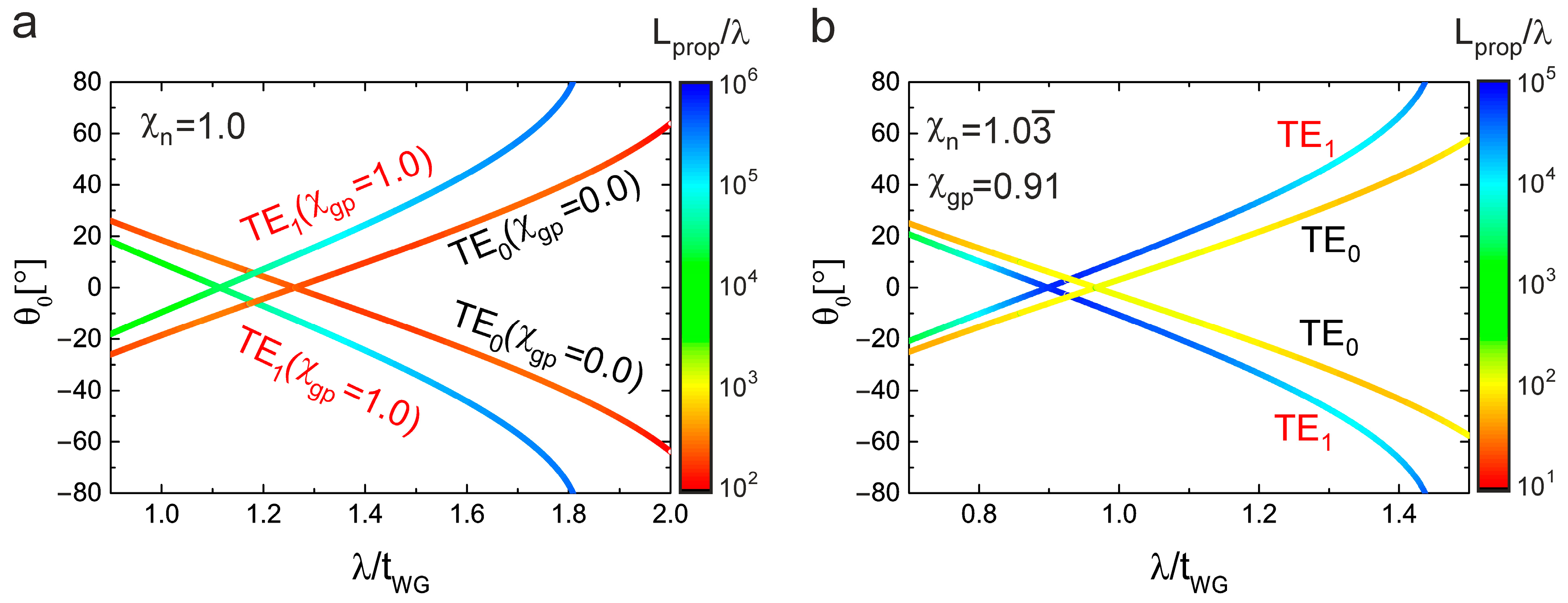
2.3. Geometry with $n_{g1}\ne n_{g2}$ with Variation in Symmetry Parameters

The grating ($t_g>0, n_{g1}\ne n_{g2}$) acts as a discrete lateral momentum reservoir providing a set of lateral momenta $k_{m,k}=k_{x,0,k}+m\frac{2\pi }{\Lambda }$ as a result of Floquet’s theorem [28]. The physical consequence of this set of momenta is that a mode of initial lateral momentum $|\frac{Re\left(k_{m,k}\right)}{k_0}|>n_s$ couples to free-space modes for $|\frac{Re\left(k_{m,k}\right)}{k_0}|<n_s$. As a result, the initially real-valued $n_{eff,TE,k}$ becomes complex-valued. The intensity of an excited mode dampens to 1/e of its initial value by radiation over the normalized propagation length $\frac{L_{prop}}{\lambda }=\frac{1}{4\pi Im\left(n_{eff,TE,k}\right)}$ due to radiation into free-space modes. Radiated light enters the free space under an angle of ${\theta }_0=\arcsin (\frac{Re\left(k_{m,k}\right)}{n_s k_0})$ and angular divergence of the diffracted light of $\Delta \theta =\frac{2Im\left(n_{eff,TE,k}\right)}{n_s cos({\theta }_0)}$. Here, we chose $n_{g1}=1.0$, $n_{g2}=1.5$, $D=0.5$ with otherwise identical parameters as for the waveguide grating discussed in Figure 2. Figure 3a,b show $L_{prop}$ and $\Delta \theta$ as functions of ${\chi }_{gp}$ with fixed values of $t_{d1}+t_{d2}=0.632 \lambda , \Lambda =0.632 \lambda$, and $t_g=0.079 \lambda$ (the grating position is shifted through a waveguide grating of fixed thickness). For ${\chi }_{gp}=0.0$, we obtained small values of $\frac{L_{prop}}{\lambda }$ of around ${10}^2$ and large values of $\Delta \theta$ of around $0.1°$, for both the ${TE}_0$ and the ${TE}_1$ mode. Strikingly, for ${\chi }_{gp}=1.0$, the ${TE}_1$ mode exhibits large values of $\frac{L_{prop}}{\lambda }=1.2\times {10}^5$ and small values of the divergence angle around $\Delta \theta =({10}^{-4})°$. The distributions of $Re\left(E_y\right)$ and ${\left|E_y\right|}^2$ in Figure 3c–e for the ${TE}_0$ and ${TE}_1$ mode at ${\chi }_{gp}=0.0$, as well as for the ${TE}_0$ mode at ${\chi }_{gp}=1.0$, are spatially distorted in comparison to the corresponding ones in Figure 2. Such distortions can be understood as radiation sources and indicate that the grating strongly couples guided waves to radiating waves. For the ${TE}_1$ mode at ${\chi }_{gp}=1.0$ (Figure 3f), almost no such distortion can be observed.

Figure 3. Variation in the asymmetry parameter ${\chi }_{gp}$ of a waveguide grating with $n_{g1}=1.0$, $n_{g2}=1.5$ and $D=0.5$ under a constant value of $t_{d1}+t_{d2}=t_d=0.632 \lambda$. All other parameters are identical to the ones discussed in Figure 2: (a) the normalized propagation length $L_{prop}/\lambda$ and (b) the divergence angle of the $T{E}_0$ mode (black) and $T{E}_1$ mode (red); (c–f) normalized electric fields $Re\left(E_y\right)$ and intensities $I\propto {\left|E_y\right|}^2$ of the $T{E}_0$ mode and $T{E}_1$ mode for ${\chi }_{gp}=0.0$ and ${\chi }_{gp}=1.0$.

This behavior of $\frac{L_{prop}}{\lambda }$, $\Delta \theta$, and the field distributions originates from the small value of $FF$ discussed in Figure 2: empirically, for thin gratings ($t_g<0.1 t_{WG}$), we find the relation

$$\frac{L_{prop}}{\lambda }\propto \frac{1}{t_g^p}$$

We observed that the ${TE}_1$ mode at ${\chi }_{gp}=1.0$ exhibits $p=6$, and thus, $\frac{L_{prop}}{\lambda }\propto =t_g^{-6}$. In comparison, the ${TE}_0$ mode at ${\chi }_{gp}=1.0$ and ${\chi }_{gp}=0.0$ as well as the ${TE}_1$ mode at ${\chi }_{gp}=0.0$ show $p=2$. These dependencies presumably occur because the radiative loss rate $\alpha$ of the grating scales with $\alpha \propto t_g^2$ and the filling factor approximately scales with $FF\propto t_g^3$ and $FF\propto t_g^1$, respectively. As a side note, gratings with dominant Ohmic losses (e.g., metallic gratings) show scalings of $p=3$ (${TE}_1$ mode, ${\chi }_{gp}=1.0$) and $p=1$ for all other cases.

Figure 4a,b show $L_{prop}/\lambda$ and $\Delta \theta$ with variation in $t_g/\lambda$ at a fixed value of $t_{d1}+t_{d2}=0.632 \lambda$. Decreasing values of $t_g/\lambda$ lead to increasing values of $L_{prop}/\lambda$ and decreasing values of $\Delta \theta$ with the explained proportionalities. These trends can be observed up to a value of $t_g=0.4 \lambda$, corresponding to $\frac{t_g}{t_{WG}}\approx 0.39$.

Figure 4. (a) The normalized propagation length $L_{prop}/\lambda$ and (b) the divergence angle of the $T{E}_0$ mode (black) and $T{E}_1$ mode (red) with variation in the normalized grating thickness $t_g/\lambda$ for ${\chi }_{gp}=0.0$ (dashed lines) and ${\chi }_{gp}=1.0$ (solid lines) and a fixed normalized waveguide grating thickness $t_{d1}+t_{d2}=0.632 \lambda$; (c,d) corresponding plots with variation in the normalized waveguide grating thickness $t_{WG}/\lambda$ and a fixed normalized grating thickness $t_g=0.079 \lambda$.

Figure 4c,d show $L_{prop}/\lambda$ and $\Delta \theta$ with variation in $t_{WG}/\lambda$ at a fixed value of $t_g=0.079 \lambda$. $L_{prop}/\lambda$ is strongly increased for the ${TE}_1$ mode at ${\chi }_{gp}=1.0$ in comparison to all other displayed cases for all values of $t_{WG}/\lambda$ above the cutoff of the ${TE}_1$ mode.

Thus, as long as $t_g$ is small, compared with $t_{WG}$, and $t_{WG}$ is large enough to support the ${TE}_1$ mode, its increased values of $L_{prop}/\lambda$ and decreased values of $\Delta \theta$ can be obtained over a broad range of waveguide grating thicknesses in the case of ${\chi }_{gp}=1.0$ and ${\chi }_n=1.0$.

To present an impression of the meaning of these values in an optical application, we considered the ${TE}_1$ mode and ${\chi }_{gp}=1.0$ for a wavelength of $\lambda =632.8$ nm with a grating thickness of $t_g=0.079 \lambda =50$ nm. For these values, we obtained $L_{prop}=7.6 \mathrm{cm}$. In comparison, the standard scenario of a ${TE}_0$ mode and ${\chi }_{gp}=0.0$ leads to $L_{prop}=110$ µm. To reach the same $L_{prop}$ as for the ${TE}_1$ mode at ${\chi }_{gp}=1.0$, the grating thickness would have to be reduced to 0.88 nm (a factor of 1/56) or the waveguide grating thickness (for $t_g=50$ nm) would have to be increased to approximately $t_{WG}=$ 7 µm (a factor of 15). Therefore, for a given grating geometry and waveguide grating thickness, using the ${TE}_1$ mode at ${\chi }_{gp}=1.0$ allows for a drastic increase in the propagation length in comparison to standard waveguide gratings using the ${TE}_0$ mode.

Figure 5a shows the dispersion relation of the ${TE}_1$ mode at ${\chi }_{gp}=1.0$ and the ${TE}_0$ mode at ${\chi }_{gp}=0.0$, with fixed ratios of all other geometry parameters (identical values to the ones in Figure 3 and Figure 4). Remarkably, large values of $L_{prop}/\lambda$ between ${10}^4$ and ${10}^6$ are observed for the ${TE}_1$ mode over a broad spectral range between $\frac{\lambda }{t_{WG}}=0.9$ and $\frac{\lambda }{t_{WG}}=2.0$. This behavior occurs due to the symmetry of the waveguide grating, which enforces the node of the ${TE}_1$ mode to remain at the center plane of the waveguide grating. Therefore, regardless of the wavelength, an equivalent situation as discussed in Figure 3 is apparent when $\frac{\lambda }{t_{WG}}$ is below the cutoff of the ${TE}_1$ mode.

Figure 5. (a) The dispersion relations and normalized propagation lengths of the TE₀ mode for ${\chi }_{gp}=0.0$ and the TE₁ mode for ${\chi }_{gp}=1.0$ under fixed ratios of all geometry parameters as used in Figure 3 (only the wavelength is varied with respect to the geometry) and ${\chi }_n=1$; (b) dispersion relations and normalized propagation lengths for an asymmetric geometry with ${\chi }_{gp}=0.91$, ${\chi }_n=1.0\overline{3}$ for both the $T{E}_0$ mode and $T{E}_1$ mode with $\frac{t_g}{t_{d1}+t_{d2}}=0.045$.

In comparison, the ${TE}_0$ mode exhibits values of $L_{prop}/\lambda$ between ${10}^2$ and ${10}^3$ for all values of $\frac{\lambda }{t_{WG}}$.

For an asymmetric geometry (${\chi }_{gp}\ne 1.0, {\chi }_n\ne 1.0$), $L_{prop}/\lambda$ shows a maximum of around ${10}^5$ at a distinct value of $\frac{\lambda }{t_{WG}}=0.96$ (Figure 5b) for the ${TE}_1$ mode. This maximum occurs since the position of the node of $Re\left(E_y\right)$ shifts through the waveguide grating with respect to the z-direction as a function of $\frac{\lambda }{t_{WG}}$, and the largest value of $L_{prop}/\lambda$ is observed when $FF$ is minimized.

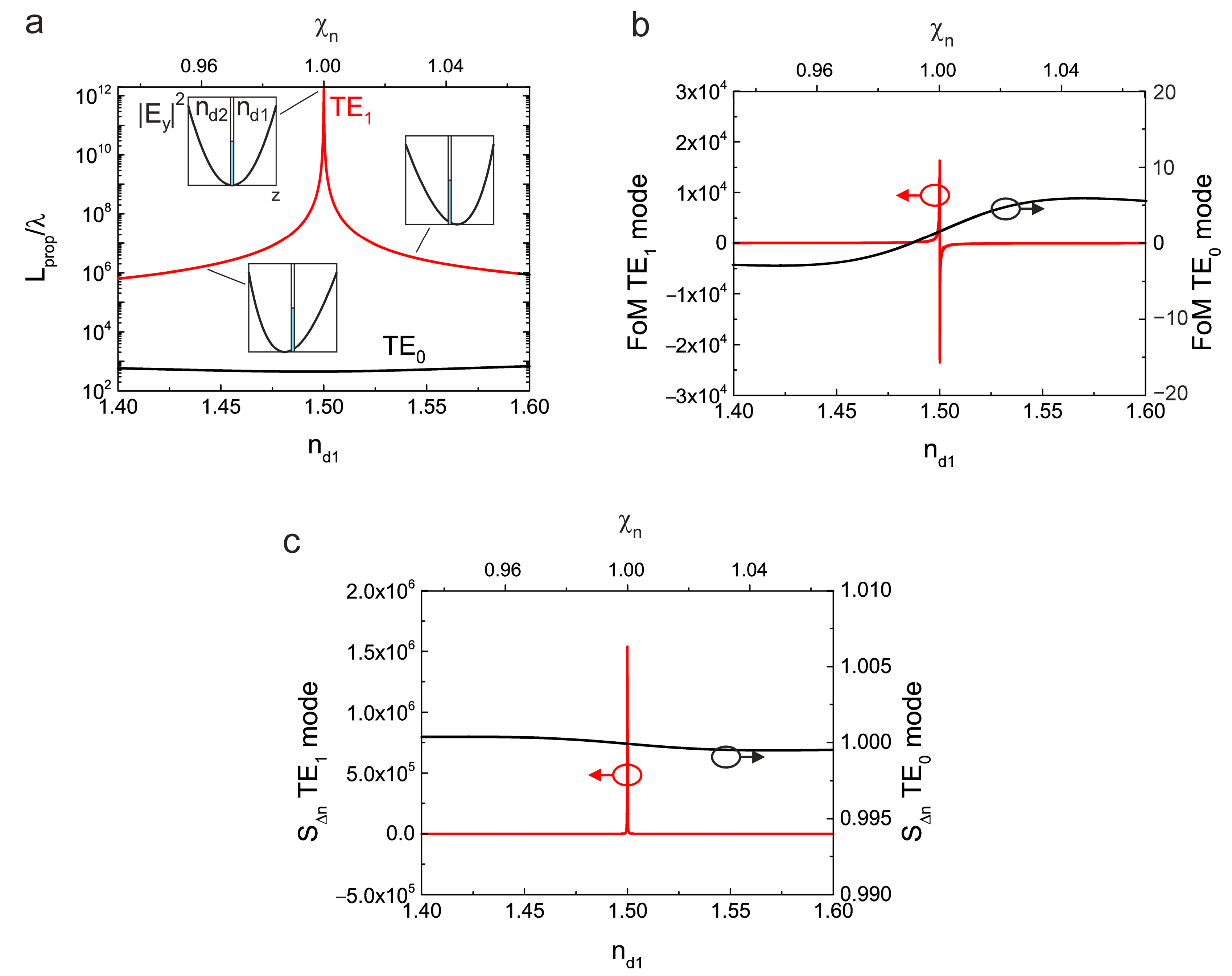
2.4. Sensitivity to Asymmetric Refractive Index Changes

In the last part of this study, we analyze the sensitivity of the waveguide grating with respect to an asymmetric change in the refractive index at ${\chi }_{gp}=1.0$. Such an asymmetric change in the refractive index means that $n_{d1}$ is varied, and $n_{d2}$ remains fixed at a value of $1.5$. As a side note, variations in both $n_{d1}$ and $n_{d2}$ at ${\chi }_n=1.0$ show almost no sensitivity for the ${TE}_1$ mode for any symmetric geometry, as $FF$ is always minimized.

For this exemplary case, the grating thickness was chosen to be $t_g=1.5\times {10}^{-3} \lambda$, whereby all other remaining geometry parameters were chosen to be the same as in Figure 3 and Figure 4.

The following two simulation observations are of interest in order to investigate the sensitivity of the waveguide grating:

(1) For small changes of the refractive index, the figure of merit

$$FoM\left(n_{d1}\right)=\frac{1}{L_{prop}\left(n_{d1}\right)}\frac{\partial L_{prop}\left(n_{d1}\right)}{\partial n_{d1}}$$

provides a measure for the sensitivity.

(2) For more practical considerations, the refractive index is commonly switched between two distinct values, with a difference of $\Delta n$. The sensitivity can be defined by

$$S_{\Delta n}=\frac{L_{prop}\left(n_{d1}+\Delta n\right)}{L_{prop}\left(n_{d1}\right)}$$

Figure 6 shows both $L_{prop}/\lambda$ and the corresponding $FoM$, as well as $S_{\Delta n}$ as a function of $n_{d1}$ for the ${TE}_0$ mode and the ${TE}_1$ mode. Similar to the variation in ${\chi }_{gp}$ in Figure 3, Figure 4 and Figure 5, the ${TE}_1$ mode exhibits high values of $L_{prop}/\lambda$ around ${10}^{12}$ of when ${\chi }_n$ approaches 1.0. Most strikingly, $L_{prop}/\lambda$ strongly varies with changing values of $n_{d1}$ (Figure 6a). In comparison, the ${TE}_0$ mode exhibits nearly constant values of $L_{prop}/\lambda$ around ${10}^3$. The $FoM$ of the ${TE}_1$ mode reaches values of up to $2\times {10}^4$, whereas the maximum $FoM$ of the ${TE}_0$ mode in the displayed range is $5.6$ (Figure 6b). The reason for this large $FoM$ for the ${TE}_1$ lies in a strong decrease in $L_{prop}/\lambda$ consequent to symmetry breaking. Concerning $S_{\Delta n}$ (Figure 6c), for a value of $\Delta n=1\times {10}^{-4}$ (e.g., in the Pockels effect [18,19]), the values of $S_{\Delta n}$ are close to 1 for the ${TE}_0$ mode.

Figure 6. (a) The normalized propagation length, (b) $FoM$, and (c) $S_{\Delta n}$ of a waveguide grating with $t_g=1.5\times {10}^{-3} \lambda$ and otherwise identical parameters to the ones in Figure 3 and Figure 4 with asymmetric refractive index changes ($n_{d1}$ is varied, and $n_{d2}$ is fixed at a value of 1.5).

However, for the ${TE}_1$ mode, it can be observed that $S_{\Delta n}$ exhibits a maximum at ${\chi }_n=1.0$, with a substantially higher value of around $1.5\times {10}^6$, in comparison to the ${TE}_0$ mode. Although fully bound modes ($L_{prop}\to \infty$) cannot be reached, as the filling factor cannot be set to zero, the ${TE}_1$ mode allows obtaining much higher propagation lengths and sensitivities with respect to asymmetric refractive index changes than the ${TE}_0$ mode using the same geometry. In comparison, reports in the literature regarding the sensitivity of the propagation length with respect to refractive index sensitivity are around $FoM\approx 3$ and $S_{\Delta n}\approx 1.005$ for $\Delta n=1\times {10}^{-4}$ [21,22].

3. Conclusions

The results presented in this study show a way to drastically increase both the propagation length and sensitivity of waveguide grating by using the $T{E}_1$ mode, as long as the grating thickness is small, compared with the waveguide grating thickness. As all results were obtained with the help of an exemplary set of waveguide grating geometries, further optimizations for specific applications such as different refractive indices and grating shapes should be considered in future studies. Nonetheless, as the increased propagation length and sensitivity result from symmetrical conditions, the concept at hand can be applied to a broad range of geometry parameters and wavelengths in general. Control over the propagation length cannot be provided only by changing the refractive index but also by breaking the geometric symmetry of the waveguide grating, e.g., by thermomechanical effects. To be sure, this property also implies the necessity of the accurate control of thickness homogeneity. From the practical point of view, symmetric and homogeneous waveguide gratings can be approached by lamination [29] and are, therefore, in principle, accessible with precise standard fabrication techniques such as roll-to-roll coating [30] in combination with lithography methods [31,32]. Thus, we anticipate this concept to be suited for large-area applications requiring control of the propagation length and divergence angle over many orders of magnitude or sensitivity to environmental changes. Obvious applications are spatially resolved refractive index sensors and light modulators.

4. Methods

All simulations in this research were conducted using rigorous coupled-wave analysis (RCWA) [28]. To ensure the stability of the simulation, we checked both the convergence of the simulated values as well as the conservation of energy (see the Supporting Information). Naturally, as the presented data were calculated for TE polarization, fast convergence and large stability were already obtained for a low number of Fourier orders.