1. Introduction
Photo-elastic modulators (PEMs) are widely used in high-sensitivity optical detection and ellipsometry applications [
1,
2,
3], thanks to their advantages that include a large acceptance angle, low power consumption, and high measurement speed [
4,
5,
6]. The incident or reflected beam’s state of polarization are modulated by a standing sound wave in the optical head of the PEM and are converted to an intensity variation using polarizers [
7,
8,
9]. The photo-elastic modulator is a kind of optical modulator that works in the resonance state [
10]. When the frequency of excitation signal is equal/close to the natural resonance frequency of the PEM, the optical modulation efficiency of the PEM reaches its maximum. Therefore, the resonance characteristics of the PEM directly determine its modulation performance, and it is very important to study the resonance characteristics of PEMs (mainly including resonance frequency and quality factor, Q).
A common method used to measure the resonance frequencies of PEMs is the use of a Doppler vibrometer [
11]. In this method, the vibration status is converted into Doppler frequency shift that is monitored by electrical signals. By adjusting the frequency of the signal source, when the amplitude of vibration is at its largest, the measured PEM is considered to reach the resonance state, and the corresponding frequency is the resonance frequency. Since the vibration of PEM is relatively weak, this method has high requirements for the measurement equipment and measurement environment. Meanwhile, this method can only judge whether the measured PEM is in resonance state by the maximum amplitude of vibration, but cannot measure the exact quality factor.
Therefore, a method of measuring admittance parameters was proposed to evaluate the performance of PEMs [
12,
13,
14]. By using this method, the authors obtained the resonance frequency and quality factor, Q. However, only rod-shaped photo-elastic modulators, in which the resonant standing vibrations only occur in the one-dimensional direction, have been studied. In fact, 2D octagonal PEMs, whose internal resonant standing vibrations occur along two directions perpendicular to each other, are most commonly used nowadays.
In this paper, for the 2D octagonal PEM, we propose a method based on impedance measurement to obtain the resonance frequency and the exact quality factor of the PEM. Using this method, the equivalent RLC circuit model, which only consists of resistances (R), inductances (L), and capacitances (C), is established for the 2D octagonal PEM. Then, this model is applied to the data analysis of impedance measurement, through which we can simultaneously obtain the resonance frequency and the exact Q-factor of PEM. Measuring experiments for the commercial PEM products are also set up to verify the above method. The experimental results indicate that this method is effective and efficient.
2. Methods
The operation of PEMs is based on the principle that uniform optical materials such as glass become birefringent when compressed along one axis. This is commonly referred to as stress-induced birefringence, or the photo-elastic effect. By coupling a piezoelectric transducer (PZT) to the optical material, a standing sound wave that oscillates at the resonance frequency is induced, causing a rapid modulation of the birefringence. After the incident light passes through the optical material, the polarization state will change, for example, the linearly polarized light will become elliptically polarized light, as shown in
Figure 1.
Compared with early one-dimensional rod-shaped PEMs, the operating principle of 2D octagonal PEMs shown in
Figure 1 is more complicated, and the requirements of design and manufacture are more critical. On the other hand, 2D PEMs can provide larger optical apertures and wider phase modulation ranges. In addition, the new structure can also reduce the residual stress birefringence caused by the support point. Therefore, this paper mainly focuses on 2D octagonal PEMs.
The impedance analysis method based on the equivalent RLC circuit model can effectively analyze the resonance characteristics of a PZT. Although PEMs are composed of a PZT and an optical material, they can be approximately rigidly connected, and the optical material is in forced vibration state. Therefore, in this paper, we propose to treat the whole PEM optical head as a simple harmonic oscillator and analyze its impedance based on the equivalent RLC circuit model.
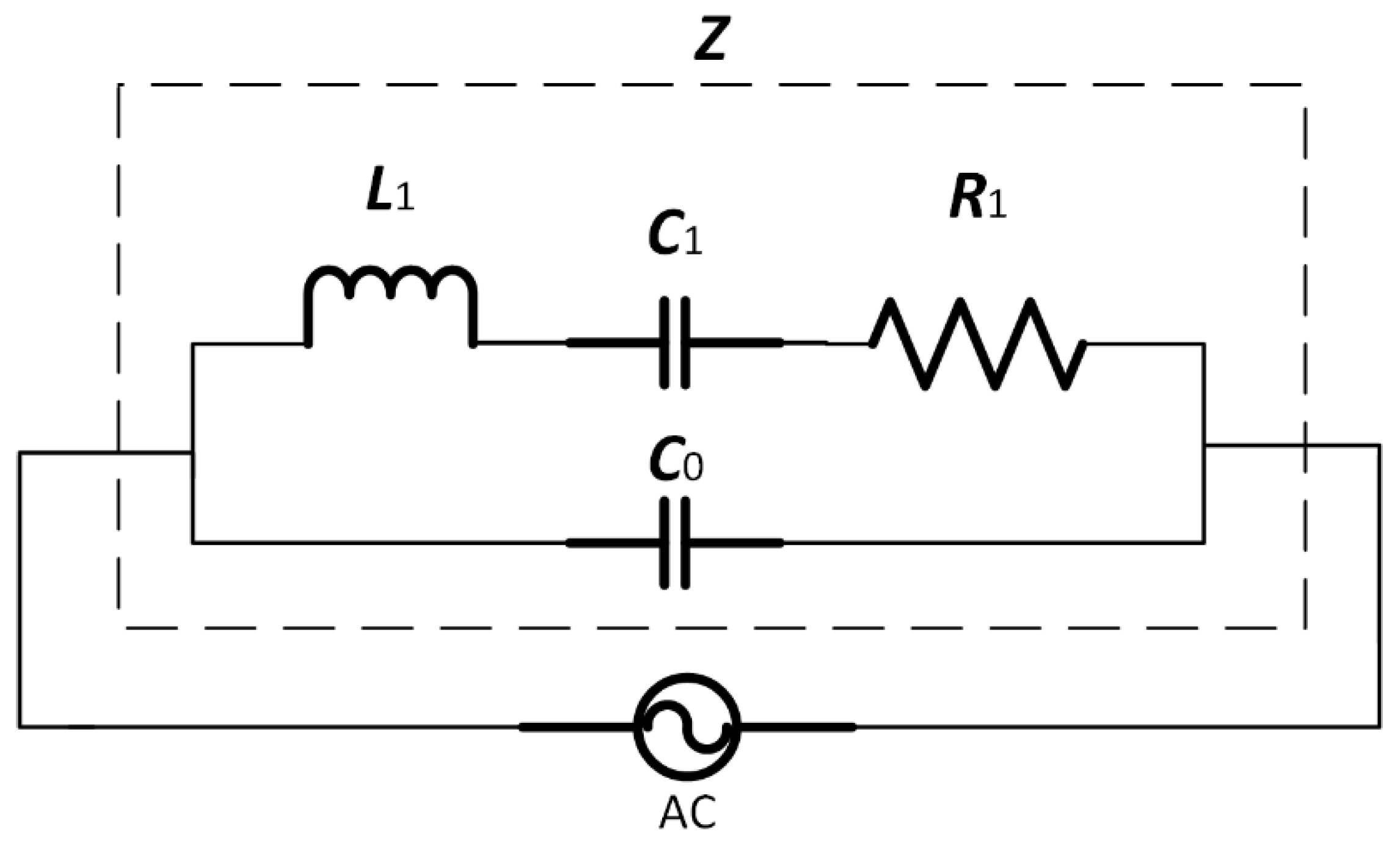
Figure 2 shows the equivalent RLC circuit model of the PEM as a single harmonic oscillator. The parameter
C0 is called static capacitance. The parameter
L1 is called dynamic inductance and
C1 is called dynamic capacitance, which are dynamic equivalent parameters of the PEM;
R1 is called dynamic resistance, which represents the mechanical loss of the PEM. Note that in this model, the above parameters,
C0,
C1,
L1 and
R1, are considered to be stable for the determined PEM. However, in fact, these parameters are affected by external conditions such as temperature, air pressure, support stress and so on. These are some of the issues we will consider in our follow-up research.
The total impedance,
Z, of the above equivalent RLC circuit is described as below:
where
and
f is the frequency of the input signal, and
Re and
Xe are the equivalent resistance and the equivalent reactance, respectively, which can be derived from Equation (4):
Z,
Re, and
Xe depend on the frequency of the input signal
f. Using Equations (1)–(3), we can calculate the frequency response curves for certain circuits.
Figure 3 shows some typical frequency response curves for different parameters. Here,
fm and
fn are the minimum impedance frequency and the maximum impedance frequency, respectively. For a resonance system with a high quality factor, such as a photo-elastic modulator, the resonance frequency can be considered as the minimum impedance frequency, while the anti-resonance frequency is the maximum impedance frequency.
In our method, the frequency response curves of the PEM to be estimated were firstly measured by using an automatic impedance measurement system built in our laboratory. Then, the calculated frequency response curves were fixed to the experimental curves by adjusting parameters
C0,
C1,
L1, and
R1. When the error between the calculated curves and the experimental curves reached the minimum, we can finally obtained the right values of
C0,
C1,
L1 and
R1. Therefore, we can use Equations (1)–(3) to obtain the resonance frequency of a PEM. Furthermore, the quality factor,
Q, can be calculated from Equation (5):
4. Results and Discussion
Figure 5 compares the impedance frequency response curve between measured data and model data for the 20 kHz commercial PEM. The blue line with diamond markings represents the actual measured data from the impedance analyzer IM3570, and the red line is the simulated data from the RLC circuit model. The curve in the black box in the lower left corner is enlarged for observation. It can be seen that the difference between the measured data and simulated data is very small, which also verifies that the RLC circuit model can effectively describe the resonance characteristics of PEMs. The light green area and the light red area represent the resonance region and the anti-resonance region, respectively. The bandwidth of the resonance region is only about 10 Hz~15 Hz, which means that the deviation between the excitation signal frequency and the natural resonant frequency of a PEM must be small enough to ensure the stable operation of the PEM.
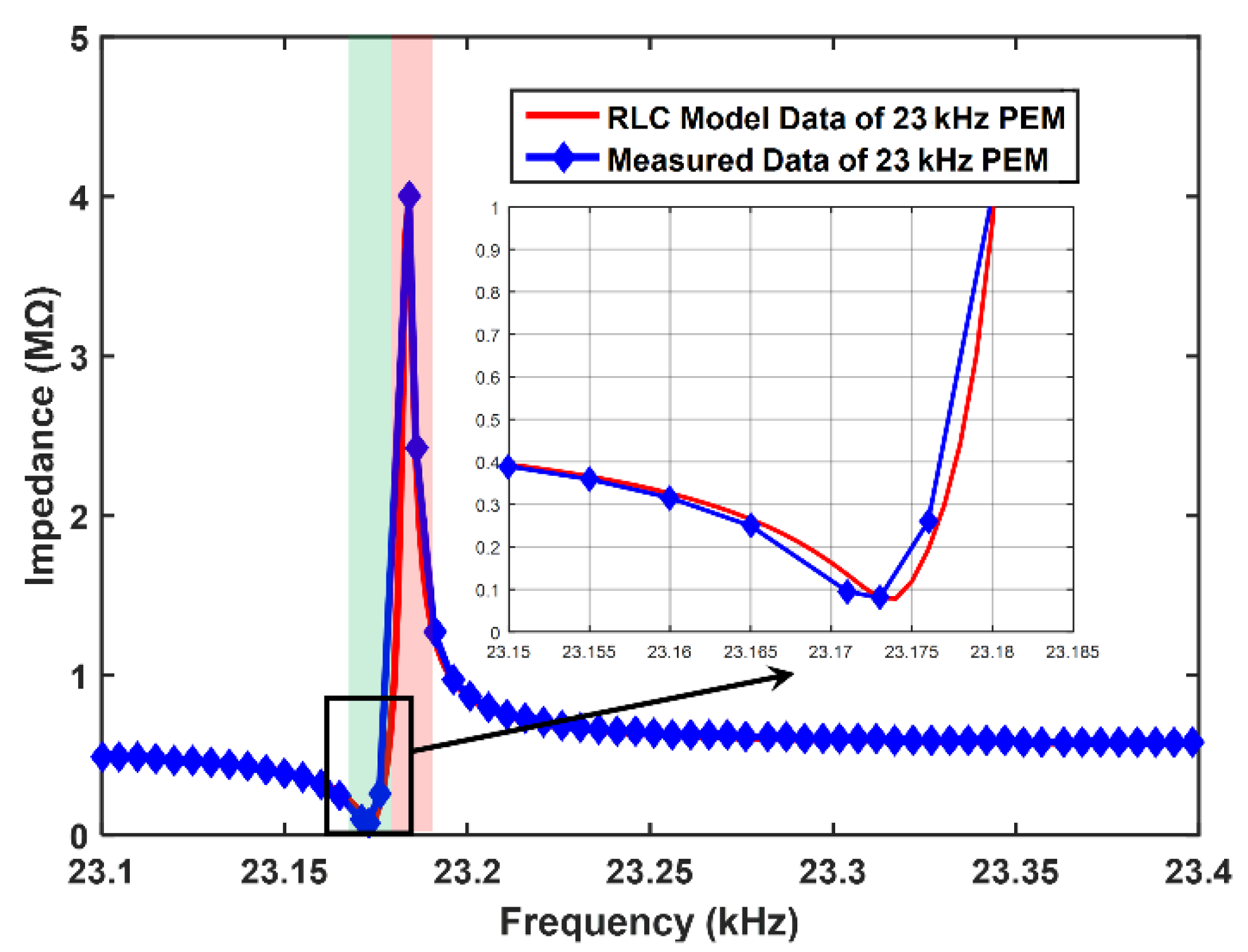
The measured data and the model data for the 23 kHz commercial PEM were also obtained and compared using the same procedure. The comparison results are displayed in
Figure 6, where all the symbol marks are consistent with
Figure 5. It can also be seen that the simulated data fit well with the measured data. The fitting RLC parameters obtained in the above two groups of experiments are listed in
Table 1, as well as the natural resonance frequency,
fR, and quality factor,
Q. The natural resonance frequency of the 20 kHz PEM is about 20.147 kHz, and that of 23 kHz PEM is about 23.174 kHz. The quality factor of the 20 kHz PEM is about 1.048 × 10
4, and that of 23 kHz PEM is about 8.747 × 10
3.
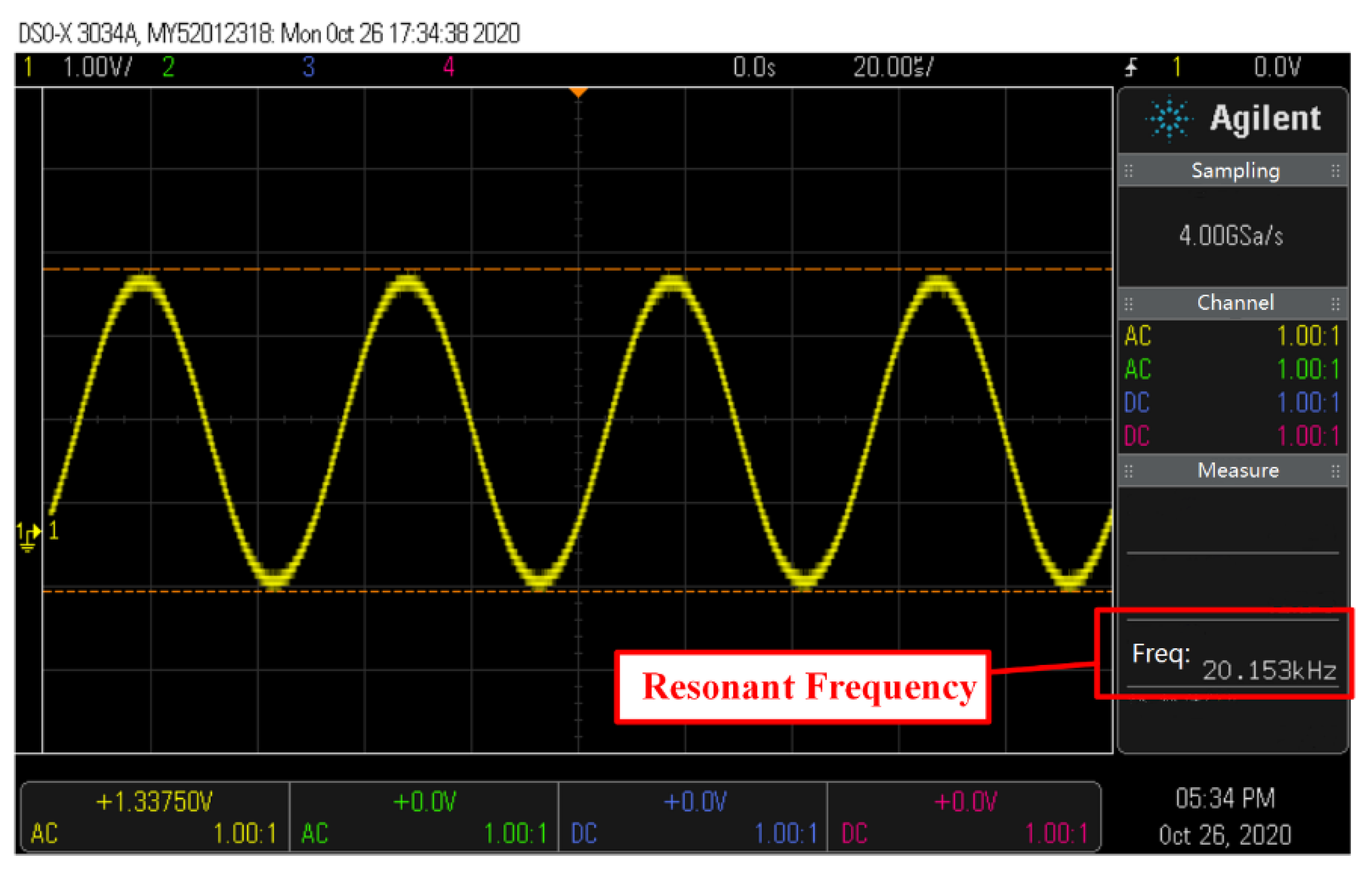
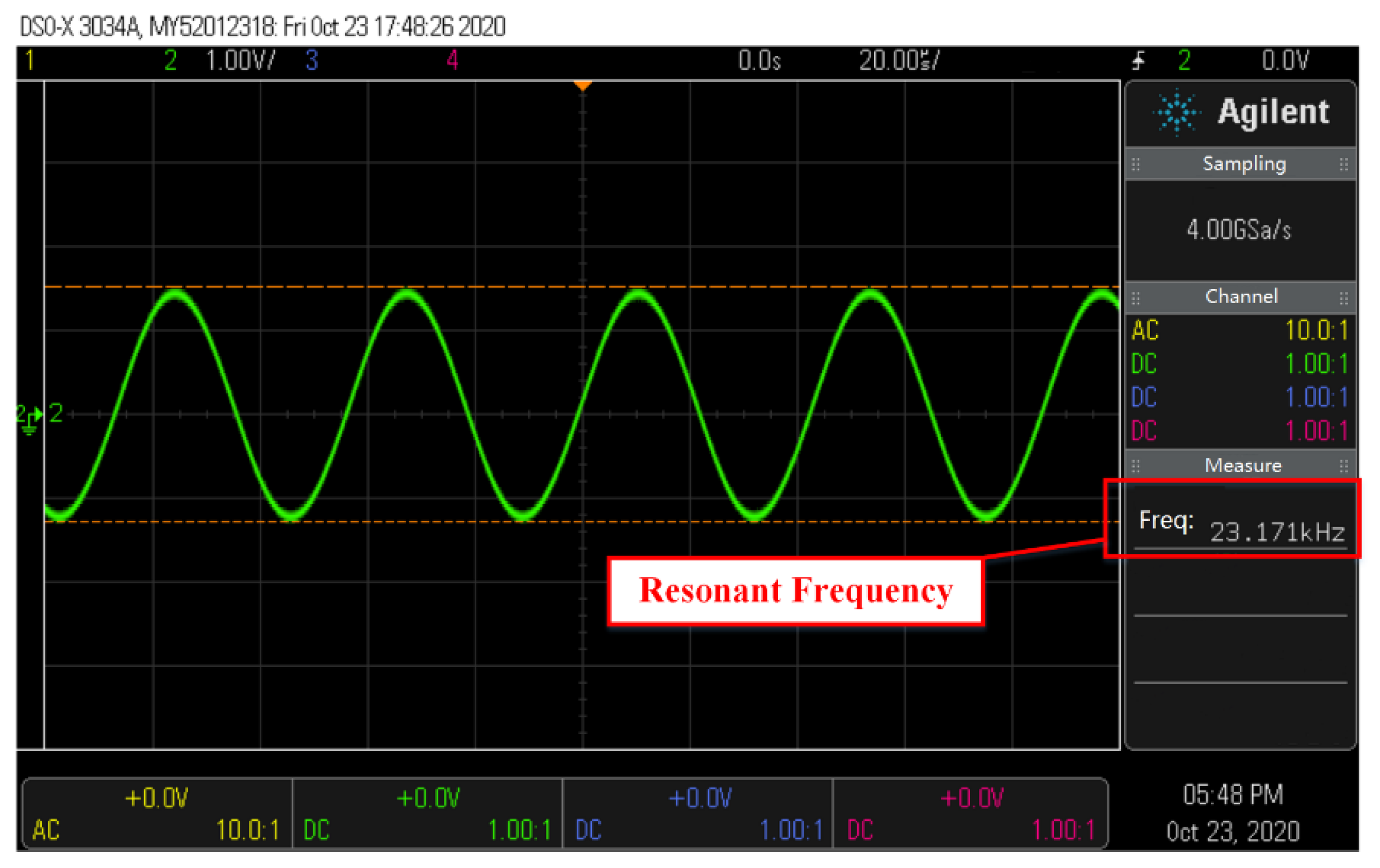
Figure 7 and
Figure 8 show the excitation signal waveforms of the 20 kHz and 23 kHz PEMs at resonance, respectively. The resonance frequency can be measured directly by the oscilloscope. For the 20 kHz PEM, the measured resonance frequency is 20.153 kHz, and for the 23 kHz PEM, the measured result is 23.171 kHz. Note that the words, ’20 kHz’ and ’23 kHz’, only serve as labels to distinguish two different PEMs, and the actual working frequency deviates slightly. It is obvious that the resonance frequencies in Table I (
fR) obtained by the RLC circuit model are consistent with the measured one. Moreover, the error range can be as low as 0.03%.
The above results verify that the electrical measurement method based on impedance analysis can evaluate the resonance performance of a two-dimensional octagonal photo-elastic modulator. Compared with the optical method based on a Doppler vibrometer, our method is much simpler and faster. In practical applications, this method can be used to quickly detect whether the resonance frequency of a PEM meets the specifications and whether the quality factor is qualified. Additionally, with the parameter values (C0, C1, L1 and R1) obtained, we may optimize the driving circuit of the PEM according to these parameter values to improve the matching degree between them, so as to further improve the performance of the PEM. This is also how we plan to continue this research.