Optical Properties of Alkali Halides in Ultraviolet Spectral Regions
Abstract
:1. Introduction
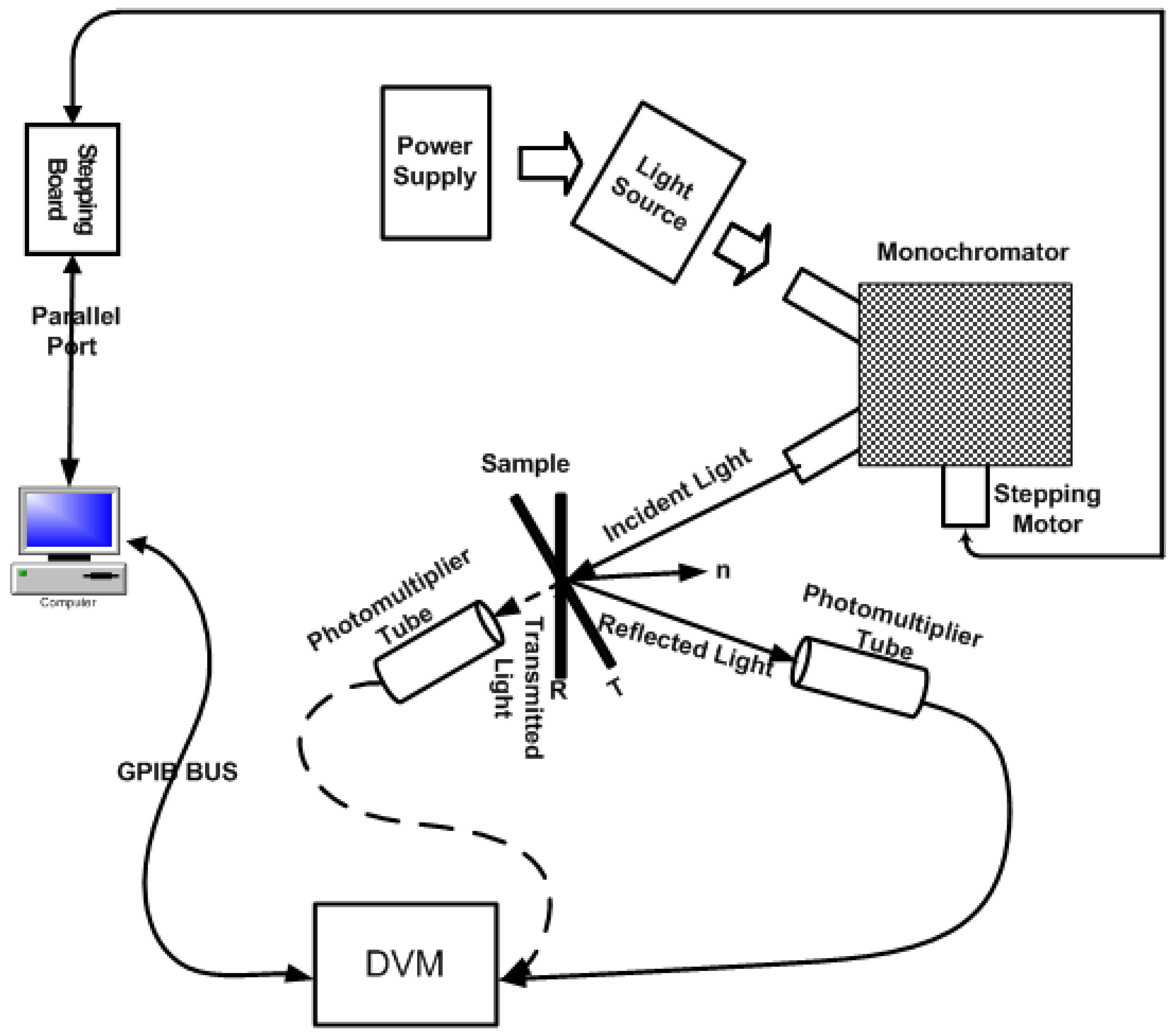
2. Apparatus
3. Experimental Methods
4. Theory
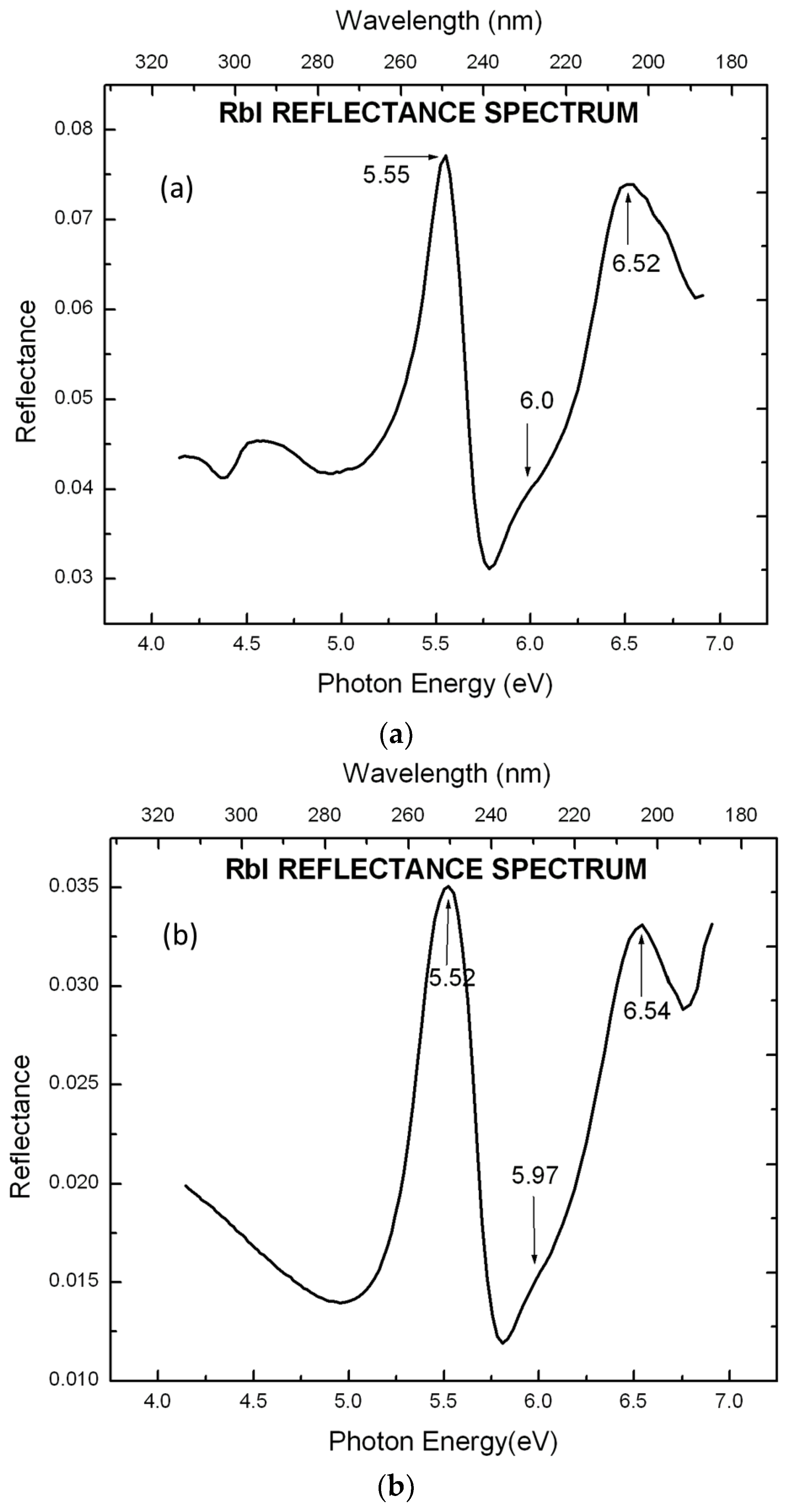
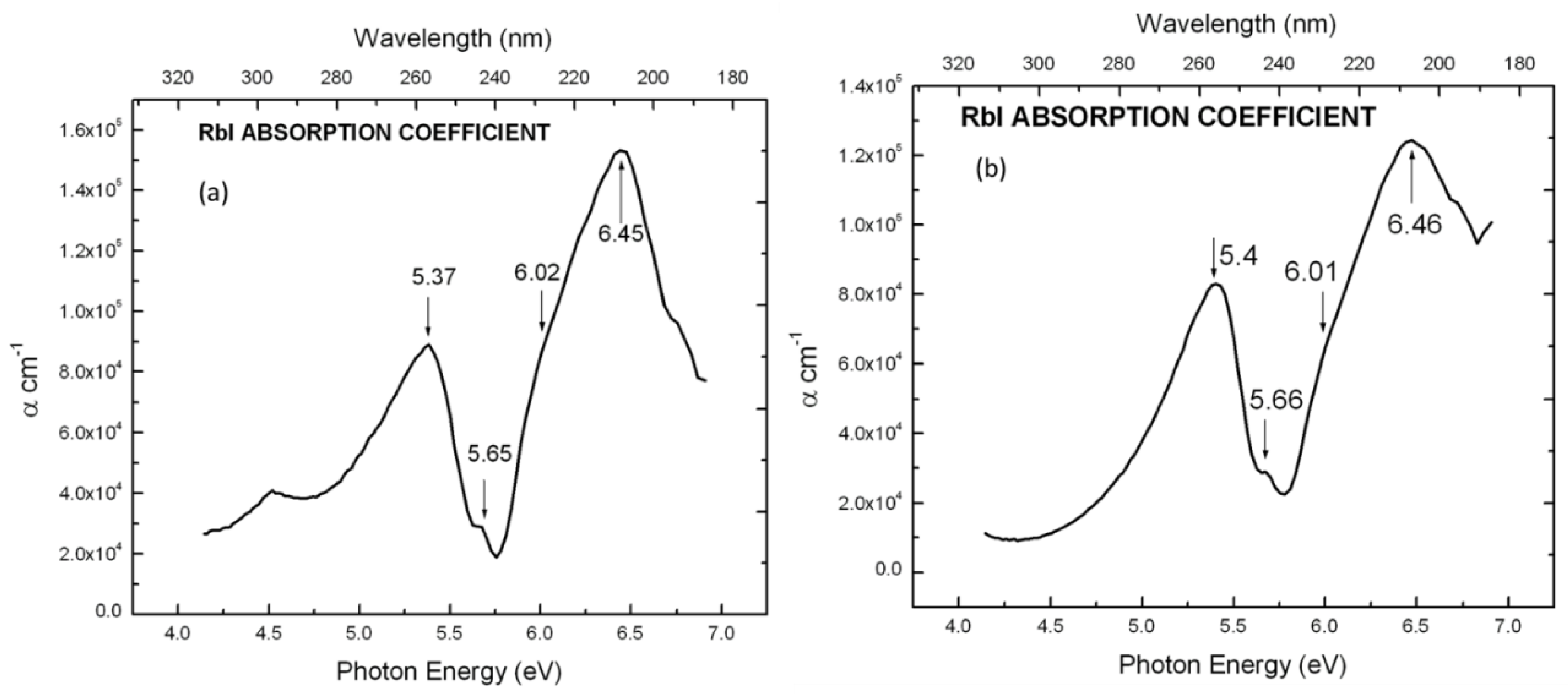
5. Results and Discussion
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Louis, C.N.; Iyakutti, K. Electronic band structure and metallization of KI and RbI under high pressure. Phys. Status Solidi 2002, 233, 339–350. [Google Scholar] [CrossRef]
- Howland, L. Band structure and cohesive energy of potassium chloride. Phys. Rev. 1958, 109, 1927. [Google Scholar] [CrossRef]
- Onodera, Y.; Okazaki, M.; Inui, T. Relativistic electronic structure of KI crystal. J. Phys. Soc. Jpn. 1966, 21, 2229–2238. [Google Scholar] [CrossRef]
- Oyama, S.; Miyakawa, T. Conduction band structure of KCl. J. Phys. Soc. Jpn. 1966, 21, 868–874. [Google Scholar] [CrossRef]
- Phillips, J. Ultraviolet absorption of insulators. III. fcc alkali halides. Phys. Rev. 1964, 136, A1705. [Google Scholar] [CrossRef]
- Amirthakumari, R.M.; Pari, G.; Rita, R.; Asokamani, R. Phase transformation and metallisation studies of some of the alkali iodides through high pressure electronic structure calculations. Phys. Status Solidi 1997, 199, 157–164. [Google Scholar] [CrossRef]
- Ching, W.; Gan, F.; Huang, M.Z. Band theory of linear and nonlinear susceptibilities of some binary ionic insulators. Phys. Rev. B 1995, 52, 1596. [Google Scholar] [CrossRef]
- Ketterson, J.B. The Physics of Solids. MRS Bull. 2018, 43, 68–69. [Google Scholar]
- Dayal, B. The specific heats of the alkali halides. Proc. Indian Acad. Sci.Sect. A 1944, 20, 77–86. [Google Scholar] [CrossRef]
- Dayal, B. Theory of the thermal expansion of the alkali halides. Proc. Indian Acad. Sci.Sect. A 1944, 20, 145–154. [Google Scholar] [CrossRef]
- White, G. The thermal expansion of alkali halides at low temperatures. Proc. R. Soc. Lond. A 1965, 286, 204–217. [Google Scholar]
- Doll, K.; Stoll, H. Cohesive properties of alkali halides. Phys. Rev. B 1997, 56, 10121. [Google Scholar] [CrossRef] [Green Version]
- Slater, J.C. Compressibility of the Alkali Halides. Phys. Rev. 1924, 23, 488–500. [Google Scholar] [CrossRef]
- Basu, A.N.; Sengupta, S. Lattice Dynamics of Alkali Halides. Phys. Rev. B 1973, 8, 2982. [Google Scholar] [CrossRef]
- Woods, A.; Cochran, W.; Brockhouse, B. Lattice dynamics of alkali halide crystals. Phys. Rev. 1960, 119, 980. [Google Scholar] [CrossRef]
- Verma, M.; Dayal, B. Fuchs’s Relations in Alkali Halides and Their Application to the Lattice Dynamics of Lithium Fluoride. Phys. Status Solidi 1966, 13, 251–256. [Google Scholar] [CrossRef]
- Singh, R.; Verma, M. Effect of Three-Body Forces on the Shell Model of Alkali Halides: Application to KBr and KI. Phys. Status Solidi 1969, 36, 335–343. [Google Scholar] [CrossRef]
- Jesser, W.A.; Matthews, J.W. Growth of copper, silver, and gold on twelve Alkali halides cleaved in vacuum. J. Cryst. Growth 1969, 5, 83–89. [Google Scholar] [CrossRef]
- Lord, D.G.; Prutton, M. Electrons and the epitaxial growth of metals on alkali halides. Thin Solid Films 1974, 21, 341–356. [Google Scholar] [CrossRef]
- Mobus, M.; Karl, N.; Kobayashi, T. Structure of perylene-tetracarboxylic-dianhydride thin films on alkali halide crystal substrates. J. Cryst. Growth 1992, 116, 495–504. [Google Scholar] [CrossRef]
- Gupta, S.C. Optoelectronic Devices and Systems; PHI Learning Pvt. Ltd.: Delhi, India, 2014. [Google Scholar]
- Hilsch, R.; Pohl, R.W. Einige Dispersionsfrequenzen der Alkalihalogenidkristalle im Schumanngebiet. Z. Phys. 1930, 59, 812–819. [Google Scholar] [CrossRef]
- Baldini, G.; Bosacchi, B. Optical properties of alkali-halide crystals. Phys. Rev. 1968, 166, 863. [Google Scholar] [CrossRef]
- Baldini, G.; Bosacchi, A.; Bosacchi, B. Exciton-phonon interaction in alkali halides. Phys. Rev. Lett. 1969, 23, 846. [Google Scholar] [CrossRef]
- Said, K.I.; Green, G.W. Optical properties of caesium iodide in the vacuum ultraviolet. J. Phys. C 1977, 10, 479–488. [Google Scholar] [CrossRef]
- Philipp, H.R.; Ehrenreich, H. Intrinsic Optical Properties of Alkali Halides. Phys. Rev. 1963, 131, 2016. [Google Scholar] [CrossRef]
- Blechschmidt, D.; Klucker, R.; Skibowski, M. Dielectric properties of KCl, KBr, and KI single crystals in the extreme ultraviolet up to 35 eV. Phys. Status Solidi 1969, 36, 625–634. [Google Scholar] [CrossRef]
- Tomiki, T.; Miyata, T.; Tsukamoto, H. Temperature Dependence of the Fundamental Spectra of Potassium-Halides in the Schumann Ultraviolet Region (4.4~13.5 eV). J. Phys. Soc. Jpn. 1973, 35, 495–507. [Google Scholar]
- Tomiki, T.; Miyata, T.; Tsukamoto, H. The Urbach rule for the sodium-and potassium-halides. Z. Naturforsch. A 1974, 29, 145–157. [Google Scholar] [CrossRef]
- Antinori, M.; Balzarotti, A.; Piacentini, M. High-resolution reflection spectra of alkali halides in the far ultraviolet. Phys. Rev.B 1973, 7, 1541. [Google Scholar] [CrossRef]
- Tomiki, T. Optical constants and Excton States in KCl Single Crystals. II. The Spectra of Reflectivity and Absorption Constant. J. Phys. Soc. Jpn. 1967, 23, 1280–1296. [Google Scholar] [CrossRef]
- Eby, J.E.; Teegarden, K.J.; Dutton, D.B. Ultraviolet Absorption of Alkali Halides. Phys. Rev. 1959, 116, 1099–1105. [Google Scholar] [CrossRef]
- Teegarden, K.; Baldini, G. Optical Absorption Spectra of the Alkali Halides at 10 K. Phys. Rev. 1967, 155, 896–907. [Google Scholar] [CrossRef]
- Saito, H.; Saito, S.; Onaka, R.; Ikeo, B. Extreme ultraviolet absorption of alkali halides. J. Phys. Soc. Jpn. 1968, 24, 1095–1098. [Google Scholar] [CrossRef]
- O’Connel-Bronin, A. Influence of cleavage in liquid helium on the shape of the n = 1 exciton reflection band in KI and RbI crystals. J. Phys. 1994, 6, 2847. [Google Scholar] [CrossRef]
- Kondo, S.I.; Nakamura, K. Strain Effects on the Fundamental Absorption in Alkali Iodides. J. Phys. Soc. Jpn. 1970, 28, 1381. [Google Scholar] [CrossRef]
- Takahashi, S.; Kobayashi, M.; Misu, A. Piezoreflectivity Studies on Excitons and Band to Band Transitions in Alkali Bromides and Iodides under Uniaxial Stress. J. Phys. Soc. Jpn. 1990, 59, 4547–4553. [Google Scholar] [CrossRef]
- Hashimoto, S.; Itoh, M. Excitonic structures of very thin RbI crystals. J. Phys. Soc. Jpn. 1986, 55, 739–741. [Google Scholar] [CrossRef]
- Cardona, M.; Lynch, D. Optical Properties of the Rubidium and Cesium Halides in the Extreme Ultraviolet. Phys. Rev. B 1970, 2, 1117. [Google Scholar] [CrossRef] [Green Version]
- Hashimoto, S.; Tomi-ie, N.; Itoh, M. Interference effect and dispersion in thin RbI crystals. Solid State Commun. 1985, 54, 1081–1084. [Google Scholar] [CrossRef]
- Peimann, C.J.; Skibowski, M. Dielectric Properties of the Rubidium Halide Crystals in the Extreme Ultraviolet up to 30 eV. Phys. Status Solidi 1971, 46, 655–665. [Google Scholar] [CrossRef]
- Roessler, D.M.; Walker, W.C. Exciton structure in the ultraviolet spectra of KI and RbI. J. Opt. Soc. Am. 1967, 57, 677–682. [Google Scholar] [CrossRef]
- Hutchings, D.C.; Sheik-Bahae, M.; Hagan, D.J.; van Stryland, E.W. Kramers-Krönig relations in nonlinear optics. Opt. Quantum Electron. 1992, 24, 1–30. [Google Scholar] [CrossRef]
- Kronig, R.D.L. On the theory of dispersion of X-rays. Josa 1926, 12, 547–557. [Google Scholar] [CrossRef]
- Lucarini, V.; Saarinen, J.J.; Peiponen, K.E.; Vartiainen, E.M. Kramers-Kronig Relations in Optical Materials Research; Springer Science & Business Media: Berlin, Germany, 2005; Volume 110. [Google Scholar]
- Aspnes, D.; Kelso, S.; Logan, R.; Bhat, R. Optical properties of Al x Ga1-x As. J. Appl. Phys. 1986, 60, 754–767. [Google Scholar] [CrossRef]
- Weast, R.C.; Astle, M.J.; Beyer, W.H. CRC Handbook of Chemistry And Physics; CRC press: Boca Raton, FL, USA, 1988; Volume 69. [Google Scholar]
- Michael, B. Properties of crystals and glasses. In Handbook of Optics: Volume IV—Optical Properties of Materials, Nonlinear Optics, Quantum Optics, 3rd ed.; The McGraw Hill Companies, Inc.: New York, NY, USA, 2010. [Google Scholar]
- Pankove, J.I. Optical Processes in Semiconductors; Dover Publicatins Inc.: New York, NY, USA, 1975. [Google Scholar]
- Portis, A.M. Electromagentic Fields: Souces and Media, 1st ed.; John Eiley & Sons Inc.: New York, NY, USA, 1978. [Google Scholar]
- Stern, F. Elementary theory of the optical properties of solids. Solid State Phys. 1963, 15, 299–408. [Google Scholar]
- Taft, E.; Philipp, H. Photoelectric emission from the valence band of some alkali halides. J. Phys. Chem. Solids 1957, 3, 1–6. [Google Scholar] [CrossRef]
- Arms, D.A.; Graber, T.J.; Macrander, A.T.; Simmons, R.O.; Schwoerer-Böhning, M.; Zhong, Y. Excitons in bulk liquid He 4. Phys. Rev. B 2005, 71, 233107. [Google Scholar] [CrossRef]
- Beaglehole, D. Reflection Studies of Excitons in Liquid and Solid Xenon. Phys. Rev. Lett. 1965, 15, 551–553. [Google Scholar] [CrossRef]
- Rowe, E.; Otte, R.; Pruett, C.; Steben, J. Operation and Performance of the University of Wisconsin-Physical Sciences Laboratory Electron Storage Ring. IEEE Trans. Nucl. Sci. 1969, 16, 159–164. [Google Scholar] [CrossRef]
- Rubloff, G.; Fritzsche, H.; Gerhardt, U.; Freeouf, J. Far ultraviolet spectroscopy of solids in the range 6–36 eV using synchrotron radiation from an electron storage ring. Rev. Sci. Instrum. 1971, 42, 1507–1513. [Google Scholar] [CrossRef]
- DeCicco, P.D. Self-Consistent Energy Bands and Cohesive Energy of Potassium Chloride. Phys. Rev. 1967, 153, 931–938. [Google Scholar] [CrossRef]
- Kunz, A. Electronic Energy Bands for Rubidium Chloride and the Face-Centered Cubic Alkali Bromides. Phys. Status Solidi 1968, 29, 115–120. [Google Scholar] [CrossRef]
- Bachrach, R.Z. The Optical Absorption of Lithium Iodide. Phys. Lett. A 1969, 30, 318–319. [Google Scholar] [CrossRef]

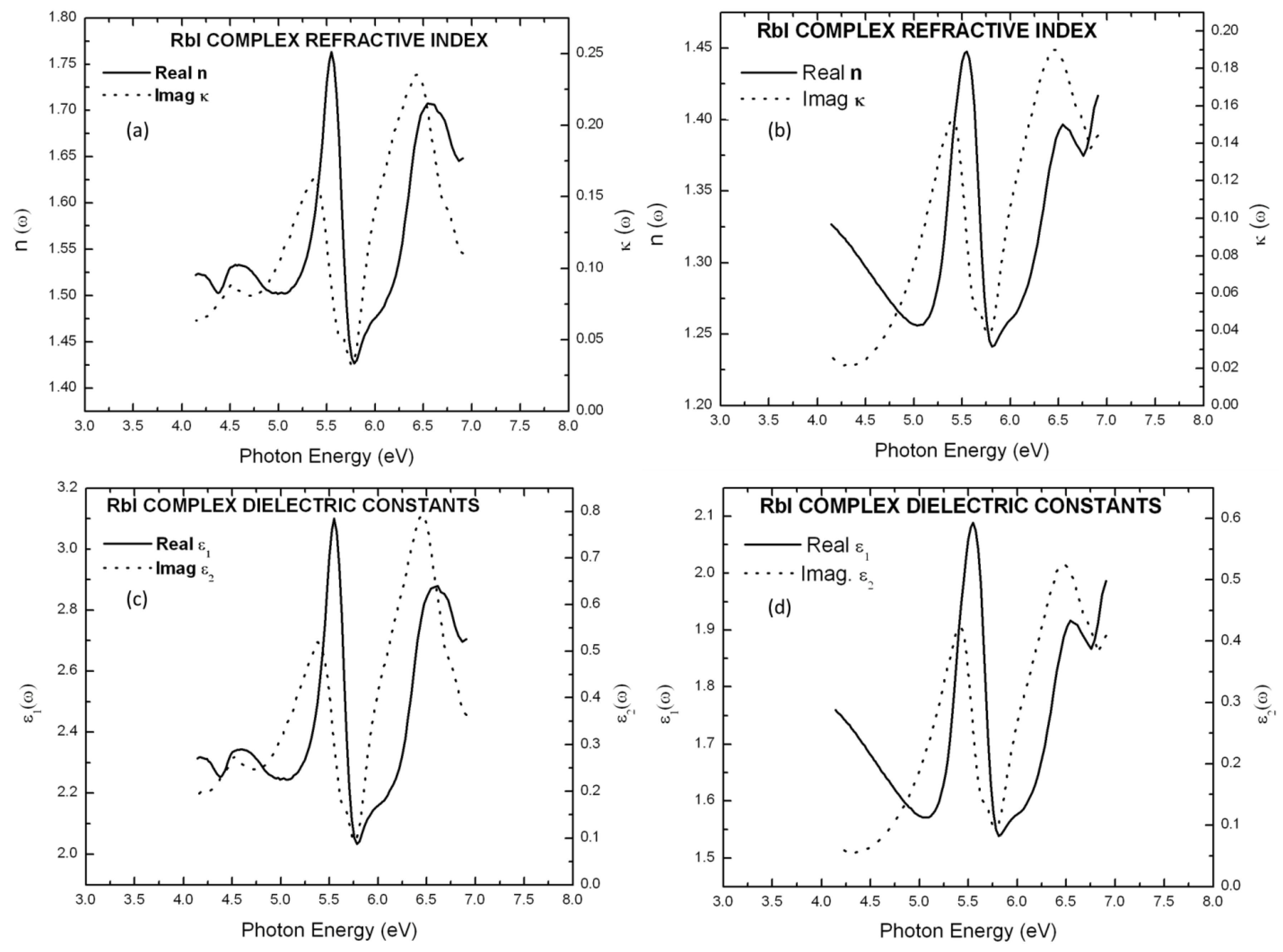
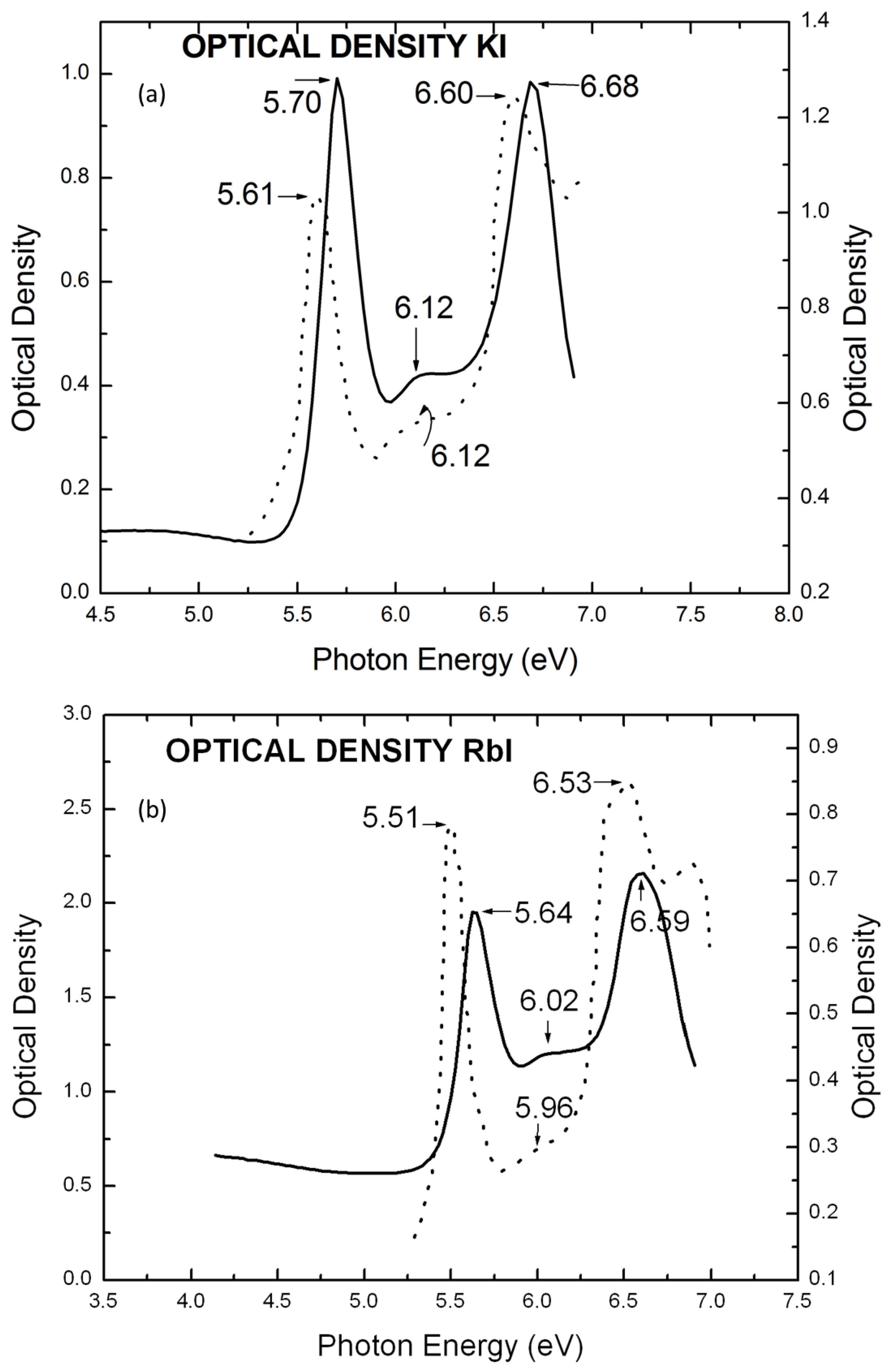
| Materials | Maximum | Minimum |
|---|---|---|
| KI | 2.04 (5.63 eV) | 1.55 (5.86 eV) |
| RbI | 1.76 (5.63 eV) | 1.43 (5.78 eV) |
| Materials | Maximum | Minimum |
|---|---|---|
| KI | 1.93 (5.65 eV) | 1.49 (5.86 eV) |
| RbI | 1.45 (5.55 eV) | 1.24 (5.81 eV) |
| Materials | Maximum | Minimum |
|---|---|---|
| KI | 4.14 (5.63 eV) | 2.40 (5.86 eV) |
| RbI | 3.10 (5.55 eV) | 2.03 (5.78 eV) |
| Materials | Maximum | Minimum |
|---|---|---|
| KI | 3.71 (5.65 eV) | 2.21 (5.86 eV) |
| RbI | 2.09 (5.55 eV) | 1.54 (5.81 eV) |
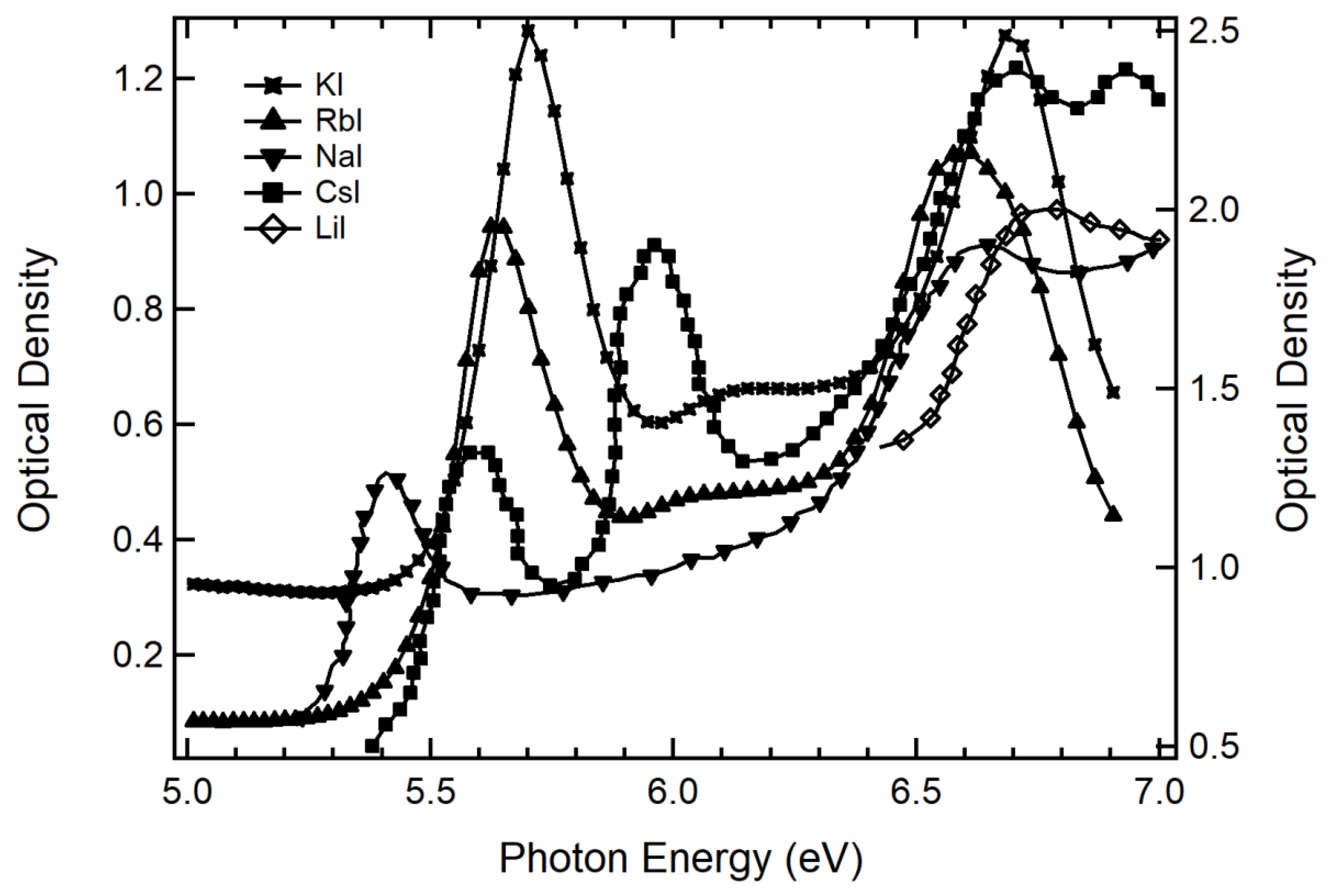
| Materials | First Peak | Second Peak | Difference |
|---|---|---|---|
| KI | 5.80 eV | 6.68 eV | 0.88 eV |
| RbI | 5.70 eV | 6.47 eV | 0.77 eV |
| NaI | 5.56 eV | 6.73 eV | 1.17 eV |
| CsI | 5.76 eV | 5.91 eV | 0.15 eV |
| LiI | uncertain | uncertain |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhandari, K.P. Optical Properties of Alkali Halides in Ultraviolet Spectral Regions. Optics 2020, 1, 18-31. https://doi.org/10.3390/opt1010002
Bhandari KP. Optical Properties of Alkali Halides in Ultraviolet Spectral Regions. Optics. 2020; 1(1):18-31. https://doi.org/10.3390/opt1010002
Chicago/Turabian StyleBhandari, Khagendra P. 2020. "Optical Properties of Alkali Halides in Ultraviolet Spectral Regions" Optics 1, no. 1: 18-31. https://doi.org/10.3390/opt1010002
APA StyleBhandari, K. P. (2020). Optical Properties of Alkali Halides in Ultraviolet Spectral Regions. Optics, 1(1), 18-31. https://doi.org/10.3390/opt1010002




