Evolution of Studies on Fracture Behavior of Composite Laminates: A Scoping Review
Abstract
1. Introduction
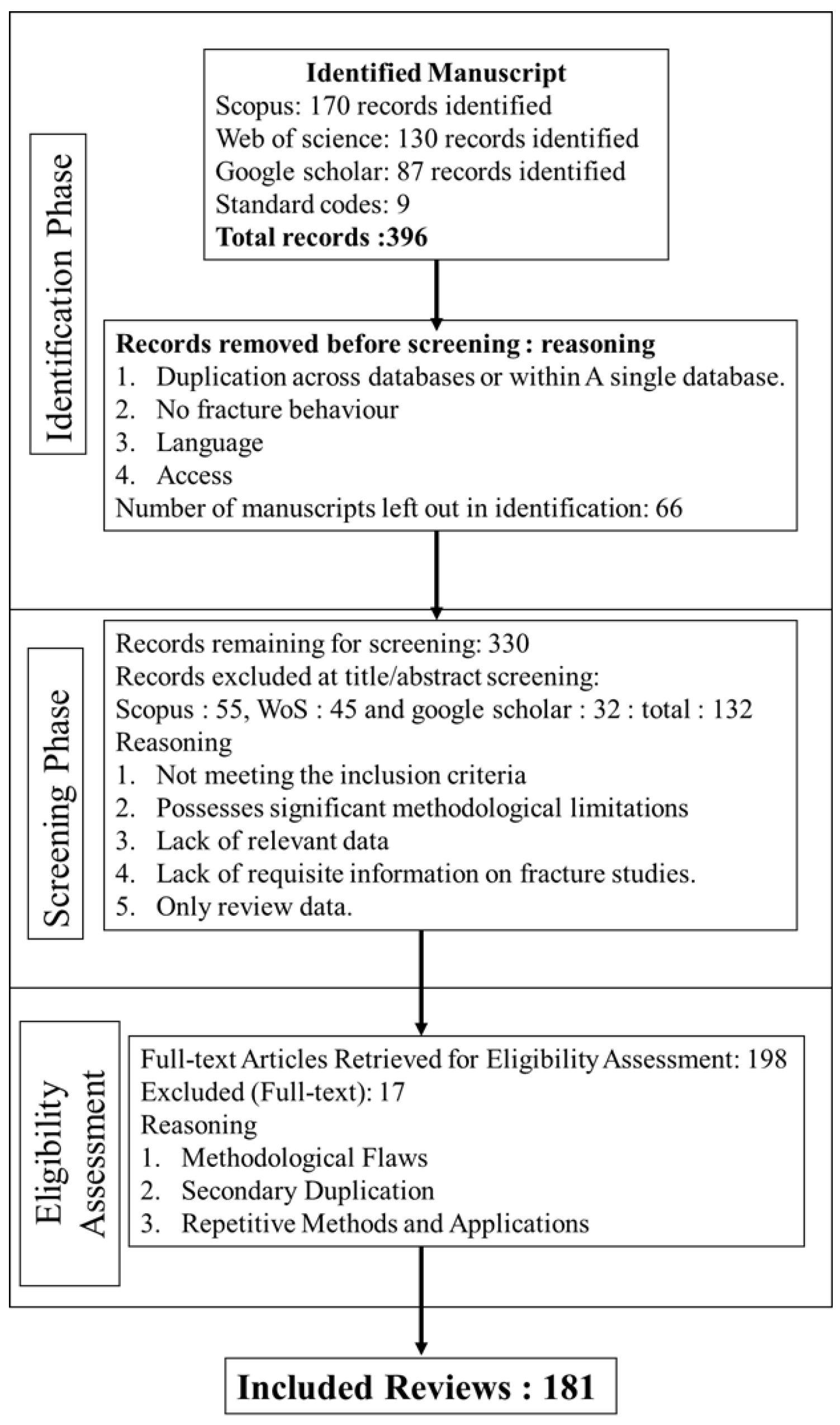
2. Review Methodology
3. Evolution of Fracture Testing in Laminated Composites
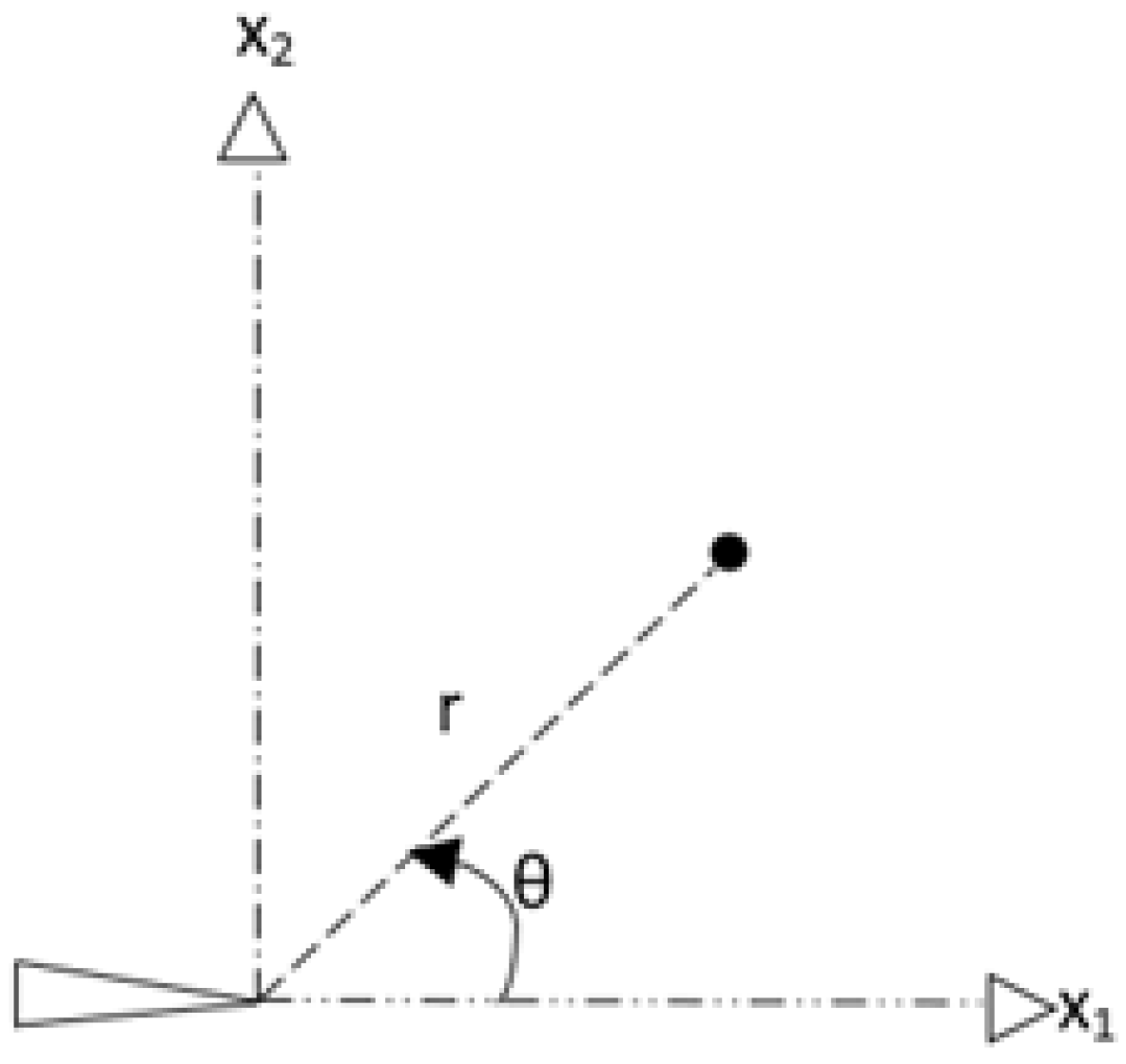
3.1. Foundation—From Griffith to Anisotropic Theories
3.2. Early Fracture Testing and Criteria for Laminates
3.2.1. Failure Prediction Criteria in Laminates
3.2.2. Applications of LEFM to Laminated Composites
3.2.3. Effect of Structural Discontinuities on Fracture Behavior
3.2.4. Influence of Matrix Type on Interlaminar Fracture Toughness
3.2.5. Influence of Manufacturing Process on Delamination Resistance
3.3. Evolution of Standardized Fracture Testing in Laminated Composites
3.3.1. Historical Context and Early Criteria for Delamination
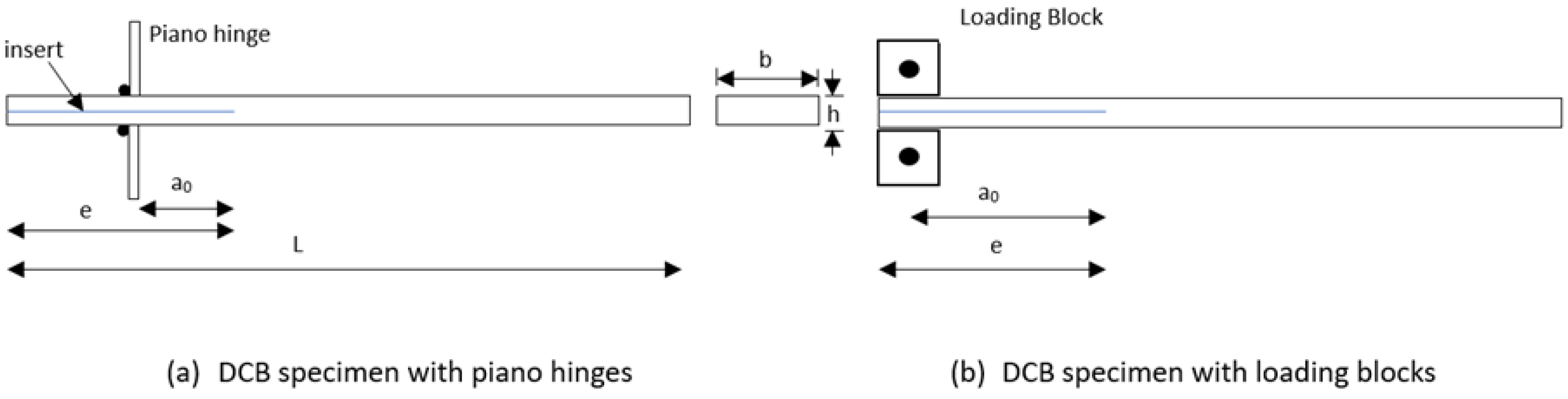
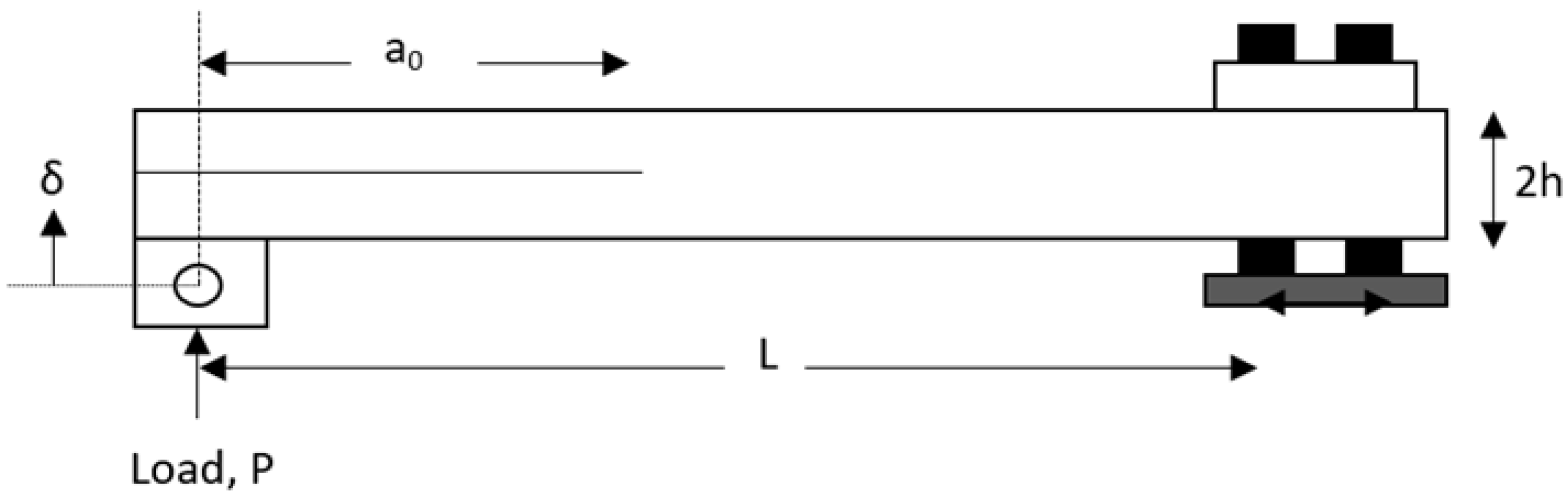
3.3.2. Mode I—Double Cantilever Beam (DCB)
3.3.3. Mode II—End-Notched Flexure (ENF) and Calibrated End-Loaded Split (C-ELS)
3.3.4. Mixed-Mode Bending (MMB)
3.3.5. Mode III Edge Crack Torsion (ECT) and Alternative Configurations
3.4. Evolution and Application of Alternative Fracture Testing and Modeling Approaches
3.4.1. J-Integral and Energy-Based Methods for Non-Linear and Toughened Systems
| Material Type | Curve Behavior | Codal Provisions | Remarks |
|---|---|---|---|
| Brittle Materials | Flat line (constant J) | Typically not characterized by curves; LEFM standards like ASTM E399, and E561 used instead [96] | Fracture toughness is defined by a single value like -integral not meaningful due to lack of plasticity. |
| Ductile Metals/Composites | Rising curve | ASTM E1820, ISO 12135 | J-integral increases with crack growth. Plastic zone develops. (initiation toughness) and R curve (resistance curve) are plotted. |
| Toughened Composites/Laminates | Steep rising curve | ASTM E1820 (extended to some composites), or modified protocols using DCB/MMB/ENF with CZM or FEM analysis | Strong crack resistance from bridging, pull-out, and deflection. For composites, ASTM D5528, D7905, and ISO 15114 for interlaminar fracture are sometimes adapted. |
3.4.2. Cohesive Zone Modeling (CZM) for Delamination Simulation
3.4.3. Virtual Crack Closure Technique (VCCT) in Delamination Analysis
3.4.4. Extended Finite Element Method (XFEM) for Arbitrary Crack Growth
3.4.5. Phase-Field Modeling of Complex Crack Evolution
3.4.6. Digital Image Correlation (DIC) for Experimental Validation of Delamination
4. Recent Advances in Composite Laminate Fracture Testing and Modeling
5. Mechanisms for Enhancing Fracture Toughness in Laminated Composites
6. Future Prospectus
6.1. Molecular Dynamics (MD) Simulations for Fracture Analysis
6.2. Machine Learning (ML) in Fracture Studies of Composite Laminates
6.3. Emerging Trends Beyond MD and ML
6.4. Strategic Research Roadmap
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thomason, J.; Xypolias, G. Hydrothermal ageing of glass fibre reinforced vinyl ester composites: A review. Polymers 2023, 15, 835. [Google Scholar] [CrossRef]
- Vijayan, D.S.; Sivasuriyan, A.; Devarajan, P.; Stefańska, A.; Wodzyński, Ł.; Koda, E. Carbon fibre-reinforced polymer (CFRP) composites in civil engineering application—A comprehensive review. Buildings 2023, 13, 1509. [Google Scholar] [CrossRef]
- Jensin Joshua, J.; Singh, D.; Venkatanarayanan, P.; Snehit, C.S.; Bipin Sai Eswar, A.; Desta, M. Experimental Estimation of Energy Absorbed and Impact Strength of Kevlar/Basalt-Epoxy Interwoven Composite Laminate Added with Al2O3 Nanoparticles after High-Velocity Bullet Impact. J. Eng. 2023, 2023, 2830575. [Google Scholar] [CrossRef]
- Velumayil, R.; Palanivel, A. Hybridization effect on mechanical properties of basalt/Kevlar/epoxy composite laminates. Polymers 2022, 14, 1382. [Google Scholar] [CrossRef]
- Slamani, M.; Chatelain, J.F. A review on the machining of polymer composites reinforced with carbon (CFRP), glass (GFRP), and natural fibers (NFRP). Discov. Mech. Eng. 2023, 2, 4. [Google Scholar] [CrossRef]
- Dharek, M.S.; Vengala, J.; Sunagar, P.; Sreekeshava, K.; Kilabanur, P.; Thejaswi, P. Biocomposites and their applications in civil engineering—An overview. In Smart Technologies for Energy, Environment and Sustainable Development, Vol 1: Select Proceedings of ICSTEESD 2020; Springer: Singapore, 2022; pp. 151–165. [Google Scholar]
- de Castro Saiki, L.E.; Gomes, G.F. Understanding and mitigating delamination in composite materials: A comprehensive review. Mech. Adv. Mater. Struct. 2024, 31, 13147–13167. [Google Scholar] [CrossRef]
- Geremew, A.; Outtier, A.; De Winne, P.; Demissie, T.A.; De Backer, H. An Experimental Investigation on the Effect of Incorporating Natural Fibers on the Mechanical and Durability Properties of Concrete by Using Treated Hybrid Fiber-Reinforced Concrete Application. Fibers 2025, 13, 26. [Google Scholar] [CrossRef]
- Olonisakin, K.; He, S.; Yang, Y.; Wang, H.; Li, R.; Yang, W. Influence of stacking sequence on mechanical properties and moisture absorption of epoxy-based woven flax and basalt fabric hybrid composites. Sustain. Struct. 2022, 2, 16. [Google Scholar] [CrossRef]
- Durão, M.L.; Nobre, L.; Mota, C.; Bessa, J.; Cunha, F.; Fangueiro, R. Self-Healing Composites: A Path to Redefining Material Resilience—A Comprehensive Recent Review. Materials 2024, 17, 4681. [Google Scholar] [CrossRef]
- Kibrete, F.; Trzepieciński, T.; Gebremedhen, H.S.; Woldemichael, D.E. Artificial intelligence in predicting mechanical properties of composite materials. J. Compos. Sci. 2023, 7, 364. [Google Scholar] [CrossRef]
- Griffith, A. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. London. Ser. A Contain. Pap. Math. Phys. Character 1997, 221, 163–198. [Google Scholar]
- Westergaard, H.M. Bearing pressures and cracks: Bearing pressures through a slightly waved surface or through a nearly flat part of a cylinder, and related problems of cracks. J. Appl. Mech. 1939, 6, A49–A53. [Google Scholar] [CrossRef]
- Irwin, G.R. Analysis of stresses and strains near the end of a crack traversing a plate. J. Appl. Mech. 1997, 24, 361–364. [Google Scholar] [CrossRef]
- Abdellah, M.Y.; Zuwawi, A.R.; Azam, S.A.; Hassan, M.K. A comparative study to evaluate the essential work of fracture to measure the fracture toughness of quasi-brittle material. Materials 2022, 15, 4514. [Google Scholar] [CrossRef]
- Lekhnitskii, S.G. Theory of Elasticity of an Anisotropic Elastic Body; Holden-Day: San Francisco, CA, USA, 1963. [Google Scholar]
- Sih, G. Plane extension of rigidly embedded line inclusions. Dev. Mech. 1965, 3, 61–79. [Google Scholar]
- Liebowitz, H.; Sih, G. Mathematical theories of brittle fracture. Fracture 1968, 2, 67–190. [Google Scholar]
- Erdogan, F.; Aksogan, O. Bonded half planes containing an arbitrarily oriented crack. Int. J. Solids Struct. 1974, 10, 569–585. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, F.; Lu, Z.; Cao, D.; Jia, X. Numerical Tensile Damage Procedure Analysis of Angle-Ply Laminate Using Multi-Scale RVEs with Smear Crack Models. Materials 2022, 15, 2002. [Google Scholar] [CrossRef] [PubMed]
- Werthen, E.; Hardt, D.; Balzani, C.; Hühne, C. Comparison of different cross-sectional approaches for the structural design and optimization of composite wind turbine blades based on beam models. Wind. Energy Sci. Discuss. 2023, 2023, 1–26. [Google Scholar] [CrossRef]
- Premanand, A.; Balle, F. Influence of pulse duration on the fatigue behavior of a carbon-fiber-reinforced composite under cyclic three-point bending at 20 kHz. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 1731–1747. [Google Scholar] [CrossRef]
- Sih, G.C. Strain-energy-density factor applied to mixed mode crack problems. Int. J. Fract. 1974, 10, 305–321. [Google Scholar] [CrossRef]
- Sih, G.; Sih, G. A three-dimensional strain energy density factor theory of crack propagation. In Mechanics of Fracture Initiation and Propagation: Surface and Volume Energy Density Applied as Failure Criterion; Springer: Dordrecht, Switzerland, 1991; pp. 23–56. [Google Scholar]
- Bouvet, C.; Vieille, B.; Pujols-Gonzalez, J. Experimental characterization and numerical modelling of the translaminar fracture of woven-ply hybrid fibers reinforced thermoplastic laminates. Eng. Fract. Mech. 2022, 276, 108867. [Google Scholar] [CrossRef]
- Toribio, J.; Matos, J.C.; González, B. Stress Intensity Factor (SIF) Solutions and Fatigue Crack Paths in Eccentric Circumferentially Cracked Round Bar (CCRB) in Tension. Materials 2023, 16, 1728. [Google Scholar] [CrossRef]
- Gdoutos, E.E.; Gdoutos, E.E. Linear elastic stress field in cracked bodies. In Fracture Mechanics; Springer: Cham, Switzerland, 2020; pp. 15–63. [Google Scholar]
- Ping, X.; Zhang, Y.; Guo, Y.; Xiao, Z.; Jalde, J.; Chen, M. Intensity of stress singularity for the circumferential V-shape corner front of a three-dimensional diamond-like defect. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 802–817. [Google Scholar] [CrossRef]
- Popejoy, D.B.; Dharani, L.R.; Tang, H. Crack growth at interfaces in bimaterial systems and composites. Int. J. Solids Struct. 1992, 29, 3113–3123. [Google Scholar] [CrossRef]
- Bambach, M.R. Tension Strength of Multi-Fastener, Single-Lap Joints in Flax and Jute Composite Plates Using Bolts or Rivets. Materials 2025, 18, 2180. [Google Scholar] [CrossRef]
- Bonhomme, J.; Viña, J.; Argüelles, A.; Viña, I.; Mollón, V. Influence of the matrix toughness in carbon-epoxy composites subjected to delamination under modes I, II, and mixed I/II. Mech. Adv. Mater. Struct. 2013, 20, 679–686. [Google Scholar] [CrossRef]
- Perez, P.G.; Bouvet, C.; Chettah, A.; Dau, F.; Ballère, L.; Peres, P. Effect of unstable crack growth on mode II interlaminar fracture toughness of a thermoplastic PEEK composite. Eng. Fract. Mech. 2019, 205, 486–497. [Google Scholar] [CrossRef]
- Song, X.; Deng, Z.P.; Li, C.B.; Song, F.; Wang, X.L.; Chen, L.; Guo, D.M.; Wang, Y.Z. A bio-based epoxy resin derived from p-hydroxycinnamic acid with high mechanical properties and flame retardancy. Chin. Chem. Lett. 2022, 33, 4912–4917. [Google Scholar] [CrossRef]
- White, S.R.; Sottos, N.R.; Geubelle, P.H.; Moore, J.S.; Kessler, M.R.; Sriram, S.; Brown, E.N.; Viswanathan, S. Autonomic healing of polymer composites. Nature 2001, 409, 794–797. [Google Scholar] [CrossRef]
- Krzak, A.; Nowak, A.J.; Heljak, M.; Antonowicz, J.; Garg, T.; Sumption, M. Mechanical and thermal analysis of duroplastic matrix composites over a range of temperatures. Polymers 2024, 16, 606. [Google Scholar] [CrossRef]
- Shen, R.; Liu, T.; Liu, H.; Zou, X.; Gong, Y.; Guo, H. An enhanced vacuum-assisted resin transfer molding process and its pressure effect on resin infusion behavior and composite material performance. Polymers 2024, 16, 1386. [Google Scholar] [CrossRef]
- Somrani, S.; Jacques, E.; Weiss, B.; Duchamp, B. Modelling the Permeabilities of Dry Filament Wound Cylindrical Reinforcements for RTM Simulation. Processes 2025, 13, 1071. [Google Scholar] [CrossRef]
- Ding, S.; Zou, B.; Liu, Q.; Wang, X.; Liu, J.; Li, L. Non-planar additive manufacturing of pre-impregnated continuous fiber reinforced composites using a three-axis printer. J. Mater. Res. Technol. 2024, 32, 4410–4419. [Google Scholar] [CrossRef]
- Friedrich, L.F.; Kosteski, L.E.; Cezar, É.S.; Colpo, A.B.; Bremm, C.; Lacidogna, G.; Iturrioz, I. A Fractal Analysis of the Size Effect in Quasi-Brittle Materials: Experimental Tests and Peridynamic Simulations. Mathematics 2024, 13, 94. [Google Scholar] [CrossRef]
- Argon, A. Fracture of composites. Treatise Mater. Sci. Technol. 2013, 1, 79–114. [Google Scholar]
- Whitney, J.M.; Nuismer, R.J. Stress fracture criteria for laminated composites containing stress concentrations. J. Compos. Mater. 1974, 8, 253–265. [Google Scholar] [CrossRef]
- Whitney, J.; Browning, C.; Hoogsteden, W. A double cantilever beam test for characterizing Mode I delamination of composite materials. J. Reinf. Plast. Compos. 1982, 1, 297–313. [Google Scholar] [CrossRef]
- Nuismer, R.; Whitney, J.M. Uniaxial failure of composite laminates containing stress concentrations. In Fracture Mechanics of Composites; ASTM International: West Conshohocken, PA, USA, 1975. [Google Scholar]
- Sih, G.; Macdonald, B. Fracture mechanics applied to engineering problems-strain energy density fracture criterion. Eng. Fract. Mech. 1974, 6, 361–386. [Google Scholar] [CrossRef]
- Braiden, P. The development of rational design criteria for brittle materials. Mater. Des. 1980, 2, 73–82. [Google Scholar] [CrossRef]
- Rybicki, E.F.; Kanninen, M.F. A finite element calculation of stress intensity factors by a modified crack closure integral. Eng. Fract. Mech. 1977, 9, 931–938. [Google Scholar] [CrossRef]
- Wang, A.; Crossman, F. Initiation and growth of transverse cracks and edge delamination in composite laminates Part 1. An energy method. J. Compos. Mater. 1980, 14, 71–87. [Google Scholar] [CrossRef]
- Nicholls, D.; Gallagher, J. Determination of GIC in angle ply composites using a cantilever beam test method. J. Reinf. Plast. Compos. 1983, 2, 2–17. [Google Scholar] [CrossRef]
- ASTM D5528-13; Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites. ASTM International: West Conshohocken, PA, USA, 2013.
- Jurf, R.A.; Pipes, R.B. Interlaminar fracture of composite materials. J. Compos. Mater. 1982, 16, 386–394. [Google Scholar] [CrossRef]
- Liu, X.; Sun, T.; Wu, Z.; He, H. Mode II interlaminar fracture toughness of unidirectional fiber-reinforced polymer matrix composites with synthetic boehmite nanosheets at room temperature and low temperature. J. Compos. Mater. 2018, 52, 945–952. [Google Scholar] [CrossRef]
- ISO 15114:2014; Fibre-Reinforced Plastic Composites—Determination of the mode II Fracture Resistance for Unidirectionally Reinforced Materials Using the Calibrated End-Loaded Split (C-ELS) Test and An Effective Crack Length Approach. International Organization for Standardization: Geneva, Switzerland, 2014.
- Sarasini, F.; Tirillò, J.; Valente, M.; Valente, T.; Cioffi, S.; Iannace, S.; Sorrentino, L. Effect of basalt fiber hybridization on the impact behavior under low impact velocity of glass/basalt woven fabric/epoxy resin composites. Compos. Part A Appl. Sci. Manuf. 2013, 47, 109–123. [Google Scholar] [CrossRef]
- ASTM D7905/D7905M-19e1; Standard Test Method for Determination of the mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites. ASTM International: West Conshohocken, PA, USA, 2014.
- Wang, S. Fracture mechanics for delamination problems in composite materials. J. Compos. Mater. 1983, 17, 210–223. [Google Scholar] [CrossRef]
- Hashemi, S.; Kinloch, A.; Williams, J. Mechanics and mechanisms of delamination in a poly (ether sulphone)—Fibre composite. Compos. Sci. Technol. 1990, 37, 429–462. [Google Scholar] [CrossRef]
- Zhou, H. Interlayer delamination and adhesion of coextruded films. J. Appl. Polym. Sci. 2004, 92, 3901–3909. [Google Scholar] [CrossRef]
- Cao, D.; Hu, H.; Duan, Q.; Song, P.; Li, S. Experimental and three-dimensional numerical investigation of matrix cracking and delamination interaction with edge effect of curved composite laminates. Compos. Struct. 2019, 225, 111154. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, P.; Bhadauria, S.S. Numerical simulation of delamination growth in fiber reinforced polymer laminates using cohesive zone modeling. Mech. Adv. Mater. Struct. 2022, 29, 213–229. [Google Scholar] [CrossRef]
- Smolnicki, M.; Duda, S. Determination of Interface Fracture Parameters in Thermoplastic Fiber Metal Laminates Under Mixed-Mode I+ II. Polymers 2025, 17, 1462. [Google Scholar] [CrossRef]
- Carroll, J.; Efstathiou, C.; Lambros, J.; Sehitoglu, H.; Hauber, B.; Spottswood, S.; Chona, R. Investigation of fatigue crack closure using multiscale image correlation experiments. Eng. Fract. Mech. 2009, 76, 2384–2398. [Google Scholar] [CrossRef]
- Durif, E.; Réthoré, J.; Combescure, A.; Fregonese, M.; Chaudet, P. Controlling stress intensity factors during a fatigue crack propagation using digital image correlation and a load shedding procedure. Exp. Mech. 2012, 52, 1021–1031. [Google Scholar] [CrossRef]
- Amsalu, C.; Negasa, D.; Merga, A. Numerical analysis of fiber reinforced composite material for structural component application. Heliyon 2024, 10, e37698. [Google Scholar] [CrossRef]
- Gong, L.; Feng, Y.; Zhang, W.; Xu, M.; Zeng, X. Vibration Performances of a Full-Scale Assembled Integral Two-Way Multi-Ribbed Composite Floor. Buildings 2025, 15, 1551. [Google Scholar] [CrossRef]
- Reeder, J.R.; Crews, J.H., Jr. Mixed-mode bending method for delamination testing. AIAA J. 1990, 28, 1270–1276. [Google Scholar] [CrossRef]
- Song, S.J.; Waas, A.M. Mode I failure of laminated polymeric composites. Eng. Fract. Mech. 1994, 49, 17–27. [Google Scholar] [CrossRef]
- De Morais, A.B. Double cantilever beam testing of multidirectional laminates. Compos. Part A Appl. Sci. Manuf. 2003, 34, 1135–1142. [Google Scholar] [CrossRef]
- Hu, X.M.; Han, K.C.; Xu, F.; Xie, W.; Kou, J.F. Mixed-Mode Bending Test for Fracture Toughness of Composite Bonding Adhesive Layer. Adv. Mater. Res. 2012, 415, 2240–2243. [Google Scholar] [CrossRef]
- Bahmani, A.; Farahmand, F.; Janbaz, M.; Darbandi, A.; Ghesmati-Kucheki, H.; Aliha, M. On the comparison of two mixed-mode I+ III fracture test specimens. Eng. Fract. Mech. 2021, 241, 107434. [Google Scholar] [CrossRef]
- Oliveira, J.; Xavier, J.; Pereira, F.; Morais, J.; de Moura, M. Direct evaluation of mixed mode I+II cohesive laws of wood by coupling MMB test with DIC. Materials 2021, 14, 374. [Google Scholar] [CrossRef]
- ASTM D6671-01; Standard Test Method for Mixed Mode I/II Interlaminar Fracture Toughness of Unidirectional Fibre Reinforced Polymer Matrix Composites. ASTM International: West Conshohocken, PA, USA, 2001.
- Gong, Y.; Zhao, L.; Zhang, J.; Hu, N.; Zhang, C. Development of a standardized test procedure and an improved data reduction method for the mixed-mode I/II delamination in composite laminates. Compos. Sci. Technol. 2021, 201, 108488. [Google Scholar] [CrossRef]
- Edelen, D.L., III; Bruck, H.A. Predicting failure modes of 3D-printed multi-material polymer sandwich structures from process parameters. J. Sandw. Struct. Mater. 2022, 24, 1049–1075. [Google Scholar] [CrossRef]
- Guseinov, K.; Kudryavtsev, O.; Bezmelnitsyn, A.; Sapozhnikov, S. Determination of interlaminar shear properties of fibre-reinforced composites under biaxial loading: A new experimental approach. Polymers 2022, 14, 2575. [Google Scholar] [CrossRef] [PubMed]
- Kanno, T.; Kurita, H.; Suzuki, M.; Tamura, H.; Narita, F. Numerical and Experimental Investigation of the Through-Thickness Strength Properties of Woven Glass Fiber Reinforced Polymer Composite Laminates under Combined Tensile and Shear Loading. J. Compos. Sci. 2020, 4, 112. [Google Scholar] [CrossRef]
- ASTM D7078; Standard Test Method for Shear Properties of Composite Materials by V-Notched Rail Shear Method. ASTM International: West Conshohocken, PA, USA, 2005.
- Saadati, Y.; Chatelain, J.F.; Lebrun, G.; Beauchamp, Y.; Bocher, P.; Vanderesse, N. A study of the interlaminar fracture toughness of unidirectional flax/epoxy composites. J. Compos. Sci. 2020, 4, 66. [Google Scholar] [CrossRef]
- Li, J.; Lee, S.M.; Lee, E.W.; O’Brien, T.K. Evaluation of the edge crack torsion (ECT) test for mode III interlaminar fracture toughness of laminated composites. Compos. Technol. Res. 1997, 19, 174–183. [Google Scholar]
- Nezamabadi, S.; Potier-Ferry, M.; Zahrouni, H.; Yvonnet, J. Compressive failure of composites: A computational homogenization approach. Compos. Struct. 2015, 127, 60–68. [Google Scholar] [CrossRef]
- Abdullah, S.S.; Bokti, S.; Wong, K.; Johar, M.; Chong, W.; Dong, Y. mode II and mode III delamination of carbon fiber/epoxy composite laminates subjected to a four-point bending mechanism. Compos. Part B Eng. 2024, 270, 111110. [Google Scholar] [CrossRef]
- De Morais, A.; Pereira, A. mode III interlaminar fracture of carbon/epoxy laminates using a four-point bending plate test. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1741–1746. [Google Scholar] [CrossRef]
- Pundir, M.; Adda-Bedia, M.; Kammer, D.S. Transonic and supershear crack propagation driven by geometric nonlinearities. Phys. Rev. Lett. 2024, 132, 226102. [Google Scholar] [CrossRef]
- Zolfagharian, A.; Khosravani, M.R.; Kaynak, A. Fracture resistance analysis of 3D-printed polymers. Polymers 2020, 12, 302. [Google Scholar] [CrossRef]
- Rice, J.R. A path independent integral and the approximate analysis of strain concentration by notches and cracks. ASME. J. Appl. Mech. 1968, 35, 379–386. [Google Scholar] [CrossRef]
- Lei, Y. J-integral evaluation for cases involving non-proportional stressing. Eng. Fract. Mech. 2005, 72, 577–596. [Google Scholar] [CrossRef]
- Sun, C.Q.; Zhang, C.; He, B. Effect of Strength Matching Performance on J-Integral of Inhomogeneous Welded Joints. Adv. Mater. Res. 2012, 472, 1267–1270. [Google Scholar] [CrossRef]
- Acharyya, S.; Dhar, S.; Chattopadhyay, J. Evaluation of critical fracture energy parameter Gfr and assessment of its transferrability. Eng. Fract. Mech. 2008, 75, 253–274. [Google Scholar] [CrossRef]
- Huang, T.; Bobyr, M. A review of delamination damage of composite materials. J. Compos. Sci. 2023, 7, 468. [Google Scholar] [CrossRef]
- Wu, D.; Liu, Z.; Li, D.; Zhang, Z.; Chen, J. Study on the stress intensity factor of a compact specimen under the pre-compressed load condition. J. Theor. Appl. Mech. 2023, 61, 37–47. [Google Scholar] [CrossRef]
- E1820-17a; Standard Test Method for Measurement of Fracture Toughness. ASTM International: West Conshohocken, PA, USA, 2017.
- ISO 12135:2002(E); Metallic Materials—Unified Method of Test for the Determination of Quasistatic Fracture Toughness. International Organization for Standardization: Geneva, Switzerland, 2002.
- E561-20; Standard Practice for R-Curve Determination. ASTM International: West Conshohocken, PA, USA, 2020. [CrossRef]
- Romanowicz, M. Predictions of fracture resistance of spruce wood under mixed mode loading using non-local fracture theory and numerical modelling. J. Theor. Appl. Mech. 2023, 61, 147–162. [Google Scholar] [CrossRef]
- Cˇervenka, J.; Saouma, V.E. Numerical evaluation of 3-D SIF for arbitrary finite element meshes. Eng. Fract. Mech. 1997, 57, 541–563. [Google Scholar] [CrossRef]
- Gosz, M.; Moran, B. An interaction energy integral method for computation of mixed-mode stress intensity factors along non-planar crack fronts in three dimensions. Eng. Fract. Mech. 2002, 69, 299–319. [Google Scholar] [CrossRef]
- E399-20; Standard Test Method for Linear-Elastic Plane-Strain Fracture Toughness of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2020. [CrossRef]
- Vala, J.; Tomáš, J. Damage behavior of Quasi-Brittle Composites: Mathematical and Computational Aspects. Appl. Sci. 2025, 15, 4214. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The formation of equilibrium cracks during brittle fracture. General ideas and hypotheses. Axially-symmetric cracks. J. Appl. Math. Mech. 1959, 23, 622–636. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Fan, C.; Jar, P.Y.B.; Cheng, J.R. Cohesive zone with continuum damage properties for simulation of delamination development in fibre composites and failure of adhesive joints. Eng. Fract. Mech. 2008, 75, 3866–3880. [Google Scholar] [CrossRef]
- Tvergaard, V.; Hutchinson, J.W. Effect of T-stress on mode I crack growth resistance in a ductile solid. Int. J. Solids Struct. 1994, 31, 823–833. [Google Scholar] [CrossRef]
- Vandellos, T.; Huchette, C.; Carrere, N. Proposition of a framework for the development of a cohesive zone model adapted to carbon-fiber reinforced plastic laminated composites. Compos. Struct. 2013, 105, 199–206. [Google Scholar] [CrossRef]
- Mageed, A.A.; Pandey, R. Mixed mode crack growth under static and cyclic loading in A1-alloy sheets. Eng. Fract. Mech. 1991, 40, 371–385. [Google Scholar] [CrossRef]
- Zhu, Y.; Liechti, K.M.; Ravi-Chandar, K. Direct extraction of rate-dependent traction–separation laws for polyurea/steel interfaces. Int. J. Solids Struct. 2009, 46, 31–51. [Google Scholar] [CrossRef]
- Halverson, H.G.; Curtin, W.A.; Reifsnider, K.L. Fatigue life of individual composite specimens based on intrinsic fatigue behavior. Int. J. Fatigue 1997, 19, 369–377. [Google Scholar] [CrossRef]
- Benzeggagh, M.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Filipescu, H.; Caplescu, C.; Pasca, N. Assessment of UMTS and averaged SED fracture criteria for U-notched specimens. Key Eng. Mater. 2014, 577, 113–116. [Google Scholar] [CrossRef]
- Karadimas, G.; Salonitis, K. Ceramic matrix composites for aero engine applications—A review. Appl. Sci. 2023, 13, 3017. [Google Scholar] [CrossRef]
- Pan, Y.; Liu, X.; Yao, J. Prediction of Mechanical Properties of Void Defect-Containing Cf/SiBCN Ceramic Matrix Composite Based on a Multiscale Analysis Approach. Materials 2025, 18, 2116. [Google Scholar] [CrossRef]
- Das, A.K.; Leung, C.K.Y. A Novel Technique for High-Efficiency Characterization of Complex Cracks with Visual Artifacts. Appl. Sci. 2024, 14, 7194. [Google Scholar] [CrossRef]
- Karihaloo, B.L.; Xiao, Q. Modelling of stationary and growing cracks in FE framework without remeshing: A state-of-the-art review. Comput. Struct. 2003, 81, 119–129. [Google Scholar] [CrossRef]
- Kim, H.G.; Howe, R.; Wiebe, R.; Spottswood, S.M.; O’Hara, P.J.; Salviato, M. Experimental characterization of traction-separation laws for interlaminar fracture in geometrically-scaled composites using progressive digital image correlation and through-thickness deformation analysis. arXiv 2023, arXiv:2312.05087. [Google Scholar]
- Blaschke, D.N.; Nguyen, T.; Nitol, M.; O’Malley, D.; Fensin, S. Machine learning based approach to predict ductile damage model parameters for polycrystalline metals. Comput. Mater. Sci. 2023, 229, 112382. [Google Scholar] [CrossRef]
- Gopalsamy, R.; Chevaugeon, N.; Chupin, O.; Hammoum, F. Variational approach to viscoelastic fracture: Comparison of a phase-field and a lip-field approach. Int. J. Fract. 2023, 244, 163–185. [Google Scholar] [CrossRef]
- Newman, B.; Randall, J.D.; Varley, R.J.; Stojcevski, F.; Henderson, L.C. Bioinspired Hard–Soft Interface Management for Superior Performance in Carbon Fibre Composites. Fibers Polym. 2023, 24, 3279–3288. [Google Scholar] [CrossRef]
- Wang, Y.; Javadi, A.A.; Fidelibus, C.; Liang, H. Improvements for the solution of crack evolution using extended finite element method. Sci. Rep. 2024, 14, 26924. [Google Scholar] [CrossRef] [PubMed]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Fageehi, Y.A. A Robust Adaptive Mesh Generation Algorithm: A Solution for Simulating 2D Crack Growth Problems. Materials 2023, 16, 6481. [Google Scholar] [CrossRef]
- Guo, F.; Li, Y.; Chen, Y.; Liu, P.; Wang, X. Investigation of the Stress Intensity Factor in Heterogeneous Materials Based on the Postprocessing Routine of Commercial Finite Element Software. Appl. Sci. 2025, 15, 5827. [Google Scholar] [CrossRef]
- Feklistova, E.; Mugatarov, A.; Wildemann, V.; Agishev, A. Fracture processes numerical modeling of elastic-brittle bodies with statistically distributed subregions strength values. Fract. Struct. Integr. 2024, 18, 425–439. [Google Scholar] [CrossRef]
- Bourdin, B. Numerical implementation of the variational formulation for quasi-static brittle fracture. Interfaces Free Bound. 2007, 9, 411–430. [Google Scholar] [CrossRef]
- Peters, W.; Ranson, W.; Sutton, M.; Chu, T.; Anderson, J. Application of digital correlation methods to rigid body mechanics. Opt. Eng. 1983, 22, 738–742. [Google Scholar] [CrossRef]
- McNeill, S.; Peters, W.; Sutton, M. Estimation of stress intensity factor by digital image correlation. Eng. Fract. Mech. 1987, 28, 101–112. [Google Scholar] [CrossRef]
- Tiwari, V.; Sutton, M.; McNeill, S. Assessment of high speed imaging systems for 2D and 3D deformation measurements: Methodology development and validation. Exp. Mech. 2007, 47, 561–579. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Schreier, H.; Orteu, J.J.; Sutton, M.A. Image correlation for shape, motion and deformation measurements: Basic concepts, theory and applications. In Image Correlation for Shape, Motion and Deformation Measurements; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Romanowicz, P.J.; Szybiński, B.; Wygoda, M. Assessment of digital image correlation effectiveness and quality in determination of surface strains of hybrid steel/composite structures. Materials 2024, 17, 3561. [Google Scholar] [CrossRef]
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the IJCAI’81: 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981; Volume 2, pp. 674–679. [Google Scholar]
- Catalanotti, G.; Camanho, P.; Xavier, J.; Dávila, C.; Marques, A. Measurement of resistance curves in the longitudinal failure of composites using digital image correlation. Compos. Sci. Technol. 2010, 70, 1986–1993. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, C. Unsupervised CNN-based DIC method for 2D displacement measurement. Opt. Lasers Eng. 2024, 174, 107981. [Google Scholar] [CrossRef]
- Rashid, S.; Rossi, E.; Diplas, S.; Carvalho, P.A.; Pucicki, D.; Kuna, R.; Sebastiani, M. A Critical Comparison Among High-Resolution Methods for Spatially Resolved Nano-Scale Residual Stress Analysis in Nanostructured Coatings. Int. J. Mol. Sci. 2025, 26, 3296. [Google Scholar] [CrossRef]
- Latifi, M.; Kouchakzadeh, M. Modeling the R-curve effects in laminate composites using the interface thick level set method. Theor. Appl. Fract. Mech. 2020, 108, 102645. [Google Scholar] [CrossRef]
- Han, N.; Fan, L.; Zhang, Y. Estimation of cohesive zone model parameters for glass/Elium composites with different processing temperature. J. Reinf. Plast. Compos. 2024, 43, 601–611. [Google Scholar] [CrossRef]
- Martulli, L.; Bernasconi, A. An efficient and versatile use of the VCCT for composites delamination growth under fatigue loadings in 3D numerical analysis: The Sequential Static Fatigue algorithm. Int. J. Fatigue 2023, 170, 107493. [Google Scholar] [CrossRef]
- Mohamed, A.F.; Abdellah, M.Y.; Hassan, M.K.; Backar, A.H. Advanced Prediction and Analysis of Delamination Failure in Graphite-Reinforced Epoxy Composites Using VCCT-Based Finite Element Modelling Techniques. Polymers 2025, 17, 771. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.; Alderliesten, R.; Benedictus, R. Delamination in fiber metal laminates (GLARE) during fatigue crack growth under variable amplitude loading. Int. J. Fatigue 2011, 33, 1292–1303. [Google Scholar] [CrossRef]
- Hofman, P.; van der Meer, F.; Sluys, L.J. Modeling of progressive high-cycle fatigue in composite laminates accounting for local stress ratios. Compos. Part A Appl. Sci. Manuf. 2024, 183, 108219. [Google Scholar] [CrossRef]
- Kalfon-Cohen, E.; Kopp, R.; Furtado, C.; Ni, X.; Arteiro, A.; Borstnar, G.; Mavrogordato, M.N.; Sinclair, I.; Spearing, S.M.; Camanho, P.P.; et al. Synergetic effects of thin plies and aligned carbon nanotube interlaminar reinforcement in composite laminates. Compos. Sci. Technol. 2018, 166, 160–168. [Google Scholar] [CrossRef]
- Yujing, C. Modeling of the mechanical degradation induced by moisture absorption in short natural fiber reinforced composites. Compos. Sci. Technol. 2014, 103, 22–27. [Google Scholar] [CrossRef]
- Wei, J.; Fang, Z.; Wu, X.; Li, D.-S.; Guo, Q.; Zhang, D.; Li, C.; Liu, Y.; Yan, Y.; Guo, J.; et al. Vibration Fatigue Behavior and Failure Mechanism of 3D Layer-to-Layer Interlock Woven Composites; SSRN: Rocheste, NY, USA, 2025. [Google Scholar]
- Bozkurt, M.O.; Ozen, E.B.; Yavuz, B.O.; Parnas, L.; Coker, D. High-speed observation of dynamic delamination failure in tapered composite laminates under tensile loading. Polym. Compos. 2024, 45, 9181–9195. [Google Scholar] [CrossRef]
- Molimard, J.; Le Riche, R.; Vautrin, A.; Lee, J.R. Identification of the four orthotropic plate stiffnesses using a single open-hole tensile test. Exp. Mech. 2005, 45, 404–411. [Google Scholar] [CrossRef]
- Kumar, V.; Singh, A. Investigation of traction-separation behavior in adhesively bonded joints under mode I and mode II loading using DIC technique and FEA. Eng. Fail. Anal. 2024, 159, 108048. [Google Scholar] [CrossRef]
- Yenigun, B.; Chaudhry, M.S.; Gkouti, E.; Czekanski, A. Characterization of Mode I and mode II Interlaminar Fracture Toughness in CNT-Enhanced CFRP under Various Temperature and Loading Rates. Nanomaterials 2023, 13, 1729. [Google Scholar] [CrossRef]
- Elango, I.; Arumugam, V.; Dhakal, H.N. Fabrication and comparison of interlaminar fracture toughness behavior of glass epoxy composites with recycled milled Kevlar-carbon hybrid fillers. Heliyon 2024, 10, e38842. [Google Scholar] [CrossRef]
- Chen, T.; Harvey, C.M.; Zhang, K.; Wang, S.; Silberschmidt, V.V.; Wei, B. Dynamic mode-I delamination in composite DCB under impact loads with attunable dynamic effect. Compos. Sci. Technol. 2023, 241, 110120. [Google Scholar] [CrossRef]
- Gong, Y.; Xia, K.; Wang, Y.; Zhao, L.; Zhang, J.; Hu, N. A semi-analytical model for the mode II fracture toughness of multidirectional composite laminates. Thin-Walled Struct. 2023, 182, 110235. [Google Scholar] [CrossRef]
- Gong, Y.; Jiang, L.; Li, L.; Zhao, J. An experimental and numerical study of the influence of temperature on mode II fracture of a T800/epoxy unidirectional laminate. Materials 2022, 15, 8108. [Google Scholar] [CrossRef]
- Yan, B.; Zhu, L.; Zhu, S.; Zhang, Y.; Shen, L.; Zhang, T.; Zhu, K.; Li, Z.; Jiang, W. Half-thickness z-pin effect on the interlaminar and the intralaminar properties of polyimide z-pin reinforced polymer composites. J. Compos. Mater. 2025, 59. [Google Scholar] [CrossRef]
- Chen, Y.; Meng, B.; Zhong, L.; Guo, D.; Sha, L.; Zhao, H.; Xu, Y.; Li, J.; Chang, Z.; Zhang, X.; et al. Novel carbon fiber/aramid fiber composite carbon paper for improved performance in proton exchange membrane fuel cells. Ind. Crops Prod. 2025, 223, 120187. [Google Scholar] [CrossRef]
- Arca, M.; Coker, D. Experimental investigation of CNT effect on curved beam strength and interlaminar fracture toughness of CFRP laminates. J. Phys. Conf. Ser. 2014, 524, 012038. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, Y.; Liu, Y.; Li, W.; Liu, K.; Han, W.; Zhang, Z. A novel rapid fabrication method and in-situ densification mechanism for ceramic matrix composite. Compos. Part B Eng. 2025, 288, 111881. [Google Scholar] [CrossRef]
- Bensadoun, F.; Verpoest, I.; Van Vuure, A.W. Interlaminar fracture toughness of flax-epoxy composites. J. Reinf. Plast. Compos. 2017, 36, 121–136. [Google Scholar] [CrossRef]
- Yang, X.; Chen, Y.; Zhang, C.; Duan, G.; Jiang, S. Electrospun carbon nanofibers and their reinforced composites: Preparation, modification, applications, and perspectives. Compos. Part B Eng. 2023, 249, 110386. [Google Scholar] [CrossRef]
- Beckermann, G.W. Nanofiber interleaving veils for improving the performance of composite laminates. Reinf. Plast. 2017, 61, 289–293. [Google Scholar] [CrossRef]
- Zhang, H.; Kuwata, M.; Bilotti, E.; Peijs, T. Integrated damage sensing in fibre-reinforced composites with extremely low carbon nanotube loadings. J. Nanomater. 2015, 2015, 785834. [Google Scholar] [CrossRef]
- Zuo, P.; Srinivasan, D.V.; Vassilopoulos, A.P. Review of hybrid composites fatigue. Compos. Struct. 2021, 274, 114358. [Google Scholar] [CrossRef]
- Abd Rased, M.; Yoon, S. Experimental study on effects of asymmetrical stacking sequence on carbon fiber/epoxy filament wound specimens in DCB, ENF, and MMB tests. Compos. Struct. 2021, 264, 113749. [Google Scholar] [CrossRef]
- Wang, L.; Su, H.; Zhou, K. A phase-field model for mixed-mode cohesive fracture in fiber-reinforced composites. Comput. Methods Appl. Mech. Eng. 2024, 421, 116753. [Google Scholar] [CrossRef]
- Benazzo, F.; Rigamonti, D.; Bettini, P.; Sala, G.; Grande, A. Interlaminar fracture of structural fibre/epoxy composites integrating damage sensing and healing. Compos. Part B Eng. 2022, 244, 110137. [Google Scholar] [CrossRef]
- Umarfarooq, M.; Gouda, P.S.; Banapurmath, N.; Kittur, M.; Khan, T.; Parveez, B.; Sebaey, T.A.; Badruddin, I.A. Post-curing and fiber hybridization effects on mode-II interlaminar fracture toughness of glass/carbon/epoxy composites. Polym. Compos. 2023, 44, 4734–4745. [Google Scholar] [CrossRef]
- Lamichhane, P.; Dhakal, D.; Jayalath, I.N.; Baxter, L.; Chaudhari, S.; Vaidyanathan, R. Polyaniline and graphene nanocomposites for enhancing the interlaminar fracture toughness and thermo-mechanical properties of carbon fiber/epoxy composites. arXiv 2022, arXiv:2207.09500. [Google Scholar]
- Süsler, S.; Kazancı, Z. Investigation of Delamination Characteristics in 3D-Printed Hybrid Curved Composite Beams. Polymers 2024, 16, 2250. [Google Scholar] [CrossRef] [PubMed]
- Kawai, M.; Koizumi, M. Nonlinear constant fatigue life diagrams for carbon/epoxy laminates at room temperature. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2342–2353. [Google Scholar] [CrossRef]
- Au-Yeung, K.; Quintanas-Corominas, A.; Martínez-Pañeda, E.; Tan, W. Hygroscopic phase field fracture modelling of composite materials. Eng. Comput. 2023, 39, 3847–3864. [Google Scholar] [CrossRef]
- Marulli, M.; Valverde-González, A.; Quintanas-Corominas, A.; Paggi, M.; Reinoso, J. A combined phase-field and cohesive zone model approach for crack propagation in layered structures made of nonlinear rubber-like materials. Comput. Methods Appl. Mech. Eng. 2022, 395, 115007. [Google Scholar] [CrossRef]
- Dawood, L.L.; AlAmeen, E.S. Influence of infill patterns and densities on the fatigue performance and fracture behavior of 3D-printed carbon fiber-reinforced PLA composites. AIMS Mater. Sci. 2024, 11, 833–857. [Google Scholar] [CrossRef]
- Santos, P.; Silva, A.P.; Reis, P.N. The effect of carbon nanofibers on the mechanical performance of epoxy-based composites: A review. Polymers 2024, 16, 2152. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, J.; Hua, Y.; Tertuliano, O.A.; Raney, J.R. Improving structural damage tolerance and fracture energy via bamboo-inspired void patterns. Bioinspir. Biomim. 2024, 19, 056005. [Google Scholar] [CrossRef]
- Kostopoulos, V.; Sarantinos, N.; Tsantzalis, S. Review of through-the-thickness reinforced z-pinned composites. J. Compos. Sci. 2020, 4, 31. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, X.; Jiang, S.; Ren, Y. Hybrid effects and interactive failure mechanisms of hybrid fiber composites under flexural loading: Carbon/Kevlar, carbon/glass, carbon/glass/Kevlar. Aerosp. Sci. Technol. 2023, 133, 108105. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, G.; Lai, J.; Yu, T.; Zhang, X. Interlaminar toughening and self-healing mechanism for hard-and-soft layered composite laminates. Compos. Part A Appl. Sci. Manuf. 2025, 189, 108623. [Google Scholar] [CrossRef]
- Karaman, A.; Yeşil, H. Determination of tensile strength perpendicular to the fibers of wooden materials reinforced with basalt, glass fiber-reinforced polymer, and plaster mesh. BioResources 2025, 20, 42. [Google Scholar] [CrossRef]
- Furtado, C.; Kopp, R.; Ni, X.; Sarrado, C.; Kalfon-Cohen, E.; Wardle, B.L.; Camanho, P.P. J-integral experimental reduction reveals fracture toughness improvements in thin-ply carbon fiber laminates with aligned carbon nanotube interlaminar reinforcement. ACS Appl. Mater. Interfaces 2024, 16, 20980–20989. [Google Scholar] [CrossRef]
- Kartsonakis, I.A.; Kontiza, A.; Kanellopoulou, I.A. Advanced Micro/Nanocapsules for Self-Healing Coatings. Appl. Sci. 2024, 14, 8396. [Google Scholar] [CrossRef]
- Rahman, R.; Haque, A. Molecular modeling of crosslinked graphene–epoxy nanocomposites for characterization of elastic constants and interfacial properties. Compos. Part B Eng. 2013, 54, 353–364. [Google Scholar] [CrossRef]
- Nguyen, H.K.; Shundo, A.; Ito, M.; Pittenger, B.; Yamamoto, S.; Tanaka, K.; Nakajima, K. Insights into mechanical dynamics of nanoscale interfaces in epoxy composites using nanorheology atomic force microscopy. ACS Appl. Mater. Interfaces 2023, 15, 38029–38038. [Google Scholar] [CrossRef]
- Wang, W.; Takao, Y.; Matsubara, T.; Kim, H. Improvement of the interlaminar fracture toughness of composite laminates by whisker reinforced interlamination. Compos. Sci. Technol. 2002, 62, 767–774. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Q.; Xie, H.; Li, Q.; Sun, G. Digital image correlation (DIC) based damage detection for CFRP laminates by using machine learning based image semantic segmentation. Int. J. Mech. Sci. 2022, 230, 107529. [Google Scholar] [CrossRef]
- Zhu, G.; Zhang, Y.; Niu, X.; Duan, C.; Wang, Z.; Zhao, X. Novel multiscale modeling strategy for hybrid fiber-reinforced composites. Int. J. Mech. Sci. 2025, 287, 109997. [Google Scholar] [CrossRef]
- Amorim, L.; Santos, A.; Nunes, J.; Viana, J. Bioinspired approaches for toughening of fibre reinforced polymer composites. Mater. Des. 2021, 199, 109336. [Google Scholar] [CrossRef]

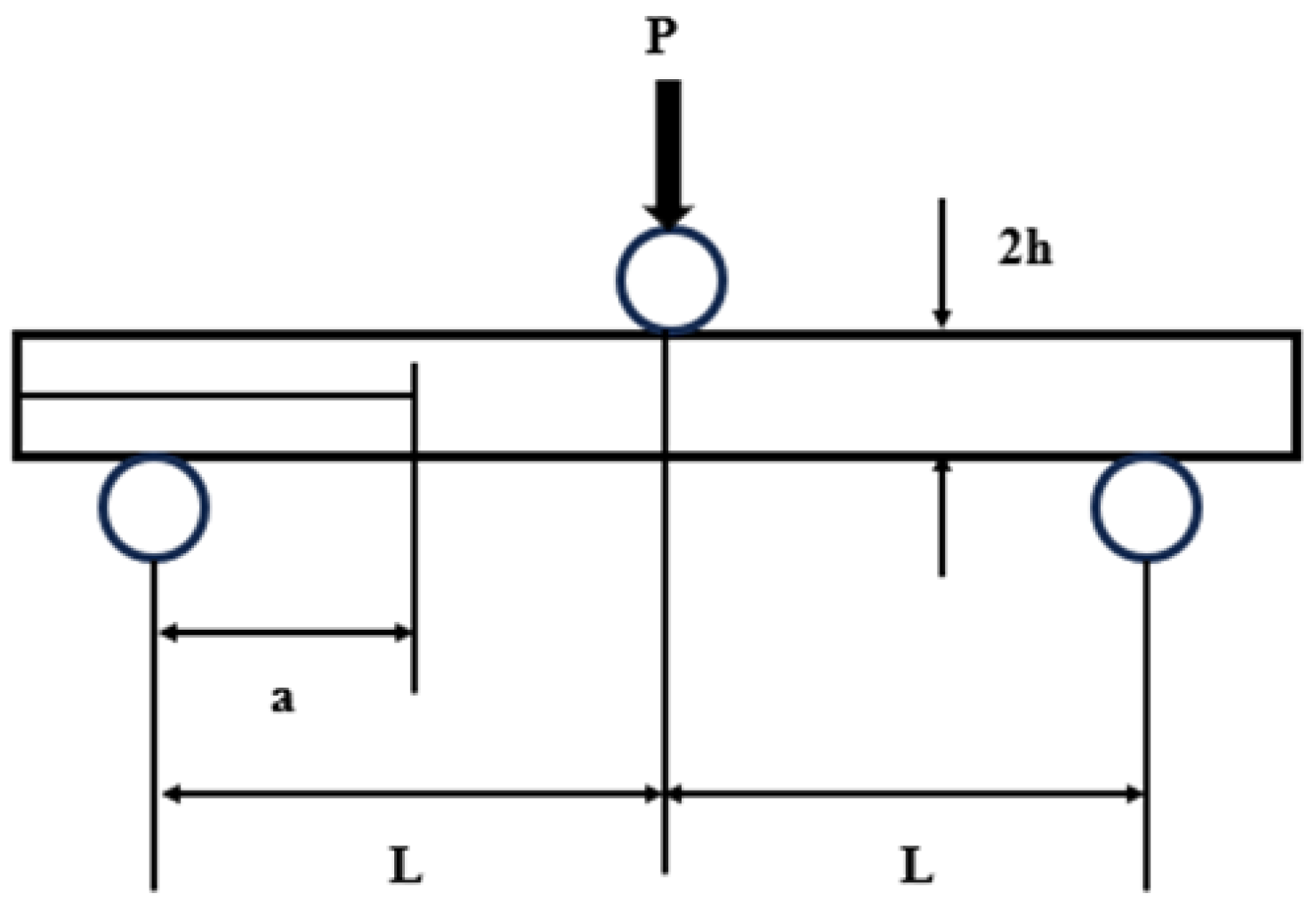
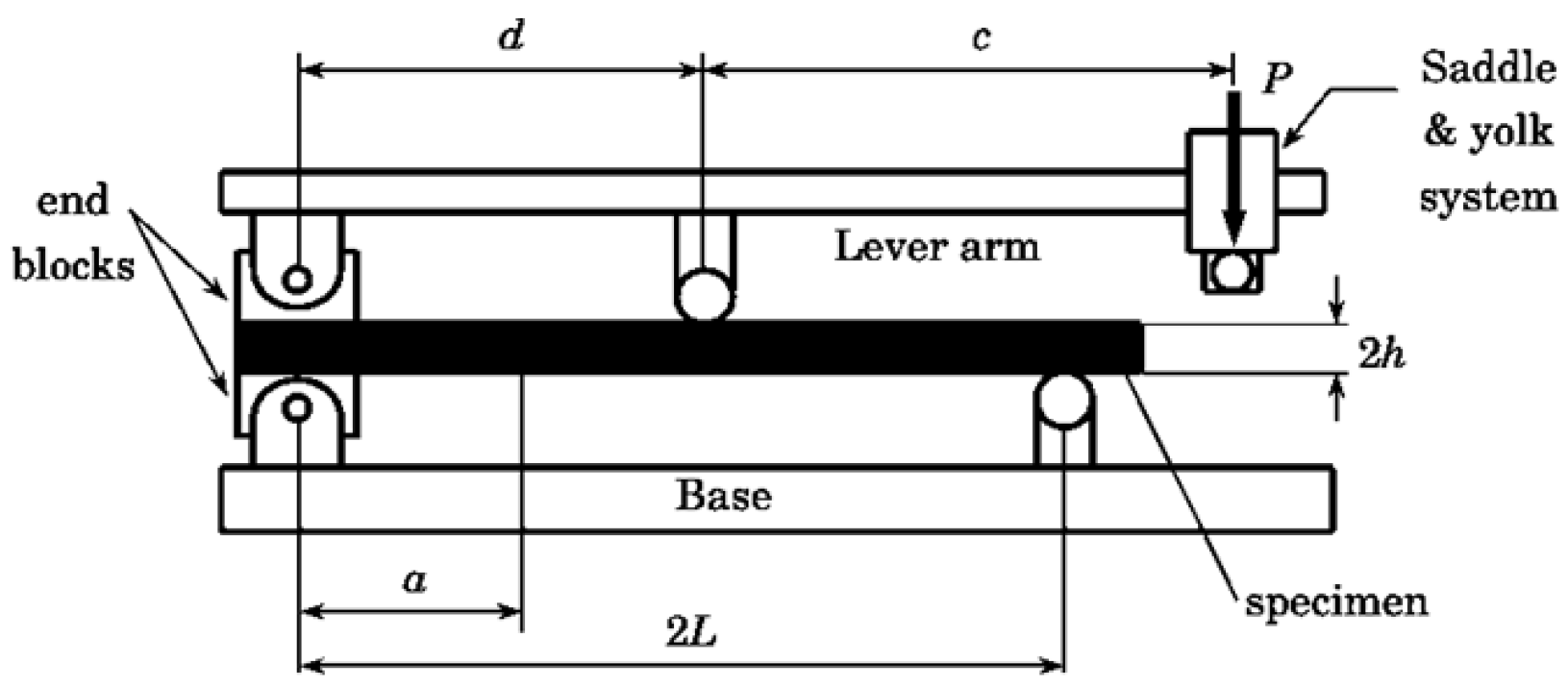
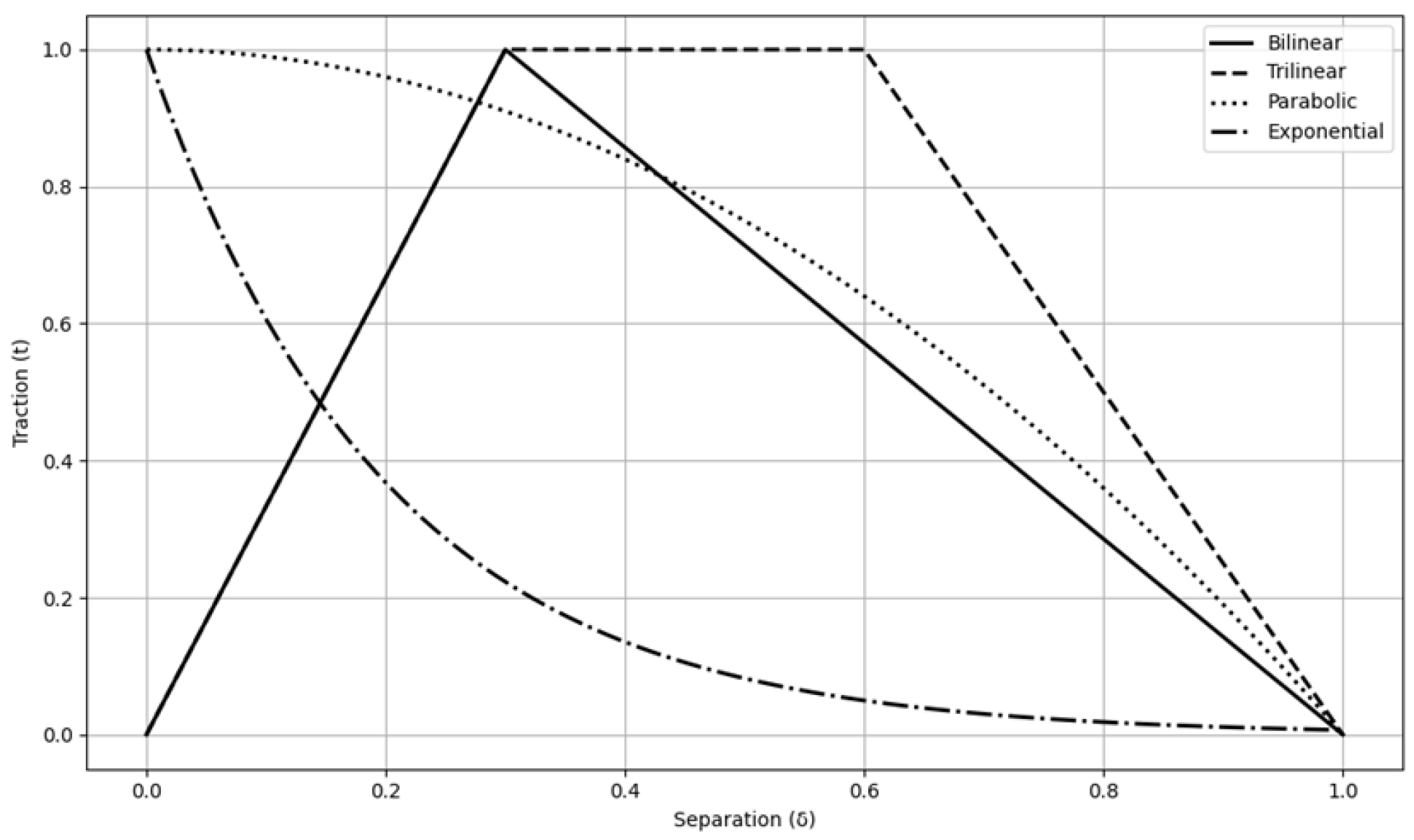
| Test Method | Standard | Mode(s) | Strengths | Limitations | Original Motivation |
|---|---|---|---|---|---|
| Double Cantilever Beam (DCB) | ASTM D5528 | Mode I | • Simple fixture • Direct crack length measurement • Extensive historical data for benchmarking | • Sensitive to fiber bridging, root rotation, and mode contamination • From initiation to propagation, the curve can differ significantly | Quantify Mode I interlaminar toughness for unidirectional laminates |
| End-Notched Flexure (ENF) | ASTM D7905 | Mode II | • Isolates shear-dominated delamination • Compliance calibration improves repeatability | • Pure Mode II difficult to maintain • Sensitive to fixture alignment and frictional effects | Address shear-driven delamination not captured by Mode I tests |
| Calibrated End-Loaded Split (C-ELS) | ISO 15114 | Mode II | • Stable crack growth • Enables R curve measurement for propagation toughness | • Requires high-resolution crack tracking • Sensitive to load symmetry | Provide Mode II propagation data and improve shear fracture characterization |
| Mixed-Mode Bending (MMB) | ASTM D6671 | Mixed-Mode I/II | • Adjustable mode mixity • Supports cohesive zone model calibration • Unified fixture for wide range | • Complex calibration • Extreme mode ratios can induce secondary effects • Limited to unidirectional laminates | Simulate realistic service load mixes in a controlled, standardized manner |
| Edge Crack Torsion (ECT) | ASTM D7078 | Mode III | • Near-pure Mode III loading • Stable crack propagation • Applicable to various laminate architectures | • Requires specialized torsional fixture • Geometry-sensitive | Provide torsional fracture data for design and certification |
| Split Cantilever Beam (SCB) | NA | Mode III (mixed) | • Simple specimen suitable for symmetric/asymmetric layups | • Mode II contamination • Contact stresses may cause crack path deviation | Explore low-cost alternatives for Mode III testing |
| Asymmetric Double Cantilever Beam (ADCB) | NA | Mode I/III | • Modifiable to tune Mode I/III interaction | • Requires numerical decomposition • Risk of unstable crack growth | Study interaction between opening and tearing modes in research settings |
| Standard | Title | Scope |
|---|---|---|
| ASTM E1820 [90] | Standard test method for measurement of fracture toughness | Determination of curves, , and crack growth in metals and ductile materials. |
| ISO 12135 [91] | Metallic materials—unified method for the determination of quasi-static fracture toughness | Provides international guidance similar to ASTM E1820. |
| ASTM E561 [92] | Standard test Method for curve determination | Primarily used for linear elastic R curves for brittle materials. |
| Mode | Traction | Strain Energy Release Rate |
|---|---|---|
| I | ||
| II |
| Sl. No. | Technique | Material Specimen and Loading | Finding | Ref. |
|---|---|---|---|---|
| 1 | Cohesive Zone Modeling (CZM) | Carbon Epoxy skin-doubler, 3-point bending | Superposes two bilinear TSLs to reproduce fiber-bridging R curves with a peak-load error ≈ 15%. | [132] |
| 2 | CZM (temperature-dependent) | Glass/Elium DCB and ENF, 24–80 °C | Inverse FE–DIC fit delivers six TSL sets predicting SBS strength within test scatter. | [133] |
| 3 | VCCT—fatigue | UD CFRP DCB/ENF, mixed-mode fatigue | 3D VCCT routine – times faster than direct-cyclic FE; Paris law accuracy retained. | [134] |
| 4 | VCCT—validation | IM7/epoxy DCB | VCCT predicts COD and peak load to within 5% of experiment over 2–6 mm opening. | [135] |
| 5 | XFEM + CZM (fatigue) | CFRP DCB/ENF and OHT, cyclic | XFEM for matrix cracks + cohesive delamination; cycle-jump strategy cuts CPU time > 90%. | [136] |
| 6 | XFEM—high-cycle | Quasi-isotropic open-hole laminate | Adaptive cycle-jump XFEM reproduces -cycle life and damage sequence. | [137] |
| 7 | J-Integral (non-linear energy) | Thin-ply CFRP DCB and ENF | Rotation-angle J-method shows +34% (Mode I) and +62% (Mode II) toughness vs. baseline, no crack length measurement needed. | [138] |
| 8 | Phase-Field Fracture (hygro-mechanical) | Carbon/epoxy laminate with moisture diffusion | Couples Fickian transport, hygroscopic strain and PF; predicts 30% toughness loss at 2% moisture. | [139] |
| 9 | Phase Field—fatigue | E-glass/epoxy under cyclic tension | Cycle-dependent degradation term reproduces S–N curve and crack branching sans remeshing. | [140] |
| 10 | High-speed stereo DIC | Tapered laminate, dynamic tension | 10 kfps DIC captures crack-tip velocity and branching; feeds dynamic CZM calibration. | [141] |
| 11 | Full-field IDIC (material ID) | Hole-plate CFRP, quasi-static | Single tension test + integrated DIC identify full orthotropic stiffness tensor. | [142] |
| 12 | DIC-driven CZM (Mode II) | Layered bi-material ENF | Energy balance algorithm fits bilinear CZM () with <5% error. | [143] |
| Sl. No. | Study Focus | Test Used | Fracture Toughness | Key Findings and Model Accuracy | Ref. |
|---|---|---|---|---|---|
| 1 | CNT-enhanced carbon fiber laminate | DCB (Mode I) | = 440 J/m2 | CNTs improved toughness by 30%. Predicted curve matched within 6%. | [144] |
| 2 | Recycled Kevlar–carbon fillers in glass/epoxy | MMB | Gmix up by 73% | Tougher interface when Mode II increases. R2 = 0.95 for curve fit. | [145] |
| 3 | Impact delamination | DCB (high-speed impact) | Up to 1.8 kJ/m2 | Toughness increases with speed. <5% error in dynamic model. | [146] |
| 4 | Acid-aged glass laminate | ENF (Mode II) | Drop from 690 to 480 J/m2 | 8 weeks in acid weakened the material. Experimental method highly repeatable. | [147] |
| 5 | High-temperature effect on CFRP | ENF (Mode II) | 2264 to 1602 J/m2 from RT to 130°C | Toughness drops as temperature increases. <4% error in CZM simulation. | [148] |
| 6 | Z-pin-reinforced CFRP | ENF | +65% with reference to standard | Z-pins slowed crack growth. Model predicted length within 8%. | [149] |
| 7 | Short aramid fibers | ENF | +69% with reference to standard | Toughening with short fibers. R2 = 0.93 with model. | [150] |
| 8 | SWCNT in glass/epoxy | DCB | nearly doubled with reference to standard | CNTs bridged crack. CZM error <10%. | [151] |
| 9 | Ceramic matrix composite | Wedge DCB | = 450 J/m2 | Wedge test showed small deviation. Error ±3% in calculated G. | [152] |
| 10 | Flax/epoxy natural-fiber laminate | DCB, ENF, MMB | = 574 J/m2, = 612 J/m2 | First full natural-fiber delamination dataset. Experimental only. | [153] |
| 11 | Plasma-treated nanofibers | ENF | +91% with reference to control mix | Surface-treated nanofibers improved bonding. High repeatability (SD < 2%). | [154] |
| 12 | Nano-veil in CFRP | DCB | +40% with reference to control | Improved energy absorption. R curve from data matched model. | [155] |
| 13 | CNT + CF-based sensors | DCB | +60% with reference to control | Real-time crack monitoring worked. Model matched within 7%. | [156] |
| 14 | Hybrid veil in GFRP | DCB | +17% with reference to control | Tougher with glass/carbon hybrid. Simple compliance method used. | [157] |
| 15 | Stacking sequence effects in MMB | MMB | Gc: 0.85 to 3.12 kJ/m2 | More Mode II = much tougher. BK model R2 = 0.97. | [158] |
| 16 | Hybrid veil in PPS/CF CFRP | DCB | +250 J/m2 in R curve | Cohesive zone improved crack control. CZM parameters extracted. | [159] |
| 17 | VCCT in fatigue | ENF | curve captured | New method was 100 times faster. SERR fit error <0.02 N/mm. | [160] |
| 18 | Post-cure epoxy hybrid | ENF | +40% | Curing at 120 °C improved bonding. <8% error in softening law. | [161] |
| 19 | Graphene nanoparticle hybrid | DCB | +79% | Graphene improved strength greatly. increased by 18% in model. | [162] |
| 20 | 3D-printed CF/nylon | 4-point bend | Delamination load +6% | Adding flat zones improved strength. XFEM predicted path (±6%). | [163] |
| 21 | Asymmetric-mode fatigue in carbon/epoxy | Mixed-mode (fatigue), Paris law fit | Threshold = 38% of Gc; growth = mm/cycle | Accurate Mode II fatigue prediction, especially in mid-life cycles. R2 > 0.98, scatter band ±15%. | [164] |
| 22 | GFRP with Kevlar–carbon fillers | DCB + ENF + MMB | Moderate toughness gains | BK model captured fracture envelope well. = 1.58, R2 = 0.95. | [145] |
| 23 | Dynamic impact DCB model | High-speed DCB, analytical vs. FE | G∝ velocity2, up to 1800 J/m2 | Analytical model matched FE predictions (<5% error). First analytical link to delamination energy. | [146] |
| 24 | Hygroscopic phase-field study | Moisture + PF (Fickian solver) | Interfacial debonding over ply cracks | ERR and crack path matched lab data within ±10%. Useful for humid conditions. | [165] |
| 25 | Multi-phase-field + CZM model | PF (ply) + CZM (interface) | Predicts delamination migration | Hybrid model matched stress field, delamination path with high accuracy. | [166] |
| No. | Mechanism | Description | Fracture Mode Improved | Key Points | Ref. |
|---|---|---|---|---|---|
| 1 | Interleaving with Tough Films | Thin ductile layers inserted between plies absorb energy through plastic deformation and delay delamination. | Mode I and II | Easy to implement during layup; improves delamination resistance without major design changes. | [167] |
| 2 | Nano-Filler Reinforcement | Matrix modification with CNTs, graphene, or nano-silica bridges arrests cracks at the nano-scale. | Mode I and II | Enhances mechanical and multifunctional properties; effective even in small volumes. | [168] |
| 3 | Fiber Bridging and Pull-Out | Fibers bridge across cracks, absorbing energy through stretching and frictional pull-out. | Mode I | Naturally occurs in composites; contributes passively without extra processing. | [169] |
| 4 | Crack Deflection and Twisting | Cracks deviate along weak interfaces or ply boundaries, increasing fracture path. | Mixed-Mode | Increases energy dissipation via geometry; effective in layered/hybrid systems. | [82] |
| 5 | Z-Pinning and Stitching (ARM) | Through-thickness reinforcements provide mechanical interlocks. | Mode I and II | High delamination resistance; ideal for aerospace applications. | [170] |
| 6 | Hybrid Fiber Reinforcement | Combines stiff (carbon) and ductile (glass/aramid) fibers for synergistic energy absorption. | Mixed Mode | Toughness–strength trade-off; effective under static/dynamic loads. | [171] |
| 7 | Bio-Inspired Architectures | Mimics nacre or Bouligand structures for crack deflection, branching, and twisting. | Mode I | High toughness with lightweight design; suited for sustainable systems. | [63] |
| 8 | Interfacial Engineering | Chemical or plasma treatments tailor the fiber–matrix interface. | Mode I and II | Enhances stress transfer and crack resistance with minimal material changes. | [8] |
| 9 | 3D Woven/Braided Composites | Through-thickness yarns improve interlaminar bonding and damage resistance. | Mode II and Mixed | High impact resistance; suitable for thick composites. | [172] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhargavi, C.; Sreekeshava, K.S.; Raghu Prasad, B.K. Evolution of Studies on Fracture Behavior of Composite Laminates: A Scoping Review. Appl. Mech. 2025, 6, 63. https://doi.org/10.3390/applmech6030063
Bhargavi C, Sreekeshava KS, Raghu Prasad BK. Evolution of Studies on Fracture Behavior of Composite Laminates: A Scoping Review. Applied Mechanics. 2025; 6(3):63. https://doi.org/10.3390/applmech6030063
Chicago/Turabian StyleBhargavi, C., K S Sreekeshava, and B K Raghu Prasad. 2025. "Evolution of Studies on Fracture Behavior of Composite Laminates: A Scoping Review" Applied Mechanics 6, no. 3: 63. https://doi.org/10.3390/applmech6030063
APA StyleBhargavi, C., Sreekeshava, K. S., & Raghu Prasad, B. K. (2025). Evolution of Studies on Fracture Behavior of Composite Laminates: A Scoping Review. Applied Mechanics, 6(3), 63. https://doi.org/10.3390/applmech6030063





