Compressive Deformation Behavior of Artificial Pumice for Reinforcement of Existing Shelter Against Ballistic Ejecta of Volcanic Eruption
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
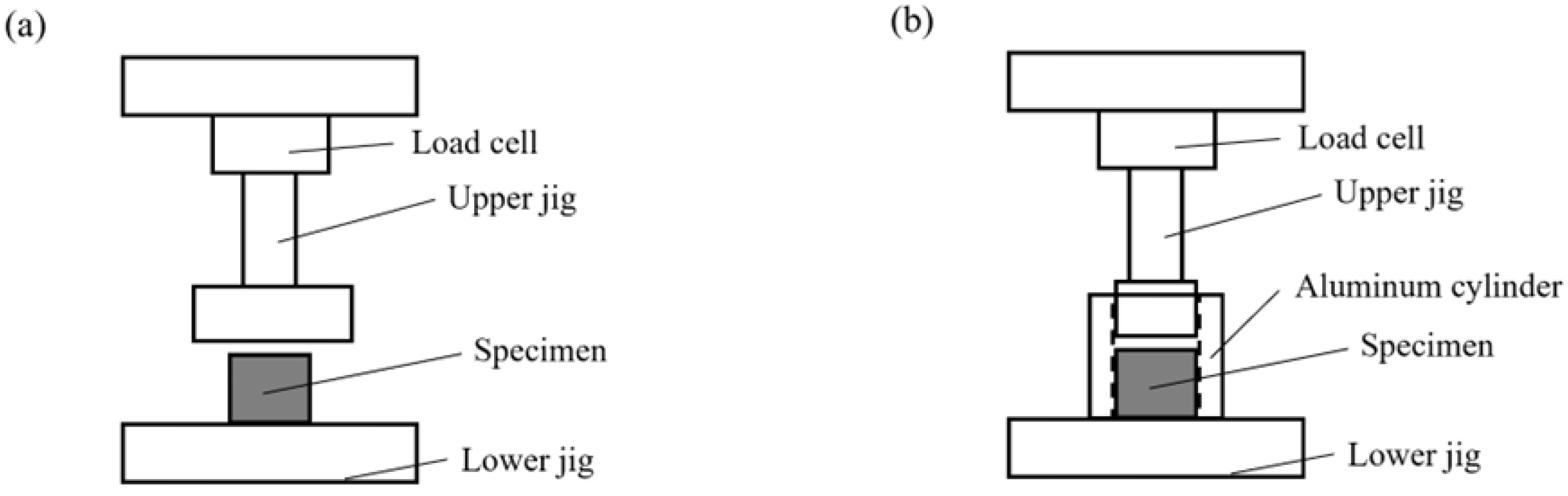
2.2. Quasi-Static Tests Under Unconfined and Oedometric Conditions
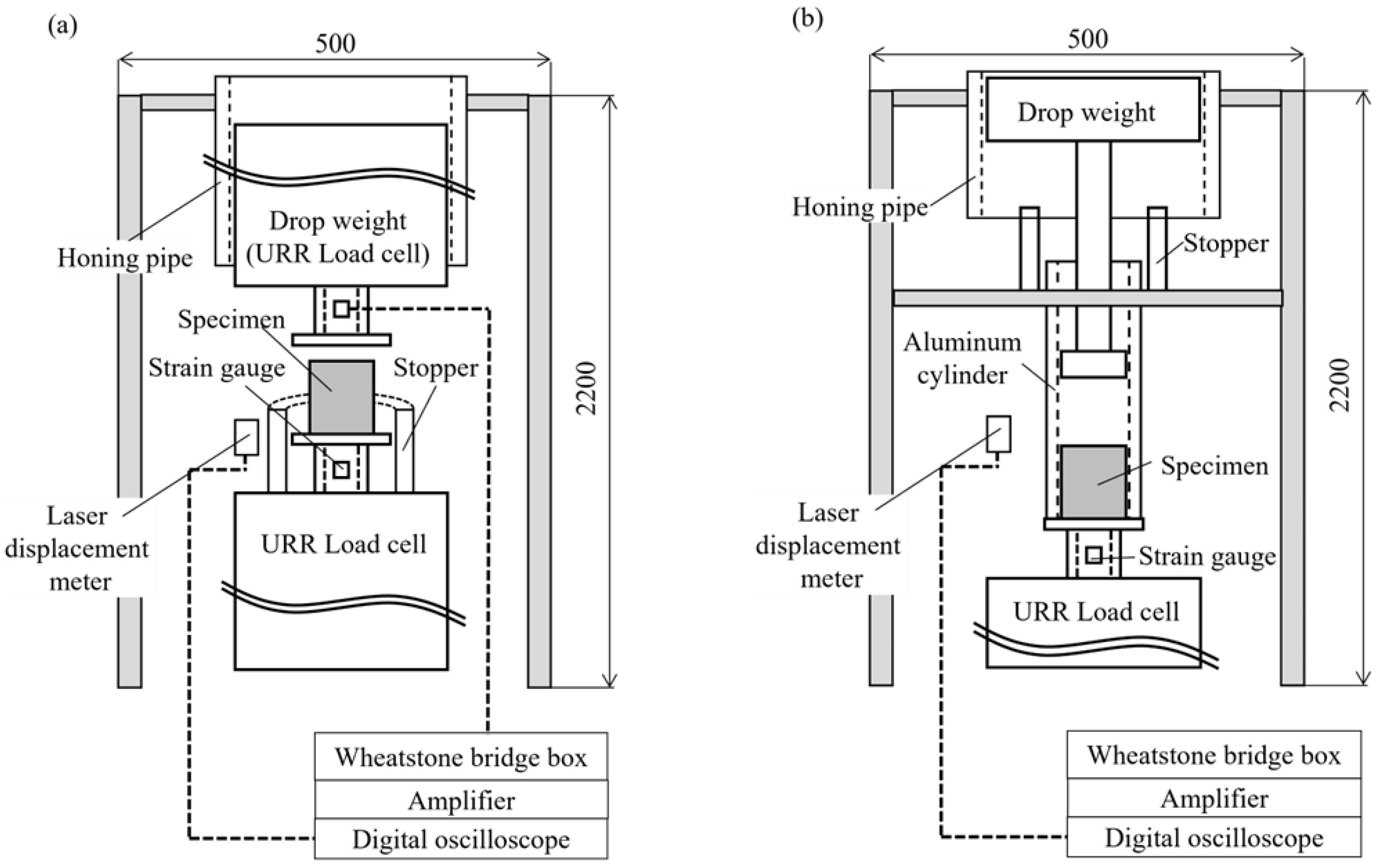
2.3. Dynamic Tests Under Unconfined and Oedometric Conditions
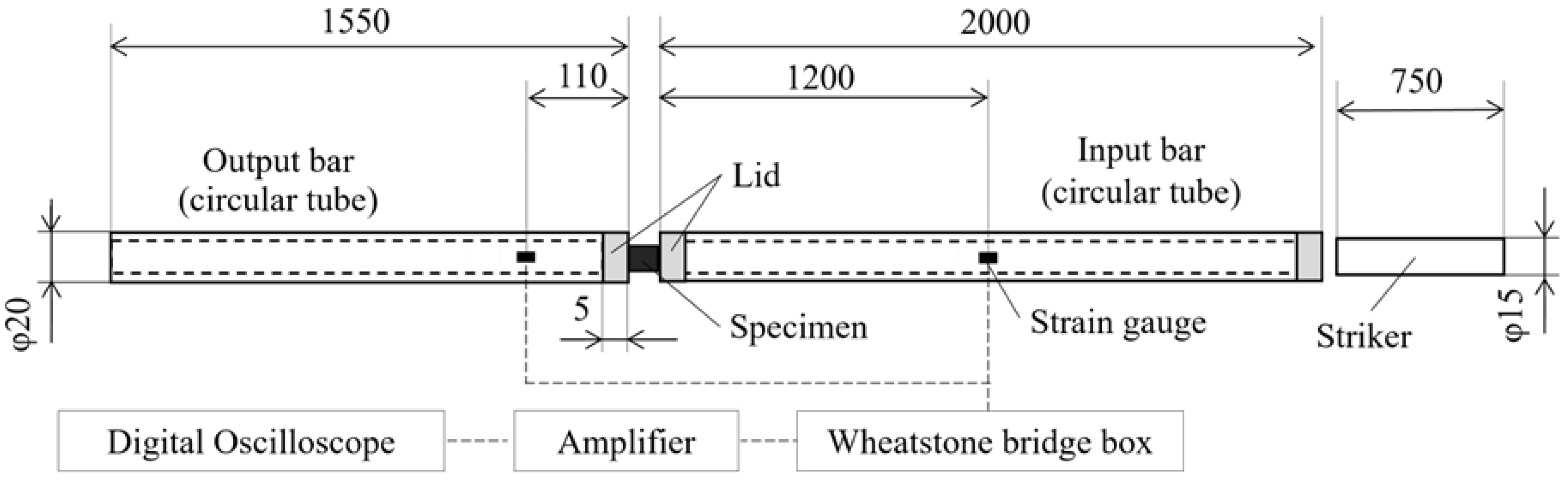
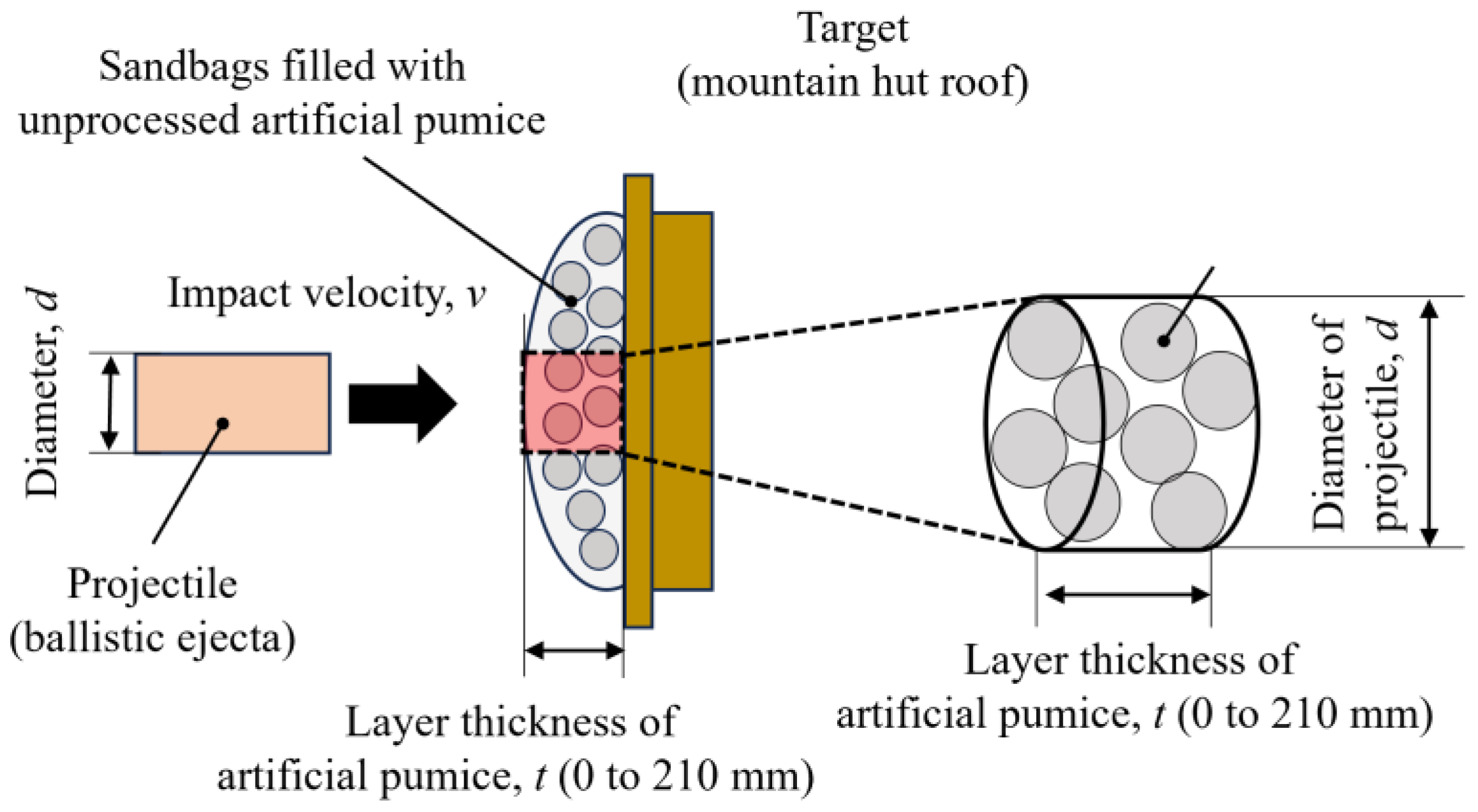
2.4. Impact Test Under Unconfined Conditions
3. Results and Discussion
3.1. Compressive Deformation Behavior of Artificial Pumice Under Unconfined Conditions
3.2. Compressive Deformation Behavior of Artificial Pumice Under Oedometric Conditions
4. Effect of Artificial Pumice Reinforcement on Penetration Resistance of Mountain Hut Roofs
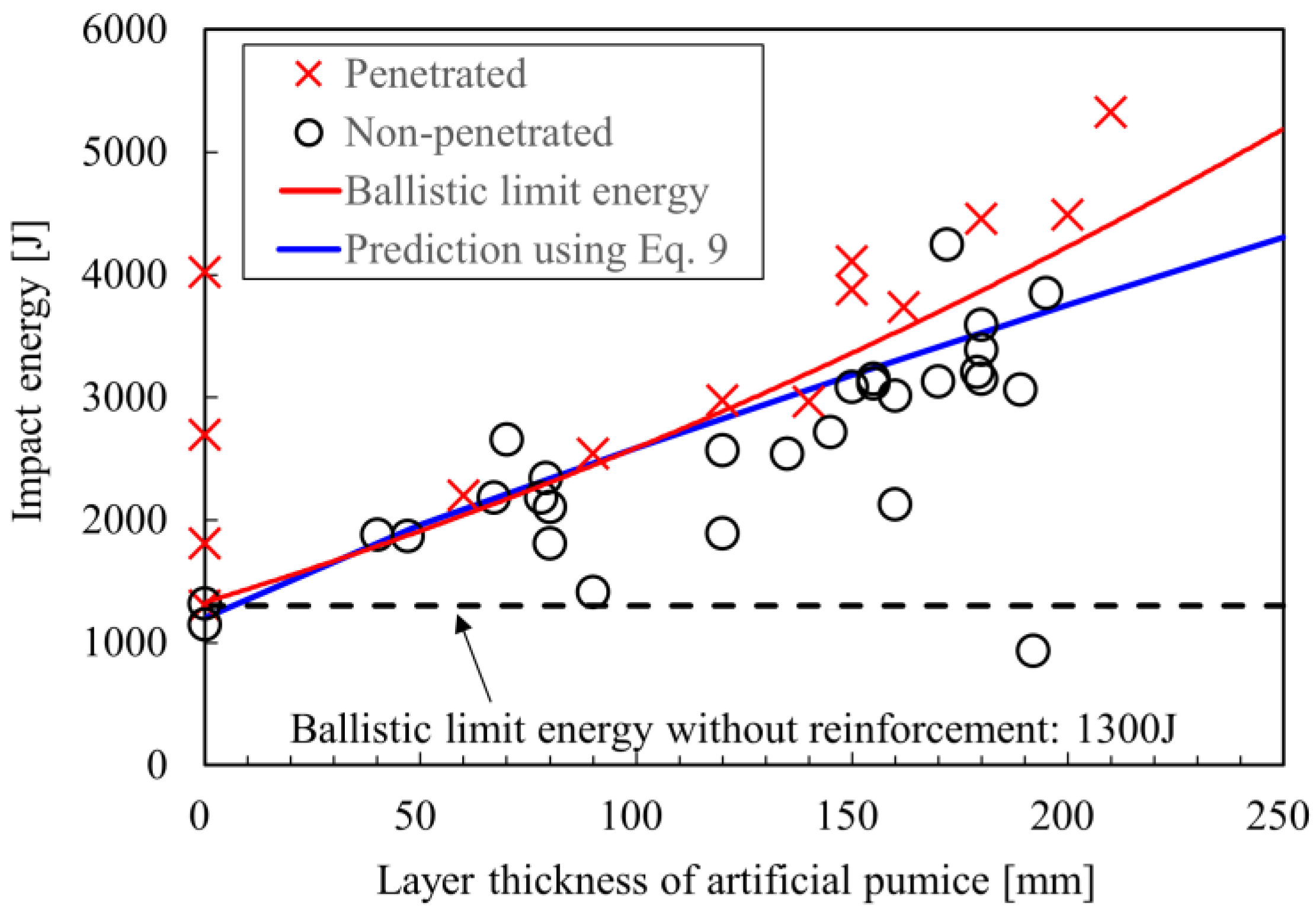
4.1. Reinforcement Effect of Artificial Pumice Obtained by Full-Scale Penetration Test
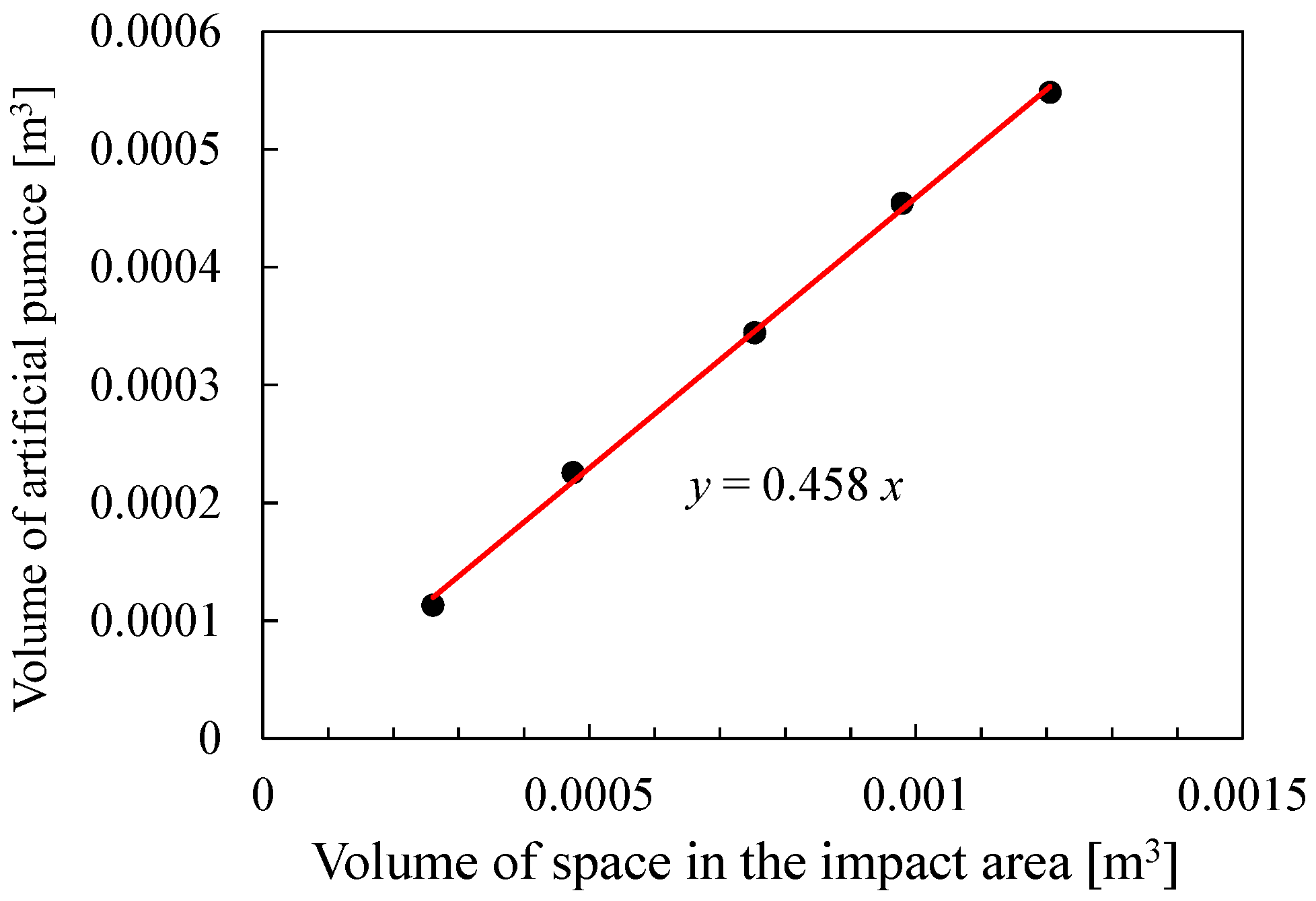
4.2. Prediction of Impact Absorption Properties of Artificial Pumice
5. Conclusions
- 1.
- In the compression tests under unconfined conditions, the specimens scattered due to fracture, allowing for evaluation only during the initial deformation stage. On the other hand, the tests under oedometric conditions enabled the observation of a three-stage deformation process—elastic, plateau, and densification—typical of cellular structures.
- 2.
- From the results of the compression tests under unconfined conditions, the initial deformation behavior of artificial pumice was classified into two types of deformation and fracture phenomena. The first type exhibited a large peak of elastic response during the initial deformation, followed by a significant decrease in stress. The second type showed no peak during the initial deformation.
- 3.
- The results of the compression tests under oedometric conditions revealed the absorbed energy of artificial pumice, which showed a positive strain rate dependence.
- 4.
- The absorbed energy predicted using the proposed method agreed well with experimental results for pumice layer thicknesses up to 150 mm. The discrepancy observed beyond 150 mm is assumed to be caused by localized deformation resulting from the absence of stress equilibrium.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SHB | Split Hopkinson bar |
References
- Oikawa, T.; Yamaoka, K.; Yoshimoto, M.; Nakada, S.; Takeshita, Y.; Maeno, F.; Ishizuka, Y.; Komori, J.; Nakano, S. The 2014 eruption of Ontake volcano, Central Japan. Bull. Volc. Soc. Jpn. 2015, 60, 411–415. (In Japanese) [Google Scholar]
- Kaneko, T.; Maeno, F.; Nakada, S. 2014 Mount Ontake eruption: Characteristics of the phreatic eruption as inferred from aerial observations. Earth Planets Space 2016, 68, 72. [Google Scholar] [CrossRef]
- Oikawa, T.; Yoshimoto, M.; Nakada, S.; Maeno, F.; Komori, J.; Shimano, T.; Takeshita, Y.; Ishizuka, Y.; Ishimine, Y. Reconstruction of the 2014 eruption sequence of Ontake volcano from recorded images and interviews. Earth Planets Space 2016, 68, 79. (In Japanese) [Google Scholar] [CrossRef]
- Erfurt-Cooper, P. Volcano and Geothermal Tourism in Kyushu, Japan. In Volcano and Geothermal Tourism; Routledge: London, UK, 2010. [Google Scholar] [CrossRef]
- Fitzgerald, R.H.; Kennedy, B.M.; Wilson, T.M.; Leonard, G.S.; Tsunematsu, K.; Keys, H. The communication and risk management of volcanic ballistic hazards. In Observing the Volcano World; Fearnley, C.J., Bird, D.K., Haynes, K., McGuire, W.J., Jolly, G., Eds.; Springer: Cham, Switzerland, 2017; pp. 121–147. [Google Scholar]
- Arreeras, S.; Arimura, M. An improvement on shelter airport selection model during large-scale volcanic disasters: A case study of Hakoneyama Japan. Asian Transp. Stud. 2022, 8, 100054. [Google Scholar] [CrossRef]
- Dolce, M.; Cardone, D.; Marnetto, R. Structural design and analysis of an impact resisting structure for volcanic shelters. Eng. Struct. 2006, 28, 1634–1649. [Google Scholar] [CrossRef]
- Dolce, M.; Cardone, D.; Moroni, C.; Nigro, D. Dynamic response of a volcanic shelter subjected to ballistic impacts. Int. J. Impact Eng. 2007, 34, 681–701. [Google Scholar] [CrossRef]
- Wilson, T.M.; Stewart, C.; Sword-Daniels, V.; Leonard, G.S.; Johnston, D.M.; Cole, J.W.; Wardman, J.; Wilson, G.; Barnard, S.T. Volcanic ash impacts on critical infrastructure. Phys. Chem. Earth 2012, 45–46, 5–23. [Google Scholar] [CrossRef]
- Yamada, H.; Tateyama, K.; Sasaki, H.; Naruke, S.; Kisimoto, H.; Yoshimoto, M. Impact resistance to ballistic ejecta of wooden buildings and a simple reinforcement method using aramid fabric. J. Volcanol. Geotherm. Res. 2018, 359, 37–46. [Google Scholar] [CrossRef]
- Yamada, H.; Tateyama, K.; Honda, R.; Yoshimoto, M.; Fujii, T. Simple structural reinforcement of roof of wooden buildings subjected to ballistic ejecta impact. Bull. Volc. Soc. Jpn. 2019, 64, 243–251. [Google Scholar]
- Liu, W.; Yu, H.; Ma, H.; Guo, J.; Mei, Q.; Wang, Y.; Zhang, J.; Wang, F. 3D mesomechanical study on the stress failure mechanism of concrete—Taking uniaxial compression as an example. Constr. Build. Mater. 2025, 467, 140381. [Google Scholar] [CrossRef]
- Ozoji, T.M.; Zhang, Z.X.; Aladejare, A.E.; Zhang, N.; Paasovaara, N.; Arrieta, M.R. Effect of strain rate on specific fracture energy and micro-fracture surface properties of rock specimen under dynamic uniaxial compression. Eng. Fract. Mech. 2024, 295, 109763. [Google Scholar] [CrossRef]
- He, Z.; Wu, G.; Zhu, J. Mechanical properties of rock under uniaxial compression tests of different control modes and loading rates. Sci. Rep. 2024, 14, 2164. [Google Scholar] [CrossRef]
- Sun, B.; Liu, S.; Zeng, S.; Wang, S.; Wang, S. Dynamic characteristics and fractal representations of crack propagation of rock with different fissures under multiple impact loadings. Sci. Rep. 2021, 11, 13071. [Google Scholar] [CrossRef]
- Parmo; Tavio; Riadi, H.; Suriani, E.; Prianto, K.; Haqi, F.I. The mechanical properties of lightweight concrete made with lightweight aggregate volcanic pumice. In Proceedings of the Built Environment, Science and Technology International Conference (BEST ICON 2018), Surabaya, Indonesia, 18–20 September 2018; SCITEPRESS: Surabaya, Indonesia, 2018; pp. 167–171. [Google Scholar]
- Sangeetha, S.P.; Divahar, R.; Mawlong, K.; Lyngkhoi, B.; Kurkalang, A. Mechanical characteristics of pumice stone as light weight aggregate in concrete. Int. J. Sci. Technol. Res. 2020, 9, 3760–3762. [Google Scholar]
- Shafiq, M.S.; Khan, F.A.; Badrashi, Y.I.; Khan, F.A.; Fahim, M.; Abbas, A.; Adil, W. Evaluation of mechanical properties of lightweight concrete with pumice aggregate. Adv. Sci. Technol. Res. J. 2021, 15, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Bakis, A. The usability of pumice powder as a binding additive in the aspect of selected mechanical parameters for concrete road pavement. Materials 2019, 12, 2743. [Google Scholar] [CrossRef]
- Forquin, P.; Francart, C.; Sapay, M.; Rack, A.; Cohen, A.; Levi-Hevroni, D.; Arrigoni, M.; Lukić, B. Analysis of microcracking processes in microconcrete under confined compression utilising synchrotron-based ultra-high speed X-ray phase contrast imaging. Int. J. Impact Eng. 2025, 198, 105167. [Google Scholar] [CrossRef]
- Tartière, J.; Arrigoni, M.; Lukic, B.; Rack, A.; Chapman, D.; Reynier, B.; Le Clanche, J.; Pradel, P.; De Resseguier, T.; Forquin, P.; et al. Experimental study and modelling of shock-induced compaction of autoclaved aerated concrete through MHz X-ray radioscopy. Int. J. Impact Eng. 2025, 204, 105376. [Google Scholar] [CrossRef]
- Saadatfar, M.; Mukherjee, M.; Madadi, M.; Schröder-Turk, G.E.; Garcia-Moreno, F.; Schaller, F.M.; Hutzler, S.; Sheppard, A.P.; Banhart, J.; Ramamurty, U. Structure and deformation correlation of closed-cell aluminium foam subject to uniaxial compression. Acta Mater. 2012, 60, 3604–3615. [Google Scholar] [CrossRef]
- Hu, Y.; Fang, Q.-Z.; Qian, J. Effect of cell structure on the uniaxial compression properties of closed-cell foam materials. Mater. Today Commun. 2021, 26, 102104. [Google Scholar] [CrossRef]
- Iqbal, S.; Kamiński, M. Review study on mechanical properties of cellular materials. Materials 2024, 17, 2682. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Zhang, X.; Zhang, J.; Lu, G.; Tse, K.M. A review on energy absorption performance of auxetic composites with fillings. Thin-Walled Struct. 2024, 205, 112348. [Google Scholar] [CrossRef]
- Nishioka, T.; Shibuya, H. Geotechnical properties of “scoria” around Mt. Fuji. J. Geotech. Geoenviron. Eng. 2014, 9, 397–415. (In Japanese) [Google Scholar]
- Tateyama, K.; Kakuno, C.; Ogasawara, N.; Yamada, H. Development of universal rate range load-cell. J. Jpn. Soc. Exp. Mech. 2017, 17, 131–138. (In Japanese) [Google Scholar]
- Kolsky, H. An investigation of the mechanical properties of materials at very high rates of loading. Proc. Phys. Soc. B 1949, 62, 676–700. [Google Scholar] [CrossRef]
- Hopkinson, B. A method of measuring the pressure in the deformation of high explosives by the impact of bullets. Philos. Trans. R. Soc. A 1914, 213, 437–452. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids, Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Cowper, G.R.; Symonds, P.S. Strain-Hardening and Strain-Rate Effects in the Impact Loading of Cantilever Beams; Division of Applied Mathematics, Brown University: Providence, RI, USA, 1957. [Google Scholar]
- Kubo, T.; Yoshimoto, M.; Honda, R.; Nishizawa, T.; Tateyama, K.; Yamada, H. Experimental study on reinforcement method of impact-resistant shelters against ballistic ejecta using artificial pumice. Bull. Volc. Soc. Jpn. 2025, 70, 3–12. (In Japanese) [Google Scholar]

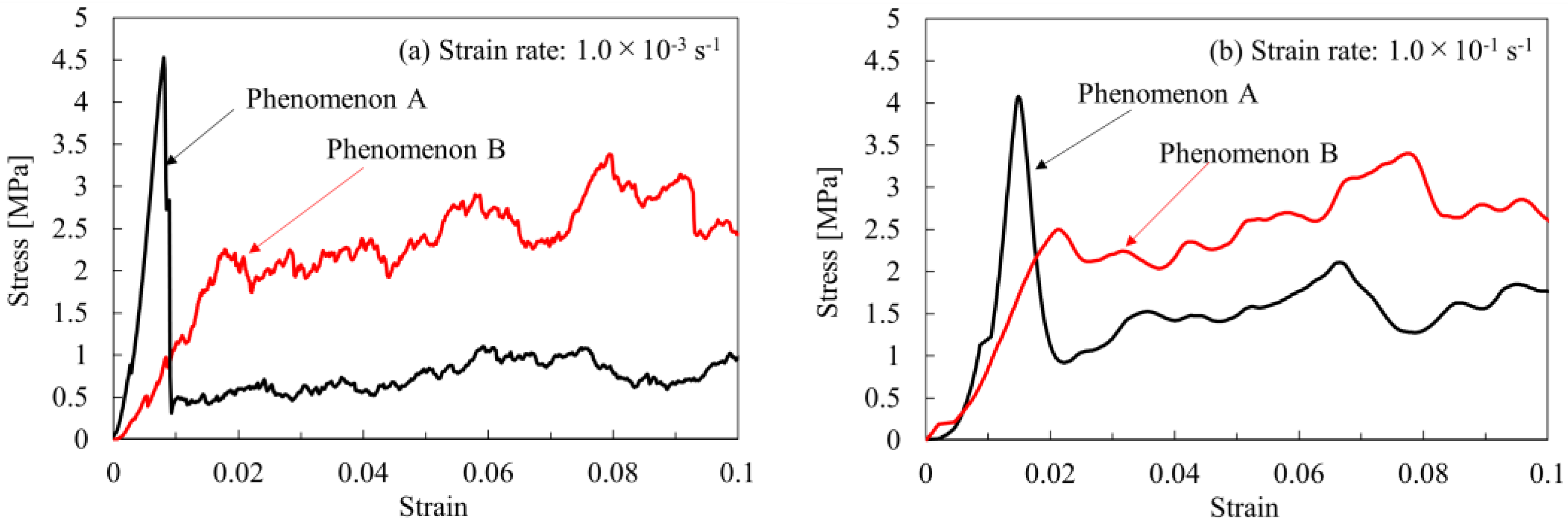

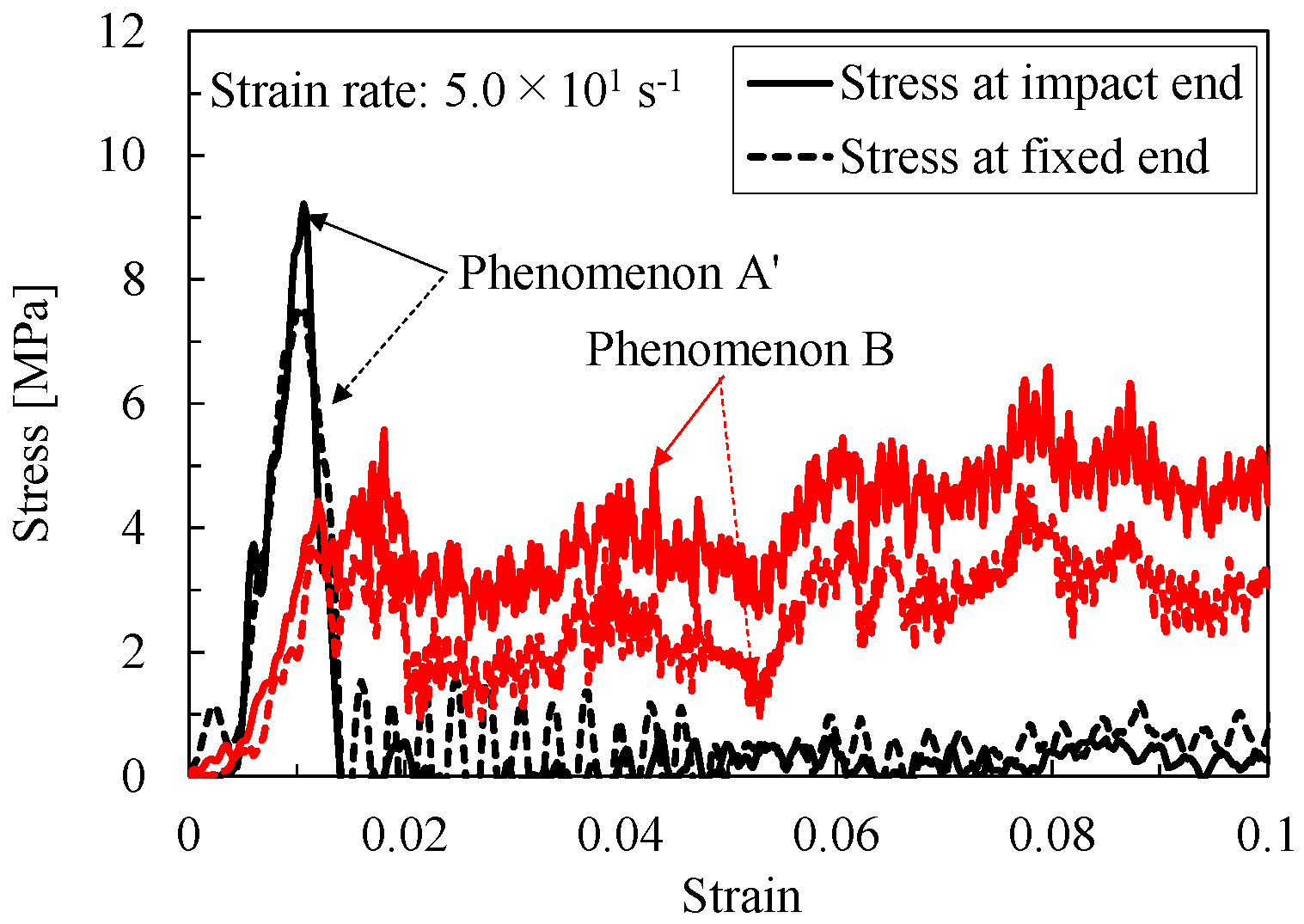

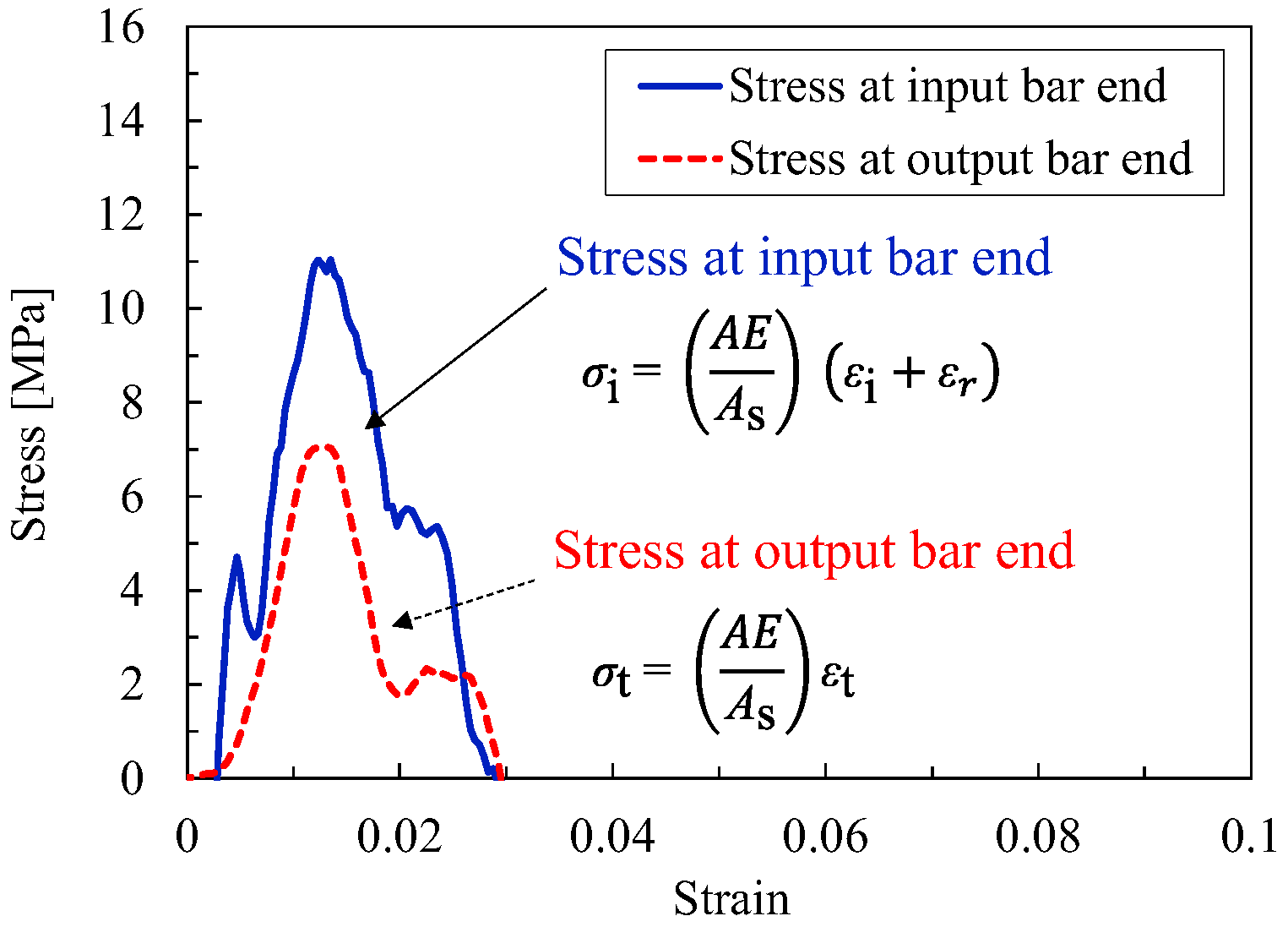
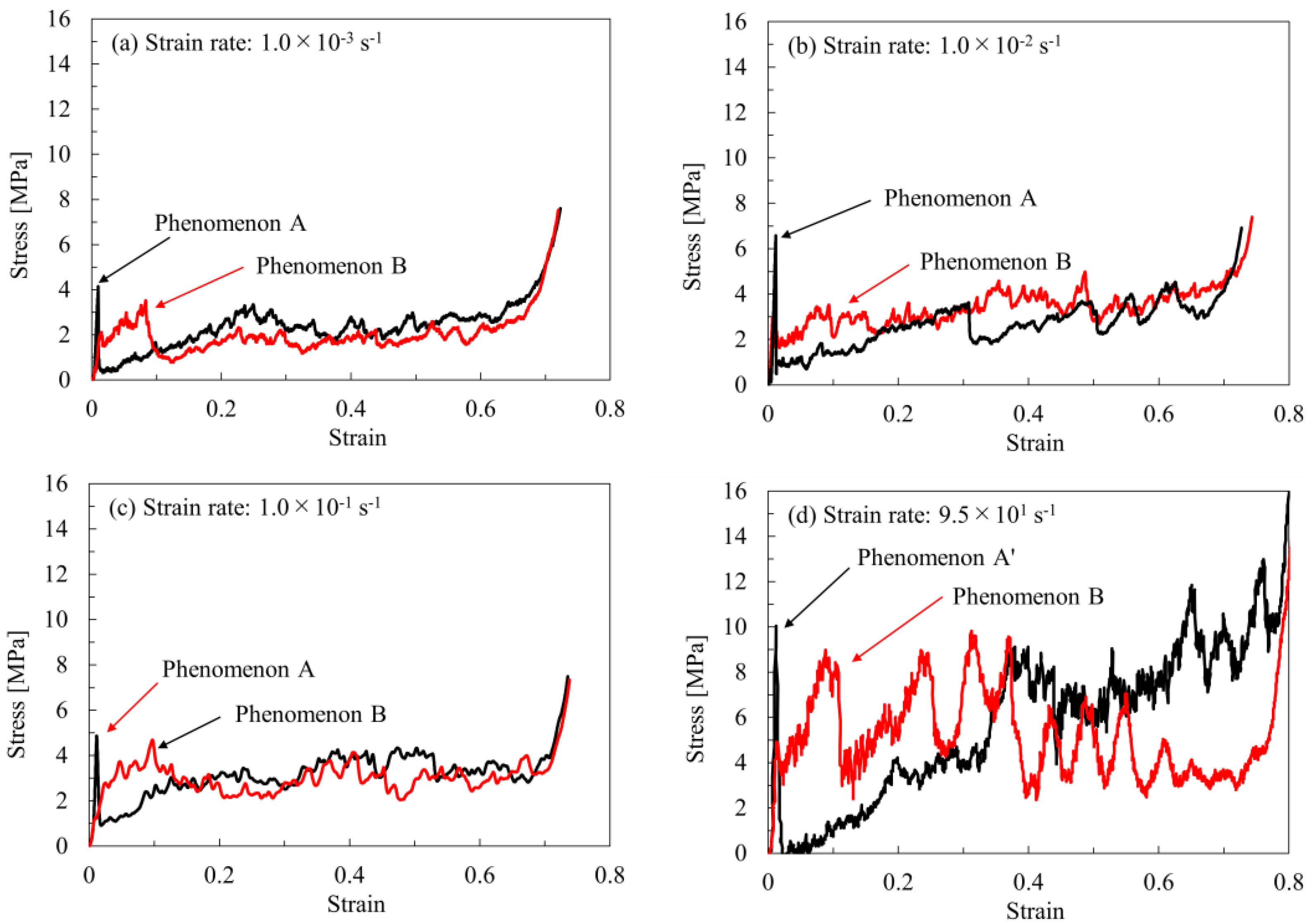
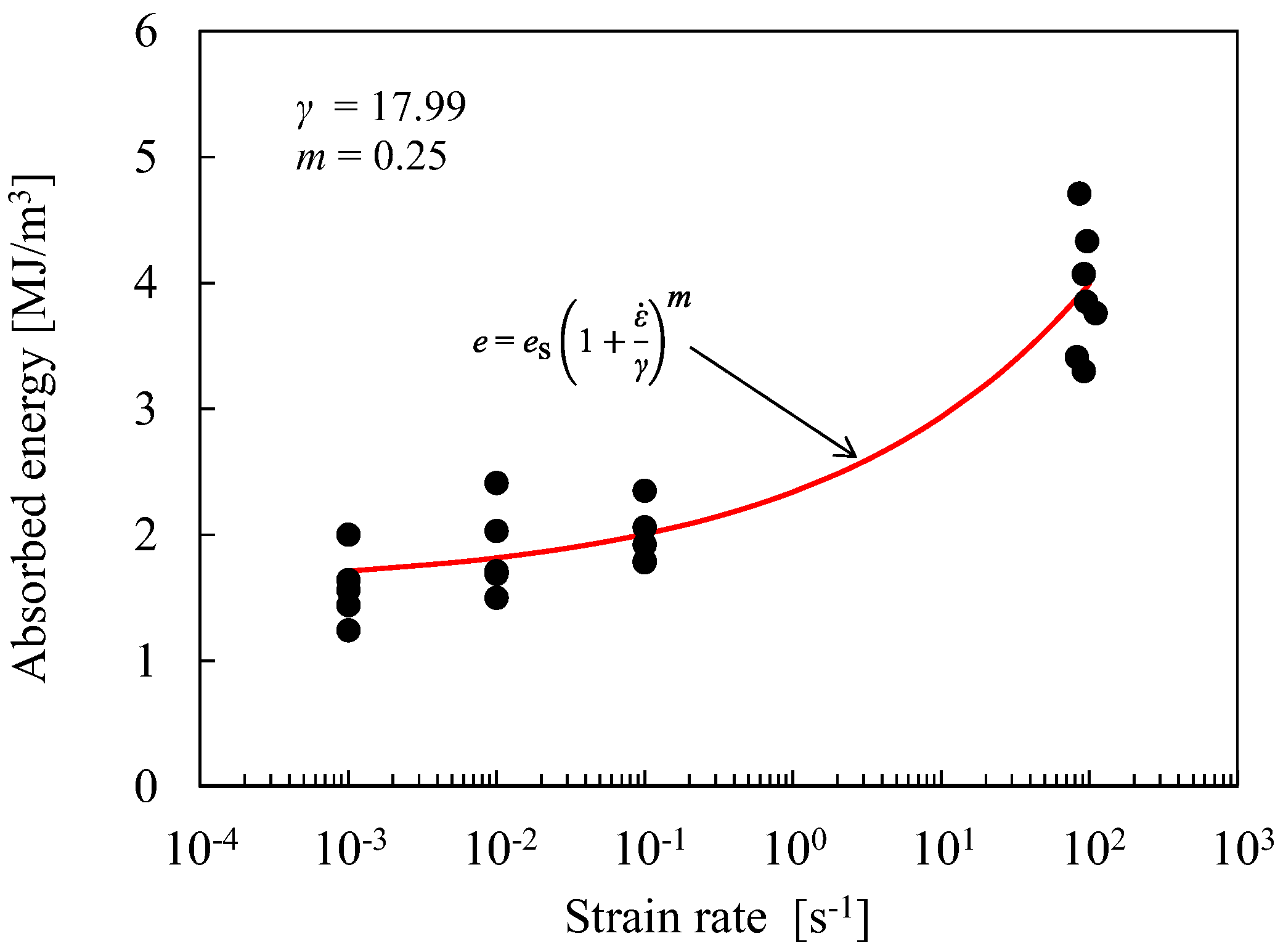
| Strain Rate [s−1] | Phenomenon | Average Absorption Energy Per Unit Volume [MJ/m3] |
|---|---|---|
| 1.0 × 10−3 | A | 1.62 |
| B | 1.47 | |
| 1.0 × 10−2 | A | 1.69 |
| B | 1.95 | |
| 1.0 × 10−1 | A | 2.06 |
| B | 1.98 | |
| 9.5 × 101 | A | 4.33 |
| B | 3.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tateyama, K.; Abe, K.; Fujiki, H.; Sasaki, H.; Yamada, H. Compressive Deformation Behavior of Artificial Pumice for Reinforcement of Existing Shelter Against Ballistic Ejecta of Volcanic Eruption. Appl. Mech. 2025, 6, 43. https://doi.org/10.3390/applmech6020043
Tateyama K, Abe K, Fujiki H, Sasaki H, Yamada H. Compressive Deformation Behavior of Artificial Pumice for Reinforcement of Existing Shelter Against Ballistic Ejecta of Volcanic Eruption. Applied Mechanics. 2025; 6(2):43. https://doi.org/10.3390/applmech6020043
Chicago/Turabian StyleTateyama, Kohei, Kazuma Abe, Hiroyuki Fujiki, Hisashi Sasaki, and Hiroyuki Yamada. 2025. "Compressive Deformation Behavior of Artificial Pumice for Reinforcement of Existing Shelter Against Ballistic Ejecta of Volcanic Eruption" Applied Mechanics 6, no. 2: 43. https://doi.org/10.3390/applmech6020043
APA StyleTateyama, K., Abe, K., Fujiki, H., Sasaki, H., & Yamada, H. (2025). Compressive Deformation Behavior of Artificial Pumice for Reinforcement of Existing Shelter Against Ballistic Ejecta of Volcanic Eruption. Applied Mechanics, 6(2), 43. https://doi.org/10.3390/applmech6020043






