A Fast Analytical Method for Elastic–Plastic Analysis of Threaded Connections
Abstract
1. Introduction
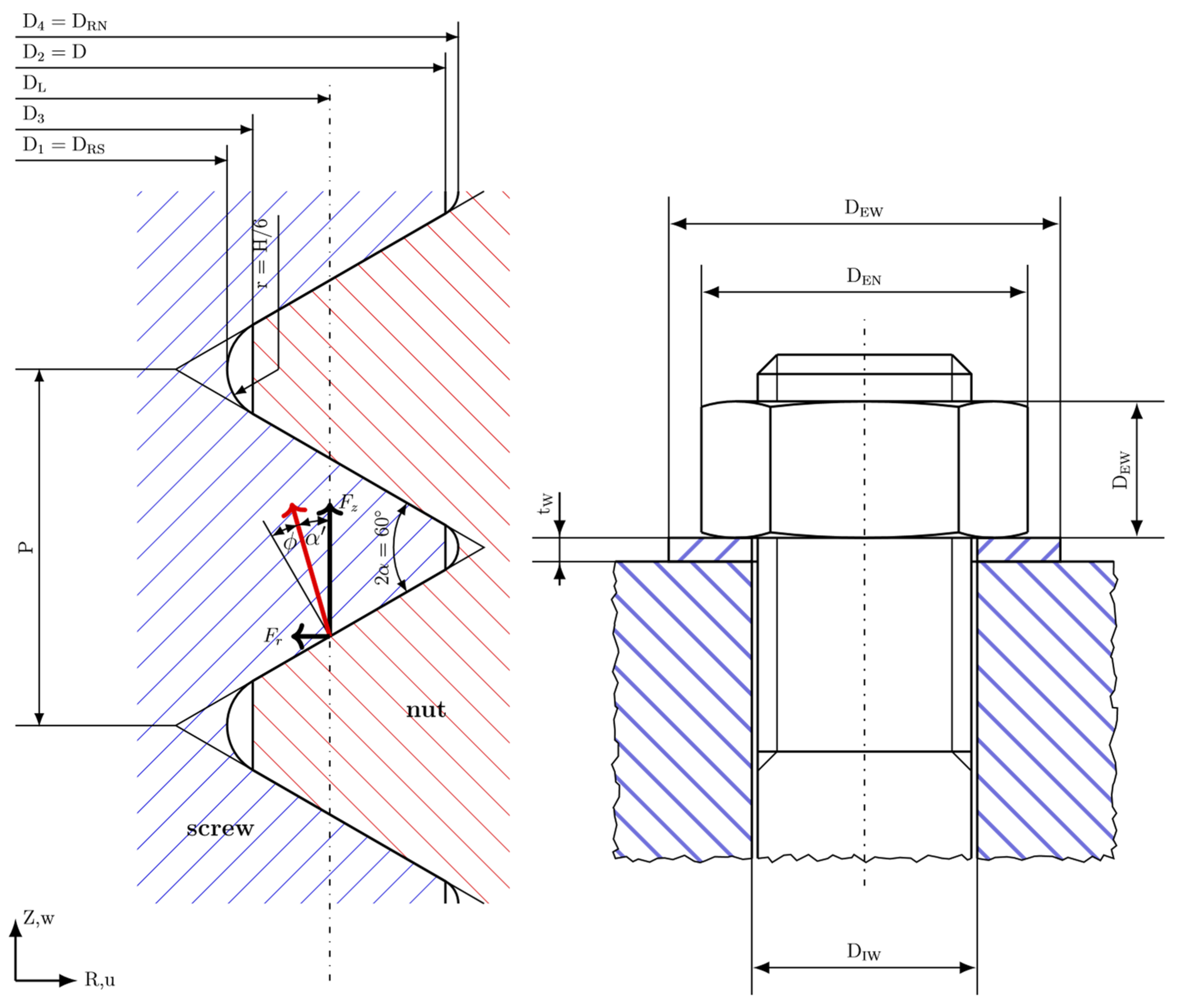
2. Theoretical Approach
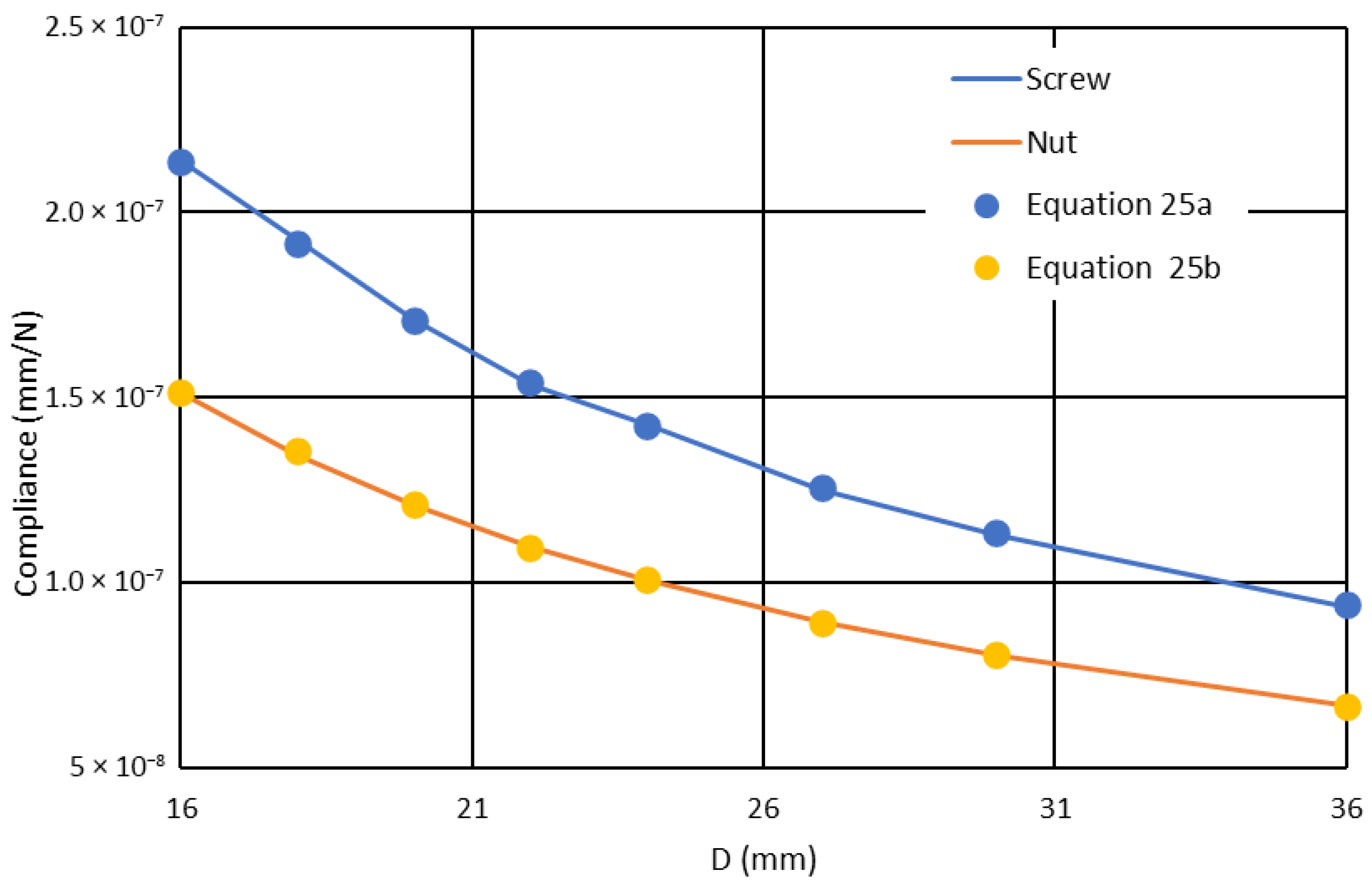
2.1. Elastic Behavior
2.2. Elastic–Plastic Behaviour
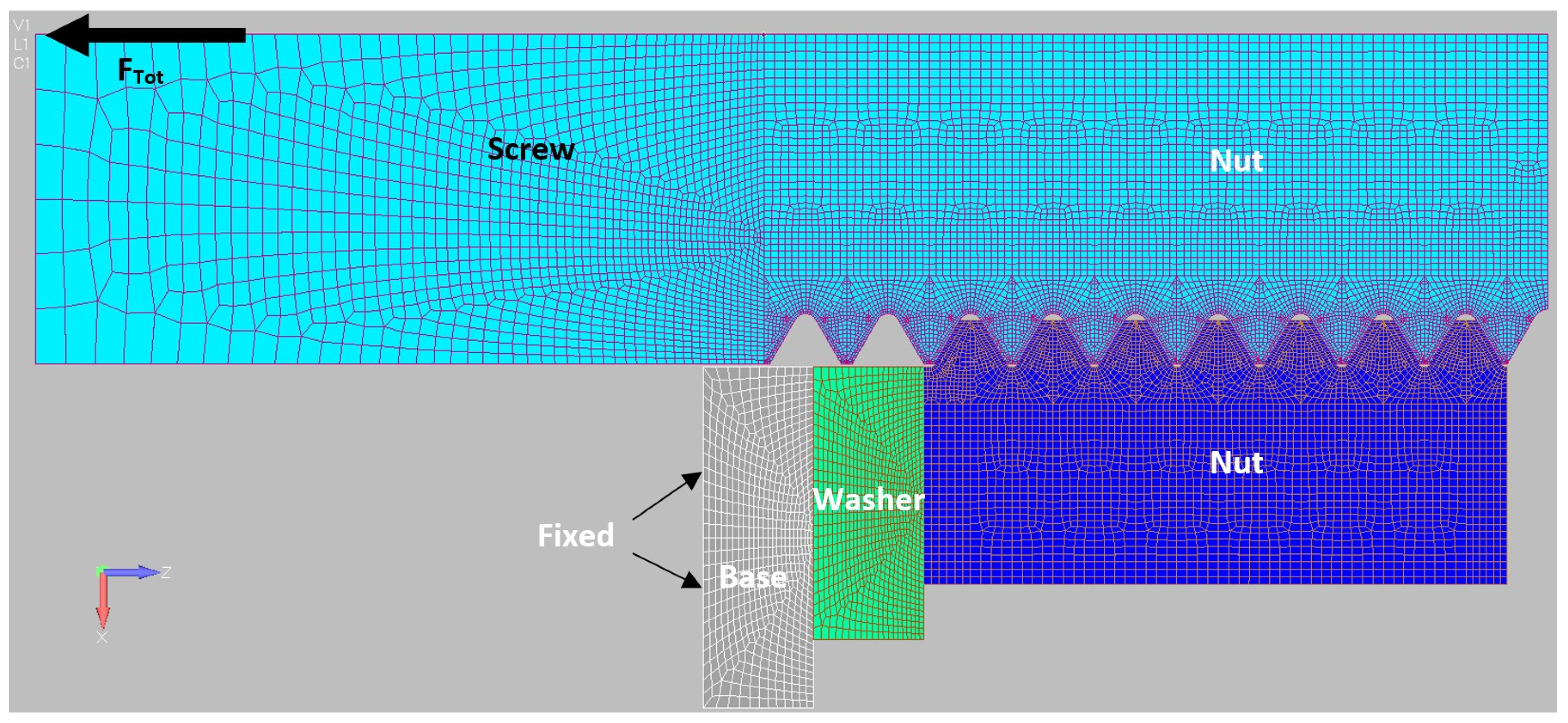
3. Numerical Models
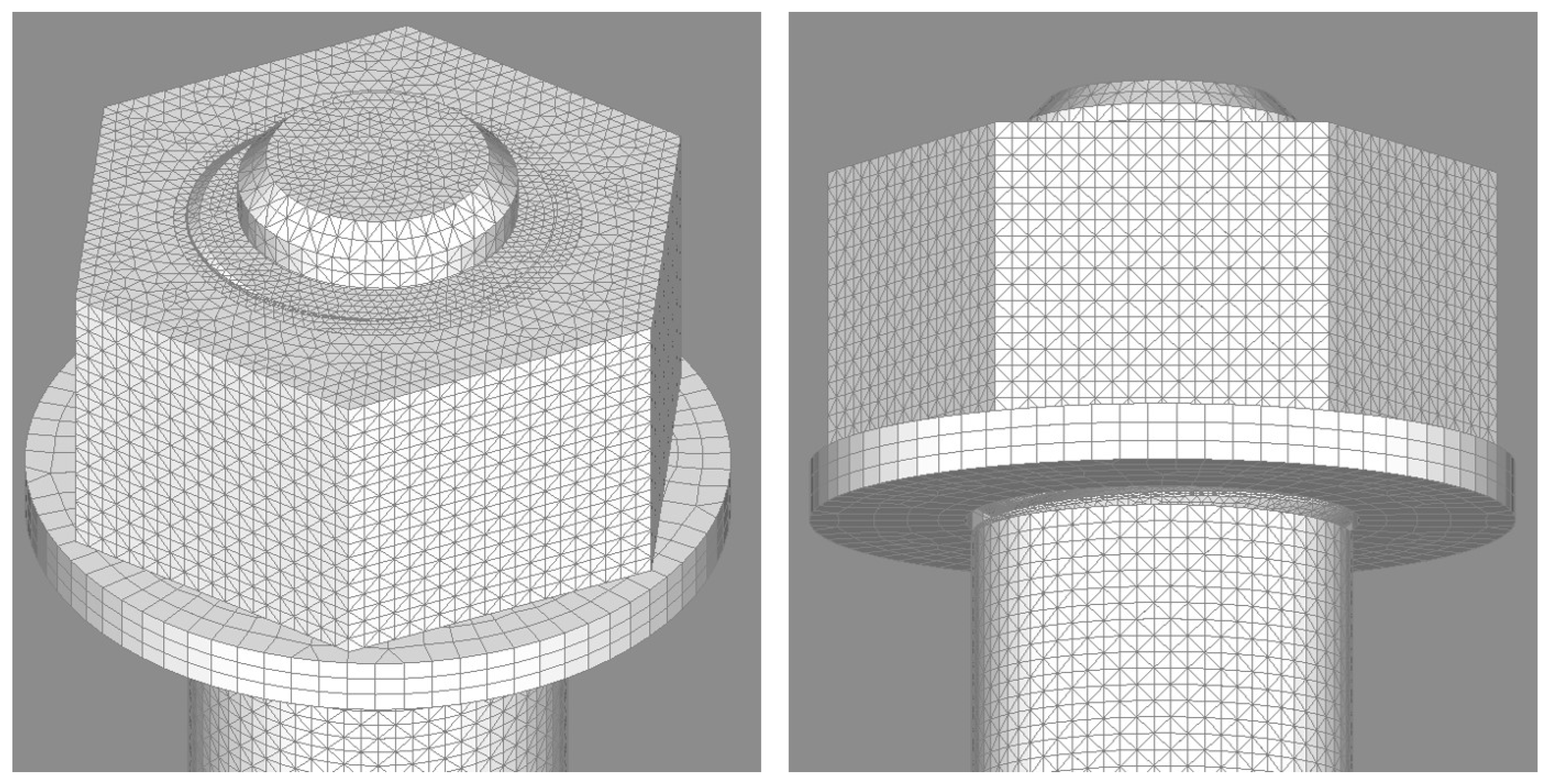
3.1. Axisymmetric FE Models
3.2. Three-Dimensional FE Models
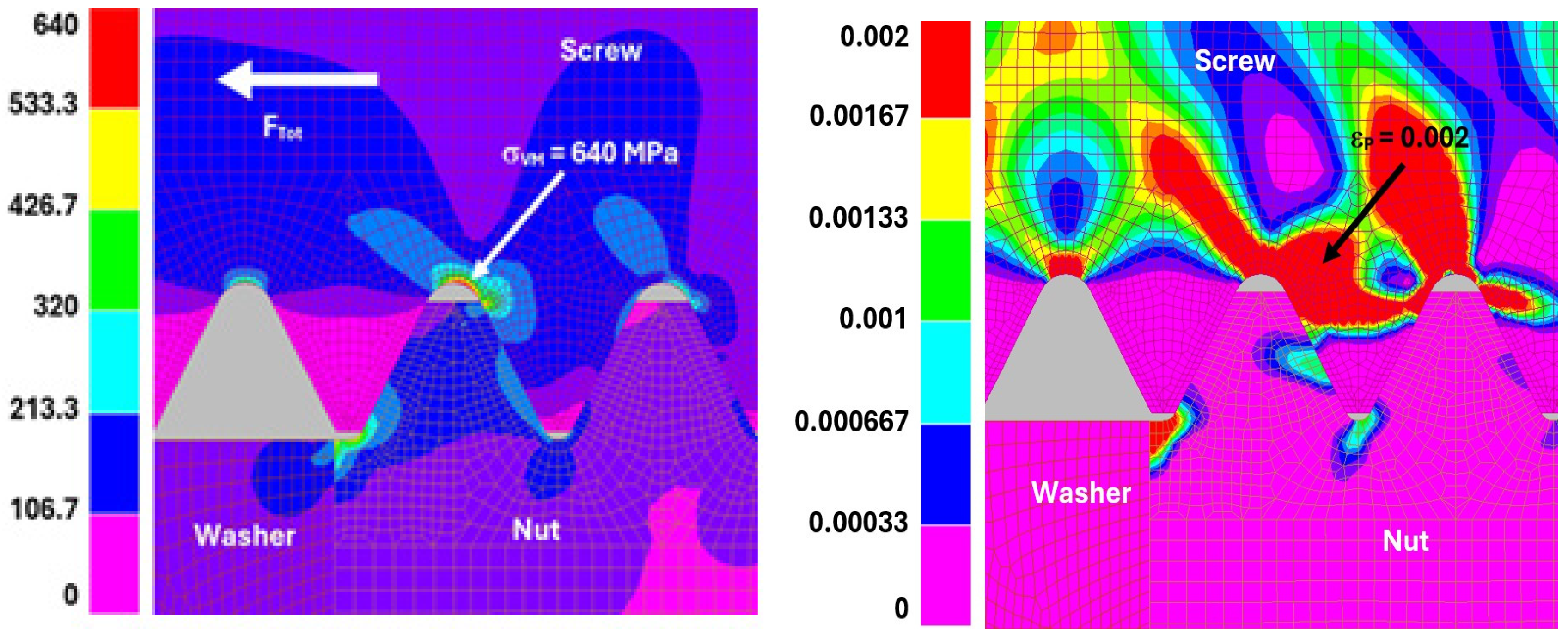
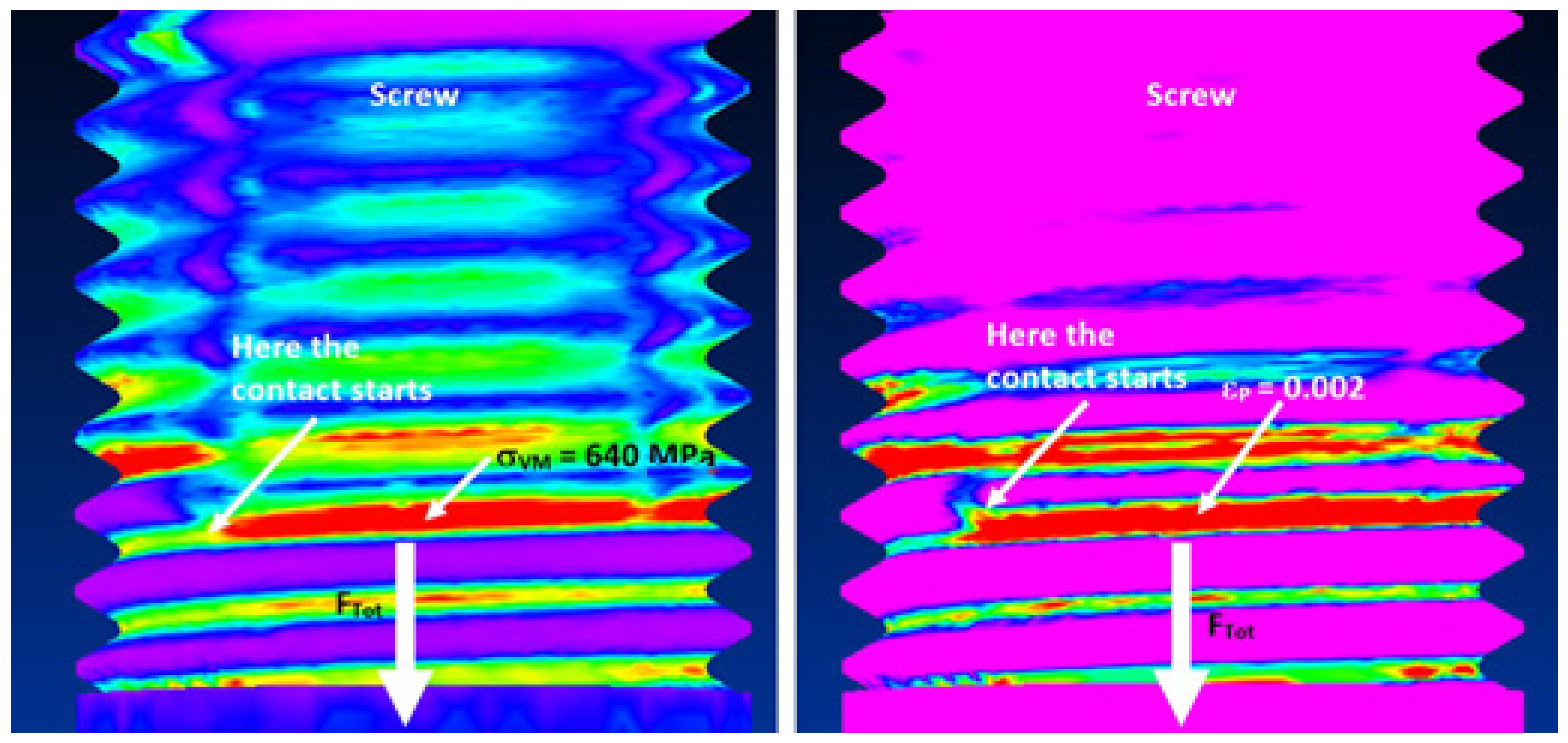
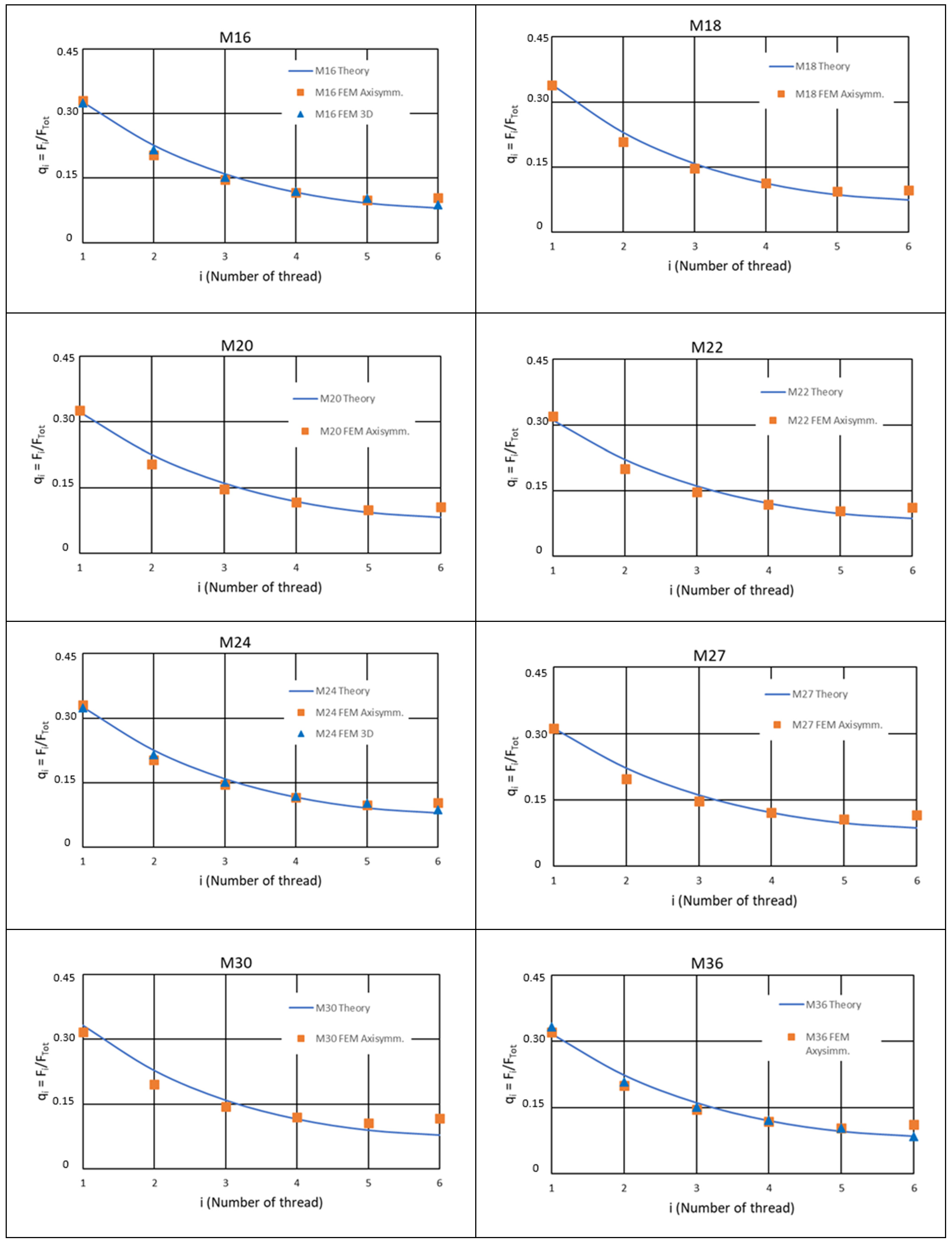
4. Results
5. Comparison with the Results Available in the Literature
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
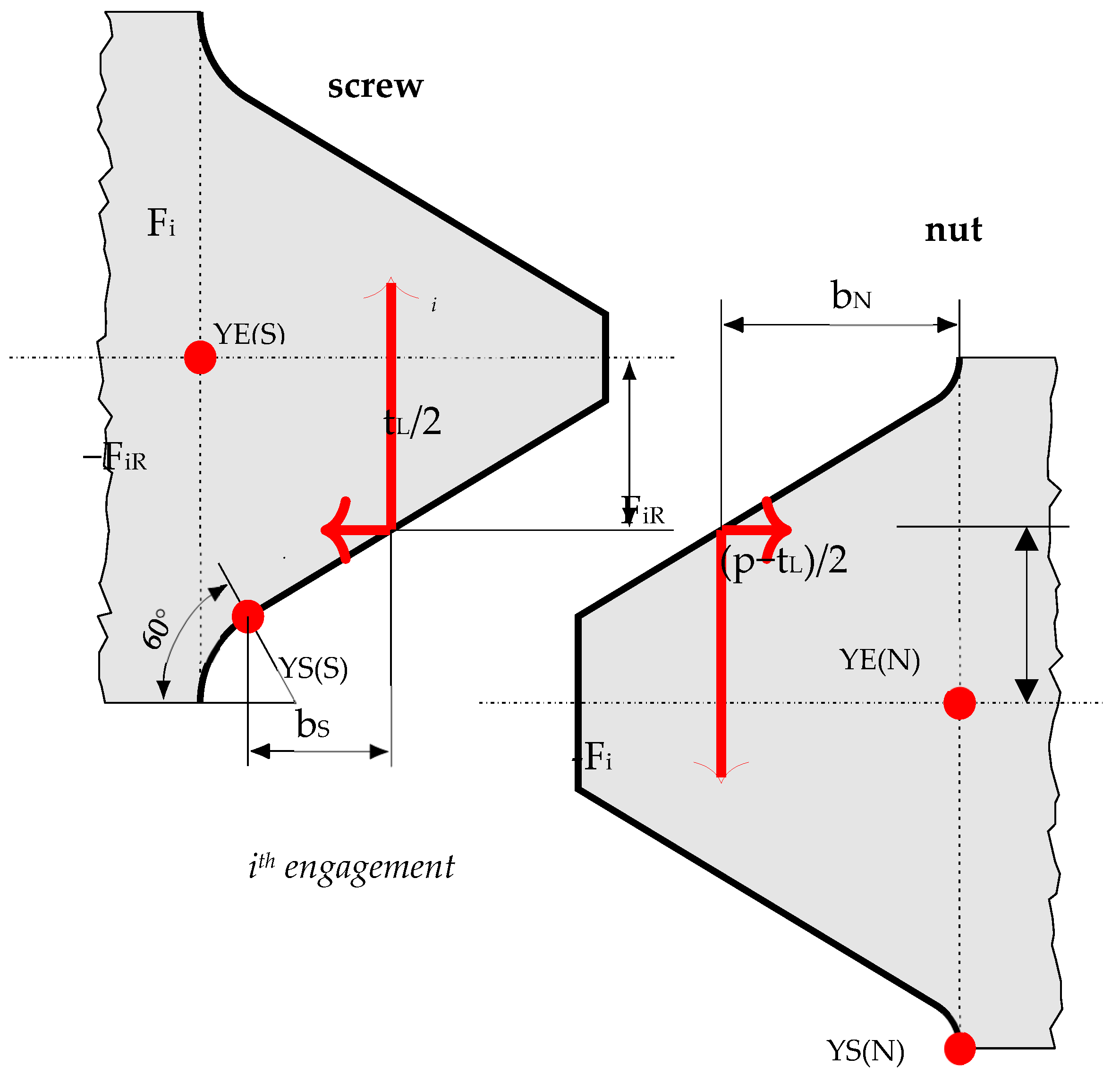
Appendix A. Stress Calculation
Appendix A.1. Point YS(S)
Appendix A.2. Point YE(S)
Appendix A.3. Point YS(N)
Appendix A.4. Point YE(N)
References
- Strizhak, V.; Penkov, I. Distribution of axial load on bolt and nut threads. In International Symposium on History of Machines and Mechanisms Proceedings HMM 2000; Springer: Dordrecht, The Netherlands, 2000; pp. 101–110. [Google Scholar]
- Mackerle, J. Finite element analysis of fastening and joining: A bibliography (1990–2002). Int. J. Press. Vessel. Pip. 2003, 80, 253–271. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Fini, S.; Khan, M.Y.; Mele, M.; Olmi, G. Optimization of bolted joints: A literature review. Metals 2023, 13, 1708. [Google Scholar] [CrossRef]
- Maduschka, L. Beanspruchung von schraubenverbindungen und zweckmäßige gestaltung der gewindeträger. Forsch. Geb. Ingenieurwesens A 1936, 7, 299–305. [Google Scholar] [CrossRef]
- Sopwith, D. The distribution of load in screw threads. Proc. Inst. Mech. Eng. 1948, 159, 373–383. [Google Scholar] [CrossRef]
- Yamamoto, A. The Theory and Computation of Threads Connection; Youkendo: Tokyo, Japan, 1980; pp. 39–54. [Google Scholar]
- Zhou, J.; Thai, H.T.; Ngo, T. Simplified finite element model for screwed connections with clip angle. Structures 2025, 74, 108479. [Google Scholar] [CrossRef]
- Zhang, D.; Gao, S.; Niu, S.; Liu, H. A prediction method for load distribution in threaded connections. J. Theor. Appl. Mech. 2018, 56, 157–168. [Google Scholar] [CrossRef]
- Hetenyi, M. A photoelastic study of bolt and nut fastenings. J. Appl. Mech. 1943, 10, A93–A100. [Google Scholar] [CrossRef]
- Kenny, B.; Patterson, E.A. The distribution of load and stress in the threads of fasteners-a review. J. Mech. Behav. Mater. 1989, 2, 87–106. [Google Scholar] [CrossRef]
- Brutti, C.; D’Eramo, M. Methods to evaluate load distribution in screw threads. In Proceedings of the 2th Canadian Conference of Applied Mechanics, Edmonton, AB, Canada, 31 May–4 June 1987; pp. 74–75. [Google Scholar]
- D’Eramo, M.; Cappa, P. An experimental validation of load distribution in screw threads. Exp. Mech. 1991, 31, 70–75. [Google Scholar] [CrossRef]
- Heywood, R. Tensile fillet stresses in loaded projections. Proc. Inst. Mech. Eng. 1948, 159, 384–398. [Google Scholar] [CrossRef]
- Patterson, E.; Kenny, B. Stress analysis of some nut-bolt connections with modifications to the external shape of the nut. J. Strain Anal. Eng. Des. 1987, 22, 187–193. [Google Scholar] [CrossRef]
- Dragoni, E. Effect of thread shape on screw stress concentration by photoelastic measurements. J. Offshore Mech. Arct. Eng. 1994, 116, 228–232. [Google Scholar] [CrossRef]
- Govindu, N.; Kumar, T.J.; Venkadesh, S. Design and optimization of screwed fasteners to reduce stress concentration factor. J. Appl. Mech. Eng. 2015, 4, 171. [Google Scholar]
- Calì, M.; Oliveri, S.M.; Biancolini, M.E. Thread couplings stress analysis by radial basis functions mesh morphing. In International Joint Conference on Mechanics, Design Engineering & Advanced Manufacturing; Springer: Cham, Switzerland, 2020; pp. 114–120. [Google Scholar]
- Fathalla, A.S.M.; Akhavan, F.A.; Moezzi, R.; Koloor, S.S.R. A numerical study of the effect of bolt thread geometry on the load distribution of continuous threads. J. Eng. Res. 2022, 10, 158–173. [Google Scholar] [CrossRef]
- Brutti, C. Load and stress distribution in screw threads with modified washers. J. Multidiscip. Eng. Sci. Technol. 2017, 4, 6523. [Google Scholar]
- Sensale, M.; Vendeuvre, T.; Schilling, C.; Grupp, T.; Rochette, M.; Dall’Ara, E. Patient-specific finite element models of posterior pedicle screw fixation: Effect of screw’s size and geometry. Front. Bioeng. Biotechnol. 2021, 9, 643154. [Google Scholar] [CrossRef]
- Cardelli, P.; Montani, M.; Gallio, M.; Biancolini, M.; Brutti, C.; Barlattani, A. Angulated abutments and perimplants stress: Fem analysis. Oral Implantol. 2009, 2, 3. [Google Scholar]
- Chen, W.; Liu, Z.; Chu, H.; Yan, X.; Li, Y. Nonlinear finite element analysis for axial load distribution of thread considering plastic deformation. J. Phys. Conf. Ser. 2024, 2819, 012057. [Google Scholar] [CrossRef]
- Wang, W.; Marshek, K. Determination of load distribution in a threaded connector with yielding threads. Mech. Mach. Theory 1996, 31, 229–244. [Google Scholar] [CrossRef]
- Fukuoka, T.; Takaki, T. Elastic plastic finite element analysis of bolted joint during tightening process. J. Mech. Des. 2003, 125, 823–830. [Google Scholar] [CrossRef]
- Sun, Y.J.; Liao, R.D. The effect of helix on the nonlinear analysis of threaded connection. Adv. Mater. Res. 2011, 148, 1741–1744. [Google Scholar] [CrossRef]
- Sawa, S.; Ishimura, M.; Omiya, Y.; Sawa, T. 3-D FEM stress analysis of screw threads in bolted joints under static tensile loadings. In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition IMECE 2014-38089, Montreal, QC, Canada, 14–20 November 2014. [Google Scholar]
- Zhang, D.; Wang, G.; Huang, F.; Zhang, K. Load-transferring mechanism and calculation theory along engaged threads of high-strength bolts under axial tension. J. Constr. Steel Res. 2020, 172, 106153. [Google Scholar] [CrossRef]
- Redondo, R.; Mehmanparast, A. Numerical analysis of stress distribution in offshore wind turbine m72 bolted connections. Metals 2020, 10, 689. [Google Scholar] [CrossRef]
- Jiang, X.; Li, Z.; Wang, Y.; Pan, F. Self-loosening behavior of bolt in curvic coupling due to materials ratcheting at thread root. Adv. Mech. Eng. 2019, 11, 168781401984113. [Google Scholar] [CrossRef]
- Zhang, D.; Gao, S.; Xu, X. A new computational method for threaded connection stiffness. Adv. Mech. Eng. 2016, 8, 1687814016682653. [Google Scholar] [CrossRef]
- Zhao, H. Stress concentration factors within bolt-nut connectors under elasto-plastic deformation. Int. J. Fatigue 1998, 20, 651–659. [Google Scholar] [CrossRef]
- Castagnetti, D.; Dragoni, E. Stress concentrations in periodic notches: A critical investigation of Neuber’s method. Mater. Werkst. 2013, 44, 364–371. [Google Scholar] [CrossRef]
- Grimsmo, E.L.; Aalberg, A.; Langseth, M.; Clausen, A.H. Failure modes of bolt and nut assemblies under tensile loading. J. Constr. Steel Res. 2016, 126, 15–25. [Google Scholar] [CrossRef]
- Zhang, M.; Sheng, Z.; Xiong, J.; Saren, Q.; Chen, X.; Zhang, Z. Accurate modeling of threaded connections and evaluation of contact surface distribution errors oriented to accurate digital twins. Measurement 2025, 247, 116821. [Google Scholar] [CrossRef]
- Mirasoli, G.; Brutti, C.; Groth, C.; Mancini, L.; Porziani, S.; Biancolini, M. Structural health monitoring of civil structures through fem high-fidelity modelling. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1214, 012019. [Google Scholar] [CrossRef]
- Rankin, A. Shrink-fit stresses and deformations. J. Appl. Mech. 1944, 11, A77–A85. [Google Scholar] [CrossRef]
- Miller, D.L.; Marshek, K.M.; Naji, M.R. Determination of load distribution in a threaded connection. Mech. Mach. Theory 1983, 18, 421–430. [Google Scholar] [CrossRef]
- Lu, S.-K.; Hua, D.-X.; Li, Y.; Cui, F.-Y.; Li, P.-Y. Stiffness calculation model of thread connection considering friction factors. Math. Probl. Eng. 2019, 2019, 8424283. [Google Scholar] [CrossRef]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw Hill: New York, NY, USA, 1959. [Google Scholar]
- EN 1090-2:2018; Execution of Steel Structures and Aluminum Structures—Part 2: Technical Requirements for Steel Structures. iTeh standards: Newark, DE, USA, 2018.
- Winter, H.; Hirth, M. Tooth root resistance based on real stresses. VDI-Z 1974, 116, 119–426. (In German) [Google Scholar]

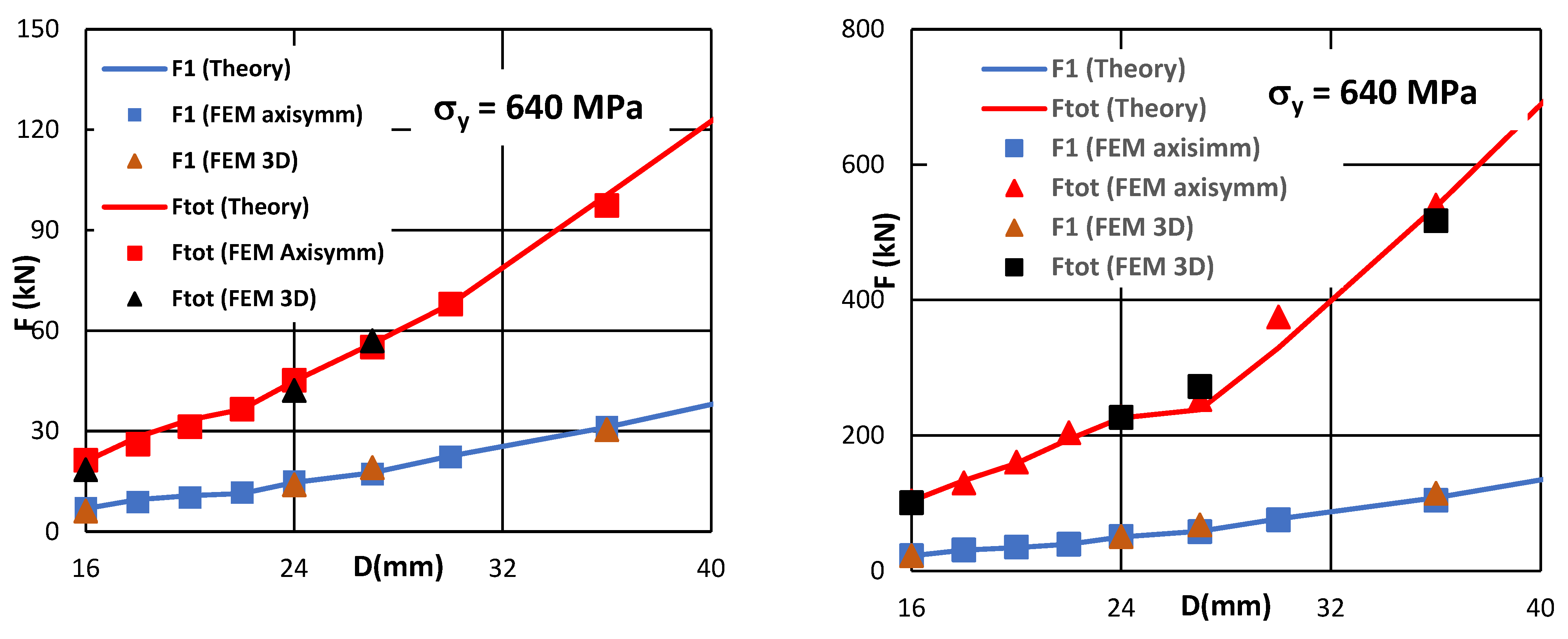

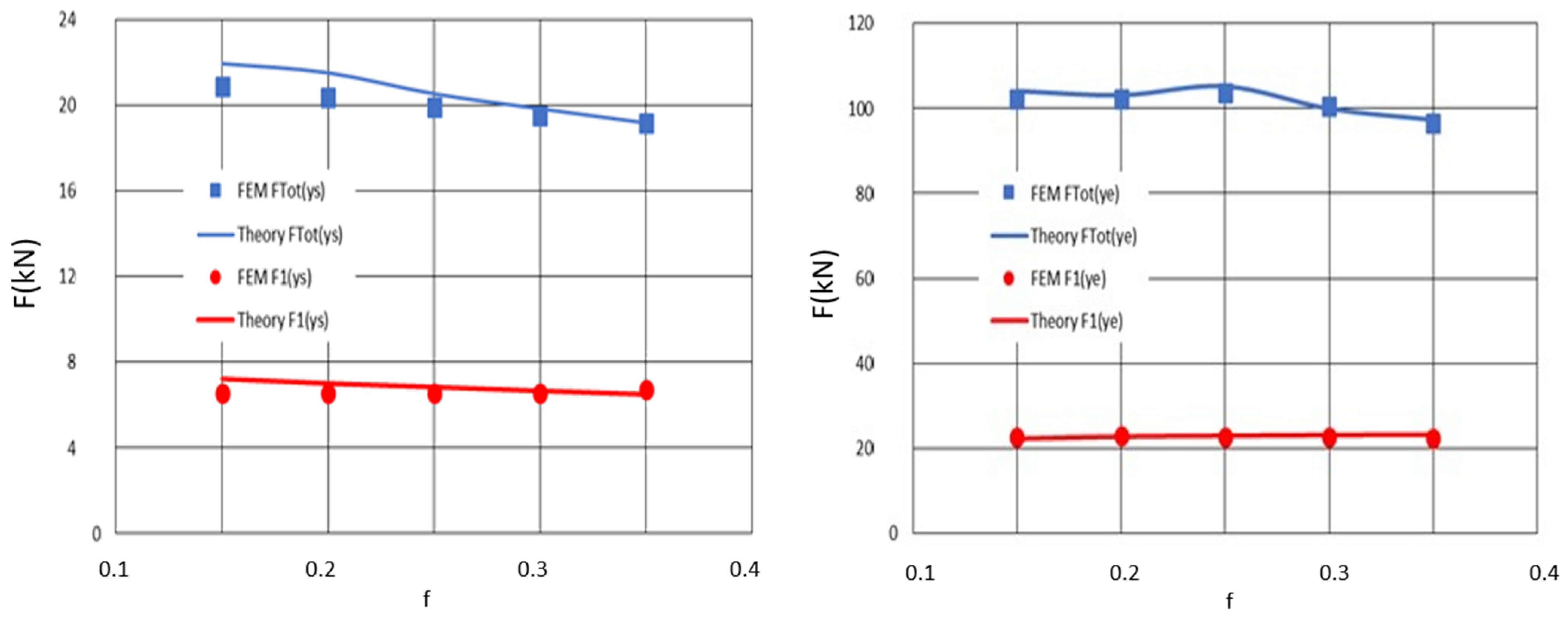

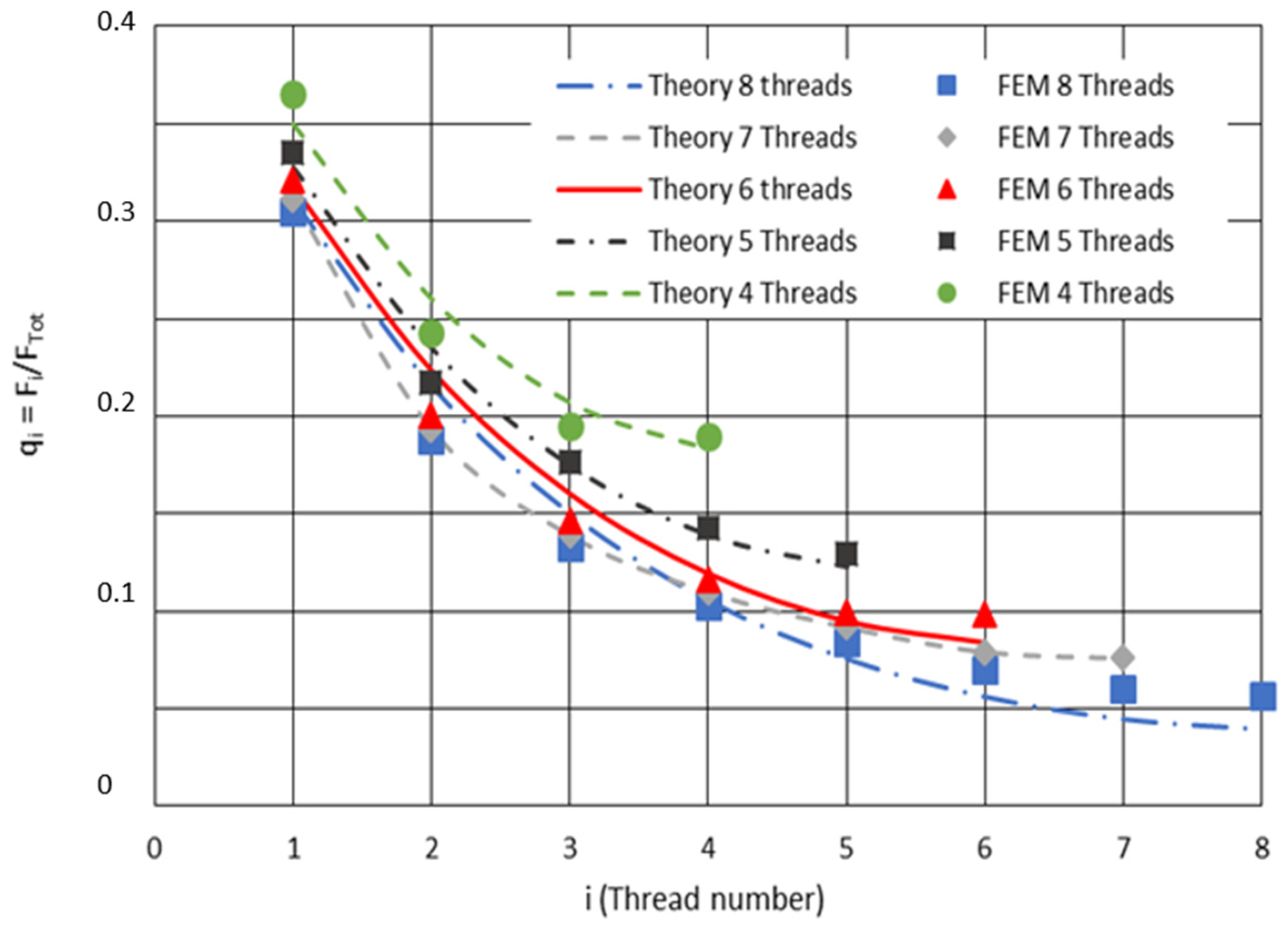

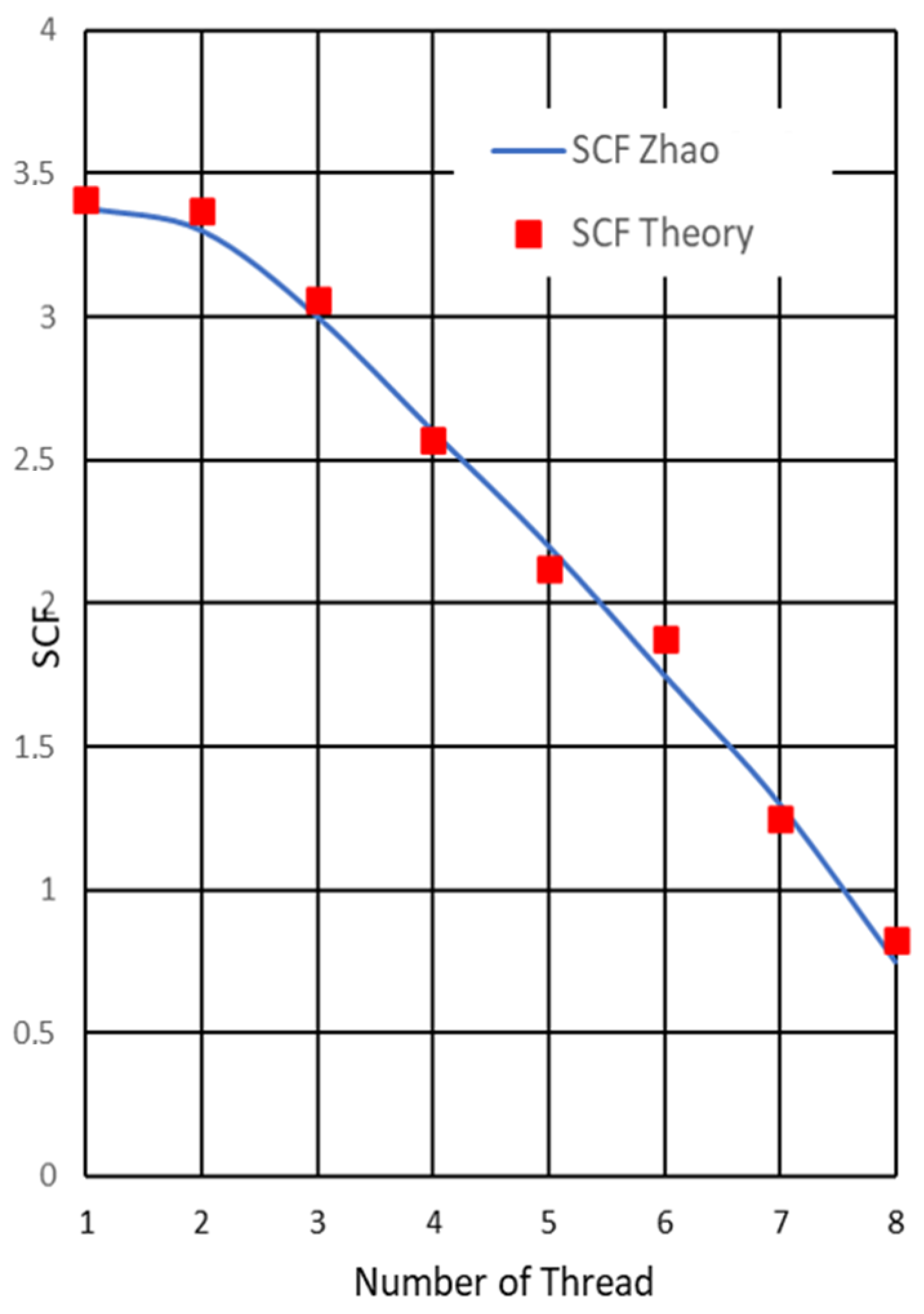
| Size | FTot (N) | Nf = 8 | Nf = 10 | Nf = 12 | Nf = 14 |
|---|---|---|---|---|---|
| M16 | 267 | 142.4 | 149.1 | 156.5 | 156.1 |
| M24 | 663 | 171.5 | 179.2 | 181.9 | 182.2 |
| M36 | 1424 | 175.9 | 179.0 | 183.7 | 184.0 |
| Case | p | D/p | R | r | DeN | HN | tw | Dew |
|---|---|---|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | ||
| M16 | 2 | 8 | 0.289 | 0.173 | 25.4 | 13 | 3 | 30 |
| M18 | 2.5 | 7.2 | 0.361 | 0.217 | 28.6 | 16.5 | 3 | 33 |
| M20 | 2.5 | 8 | 0.361 | 0.217 | 31.8 | 16.5 | 3 | 37 |
| M22 | 2.5 | 8.8 | 0.361 | 0.217 | 32.8 | 16.5 | 3.5 | 42 |
| M24 | 3 | 8 | 0.433 | 0.26 | 38 | 19.5 | 4 | 44 |
| M27 | 3 | 9 | 0.433 | 0.26 | 43.3 | 19.5 | 4 | 47 |
| M30 | 3.5 | 8.57 | 0.505 | 0.303 | 51 | 22 | 4.5 | 56 |
| M36 | 4 | 9 | 0.577 | 0.346 | 58.2 | 26 | 5 | 66 |
| Parameter | Ref. | Type | Value | Our Method | E% | Notes |
|---|---|---|---|---|---|---|
| q1 = F1/FTot | [30] | Th/El | 0.300 | 0.305 | +1.7 | M24: f = 0.15; n = 7; HN = 21 mm |
| q1 = F1/FTot | [30] | Nu/EP | 0.213 | 0.212 | −0.5 | M24: idem; σy = 673.7 MPa |
| FYE | [30] | EXP/EP | 250 kN | 253 kN | +1.2 | M24: idem |
| FYu | [30] | EXP/EP | 319 kN | 322 kN | +0.9 | M24: idem; σu = 856.9 MPa |
| q1 = F1/FTot | [22] | Nu/EP | 0.202 | 0.201 | −0.5 | M16: f = 0.15; n = 7; σy = 480 MPa |
| FYE | [22] | Nu/EP | 90 kN | 86 kN | −4.4 | M16: idem |
| FYE | [33] | EXP/EP | 149 kN | 157 kN | +5.3 | M18: f = 0.20; n = 6; σy = 908 MPa |
| K(thread) | [34] | Exp/El | 5.23 × 106 N/mm | 5.37 × 106 N/mm | +2.6 | M36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brutti, C.; Groth, C.; Biancolini, M.E. A Fast Analytical Method for Elastic–Plastic Analysis of Threaded Connections. Appl. Mech. 2025, 6, 42. https://doi.org/10.3390/applmech6020042
Brutti C, Groth C, Biancolini ME. A Fast Analytical Method for Elastic–Plastic Analysis of Threaded Connections. Applied Mechanics. 2025; 6(2):42. https://doi.org/10.3390/applmech6020042
Chicago/Turabian StyleBrutti, Carlo, Corrado Groth, and Marco Evangelos Biancolini. 2025. "A Fast Analytical Method for Elastic–Plastic Analysis of Threaded Connections" Applied Mechanics 6, no. 2: 42. https://doi.org/10.3390/applmech6020042
APA StyleBrutti, C., Groth, C., & Biancolini, M. E. (2025). A Fast Analytical Method for Elastic–Plastic Analysis of Threaded Connections. Applied Mechanics, 6(2), 42. https://doi.org/10.3390/applmech6020042






