Influence of Panel Zone Modeling on the Seismic Behavior of Steel Moment-Resisting Frames: A Numerical Study
Abstract
1. Introduction
2. Design and Modeling of the Steel MRFs
2.1. Seismic Design of Frames
2.2. Seismic Records Considered
2.3. Frame Modeling and Nonlinear Time History Analyses
| Performance Level | IDR | θp |
|---|---|---|
| SP1 or IO | 0.7% | 0 |
| SP2 or DL | 1.5% | θy |
| SP3 or LS | 2.5% | 3.5 θy |
| SP4 or CP | 5.0% | 6.5 θy |
3. Computation of Seismic Behavior Factor q
4. Analysis Results
4.1. Influence of Panel Zone on the Modal Characteristics of Steel MRFs
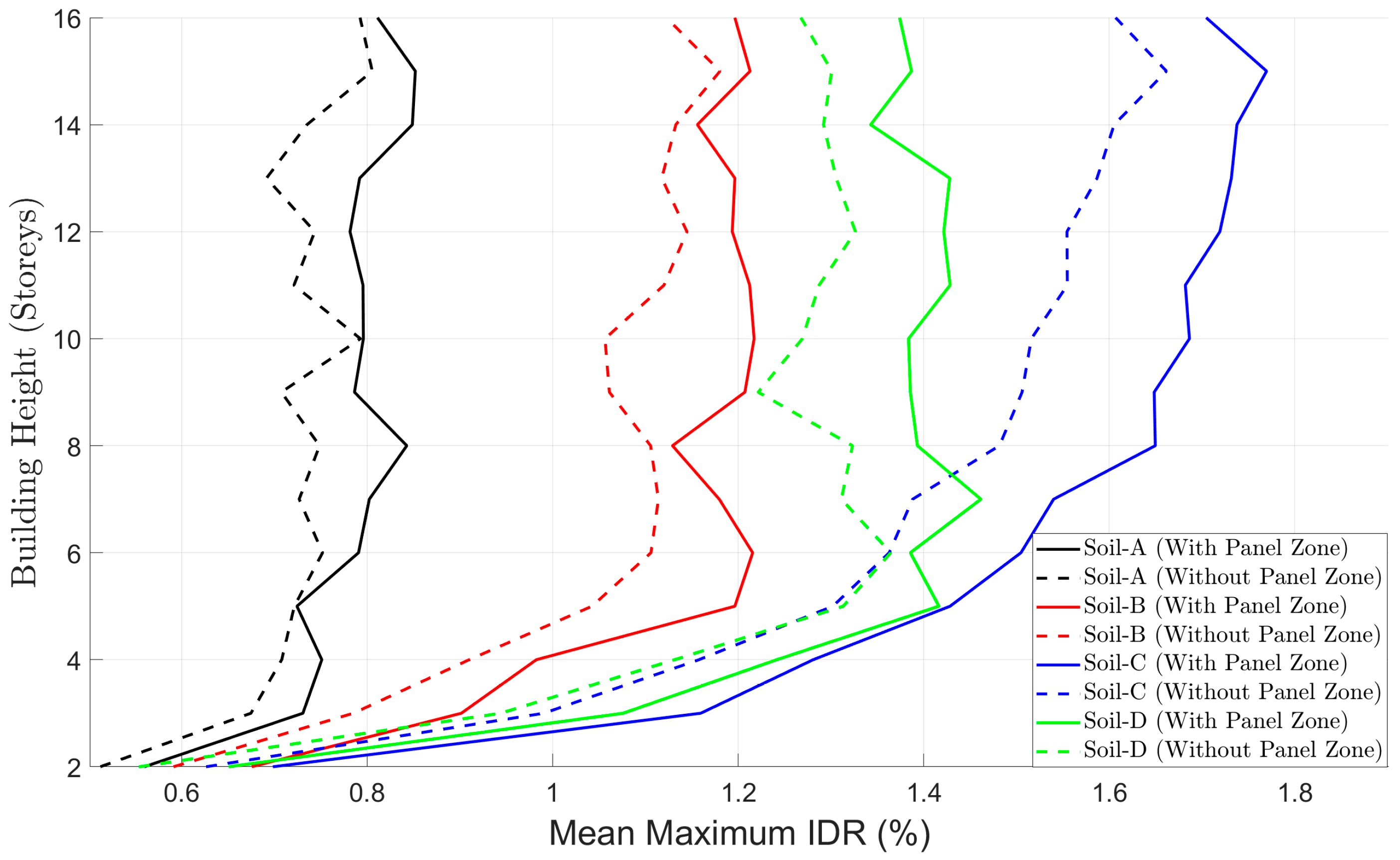
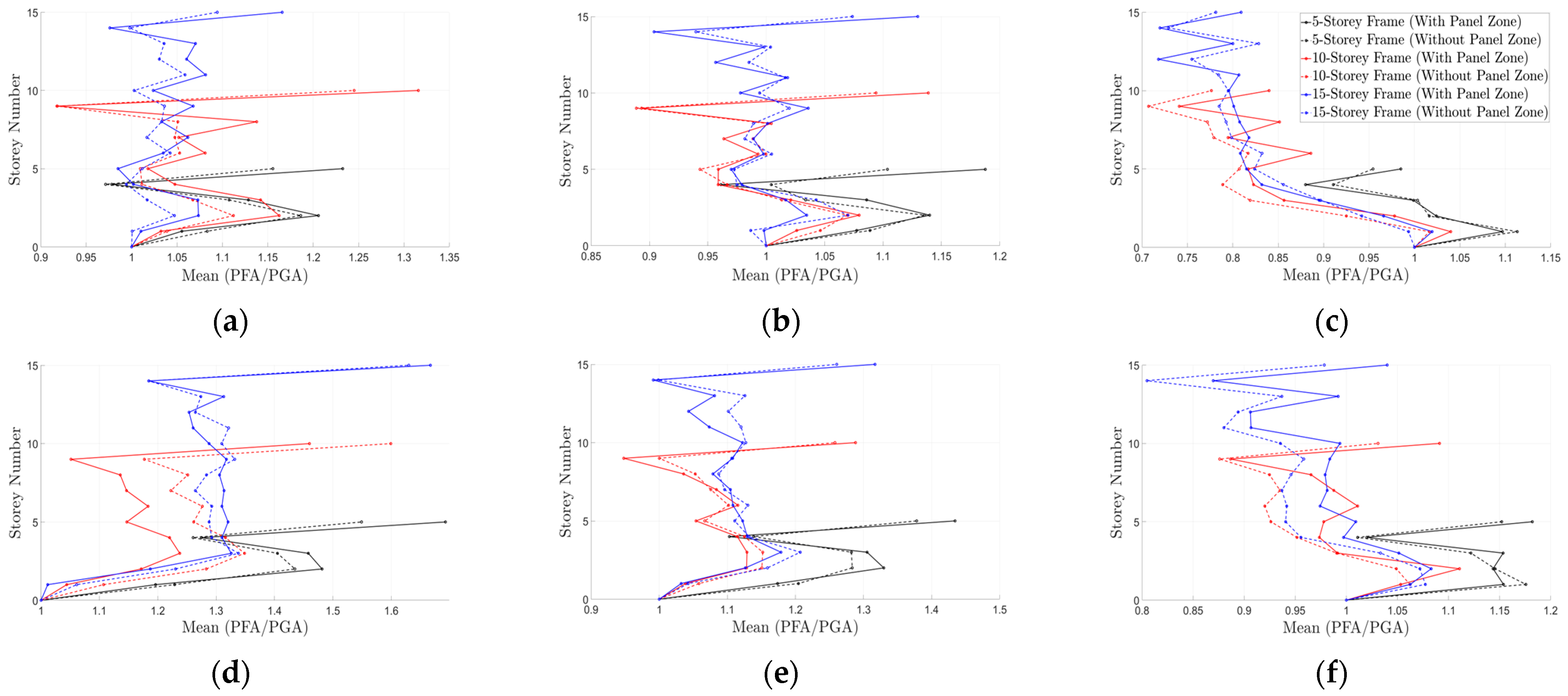
4.2. Influence of Panel Zone on the Seismic Behavior of Steel MRFs
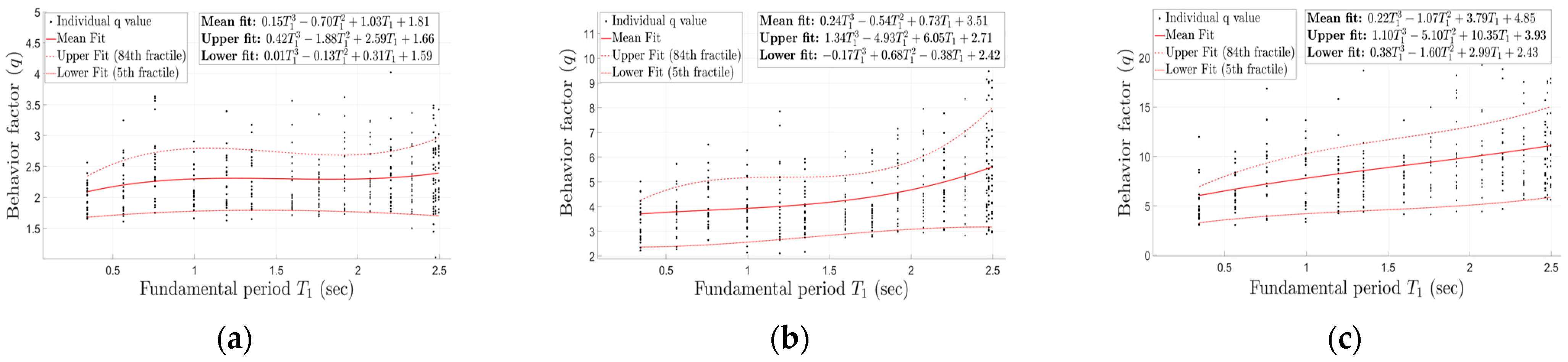
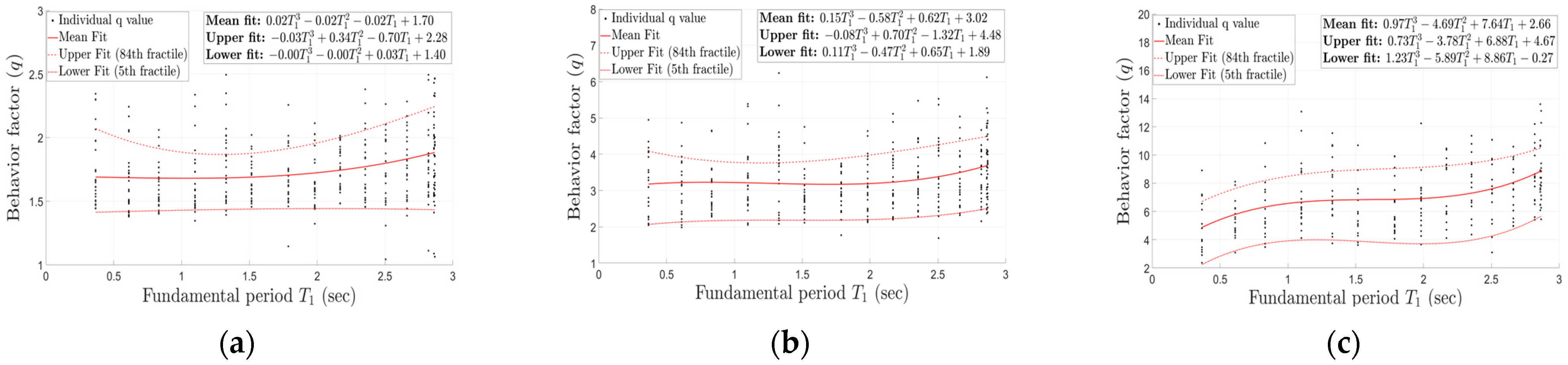
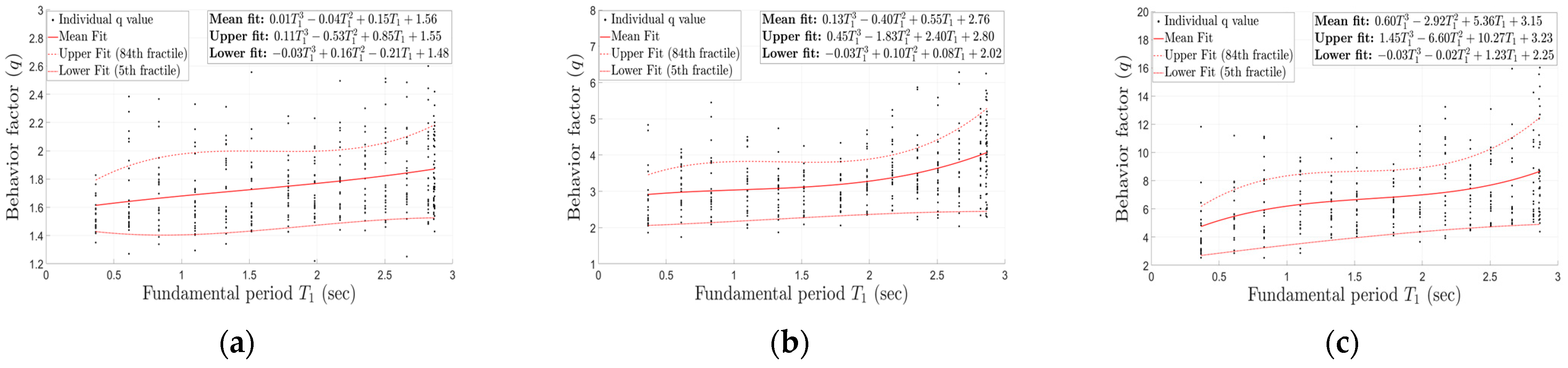
4.3. Influence of Panel Zone on the Behavior Factor
5. Discussion
6. Conclusions
- Including the panel zone in the analytical model reduces overall frame stiffness, thereby increasing the fundamental periods. For 16-story (and taller) buildings, the first-mode period increases by more than 15% and the second-mode period by over 13%, relative to models that neglect panel-zone action.
- Omitting the modeling of the panel zone leads to higher stiffness estimates and, therefore, larger base shear values during seismic analysis. Although this results in a more conservative design, improving safety margins, it also raises construction costs.
- As building height increases, the difference in base shear between two similar steel MRFs with and without panel zone consideration becomes more evident.
- Softer soils (e.g., type C or D) amplify ground motions over a broader period range, increasing mean maximum IDR values. The consideration of panel zone flexibility further raises drift response, especially in taller frames.
- The panel zone action contributes to the frame’s inelastic deformation, reduces stiffness, and decreases PGA amplification, especially at higher levels. Ignoring the panel zone influence results in an artificially stiff model, leading to increased floor accelerations.
- Because the panel zone lowers global stiffness, less seismic intensity is needed to reach a given damage level, reducing ratio and, hence, the corresponding behavior factor q.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krawinkler, H. Shear in Beam-Column Joints in Seismic Design of Steel Frames. Eng. J. Am. Inst. Steel Constr. 1978, 15, 82–91. [Google Scholar] [CrossRef]
- Castro, J.M.; Elghazouli, A.Y.; Izzuddin, B.A. Modelling of the Panel Zone in Steel and Composite Moment Frames. Eng. Struct. 2005, 27, 129–144. [Google Scholar] [CrossRef]
- Castro, J.M.; Dávila-Arbona, F.J.; Elghazouli, A.Y. Seismic Design Approaches for Panel Zones in Steel Moment Frames. J. Earthq. Eng. 2008, 12 (Suppl. S1), 34–51. [Google Scholar] [CrossRef]
- Schneider, S.P.; Amidi, A. Seismic Behavior of Steel Frames with Deformable Panel Zones. J. Struct. Eng. 1998, 124, 35–42. [Google Scholar] [CrossRef]
- Miri, M.; Naghipour, M.; Kashiryfar, A. Panel Zone Rigidity Effects on Special Steel Moment-Resisting Frames According to the Performance Based Design. World Acad. Sci. Eng. Technol. 2009, 50, 925–931. [Google Scholar]
- Sui, W.; Dong, Z.; Zhang, X.; Wang, Z. Experimental Study of the Influence of the Shear Strength of Panel Zones on the Mechanical Properties of Steel Frame Structures. Structures 2022, 44, 42–57. [Google Scholar] [CrossRef]
- Garlock, M.M.; Ricles, J.M.; Sause, R. Influence of Design Parameters on Seismic Response of Post-Tensioned Steel MRF Systems. Eng. Struct. 2008, 30, 1037–1047. [Google Scholar] [CrossRef]
- Herrera, R.A.; Muhummud, T.; Ricles, J.M.; Sause, R. Modeling of Composite MRFs with CFT Columns and WF Beams. Steel Compos. Struct. 2022, 43, 327–340. [Google Scholar] [CrossRef]
- Herrera, R.; Nunez, E.; Hernandez, M. Seismic-Resistant Performance of Double Built-Up T Moment Connections. J. Struct. Eng. 2025, 151, 04024193. [Google Scholar] [CrossRef]
- Du, H.; Zhao, P.; Wang, Y.; Sun, W. Seismic Experimental Assessment of Beam-Through Beam-Column Connections for Modular Prefabricated Steel Moment Frames. J. Constr. Steel Res. 2022, 192, 107208. [Google Scholar] [CrossRef]
- Mansouri, I.; Saffari, H. A New Steel Panel Zone Model Including Axial Force for Thin to Thick Column Flanges. Steel Compos. Struct. 2014, 16, 417–436. [Google Scholar] [CrossRef]
- Sazmand, E.; Aghakouchak, A.A. Modeling the Panel Zone in Steel MR Frames Composed of Built-Up Columns. J. Constr. Steel Res. 2012, 77, 54–68. [Google Scholar] [CrossRef]
- Xu, Z.-G.; Zhao, Y.-T.; Wu, H.-J.; Bao, E.-H. Research on the Influence of Panel Zone on Dynamic Damage of Multi-Story Steel Structure. Eur. J. Environ. Civ. Eng. 2024, 28, 518–533. [Google Scholar] [CrossRef]
- Skiadopoulos, A.; Lignos, D.G. Seismic Demands of Steel Moment-Resisting Frames with Inelastic Beam-to-Column Web Panel Zones. Earthq. Eng. Struct. Dyn. 2022, 51, 1591–1609. [Google Scholar] [CrossRef]
- Skiadopoulos, A.; Elkady, A.; Lignos, D.G. Proposed Panel Zone Model for Seismic Design of Steel Moment-Resisting Frames. J. Struct. Eng. 2021, 147, 04021006. [Google Scholar] [CrossRef]
- Isaincu, A.; D’Aniello, M.; Stratan, A. Implications of Structural Model on the Design of Steel Moment Resisting Frames. Open Constr. Build. Technol. J. 2018, 12 (Suppl. S1), 124–131. [Google Scholar] [CrossRef]
- Rigi, A.; JavidSharifi, B.; Hadianfard, M.A.; Yang, T.Y. Study of the Seismic Behavior of Rigid and Semi-Rigid Steel Moment-Resisting Frames. J. Constr. Steel Res. 2021, 186, 106910. [Google Scholar] [CrossRef]
- Sepasdar, R.; Banan, M.R.; Banan, M.R. A Numerical Investigation on the Effect of Panel Zones on Cyclic Lateral Capacity of Steel Moment Frames. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 439–448. [Google Scholar] [CrossRef]
- Lu, L.; Zhang, J.; Zhang, G.; Peng, H.; Liu, B.; Hao, H. The Influence of Box-Strengthened Panel Zone on Steel Frame Seismic Performance. Buildings 2023, 13, 3042. [Google Scholar] [CrossRef]
- Tuna, M.; Topkaya, C. Panel Zone Deformation Demands in Steel Moment Resisting Frames. J. Constr. Steel Res. 2015, 110, 65–75. [Google Scholar] [CrossRef]
- SEAOC. Recommended Lateral Force Requirements and Commentary; Structural Engineers Association of California: Sacramento, CA, USA, 1999. [Google Scholar]
- EN 1998-1; Eurocode 8. Design of Structures for Earthquake Resistance, Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2009.
- EN 1993-1-1; Eurocode 3. Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2005.
- SAP2000 (Version 19); Analysis Reference Manual. Computers and Structures Inc.: Berkeley, CA, USA, 2019.
- PEER. Pacific Earthquake Engineering Research Center, Strong Ground Motion Database; University of California: Berkeley, CA, USA, 2009; Available online: http://peer.berkeley.edu/ (accessed on 1 January 2015).
- COSMOS. Consortium of Organizations for Strong Motion Observation Systems; COSMOS: San Francisco, CA, USA, 2013; Available online: http://www.cosmos-eq.org/ (accessed on 1 January 2015).
- Kalapodis, N.A.; Papagiannopoulos, G.A.; Beskos, D.E. Modal Strength Reduction Factors for Seismic Design of Plane Steel Braced Frames. J. Constr. Steel Res. 2018, 147, 549–563. [Google Scholar] [CrossRef]
- Carr, A.J. Theory and User Guide to Associated Programs—Ruaumoko Manual; Department of Engineering, University of Canterbury: Christchurch, New Zealand, 2006. [Google Scholar]
- Lignos, D.G.; Krawinkler, H. Deterioration Modeling of Steel Components in Support of Collapse Prediction of Steel Moment Frames Under Earthquake Loading. J. Struct. Eng. 2011, 137, 1291–1302. [Google Scholar] [CrossRef]
- FEMA 356. Prestandard and Commentary for the Seismic Rehabilitation of Buildings; Federal Emergency Management Agency: Washington, DC, USA, 2000. [Google Scholar]
- Lee, C.H.; Jeon, S.W.; Kim, J.H.; Uong, C.M. Effects of Panel Zone Strength and Beam-Web Connection Method on Seismic Performance of Reduced Beam Section Steel Moment Connections. J. Struct. Eng. 2005, 131, 1854–1865. [Google Scholar] [CrossRef]
- MATLAB, version 2018a; The MathWorks, Inc.: Natick, MA, USA, 2018.
- De Luca, F.; Iervolino, I.; Cosenza, E. Unscaled, Scaled, Adjusted and Artificial Spectral Matching Accelerograms: Displacement and Energy-Based Assessment. In Proceedings of the 13th Congress of the Italian National Association of Earthquake Engineering (ANIDIS), Bologna, Italy, 28 June–2 July 2009. [Google Scholar]
- Krawinkler, H.; Seneviratna, G.D.P.K. Pros and Cons of a Pushover Analysis of Seismic Performance Evaluation. Eng. Struct. 1998, 20, 452–464. [Google Scholar] [CrossRef]
- Fajfar, P. Capacity Spectrum Method Based on Inelastic Demand Diagrams. Earthq. Eng. Struct. Dyn. 1999, 28, 979–993. [Google Scholar] [CrossRef]
- Uang, C.M. Establishing R (or Rw) and Cd Factors for Building Seismic Provisions. J. Struct. Eng. 1991, 117, 19–28. [Google Scholar] [CrossRef]
- Miranda, E.; Taghavi, S. Approximate Floor Acceleration Demands in Multistory Buildings. I: Formulation. J. Struct. Eng. 2005, 131, 203–211. [Google Scholar] [CrossRef]
- Kalapodis, N.A.; Muho, E.V.; Papagiannopoulos, G.A. Integration of Peak Seismic Floor Velocities and Accelerations into the Performance-Based Design of Steel Structures. Soil Dyn. Earthq. Eng. 2022, 154, 107160. [Google Scholar] [CrossRef]
- ASCE/SEI 7-16; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2017.
- Charney, F.A.; Marshall, J. A Comparison of the Krawinkler and Scissors Models for Including Beam–Column Joint Deformations in the Analysis of Moment-Resisting Steel Frames. Eng. J. (AISC) 2006, 43, 31–48. [Google Scholar] [CrossRef]
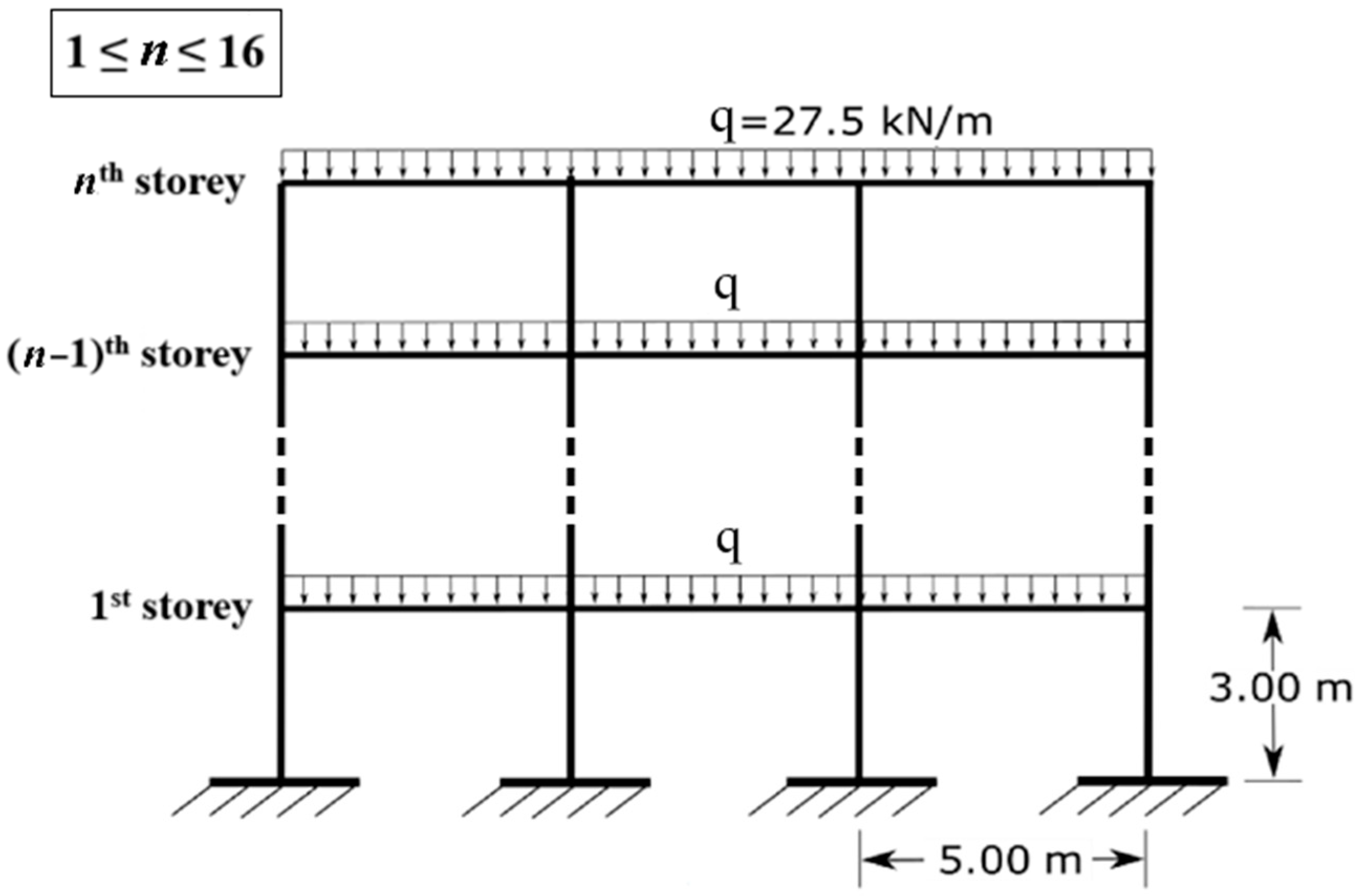
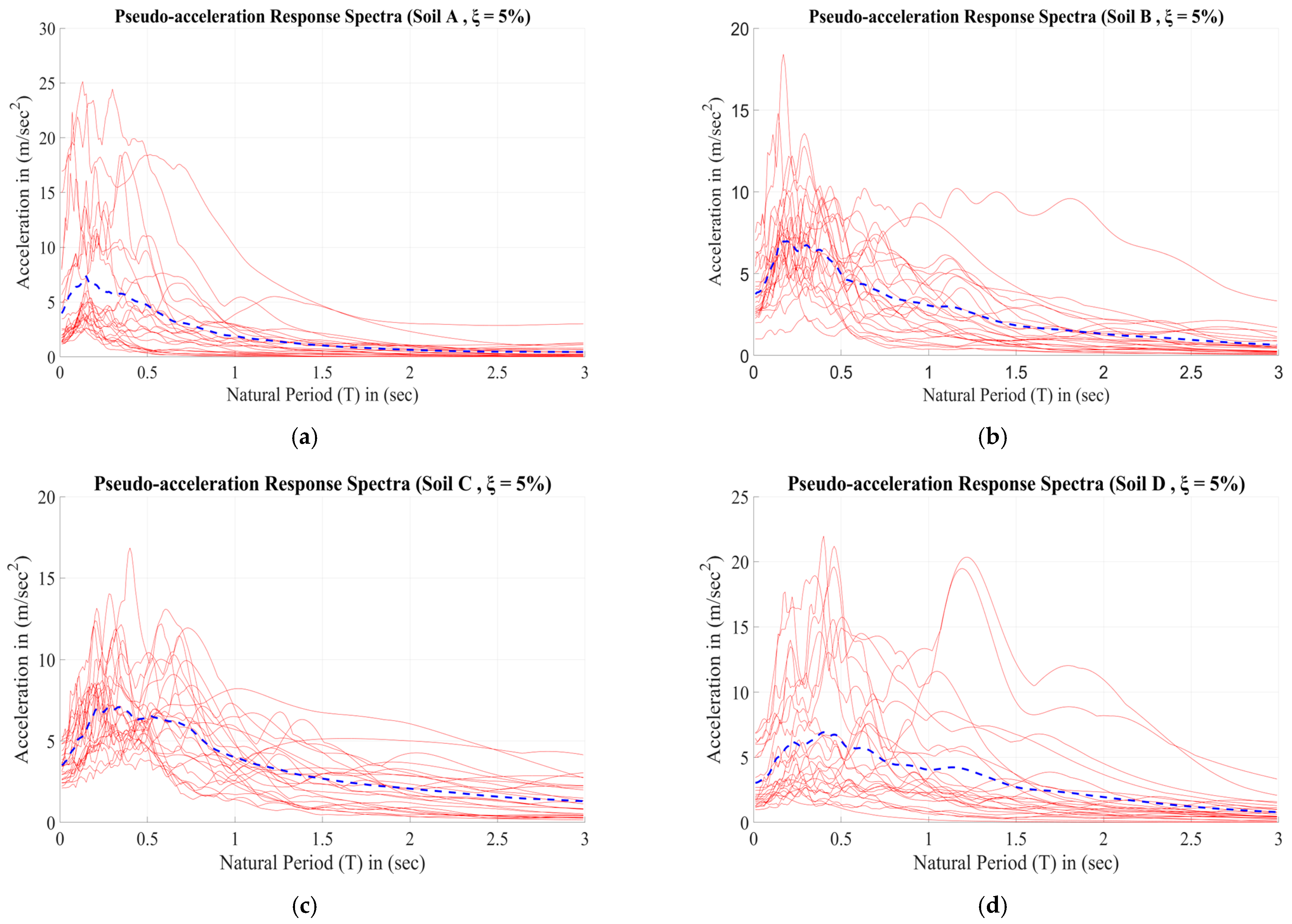
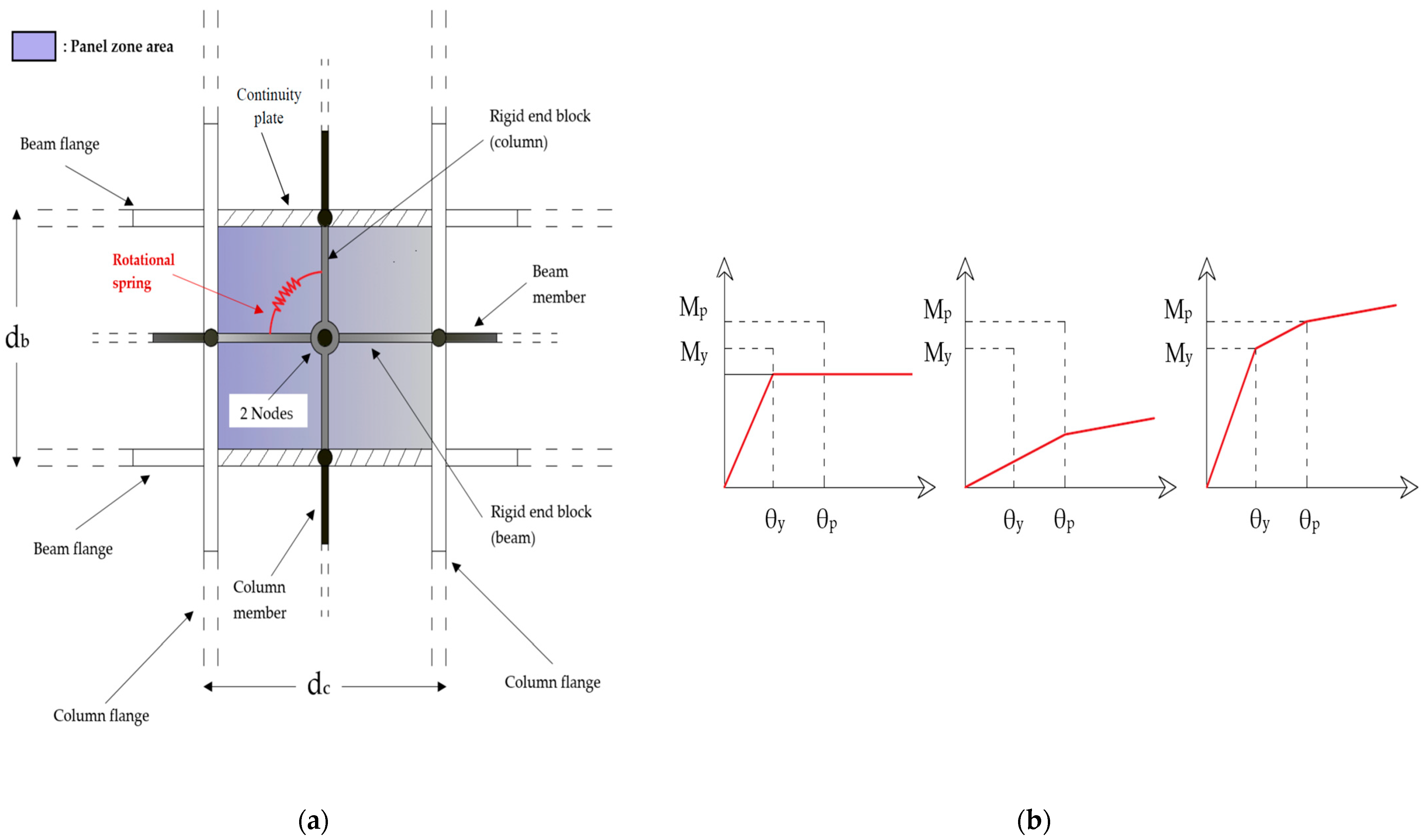
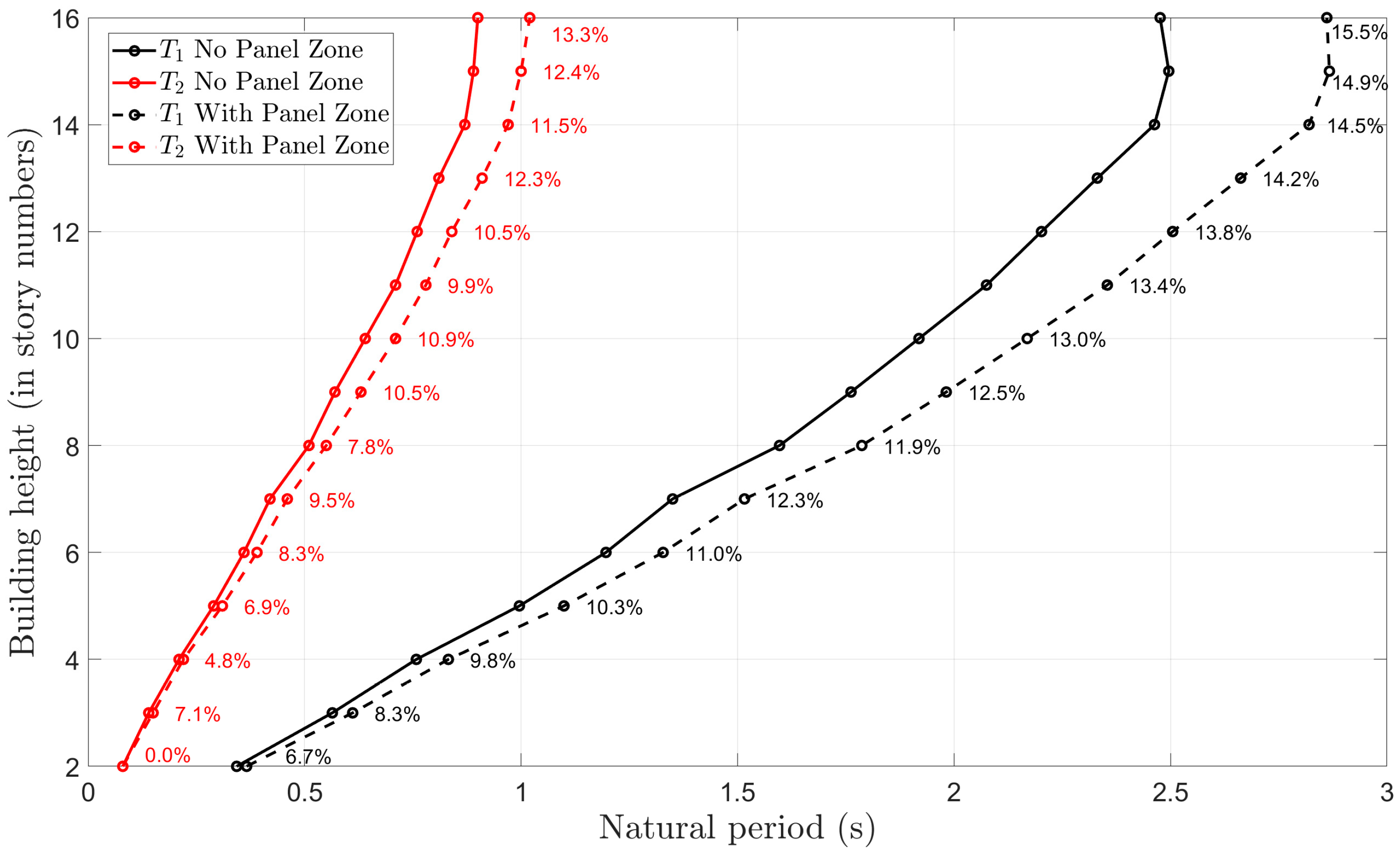



| Frame | Story | Frame Sections HEB (Columns)—IPE (Beams) | T1, no PZ (s) | T2, no PZ (s) | T1, with PZ (s) | T2, with PZ (s) |
|---|---|---|---|---|---|---|
| 1 | 2 | 400-300 (1), 360-270 (2) | 0.343 | 0.08 | 0.37 | 0.08 |
| 2 | 3 | 400-300 (1), 360-270 (2–3) | 0.564 | 0.14 | 0.611 | 0.15 |
| 3 | 4 | 400-300 (1–2), 360-270 (3–4) | 0.758 | 0.21 | 0.832 | 0.22 |
| 4 | 5 | 400-300 (1–2), 360-270 (3–5) | 0.996 | 0.29 | 1.099 | 0.31 |
| 5 | 6 | 400-300 (1–3), 360-270 (4–6) | 1.196 | 0.36 | 1.328 | 0.39 |
| 6 | 7 | 450-330 (1), 400-300 (2–4), 360-270 (5–7) | 1.350 | 0.42 | 1.516 | 0.46 |
| 7 | 8 | 450-330 (1), 400-300 (2–4), 360-270 (5–8) | 1.597 | 0.51 | 1.787 | 0.55 |
| 8 | 9 | 450-330 (1–2), 400-300 (3–5), 360-270 (6–9) | 1.762 | 0.57 | 1.982 | 0.63 |
| 9 | 10 | 450-330 (1–3), 400-300 (4–6), 360-270 (7–10) | 1.919 | 0.64 | 2.169 | 0.71 |
| 10 | 11 | 450-330 (1–4), 400-300 (5–7), 360-270 (8–11) | 2.075 | 0.71 | 2.354 | 0.78 |
| 11 | 12 | 500-360 (1), 450-330 (2–5), 400-300 (6–8), 360-270 (9–12) | 2.202 | 0.76 | 2.505 | 0.84 |
| 12 | 13 | 500-360 (1–2), 450-330 (3–6), 400-300 (7–9), 360-270 (10–13) | 2.331 | 0.81 | 2.662 | 0.91 |
| 13 | 14 | 500-360 (1–3), 450-330 (4–7), 400-300 (8–10), 360-270 (11–14) | 2.463 | 0.87 | 2.820 | 0.97 |
| 14 | 15 | 550-400 (1–2), 500-360 (3–5), 450-330 (6–8), 400-300 (9–11), 360-270 (12–15) | 2.496 | 0.89 | 2.867 | 1.00 |
| 15 | 16 | 550-400 (1–4), 500-360 (5–7), 450-330 (8–10), 400-300 (11–13), 360-270 (14–16) | 2.476 | 0.9 | 2.861 | 1.02 |
| No. | Date | Record Name | Comp. | Station Name | PGA (g) |
|---|---|---|---|---|---|
| 1 | 10/4/1987 | Whittier Narrows | NS | 24399 Mt Wilson-CIT Station | 0.158 |
| 2 | 10/4/1987 | Whittier Narrows | EW | 24399 Mt Wilson-CIT Station | 0.142 |
| 3 | 9/20/1999 | Chi-Chi, Taiwan | 056-N | HWA056 | 0.107 |
| 4 | 9/20/1999 | Chi-Chi, Taiwan | 056-N | HWA056 | 0.107 |
| 5 | 10/1/1987 | Whittier Narrows | NS | 24399 Mt Wilson-CIT Station | 0.186 |
| 6 | 10/1/1987 | Whittier Narrows | EW | 24399 Mt Wilson-CIT Station | 0.123 |
| 7 | 2/9/1971 | San Fernando | N069 | 127 Lake Hughes 9 | 0.157 |
| 8 | 2/9/1971 | San Fernando | N159 | 127 Lake Hughes 9 | 0.134 |
| 9 | 1/17/1994 | Northridge | NS | 90019 San Gabriel-E. Gr. Ave. | 0.256 |
| 10 | 1/17/1994 | Northridge | EW | 90019 San Gabriel-E. Gr. Ave. | 0.141 |
| 11 | 9/20/1999 | Chi-Chi, Taiwan | NS | TAP103 | 0.177 |
| 12 | 9/20/1999 | Chi-Chi, Taiwan | EW | TAP103 | 0.122 |
| 13 | 1/17/1994 | Northridge | N005 | 90017 LA-Wonderland Ave | 0.172 |
| 14 | 1/17/1994 | Northridge | N175 | 90017 LA-Wonderland Ave | 0.112 |
| 15 | 6/7/1975 | Northern Calif. | N060 | 1249 Cape Mendocino, Petrolia | 0.115 |
| 16 | 6/7/1975 | Northern Calif. | N150 | 1249 Cape Mendocino, Petrolia | 0.179 |
| 17 | 7/8/1986 | N. Palm Springs | NS | 12206 Silent Valley | 0.139 |
| 18 | 10/18/1989 | Loma Prieta | N205 | 58539 San Francisco | 0.105 |
| 19 | 10/18/1989 | Loma Prieta | NS | 47379 Gilroy Array 1 | 0.473 |
| 20 | 10/18/1989 | Loma Prieta | EW | 47379 Gilroy Array 1 | 0.411 |
| 21 | 8/17/1999 | Kocaeli, Turkey | NS | Gebze | 0.137 |
| 22 | 8/17/1999 | Kocaeli, Turkey | EW | Gebze | 0.244 |
| 23 | 6/28/1992 | Landers | NS | 21081 Amboy | 0.115 |
| 24 | 6/28/1992 | Landers | EW | 21081 Amboy | 0.146 |
| 25 | 9/20/1999 | Chi-Chi, Taiwan | N034 | TCU046 | 0.133 |
| No. | Date | Record Name | Comp. | Station Name | PGA (g) |
|---|---|---|---|---|---|
| 1 | 4/25/1992 | Cape Mendocino | NS | 89509 Eureka | 0.154 |
| 2 | 4/25/1992 | Cape Mendocino | EW | 89509 Eureka | 0.178 |
| 3 | 6/9/1980 | Victoria, Mexico | N045 | 6604 Cerro Prieto | 0.621 |
| 4 | 6/9/1980 | Victoria, Mexico | N135 | 6604 Cerro Prieto | 0.587 |
| 5 | 4/25/1992 | Cape Mendocino | EW | 89324 Rio Dell Overpass | 0.385 |
| 6 | 4/25/1992 | Cape Mendocino | NS | 89324 Rio Dell Overpass | 0.549 |
| 7 | 8/13/1978 | Santa Barbara | N048 | 283 Santa Barbara Courthouse | 0.203 |
| 8 | 8/13/1978 | Santa Barbara | N138 | 283 Santa Barbara Courthouse | 0.102 |
| 9 | 9/20/1999 | Chi-Chi, Taiwan | NS | TCU095 | 0.712 |
| 10 | 9/20/1999 | Chi-Chi, Taiwan | EW | TCU095 | 0.378 |
| 11 | 8/6/1979 | Coyote Lake | N213 | 1377 San Juan Bautista | 0.108 |
| 12 | 8/6/1979 | Coyote Lake | N303 | 1377 San Juan Bautista | 0.107 |
| 13 | 1/17/1994 | Northridge | NS | 90021 LA-N Westmoreland | 0.361 |
| 14 | 1/17/1994 | Northridge | EW | 90021 LA-N Westmoreland | 0.401 |
| 15 | 7/8/1986 | N. Palm Springs | NS | 12204 San Jacinto-Soboba | 0.239 |
| 16 | 7/8/1986 | N. Palm Springs | EW | 12204 San Jacinto-Soboba | 0.25 |
| 17 | 9/12/1970 | Lytle Creek | N115 | 290 Wrightwood | 0.162 |
| 18 | 9/12/1970 | Lytle Creek | N205 | 290 Wrightwood | 0.2 |
| 19 | 10/18/1989 | Loma Prieta | NS | 58065 Saratoga-Aloha Ave | 0.324 |
| 20 | 10/18/1989 | Loma Prieta | EW | 58065 Saratoga-Aloha Ave | 0.512 |
| 21 | 6/28/1992 | Landers | NS | 22170 Joshua Tree | 0.284 |
| 22 | 6/28/1992 | Landers | EW | 22170 Joshua Tree | 0.274 |
| 23 | 9/15/1976 | Friuli, Italy | NS | 8014 Forgaria Cornino | 0.212 |
| 24 | 9/15/1976 | Friuli, Italy | EW | 8014 Forgaria Cornino | 0.26 |
| 25 | 9/20/1999 | Chi-Chi, Taiwan | N045 | TCU045 | 0.512 |
| No. | Date | Record Name | Comp. | Station Name | PGA (g) |
|---|---|---|---|---|---|
| 1 | 9/20/1999 | Chi-Chi, Taiwan | NS | NST | 0.388 |
| 2 | 9/20/1999 | Chi-Chi, Taiwan | EW | NST | 0.309 |
| 3 | 5/2/1983 | Coalinga | EW | 36227 Parkfield | 0.147 |
| 4 | 5/2/1983 | Coalinga | NS | 36227 Parkfield | 0.131 |
| 5 | 11/12/1999 | Duzce, Turkey | NS | Bolu | 0.728 |
| 6 | 11/12/1999 | Duzce, Turkey | EW | Bolu | 0.822 |
| 7 | 10/15/1979 | Imperial Valley | N015 | 6622 Computertas | 0.186 |
| 8 | 10/15/1979 | Imperial Valley | N285 | 6622 Computertas | 0.147 |
| 9 | 10/15/1979 | Imperial Valley | N012 | 6621 Chihuahua | 0.27 |
| 10 | 10/15/1979 | Imperial Valley | N282 | 6621 Chihuahua | 0.284 |
| 11 | 8/17/1999 | Kocaeli, Turkey | NS | Atakoy | 0.105 |
| 12 | 8/17/1999 | Kocaeli, Turkey | EW | Atakoy | 0.164 |
| 13 | 10/18/1989 | Loma Prieta | NS | 1028 Hollister City Hall | 0.247 |
| 14 | 10/18/1989 | Loma Prieta | EW | 1028 Hollister City Hall | 0.215 |
| 15 | 4/24/1984 | Morgan Hill | NS | 57382 Gilroy Array # 4 | 0.224 |
| 16 | 4/24/1984 | Morgan Hill | EW | 57382 Gilroy Array # 4 | 0.348 |
| 17 | 1/17/1994 | Northridge | NS | 90057 Canyon Country | 0.482 |
| 18 | 1/17/1994 | Northridge | EW | 90057 Canyon Country | 0.41 |
| 19 | 2/9/1971 | San Fernando | EW | 135 LA–Hollywood | 0.21 |
| 20 | 2/9/1971 | San Fernando | NS | 135 LA-Hollywood | 0.174 |
| 21 | 4/26/1981 | Westmorland | NS | 5169 Westmorland Fire Sta | 0.368 |
| 22 | 4/26/1981 | Westmorland | EW | 5169 Westmorland Fire Sta | 0.496 |
| 23 | 11/24/1987 | Superstition Hills (B) | NS | 01335 El Centro Imp. Co. Cent | 0.258 |
| 24 | 11/24/1987 | Superstition Hills (B) | EW | 01335 El Centro Imp. Co. Cent | 0.358 |
| 25 | 1/27/1980 | Livermore | EW | 57187 San Ramon | 0.301 |
| No. | Date | Record Name | Comp. | Station Name | PGA (g) |
|---|---|---|---|---|---|
| 1 | 4/26/1981 | Westmorland | N045 | 5062 Salton Sea Wildlife Ref. | 0.199 |
| 2 | 4/26/1981 | Westmorland | N135 | 5062 Salton Sea Wildlife Ref. | 0.176 |
| 3 | 11/24/1987 | Superstition Hills | N045 | 5062 Salton Sea Wildlife Refuge | 0.119 |
| 4 | 11/24/1987 | Superstition Hills | N135 | 5062 Salton Sea Wildlife Refuge | 0.167 |
| 5 | 1/17/1994 | Northridge | N064 | 90011 Montebello-Bluff Rd. | 0.128 |
| 6 | 1/17/1994 | Northridge | N154 | 90011 Montebello-Bluff Rd. | 0.179 |
| 7 | 10/18/1989 | Loma Prieta | NS | 58117 Treasure Island | 0.159 |
| 8 | 10/18/1989 | Loma Prieta | EW | 58117 Treasure Island | 0.1 |
| 9 | 8/17/1999 | Kocaeli, Turkey | NS | Ambarlı | 0.184 |
| 10 | 8/17/1999 | Kocaeli, Turkey | EW | Ambarlı | 0.249 |
| 11 | 10/18/1989 | Loma Prieta | N043 | 1002 APEEL 2-Redwood City | 0.274 |
| 12 | 10/18/1989 | Loma Prieta | N133 | 1002 APEEL 2-Redwood City | 0.22 |
| 13 | 10/15/1979 | Imperial Valley | N040 | 5057 El Centro Array 3 | 0.112 |
| 14 | 10/15/1979 | Imperial Valley | N130 | 5057 El Centro Array 3 | 0.179 |
| 15 | 9/20/1999 | Chi-Chi, Taiwan | N041 | CHY041 | 0.639 |
| 16 | 9/20/1999 | Chi-Chi, Taiwan | N131 | CHY041 | 0.302 |
| 17 | 10/18/1989 | Loma Prieta | N047 | 1002 APEEL 2-Redwood City | 0.274 |
| 18 | 10/18/1989 | Loma Prieta | N137 | 1002 APEEL 2-Redwood City | 0.22 |
| 19 | 9/20/1999 | Chi-Chi, Taiwan | EW | TAP003 | 0.126 |
| 20 | 9/20/1999 | Chi-Chi, Taiwan | NS | TAP003 | 0.106 |
| 21 | 1/16/1995 | Kobe | NS | Nishi-Akashi | 0.503 |
| 22 | 1/16/1995 | Kobe | EW | Nishi-Akashi | 0.509 |
| 23 | 9/20/1999 | Chi-Chi, Taiwan | N040 | TCU040 | 0.123 |
| 24 | 9/20/1999 | Chi-Chi, Taiwan | N130 | TCU040 | 0.149 |
| 25 | 1/16/1995 | Kobe | NS | Kakogawa | 0.345 |
| Performance Level | Limits | Soil Type—A | Soil Type—B | Soil Type—C | Soil Type—D |
|---|---|---|---|---|---|
| Damage limitation (DL) 0.7% < IDRmax ≤ 1.5% | Upper | ||||
| Mean | |||||
| Lower | |||||
| Life safety (LS) 1.5% < IDRmax ≤ 2.5% | Upper | ||||
| Mean | |||||
| Lower | |||||
| Collapse prevention (CP) 2.5% < IDRmax ≤ 5% | Upper | ||||
| Mean | |||||
| Lower |
| Performance Level | Limits | Soil Type—A | Soil Type—B | Soil Type—C | Soil Type—D |
|---|---|---|---|---|---|
| Damage limitation (DL)0.7% < IDRmax ≤ 1.5% | Upper | ||||
| Mean | |||||
| Lower | |||||
| Life safety (LS)1.5% < IDRmax ≤ 2.5% | Upper | ||||
| Mean | |||||
| Lower | |||||
| Collapse prevention (CP)2.5% < IDRmax ≤ 5% | Upper | ||||
| Mean | |||||
| Lower |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalapodis, N.A. Influence of Panel Zone Modeling on the Seismic Behavior of Steel Moment-Resisting Frames: A Numerical Study. Appl. Mech. 2025, 6, 22. https://doi.org/10.3390/applmech6010022
Kalapodis NA. Influence of Panel Zone Modeling on the Seismic Behavior of Steel Moment-Resisting Frames: A Numerical Study. Applied Mechanics. 2025; 6(1):22. https://doi.org/10.3390/applmech6010022
Chicago/Turabian StyleKalapodis, Nicos A. 2025. "Influence of Panel Zone Modeling on the Seismic Behavior of Steel Moment-Resisting Frames: A Numerical Study" Applied Mechanics 6, no. 1: 22. https://doi.org/10.3390/applmech6010022
APA StyleKalapodis, N. A. (2025). Influence of Panel Zone Modeling on the Seismic Behavior of Steel Moment-Resisting Frames: A Numerical Study. Applied Mechanics, 6(1), 22. https://doi.org/10.3390/applmech6010022





