On the Need of Compressive Regularization in Damage Models for Concrete: Demonstration on a Modified Mazars Model
Abstract
1. Introduction
2. Original Mazars’ Model and Regularization in Tension
2.1. Original Formulation
- The maximum stress in tension must be equal to ( in compression);
- The asymptotic tension stress with infinite strains should be 0 (hence );
- The peak compression stress must be reached at the strain .
2.2. Mazars’ Model with Tension Energy Regularization
2.3. Application of the Mazars’ RT Model to the Pushout Test
3. Towards a Regularized Model in Compression
3.1. Proposition of a Modified Mazars’ Model Combining Tensile and Compressive Energy Regularization
- The definition of the facture energy (as written in Equation (2)), as the stress never goes back to zero; hence, the absorbed energy according to Equation (2) tends to infinity;
- The physical consistency of the model, as the residual stress is mesh-dependent, located between 0 and (with the Poisson ratio set to 0.2).
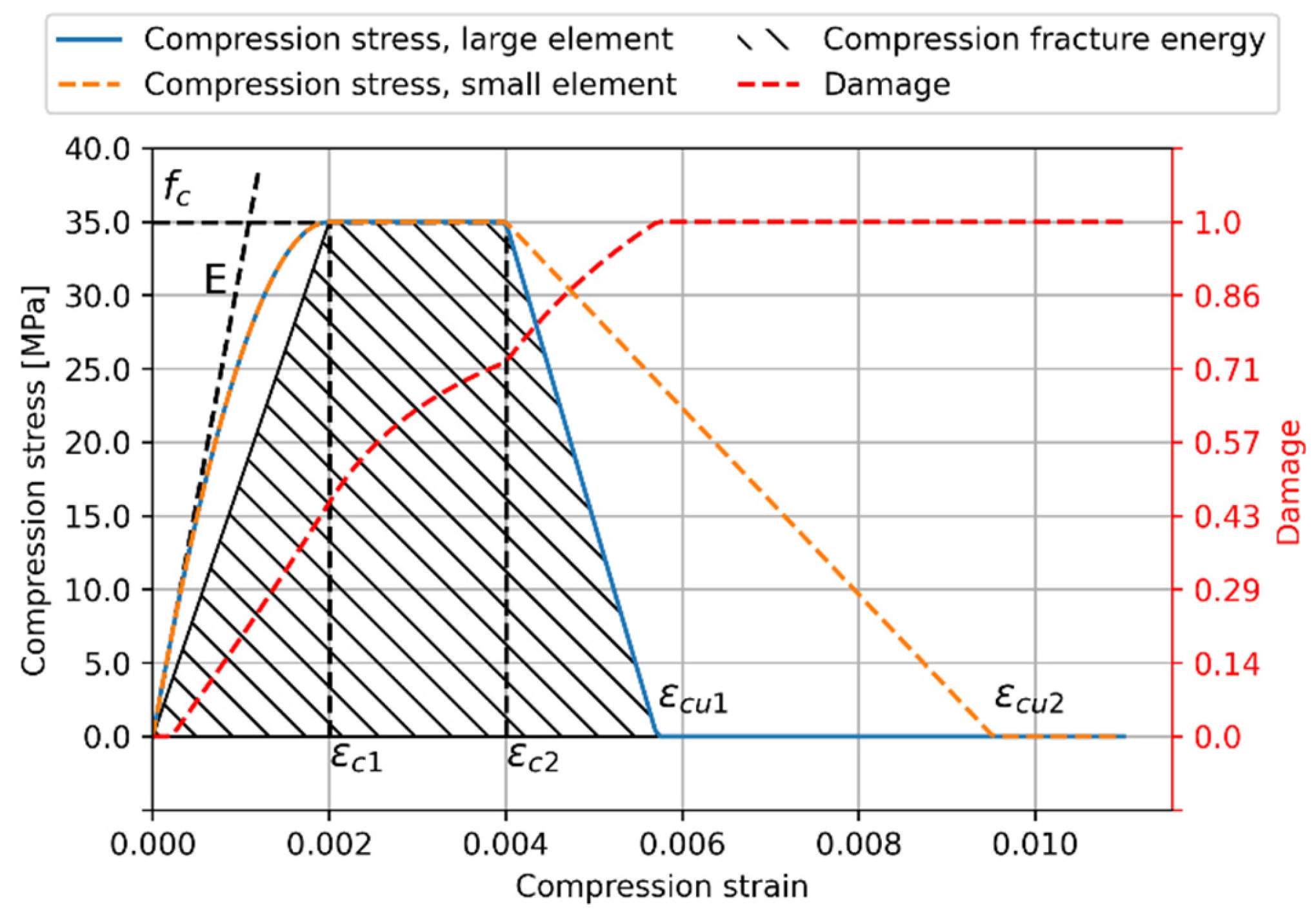
- An initial elastic phase between strains and .
- The first softening phase is adapted from the Model Code 2010 model for non-linear concrete [33].
- The second phase is a plateau at the stress between the strains and .
- The third phase is a linear softening branch from to 0, between the strains and .
- A fractured phase where (or a close value to avoid zero-stiffness) after having reached .
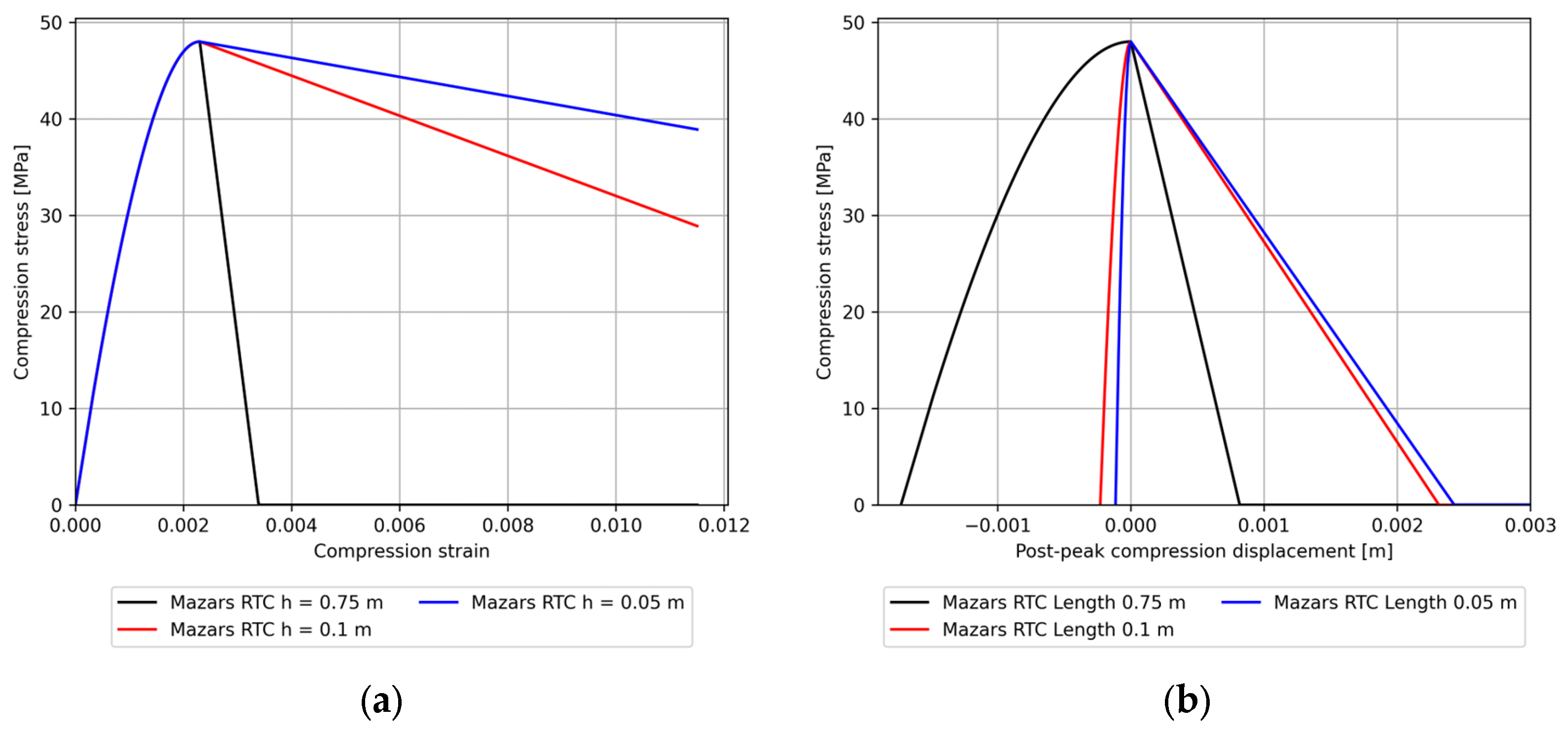
3.2. Validation on a Cube under Uniaxial Compression
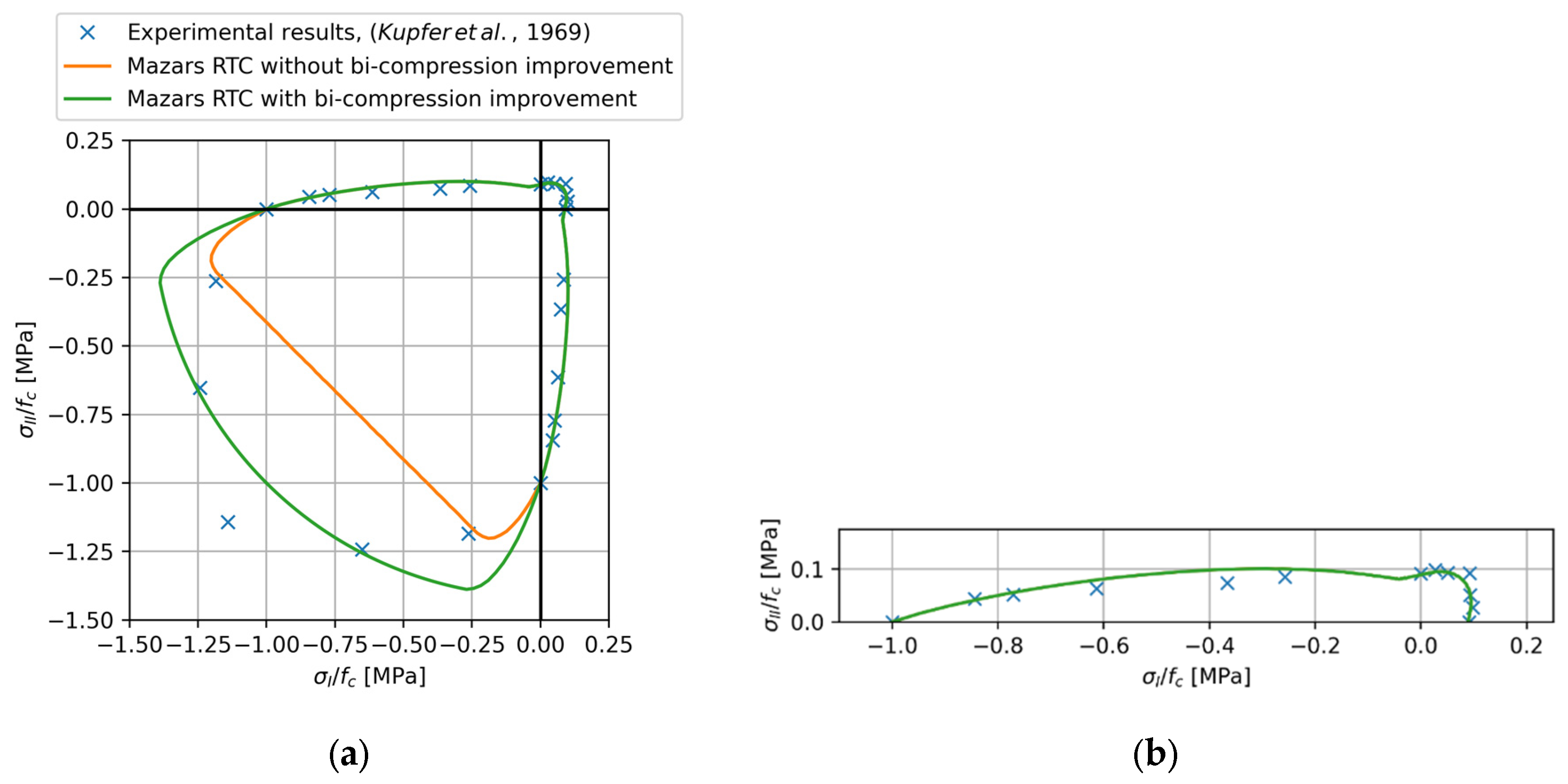
3.3. Cube under Bi-Axial Compression
4. Validation of Mazars’ RTC Model in Structural Compression
- a skewed crack prism under compression load adapted from [34];
- a 3-point bending test on a regular reinforced concrete beam [35];
- the pushout test from Section 2.3 [15].
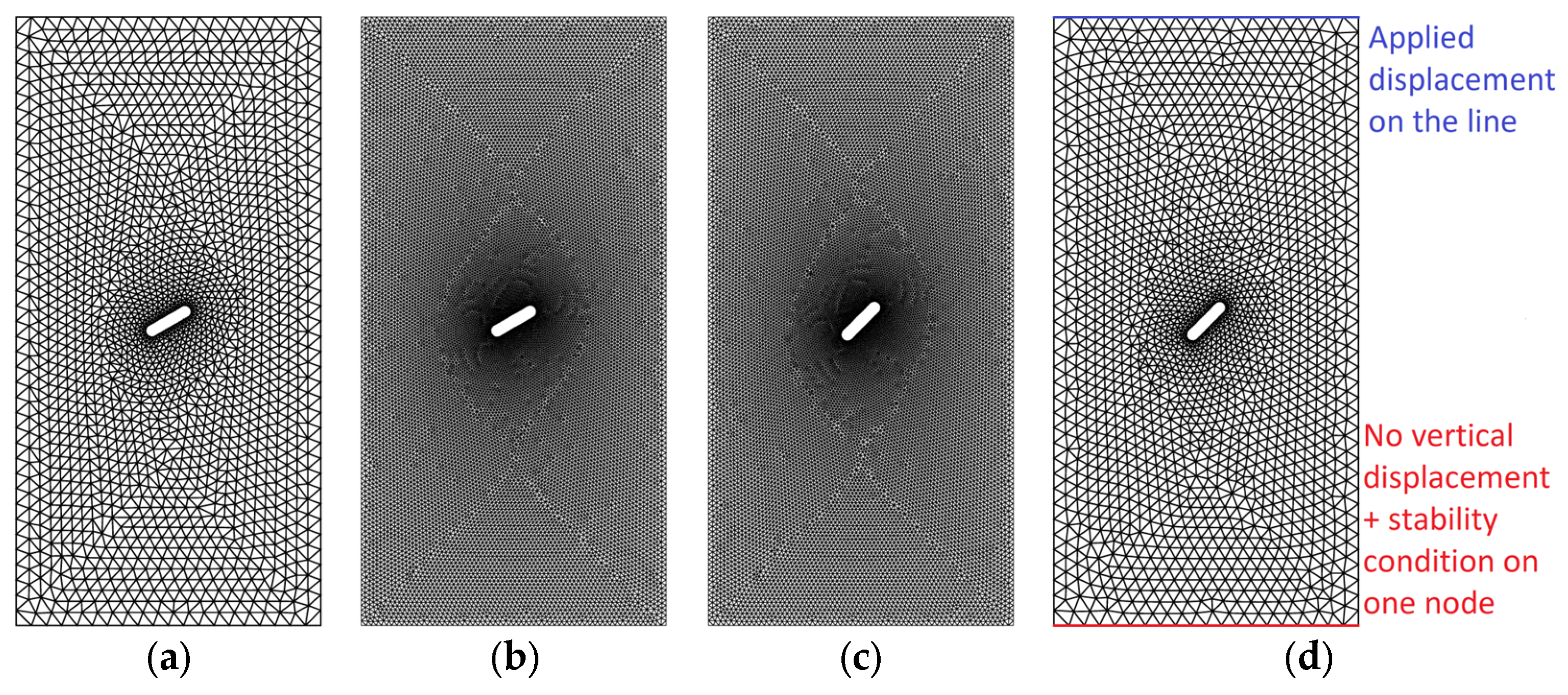
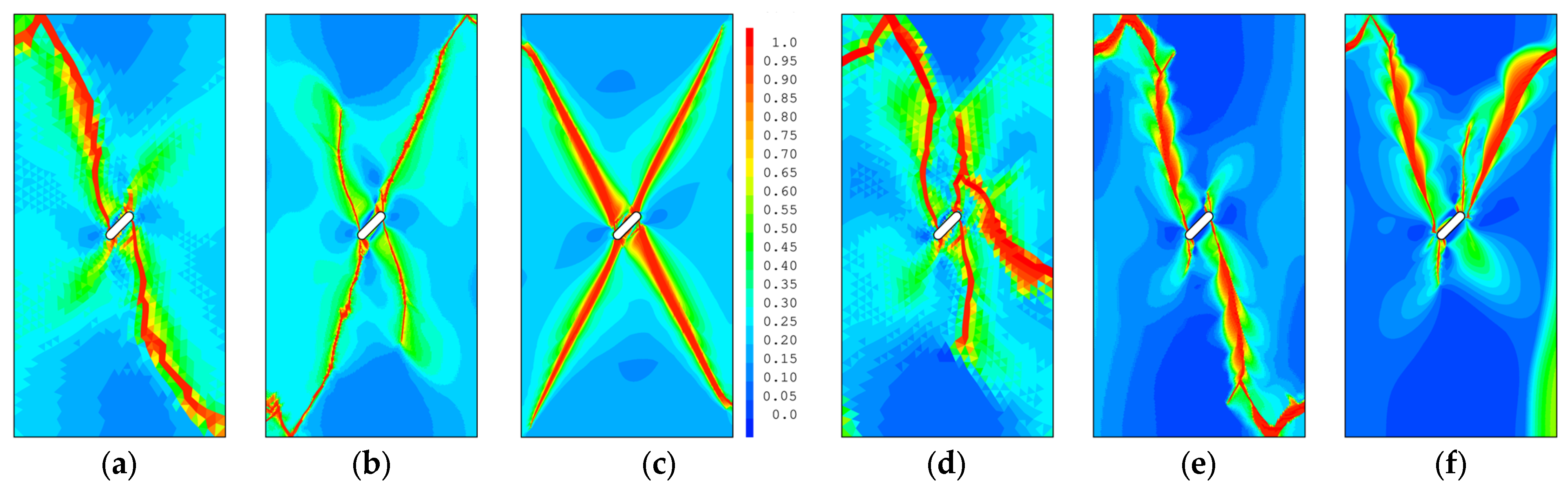
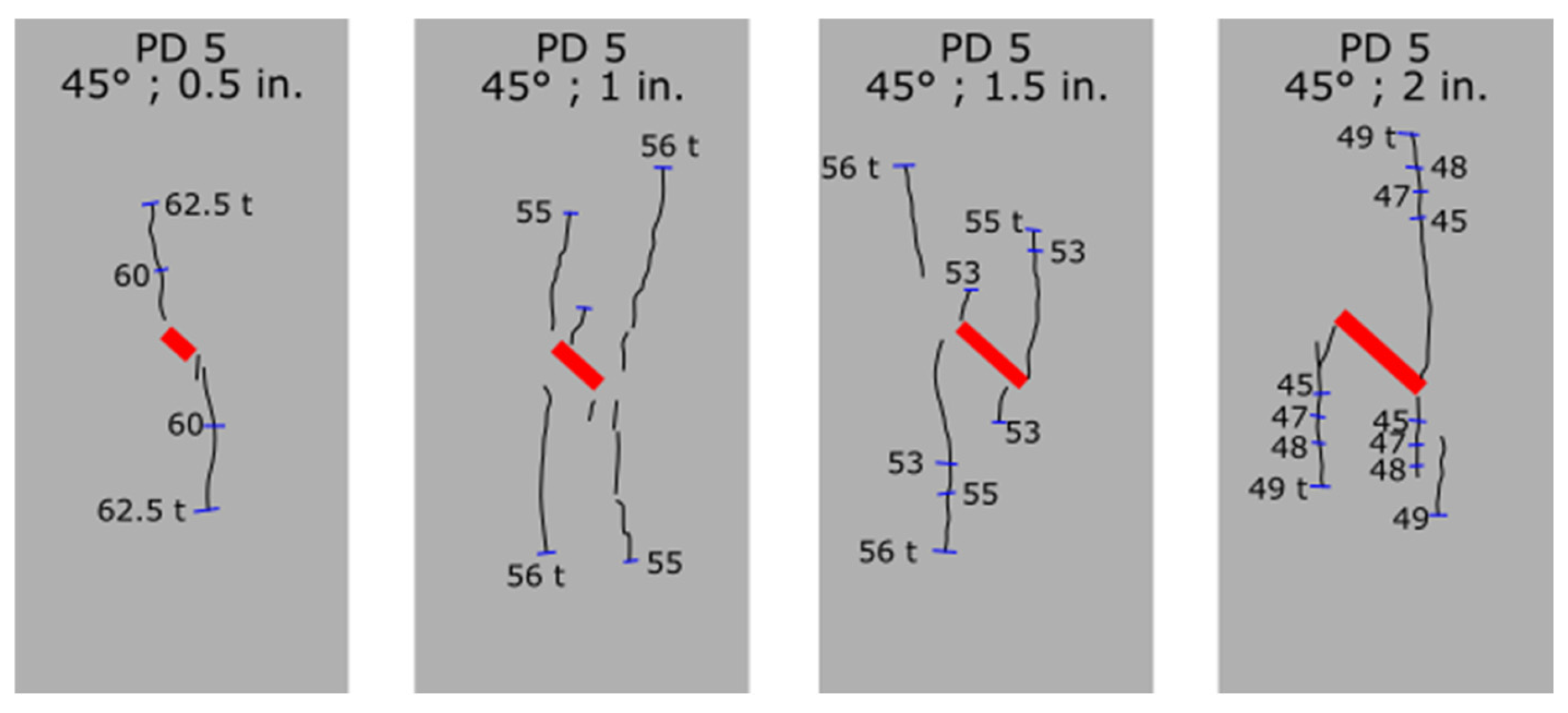
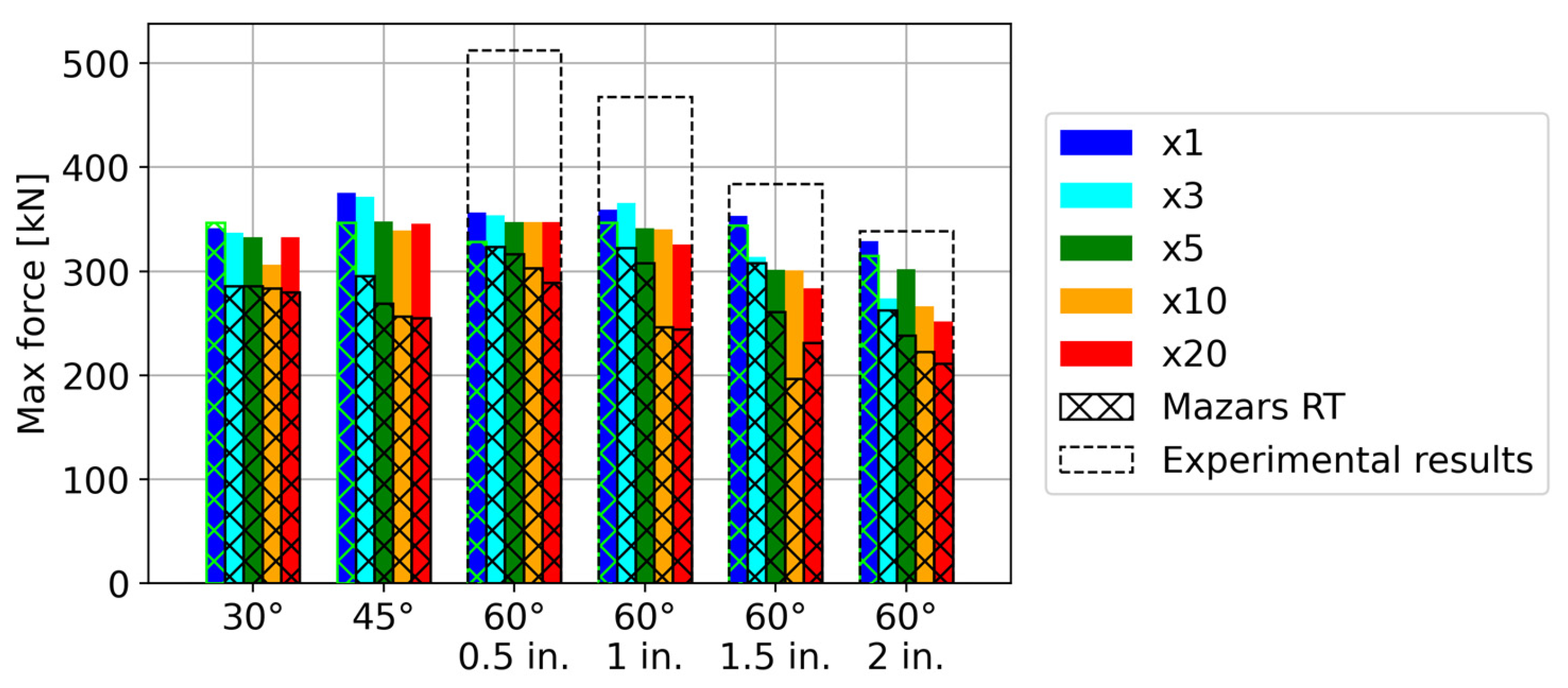
4.1. Skewed Crack Prisms
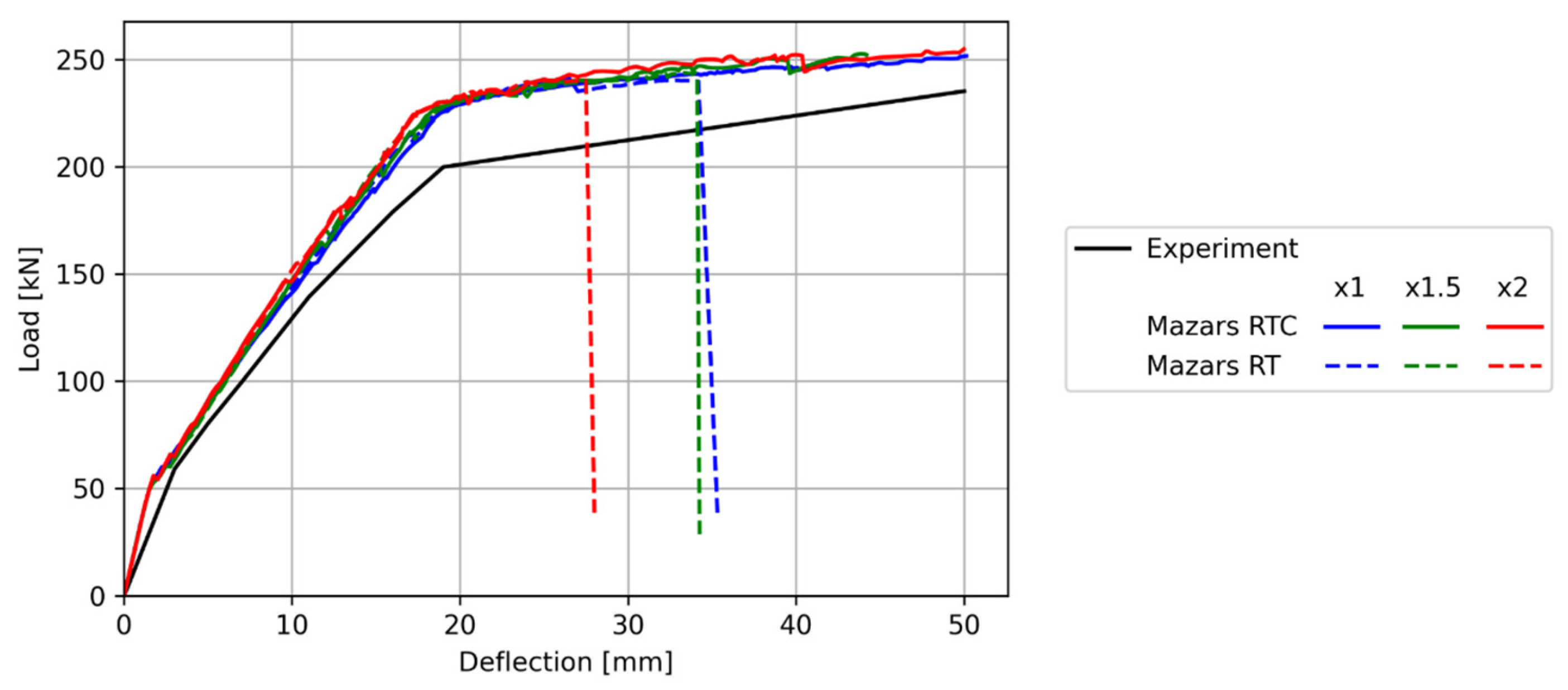
4.2. Three-Point Bending
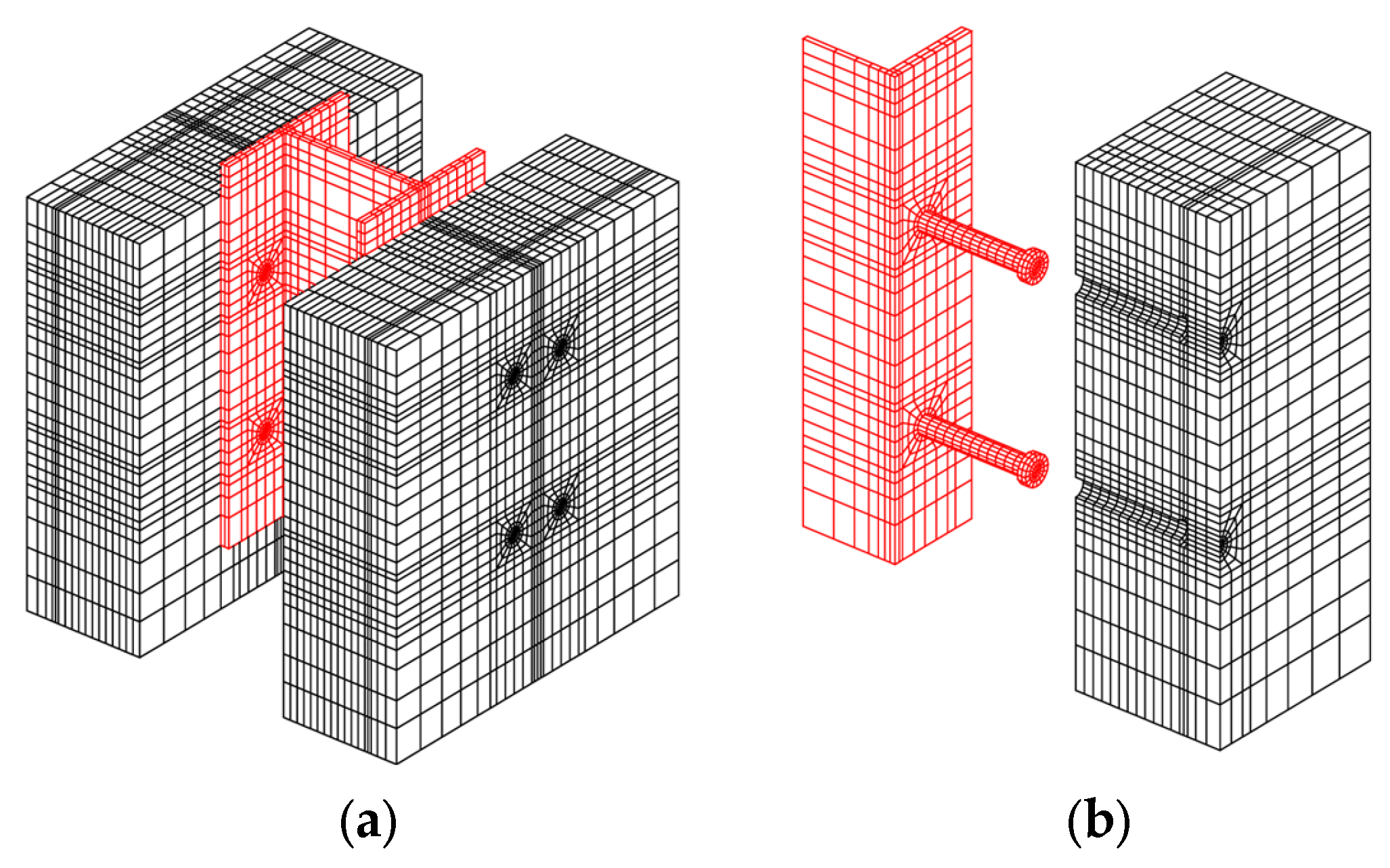
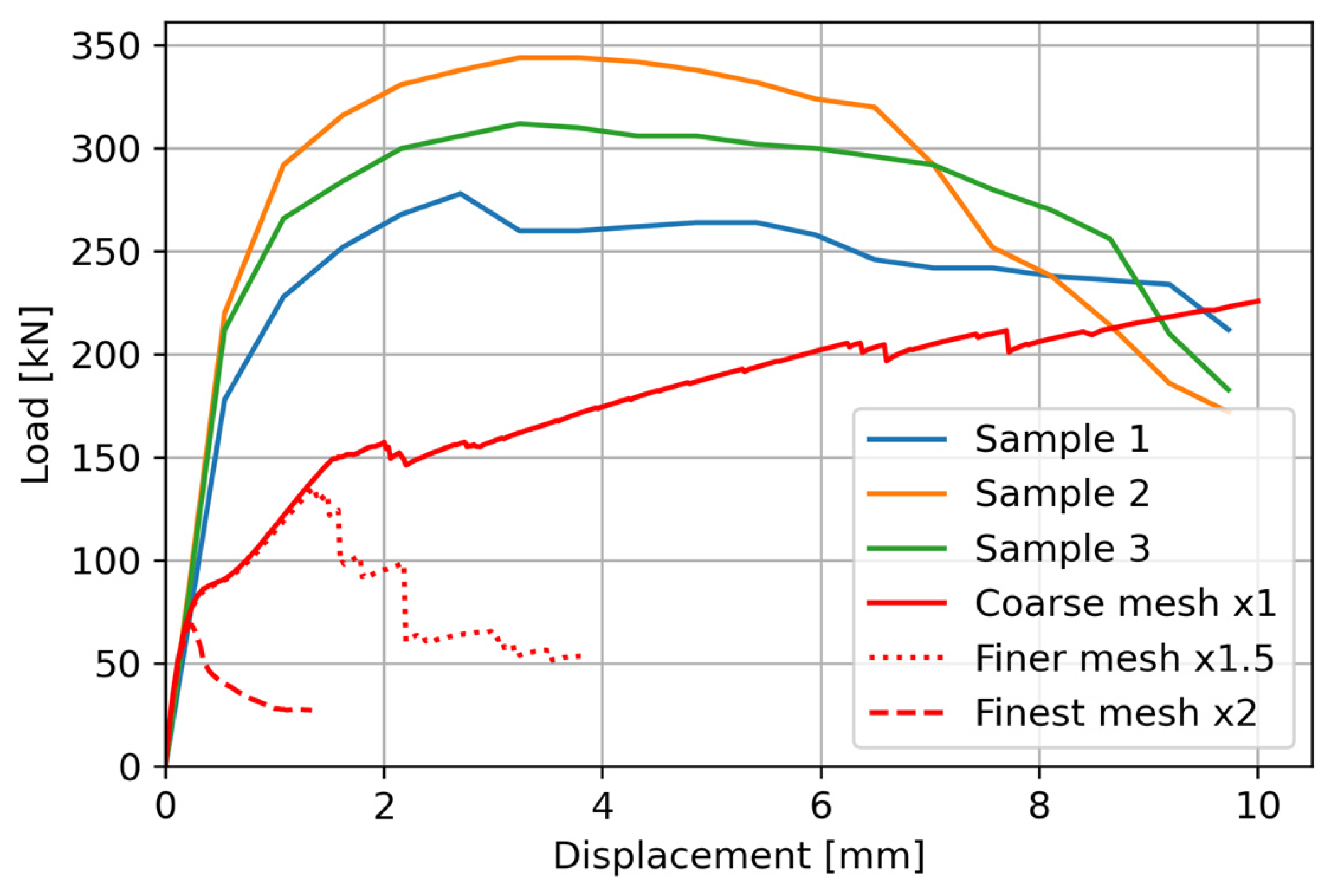
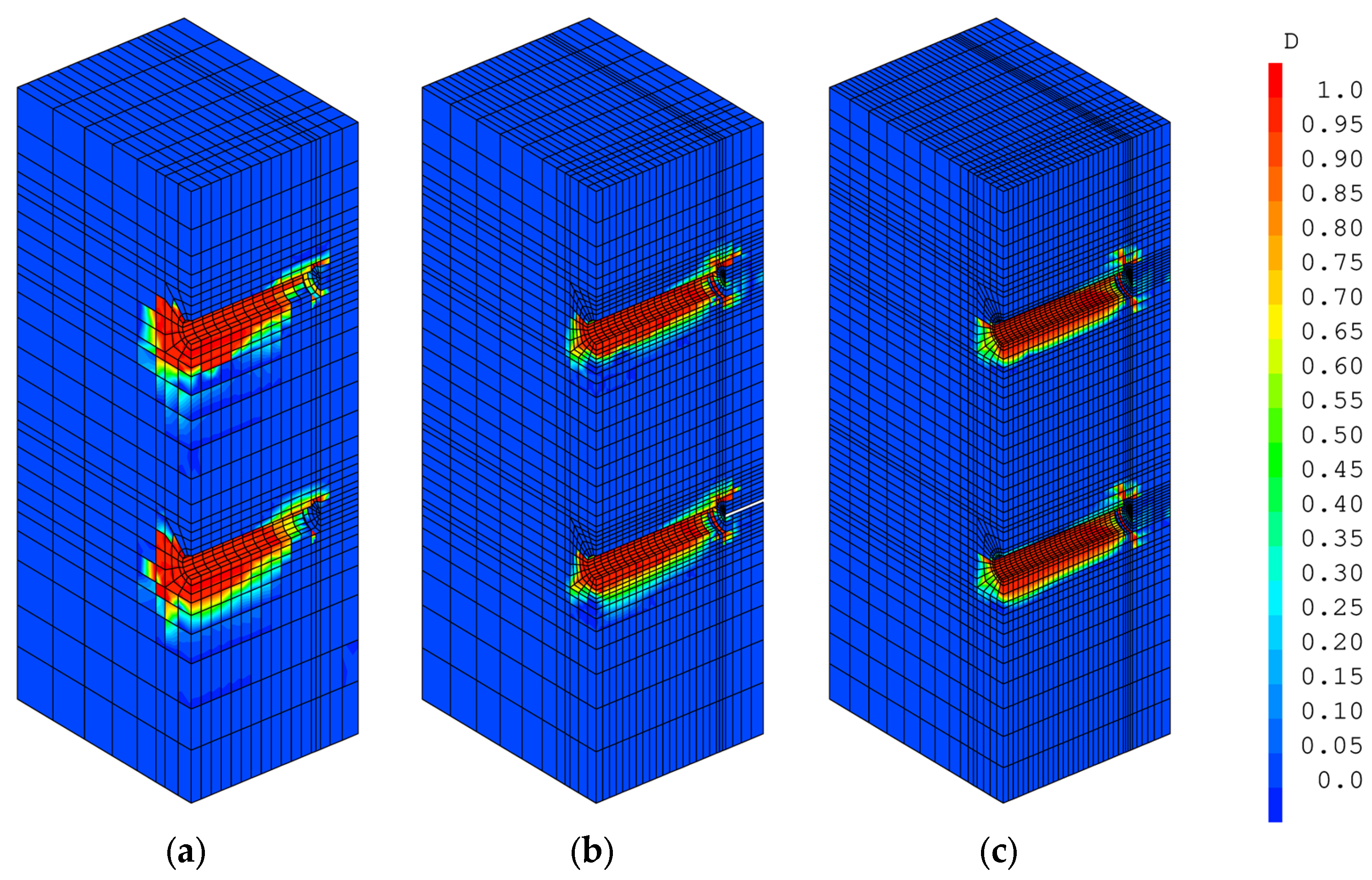
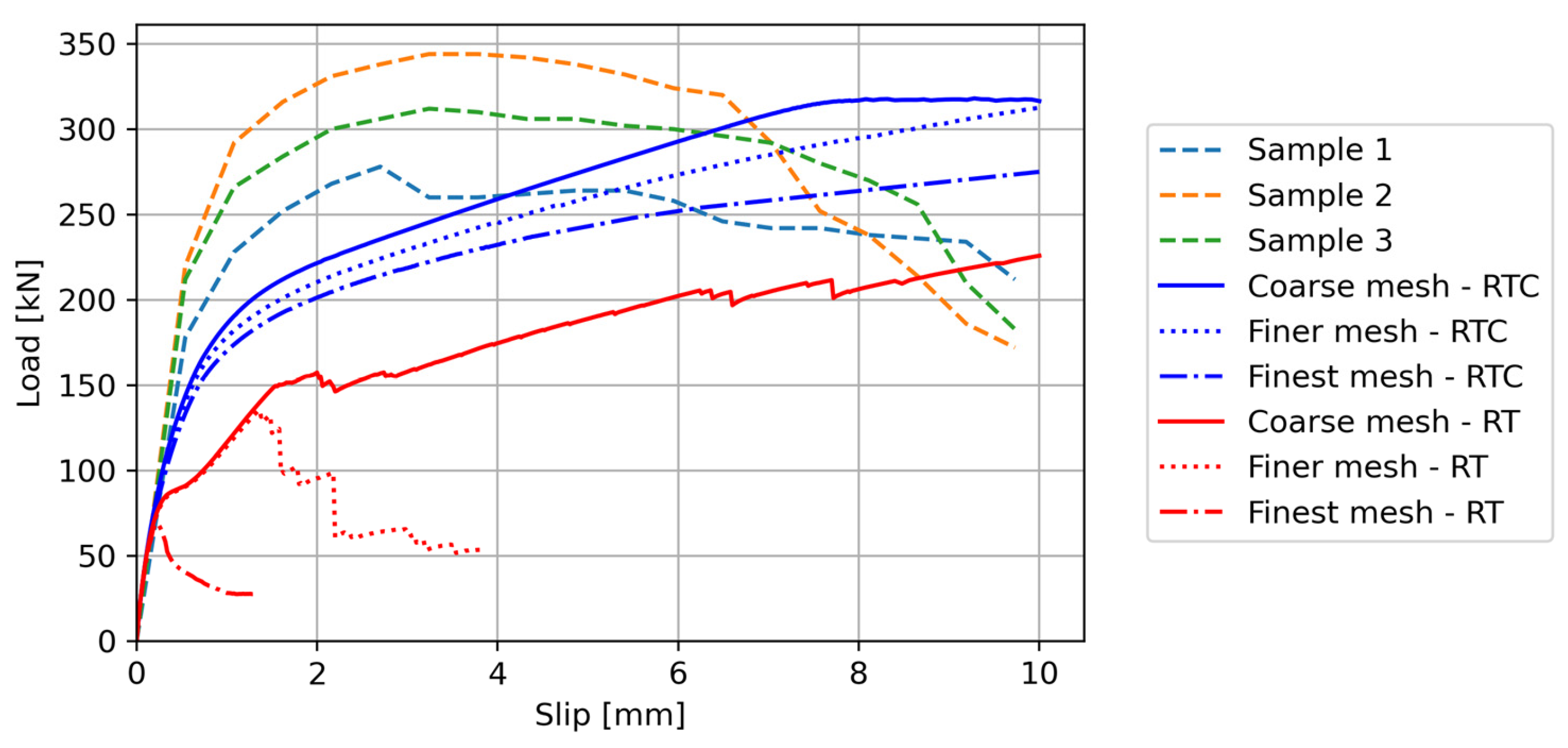
4.3. Pushout Tests
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rashid, Y.R. Ultimate Strength Analysis of Prestressed Concrete Pressure Vessels. Nucl. Eng. Des. 1968, 7, 334–344. [Google Scholar] [CrossRef]
- Ingraffea, A.R.; Saouma, V. Numerical Modeling of Discrete Crack Propagation in Reinforced and Plain Concrete. In Fracture Mechanics of Concrete: Structural Application and Numerical Calculation; Springer: Dordrecht, The Netherlands, 1985; Volume 4, pp. 171–225. ISBN 978-94-009-6152-4. [Google Scholar]
- Melenk, J.M.; Babuška, I. The Partition of Unity Finite Element Method: Basic Theory and Applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef]
- Cicekli, U.; Voyiadjis, G.Z.; Abu Al-Rub, A.K. A Plasticity and Anisotropic Damage Model for Plain Concrete. Int. J. Plast. 2007, 23, 1874–1900. [Google Scholar] [CrossRef]
- Alfarah, B.; López-Almansa, F.; Oller, S. New Methodology for Calculating Damage Variables Evolution in Plastic Damage Model for RC Structures. Eng. Struct. 2017, 132, 70–86. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Mazars, J. A Description of Micro- and Macroscale Damage of Concrete Structures. Eng. Fract. Mech. 1986, 25, 729–737. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.-E. Analysis of Crack Formation and Crack Growth in Concrete by Means of Fracture Mechanics and Finite Elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Oh, B.H. Crack Band Theory for Fracture of Concrete. Matér. Constr. 1983, 16, 155–177. [Google Scholar] [CrossRef]
- Pijaudier-Cabot, G.; Bažant, Z.P. Nonlocal Damage Theory. J. Eng. Mech. 1987, 113, 1512–1533. [Google Scholar] [CrossRef]
- Peerlings, R.H.J.; Geers, M.G.D.; de Borst, R.; Brekelmans, W.A.M. A Critical Comparison of Nonlocal and Gradient-Enhanced Softening Continua. Int. J. Solids Struct. 2001, 38, 7723–7746. [Google Scholar] [CrossRef]
- Giry, C.; Dufour, F.; Mazars, J. Stress-Based Nonlocal Damage Model. Int. J. Solids Struct. 2011, 48, 3431–3443. [Google Scholar] [CrossRef]
- Coleman, J.; Spacone, E. Localization Issues in Force-Based Frame Elements. J. Struct. Eng. 2001, 127, 1257–1265. [Google Scholar] [CrossRef]
- Calixte, R.; Davenne, L.; Jason, L. Refined and Simplified Modelling of Steel-Concrete-Steel (SCS) Composite Beams. In Computational Modelling of Concrete and Concrete Structures; CRC Press: London, UK, 2022; pp. 332–340. [Google Scholar]
- Shim, C.-S.; Lee, P.-G.; Yoon, T.-Y. Static Behavior of Large Stud Shear Connectors. Eng. Struct. 2004, 26, 1853–1860. [Google Scholar] [CrossRef]
- Červenka, J.; Červenka, V.; Laserna, S. On Crack Band Model in Finite Element Analysis of Concrete Fracture in Engineering Practice. Eng. Fract. Mech. 2018, 197, 27–47. [Google Scholar] [CrossRef]
- Lertsrisakulrat, T.; Watanabe, K.; Matsuo, M.; Niwa, J. Experimental Study on Parameters in Localization of Concrete Subjected to Compression. J. Mater. Concr. Struct. Pavements JSCE 2001, 50, 309–321. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, H.; Higai, T. Compressive Fracture Energy and Fracture Zone Length of Concrete. In Modeling of Inelastic Behavior of RC Structures under Seismic Loads; ASCE: Reston, VA, USA, 2001; pp. 471–487. [Google Scholar]
- Oliver, J. A Consistent Characteristic Length for Smeared Cracking Models. Int. J. Numer. Methods Eng. 1989, 28, 461–474. [Google Scholar] [CrossRef]
- Arruda, M.R.T.; Pacheco, J.; Castro, L.M.S.; Julio, E. A Modified Mazars Damage Model with Energy Regularization. Eng. Fract. Mech. 2022, 259, 108129. [Google Scholar] [CrossRef]
- Comi, C.; Perego, U. Fracture Energy Based Bi-Dissipative Damage Model for Concrete. Int. J. Solids Struct. 2001, 38, 6427–6454. [Google Scholar] [CrossRef]
- Pijaudier-Cabot, G.; Mazars, J.; Pulikowski, J. Steel-Concrete Bond Analysis with Nonlocal Continuous Damage. J. Struct. Eng. 1991, 117, 862–882. [Google Scholar] [CrossRef]
- European Committee for Standardization. Eurocode 2: Design of Concrete Structures, Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Kupfer, H.; Hilsdorf, H.K.; Rusch, H. Behavior of Concrete under Biaxial Stresses. J. Proc. 1969, 66, 656–666. [Google Scholar] [CrossRef]
- Davenne, L.; Saouridis, C.; Piau, J. Un Code de Calcul Pour La Prévision Du Comportement de Structures Endommageables En Béton, En Béton Armé, Ou En Béton de Fibres. Ann. Inst. Tech. Bâtim. Trav. Publics 1989, B267, 137–156. [Google Scholar]
- Feenstra, P.H.; De Borst, R. A Composite Plasticity Model for Concrete. Int. J. Solids Struct. 1996, 33, 707–730. [Google Scholar] [CrossRef]
- Jirásek, M.; Bauer, M. Numerical Aspects of the Crack Band Approach. Comput. Struct. 2012, 110–111, 60–78. [Google Scholar] [CrossRef]
- European Committee for Standardization. Eurocode 4, Design of Composite Steel and Concrete Structures, Part 1-1, General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Calixte, R.; Jason, L.; Davenne, L. Refined and Simplified Simulations for Steel–Concrete–Steel Structures. Appl. Mech. 2023, 4, 1078–1099. [Google Scholar] [CrossRef]
- CEA CAST3M 2024. Available online: https://www-cast3m.cea.fr/ (accessed on 11 June 2004).
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Kim, S.E. Finite Element Modeling of Push-out Tests for Large Stud Shear Connectors. J. Constr. Steel Res. 2009, 65, 1909–1920. [Google Scholar] [CrossRef]
- Fib Model Code 2010; Bulletins 55, 56, 65 and 66; Wilhelm Ernst & Sohn: Berlin, Germany, 2012.
- Desayi, P. Fracture of Concrete in Compression. Matér. Constr. 1977, 10, 139–144. [Google Scholar] [CrossRef]
- Péra, J. Poutres Hyperstatiques en Béton Armé: Analyse Théorique et Expérimentale. Ph.D. Thesis, INSA Lyon, Villeurbanne, France, 1973. [Google Scholar]
- Arrea, M.; Ingraffea, A.R. Mixed Mode Crack Propagation in Mortar and Concrete; Cornell University, Department of Structural Engineering: Ithaca, NY, USA, 1981. [Google Scholar]
- Dawari, V.B.; Vesmawala, G.R. Application of Nonlinear Concrete Model for Finite Element Analysis of Reinforced Concrete Beams. Int. J. Sci. Eng. Res. 2014, 5, 776–782. [Google Scholar]
- Kwak, H.G.; Filippou, F.C. Finite Element Analysis of Reinforced Concrete Structures under Monotonic Loads; University of California: Berkeley, CA, USA, 1990. [Google Scholar]







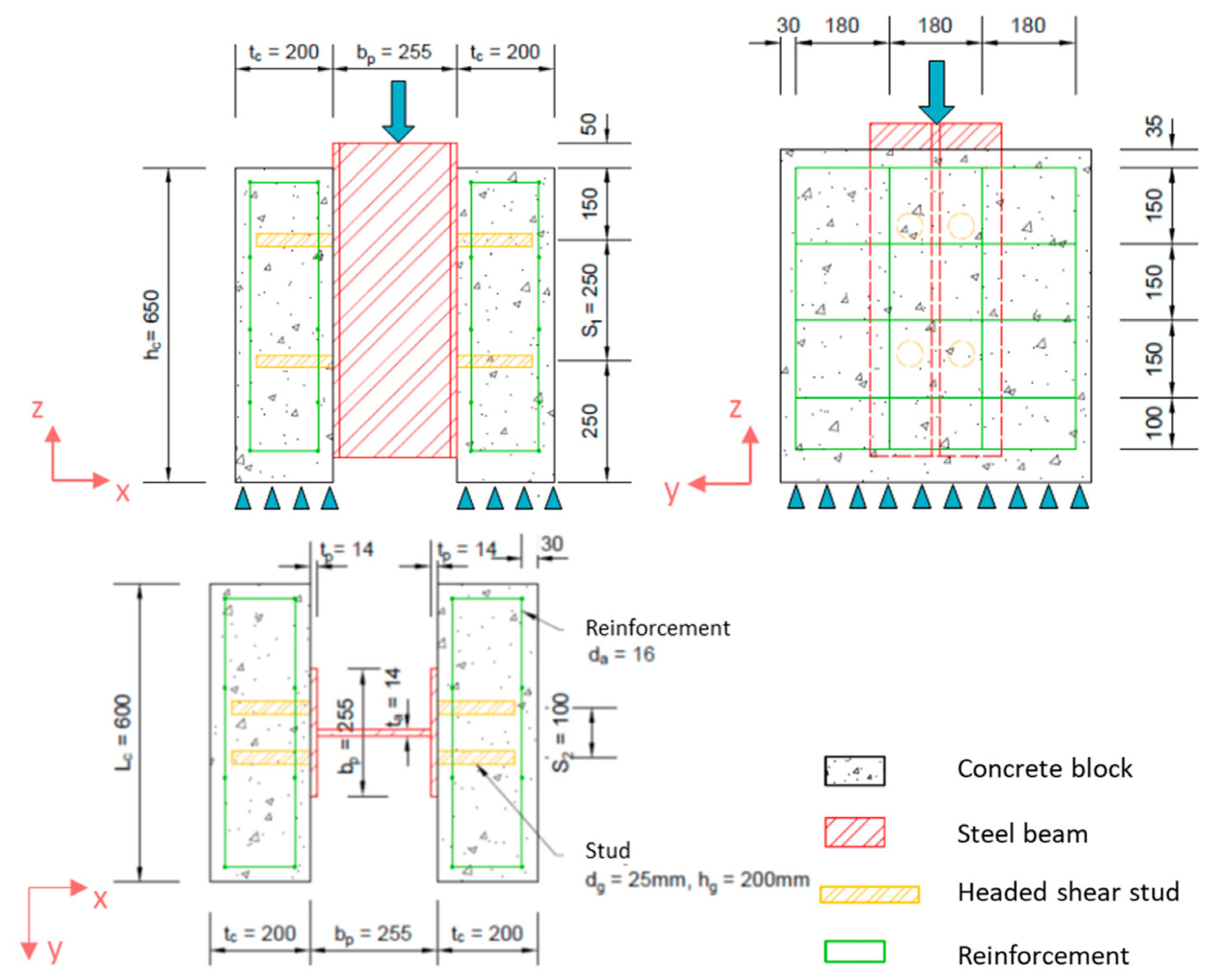
| Stud Diameter | Stud Length (Including Head) | Head Diameter | Head Length |
|---|---|---|---|
| 25 mm | 155 mm | 38 mm | 11 mm |
| Concrete | Compression Strength | Young’s Modulus | Poisson Ratio | Tension Strength | Compressive Fracture Energy | Tensile Fracture Energy |
| 35.3 MPa | 32.1 GPa | 0.2 | 3.23 MPa | 50.0 kN/m | 150 N/m | |
| W-flange beam Steel | Yield strength | Young’s modulus | Poisson ratio | Hardening modulus | – | – |
| 235 MPa | 210 GPa | 0.3 | 9 GPa | – | – | |
| Stud steel | Yield strength | Young’s modulus | Poisson ratio | Hardening modulus | – | – |
| 426 MPa | 210 GPa | 0.3 | 9 GPa | – | – |
| Size | Mazars’ RTC Parameters | |||||
|---|---|---|---|---|---|---|
| 0.75 m | ||||||
| 0.1 m | ||||||
| 0.05 m | ||||||
| Height | Length | Thickness | Length of the Crack | Angle of the Crack |
|---|---|---|---|---|
| 12 in. (30.48 cm) | 6 in. (15.24 cm) | 6 in. (15.24 cm) | 0.5, 1.0, 1.5 and 2.0 in. (1.3, 2.5, 3.8 and 5.1 cm) | 30°, 45°, and 60° |
| Specimen Angle | Concrete Strength [MPa] | Young’s Modulus [GPa] | Poisson’s Ratio | Tension Strength [MPa] | Tension Fracture Energy [N/m] | Compression Fracture Energy [N/m] |
|---|---|---|---|---|---|---|
| 60° | 25.3 | 29.0 | 0.2 | 2.0 | 130 | 44,300 |
| 45° | 26.4 | 29.4 | 0.2 | 2.1 | 130 | 45,200 |
| 30° | 24.6 | 28.8 | 0.2 | 1.9 | 130 | 43,600 |
| Concrete | Compression Strength | Young’s Modulus | Poisson Ratio | Tension Strength | Compressive Fracture Energy | Tensile Fracture Energy |
| 38.3 MPa | 37.3 GPa | 0.2 | 3.9 MPa | 54.0 kN/m | 110 N/m | |
| Rebar Steel | Yield strength | Young’s modulus | Poisson ratio | Hardening modulus | – | – |
| 400 MPa | 200 GPa | 0.33 | 3.28 GPa | – | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Debuisne, M.; Davenne, L.; Jason, L. On the Need of Compressive Regularization in Damage Models for Concrete: Demonstration on a Modified Mazars Model. Appl. Mech. 2024, 5, 490-512. https://doi.org/10.3390/applmech5030028
Debuisne M, Davenne L, Jason L. On the Need of Compressive Regularization in Damage Models for Concrete: Demonstration on a Modified Mazars Model. Applied Mechanics. 2024; 5(3):490-512. https://doi.org/10.3390/applmech5030028
Chicago/Turabian StyleDebuisne, Martin, Luc Davenne, and Ludovic Jason. 2024. "On the Need of Compressive Regularization in Damage Models for Concrete: Demonstration on a Modified Mazars Model" Applied Mechanics 5, no. 3: 490-512. https://doi.org/10.3390/applmech5030028
APA StyleDebuisne, M., Davenne, L., & Jason, L. (2024). On the Need of Compressive Regularization in Damage Models for Concrete: Demonstration on a Modified Mazars Model. Applied Mechanics, 5(3), 490-512. https://doi.org/10.3390/applmech5030028