Measuring Residual Stresses with Crack Compliance Methods: An Ill-Posed Inverse Problem with a Closed-Form Kernel
Abstract
1. Introduction
- In Section 2, crack compliance methods and their fundamental equations are introduced, drawing on some basic concepts of fracture mechanics and thus arriving at the equation of the problem concerning the reconstruction of residual stresses.
- In Section 3, the obtained equations are used to run some numerical experiments that expose the peculiar features of ill-posedness.
- In Section 4, the practical consequences for the analyst who must navigate ill-posedness in a residual stress measurement are discussed.
2. Theoretical Background
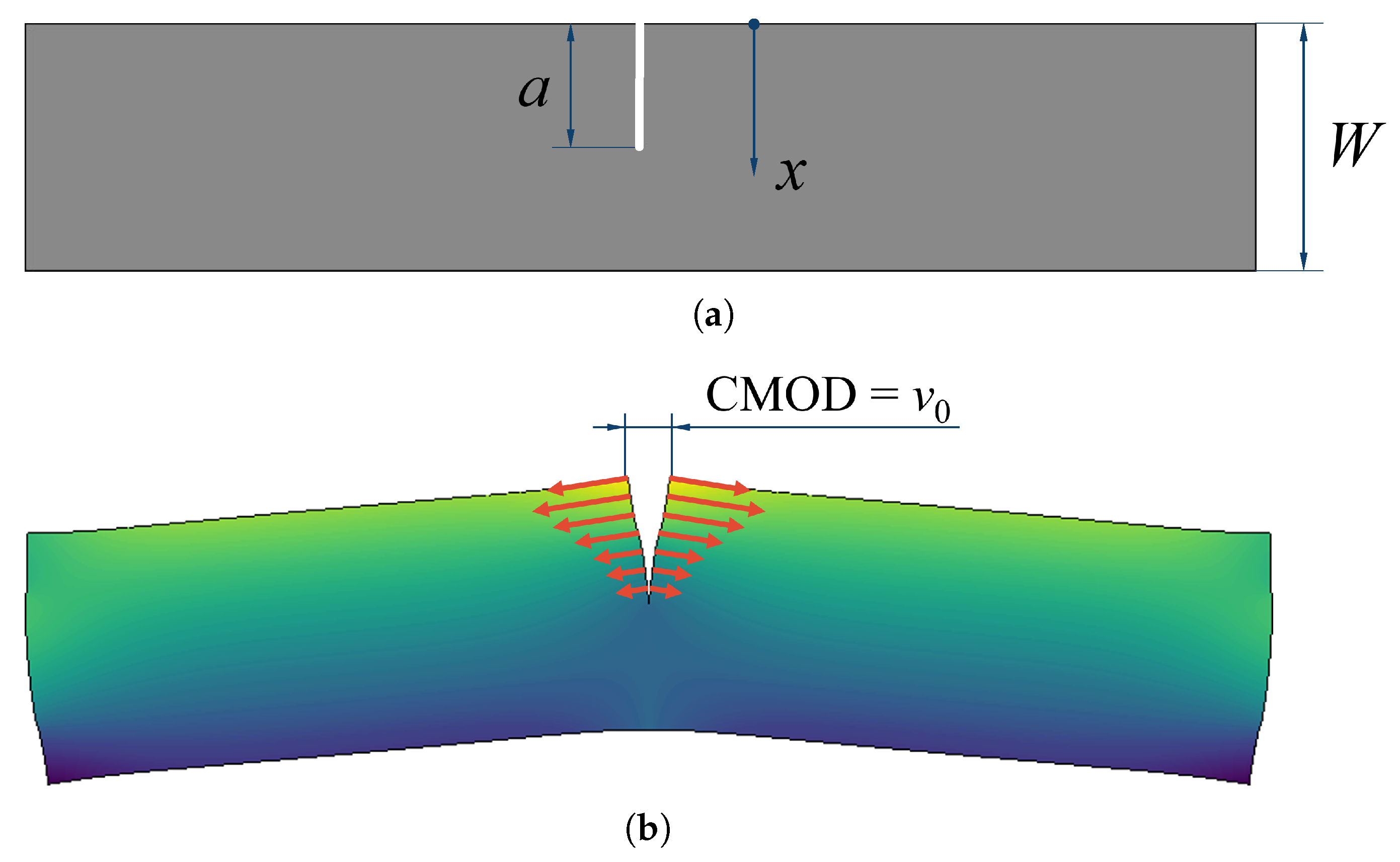
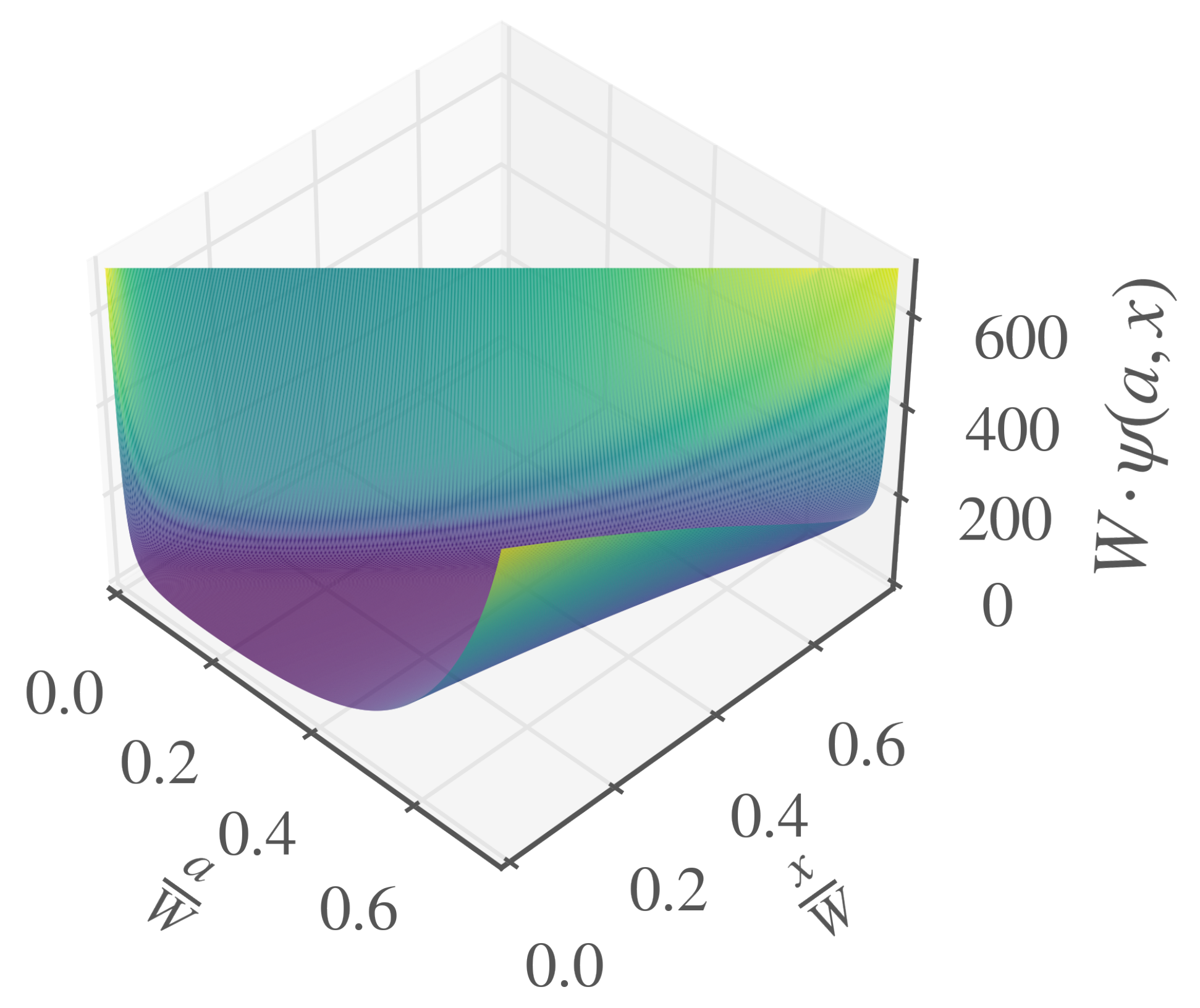
2.1. Crack Compliance Methods
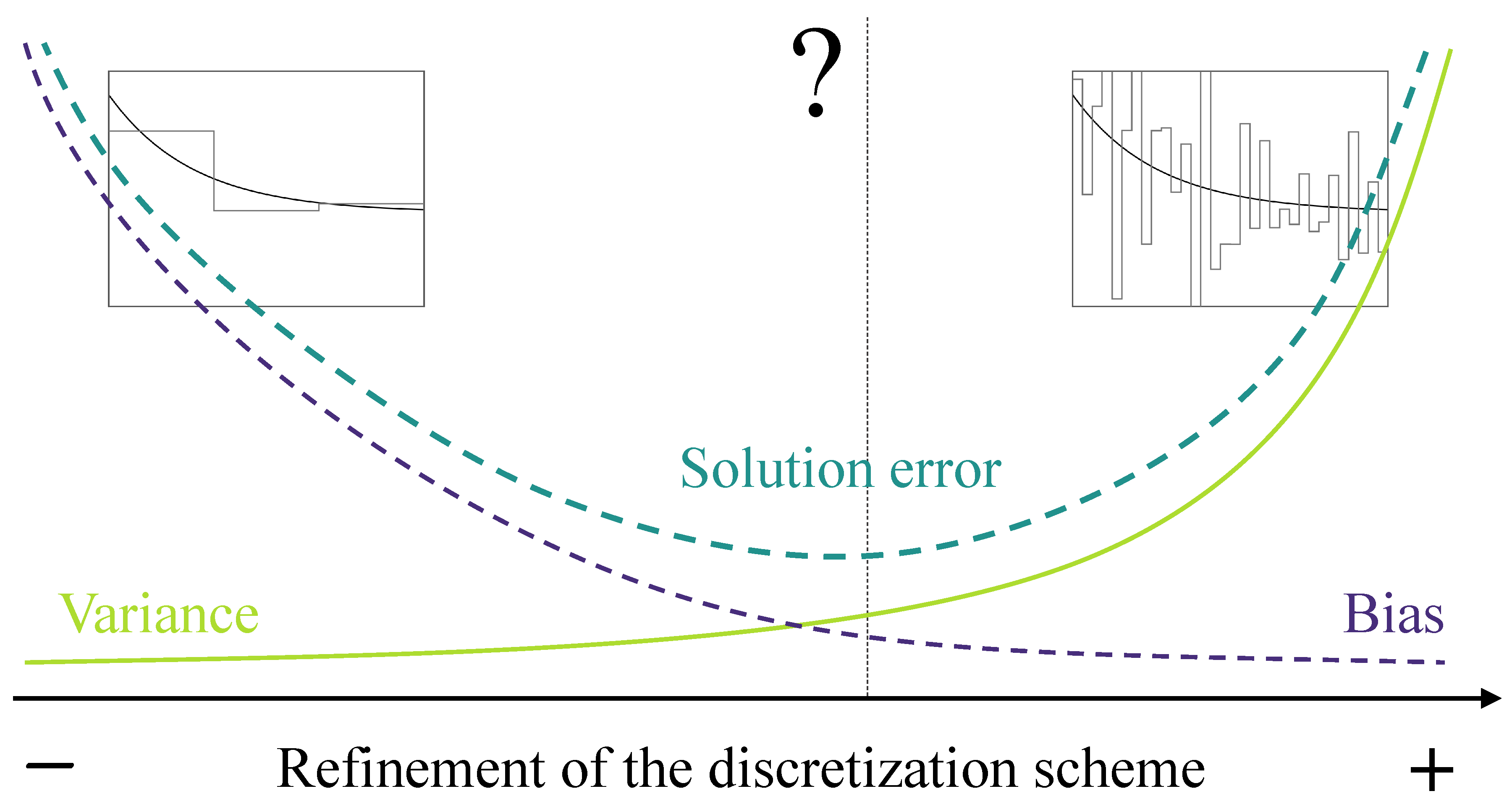
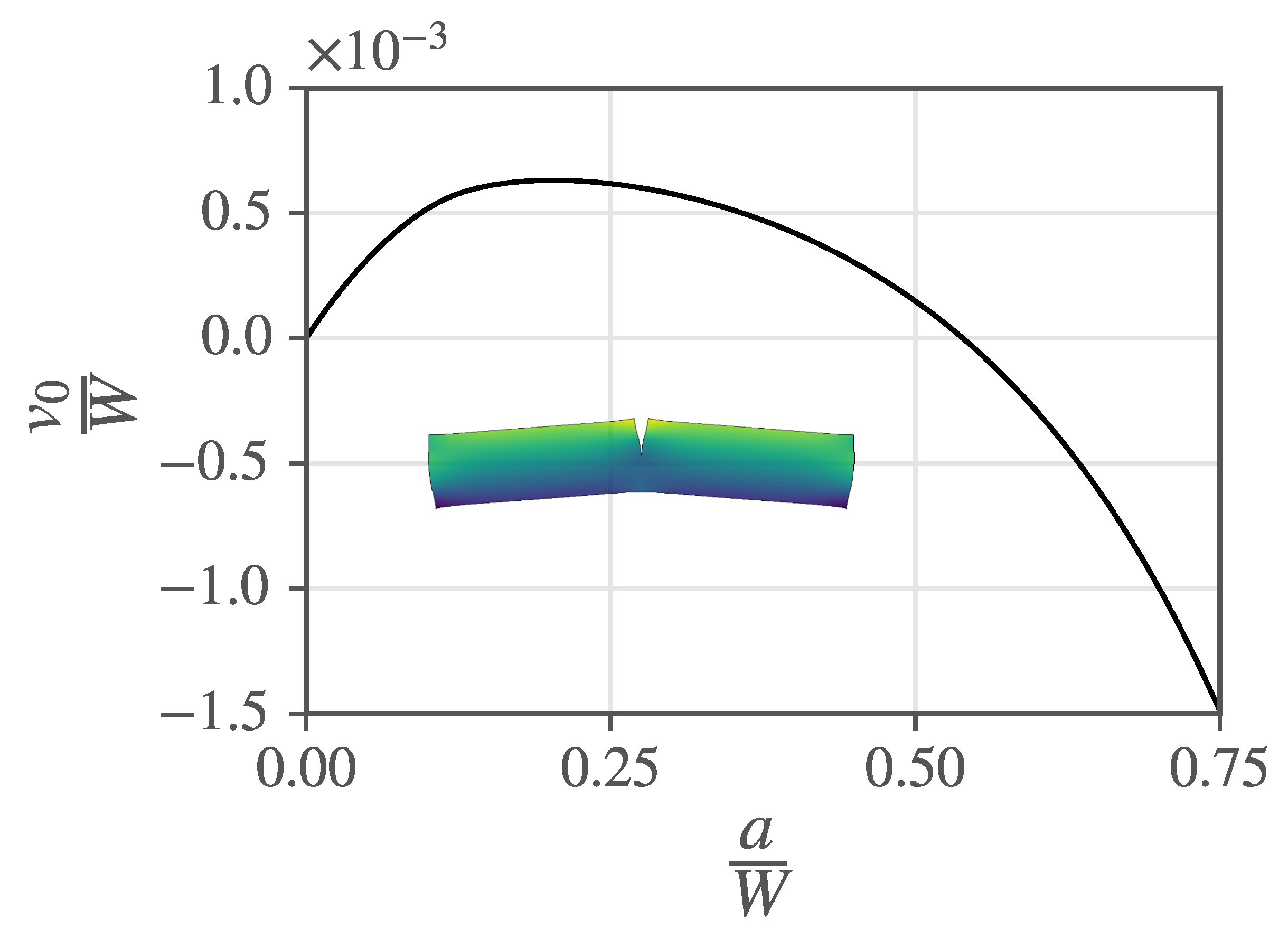
2.2. Ill-Posedness
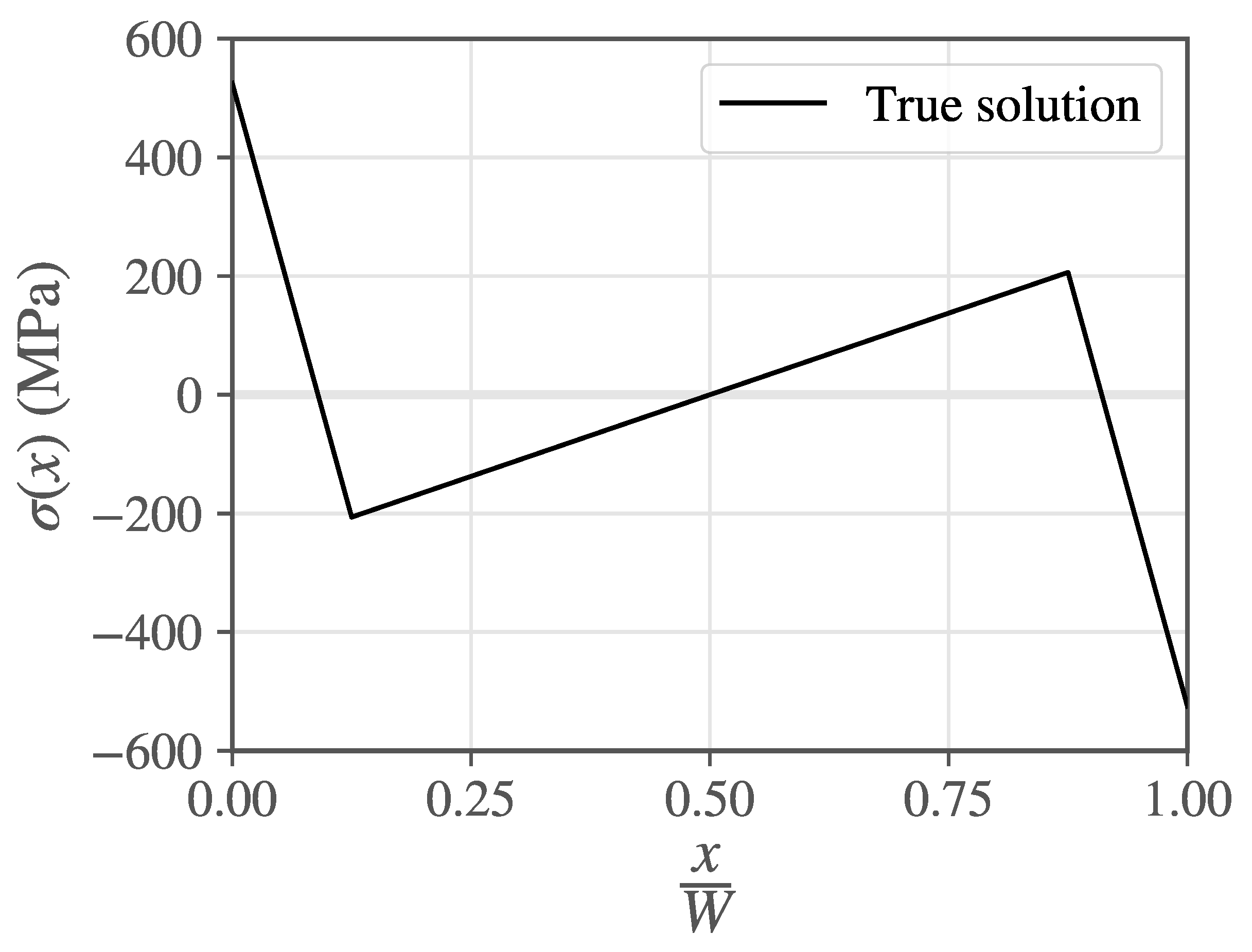
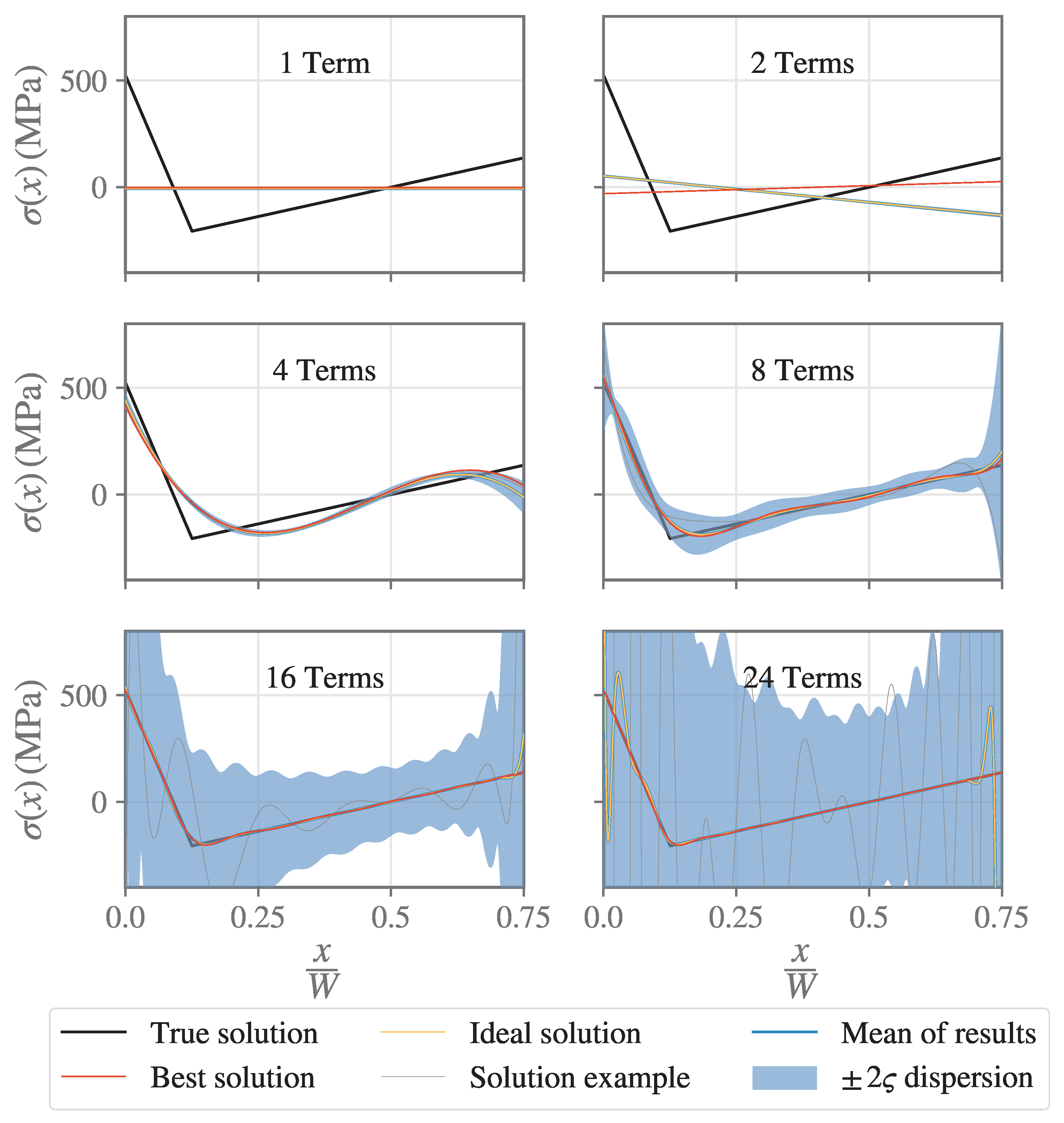
3. Numerical Investigations
- The ideal solution, which is the one corresponding to perfect, errorless CMOD measurements.
- The best solution, which is the element of the chosen stress basis that best approximates the true solution in a least-squares sense.
4. Discussion
5. Conclusions
- The ill-posedness of the problem of reconstructing residual stresses from measurements of crack opening displacement following a progressive cut introduced in the specimen is demonstrated and clearly distinguished from its more general property of being ill-conditioned.
- Through a numerical example, the typical indicator of an ill-posed problem, namely the bias–variance tradeoff, is presented, together with its potentially devastating consequences on the ability to rigorously quantify uncertainties. Therefore, it is extremely important to recognize its presence and avoid actions that only seemingly improve the quality of the solution.
- As stressed in the authors’ previous works, it is again underlined that no mathematical machinery can permanently overcome the infinite sensitivity to input errors that is inherent to ill-posed problems. The solution is to be found in the physics of the problem, aiming at pieces of information that would allow one to tame the solution variance without introducing significant and, above all, uncomputable biases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
Abbreviations
| CMOD | Crack mouth opening displacement |
| FE | Finite element |
| SIF | Stress intensity factor |
| WF | Weight function |
References
- Timoshenko, S. History of Strength of Materials: With a Brief Account of the History of Theory of Elasticity and Theory of Structures; Courier Corporation: North Chelmsford, MA, USA, 1983. [Google Scholar]
- Schajer, G.S.; Winiarski, B.; Withers, P.J. Hole-Drilling Residual Stress Measurement with Artifact Correction Using Full-Field DIC. Exp. Mech. 2013, 53, 255–265. [Google Scholar] [CrossRef]
- Baldi, A. Residual Stress Measurement Using Hole Drilling and Integrated Digital Image Correlation Techniques. Exp. Mech. 2014, 54, 379–391. [Google Scholar] [CrossRef]
- Harrington, J.S.; Schajer, G.S. Measurement of Structural Stresses by Hole-Drilling and DIC. Exp. Mech. 2017, 57, 559–567. [Google Scholar] [CrossRef]
- Hagara, M.; Trebuňa, F.; Pástor, M.; Huňady, R.; Lengvarský, P. Analysis of the aspects of residual stresses quantification performed by 3D DIC combined with standardized hole-drilling method. Measurement 2019, 137, 238–256. [Google Scholar] [CrossRef]
- Salehi, S.D.; Rastak, M.A.; Shokrieh, M.M.; Barrallier, L.; Kubler, R. Full-field measurement of residual stresses in composite materials using the incremental slitting and digital image correlation techniques. Exp. Mech. 2020, 60, 1239–1250. [Google Scholar] [CrossRef]
- Petzing, J.N.; Tyrer, J.R. Recent developments and applications in electronic speckle pattern interferometry. J. Strain Anal. Eng. Des. 1998, 33, 153–169. [Google Scholar] [CrossRef]
- Schajer, G.S.; Steinzig, M. Full-field calculation of hole drilling residual stresses from electronic speckle pattern interferometry data. Exp. Mech. 2005, 45, 526–532. [Google Scholar] [CrossRef]
- Gubbels, W.L.; Schajer, G.S. Development of 3-D Digital Image Correlation Using a Single Color-Camera and Diffractive Speckle Projection. Exp. Mech. 2016, 56, 1327–1337. [Google Scholar] [CrossRef]
- Schajer, G.S.; Prime, M.B.; Withers, P.J. Why Is It So Challenging to Measure Residual Stresses? Exp. Mech. 2022, 62, 1521–1530. [Google Scholar] [CrossRef]
- Noyan, I.C.; Cohen, J.B. Residual Stress: Measurement by Diffraction and Interpretation; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sachs, G.; Espey, G. The measurement of residual stresses in metal. Iron Age 1941, 148, 148. [Google Scholar]
- Treuting, R.G.; Read, W.T. A Mechanical Determination of Biaxial Residual Stress in Sheet Materials. J. Appl. Phys. 1951, 22, 130–134. [Google Scholar] [CrossRef]
- Beaney, E.M. Accurate measurement of residual stress on any steel using the centre hole method. Strain 1976, 12, 99–106. [Google Scholar] [CrossRef]
- Schajer, G.S. Application of Finite Element Calculations to Residual Stress Measurements. J. Eng. Mater. Technol. 1981, 103, 157–163. [Google Scholar] [CrossRef]
- Prime, M.B. Residual Stress Measurement by Successive Extension of a Slot: The Crack Compliance Method. Appl. Mech. Rev. 1999, 52, 75–96. [Google Scholar] [CrossRef]
- Prime, M.B. Cross-Sectional Mapping of Residual Stresses by Measuring the Surface Contour After a Cut. J. Eng. Mater. Technol. 2001, 123, 162–168. [Google Scholar] [CrossRef]
- Schajer, G.S. Practical Residual Stress Measurement Methods; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Schajer, G.S. Hole Eccentricity Correction for Hole-Drilling Residual Stress Measurements. Exp. Mech. 2022, 62, 1603–1613. [Google Scholar] [CrossRef]
- Bueckner, H.F. Novel principle for the computation of stress intensity factors. Z. Fuer Angew. Math. Mech. 1970, 50, 529–546. [Google Scholar]
- Schajer, G.S.; Prime, M.B. Use of Inverse Solutions for Residual Stress Measurements. J. Eng. Mater. Technol. 2006, 128, 375. [Google Scholar] [CrossRef]
- Schajer, G.S. Measurement of Non-Uniform Residual Stresses Using the Hole-Drilling Method. Part I Stress Calculation Procedures. J. Eng. Mater. Technol. 1988, 110, 338–343. [Google Scholar] [CrossRef]
- Schajer, G.S. Measurement of Non-Uniform Residual Stresses Using the Hole-Drilling Method. Part II Practical Application of the Integral Method. J. Eng. Mater. Technol. 1988, 110, 344–349. [Google Scholar] [CrossRef]
- Schajer, G.S.; Prime, M.B. Residual stress solution extrapolation for the slitting method using equilibrium constraints. J. Eng. Mater. Technol. 2007, 129, 227–232. [Google Scholar] [CrossRef]
- Schajer, G.S.; Altus, E. Stress Calculation Error Analysis for Incremental Hole-Drilling Residual Stress Measurements. J. Eng. Mater. Technol. 1996, 118, 120–126. [Google Scholar] [CrossRef]
- Beghini, M.; Grossi, T.; Prime, M.; Santus, C. Ill-Posedness and the Bias-Variance Tradeoff in Residual Stress Measurement Inverse Solutions. Exp. Mech. 2023, 63, 495–516. [Google Scholar] [CrossRef]
- Beghini, M.; Grossi, T. Towards a Reliable Uncertainty Quantification in Residual Stress Measurements with Relaxation Methods: Finding Average Residual Stresses is a Well-Posed Problem. Exp. Mech. 2024, 64, 851–874. [Google Scholar] [CrossRef]
- Beghini, M.; Bertini, L.; Cococcioni, M.; Grossi, T.; Santus, C.; Benincasa, A. Regularization of Hole-Drilling Residual Stress Measurements with Eccentric Holes: An Approach with Influence Functions. J. Mater. Eng. Perform. 2024, 1–7. [Google Scholar] [CrossRef]
- Beghini, M.; Grossi, T.; Santus, C. Validation of a strain gauge rosette setup on a cantilever specimen: Application to a calibration bench for residual stresses. Mater. Today Proc. 2023, 93, 719–724. [Google Scholar] [CrossRef]
- Beghini, M.; Grossi, T.; Santus, C.; Valentini, E. A calibration bench to validate systematic error compensation strategies in hole drilling measurements. In Proceedings of the ICRS 11–11th International Conference on Residual Stresses, Nancy, France, 27–30 March 2022. [Google Scholar] [CrossRef]
- Beghini, M.; Grossi, T.; Santus, C.; Seralessandri, L.; Gulisano, S. Residual stress measurements on a deep rolled aluminum specimen through X-Ray Diffraction and Hole-Drilling, validated on a calibration bench. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1275, 012036. [Google Scholar] [CrossRef]
- Cheng, W.; Finnie, I. Residual Stress Measurement and the Slitting Method; Mechanical Engineering Series; Springer: New York, NY, USA, 2007. [Google Scholar]
- Vaidyanathan, S.; Finnie, I. Determination of Residual Stresses From Stress Intensity Factor Measurements. J. Basic Eng. 1971, 93, 242–246. [Google Scholar] [CrossRef]
- Schindler, H.J.; Cheng, W.; Finnie, I. Experimental determination of stress intensity factors due to residual stresses. Exp. Mech. 1997, 37, 272–277. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Rice, J.R. Some remarks on elastic crack-tip stress fields. Int. J. Solids Struct. 1972, 8, 751–758. [Google Scholar] [CrossRef]
- Lamm, P.K. A Survey of Regularization Methods for First-Kind Volterra Equations. In Surveys on Solution Methods for Inverse Problems; Colton, D., Engl, H.W., Louis, A.K., McLaughlin, J.R., Rundell, W., Eds.; Springer: Vienna, Austria, 2000; pp. 53–82. [Google Scholar]
- von Mises, R. On Saint Venant’s principle. Bull. Am. Math. Soc. 1945, 51, 555–562. [Google Scholar] [CrossRef]
- Goldberg, R.R. Methods of Real Analysis; Oxford and IBH Publishing: Delhi, India, 1970. [Google Scholar]
- Rudin, W. Real and Complex Analysis, 3rd ed.; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Wu, X.R.; Carlsson, J. Weight Functions and Stress Intensity Factor Solutions; Pergamon Press: Oxford, UK, 1991. [Google Scholar]
- Prime, M.B.; Hill, M.R. Uncertainty, Model Error, and Order Selection for Series-Expanded, Residual-Stress Inverse Solutions. J. Eng. Mater. Technol. 2006, 128, 175–185. [Google Scholar] [CrossRef]
- Zuccarello, B. Optimal calculation steps for the evaluation of residual stress by the incremental hole-drilling method. Exp. Mech. 1999, 39, 117–124. [Google Scholar] [CrossRef]
- Zuccarello, B. Optimization of depth increment distribution in the ring-core method. J. Strain Anal. Eng. Des. 1996, 31, 251–258. [Google Scholar] [CrossRef]
- Olson, M.D. Measurement Layout for Residual Stress Mapping Using Slitting. Exp. Mech. 2022, 62, 393–402. [Google Scholar] [CrossRef]
- Schajer, G.S. Compact Calibration Data for Hole-Drilling Residual Stress Measurements in Finite-Thickness Specimens. Exp. Mech. 2020, 60, 665–678. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Goncharsky, A.V.; Stepanov, V.V.; Yagola, A.G. Numerical Methods for the Solution of Ill-Posed Problems; Springer: Dordrecht, The Netherlands, 1995. [Google Scholar] [CrossRef]
- Schajer, G.S. Hole-Drilling Residual Stress Profiling with Automated Smoothing. J. Eng. Mater. Technol. 2007, 129, 440–445. [Google Scholar] [CrossRef]
- Smit, T.C.; Reid, R. Tikhonov Regularization for the Fully Coupled Integral Method of Incremental Hole-Drilling. Exp. Mech. 2024, 64, 275–290. [Google Scholar] [CrossRef]
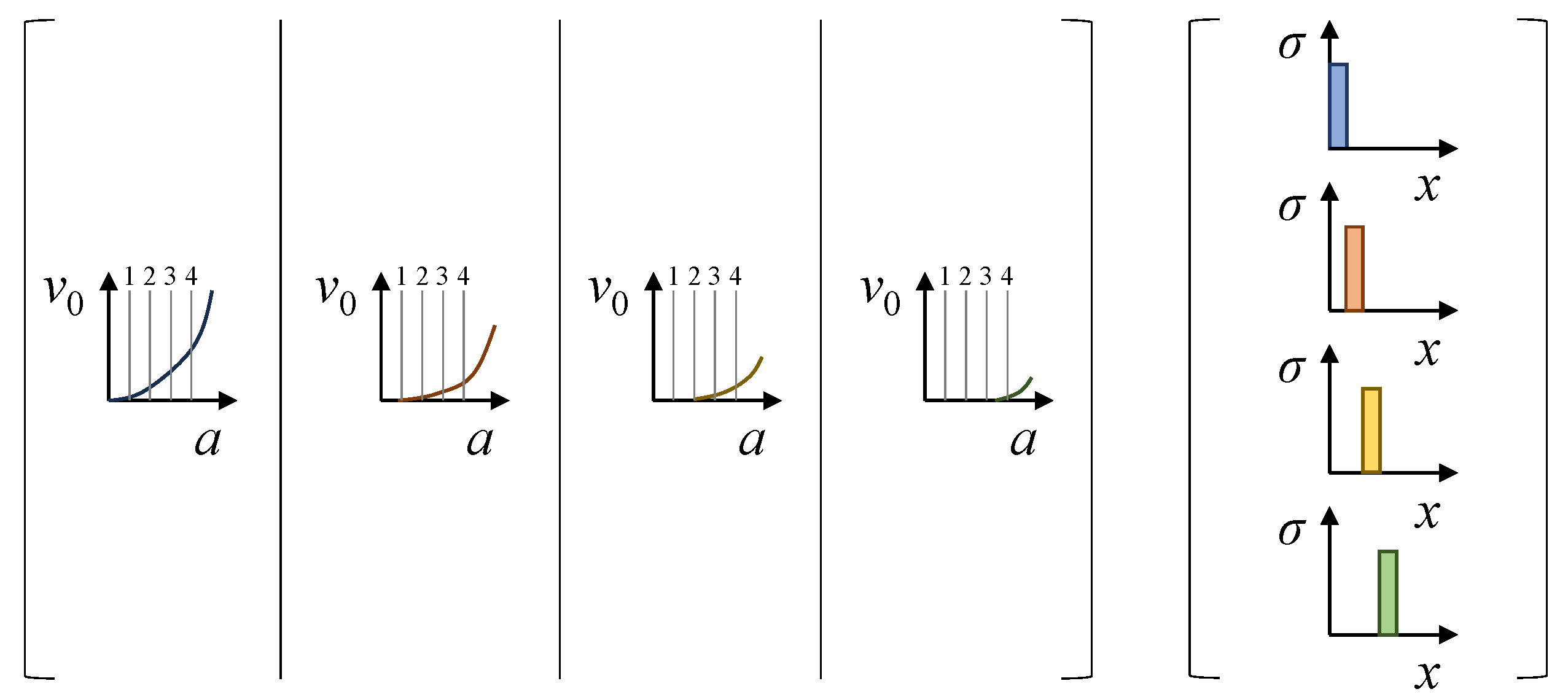

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beghini, M.; Grossi, T. Measuring Residual Stresses with Crack Compliance Methods: An Ill-Posed Inverse Problem with a Closed-Form Kernel. Appl. Mech. 2024, 5, 475-489. https://doi.org/10.3390/applmech5030027
Beghini M, Grossi T. Measuring Residual Stresses with Crack Compliance Methods: An Ill-Posed Inverse Problem with a Closed-Form Kernel. Applied Mechanics. 2024; 5(3):475-489. https://doi.org/10.3390/applmech5030027
Chicago/Turabian StyleBeghini, Marco, and Tommaso Grossi. 2024. "Measuring Residual Stresses with Crack Compliance Methods: An Ill-Posed Inverse Problem with a Closed-Form Kernel" Applied Mechanics 5, no. 3: 475-489. https://doi.org/10.3390/applmech5030027
APA StyleBeghini, M., & Grossi, T. (2024). Measuring Residual Stresses with Crack Compliance Methods: An Ill-Posed Inverse Problem with a Closed-Form Kernel. Applied Mechanics, 5(3), 475-489. https://doi.org/10.3390/applmech5030027




