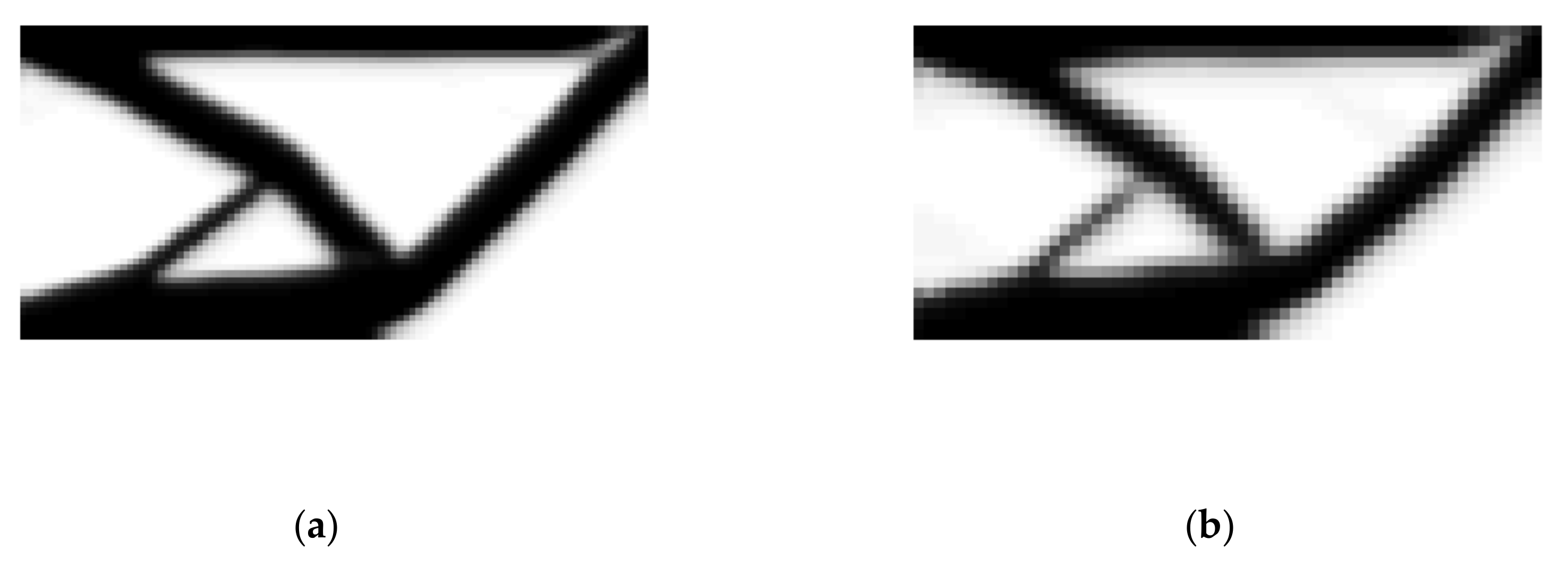Τopology Optimization under a Single Displacement Constraint Using a Strain Energy Criterion

Abstract

Based on a previous concept that has been successfully applied to the sizing optimization of truss and frame structures, this work extends and improves the strain energy criterion in the topology optimization of 2D continuum structures under a single displacement constraint. To make the proposed methodology transparent to other researchers and at the same time meaningful, the numerical value of the displacement constraint was taken to be equal to that obtained through the well-known Solid Isotropic Material with Penalization (SIMP) method under the same boundary conditions and the same external forces. The proposed method is more efficient than the SIMP method while leading to topologies very close to those obtained by the latter.

1. Introduction

Topology optimization is a mathematical method that optimizes the material layout within a given design space for a given set of loads, boundary conditions and constraints with the goal of maximizing the performance of the system. Topology optimization is different from sizing optimization and shape optimization, in the sense that the design can attain any shape within the design space instead of dealing with predefined configurations, thus also allowing one or more holes and openings, or cellular structures, such as those involved in 3D printing and additive manufacturing.

The history of topology optimization spans over 150 years to date. Based on a consideration of Maxwell’s study [1] on the virtual work of the forces and internal stresses applied during the imposed uniform tension—or compression—of a frame, Michell’s breakthrough paper [2] discovered that for the lightest, fully stressed structure, one can indicate a virtual displacement field in which this structure is embedded so that the virtual work is maximal. Considering uniform values for the elastic modulus, the mass density and the allowable stress means, in simple words, that the minimum volume (weight) occurs when the stress reaches its allowable value everywhere, hence the terminology Fully Stressed Design (FSD). Otherwise, in areas where the stress is lower than this value, there is an excess of mass that should be reduced, whereas in places where the stress is higher than the allowable value, an additional mass has to be set. A significant contribution to the topic of discrete optimum trusses was made by Prager [3], who used the method of the circle of relative displacements to arrive at the optimal topology of such trusses (typically cantilevers).

According to a historical review by Lógó [4], finite-element-based topology optimization was first explored by Rossow and Taylor (1973) [5], and, later, by Cheng and Olhoff (1981) [6]. In 1988, a new generation of problem formulation (the modern topology optimization research) was created by Bendsøe and Kikuchi (1988) [7] using homogenization. After that, a variety of new methods were presented, such as the Solid Isotropic Material with Penalization (SIMP) method [8] (the relevant textbook includes 680 references), the Evolutionary Structural Optimization (ESO) method [9], the Independent Continuum and Mapping method (ICM) (see [10,11] and papers therein), the Lever Set Method (LSM) [12], the Method of Moving Asymptotes (MMA) [13,14,15], etc. For a detailed review of the 188 papers on topology optimization, the reader is referred to [16]. Moreover, Evolutionary Topology Optimization (ETO) [17], Smooth-Edged Material Distribution for Optimizing Topology (SEMDOT) [18] and Floating Projection Topology Optimization (FPTO) [19] algorithms have recently appeared. In addition to the aforementioned linear elasticity problems, topology optimization has also been applied to elastoplastic [20] and geometrically nonlinear structures [21].

Although the size optimization of structures is not the central topic of this paper, it is worth mentioning a few relevant things, because topology optimization may also depend on it. As Prager and Taylor (1968) [22] showed, if the work of the applied loads is limited to an equality constraint, the optimum structure with uniform material properties has a uniform energy density distribution. A similar criterion was proposed by Venkayya et al. (1968, 1969) [23,24,25] for discretized structures, stating that at optimum size “The average strain energy density is the same for all elements.” Similar ideas were developed by Berke [26], as well as Gellatly and Berke [27,28].

In topology optimization, a detailed description of the continuum-type optimality criteria method was reported in Rozvany’s books [29,30], covering the period up to the year 1997. The period 2000–2014 is covered by [31], while the abovementioned review paper by Lógó [16] covers the period up to the year 2020. In general, the high number of parameters involved in the problem of topology optimization does not allow the use of Mathematical Programming (MP) methods; thus, the Optimality Criteria (OC) approach is preferred. Among these methods, of particular interest (from an academic and industrial point of view) are probably the SIMP and ESO methods as well as their variations. Moreover, according to a critical review by Rosvany [32], it is accepted that the SIMP method is more robust and efficient compared with the ESO method. As a result, the SIMP method has now been incorporated in integrated CAD/CAE systems such as SolidWorks^® and ANSYS^®. Therefore, we shall focus on the SIMP method below as a reference solution.

It is known that the SIMP method, as a density-based method, operates on a fixed domain of finite elements with the basic goal of minimizing an objective function by identifying whether each element should consist of solid material or void [31]. This problem has many design variables and is therefore a challenging large-scale integer programming problem. For this reason, it is desirable to replace the discrete variables with continuous variables. This is accomplished with an interpolation function, where the continuous design variables are explicitly interpreted as the material density of each element. Penalty methods are then utilized to force solutions into suitable “0/1” topologies.

The vast majority of published papers are focused on problems in which the objective function is compliance, and constraints are placed on the amount of material that can be utilized. According to Yang et al. [33], less effort has been devoted to the topology optimization of continuum structures subjected to displacement constraints. This is because of the following reasons: (i) it is difficult to establish the explicit function expression between the topological variables and displacement constraints using the current methods, and (ii) the large quantities of design variables in the problem make it hard to deal with using the formal mathematical programming approach.

In contrast with the abovementioned continuum methods, as already mentioned, a plethora of methods that solve the size-optimization problem subjected to displacement constraints have been established for discrete structures such as trusses. More specifically, many Optimality Criteria are capable of managing efficiently a large number of design variables and of reaching an optimum structure. Almost every Optimality Criterion used for this purpose is an energy criterion that describes the optimality conditions. In the early 1970s, Verkayya [25] stated that the optimum structure is the one in which the average strain energy density is the same across all of its elements. Makris and Provatidis [34] proposed an iterative procedure whereby an optimality criterion demanding a uniform virtual strain energy density distribution over the entire structure was introduced into their redesign formula as a normalized penalized factor. The latter method identifies the virtual strain energy density by implementing the unit load theorem. An extension of the same idea from trusses to frame structures was also successful [35]. Furthermore, another extension combining layout optimization with skeletal structures performed well [36], while the implementation in continua is still missing.

Despite the abovementioned plethora of publications, the topic of topology optimization continues to attract the interest of researchers in several topics, such as reviews [37,38], Michell structures [39,40], optimality criteria [41,42,43,44], and the efficient implementation of Lagrange multipliers [45], while regularization techniques (filtering [15,46] and projection (erode, dilate or hyperbolic tangent) [47,48,49,50]) are used to avoid hinges.

While the abovementioned optimization methods based on a strain energy criterion are efficient and perform well in conjunction with skeletal structures [34,35,36], so far, no application to the topology optimization of continua has been reported. Within this context, this paper (i) implemented a proper expression of the unit load theorem in the continuum, and (ii) improved previously used recursive formulas applicable to trusses [34] so that the proposed algorithm converged more rapidly toward the optimal element thicknesses (design variables) than other methods. In order to validate the quality of the obtained solution (mass distribution), the proposed method was successfully compared with the well-known SIMP method [7]. Surprisingly, when comparing both methodologies using the same maximum allowable displacement, it was found that both of them led to almost identical topologies in most of the test cases analyzed in this paper. Moreover, this investigation revealed a particular example (the L-shaped domain) in which the proposed method performed better than the SIMP method in the sense that it converged to a smaller volume.

2. Materials and Methods

2.1. The Truss Analog

Makris and Provatidis [34] showed that in truss-sizing optimization under stress and a single displacement constraint $u<u_{allow}$, the recursive formula for calculating the optimum (i.e., the minimum weight of the structure) may be

$$A_i^{new}=A_i^{old}\left(1+f{\eta }_i\frac{u^{old}-u_{allow}}{u_{allow}}\right)$$

(1)

where $A_i^{new}$ and $A_i^{old}$ are the new and old cross-sectional areas, respectively, of the $i$-th bar in the truss, $u_{old}$ is the current maximum nodal displacement in the truss, $u_{allow}$ is the maximum allowable nodal displacement of the structure (i.e., the constraint), and $f$ is an accelerating factor, such as:

$$f={0.01}^{\left(1/k\right)}$$

(2)

where $k$ is the current number of the iteration at which $A_i^{old}$ occurs, while the weighting factor ${\eta }_i$ refers to the contribution of the $i$-th bar in the totality of the truss members, where

$${\eta }_i=\frac{U_i}{\overline{U}}=\frac{U_i}{\left(\frac{1}{N}\right){{\displaystyle \sum }}_{j=1}^N\left|U_j\right|}$$

(3)

In Equation (3), $N$ is the number of truss members (bars) while $U_i$ denotes the virtual energy per unit volume (virtual strain energy density), which can be expressed in terms of the actual force $F_i^P$ and virtual force $F_i^Q$ by

$$U_i=\frac{F_i^P{F}_i^Q}{E{A}_i^2}$$

(4)

with $E$ denoting the elastic modulus.

Clearly, the denominator $\left(\frac{1}{N}\right){{\displaystyle \sum }}_{j=1}^N\left|U_j\right|$ in Equation (3) is the arithmetic mean of all truss members under consideration.

While Equation (1) performs well in the sizing optimization of trusses [34] and frames [35], it has some difficulties when applied to topology and layout optimization. Within this context, Venetsanos and Provatidis [36] introduced a new categorization of the structural elements according to which members that are simultaneously force-passive and area-active may lead the search methods to the local minima. A preliminary report from the same laboratory showed that the addition of a third term in Equation (1), in conjunction with giving $u_{allow}$ an artificially smaller value than the imposed lower bound, generally leads to a better solution (see Tsoumakis [50]). Below, we deal with the 2D continuum.

2.2. Theoretical Approach for 2D Continuum

Let us now assume that the two-dimensional continuum (on the $xy$-plane) is divided into $N$ bilinear finite elements so that the $i$-th element is of thickness $t_i$. Comparing this case with the abovementioned truss in Section 2.1, the analogy is based on the fact that the latter’s cross-sectional area $A_i$ has to be replaced by the thickness $t_i$ of the former. Obviously, the area $A_i$ of each finite element (on the $xy$-plane) is preserved at its initially given value.

Given a constant mass density $\rho$ throughout the domain, the topology optimization problem under a single displacement constraint aiming at weight minimization can be stated as:

$$\mathrm{minimize} W={{\displaystyle \sum }}_{i=1}^N{\rho }_i{A}_i{t}_i$$

(5)

$$\mathrm{subject} \mathrm{to} u_{ }<u_{allow}, t_i<t_{max} \mathrm{and} t_i>t_{min},$$

(6)

where $W$ is the weight of the structure, $A_i$ is the constant area of the $i$-th finite element, $t_i$ is the variable thickness of the same element, $u$ is the maximum nodal displacement component which appears on the $xy$-plane, $u_{allow}$ is the maximum allowable displacement$, t_{max}$ is the maximum allowable thickness, $t_{min}$ is the minimum allowable thickness of an element, and $N$ is the number of elements in the structure.

According to the method of Lagrange multipliers, the Lagrangian function of the aforementioned problem can be stated as:

$$L={{\displaystyle \sum }}_{i=1}^{nel}{\rho }_i{A}_i{t}_i+{\lambda }_1\left(u_i-u_{allow}\right)$$

(7)

where ${\lambda }_1$ is the Lagrange multiplier of the displacement constraint.

It is well known that in the 2D continuum, the unit load theorem depicts that the actual displacement at any point $\left(x,y\right)$ of the structure can be expressed as:

$$u={{\displaystyle \int }}_V^{ }{\left\{{\sigma }^Q\right\}}^{{\rm T}}\left\{{\epsilon }^P\right\}dV$$

(8)

where $V$ is the volume of the structure,$\left\{{\epsilon }^P\right\}$ is the strain vector caused by the actual loads and $\left\{{\sigma }^Q\right\}$ is the stress vector produced by a virtual unit load applied to the abovementioned point $\left(x,y\right)$. Introducing Equation (8) into Equation (7) yields

$$L={{\displaystyle \sum }}_{i=1}^N\left({\rho }_i{A}_i{t}_i\right)+{\lambda }_1\left({{\displaystyle \int }}_V^{ }{\left\{{\sigma }^Q\right\}}^{{\rm T}}\left\{{\epsilon }^P\right\}dV-u_{allow}\right)$$

(9)

Thus, replacing the volume integral with the summation of all the $N$ finite elements, we obtain the discretized Lagrangian function:

$$L={{\displaystyle \sum }}_{i=1}^N\left({\rho }_i{A}_i{t}_i\right)+{\lambda }_1\left({{\displaystyle \sum }}_{i=1}^N{\left\{{\sigma }_i^Q\right\}}^{{\rm T}}\left\{{\epsilon }_i^P\right\}{A}_i{t}_i-u_{allow}\right)$$

(10)

According to the method of Lagrange multipliers, the optimality condition can be met when (note that the subscript $‘t’$ in the Nabla operator stands for the word ‘thickness’)

$${\mathsf{\nabla }}_{t}L=0$$

(11)

By virtue of Equation (11), the partial derivative of Equation (10) with respect to the element thickness $t_i$ equals

$${\mathsf{\nabla }}_{t}L={\rho }_i{A}_i+{\lambda }_1{\left\{{\sigma }_i^Q\right\}}^{{\rm T}}\left\{{\epsilon }_i^P\right\}{A}_i=0$$

(12)

Obviously, Equation (12) stands provided that $A_i$ and ${\rho }_i$ are constants of each finite element. As we know, the Lagrange multiplier ${\lambda }_1$ is a constant; thus, Equation (12) can be written as follows:

$${\left\{{\sigma }_i^Q\right\}}^{{\rm T}}\left\{{\epsilon }_i^P\right\}=-\frac{{\rho }_{ }}{{\lambda }_1}=const$$

(13)

The left-hand side of Equation (13) represents the virtual strain energy density

$$U_i={\left\{{\sigma }_i^Q\right\}}^{{\rm T}}\left\{{\epsilon }_i^P\right\}, \mathrm{with} i=1,\cdots ,N$$

(14)

of the $i$-th element of the examined two-dimensional structure. According to the previous equations, the value of the virtual strain energy density is the same in the design that corresponds to the minimum weight under a single displacement constraint as in the active part of the optimized structure. However, the aforementioned optimality criterion does not provide a method for reaching this energy state; thus, a redesign formula of recursive form is still required.

To make this point clear, let us consider the discretized form of Equation (8) as follows:

$$u={{\displaystyle \sum }}_{i=1}^N{\left\{{\sigma }_i^Q\right\}}^{{\rm T}}\left\{{\epsilon }_i^P\right\}{A}_i{t}_i\equiv {{\displaystyle \sum }}_{i=1}^N{U}_i{A}_i{t}_i$$

(15)

Equation (15) shows that the displacement at a certain point of the structure, usually where the maximum displacement occurs, is formed by the contribution of all the $N$ finite elements to the computational mesh. A large value $U_i$ in Equation (15) entails a significant contribution, while a small value $U_i$ entails a minor influence on the total displacement $u$. Similar to the methodology previously applied to trusses [34], the weighting factor ${\eta }_i$ (associated with the $i$-th finite element) was again chosen to be proportional to the virtual strain energy density $U_i$; however, as ${\eta }_i$ should be a non-dimensional quantity, $U_i$’s mean average value $\overline{U}$ was used in the normalization. Concretely, in two-dimensional problems, ${\eta }_i$ is defined again according to Equation (3), whereas $U_i$ is now calculated according to Equation (14). Thus, we eventually obtain

$${\eta }_i=\frac{U_i}{\overline{U}}=\frac{{\left\{{\sigma }_i^Q\right\}}^{{\rm T}}\left\{{\epsilon }_i^P\right\}}{\left(\frac{1}{N}\right){{\displaystyle \sum }}_{j=1}^N{\left\{{\sigma }_j^Q\right\}}^{{\rm T}}\left\{{\epsilon }_j^P\right\}}$$

(16)

Regarding the abovementioned updated desirable formula for the element thicknesses, the obvious choice would be to take the analog of Equation (1) in which the cross-sectional area $A_i$ (of the corresponding $i$-th bar in the truss) is now replaced by the thickness $t_i$ of the $i$-th plane of the elasticity finite element. Although this analogy works, a preliminary investigation by Tsoumakis [51], mainly on skeletal equivalents, showed that the quality of the convergence as well as the final solution (the topology at convergence) are favorably affected by the power ${\eta }_i^p$ of the weighting factor.

Within the context of this paper which aims to stabilize the computational procedure, it is eventually proposed that Equation (1) be replaced by the following version:

$$t_i^k=t_i^{k-1}\left(1+f\frac{U_i-U_{max}}{U_{max}}+f{\eta }_i^p\frac{\left(u_{max}-u_{allow}\right)}{u_{allow}}\right), i=1,\cdots ,N$$

(17)

In Equation (17), $k$ is the current iteration in which the updated thickness $t_i^k$ is desired, $f$ is an acceleration factor given by Equation (2), $U_i$ is the virtual energy density, $U_{max}$ is its maximum value over all the $N$ finite elements, ${\eta }_i$ is the weighting factor raised to a power of, preferably, $p=3$, $u_{max}$ is the maximum displacement component (in most cases, at the point where the force is exerted), and $u_{allow}$ is the previously mentioned maximum allowable value of the displacement.

Numerical experimentation recently showed that the reasonable value $U_{max}$ in Equation (17), which obviously depends on the iteration number $k$, can also be safely replaced by the prescribed value $u_{allow}$. This is not a surprise, since we should not forget that the virtual energy density practically corresponds to a displacement, according to Equation (15).

Using the above theoretical approach, it becomes clear that the application of the unit load theorem gives the optimality condition without the use of partial derivatives in the Lagrangian function, thus leading to a derivative-free recursive formula.

2.3. Linear Filtering

According to Svanberg and Svard [15], linear filtering consists in the re-determination of element thickness according to the formula:

$$t_i={{\displaystyle \sum }}_j^{ }{w}_{ij}{t}_j$$

(18)

where $w_{ij}$ are filtering weighting factors based on the distance between elements $i$ and $j$ (which is obviously irrelevant to the abovementioned factors ${\eta }_i$). A reasonable requirement is that if all design variables are equal to a certain value, then the filtered thickness should also obtain this value. This motivates the condition

$${{\displaystyle \sum }}_j^{ }{w}_{ij}=1$$

(19)

The filtering weighting factors $w_{ij}$ are normally positive values in the neighborhood $N_i$ of the $i$-th element and are equal to zero outside this neighborhood. The neighborhood is circular, its radius is $R$ and $N_i=\left\{j: d\left(i,j\right)\le R\right\}$ where $d\left(i,j\right)$ is the distance between the centroids of elements $i$ and $j$. In this study, the filtering weighting factors are defined as

$$w_{ij}=\frac{R-d\left(i,j\right)}{{{\displaystyle \sum }}_k^{ }\left(R-d\left(i,k\right)\right)} \mathrm{if} j\in N_i, \mathrm{while} w_{ij}=0 \mathrm{if} j\notin N_i$$

(20)

2.4. Computational Implementation of the Proposed Method

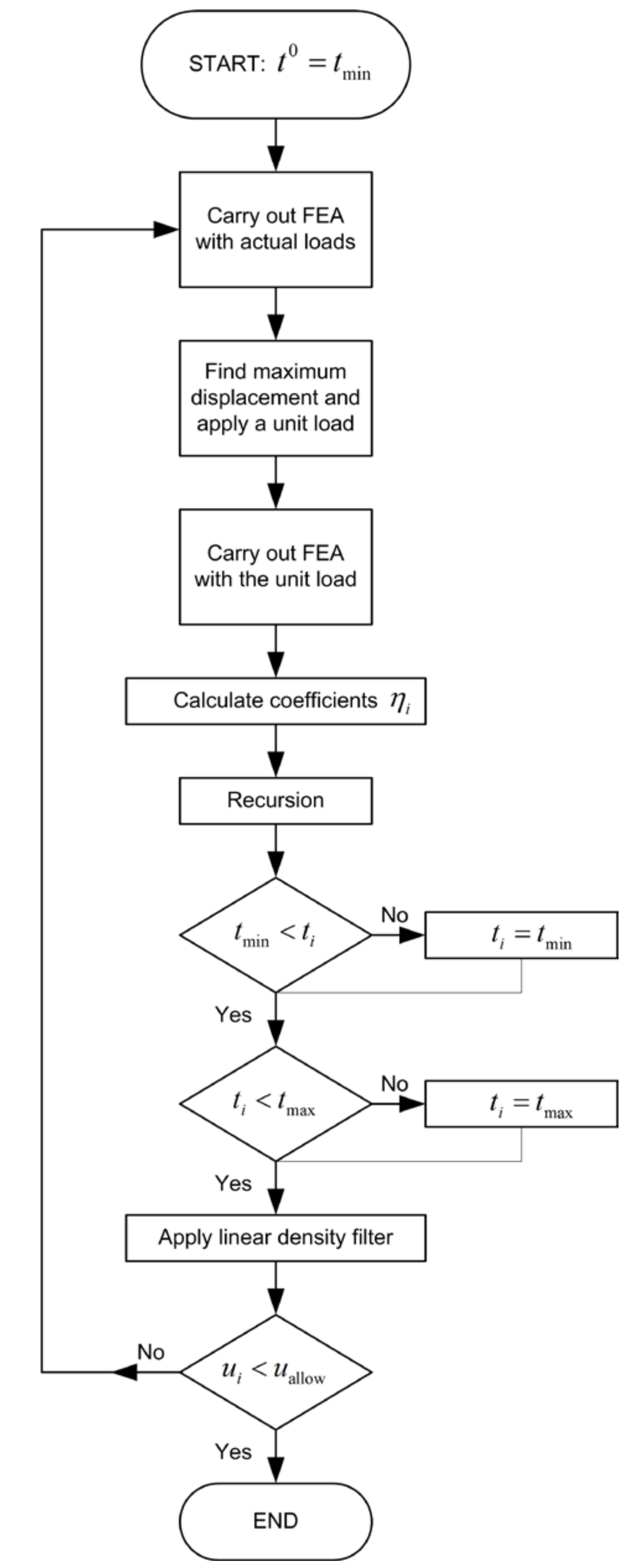
The proposed procedure that minimizes the weight of a 2D continuum structure under a single displacement constraint is as follows:

Step 1: Start from a very small value, for example, 1% of the maximum allowable thickness, or from the minimum allowable thickness of all elements of the structure.

Step 2: Carry out a Finite Element Analysis (FEA) with the actual loads and determine the nodal displacements and the actual strains ${\left\{\epsilon \right\}}^P$ of every element.

Step 3: Find the node where the maximum nodal displacement $u_{max}$ occurs, and then apply a unit load on it in the direction of the aforementioned $u_{max}$.

Step 4: Carry out an FEA, using the virtual unit load in Step 3, and determine the virtual stresses ${\left\{\sigma \right\}}^Q$ for every element.

Step 5: Determine the coefficient ${\eta }_i$ of every element according to Equation (16).

Step 6: Redesign the structure using Equation (17).

Step 7: Check whether the element thickness is within the allowable limits. If the thickness of an element exceeds the limits, assign to it the value of the nearest limit.

Step 8: Filter the new thicknesses with a linear density filter to prevent the checkerboard problem. Except for this, the aforementioned linear density filter has good convergence properties.

Step 9: Apply Steps 2 to 8 iteratively until displacement constraint is fulfilled.

The whole procedure is schematically illustrated in Figure 1.

2.5. Comparison of the Proposed Method with the SIMP Method

In this subsection, we discuss how the efficiency of the proposed methodology compares to the well-known SIMP method. Note that this comparison is not direct, as we will explain below. Specifically:

(1)

Regarding the SIMP method, a popular optimization objective is to maximize the overall stiffness of a structure or minimize its compliance under a given amount of mass removal (fraction of volume reduction).

(2)

Regarding the proposed Optimality Criteria method, it handles the volume minimization problem under the constraint of a prescribed upper displacement bound.

In order to compare these two methods, we follow the procedure below:

• Apply the SIMP method (according to [52]) with a specific volume fraction.
• Convert density variables of the SIMP method to thickness by multiplying densities with the thickness of the design domain.
• Carry out an FEA in the optimized structure and determine the maximum displacement.
• Apply the proposed algorithm, considering as displacement constraint the value of displacement which was determined in Step 3.
• Calculate the volume of the arising topology and divide it by the volume of the design domain, thus determining the volume fraction.
• Compare the volume fractions in the two methods.

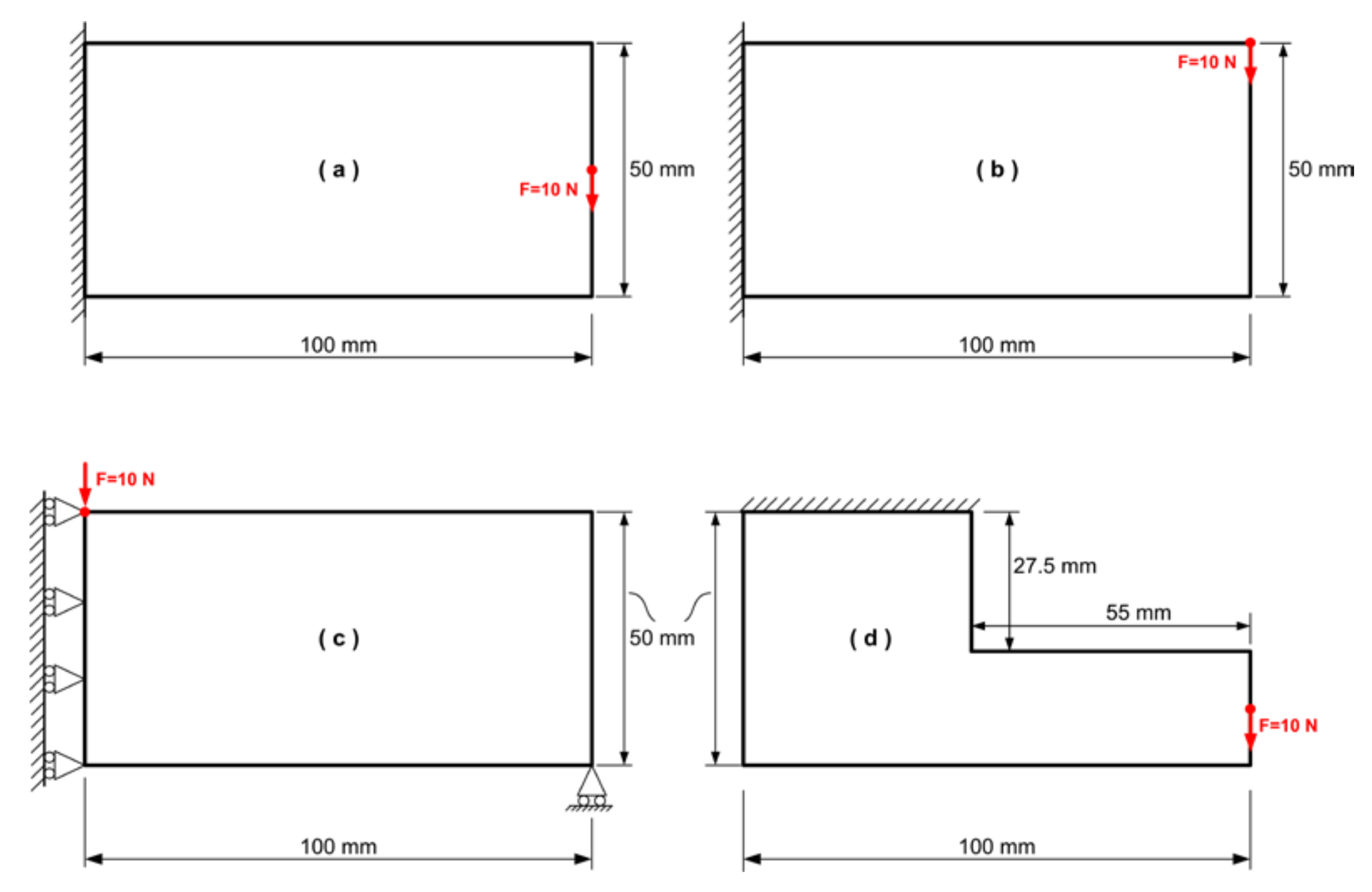
2.6. Benchmark Problems

The abovementioned methodology was implemented in four benchmark problems. The geometry and boundary conditions of these benchmark tests are shown in Figure 2.

The thickness of all design domains is defined as $t=2$ mm, which is the maximum allowable thickness. The material properties are $E=210$ GPa, $\nu =0.3$. The value of the concentrated load in all cases is $F=10$ N. The minimum allowable thickness is set to $t_{min}=0.001$ mm. The rectangular design domain is discretized using a set of 50 × 25 four-node quadrilateral finite elements. In the particular case of the L-shaped domain (see Figure 2a), the upper sub-rectangle (linked to the fixed side) is discretized using 18 × 40 four-node quadrilateral elements, whereas the lower sub-rectangle uses a mesh of 22 × 18 elements. The stress provided by the FEA is calculated at the centroid of each element.

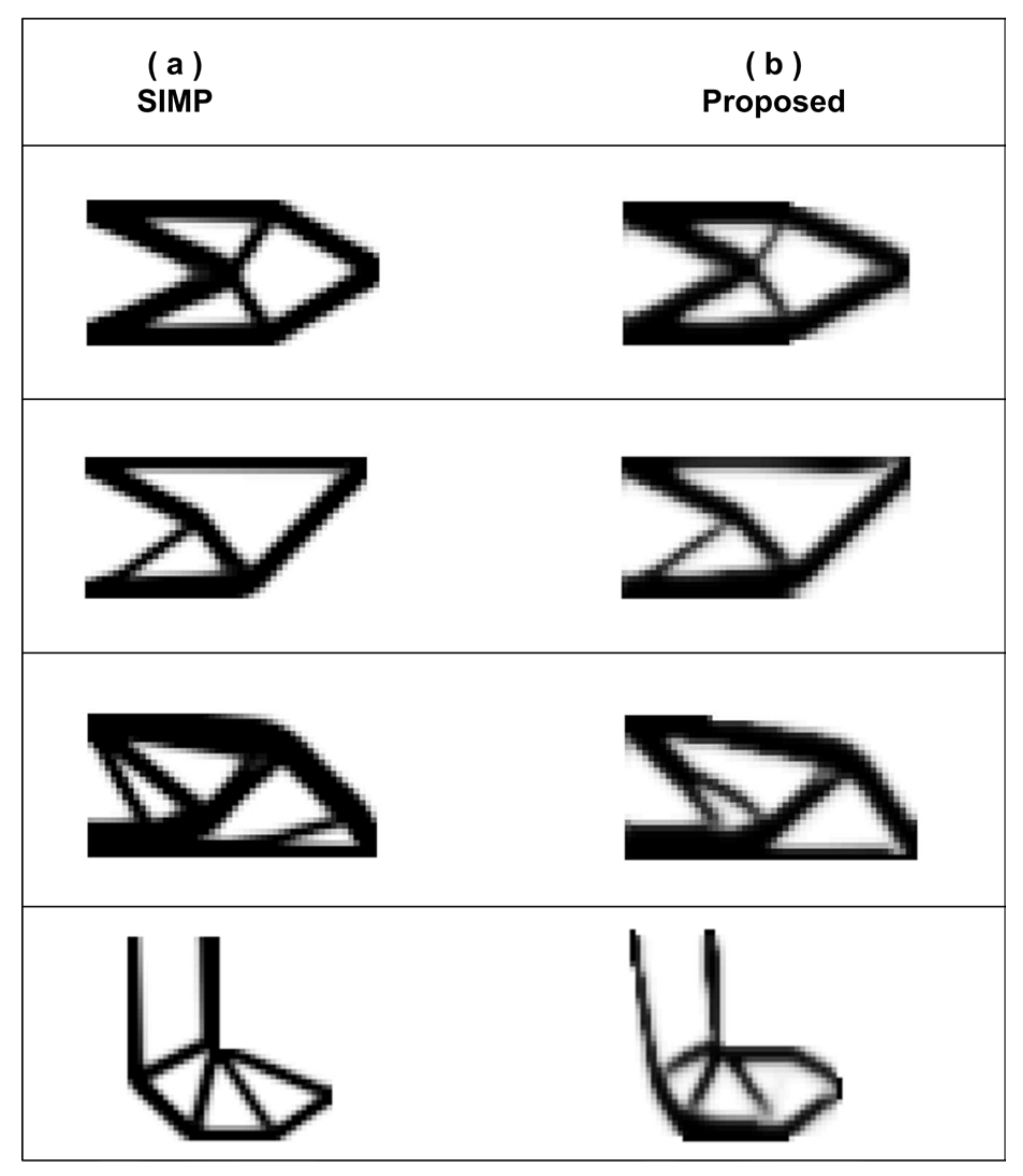
3. Results

The final solutions to which both methods converged are shown in Figure 3. One may observe that in the first two cases—which correspond to the cantilever beam defined in Figure 2a,b—there are no obvious differences. In the last two cases (i.e., the MBB beam defined in Figure 2c and the L-shaped structure in Figure 2d) there are some differences, but they are not very intensive. Qualitative details are given in

Table 1. Overall results obtained in the four case studies.

Case Study	Initial Volume (mm3)	Proposed Method		SIMP		Maximum Displacement (μm)
		Final Volume (mm3)	Volume Fraction	Final Volume (mm3)	Volume Fraction
Cantiliver Load in middle (Figure 2a)	10,000	4940	0.4947	5000	0.5	1.4324
Cantiliver Load in corner (Figure 2b)	10,000	3974	0.3974	4000	0.4	1.9366
Half-MBB (Figure 2c)	10,000	4950	0.4904	5000	0.5	1.7506
L-shaped (Figure 2d)	6975	2511	0.3603	2790	0.4	5.8786

.

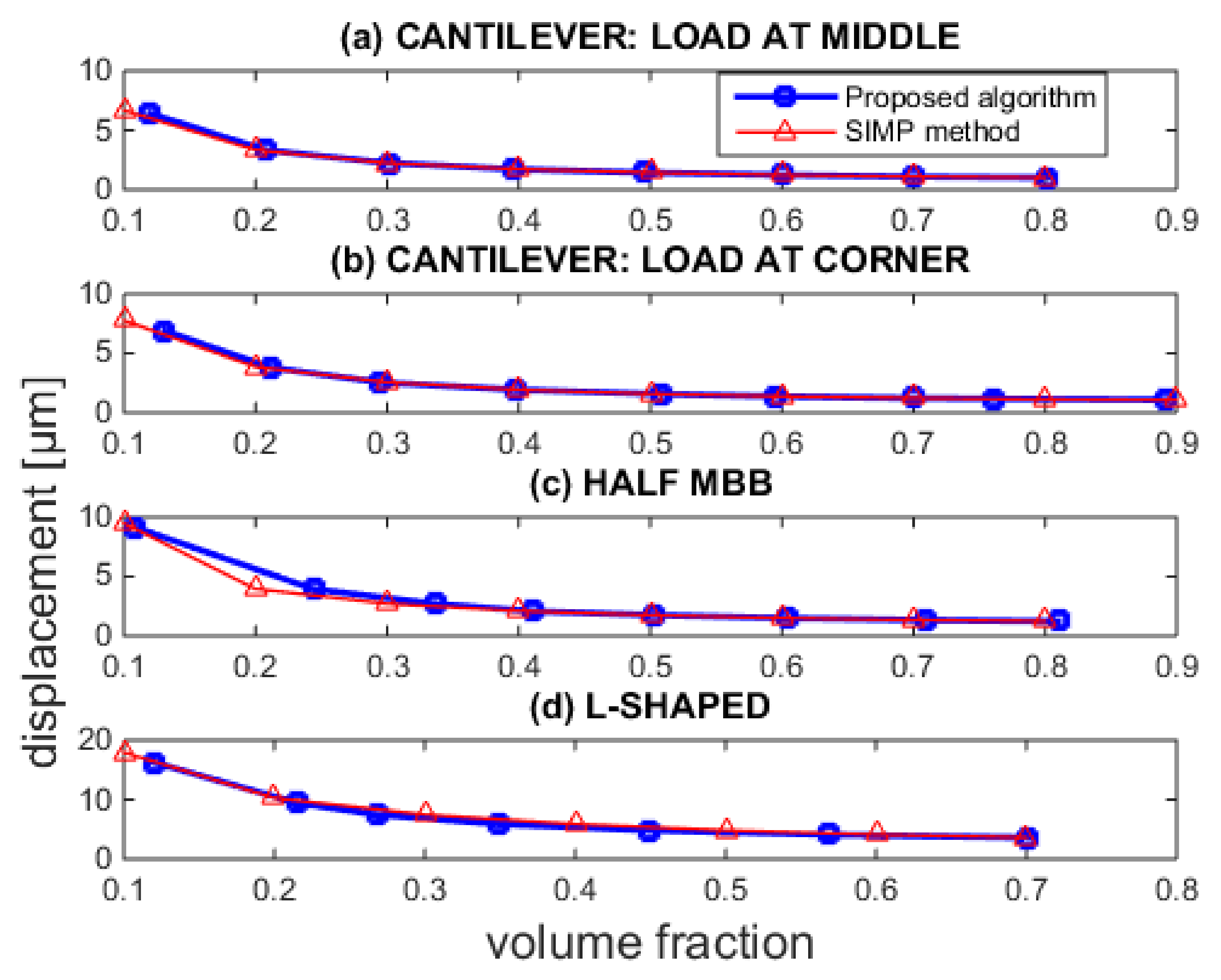
One may observe that in all the cases the proposed method leads either to almost the same volume (or a very slightly smaller volume) or performs better. For example, in the L-shaped domain, the achieved volume fraction of 0.36 instead of 0.40 is 4% smaller than that achieved by the SIMP method with respect to the initial volume.

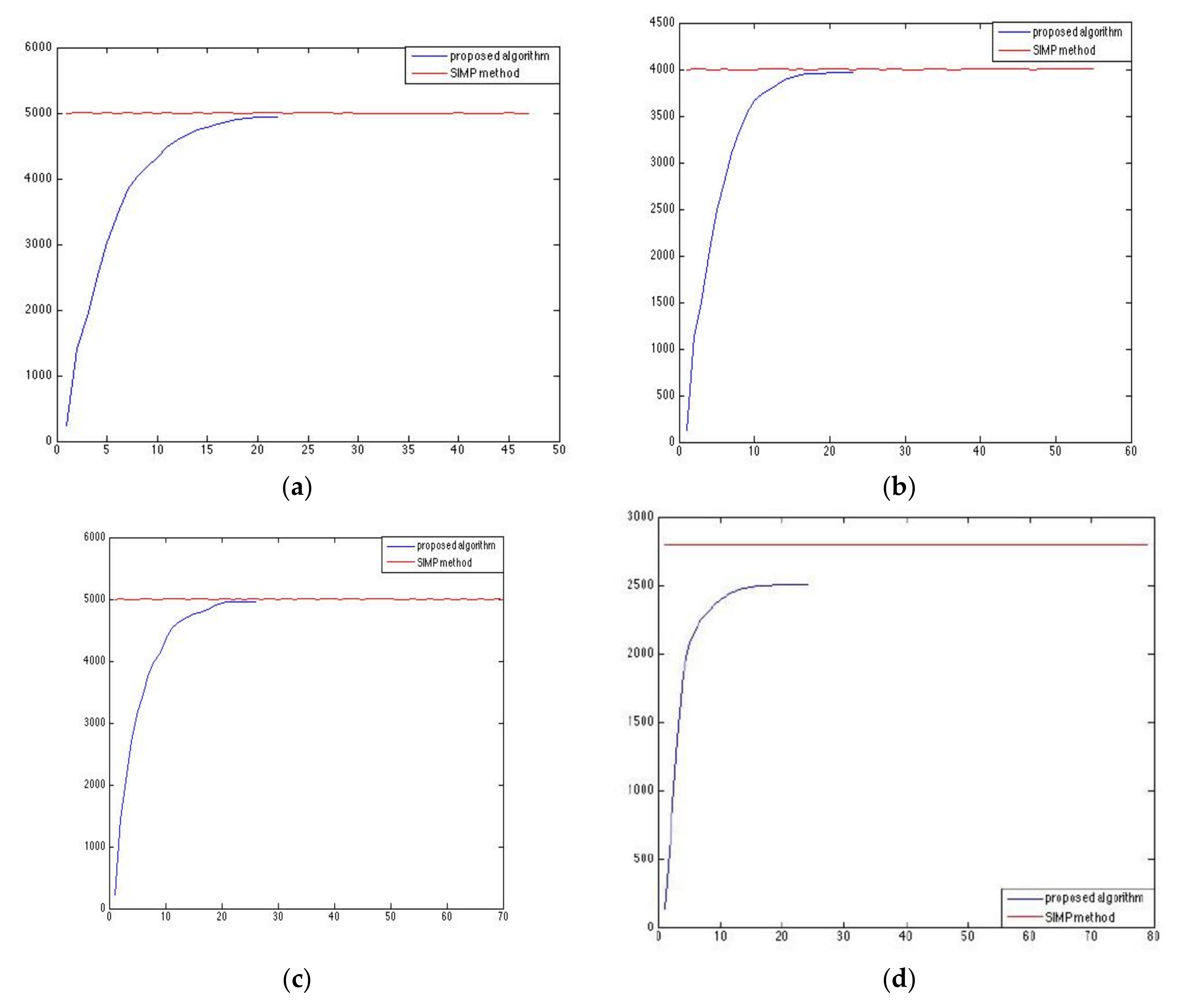
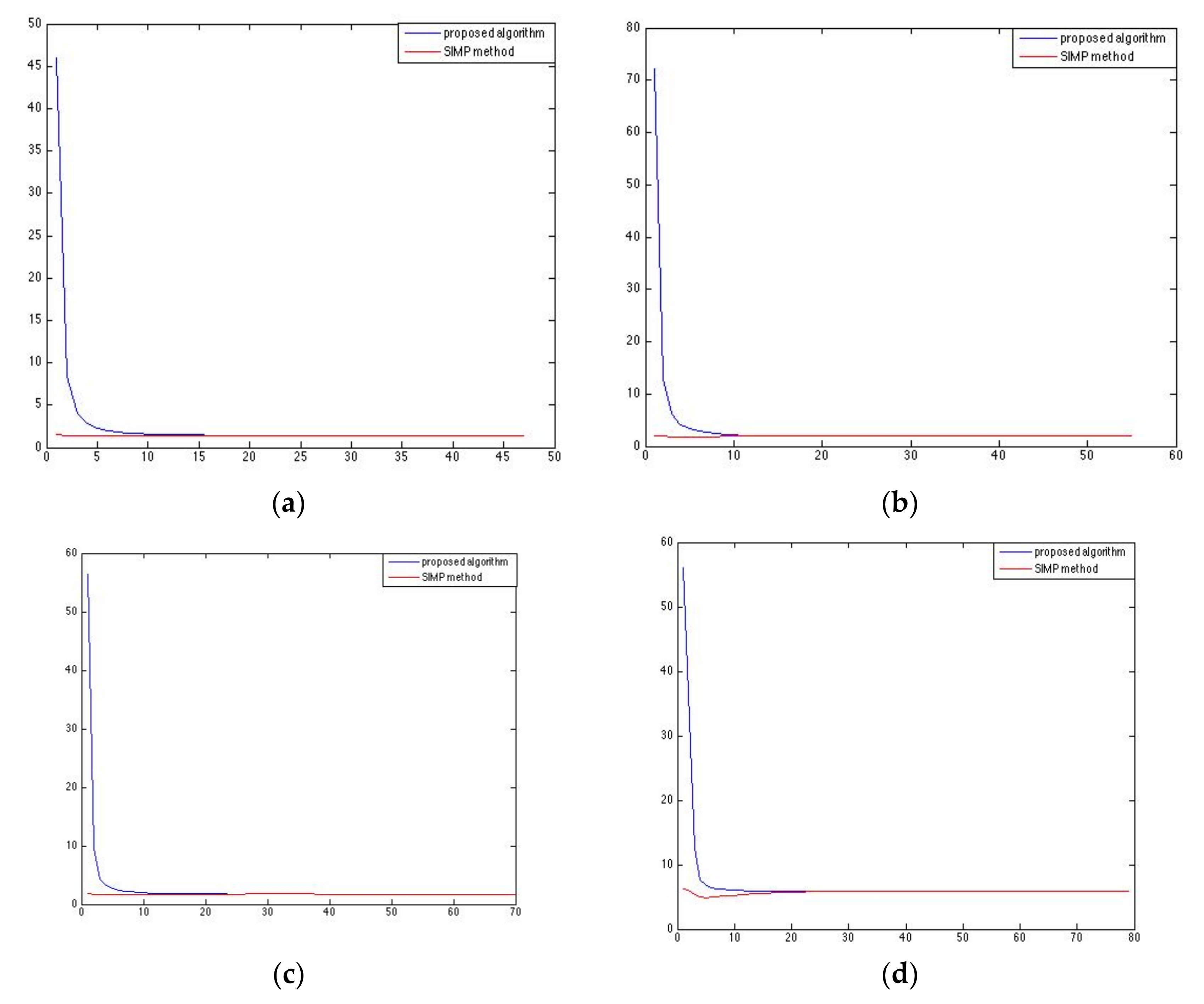
The convergence quality of the weight in the two competitive methods and for all four benchmark tests is shown in Figure 4. The horizontal axis refers to the number of iterations.

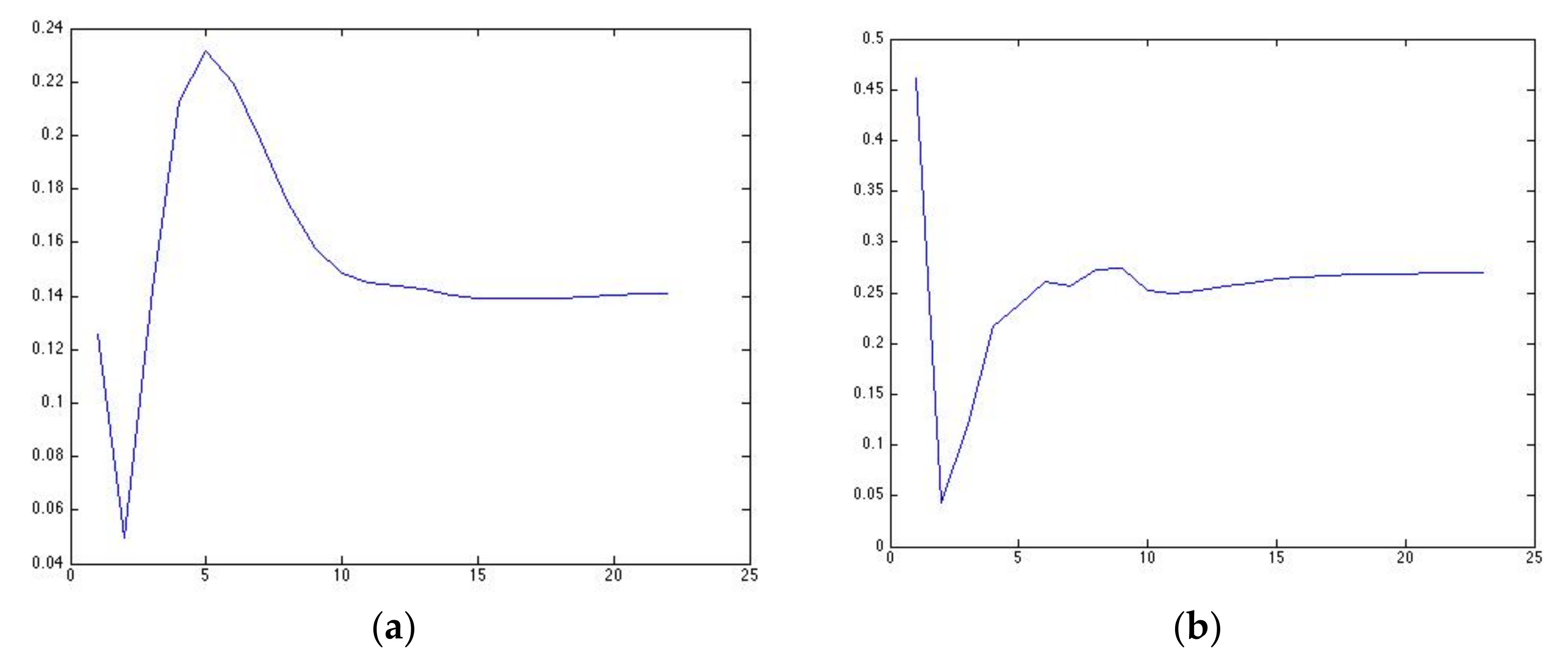
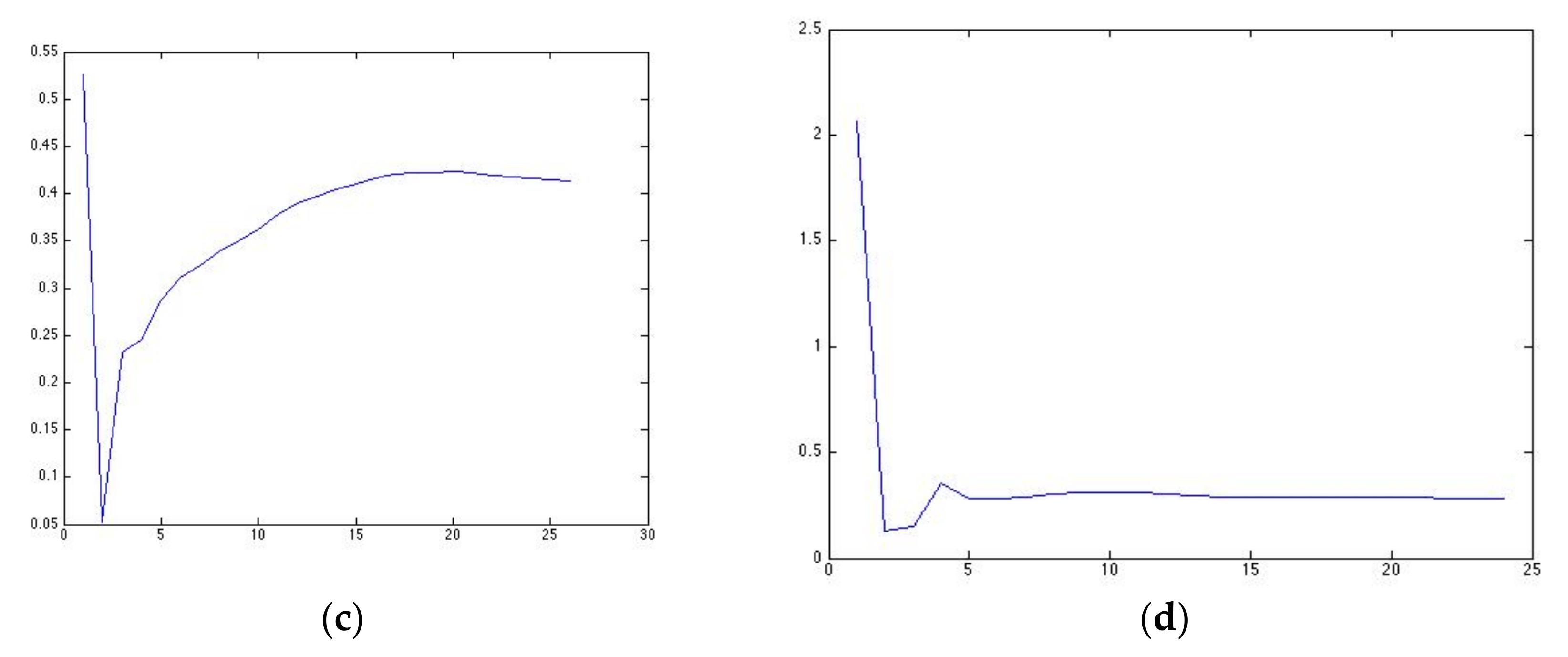
Figure 5 shows the history of the maximum displacement of each case. Again, the horizontal axis refers to the number of iterations.

In addition, for every case study, the history of the maximum value of the weighting coefficient $\eta$ was investigated and the results are presented in Figure 6. Again, the horizontal axis refers to the number of iterations.

4. Discussion

As shown in Figure 3, the optimized structures obtained by the proposed method and the SIMP method have almost the same topology, apart from the L-shaped beam. On the other hand, in Table 1, one may observe that in all the case studies used in this paper, the proposed method converged in structures lighter than those produced using the SIMP method for the specific maximum displacement determined by the SIMP method. In particular, in the L-shaped beam, the proposed method performed better as it converged to a volume that was 4% lighter than that obtained by the SIMP algorithm. Based on these findings, we can claim that the position of the load, the boundary conditions and the shape of the initial structure do not generally affect the efficiency of the method.

In Figure 4 we presented the convergence of the final volumes. As has already been mentioned, the proposed method starts from the minimum allowable thickness where the volume is minimal and, for this reason, the volume increases until convergence. On the other hand, the SIMP method has an almost stable volume because it is a constraint set from the beginning of the iterative procedure.

It is worth noticing that, according to Figure 5, the history of maximum displacement during the optimization procedure has the same hyperbolic shape in all test cases. This shape is indicative of both the stability and the efficiency of the method. In the initial iterative steps, the algorithm has huge maximum displacement values due to the small initial thickness, which was selected on purpose, in contrast to the SIMP method in which the displacement is almost stable. 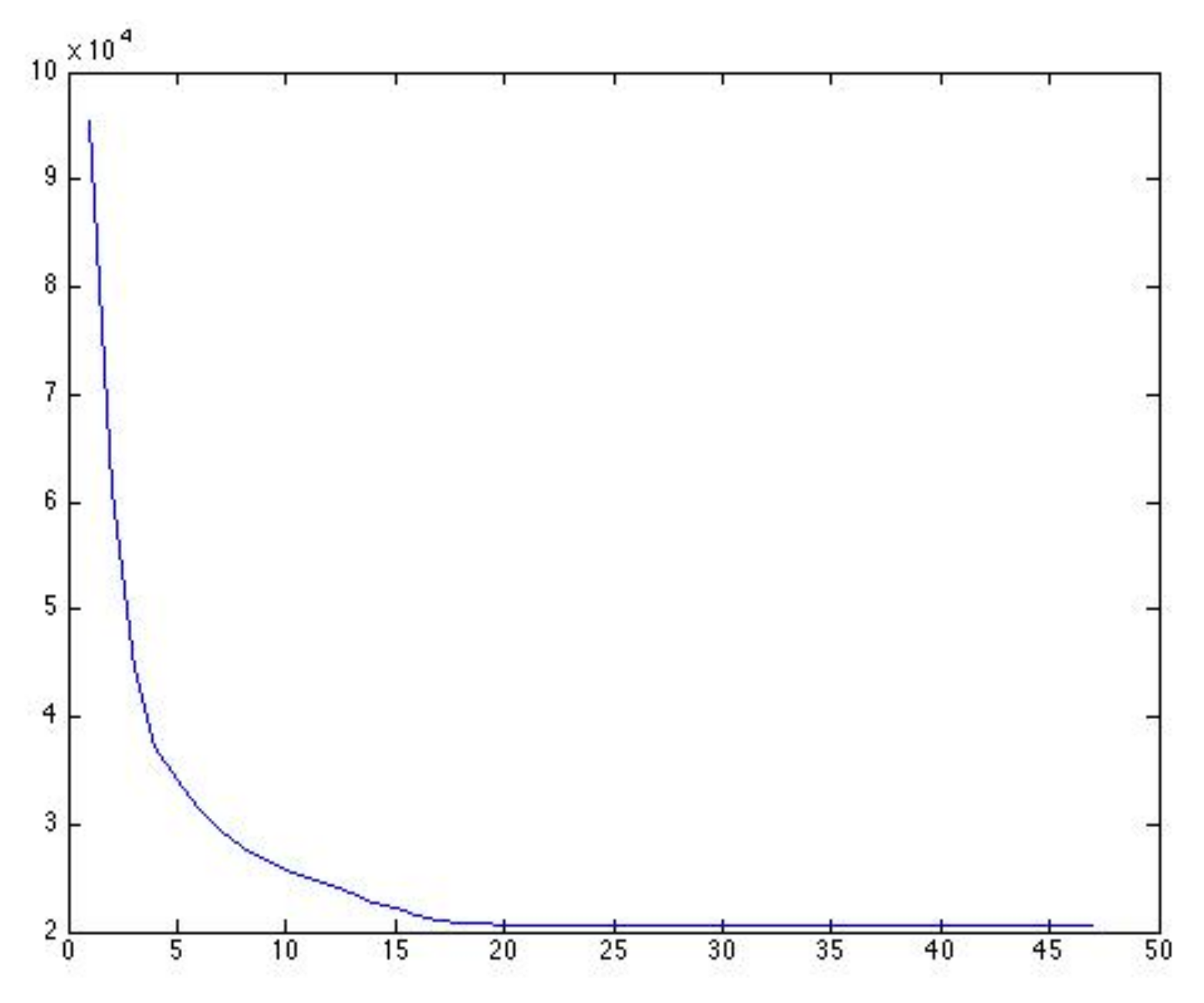If, for example, we focus on case (a) with the cantilever loaded in the middle, the convergence of the compliance in both methodologies is the same as in Figure 5a multiplied by a factor of 10, which corresponds to the external force $F=10$ N. Having said this, it is worth noticing that the objective function of the SIMP method, that is, penalized compliance, has a similar hyperbolic shape to that of the proposed method, as shown in Figure 7.

Another remarkable point is the history of the maximum value of the coefficient $\eta$ of all the finite elements, which is the “heart” of the proposed algorithm. As shown in Figure 6, the maximum coefficient $\eta$ fluctuates until its convergence. However, in the last iterations, its value becomes stable, which means that the optimality condition of Equation (12) is fulfilled.

In addition to the selected conditions described in Section 3 (Results), the proposed algorithm was further performed for a large range of volume fractions and was also compared with the SIMP method. The results of this implementation are collectively presented in Figure 8. One may observe that both methods have, under the vast majority of constraints, similar efficiency. However, the SIMP method performs better than the proposed algorithm under some constraints in the half-MBB beam. On the other hand, the proposed method continues to be the most advantageous in the L-shaped structure.

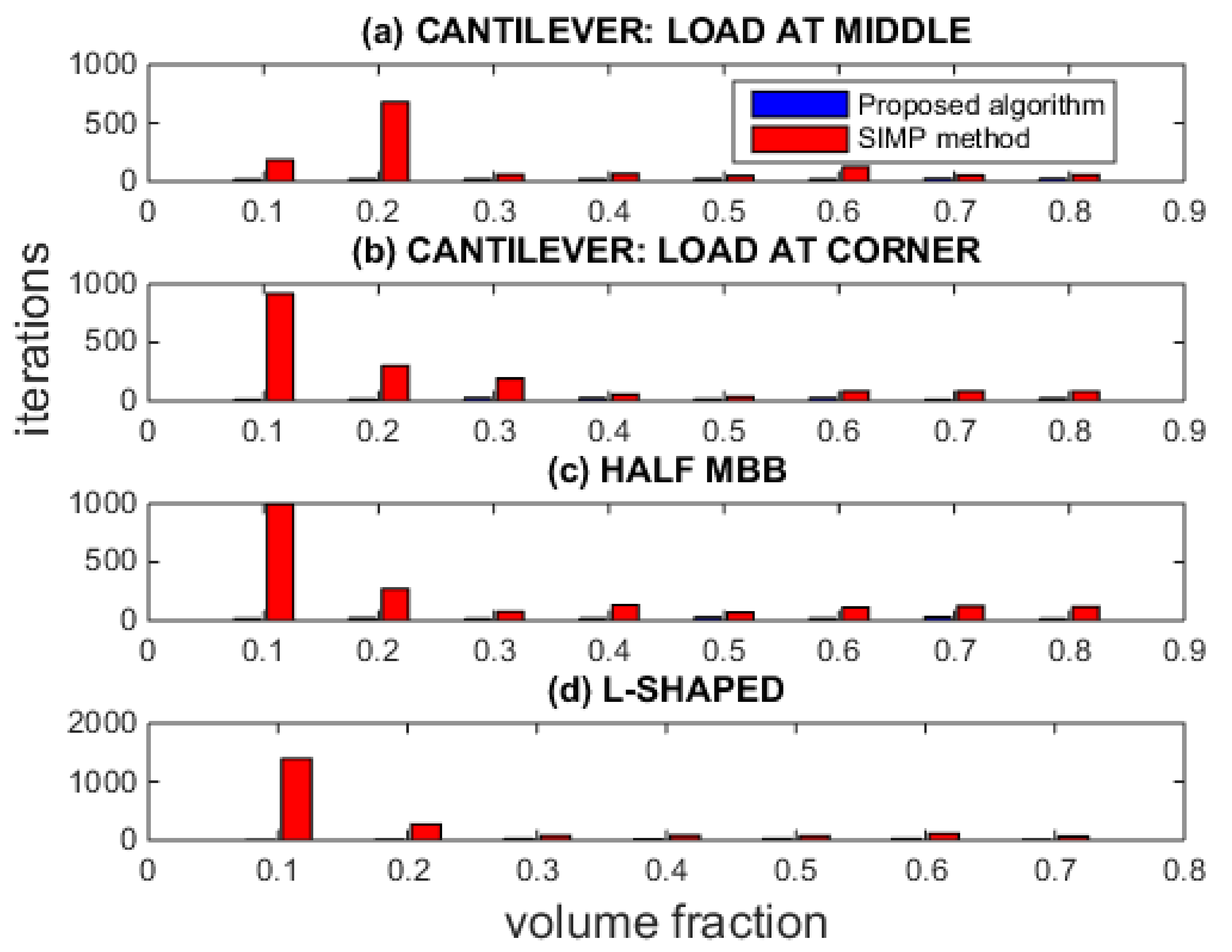
As shown in Figure 9, the proposed algorithm is incomparably advantageous in terms of the number of iterations performed. More specifically, the proposed method mainly optimizes the benchmark structures after only 20–25 iteration steps, as an average. On the contrary, the SIMP method demands more iteration steps (50–1000).

Another remarkable issue is that the proposed algorithm and the SIMP method reach almost the same topology from different paths. More specifically, the intermediate topologies of the two methods are illustrated in Figure 10. It is obvious that, although the intermediate solutions are different, the final results are very similar.

One of the most encouraging characteristics of the proposed algorithm is the mesh independency of the optimization procedure. Specifically, as shown in Figure 11, the method reaches the same topology with the same predefined volume, independently of the number of elements. This particular finding corresponds to the particular case of a cantilever with a load in the corner, where, in the setup of 100 × 50 elements, the convergence was achieved in 13 steps, whereas it was achieved in only 11 steps in the setup of 60 × 30 elements. Beyond this, the proposed algorithm is also independent of the aspect ratio of the discretization.

Finally, it was found that the algorithm behaved in the same in other aspect ratios of the cantilever beam, i.e., shorter or larger than the particular ratio 2:1 which was presented above. The same thing occurred in the MBB beam and the L-shape.

The secret to ensuring the good performance of the proposed method is to set a smaller allowable displacement$—u_{allow}$ in Equation (16)—than the value obtained at the point where the SIMP method converged, and then to scale up the element thickness.

The main disadvantage of the proposed method is the presence of more “gray” regions compared to the SIMP method. This fact can be attributed to the linear density filter, which produces solutions with a relatively large number of gray elements. However, the linear density filter helps the optimization procedure to converge (Svanberg and Svard [15]). Furthermore, the proposed method can also be used in conjunction with the Smooth-Edged Material Distribution for Optimizing Topology (SEMDOT) method [18], using the nodal stresses instead of the element ones, to obtain smooth boundaries. However, this task is left to be carried out in the future.

Moreover, future research may be conducted on the simultaneous handling of stress and displacement constraints during each iteration cycle of the proposed method. The extension into three dimensions is anticipated to be straightforward.

5. Conclusions

In this paper, a previously known strain energy optimality criterion applicable to skeletal structures was extensively revised and then implemented to minimize the volume of 2D continuum structures subject to a single displacement constraint. The new optimality criterion is derivative-free and highly influenced by the unit load theorem and the associated virtual strain energy density. The topology optimization problem has been stated in a different way than the well-known SIMP method. In the proposed method, the objective function is the total weight, which is built from all the finite elements of the structure, while the (displacement) constraint has to be ensured at all the nodal points, and thus has a local character. In contrast, in the SIMP method, the objective function is compliance, while the constraint is the given volume fraction (with a global character). Under these circumstances, it is obvious that the proposed method is capable of managing the problems within each iteration cycle as well as those arising from the stress constraints if we wish it. The performance of the proposed algorithm has been tested using four examples retrieved from the literature during which it was proven to require far fewer iterations than the SIMP method while providing similar—and sometimes slightly better—results. However, the resulting topologies have large “gray” regions, due to the linear density filter utilized.