AFM Indentation on Highly Heterogeneous Materials Using Different Indenter Geometries
Abstract
1. Introduction
2. Materials and Methods
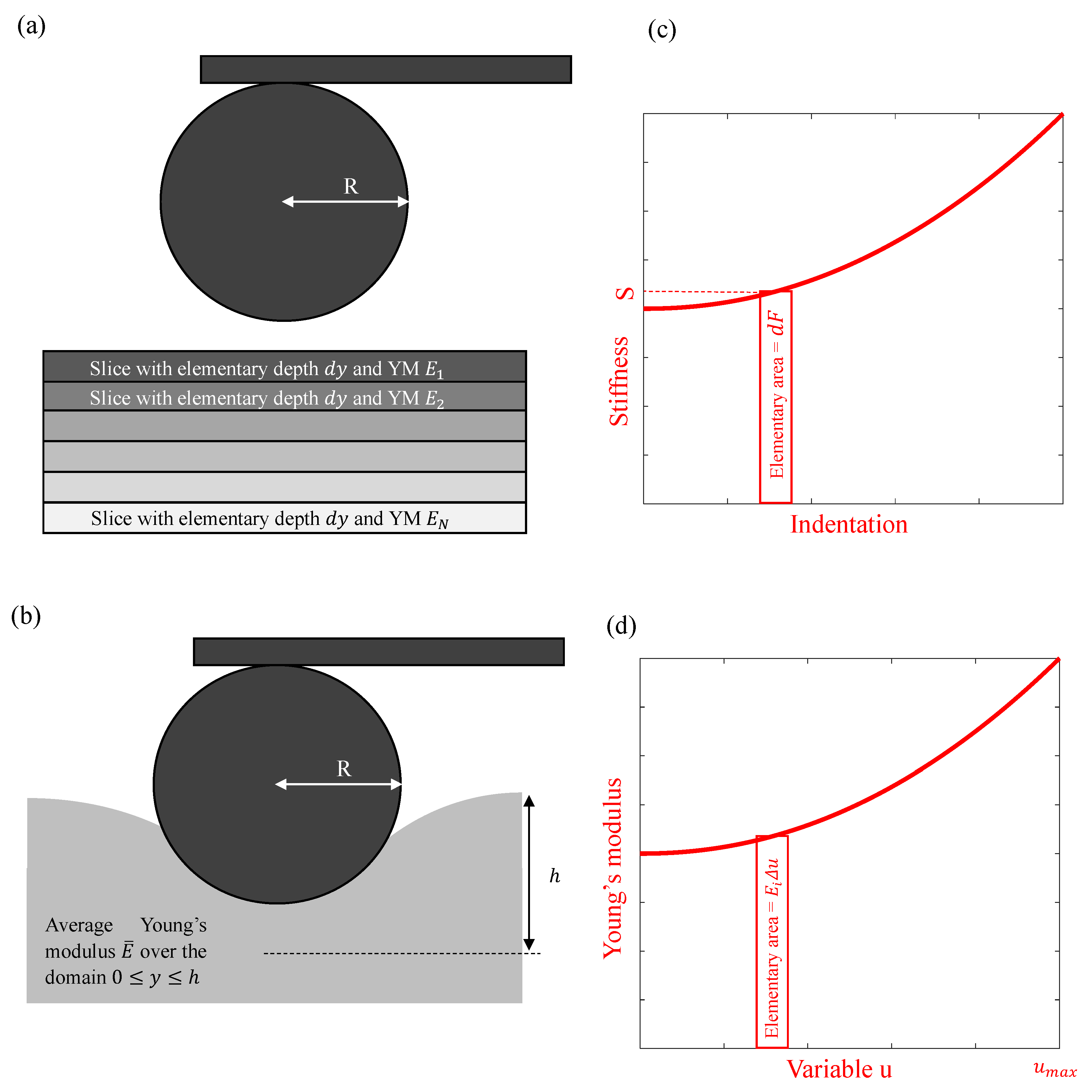
2.1. Theoretical Analysis
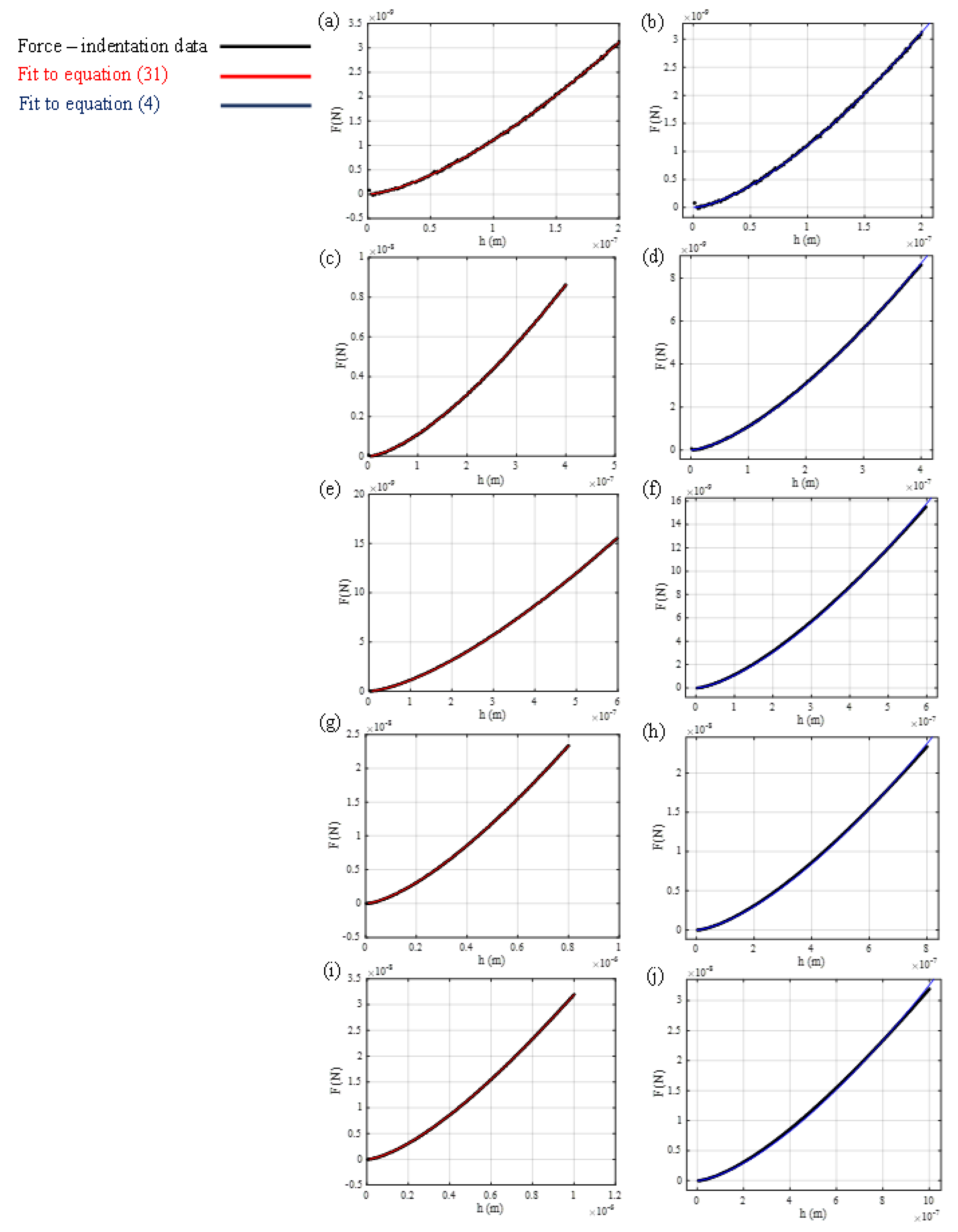
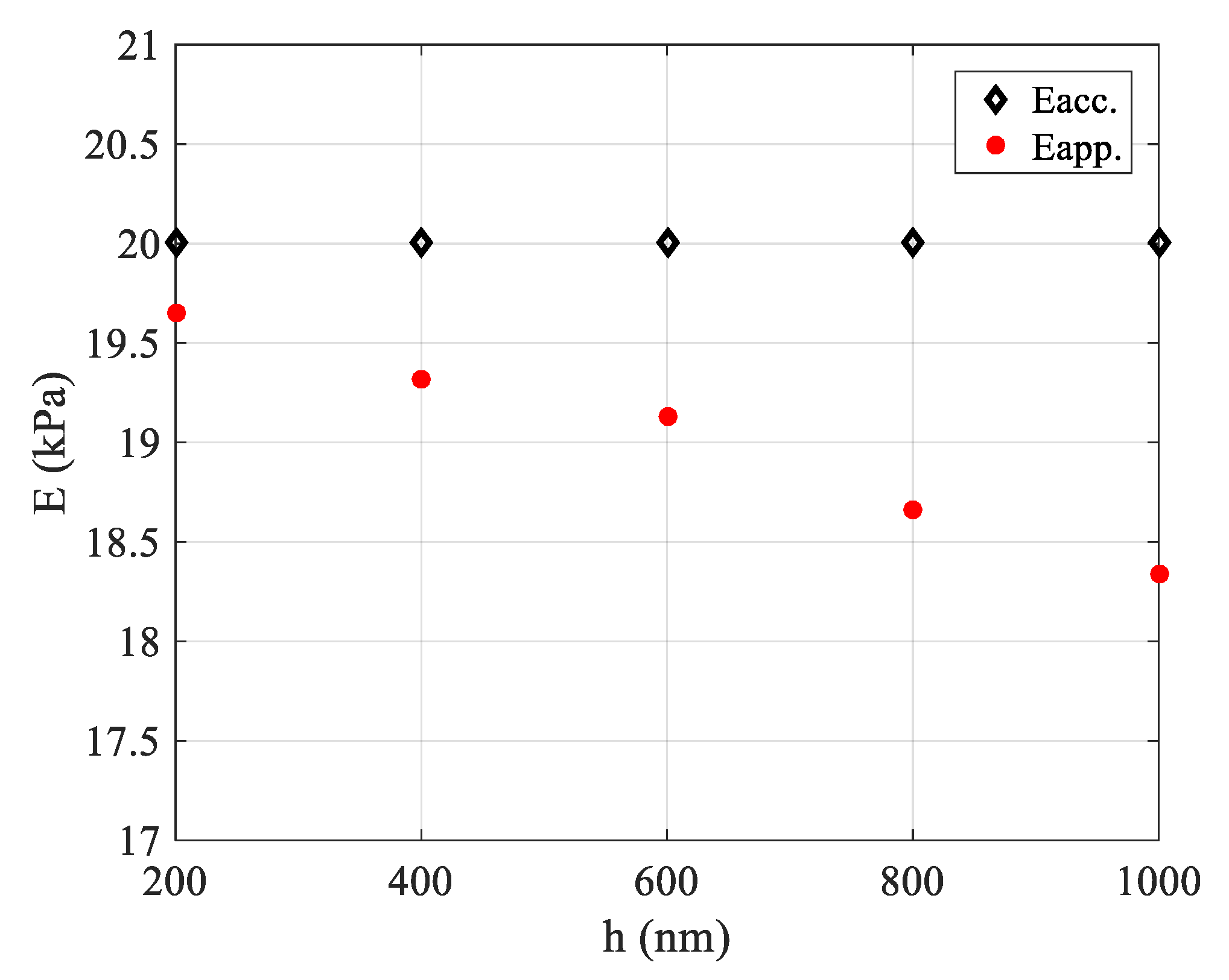
2.2. Open Access Synthetic Data
2.3. Experiments on H4 Human Glioma Cells
3. Results
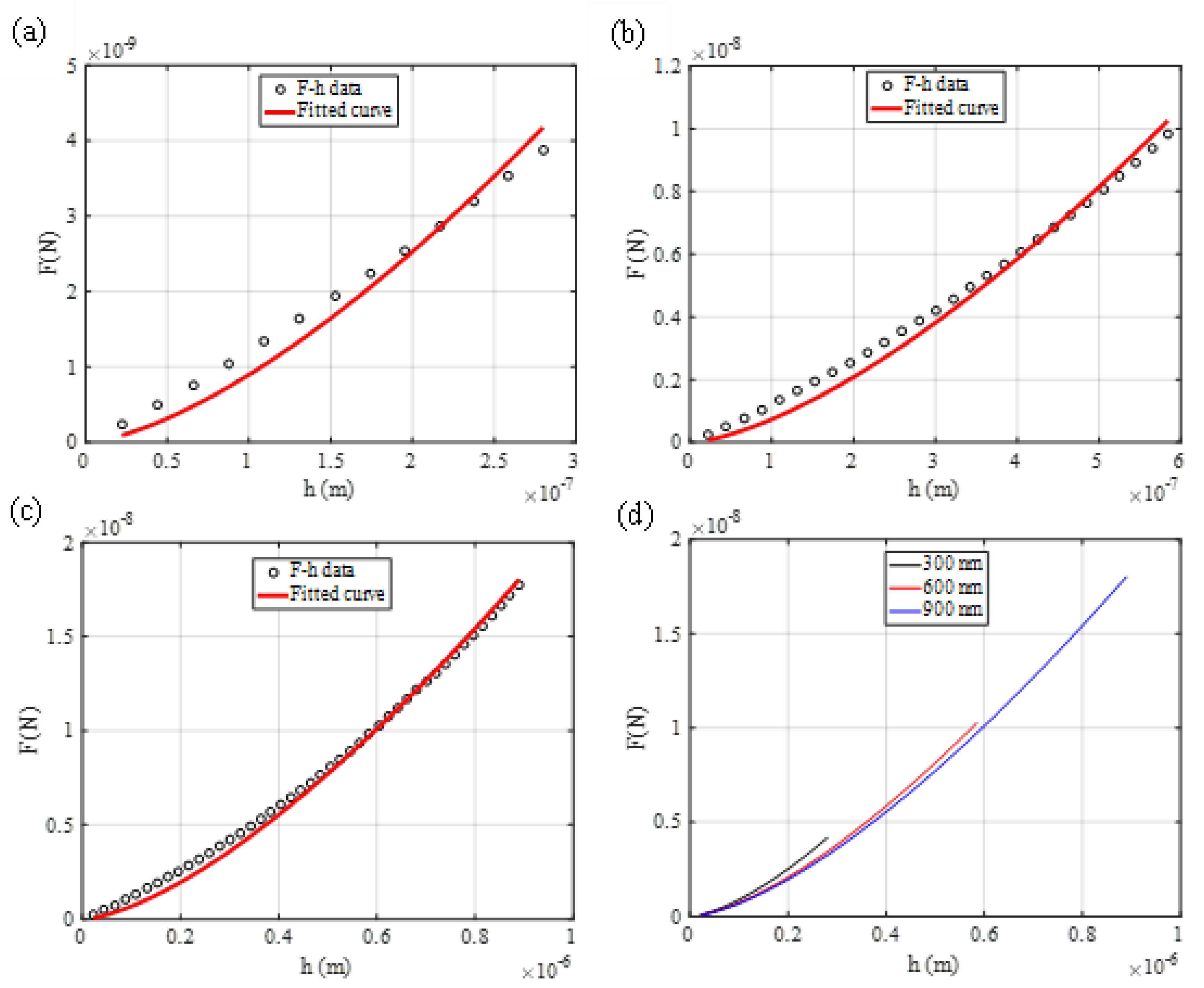
3.1. The Average Young’s Modulus for Deep Spherical Indentations
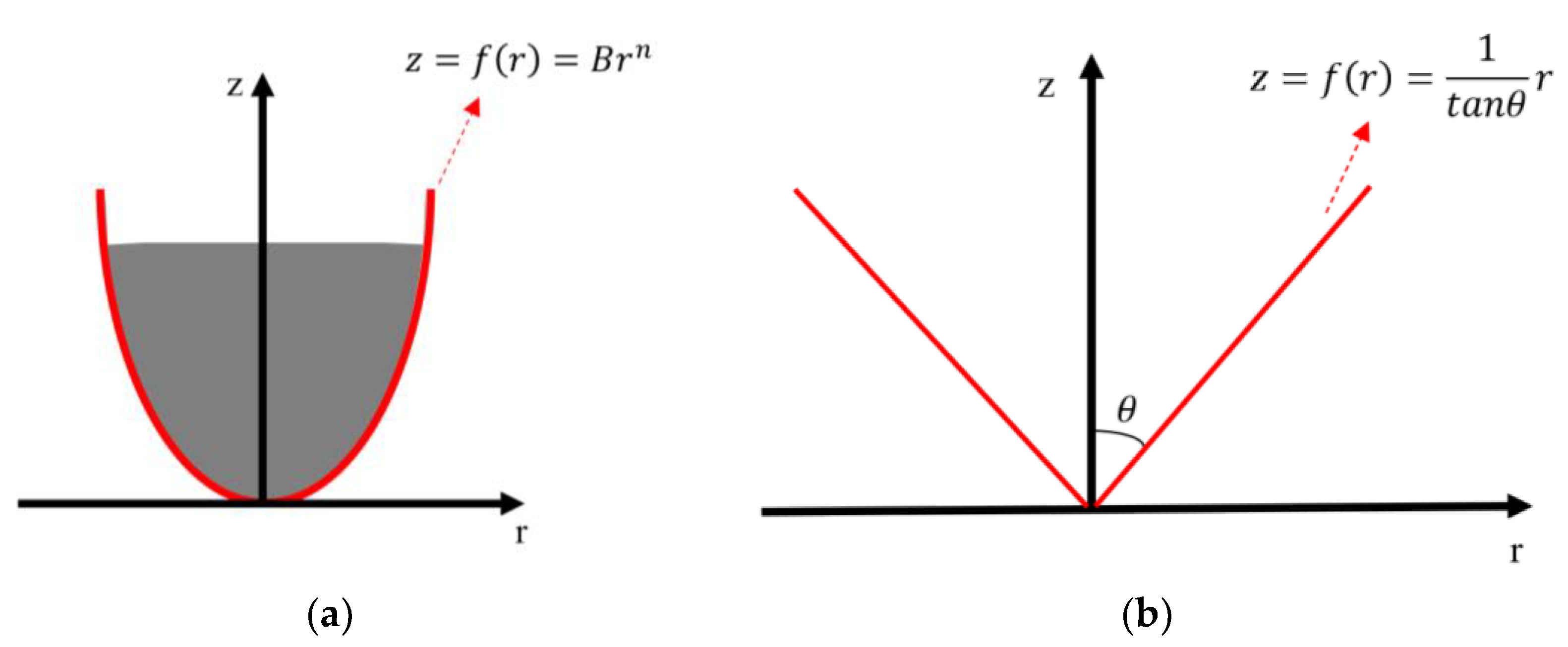
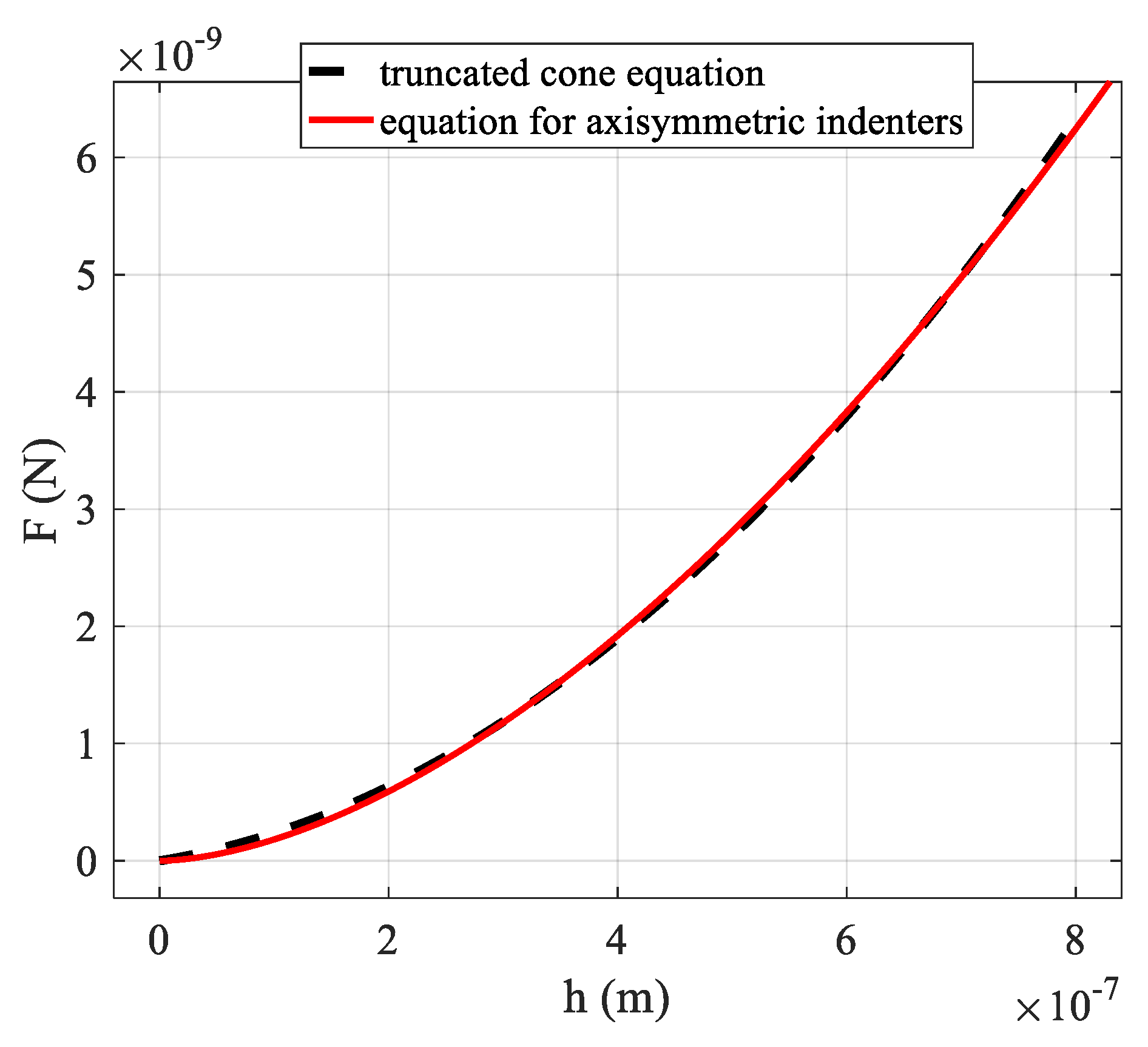
3.2. Axisymmetric Indenters with General Shape
3.3. Avoiding a Pseudo-Softening Behavior
3.4. An Example on a H4 Human Glioma Cell
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lekka, M.; Laidler, P. Applicability of AFM in cancer detection. Nat. Nanotechnol. 2009, 4, 72. [Google Scholar] [CrossRef] [PubMed]
- Stylianou, A.; Lekka, M.; Stylianopoulos, T. AFM assessing of nanomechanical fingerprints for cancer early diagnosis and classification: From single cell to tissue level. Nanoscale 2018, 10, 20930–20945. [Google Scholar] [CrossRef] [PubMed]
- Krieg, M.; Fläschner, G.; Alsteens, D.; Gaub, B.M.; Roos, W.H.; Wuite, G.J.L.; Gaub, H.E.; Gerber, C.; Dufrêne, Y.F.; Müller, D.J. Atomic force microscopy-based mechanobiology. Nat. Rev. Phys. 2019, 1, 41–57. [Google Scholar] [CrossRef]
- Plodinec, M.; Loparic, M.; Monnier, C.A.; Obermann, E.C.; Zanetti-Dallenbach, R.; Oertle, P.; Hyotyla, J.T.; Aebi, U.; Bentires-Alj, M.; Lim, R.Y.H.; et al. The nanomechanical signature of breast cancer. Nat. Nanotechnol. 2012, 7, 757–765. [Google Scholar] [CrossRef] [PubMed]
- Stylianou, A.; Kontomaris, S.V.; Grant, C.; Alexandratou, E. Atomic Force Microscopy on Biological Materials Related to Pathological Conditions. Scanning 2019, 2019, 8452851. [Google Scholar] [CrossRef]
- Stolz, M.; Gottardi, R.; Raiteri, R.; Miot, S.; Martin, I.; Imer, R.; Staufer, U.; Raducanu, A.; Dueggelin, M.; Baschong, W.; et al. Early detection of aging cartilage and osteoarthritis in mice and patient samples using atomic force microscopy. Nat. Nanotechnol. 2009, 4, 186–192. [Google Scholar] [CrossRef]
- Stolz, M.; Raiteri, R.; Daniels, A.U.; Van Landingham, A.M.W.R.; Baschong, W.; Aebi, U. Dynamic elastic modulus of porcine articular cartilage determined at two different levels of tissue organization by indentation-type atomic force microscopy. Biophys. J. 2004, 86, 3269–3283. [Google Scholar] [CrossRef]
- Drolle, E.; Hane, F.; Lee, B.; Leonenko, Z. Atomic force microscopy to study molecular mechanisms of amyloid fibril formation and toxicity in Alzheimer’s disease. Drug Metab. Rev. 2014, 46, 207–223. [Google Scholar] [CrossRef]
- Li, N.; Jang, H.; Yuan, M.; Li, W.; Yun, X.; Lee, J.; Du, Q.; Nussinov, R.; Hou, J.; Lal, R.; et al. Graphite-templated amyloid nanostructures formed by a potential pentapeptide inhibitor for Alzheimer’s disease: A combined study of real-time atomic force microscopy and molecular dynamics simulations. Langmuir 2017, 33, 6647–6656. [Google Scholar] [CrossRef]
- Ramalho, R.; Rankovic, S.; Zhou, J.; Aiken, C.; Rousso, I. Analysis of the mechanical properties of wild type and hyperstable mutants of the HIV-1 capsid. Retrovirology 2016, 13, 17. [Google Scholar] [CrossRef]
- Zhao, G.; Perilla, J.R.; Yufenyuy, E.L.; Meng, X.; Chen, B.; Ning, J.; Ahn, J.; Gronenborn, A.M.; Schulten, K.; Aiken, C.; et al. Mature HIV-1 capsid structure by cryo-electron microscopy and all-atom molecular dynamics. Nature 2013, 497, 643–646. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Georgakopoulos, A.; Malamou, A.; Stylianou, A. The average Young’s modulus as a physical quantity for describing the depth-dependent mechanical properties of cells. Mech. Mater. 2021, 158, 103846. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Stylianou, A.; Georgakopoulos, A.; Malamou, A. Is it mathematically correct to fit AFM data (obtained on biological materials) to equations arising from Hertzian mechanics? Micron 2022, 164, 103384. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Malamou, A.; Stylianou, A. The Hertzian theory in AFM nanoindentation experiments regarding biological samples: Overcoming limitations in data processing. Micron 2022, 155, 103228. [Google Scholar] [CrossRef]
- Ding, Y.; Xu, G.K.; Wang, G.F. On the determination of elastic moduli of cells by AFM based indentation. Sci. Rep. 2017, 7, 45575. [Google Scholar] [CrossRef]
- Li, Q.S.; Lee, G.Y.H.; Ong, C.N.; Lim, C.T. AFM indentation study of breast cancer cells. Biochem. Biophys. Res. Commun. 2018, 374, 609–613. [Google Scholar]
- Guz, N.; Dokukin, M.; Kalaparthi, V.; Sokolov, I. If cell mechanics can be described by elastic modulus: Study of different models and probes used in indentation experiments. Biophys. J. 2014, 107, 564–575. [Google Scholar] [CrossRef]
- Gavara, N. A beginner’s guide to atomic force microscopy probing for cell mechanics. Microsc. Res. Tech. 2017, 80, 75–84. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Malamou, A. Hertz model or Oliver & Pharr analysis? Tutorial regarding AFM nanoindentation experiments on biological samples. Mater. Res. Express 2020, 7, 033001. [Google Scholar]
- Ding, Y.; Wang, J.; Xu, G.K.; Wang, G.F. Are elastic moduli of biological cells depth dependent or not? Another explanation using a contact mechanics model with surface tension. Soft Matter 2018, 14, 7534–7541. [Google Scholar] [CrossRef]
- Hermanowicz, P.; Sarna, M.; Burda, K.; Gabryś, H. An open source software for analysis of force curves. Rev. Sci. Instrum. 2014, 85, 063703. [Google Scholar] [CrossRef] [PubMed]
- Bontempi, M.; Salamanna, F.; Capozza, R.; Visani, A.; Fini, M.; Gambardella, A. Nanomechanical Mapping of Hard Tissues by Atomic Force Microscopy: An Application to Cortical Bone. Materials 2022, 15, 7512. [Google Scholar] [CrossRef]
- Butt, H.J.; Jaschke, M. Calculation of thermal noise in atomic force microscopy. Nanotechnology 1995, 6, 1. [Google Scholar] [CrossRef]
- Sneddon, I.N. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Malamou, A. A novel approximate method to calculate the force applied on an elastic half space by a rigid sphere. Eur. J. Phys. 2021, 42, 025010. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J Mater. Res. 2004, 19, 3. [Google Scholar] [CrossRef]
- Pogoda, K.; Jaczewska, J.; Wiltowska-Zuber, J.; Klymenko, O.; Zuber, K.; Fornal, M.; Lekka, M. Depth-sensing analysis of cytoskeleton organization based on AFM data. Eur. Biophys. J. 2012, 41, 79–87. [Google Scholar] [CrossRef]
- Chen, S.W.; Teulon, J.M.; Kaur, H.; Godon, C.; Pellequer, J.L. Nano-structural stiffness measure for soft biomaterials of heterogeneous elasticity. Nanoscale Horiz. 2023, 8, 75–82. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Malamou, A. The truncated cone effect in AFM nanoindentation on soft materials. Micro Nanosyst. 2023. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Stylianou, A.; Georgakopoulos, A.; Malamou, A. 3D AFM Nanomechanical Characterization of Biological Materials. Nanomaterials 2023, 13, 395. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Stylianou, A.; Chliveros, G.; Malamou, A. Determining Spatial Variability of Elastic Properties for Biological Samples Using AFM. Micromachines 2023, 14, 182. [Google Scholar] [CrossRef]
- Islam, M.T.; Tang, S.; Liverani, C.; Saha, S.; Tasciotti, E.; Righetti, R. Non-invasive imaging of Young’s modulus and Poisson’s ratio in cancers in vivo. Sci. Rep. 2020, 10, 7266. [Google Scholar] [CrossRef]
- Chen, X.; Hughes, R.; Mullin, N.; Hawkins, R.J.; Holen, I.; Brown, N.J.; Hobbs, J.K. Mechanical Heterogeneity in the Bone Microenvironment as Characterized by Atomic Force Microscopy. Biophys. J. 2020, 119, 502–513. [Google Scholar] [CrossRef]
- Louca, M.; Stylianou, A.; Minia, A.; Pliaka, V.; Alexopoulos, L.G.; Gkretsi, V.; Stylianopoulos, T. Ras suppressor-1 (RSU-1) promotes cell invasion in aggressive glioma cells and inhibits it in non-aggressive cells through STAT6 phospho-regulation. Sci. Rep. 2019, 9, 7782. [Google Scholar] [CrossRef]
- Kilpatrick, J.I.; Revenko, I.; Rodriguez, B.J. Nanomechanics of cells and biomaterials studied by atomic force microscopy. Adv. Healthc. Mater. 2015, 4, 2456–2474. [Google Scholar] [CrossRef]
- Wu, P.-H.; Aroush, D.R.-B.; Asnacios, A.; Chen, W.-C.; Dokukin, M.E.; Doss, B.L.; Durand-Smet, P.; Ekpenyong, A.; Guck, J.; Guz, N.V.; et al. A comparison of methods to assess cell mechanical properties. Nat. Methods 2018, 15, 491–498. [Google Scholar] [CrossRef]
- Grant, C.A.; Brockwell, D.J.; Radford, S.E.; Thomson, N.H. Effects of hydration on the mechanical response of individual collagen fibrils. Appl. Phys. Lett. 2008, 92, 233902. [Google Scholar] [CrossRef]
- Heim, A.J.; Matthews, W.G.; Koob, T.J. Determination of the elastic modulus of native collagen fibrils via radial indentation. Appl. Phys. Lett. 2006, 89, 181902. [Google Scholar] [CrossRef]
- Minary-Jolandan, M.; Yu, M.F. Nanomechanical heterogeneity in the gap and overlap regions of type I collagen fibrils with implications for bone heterogeneity. Biomacromolecules 2009, 10, 2565–2570. [Google Scholar] [CrossRef]
- Yadavalli, V.K.; Svintradze, D.V.; Pidaparti, R.M. Nanoscale measurements of the assembly of collagen to fibrils. Int. J. Biol. Macromol. 2010, 46, 458–464. [Google Scholar] [CrossRef]
- Andriotis, O.G.; Manuyakorn, W.; Zekonyte, J.; Katsamenis, O.L.; Fabri, S.; Howarth, P.H.; Davies, D.E.; Thurner, P.J. Nanomechanical assessment of human and murine collagen fibrils via atomic force microscopy cantilever-based nanoindentation. J. Mech. Behav. Biomed. Mater. 2014, 39, 9–26. [Google Scholar] [CrossRef] [PubMed]
- Baldwin, S.J.; Kreplak, L.; Lee, J.M. Characterization via atomic force microscopy of discrete plasticity in collagen fibrils from mechanically overloaded tendons: Nano-scale structural changes mimic rope failure. J. Mech. Behav. Biomed. Mater. 2016, 60, 356–366. [Google Scholar] [CrossRef] [PubMed]
- Andriotis, O.G.; Elsayad, K.; Smart, D.E.; Nalbach, M.; Davies, D.E.; Thurner, P.J. Hydration and nanomechanical changes in collagen fibrils bearing advanced glycation end-products. Biomed. Opt. Express 2019, 10, 1841–1855. [Google Scholar] [CrossRef] [PubMed]
- Papi, M.; Paoletti, P.; Geraghty, B.; Akhtar, R. Nanoscale characterization of the biomechanical properties of collagen fibrils in the sclera. Appl. Phys. Lett. 2014, 104, 103703. [Google Scholar] [CrossRef]
- Kazaili, A.; Al-Hindy, H.A.A.; Madine, J.; Akhtar, R. Nano-scale stiffness and collagen fibril deterioration: Probing the cornea following enzymatic degradation using peakforce-qnm afm. Sensors 2021, 21, 1629. [Google Scholar] [CrossRef]
- Läubli, N.F.; Burri, J.T.; Marquard, J.; Vogler, H.; Mosca, G.; Vertti-Quintero, N.; Shamsudhin, N.; de Mello, A.; Grossniklaus, U.; Ahmed, D.; et al. 3D mechanical characterization of single cells and small organisms using acoustic manipulation and force microscopy. Nat. Commun. 2021, 12, 2583. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kontomaris, S.V.; Stylianou, A.; Chliveros, G.; Malamou, A. AFM Indentation on Highly Heterogeneous Materials Using Different Indenter Geometries. Appl. Mech. 2023, 4, 460-475. https://doi.org/10.3390/applmech4020026
Kontomaris SV, Stylianou A, Chliveros G, Malamou A. AFM Indentation on Highly Heterogeneous Materials Using Different Indenter Geometries. Applied Mechanics. 2023; 4(2):460-475. https://doi.org/10.3390/applmech4020026
Chicago/Turabian StyleKontomaris, Stylianos Vasileios, Andreas Stylianou, Georgios Chliveros, and Anna Malamou. 2023. "AFM Indentation on Highly Heterogeneous Materials Using Different Indenter Geometries" Applied Mechanics 4, no. 2: 460-475. https://doi.org/10.3390/applmech4020026
APA StyleKontomaris, S. V., Stylianou, A., Chliveros, G., & Malamou, A. (2023). AFM Indentation on Highly Heterogeneous Materials Using Different Indenter Geometries. Applied Mechanics, 4(2), 460-475. https://doi.org/10.3390/applmech4020026







