Shear Deterioration of the Hierarchical Structure of Cellulose Microfibrils under Water Condition: All-Atom Molecular Dynamics Analysis
Abstract
1. Introduction
2. Computational Methods and Models
3. Calculation Condition and Computation Procedures
3.1. Structural Relaxation of Single CMF
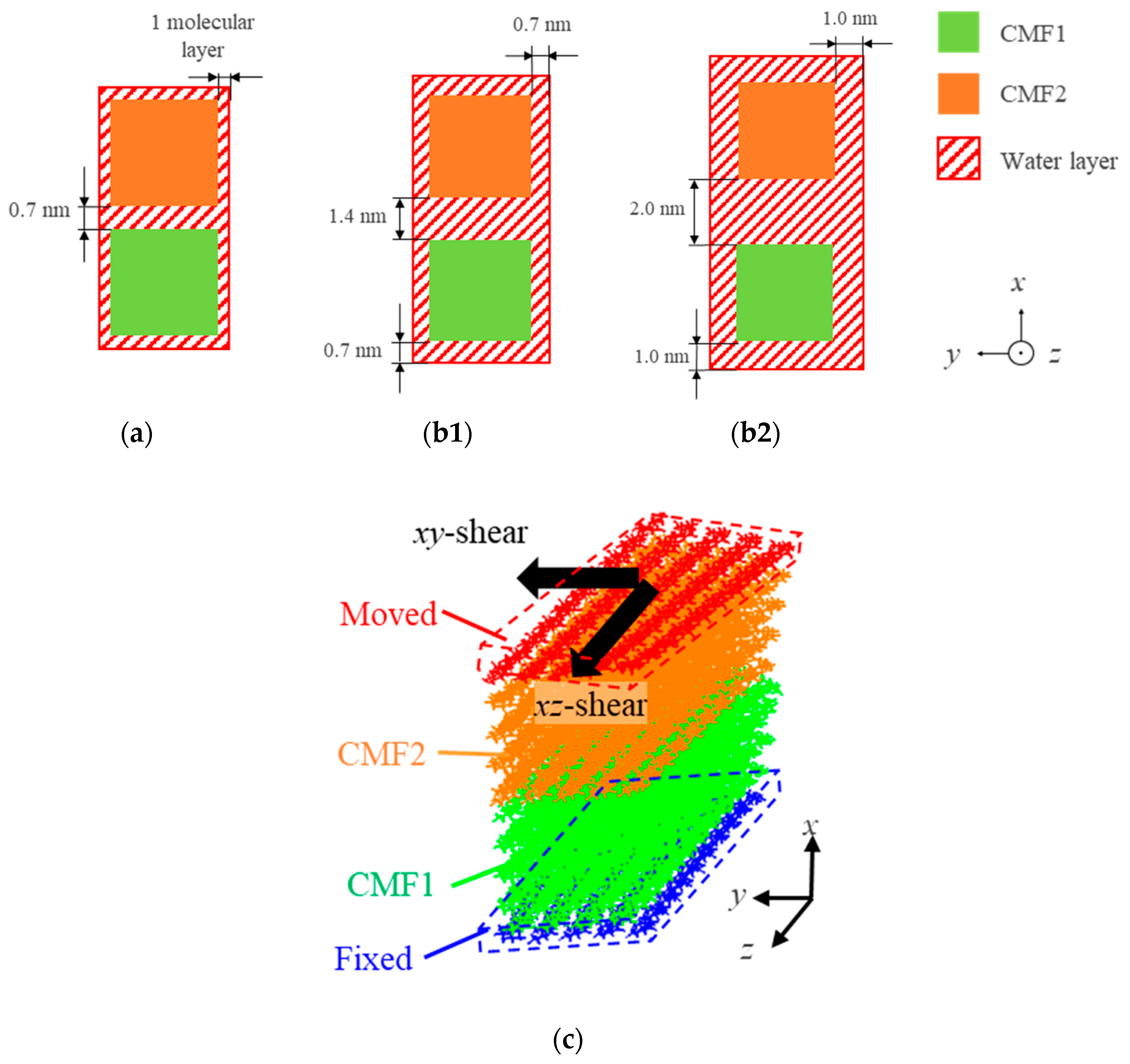
3.2. Hierarchical Structure Simulation of Two CMFs
4. Result and Discussion
4.1. Hierarchical Structure Simulation Using Two CMFs
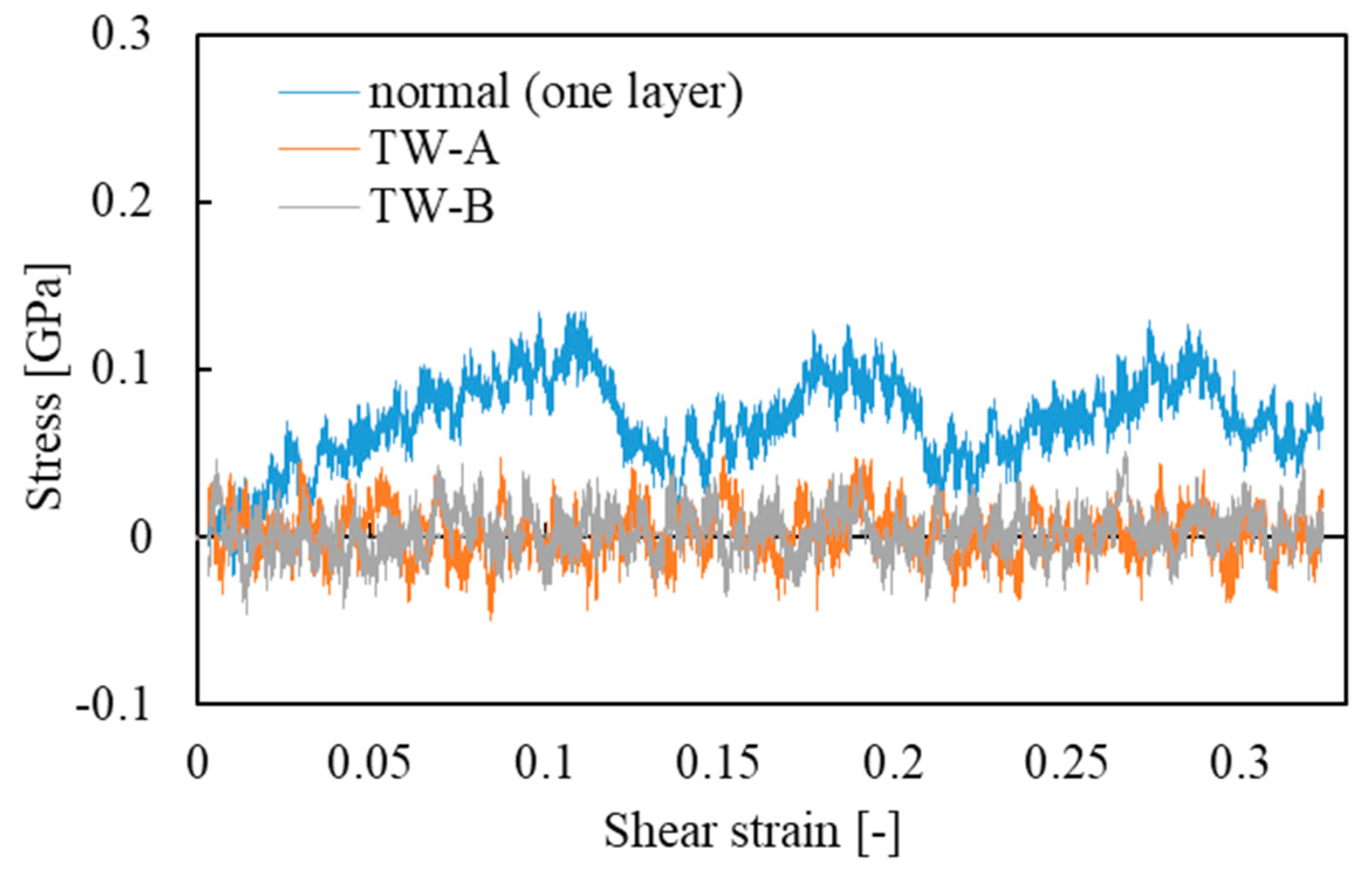
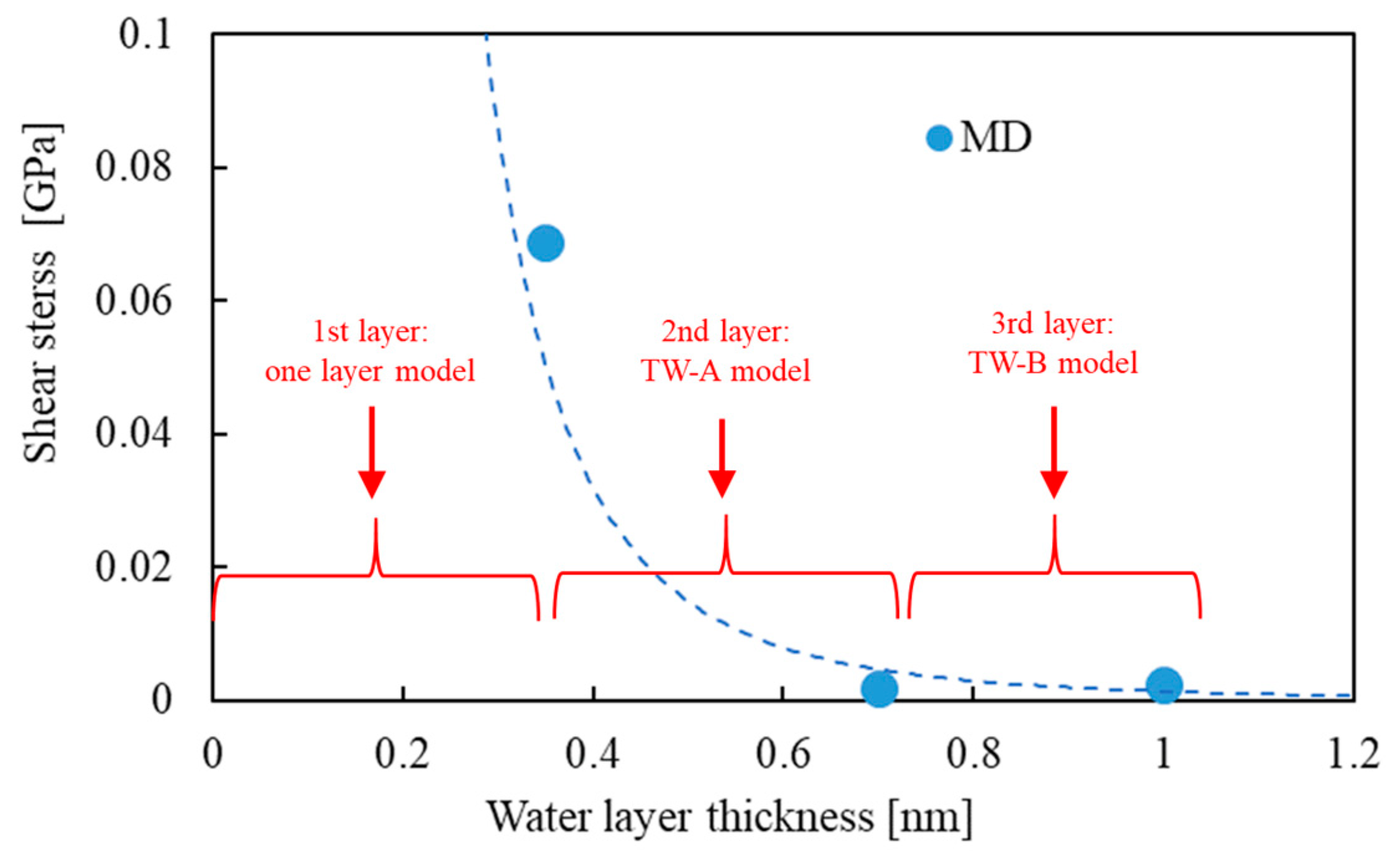
4.2. Effect of Water Thickness on the Mechanical Properties of Hierarchical Structure of Two CMFs (Results of Thick Water Models: TW-A and TW-B)
5. Conclusions
- ◆
- In vacuum condition, shear failure may occur inside the CMF, not at the interface. In the water condition, interfacial slip tends to occur in shear deformation.
- ◆
- The behavior of the water molecules at the interface is largely changed by the temperature. For example, at 300 K, the hydrogen bonds between the surfaces via water the molecules were reduced, and both the shear modulus and shear strength showed smaller values than in the vacuum condition.
- ◆
- There is strong anisotropy in shear moduli. The strength depends on the joining direction, with regard to the direction of molecular sheets.
- ◆
- When the length of water thickness exceeds 0.35 or 0.7 nm, the hydrogen bonds cannot directly connect two CMFs, interfacial sliding occurs easily, and shear stress on average is reduced to almost zero.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Klemm, D.; Kramer, F.; Moritz, S.; Lindström, T.; Ankerfors, M.; Gray, D.; Dorris, A. Nanocelluloses: A New Family of nature-based materials. Angew. Chem. Int. Ed. 2011, 50, 5438–5466. [Google Scholar] [CrossRef] [PubMed]
- Moon, R.J.; Martini, A.; Nairn, J.; Simonsen, J.; Youngblood, J. Cellulose nanomaterials review: Structure, properties and nanocomposites. Chem. Soc. Rev. 2011, 40, 3941–3994. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.-Y.; Aitomäki, Y.; Berglund, L.A.; Oksman, K.; Bismarck, A. On the use of nanocellulose as reinforcement in polymer matrix composites. Compos. Sci. Technol. 2014, 105, 15–27. [Google Scholar] [CrossRef]
- Reising, A.B.; Moon, R.J.; Youngblood, J.P. Effect of particle alignment on mechanical properties of neat cellulose nanocrystal films. J. Sci. Technol. Forest Prod. Process. 2012, 2, 32–41. Available online: https://www.fs.usda.gov/treesearch/pubs/44003 (accessed on 15 January 2023).
- Nishino, T. Structures and critical mechanical properties of cellulose. J. Soc. Mater. Sci. Jpn. 2008, 57, 97–103. [Google Scholar] [CrossRef]
- Milanez, D.H.; Morato do Amaral, R.; Lopes de Faria, L.I.; Gregolin, J.A.R. Technological indicators of nanocellulose advances obtained from data and text mining applied to patent documents. Mater. Res. 2014, 17, 1513–1522. [Google Scholar] [CrossRef]
- Guhados, G.; Wan, W.; Hutter, J.L. Measurement of the elastic modulus of single bacterial cellulose fibers using atomic force microscopy. Langmuir 2005, 21, 6642–6646. [Google Scholar] [CrossRef]
- Wu, X.; Moon, R.J.; Martini, A. Tensile strength of Iβ crystalline cellulose predicted by molecular dynamics simulation. Cellulose 2014, 21, 2233–2245. [Google Scholar] [CrossRef]
- Heiner, A.P.; Teleman, O. Structural reporter parameters for the characterisation of crystalline cellulose. Pure Appl. Chem. 1996, 68, 2187–2192. [Google Scholar] [CrossRef]
- Yui, T.; Nishimura, S.; Akiba, S.; Hayashi, S. Swelling behavior of the cellulose Iβ crystal models by molecular dynamics. Carbohydr. Res. 2006, 341, 2521–2530. [Google Scholar] [CrossRef]
- Nishiyama, Y.; Johnson, G.P.; French, A.D. Diffraction from nonperiodic models of cellulose crystal. Cellulose 2012, 19, 319–336. [Google Scholar] [CrossRef]
- Hadden, J.A.; French, A.D.; Woods, R.J. Effect of microfibril twisting on theoretical powder diffraction patterns of cellulose Iβ. Cellulose 2014, 21, 879–884. [Google Scholar] [CrossRef] [PubMed]
- Shklyaev, O.E.; Kubicki, J.D.; Watts, H.D.; Crespi, V.H. Constraints on Iβ cellulose twist from DFT calculations of 13C NMR chemical shifts. Cellulose 2014, 21, 3979–3991. [Google Scholar] [CrossRef]
- Uto, T.; Mawatari, S.; Yui, T. Theoretical study of the structural stability of molecular chain sheet models of cellulose crystal allomorphs. J. Phys. Chem. B 2014, 118, 9313–9321. [Google Scholar] [CrossRef]
- Paavilainen, S.; Róg, T.; Vattulainen, I. Analysis of twisting of cellulose nanofibrils in atomistic molecular dynamics simulations. J. Phys. Chem. B 2011, 115, 3747–3755. [Google Scholar] [CrossRef] [PubMed]
- Kannam, S.K.; Oehme, D.P.; Doblin, M.S.; Gidley, M.J.; Bacic, A.; Downton, M.T. Hydrogen bonds and twist in cellulose microfibrils. Carbohydr. Polym. 2017, 175, 433–439. [Google Scholar] [CrossRef]
- Wang, J.-S.; Wang, G.; Feng, X.-Q.; Kitamura, T.; Kang, Y.-L.; Yu, S.-W.; Qin, Q.-H. Hierarchical chirality transfer in the growth of towel gourd tendrils. Sci. Rep. 2013, 3, 3102. [Google Scholar] [CrossRef] [PubMed]
- Northolt, M.G.; Boerstoel, H.; Maatman, H.; Huisman, R.; Veurink, J.; Elzerman, H. The structure and properties of cellulose fibres spun from an anisotropic phosphoric acid solution. Polymer 2001, 42, 8249–8264. [Google Scholar] [CrossRef]
- Zhao, Z.; Shklyaev, O.E.; Nili, A.; Mohamed, M.N.A.; Kubicki, J.D.; Crespi, V.H.; Zhong, L. Cellulose microfibril twist, mechanics, and implication for cellulose biosynthesis. J. Phys. Chem. A 2013, 117, 2580–2589. [Google Scholar] [CrossRef]
- Takada, K.; Saitoh, K.-I.; Takuma, M.; Takahashi, Y.; Sato, T. Molecular dynamics study on transmission mechanism of torsional deformation in cellulose nanofibers with hierarchical structure. Soft Nanosci. Lett. 2019, 9, 45–57. [Google Scholar] [CrossRef]
- Izumi, Y.; Saitoh, K.; Takuma, M.; Takahashi, Y.; Sato, T. Mechanical behavior and hierarchical transmission mMechanism of cellulose nanofiber by all-atom molecular dynamics model. Proc. Mech. Eng. Congr. Jpn. 2020, 2020, J03132. [Google Scholar] [CrossRef]
- Sinko, R.; Keten, S. Traction–separation laws and stick–slip shear phenomenon of interfaces between cellulose nanocrystals. J. Mech. Phys. Solid. 2015, 78, 526–539. [Google Scholar] [CrossRef]
- Hou, Y.; Guan, G.-F.; Xia, J.; Ling, Z.-C.; He, Z.; Han, Z.-M.; Yang, H.-B.; Gu, P.; Zhu, Y.; Yu, S.-H.; et al. Strengthening and toughening hierarchical nanocellulose via humidity-mediated interface. ACS Nano 2021, 15, 1310–1320. [Google Scholar] [CrossRef]
- Paajanen, A.; Ceccherini, S.; Maloney, T.; Ketoja, J.A. Chirality and bound water in the hierarchical cellulose structure. Cellulose 2019, 26, 5877–5892. [Google Scholar] [CrossRef]
- Hoeger, I.; Rojas, O.J.; Efimenko, K.; Velev, O.D.; Kelley, S.S. Ultrathin film coatings of aligned cellulose nanocrystals from a convective-shear assembly system and their surface mechanical properties. Soft Matter 2011, 7, 1957–1967. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017; ISBN 9780198803195. [Google Scholar]
- Lesar, R. Introduction to Computational Materials Science: Fundamentals to Applications; Cambridge University Press: Cambridge, UK, 2014; ISBN 0521845874. [Google Scholar]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comp. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef]
- Mackerell, A.D.; Bashford, D.; Bellontt, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.M.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef] [PubMed]
- Matthews, J.F.; Beckham, G.T.; Bergenstrahle-Wohlert, M.; Brady, J.W.; Himmel, M.E.; Crowley, M.F. Comparison of cellulose Iβ simulations with three carbohydrate force fields. J. Chem. Theory Comput. 2012, 8, 735–748. [Google Scholar] [CrossRef]
- Miyamoto, H.; Schnupf, U.; Crowley, M.F.; Brady, J.W. Comparison of the simulations of cellulosic crystals with three carbohydrate force fields. Carbohydr. Res. 2016, 422, 17–23. [Google Scholar] [CrossRef]
- Gomes, T.C.F.; Skaf, M.S. Cellulose-Builder: A toolkit for building crystalline structures of cellulose. J. Comp. Chem. 2012, 33, 1338–1346. [Google Scholar] [CrossRef]
- Jakob, H.F.; Fengel, D.; Tschegg, S.E.; Fratzl, P. The Elementary Cellulose Fibril in Picea abies: Comparison of transmission electron microscopy, small-angle X-ray scattering, and wide-angle X-ray scattering results. Macromolecules 1995, 28, 8782–8787. [Google Scholar] [CrossRef]
- Schlick, T. Molecular Modeling and Simulation: An Interdisciplinary Guide; Springer Science+Business Media: New York, NY, USA, 2002; p. 435. ISBN 978-0-387-22464-0. Available online: https://link.springer.com/book/10.1007/978-0-387-22464-0 (accessed on 15 January 2023).
- Hardy, D.J.; Wu, Z.; Phillips, J.C.; Stone, J.E.; Skeel, R.D.; Schulten, K. Multilevel summation, method for electrostatic force evaluation. J. Chem. Theory Comput. 2015, 11, 766–779. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Koch, M.; Tenbohlen, S.; Stirl, T. Diagnostic application of moisture equilibrium for power transformers. IEEE Trans. Power Deliv. 2010, 25, 2574–2581. [Google Scholar] [CrossRef]
- Take, Y.; Ota, T.; Yasoshima, H. Problems on paper strength: Chap. 4, Effect of moisture containing on paper strength. Jpn. TAPPI J. 1964, 18, 155–159. (In Japanese) [Google Scholar] [CrossRef]
- Fernandes, A.N.; Thomas, L.H.; Altaner, C.M.; Callow, P.; Forsyth, V.T.; Apperley, D.C.; Kennedy, C.J.; Jarvis, M.C. Nanostructure of cellulose microfibrils in spruce wood. Proc. Natl. Acad. Sci. USA 2011, 108, E1195–E1203. [Google Scholar] [CrossRef]
- Niinivaara, E.; Faustini, M.; Tammelin, T.; Kontturi, E. Water vapor uptake of ultrathin films of biologically derived nanocrystals: Quantitative assessment with quartz crystal microbalance and spectroscopic ellipsometry. Langmuir 2015, 31, 12170–12176. [Google Scholar] [CrossRef] [PubMed]
- Steered/Interactive Molecular Dynamics. Available online: http://www.ks.uiuc.edu/Research/smd_imd/ (accessed on 10 January 2023).
- Pradhan, S.M.; Katti, D.R.; ASCE, M.; Katti, K.S. Steered molecular dynamics study of mechanical response of full length and short collagen molecules. J. Nanomech. Micromech. 2011, 1, 104–110. [Google Scholar] [CrossRef]
- Jeffrey, G.A. An Introduction to Hydrogen Bonding; Oxford University Press: New York, NY, USA, 1997; ISBN 0-19-509549-9. [Google Scholar]
- Muthoka, R.M.; Kim, H.C.; Kim, J.W.; Zhai, L.; Panicker, P.S.; Kim, J. Steered pull simulation to determine nanomechanical properties of cellulose nanofiber. Materials 2020, 13, 710. [Google Scholar] [CrossRef]
- Müller, U.; Sretenovic, A.; Gindl, W.; Teischinger, A. Longitudinal shear properties of Europe larch wood related to cell-wall structure. Wood Fiber Sci. 2004, 36, 143–151. Available online: http://wfs.swst.org/index.php/wfs/article/view/751 (accessed on 15 January 2023).
- Shishehbor, M.; Dri, F.L.; Moon, R.J.; Zavattieri, P.D. A continuum-based structural modeling approach for cellulose nanocrystals (CNCs). J. Mech. Phys. Solid. 2018, 111, 308–332. [Google Scholar] [CrossRef]
- Izumi, Y.; Saitoh, K.; Takuma, M.; Takahashi, Y.; Sato, T. Molecular dynamics analysis of shear deformation and friction behavior in hierarchical structure of cellulose nanofibers with water molecules. Proc. Mech. Eng. Congr. Jpn. 2021, 2021, J031-29. (In Japanese) [Google Scholar] [CrossRef]
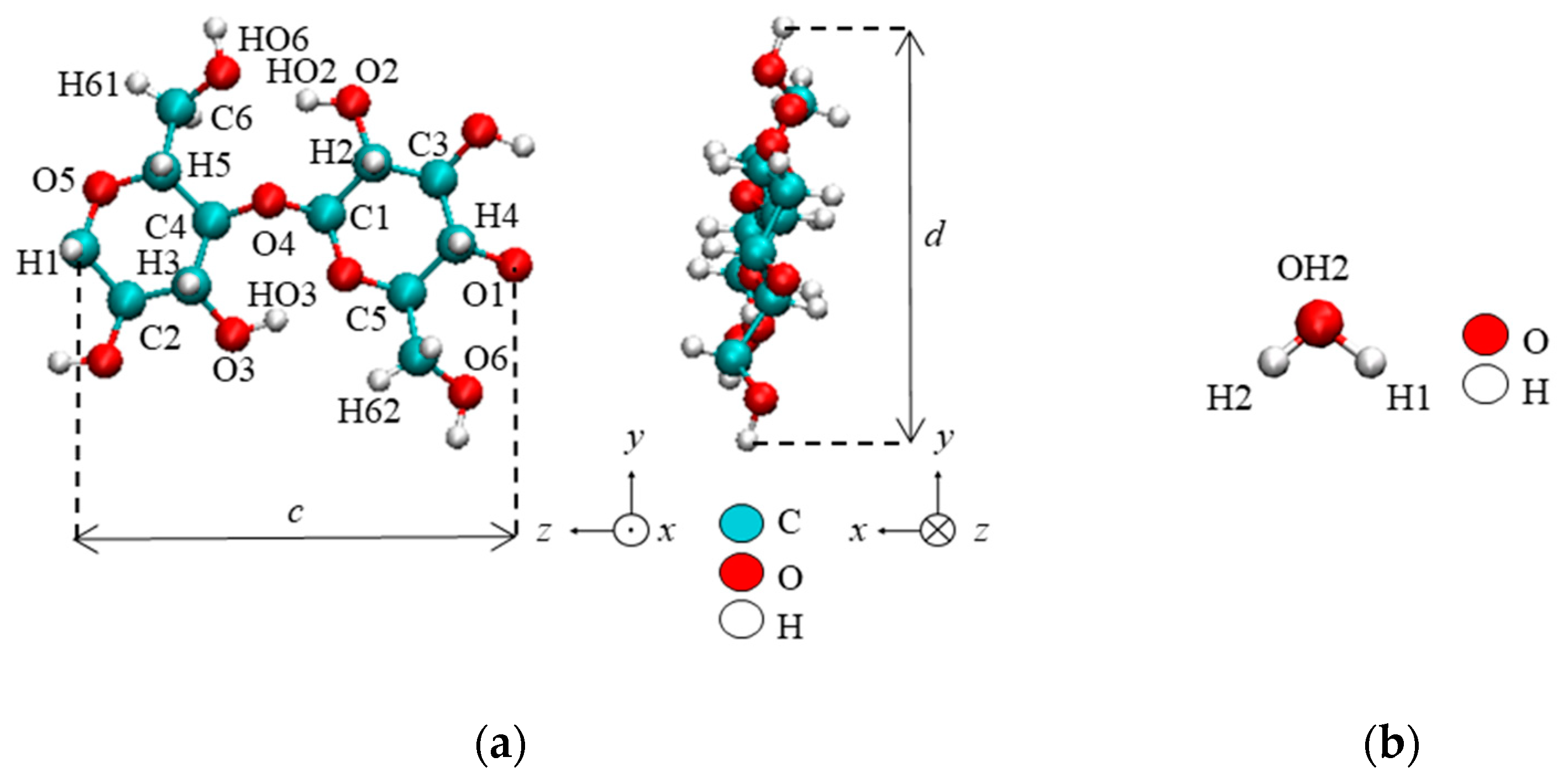
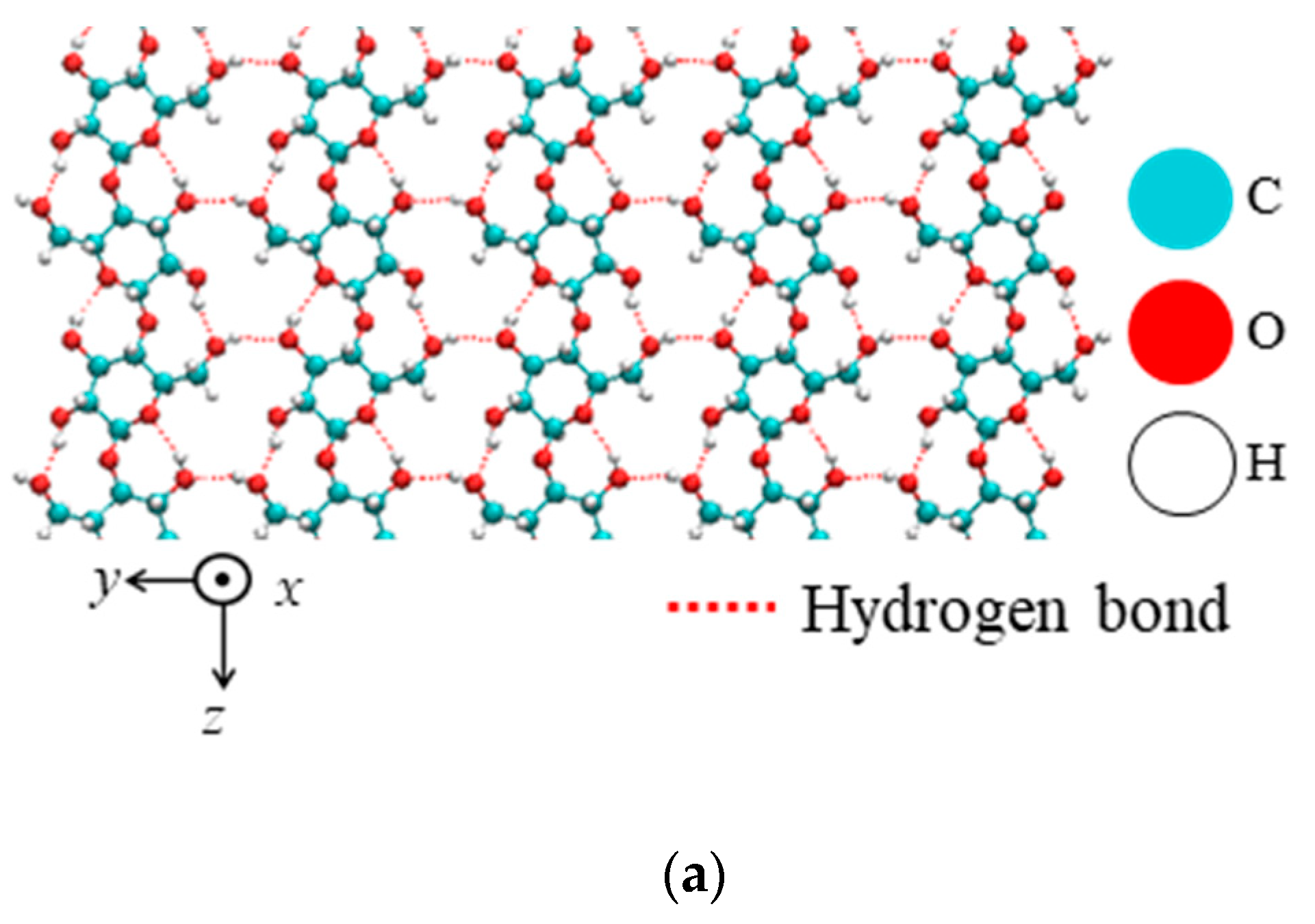
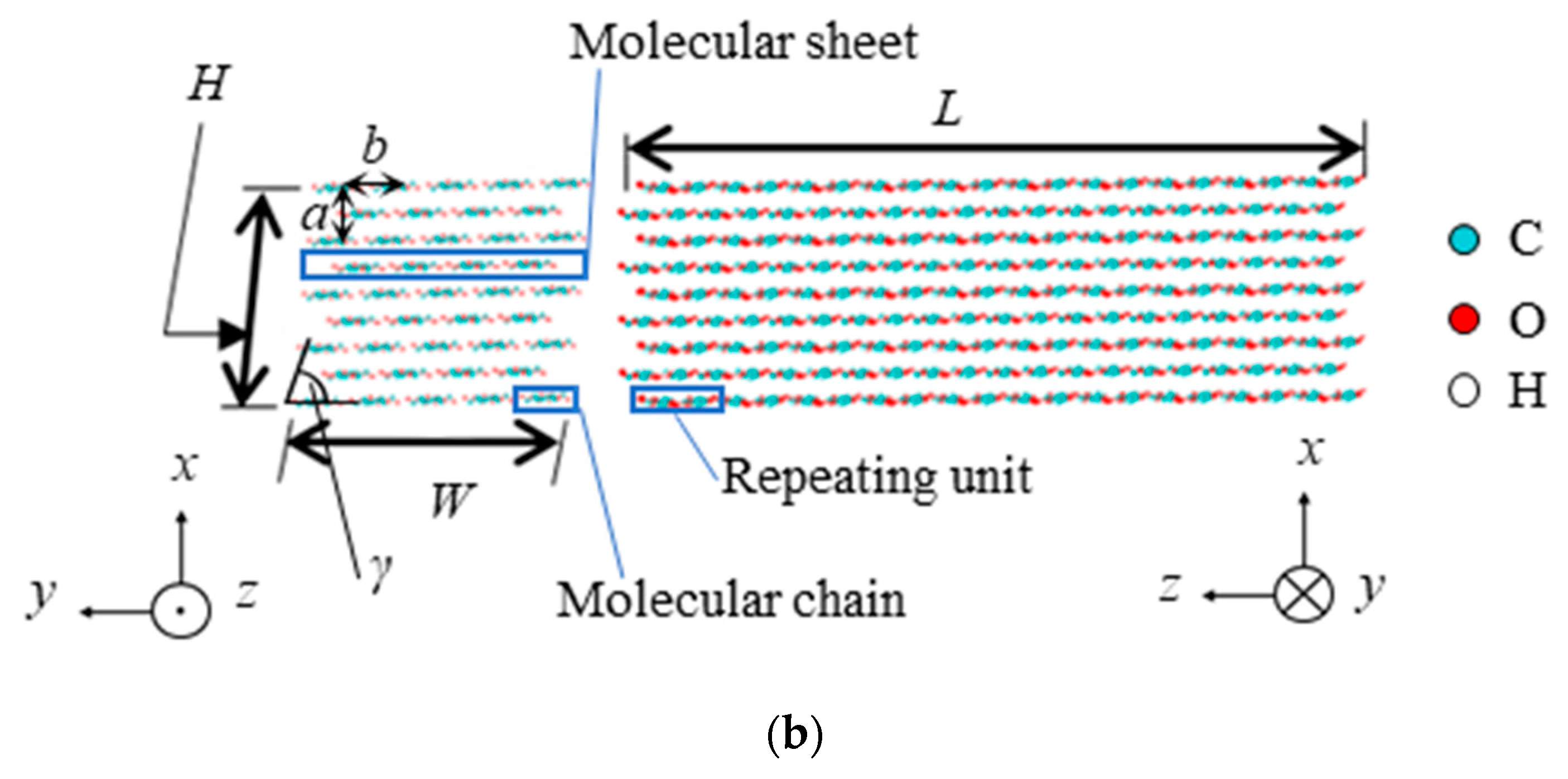
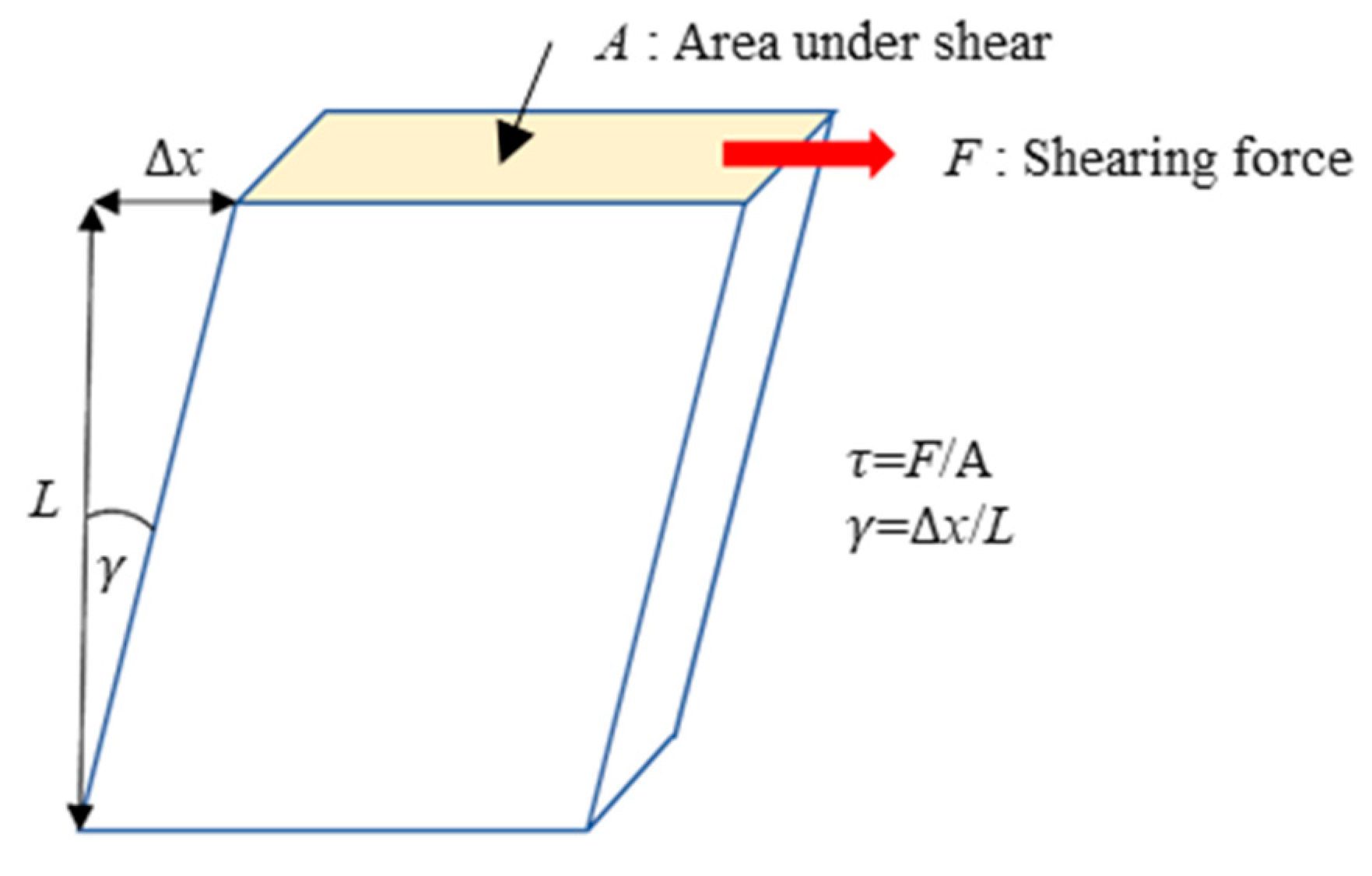

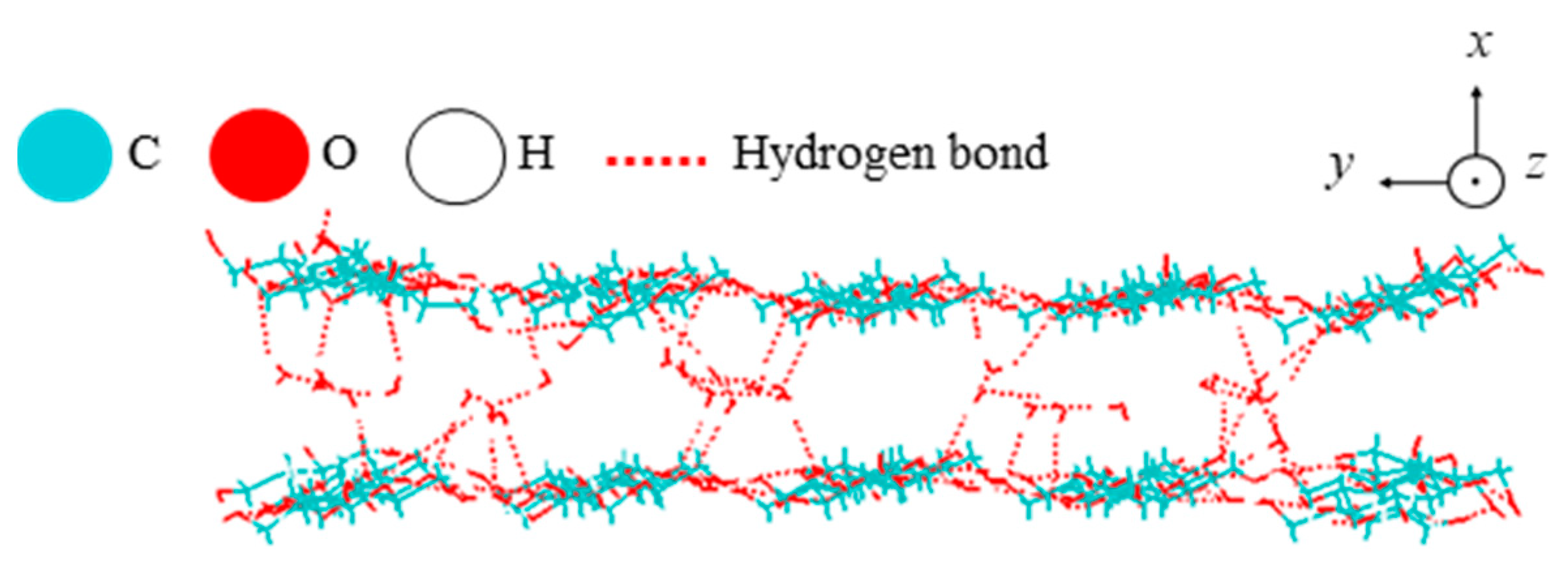

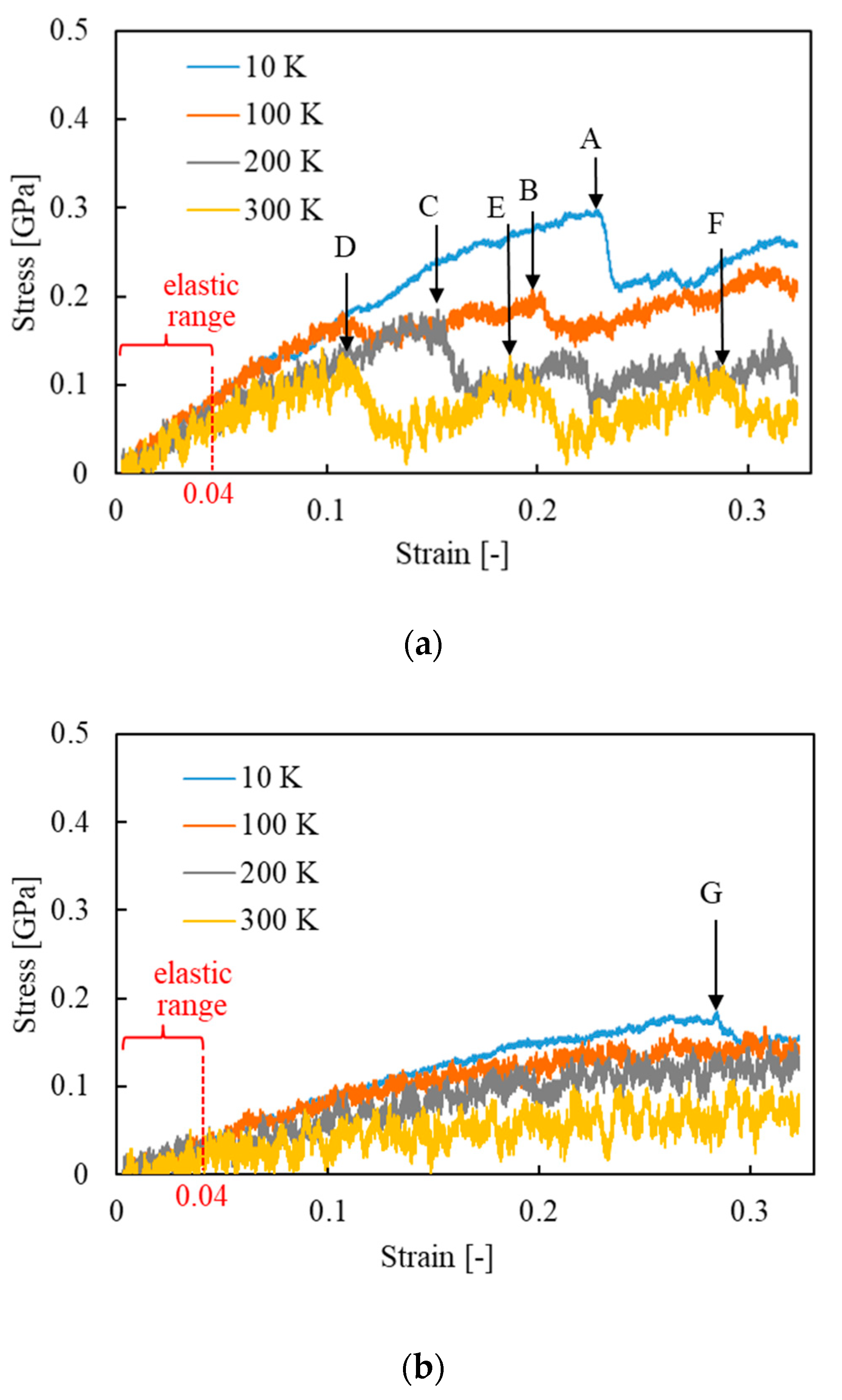
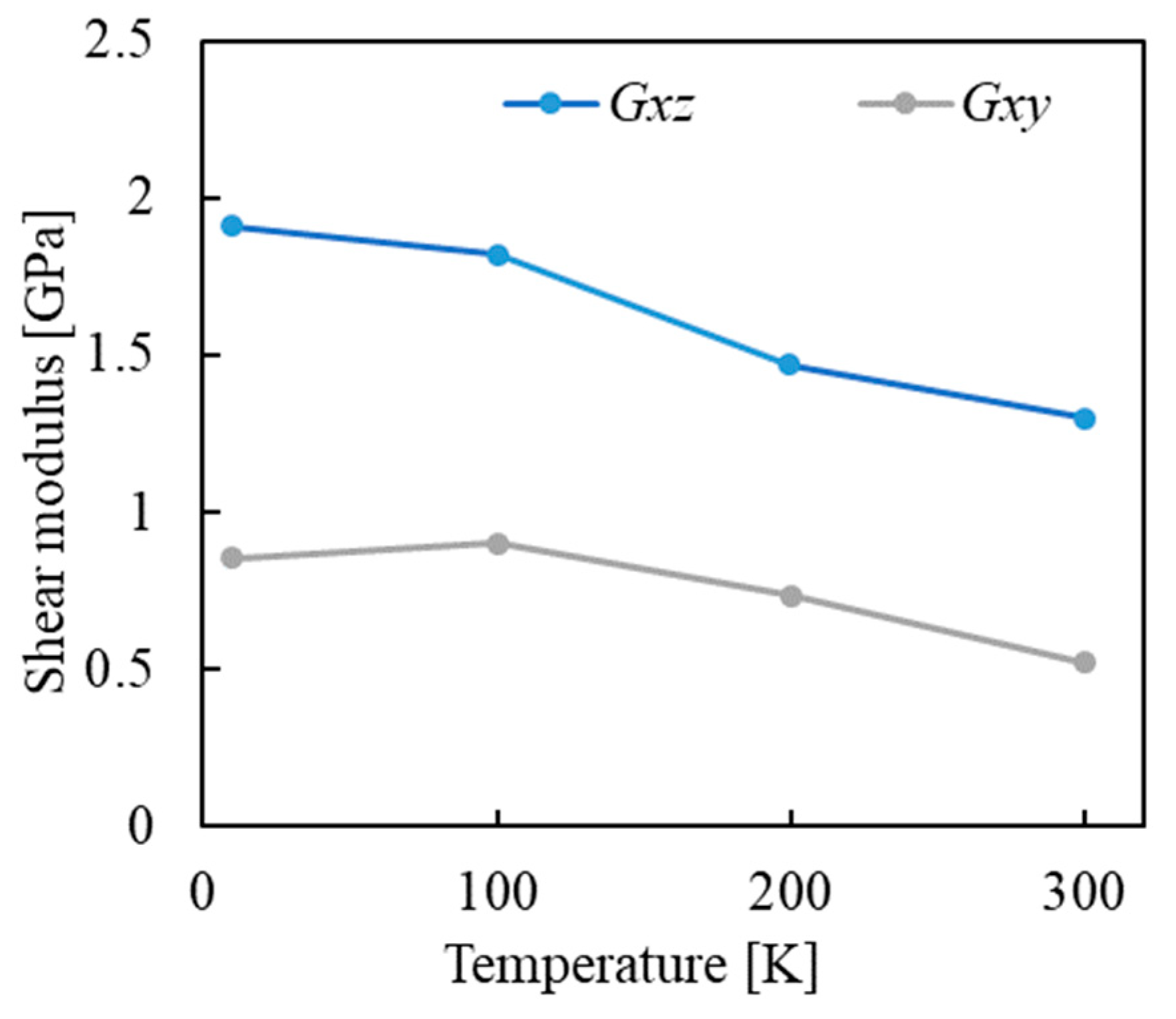
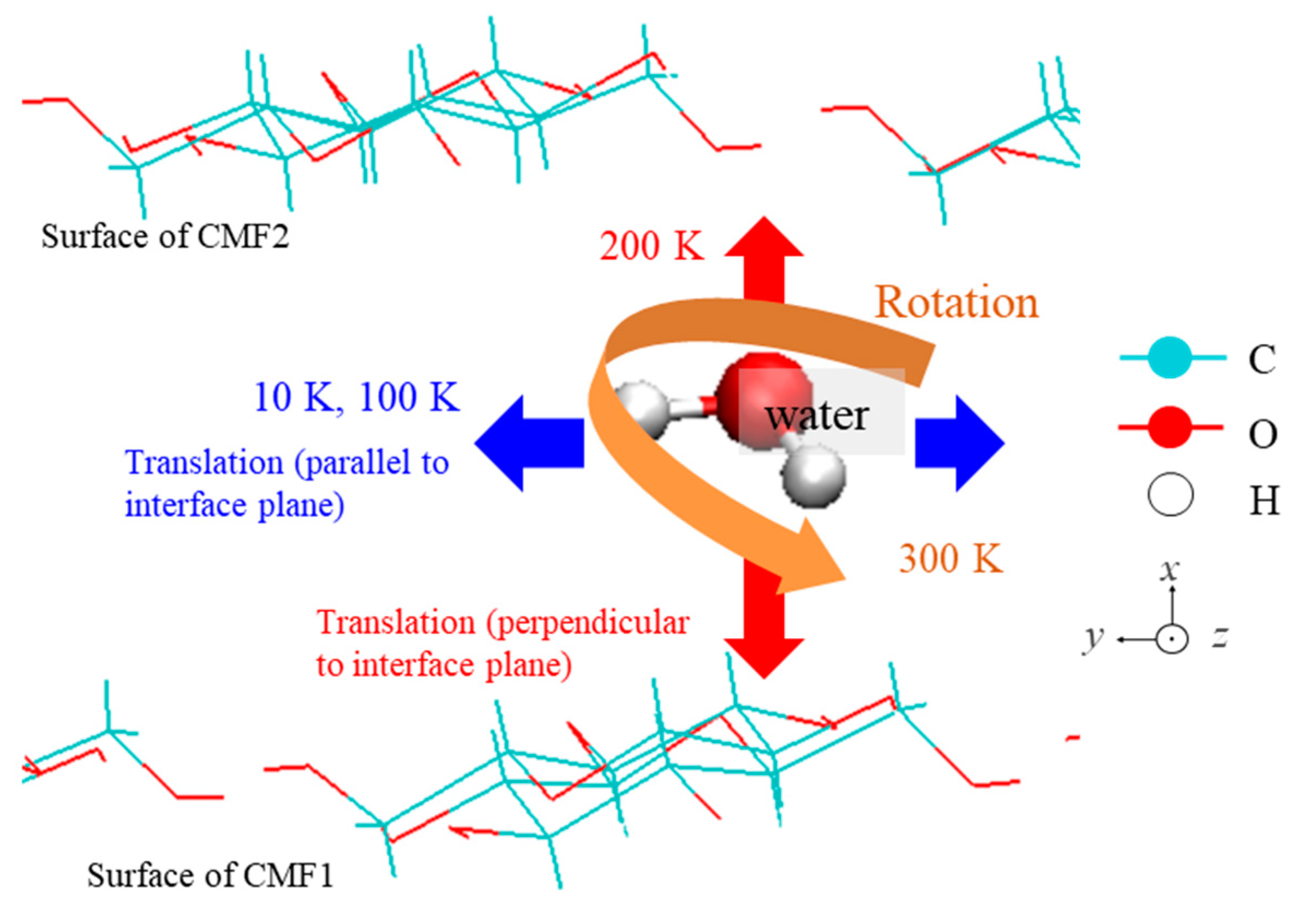
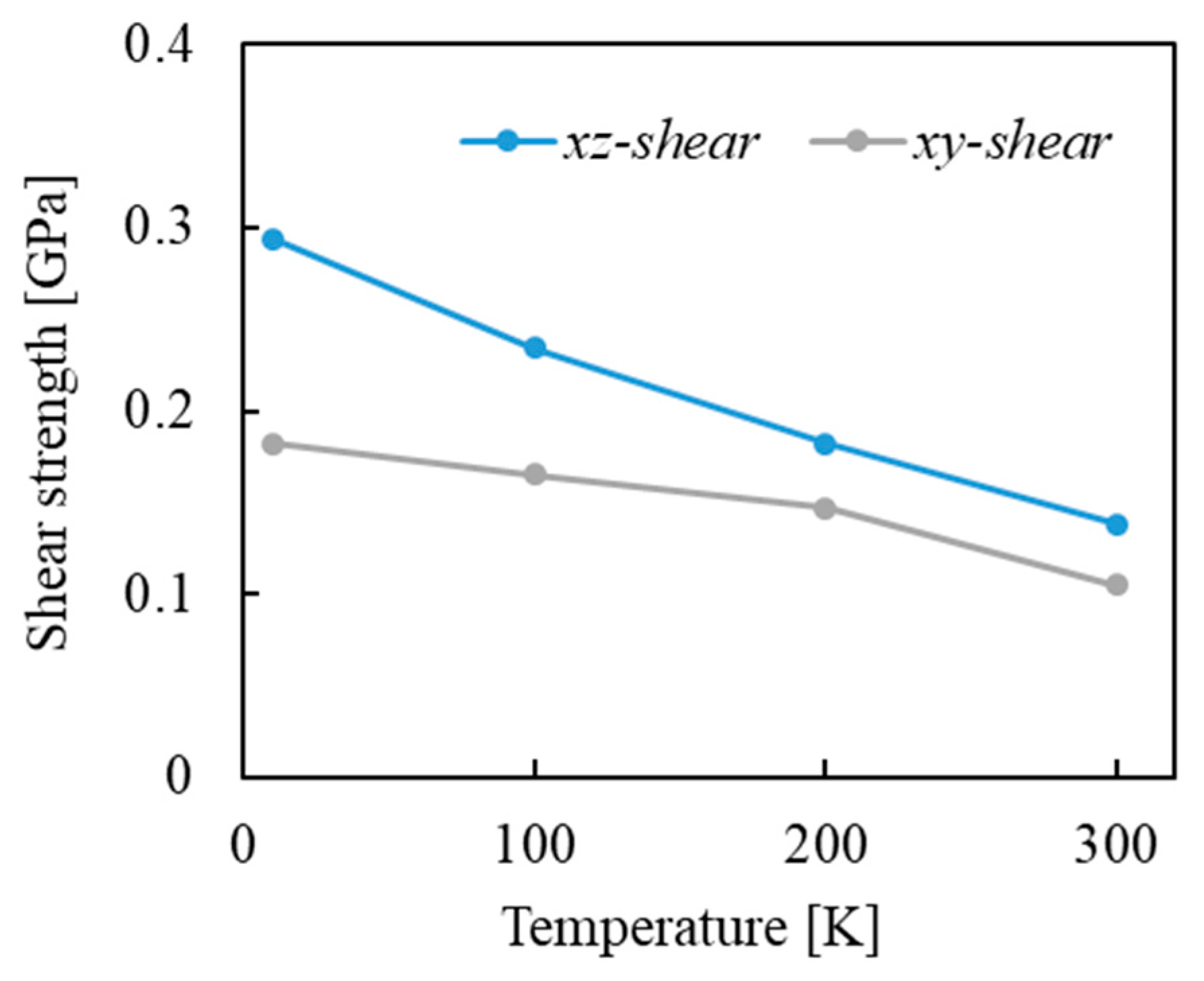
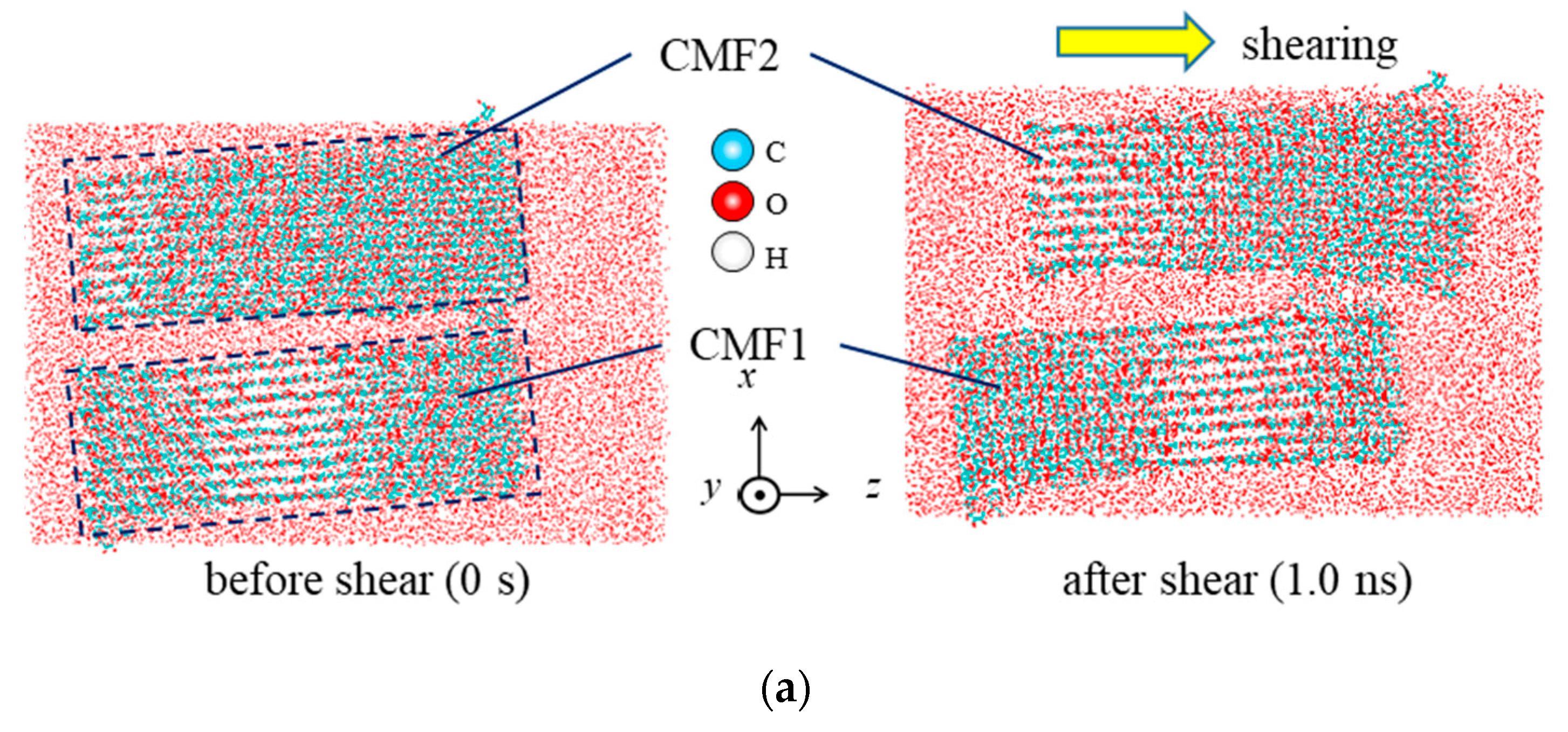
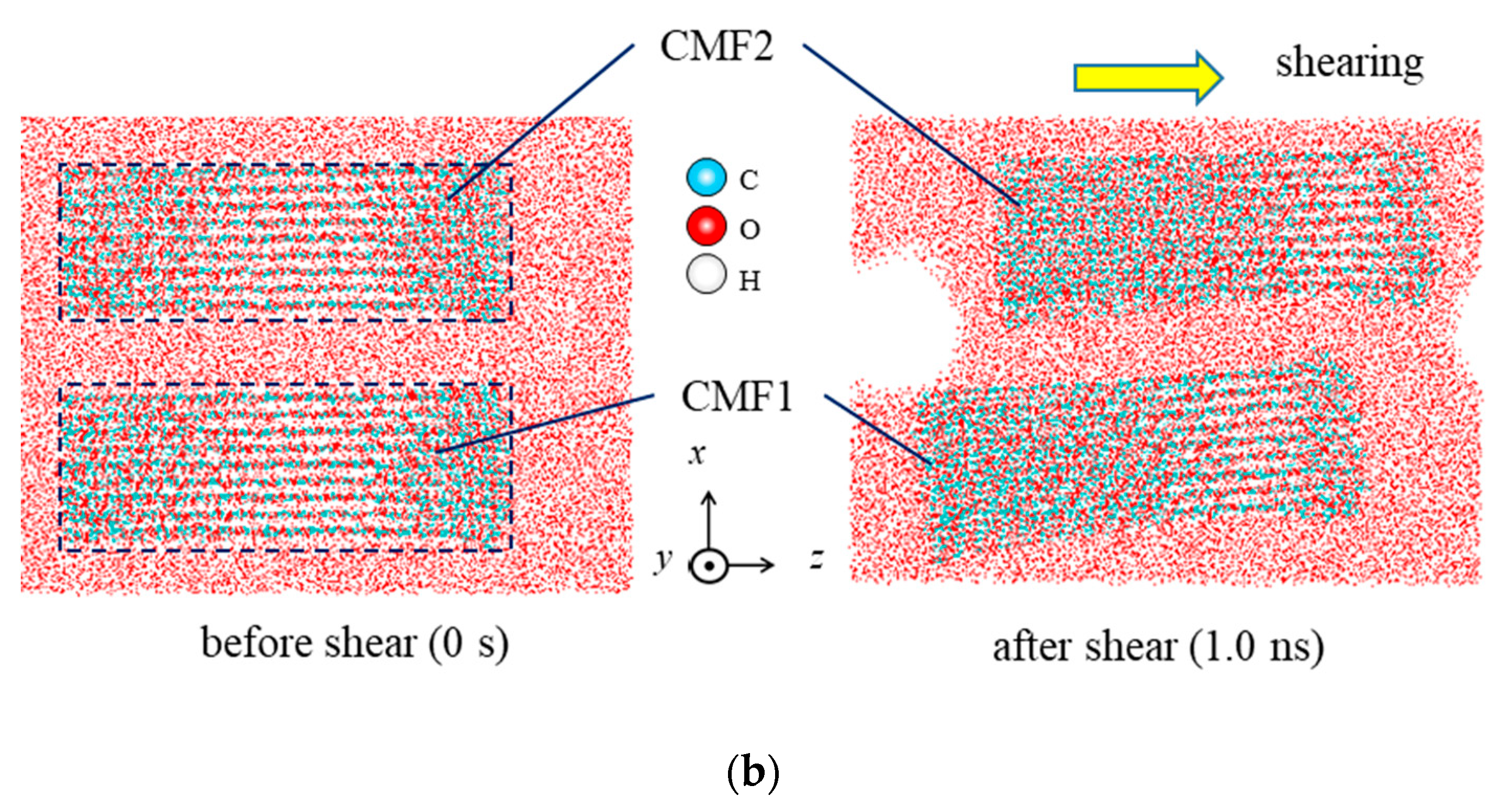
| Property | Value |
|---|---|
| c (nm) | 1.038 |
| d (nm) | 0.873 |
| (nm) | 0.09572 |
| () | 104.52 |
| (e) | −0.834 |
| (e) | 0.417 |
| (kcal/mol) | 0.1521 |
| (nm) | 0.3156 |
| Property | Value(s) |
|---|---|
| Lattice parameter a, b, c (nm) | 0.7784, 0.8201, 1.038 |
| Lattice parameter () | 83.5 |
| Degree of polymerization | 10 |
| The number of molecular chains | 41 |
| The number of atoms | 17343 |
| Length L (nm) | 10.38 |
| Width, height W, H (nm) | 3.2804, 3.1136 |
| Property | Value(s) |
|---|---|
| Cutoff length for intermolecular potential (nm) | 1.3 |
| Temperature T (K) | 10, 100, 200, 300 |
| Duration of structure relaxation (ns) | 1.0 |
| Time increment (fs) | 1.0 |
| Conditions in Common | |||
|---|---|---|---|
| Model Name | Normal | TW-A | TW-B |
| Water thickness between CMFs (nm) | 0.7 | 1.4 | 2.0 |
| Temperature T (K) | 10, 100, 200, 300 | 300 | |
| Duration of structure relaxation (ns) | 1.0 | ||
| Cutoff length for intermolecular potential (nm) | 1.3 | ||
| Time increment (fs) | 1.0 | ||
| Shear simulation by SMD | |||
| Model name | Normal | TW-A | TW-B |
| Shear direction | z, y | z | z |
| Shear velocity (m/s) | 2.0 | ||
| Duration of shearing (ns) | 1.0 | ||
| Spring constant (kcal/mol) | |||
| Shear Direction/Type | Shear Modulus [GPa] |
|---|---|
| (averaged value of our MD results) | 0.753 |
| (averaged value of our MD results) | 1.63 |
| Larch (experimental) [43] | 1~3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izumi, Y.; Saitoh, K.-i.; Sato, T.; Takuma, M.; Takahashi, Y. Shear Deterioration of the Hierarchical Structure of Cellulose Microfibrils under Water Condition: All-Atom Molecular Dynamics Analysis. Appl. Mech. 2023, 4, 230-247. https://doi.org/10.3390/applmech4010013
Izumi Y, Saitoh K-i, Sato T, Takuma M, Takahashi Y. Shear Deterioration of the Hierarchical Structure of Cellulose Microfibrils under Water Condition: All-Atom Molecular Dynamics Analysis. Applied Mechanics. 2023; 4(1):230-247. https://doi.org/10.3390/applmech4010013
Chicago/Turabian StyleIzumi, Yukihiro, Ken-ichi Saitoh, Tomohiro Sato, Masanori Takuma, and Yoshimasa Takahashi. 2023. "Shear Deterioration of the Hierarchical Structure of Cellulose Microfibrils under Water Condition: All-Atom Molecular Dynamics Analysis" Applied Mechanics 4, no. 1: 230-247. https://doi.org/10.3390/applmech4010013
APA StyleIzumi, Y., Saitoh, K.-i., Sato, T., Takuma, M., & Takahashi, Y. (2023). Shear Deterioration of the Hierarchical Structure of Cellulose Microfibrils under Water Condition: All-Atom Molecular Dynamics Analysis. Applied Mechanics, 4(1), 230-247. https://doi.org/10.3390/applmech4010013





