1. Introduction
Mathematical modeling and numerical methods for contact mechanics can be found in many textbooks, for instance [
1,
2,
3,
4]. There are different possibilities to treat the contact constraint: Lagrange multiplier and augmented Lagrangian methods [
5], mortar method [
6], penalty methods [
7,
8], semismooth Newton methods [
9], active set method [
10,
11,
12], multigrid method [
13], Nitsche’s method [
14], smoothed finite element method [
15] and cut finite element method [
16].
The incremental method (see [
17], Section 6.10–6.12) varies the forces and the imposed displacement by small increments from zero to desired values to successively solve linearized problems written in the undeformed domain. The Updated Lagrangian method is similar, but the linear problem to be solved is written in the updated domain (see [
18] Section 2.6–2.8 or [
19] Section 14.8). This method was developed initially for nonlinear elasticity, but recently it was successfully employed for dynamic fluid-structure interaction [
20]. An advantage of this approach is that at each time step, only a linear system is solved. A stability result is obtained in [
21].
Nonlinear elasticity equations with frictionless contact can be formulated in term of a constrained nonlinear optimization problem: the nonlinear cost function is the deformation elastic energy, and the constraints are the non-penetration condition of the elastic structure into the obstacle and the imposed displacement on some boundary. The Lagrange multiplier and augmented Lagrangian methods, as well as the mortar, penalty and active set methods come from the constrained nonlinear programming algorithms, where the cost function is written in the undeformed domain.
By introducing a positive function defined on the contact zone, in Nitsche’s method the problem is formulated as a system of equations which can be solved by generalized Newton’s method. The semismooth Newton method can be considered related: the problem is reformulated using non-differentiable approximating equations.
The purpose of this paper is to present the Updated Lagrangian method for nonlinear elasticity with contact. The novelty is to use this method for contact problem. We can also highlight that the linearized problem written in the undeformed domain for Neo-Hookean and Ogden compressible materials are derived.
In the second section we describe the Total Lagrangian for compressible Neo-Hookean material. In
Section 3 and
Section 4, we introduce the Updated Lagrangian formulation for Neo-Hookean and Ogden compressible materials with contact. The last section is devoted to the numerical results.
2. Contact without Friction in Non-Linear Elasticity Using Total Lagrangian Framework
We consider an undeformed structure domain, and we assume that it is an open, bounded and connected subset. Its boundary is Lipschitz and admits the decomposition , where , and are relatively open subsets, mutually disjointed. On we impose a given displacement , in volume forces are applied, and it is subjected to surface loads on . A portion of will be in contact with a rigid foundation after deformation.
A particle of the structure whose initial position was the point will occupy the position in the deformed domain , where denotes the displacement.
If is a square matrix, we denote by , , , the determinant, the trace, the inverse and the transpose matrix of A, respectively. We write , and is the cofactor matrix of .
We denote by
the gradient of the deformation, where
is the unity matrix, and we write
,
. The first and the second Piola–Kirchhoff stress tensors are denoted by
and
, respectively, and the following equality holds:
. For the hyperelastic material, there exists a strain energy function
such that
and
(see [
22], Chapter 6). The Cauchy stress tensor
is computed by
, where
.
The rigid foundation is modeled as the graph of a function
, and we denote its graph by
and its epigraph by
We assume that the undeformed structure domain is into .
The problem to solve is
subject to
3. Updated Lagrangian for Compressible Neo-Hookean Material with Contact
We suppose that the material is homogeneous, isotropic and can be described by the compressible Neo-Hookean model ([
18], p. 239); the strain energy function is
and the second Piola–Kirchhoff stress is
where
,
are the Lamé constants of the linearized theory (see [
23], Chapter 5).
We denote by
the image of
via the map
, and we set
the computational domain at the increment
n. The map from
to
defined by
; the composition of the map from
to
is defined by
, and the map from
to
defined by
With the notations
and
,
, we obtain
For the Neo-Hoohean material, we have
, and we set
. Let us introduce the tensor
For
, we define
and
by
Since
and
(see [
17], Section 2.6), and taking into account (
5), we get
Using (
4), it follows that
then
If
is a square matrix, by linearization, we have:
(see [
23], Chapter 3.2). We can linearize the map
by
For simplicity, we assume that the displacement on , the volume forces in and the surface loads on are constant. Let be the number of increments. We will solve successively N linearized problems written in the updated configuration , for .
The boundaries
,
,
of
are obtained, respectively, from
,
,
via the map
. Let us introduce the linear application of the increments of the forces
In the case of small displacements
, the constraint of non-penetration of the elastic structure into the rigid obstacle can be approached by
see [
1]. We introduce the convex set
The linearized problem written in the updated configuration to be solved is the variational inequality: find
such that
Proposition 1. The bi-linear application is symmetric.
Proof. If
,
,
are square matrices, we have
and
. We obtain
then the second term of
is symmetric. Using also
, we get
then the third term of
is symmetric. □
Let as introduce the quadratic optimization problem with affine constraints
A solution of (
11) is also a solution of (
10). If
is coercive, the variational inequality (
10) has a unique solution which is also the unique solution of optimization problem (
11) (see [
5]).
Problem (
11) will be solved numerically by the Interior Point algorithm implemented in the software
FreeFem++ (see [
24]). The novelty of this approach is that Problem (
11) is written in the updated configuration.
4. Updated Lagrangian for Compressible Ogden Material with Contact
We suppose that the compressible material is of type Ogden [
25] with the strain energy function
with
,
,
and
. The first two terms correspond to the Mooney–Rivlin material, and the volumetric part of strain-energy functions used here
was proposed in [
26] in order to obtain polyconvexity and the coerciveness of the strain energy function.
From the Cayley–Hamilton theorem in 2D, we have
and using that
is symmetric, we get
As in the preceding section, using (
5) and (
4), we obtain
and employing
,
we linearize the map
by
Proposition 2. The bi-linear application is symmetric.
As previously, the linearized problem written in the updated configuration to be solved is the variational inequality: find
such that
The associated optimization problem is
5. Numerical Results
Let
be a triangulation of
of size
h, with
vertices. We set
the shape function associated with vertex
, which is a piecewise linear function and is globally continuous. For the two-dimension displacements, we introduce the basis
for
defined by
We define the matrix
and the vector
by
and
The constraint
will be treated weakly. Thus, we introduce matrix
, where
is the number of vertex
and the vector
by
for
and
and
for
. The discrete version of (
11) is
For the numerical tests, we employed the software
FreeFem++ (see [
24]). The optimization problem (
15), (
16), (
17) is solved by the library IPOPT “Interior Point OPTimizer”, which has an interface in
FreeFem++.
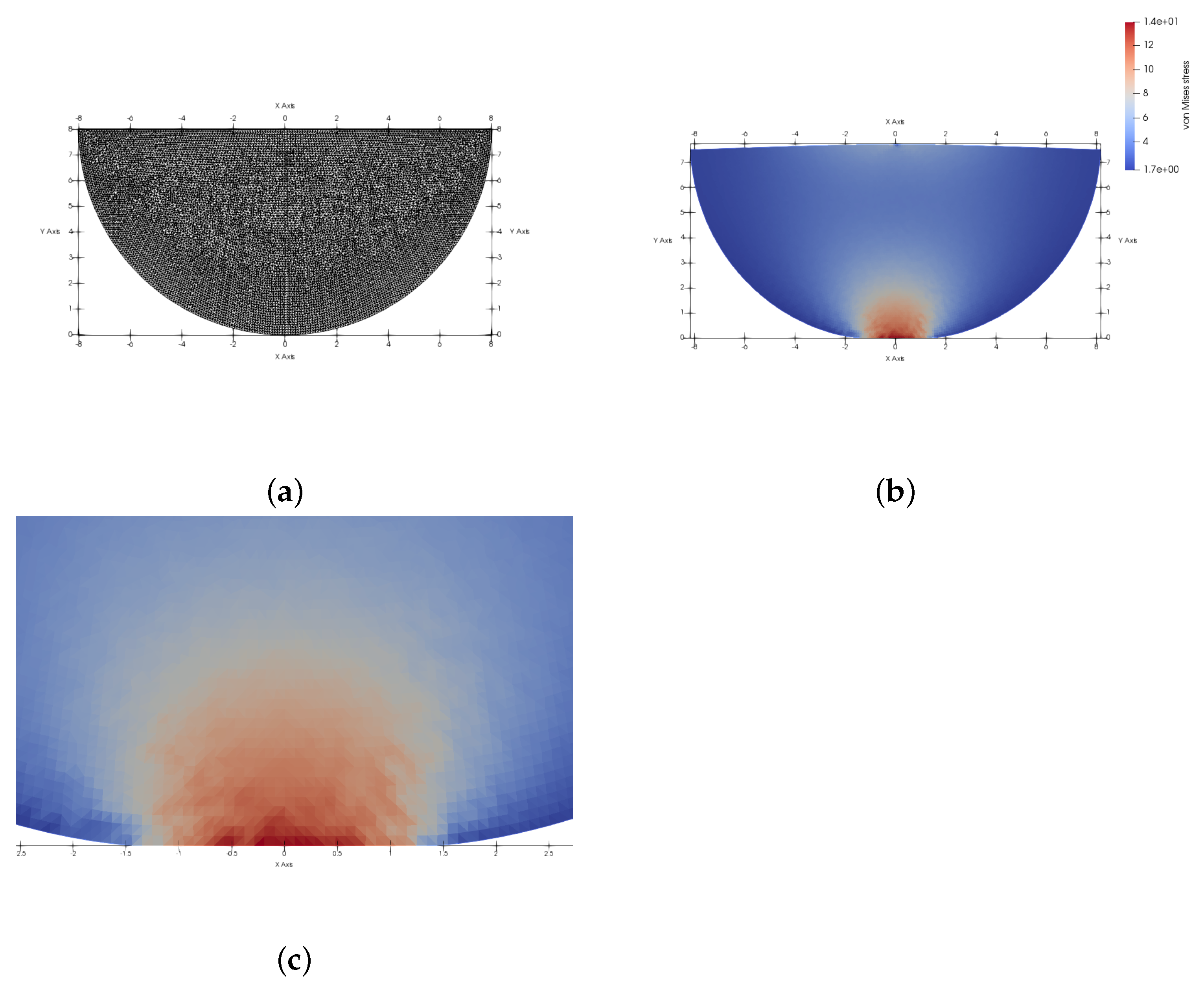
5.1. Compression of a Hertz Half Ball against a Foundation
This example is adapted from [
11]. The undeformed structure domain
is a half ball of radius
R = 8 m with center
, and the rigid foundation is given by
. The boundary
is the little segment
,
is the half of a circle
, and
is the rest of
.
On
we impose zero horizontal displacement, in
volume forces
Pa/m
are applied, and surface loads
Pa/m
are applied on
. We set Young’s modulus
Pa and Poisson’s ratio
. The structure verifies the linear elasticity equation; the stress tensor of the structure written in the Lagrangian framework is
, where
are the Lamé coefficients,
. In this case, the bi-linear form
a and the linear form
ℓ are given by
and
and the increment number is just
.
The quadratic optimization problem with affine constraints is
where
The analytical normal stress in the contact zone given by the Hertz theory is
The contact zone is and .
The number of nodes on
is 252; the mesh of
has 11,759 vertices and 23,096 triangles. For
and
, the analytical value for
b is
and for the normal stress is
, while the computed normal stress is
. In
Figure 1, we can see: the initial mesh, the von Mises stress and a zoom of the contact zone. The numerical solution is consistent with the analytical solution. The IPOPT algorithm solves the optimization problem after 10 iterations.
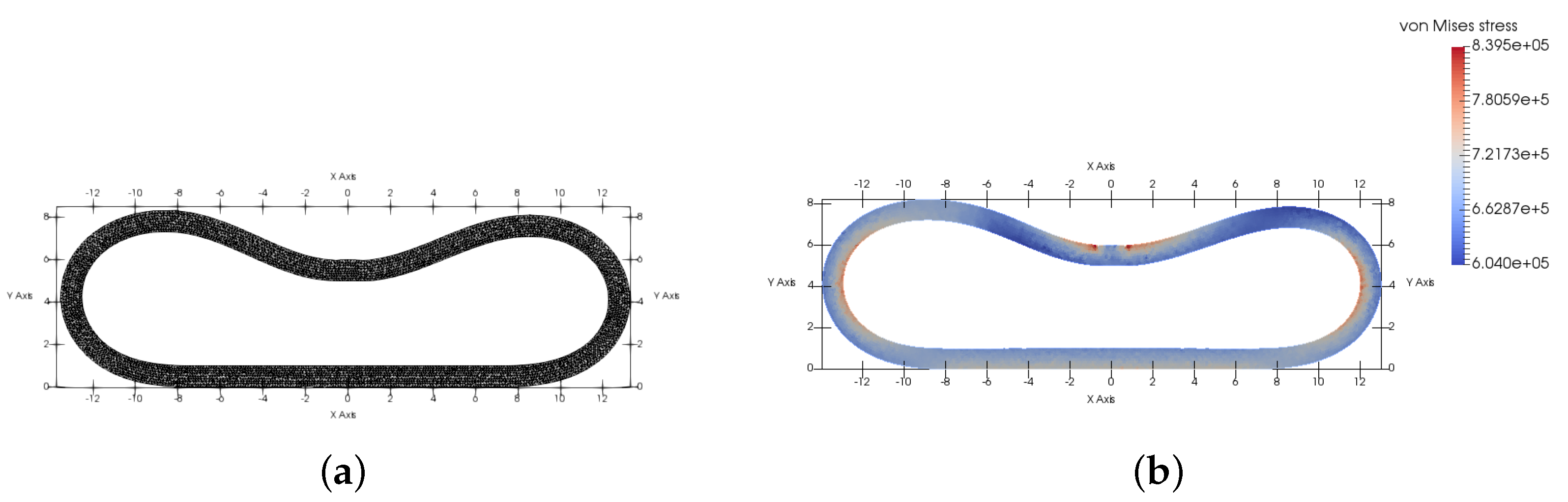
5.2. Compression of a Hyperelastic Ring against a Flat Rigid Foundation
This example is adapted from [
11]. The undeformed structure domain
is a ring of exterior radius
= 10 m, interior radius
= 9 m and center
, and the rigid foundation is given by
. The boundary
is the arc of a circle
,
is the inferior half of a circle
, and
is the rest of
.
On , we impose displacement m, in , volume forces Pa/m are applied, and surface loads Pa/m are applied on .
For the Neo-Hookean material, we use Young’s modulus
MPa and Poisson’s ratio
, which gives the Lamé constants
MPa and
= 344,828 Pa. For the Ogden-like material, we use, as in [
11],
MPa,
MPa,
a = 0.35 MPa.
The number of nodes on is 240; the mesh of has 4342 vertices and 7734 triangles. We employ finite element , and we set as the number of increments. The average number of iterations of the IPOPT algorithm in order to solve, at each increment, the optimization problem is 12.
We can see in
Figure 2 the final mesh and the von Mises stress for Neo-Hookean-like material, and in
Figure 3 the initial, intermediate and final meshes for the Ogden material. We denote by
the solution in the case of the Neo-Hookean material and by
for the Ogden-like material. We have
. Our solution for the Ogden-like material is similar to the one obtained in [
11].
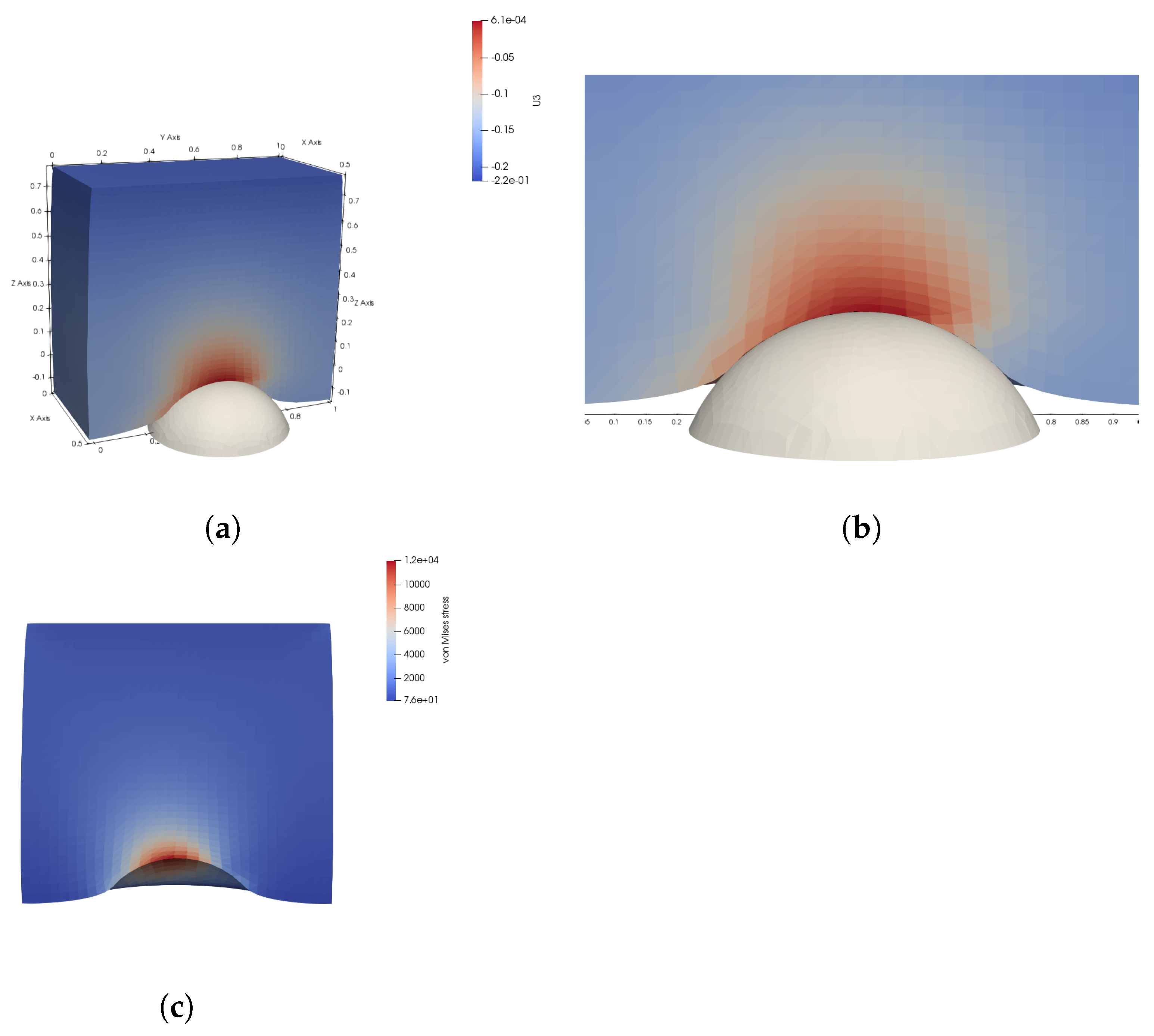
5.3. Contact of an Elastic Cube and a Ball
This example is adapted from [
13]. The undeformed structure domain
is the cube
, and the obstacle is a ball with center
and radius
, see
Figure 4.
The boundary
is the upper side,
is the bottom side, and
is the rest of
. On
, we impose the displacement
and we set
and
. Contrary to [
13], where the strain energy function is
with
and the parameters
,
,
, we consider the Neo-Hookean material as discussed in
Section 3, with Lamé constants
,
.
For 3D, we have the same formula for (
7), but (
9) is replaced by
The mesh is controled by the number k of segments on each edge of the cube. The mesh of has: 9261 vertices and 48,000 tetrahedrons for , 35,937 vertices and 197,608 tetrahedrons for and 68,921 vertices and 384,000 tetrahedrons for . We employ the finite element , and we set as the number of increments.
The optimization problem has
: 27,783 variables, 361 inequality constraints, 441 variables with imposed displacement;
: 107,811 variables, 961 inequality constraints, 1089 variables with imposed displacement;
: 206,763 variables, 1531 inequality constraints, 1681 variables with imposed displacement.
The average number of iterations of the IPOPT algorithm is 14 for and for . The total CPU time on an Intel Sandy Bridge 16 × 3.30 GHz and 64 GB RAM was 6 min for , 24 min for and 50 min for .
We denote by , , the solutions for , , , respectively. The error between computed solutions are: , , .
In
Figure 5, we plot the vertical displacement and von Mises stress at the final configuration for
.
6. Conclusions
An Updated Lagrangian method for nonlinear elasticity with frictionless contact was presented. The linearized problem written in the updated configuration for Neo-Hookean and Ogden compressible materials were derived. At each iteration, only a linear system was solved. Two- and three-dimensional numerical simulations were performed.