Modal Analysis of Optimized Trapezoidal Stiffened Plates under Lateral Pressure and Uniaxial Compression
Abstract
:1. Introduction
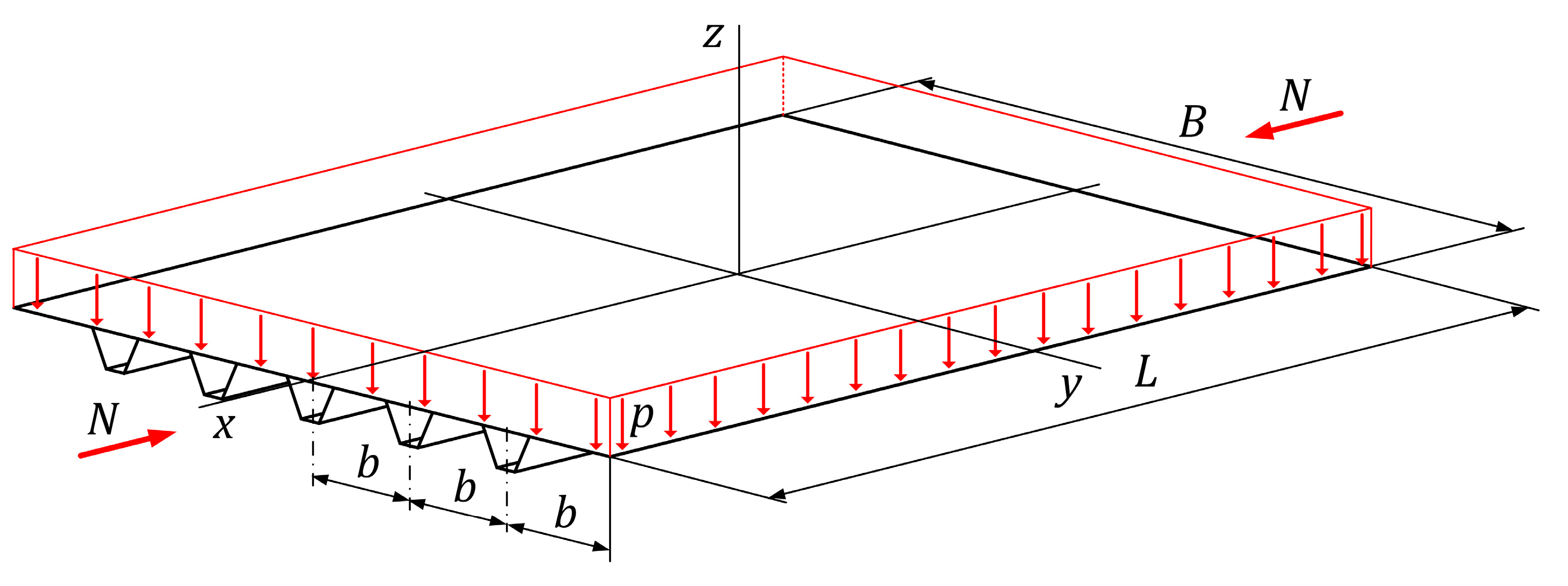
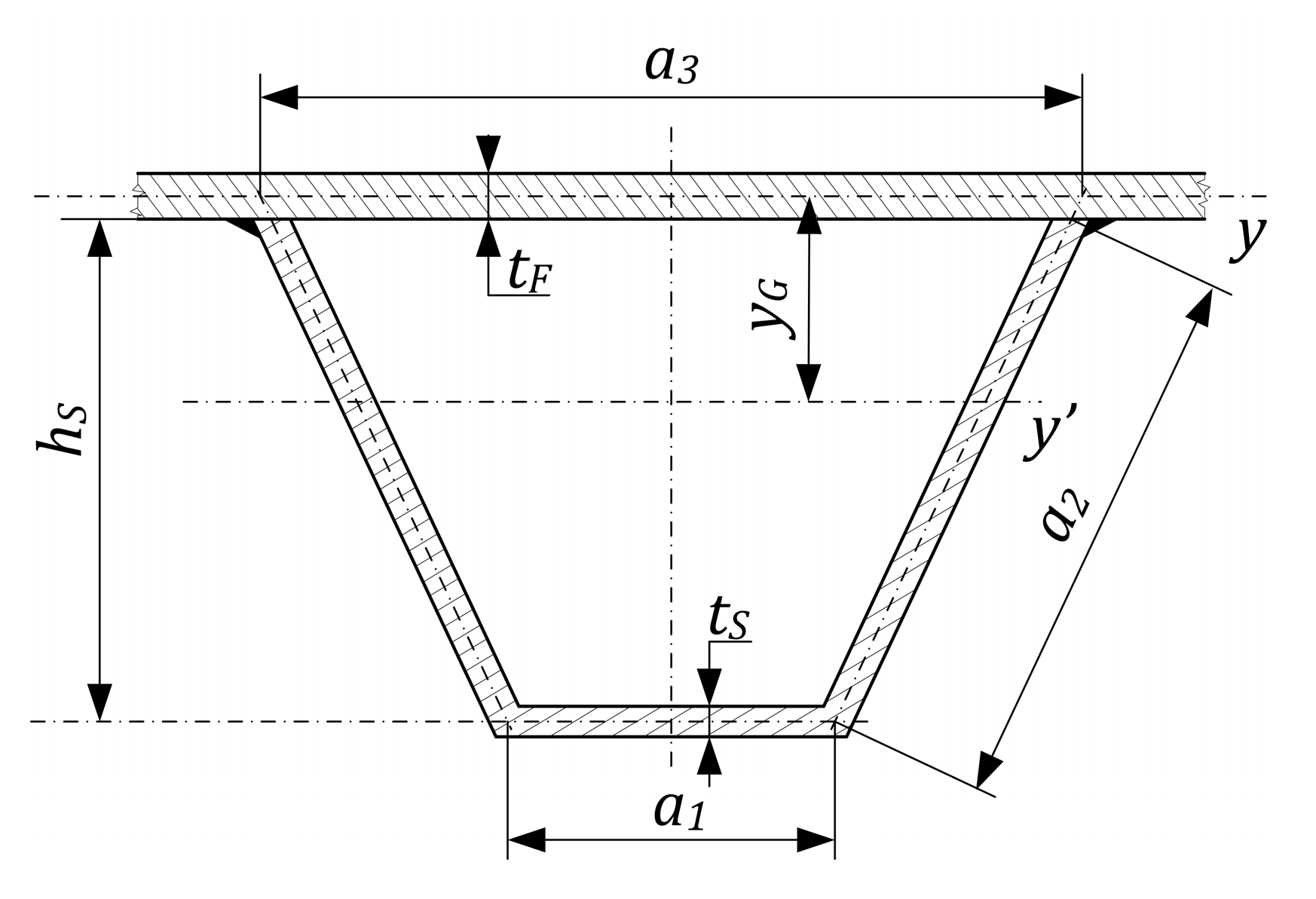
2. Designed Constraints
2.1. Calculation of the Deflection Due to Compression and Lateral Pressure
2.2. Deflection Due to the Shrinkage of Longitudinal Welds
2.3. Calculation of Stress Constraint
3. Optimizing Method and Objective Function
4. Modal Analysis
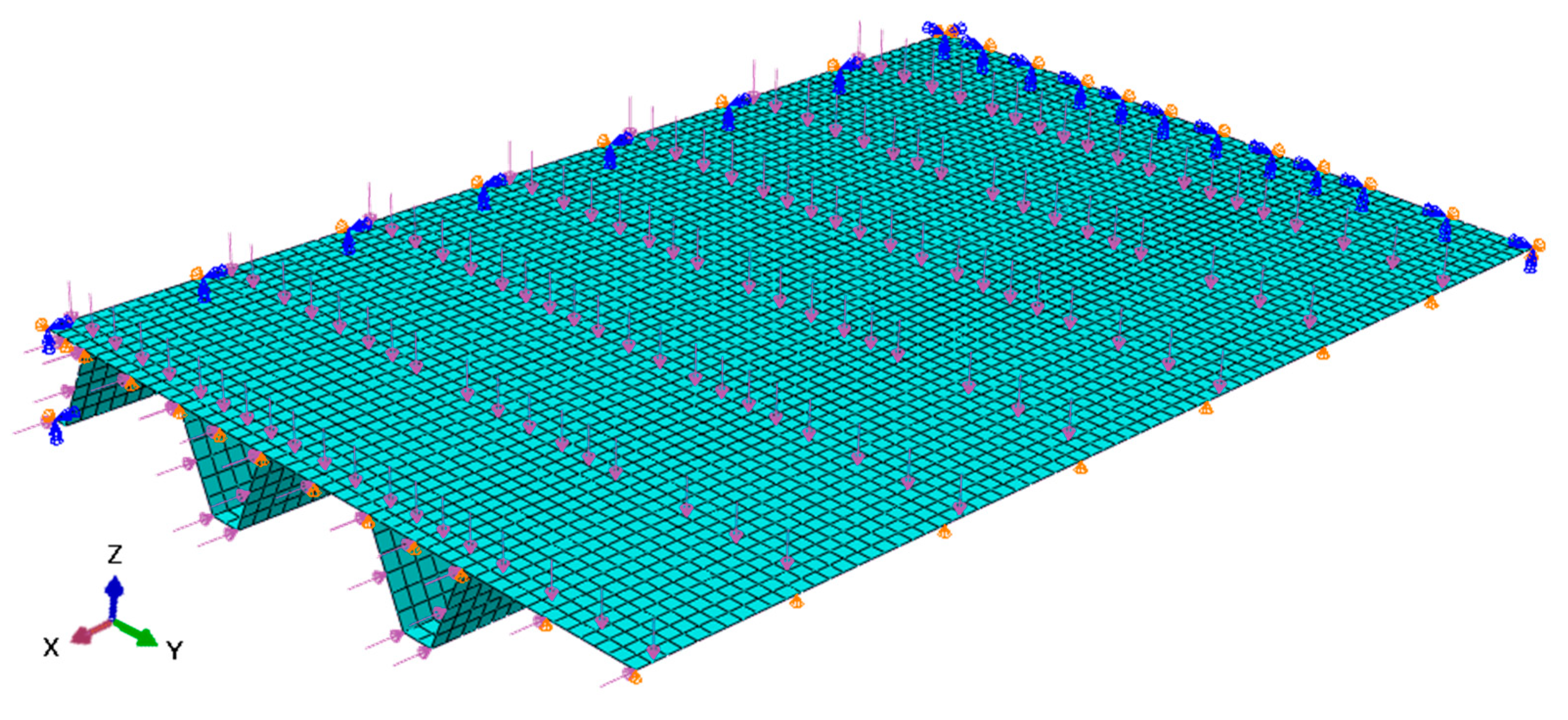
4.1. FE Model Description
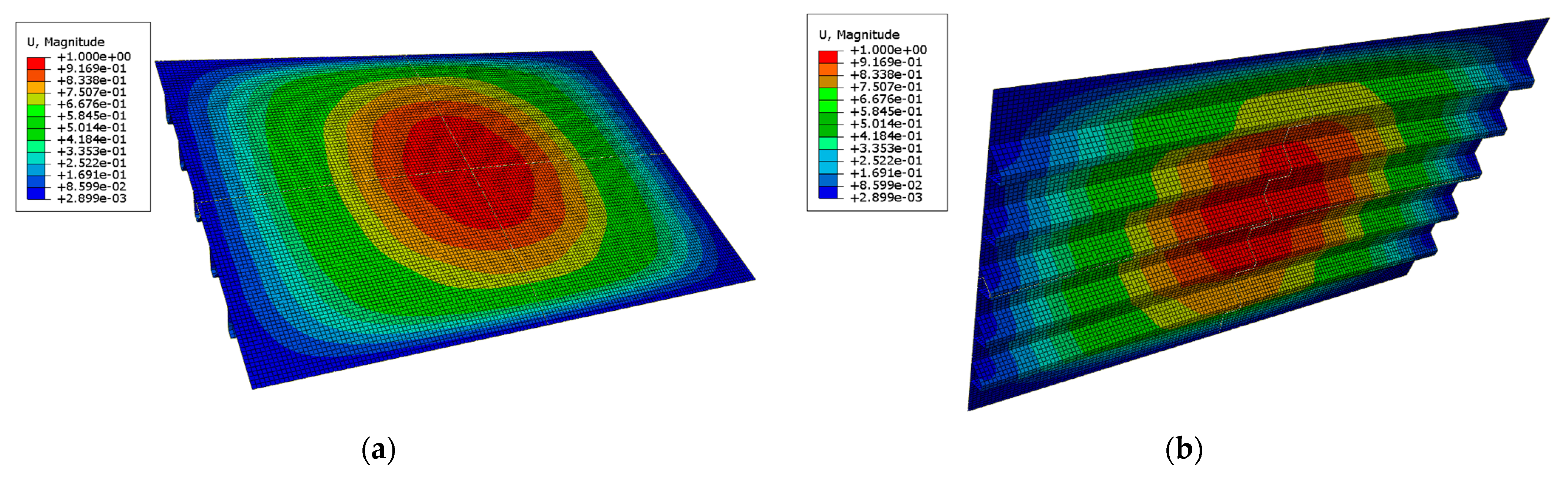
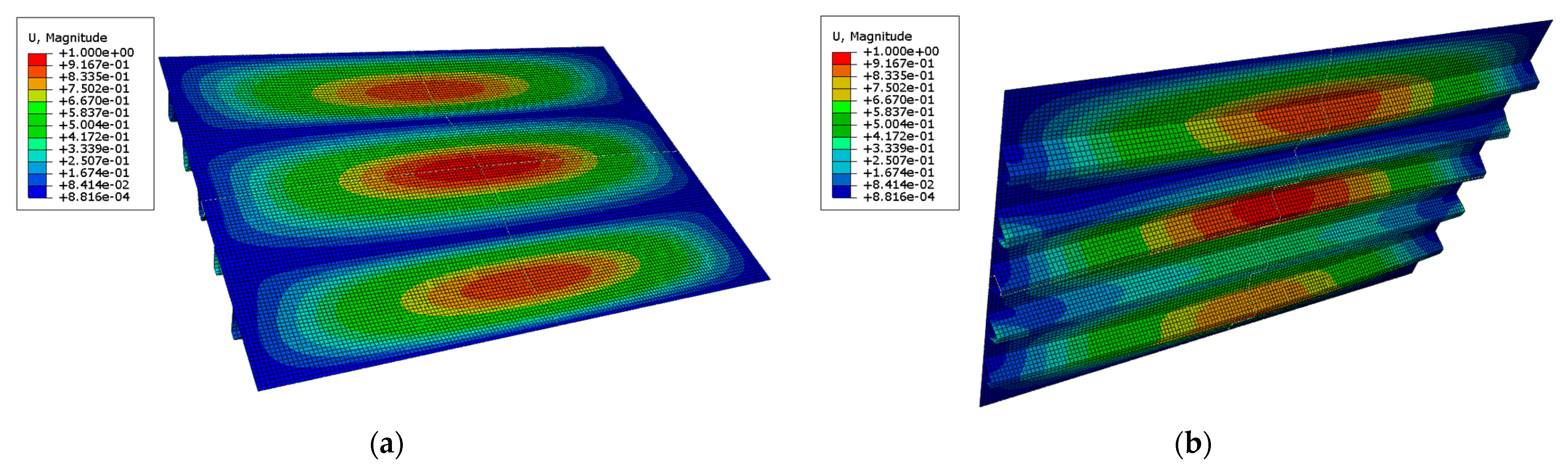
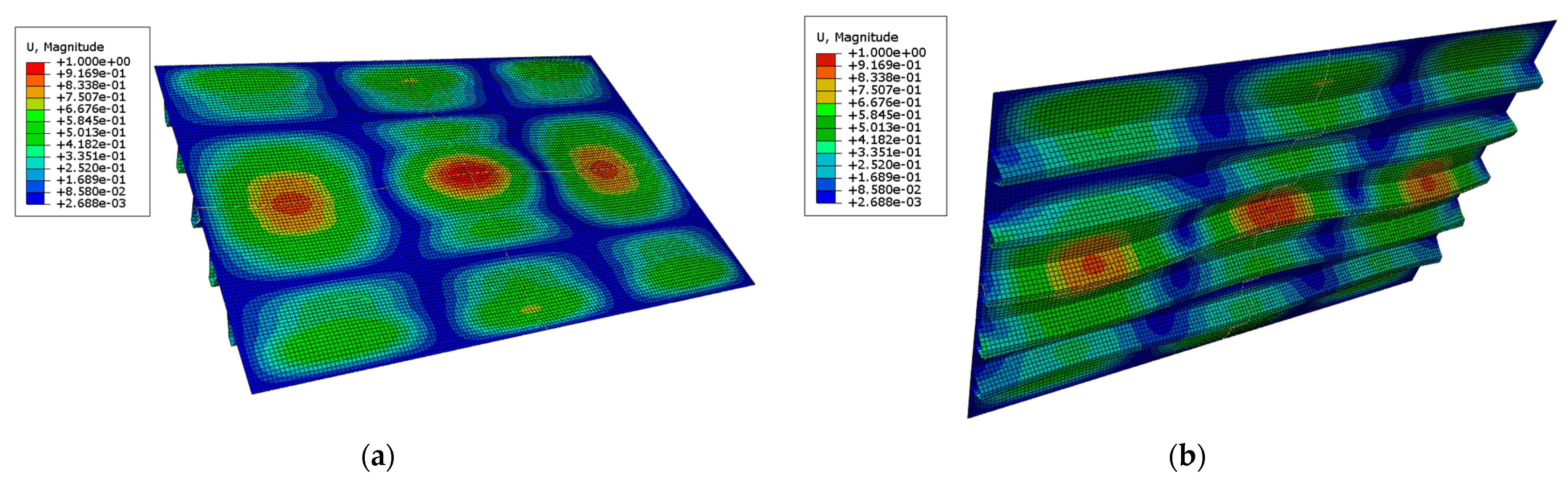
4.2. Modal Analysis Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, D.K.; Yu, S.Y.; Lim, H.L.; Cho, N.-K. Ultimate Compressive Strength of Stiffened Panel: An Empirical Formulation for Flat-Bar Type. J. Mar. Sci. Eng. 2020, 8, 605. [Google Scholar] [CrossRef]
- De Queiroz, J.P.T.P.; Cunha, M.L.; Pavlovic, A.; Rocha, L.A.O.; Dos Santos, E.D.; Troina, G.d.S.; Isoldi, L.A. Geometric Evaluation of Stiffened Steel Plates Subjected to Transverse Loading for Naval and Offshore Applications. J. Mar. Sci. Eng. 2019, 7, 7. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Dong, S.; Wang, T.; Xu, W.; Zhou, X. Numerical Investigation on Ultimate Compressive Strength of Welded Stiffened Plates Built by Steel Grades of S235–S390. Appl. Sci. 2019, 9, 2088. [Google Scholar] [CrossRef] [Green Version]
- Troina, G.; Cunha, M.; Pinto, V.; Rocha, L.; dos Santos, E.; Fragassa, C.; Isoldi, L. Computational Modeling and Constructal Design Theory Applied to the Geometric Optimization of Thin Steel Plates with Stiffeners Subjected to Uniform Transverse Load. Metals 2020, 10, 220. [Google Scholar] [CrossRef] [Green Version]
- Reis Amaral, R.; Troina, G.; Fragassa, C.; Pavlovic, A.; Cunha, M.; Rocha, L.; dos Santos, E.; Isoldi, L. Constructal design method dealing with stiffened plates and symmetry boundaries. Theor. Appl. Mech. Lett. 2020, 10, 366–376. [Google Scholar] [CrossRef]
- Al-Fatlawi, A.; Jármai, K.; Kovács, G. Optimal design of a fiber reinforced plastic composite sandwich structure for the base plate of aircraft pallets in order to reduce weight. Polymers 2021, 13, 834. [Google Scholar] [CrossRef] [PubMed]
- Al-Fatlawi, A.; Jármai, K.; Kovács, G. Optimization of a Totally Fiber-Reinforced Plastic Composite Sandwich Construction of Helicopter Floor for Weight Saving, Fuel Saving and Higher Safety. Polymers 2021, 13, 2735. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, Y.; Zeng, W. A Numerical Investigation on Stress Modal Analysis of Composite Laminated Thin Plates. Aerospace 2021, 8, 63. [Google Scholar] [CrossRef]
- Guan, C.; Zhang, H.; Wang, X.; Miao, H.; Zhou, L.; Liu, F. Experimental and Theoretical Modal Analysis of Full-Sized Wood Composite Panels Supported on Four Nodes. Materials 2017, 10, 683. [Google Scholar] [CrossRef] [Green Version]
- Jafarpour, S.; Khedmati, M.; Azkat, S. Vibration analysis of stiffened plates using Finite Element Method. Lat. Am. J. Solids Struct. 2011, 9, 1–20. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
- Abaqus 6.13 Online Documentation; Dassault Systems. 2015. Available online: http://130.149.89.49:2080/v6.13/index.html (accessed on 9 September 2021).
- Sabir, A.B.; Davies, G.T. Natural frequencies of plates with square holes when subjected to in-plane uniaxial, biaxial or shear loading. Thin-Walled Struct. 1997, 28, 321–335. [Google Scholar] [CrossRef]
- Jafari, M.; Hoseyni, S.A.M.; Altenbach, H.; Craciun, E.-M. Optimum Design of Infinite Perforated Orthotropic and Isotropic Plates. Mathematics 2020, 8, 569. [Google Scholar] [CrossRef] [Green Version]
- Vörös, G.M. Buckling and free vibration analysis of stiffened panels. Thin-Walled Struct. 2009, 47, 382–390. [Google Scholar] [CrossRef]
- Wu, Q.; Gao, H.; Zhang, Y.; Chen, L. Dynamical analysis of a thin-walled rectangular plate with preload force. J. Vibroeng. 2017, 19, 5735–5745. [Google Scholar] [CrossRef]
- Čorović, S.; Miljavec, D. Modal Analysis and Rotor-Dynamics of an Interior Permanent Magnet Synchronous Motor: An Experimental and Theoretical Study. Appl. Sci. 2020, 10, 5881. [Google Scholar] [CrossRef]
- Wang, C.; Huang, H.; Lai, X.; Chen, J. A New Online Operational Modal Analysis Method for Vibration Control for Linear Time-Varying Structure. Appl. Sci. 2020, 10, 48. [Google Scholar] [CrossRef] [Green Version]
- Szirbik, S.; Virág, Z. Finite element analysis of an optimized hybrid stiffened plate. MATEC Web Conf. 2021, 342, 06003. [Google Scholar] [CrossRef]
- Virág, Z.; Jármai, K. Optimum design of stiffened plates for static or dynamic loadings using different ribs. Struct. Eng. Mech. 2020, 74, 255–266. [Google Scholar]
- Kovács, G.; Farkas, J. Optimal design of a composite sandwich structure. Sci. Eng. Compos. Mater. 2016, 23, 237–243. [Google Scholar] [CrossRef]
- Paik, J.K.; Thayamballi, A.K.; Kim, B.J. Large deflection orthotropic plate approach to develop ultimate strength formulations for stiffened panels under combined biaxial compression/tension and lateral pressure. Thin-Walled Struct. 2001, 39, 215–246. [Google Scholar] [CrossRef]
- Kim, D.K.; Poh, B.Y.; Lee, J.R.; Paik, J.K. Ultimate strength of initially deflected plate under longitudinal compression: Part I = An advanced empirical formulation. Struct. Eng. Mech. 2018, 68, 247–259. [Google Scholar]
- Mikami, I.; Niwa, K. Ultimate compressive strength of orthogonally stiffened steel plates. J. Struct. Eng. ASCE 1996, 122, 674–682. [Google Scholar] [CrossRef]
- Ghafiland, H.N.; Jármai, K. Research and application of industrial robot manipulators in vehicle and automotive engineering, a survey. In Vehicle and Automotive Engineering 2; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2018; pp. 611–623. [Google Scholar]
- Farkas, J.; Jármai, K. Analysis and Optimum Design of Metal Structures; Balkema Publishers: Rotterdam, The Netherlands, 1997. [Google Scholar]
- Farkas, J.; Jármai, K. Optimum Design of Steel Structures; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]



| No. | p [MPa] | [MPa] | [mm] | [mm] | [-] | b [mm] | ||
|---|---|---|---|---|---|---|---|---|
| 1. | 0.02 | 235 | 23 | 9 | 3 | 1000 | 5317 | 6437 |
| 2. | 0.01 | 235 | 23 | 8 | 3 | 1000 | 5122 | 6132 |
| 3. | 0.005 | 235 | 22 | 8 | 3 | 1000 | 4934 | 5932 |
| 4. | 0.02 | 355 | 17 | 10 | 4 | 800 | 4991 | 6431 |
| 5. | 0.01 | 355 | 18 | 8 | 5 | 666.67 | 4700 | 5845 |
| 6. | 0.005 | 355 | 15 | 8 | 5 | 666.67 | 4320 | 5621 |
| No. | Mode Sequence Number | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1. | 116.39 | 253.72 | 553.46 | 629.09 | 746.49 | 844.18 |
| 2. | 88.870 | 239.44 | 555.24 | 601.75 | 733.92 | 772.18 |
| 3. | 88.026 | 231.55 | 534.53 | 581.81 | 694.87 | 766.37 |
| 4. | 117.05 | 235.98 | 578.32 | 760.09 | 785.89 | 862.40 |
| 5. | 64.490 | 212.70 | 574.14 | 674.46 | 773.65 | 851.75 |
| 6. | 72.286 | 209.47 | 406.64 | 753.10 | 792.69 | 865.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Virág, Z.; Szirbik, S. Modal Analysis of Optimized Trapezoidal Stiffened Plates under Lateral Pressure and Uniaxial Compression. Appl. Mech. 2021, 2, 681-693. https://doi.org/10.3390/applmech2040039
Virág Z, Szirbik S. Modal Analysis of Optimized Trapezoidal Stiffened Plates under Lateral Pressure and Uniaxial Compression. Applied Mechanics. 2021; 2(4):681-693. https://doi.org/10.3390/applmech2040039
Chicago/Turabian StyleVirág, Zoltán, and Sándor Szirbik. 2021. "Modal Analysis of Optimized Trapezoidal Stiffened Plates under Lateral Pressure and Uniaxial Compression" Applied Mechanics 2, no. 4: 681-693. https://doi.org/10.3390/applmech2040039
APA StyleVirág, Z., & Szirbik, S. (2021). Modal Analysis of Optimized Trapezoidal Stiffened Plates under Lateral Pressure and Uniaxial Compression. Applied Mechanics, 2(4), 681-693. https://doi.org/10.3390/applmech2040039





