On the Generation of Harmonics by the Non-Linear Buckling of an Elastic Beam
Abstract
:1. Introduction
2. Non-Linear Bending of a Beam with Large Slope
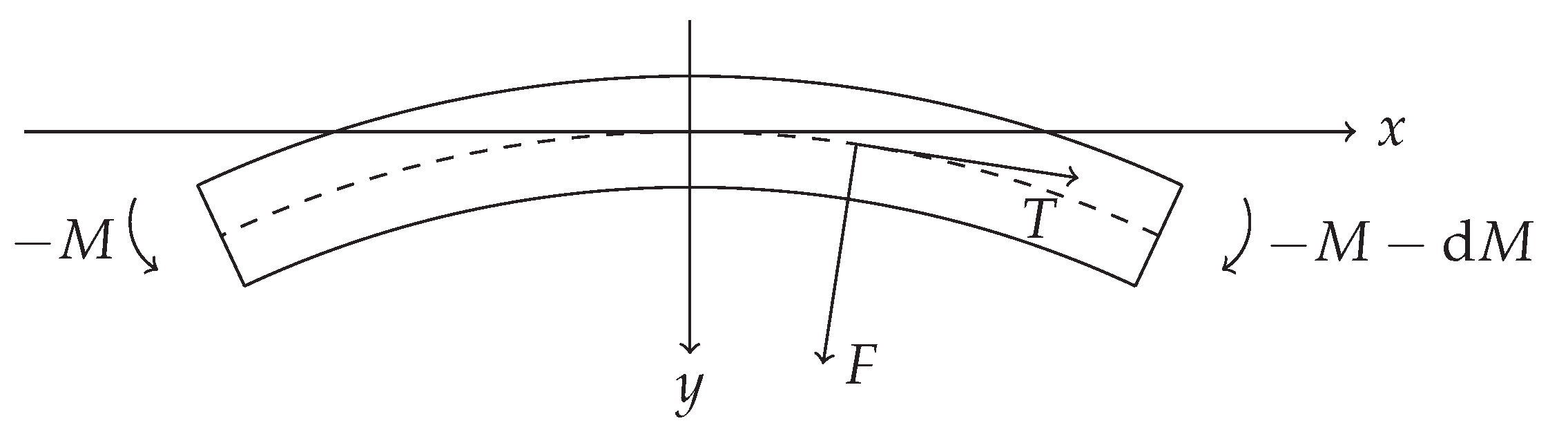
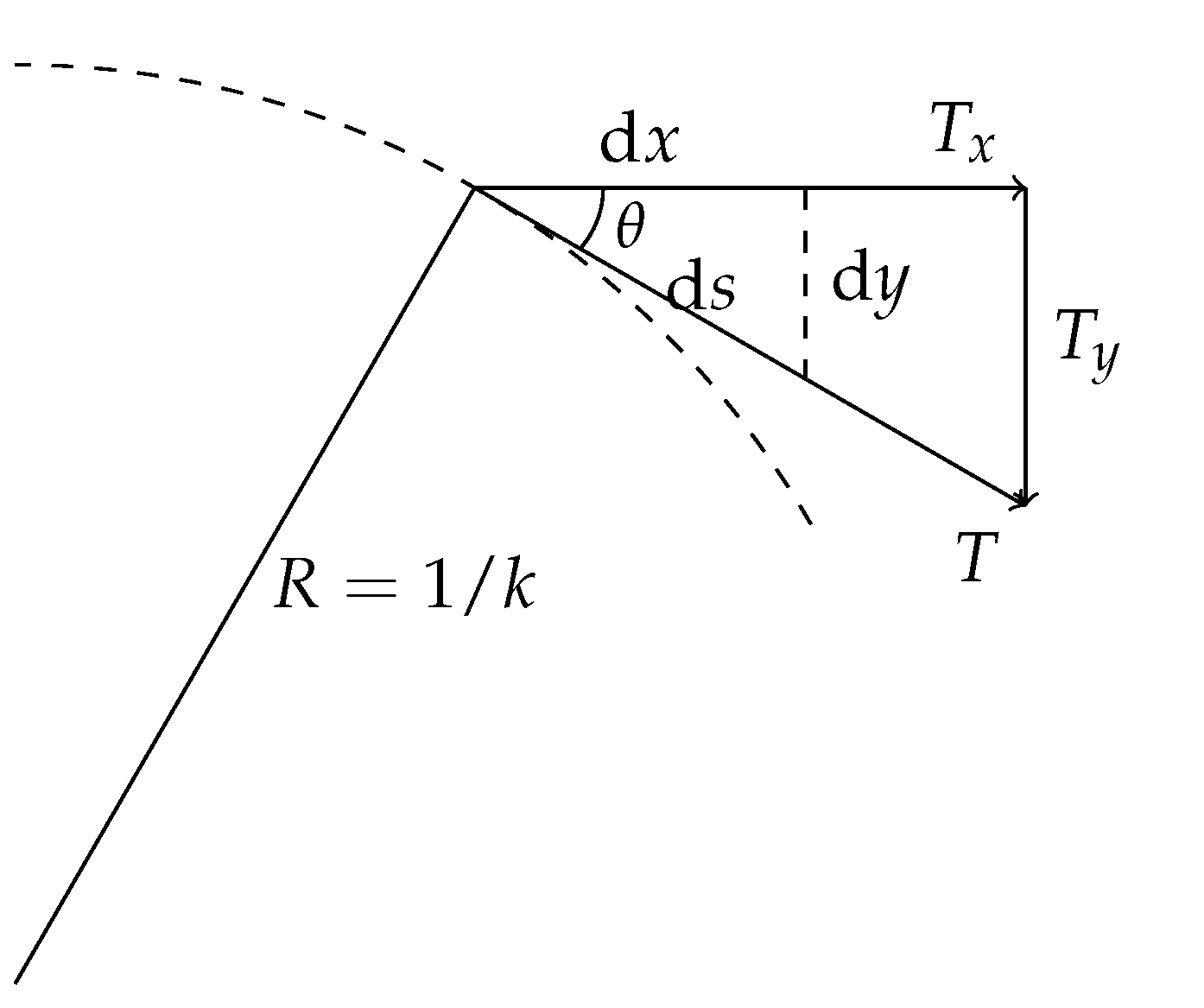
2.1. Bending Moment, Transverse Force and Shear Stress
2.2. Linear Buckling for Small Slope
2.3. Lowest-Order Non-Linear Buckling for Large Slope
2.4. Linear and Non-Linear Boundary Conditions at a Free End
3. Non-Linear Buckling of a Cantilever Beam
3.1. Non-Linear Elastica of a Cantilever Beam
3.2. Linear Approximation and Non-Linear Corrections of All Orders
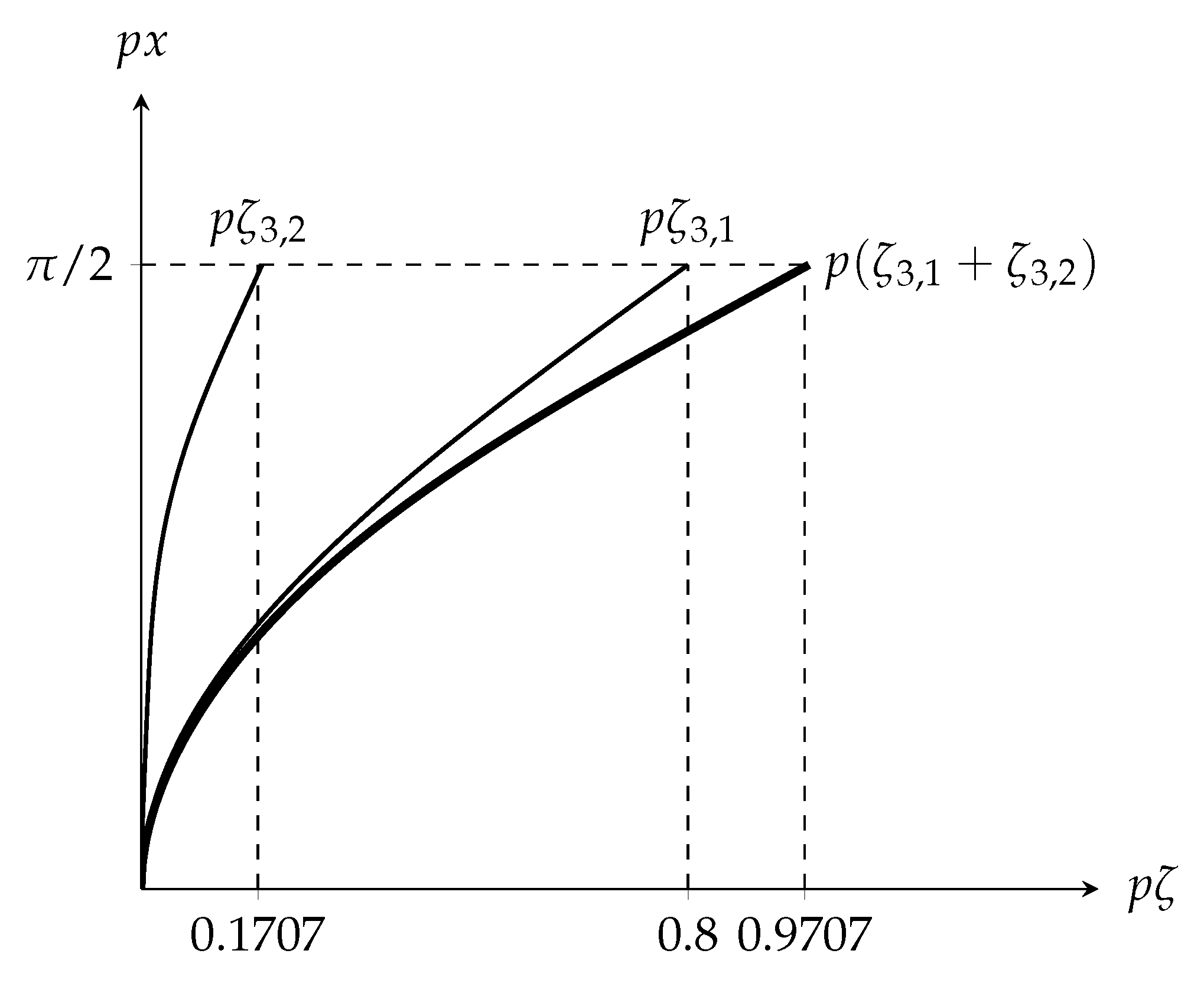
3.3. Truncation of the Series in the Shape of the Elastica
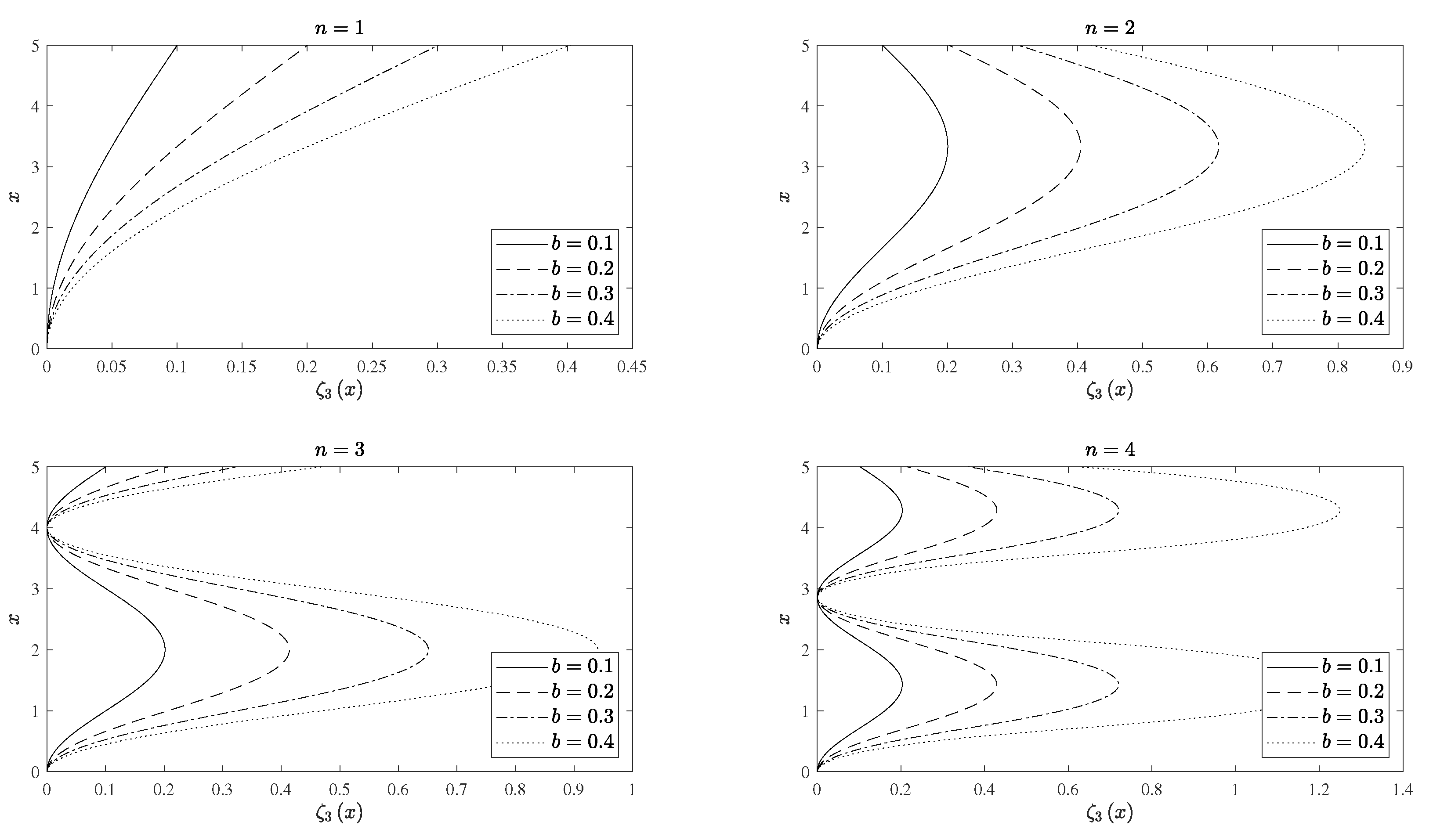
3.4. Numerical Results for the Buckling of a Cantilever Beam
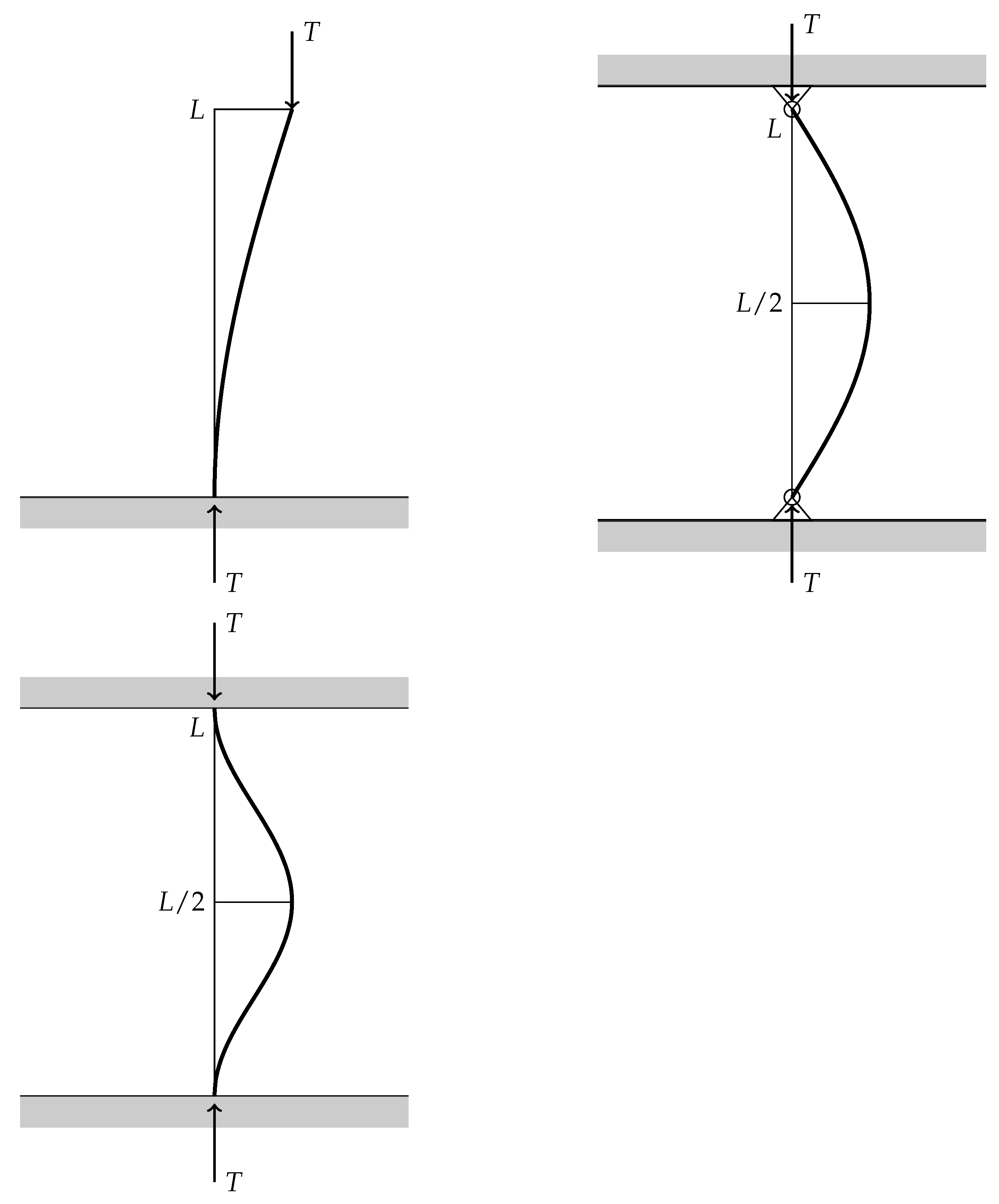
4. Non-Linear Buckling of Clamped and Pinned Beams
4.1. Non-Linear Effects of Large Slope
4.2. Coincidence of Linear and Non-Linear Critical Buckling Loads
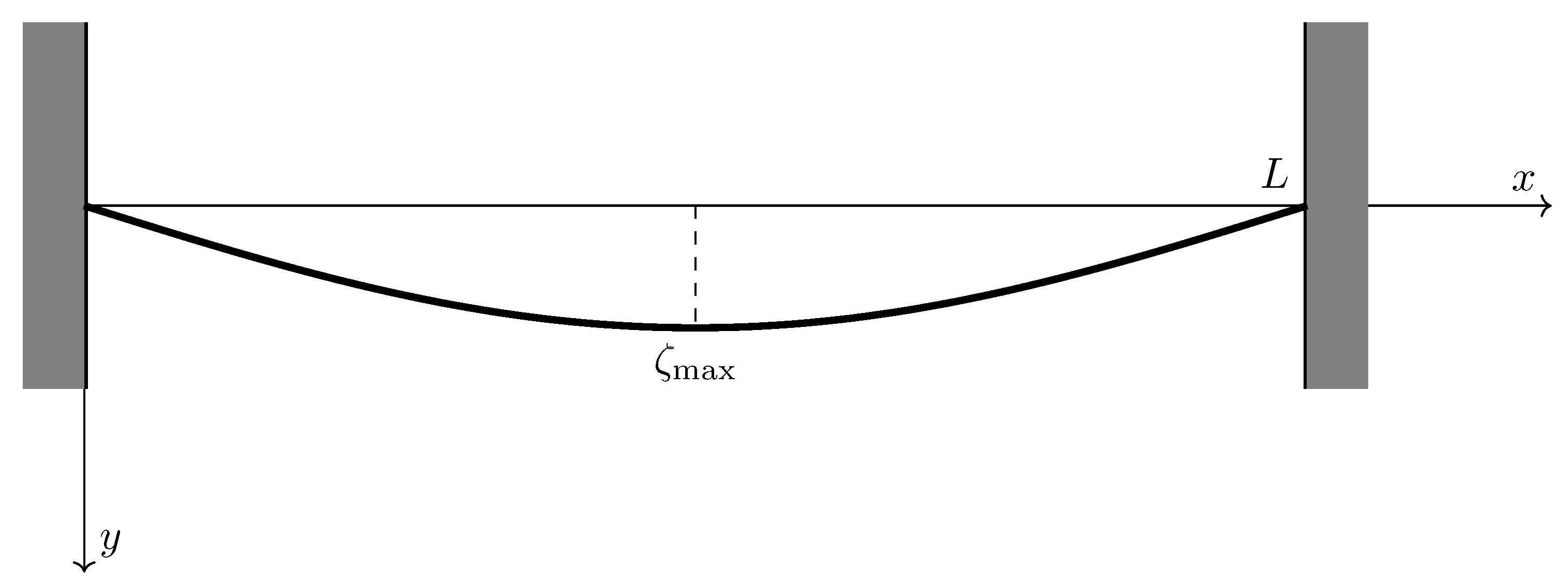
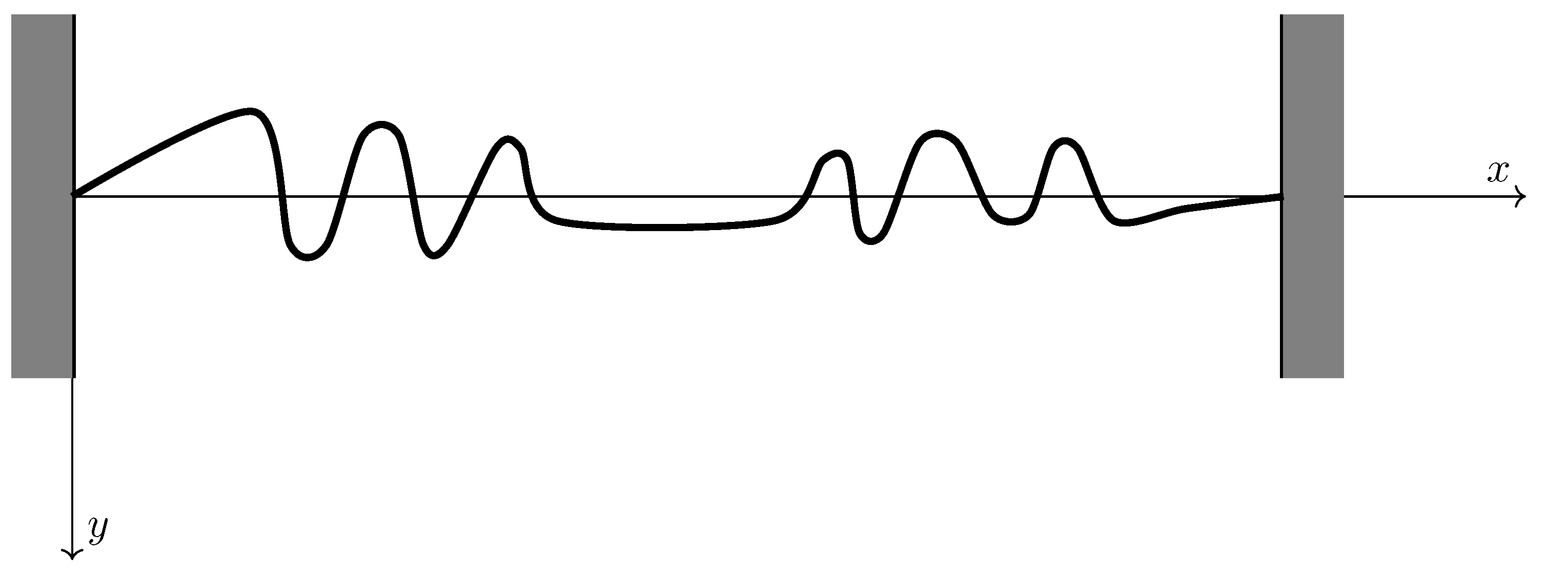
4.3. Non-Linear Effect of the Generation of Harmonics in the Shape of the Buckled Elastica
4.4. Numerical Results for the Buckling of a Clamped and Pinned Beams
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bernoulli, J. Véritable hypothèse de la résistance des solides, avec la démonstration de la courbure de corps qui font resort. In Mémoires de Mathématique et de Physique de l’Académie Royale des Sciences; Académie Royale des Sciences: Paris, France, 1705; pp. 176–186. [Google Scholar]
- Euler, L. Methodus Inveniendi líneas Curvas Maximi Minimive Proprietate Gaudantes, Sive Solutio Problematis Isoperimetrici Latíssimo Sensu Accepti; Apud Marcum-Michaelem Bousquet & Socios: Laussane/Geneva, Switzerland, 1744. [Google Scholar]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity, 4th ed.; Dover Books on Engineering; Dover Publications, Inc.: New York, NY, USA, 1944. [Google Scholar]
- Timoshenko, S.P.; Monroe, J.G. Theory of Elastic Stability, 2nd ed.; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1961. [Google Scholar]
- Prescott, J. Applied Elasticity, 1st ed.; Dover Publications: New York, NY, USA, 1946. [Google Scholar]
- Muskhelishvili, N.l. Some Basic Problems of the Mathematical Theory of Elasticity. Basic Equations, the Plane Theory of Elasticity, Torsion and Bending, 5th ed.; Nauka: Moscow, Russia, 1966. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity, 2nd ed.; Course of Theoretical Physics; Pergamon Press Ltd.: Oxford, UK, 1970; Volume 7. [Google Scholar]
- Lekhnitskii, S.G. Theory of Elasticity of an Anisotropic Elastic Body; Mir Publishers: Moscow, Russia, 1981. [Google Scholar]
- Rekach, V.G. Manual of the Theory of Elasticity, 1st ed.; Mir Publishers: Moscow, Russia, 1979. [Google Scholar]
- Parton, V.Z.; Perline, P.I. Méthodes de la Théorie Mathématique de L’élasticité; Éditions Mir: Moscow, Russia, 1984; Volume 2. [Google Scholar]
- Antman, S.S. Nonlinear Problems of Elasticity, 1st ed.; Applied Mathematical Sciences; Springer Science+Business Media: New York, NY, USA, 1995; Volume 107. [Google Scholar] [CrossRef]
- Chan, S.L. Geometric and material non-linear analysis of beam-columns and frames using the minimum residual displacement method. Int. J. Numer. Methods Eng. 1988, 26, 2657–2669. [Google Scholar] [CrossRef]
- Kapania, R.K.; Raciti, S. Recent Advances in Analysis of Laminated Beams and Plates, Part I: Shear Effects and Buckling. AIAA J. 1989, 27, 923–935. [Google Scholar] [CrossRef]
- Huang, H.; Kardomateas, G.A. Buckling and Initial Postbuckling Behavior of Sandwich Beams Including Transverse Shear. AIAA J. 2002, 40, 2331–2335. [Google Scholar] [CrossRef] [Green Version]
- Silvestre, N. Generalised beam theory to analyse the buckling behaviour of circular cylindrical shells and tubes. Thin-Walled Struct. 2007, 45, 185–198. [Google Scholar] [CrossRef]
- Machado, S.P. Non-linear buckling and postbuckling behavior of thin-walled beams considering shear deformation. Int. J. Non-Linear Mech. 2008, 43, 345–365. [Google Scholar] [CrossRef]
- Ruta, G.C.; Varano, V.; Pignataro, M.; Rizzi, N.L. A beam model for the flexural–torsional buckling of thin-walled members with some applications. Thin-Walled Struct. 2008, 46, 816–822. [Google Scholar] [CrossRef]
- Mancusi, G.; Feo, L. Non-linear pre-buckling behavior of shear deformable thin-walled composite beams with open cross-section. Compos. Part B Eng. 2013, 47, 379–390. [Google Scholar] [CrossRef]
- Lanc, D.; Turkalj, G.; Vo, T.P.; Brnić, J. Nonlinear buckling behaviours of thin-walled functionally graded open section beams. Compos. Struct. 2016, 152, 829–839. [Google Scholar] [CrossRef] [Green Version]
- Hutchinson, J.W.; Budiansky, B. Dynamic Buckling Estimates. AIAA J. 1966, 4, 525–530. [Google Scholar] [CrossRef]
- Zhao, J.; Jia, J.; He, X.; Wang, H. Post-buckling and Snap-Through Behavior of Inclined Slender Beams. J. Appl. Mech. 2008, 75. [Google Scholar] [CrossRef] [Green Version]
- Vega-Posada, C.; Areiza-Hurtado, M.; Aristizabal-Ochoa, J.D. Large-deflection and post-buckling behavior of slender beam-columns with non-linear end-restraints. Int. J. Non-Linear Mech. 2011, 46, 79–95. [Google Scholar] [CrossRef]
- Goriely, A.; Vandiver, R.; Destrade, M. Nonlinear Euler buckling. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 3003–3019. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Buckling analysis of size-dependent nonlinear beams based on a nonlocal strain gradient theory. Int. J. Eng. Sci. 2015, 97, 84–94. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Kreider, W.; Anderson, T.J. Investigation of natural frequencies and mode shapes of buckled beams. AIAA J. 1995, 33, 1121–1126. [Google Scholar] [CrossRef]
- Lestari, W.; Hanagud, S. Nonlinear vibration of buckled beams: Some exact solutions. Int. J. Solids Struct. 2001, 38, 4741–4757. [Google Scholar] [CrossRef]
- Abou-Rayan, A.M.; Nayfeh, A.H.; Mook, D.T.; Nayfeh, M.A. Nonlinear Response of a Parametrically Excited Buckled Beam. Nonlinear Dyn. 1993, 4, 499–525. [Google Scholar] [CrossRef]
- Kreider, W.; Nayfeh, A.H. Experimental Investigation of Single-Mode Responses in a Fixed-Fixed Buckled Beam. Nonlinear Dyn. 1998, 15, 155–177. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Lacarbonara, W.; Chin, C.M. Nonlinear Normal Modes of Buckled Beams: Three-to-One and One-to-One Internal Resonances. Nonlinear Dyn. 1999, 18, 253–273. [Google Scholar] [CrossRef]
- Jensen, J.S. Buckling of an elastic beam with added high-frequency excitation. Int. J. Non-Linear Mech. 2000, 35, 217–227. [Google Scholar] [CrossRef]
- Emam, S.A.; Nayfeh, A.H. Nonlinear Responses of Buckled Beams to Subharmonic-Resonance Excitations. Nonlinear Dyn. 2004, 35, 105–122. [Google Scholar] [CrossRef]
- Emam, S.A.; Nayfeh, A.H. On the Nonlinear Dynamics of a Buckled Beam Subjected to a Primary-Resonance Excitation. Nonlinear Dyn. 2004, 35, 1–17. [Google Scholar] [CrossRef]
- Emam, S.A.; Nayfeh, A.H. Non-linear response of buckled beams to 1:1 and 3:1 internal resonances. Int. J. Non-Linear Mech. 2013, 52, 12–25. [Google Scholar] [CrossRef]
- Pinto, O.C.; Gonçalves, P.B. Non-linear control of buckled beams under step loading. Mech. Syst. Signal Process. 2000, 14, 967–985. [Google Scholar] [CrossRef]
- Li, S.; Zhou, Y. Post-buckling of a hinged-fixed beam under uniformly distributed follower forces. Mech. Res. Commun. 2005, 32, 359–367. [Google Scholar] [CrossRef]
- Li, S.R.; Zhang, J.H.; Zhao, Y.G. Thermal post-buckling of Functionally Graded Material Timoshenko beams. Appl. Math. Mech. 2006, 27, 803–810. [Google Scholar] [CrossRef]
- Li, S.R.; Batra, R.C. Thermal Buckling and Postbuckling of Euler–Bernoulli Beams Supported on Nonlinear Elastic Foundations. AIAA J. 2007, 45, 712–720. [Google Scholar] [CrossRef] [Green Version]
- Song, X.; Li, S.R. Thermal buckling and post-buckling of pinned–fixed Euler–Bernoulli beams on an elastic foundation. Mech. Res. Commun. 2007, 34, 164–171. [Google Scholar] [CrossRef]
- Kirchhoff, G. Ueber die Transversalschwingungen eines Stabes von veränderlichem Querschnitt. Ann. Phys. 1880, 246, 501–512. [Google Scholar] [CrossRef] [Green Version]
- Wrinch, D. On the lateral vibrations of bars of conical type. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1922, 101, 493–508. [Google Scholar] [CrossRef] [Green Version]
- Ono, A. Lateral vibrations of tapered bars. J. Soc. Mech. Eng. 1925, 28, 429–441. [Google Scholar] [CrossRef]
- Conway, H.D.; Becker, E.C.H.; Dubil, J.F. Vibration Frequencies of Tapered Bars and Circular Plates. J. Appl. Mech. 1964, 31, 329–331. [Google Scholar] [CrossRef]
- Gaines, J.H.; Volterra, E. Transverse Vibrations of Cantilever Bars of Variable Cross Section. J. Acoust. Soc. Am. 1966, 39, 674–679. [Google Scholar] [CrossRef]
- Wang, H.C.; Worley, W.J. Tables of Natural Frequencies and Nodes for Transverse Vibration of Tapered Beams; Technical Report; University of Illinois: Washington, DC, USA, 1966. [Google Scholar]
- Wang, H.C. Generalized Hypergeometric Function Solutions on the Transverse Vibration of a Class of Nonuniform Beams. J. Appl. Mech. 1967, 34, 702–708. [Google Scholar] [CrossRef]
- Lau, J.H. Vibration Frequencies of Tapered Bars With End Mass. J. Appl. Mech. 1984, 51, 179–181. [Google Scholar] [CrossRef]
- Naguleswaran, S. Vibration of an Euler–Bernoulli beam of constant depth and with linearly varying breadth. J. Sound Vib. 1992, 153, 509–522. [Google Scholar] [CrossRef]
- Downs, B. Transverse Vibrations of Cantilever Beams Having Unequal Breadth and Depth Tapers. J. Appl. Mech. 1977, 44, 737–742. [Google Scholar] [CrossRef]
- Sato, K. Transverse vibrations of linearly tapered beams with ends restrained elastically against rotation subjected to axial force. Int. J. Mech. Sci. 1980, 22, 109–115. [Google Scholar] [CrossRef]
- Chen, R.S. Evaluation of natural vibration frequency and buckling loading of bending bar by searching zeros of a target function. Commun. Numer. Methods Eng. 1997, 13, 695–704. [Google Scholar] [CrossRef]
- Amabili, M.; Garziera, R. A technique for the systematic choice of admissible functions in the Rayleigh-Ritz method. J. Sound Vib. 1999, 224, 519–539. [Google Scholar] [CrossRef]
- Zhou, D.; Cheung, Y.K. The free vibration of a type of tapered beams. Comput. Methods Appl. Mech. Eng. 2000, 188, 203–216. [Google Scholar] [CrossRef]
- Bayat, M.; Pakar, I.; Bayat, M. Analytical study on the vibration frequencies of tapered beams. Lat. Am. J. Solids Struct. 2011, 8, 149–162. [Google Scholar] [CrossRef]
- Cazzani, A.; Rosati, L.; Ruge, P. The contribution of Gustav R. Kirchhoff to the dynamics of tapered beams. Z. Angew. Math. Mech. 2017, 97, 1174–1203. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.Y. Vibration of a tapered cantilever of constant thickness and linearly tapered width. Arch. Appl. Mech. 2013, 83, 171–176. [Google Scholar] [CrossRef]
- Storti, D.; Aboelnaga, Y. Bending Vibrations of a Class of Rotating Beams with Hypergeometric Solutions. J. Appl. Mech. 1987, 54, 311–314. [Google Scholar] [CrossRef]
- Auciello, N.M.; Maurizi, M.J. On the natural vibrations of tapered beams with attached inertia elements. J. Sound Vib. 1997, 199, 522–530. [Google Scholar] [CrossRef]
- Yoo, H.H.; Shin, S.H. Vibration analysis of rotating cantilever beams. J. Sound Vib. 1998, 212, 807–828. [Google Scholar] [CrossRef]
- Balakrishnan, A.V.; Iliff, K.W. Continuum Aeroelastic Model for Inviscid Subsonic Bending-Torsion Wing Flutter. J. Aerosp. Eng. 2007, 20, 152–164. [Google Scholar] [CrossRef]
- Chang, C.S.; Hodges, D.H. Parametric Studies on Ground Vibration Test Modeling for Highly Flexible Aircraft. J. Aircr. 2007, 44, 2049–2059. [Google Scholar] [CrossRef]
- Su, W.; Cesnik, C.E.S. Dynamic Response of Highly Flexible Flying Wings. AIAA J. 2011, 49, 324–339. [Google Scholar] [CrossRef]
- Saltari, F.; Riso, C.; Matteis, G.D.; Mastroddi, F. Finite-Element-Based Modeling for Flight Dynamics and Aeroelasticity of Flexible Aircraft. J. Aircr. 2017, 54, 2350–2366. [Google Scholar] [CrossRef]
- Changchuan, X.; Lan, Y.; Yi, L.; Chao, Y. Stability of Very Flexible Aircraft with Coupled Nonlinear Aeroelasticity and Flight Dynamics. J. Aircr. 2018, 55, 862–874. [Google Scholar] [CrossRef]
- Rui, X.; Abbas, L.K.; Yang, F.; Wang, G.; Yu, H.; Wang, Y. Flapwise Vibration Computations of Coupled Helicopter Rotor/Fuselage: Application of Multibody System Dynamics. AIAA J. 2018, 56, 818–835. [Google Scholar] [CrossRef]
- da Costa Campos, L.M.B. Generalized Calculus with Applications to Matter and Forces, 1st ed.; Mathematics and Physics for Science and Technology; CRC Press: Boca Raton, FL, USA, 2014; Volume 3. [Google Scholar]
- da Costa Campos, L.M.B. Higher-Order Differential Equations and Elasticity, 1st ed.; Mathematics and Physics for Science and Technology; Book 6; CRC Press: Boca Raton, FL, USA, 2019; Volume 4. [Google Scholar]
- Forsyth, A.R. Theory of Differential Equations; Cambridge University Press: Cambridge, UK, 1906; Volumes 1–6. [Google Scholar]
- Moulton, F.R. Differential Equations; Dover Publications: New York, NY, USA, 1958. [Google Scholar]
- Franklin, P. Differential Equations for Engineers; Dover Publications: New York, NY, USA, 1960. [Google Scholar]
- Poole, E.G.C. Introduction to the Theory of Linear Differential Equations; Clarendon Press—Oxford University Press: Oxford, UK, 1936. [Google Scholar]
- Tricomi, F.G. Equazioni Differenziali, 3rd ed.; Paolo Boringhieri: Rome, Italy, 1961. [Google Scholar]
- Kamke, E. Differentialgleichungen. Lösungsmethoden und Lösungen; Chelsea: New York, NY, USA, 1944; Volumes 1–2. [Google Scholar]
- Forsyth, A.R. A Treatise on Differential Equations, 6th ed.; Macmillan & Co. Ltd.: London, UK, 1956. [Google Scholar]
- Ince, E.L. Ordinary Differential Equations; Dover Books on Mathematics; Dover Publications, Inc.: Mineola, NY, USA, 1956. [Google Scholar]
- Greenspan, D. Theory and Solution of Ordinary Differential Equations; Macmillan: New York, NY, USA, 1960. [Google Scholar]
- Pontriaguine, L. Équations Différentielles Ordinaires; Éditions Mirr: Moscow, Russia, 1975. [Google Scholar]
- Braun, M. Differential Equations and Their Applications, 3rd ed.; Applied Mathematical Sciences; Springer: New York, NY, USA, 1983; Volume 15. [Google Scholar] [CrossRef]
- da Costa Campos, L.M.B. Linear Differential Equations and Oscillators, 1st ed.; Mathematics and Physics for Science and Technology; Book 4; CRC Press: Boca Raton, FL, USA, 2019; Volume 4. [Google Scholar] [CrossRef]
- da Costa Campos, L.M.B. Non-Linear Differential Equations and Dynamical Systems, 1st ed.; Mathematics and Physics for Science and Technology; Book 5; CRC Press: Boca Raton, FL, USA, 2019; Volume 4. [Google Scholar] [CrossRef]
- Briot, C.A.A.; Bouquet, J.C. Théorie des Fonctions Elliptiques, 2nd ed.; Gauthier-Villars: Paris, France, 1875. [Google Scholar]
- Laurent, P.M.H. Théorie Élémentaire des Fonctions Elliptiques; Gauthier-Villars: Paris, France, 1880. [Google Scholar]
- Greenhill, A.G. The Applications of Elliptic Functions; Macmillan and Company: London, UK, 1892. [Google Scholar]
- Cayley, A. An Elementary Treatise on Elliptic Functions; Deighton, Bell, and Company: Cambridge, UK, 1876. [Google Scholar]
- da Costa Campos, L.M.B. Complex Analysis with Applications to Flows and Fields, 1st ed.; Mathematics and Physics for Science and Technology; CRC Press: Boca Raton, FL, USA, 2011; Volume 1. [Google Scholar]
- da Costa Campos, L.M.B. Singular Differential Equations and Special Functions, 1st ed.; Mathematics and Physics for Science and Technology; Book 8; CRC Press: Boca Raton, FL, USA, 2019; Volume 4. [Google Scholar] [CrossRef]
- Barten, H.J. On the deflection of a cantilever beam. Q. Appl. Math. 1944, 2, 168–171. [Google Scholar] [CrossRef] [Green Version]
- Bisshopp, K.E.; Drucker, D.C. Large deflection of cantilever beams. Q. Appl. Math. 1945, 3, 272–275. [Google Scholar] [CrossRef] [Green Version]
- Mattiasson, K. Numerical results from large deflection beam and frame problems analysed by means of elliptic integrals. Int. J. Numer. Methods Eng. 1981, 17, 145–153. [Google Scholar] [CrossRef]
- Lau, J.H. Large deflection of beams with combined loads. ASCE J. Eng. Mech. 1982, 108, 180–185. [Google Scholar]
- Chucheepsakul, S.; Buncharoen, S.; Wang, C.M. Large Deflection of Beams under Moment Gradient. ASCE J. Eng. Mech. 1994, 120, 1848–1860. [Google Scholar] [CrossRef]
- Chucheepsakul, S.; Wang, C.M.; He, X.Q.; Monprapussorn, T. Double Curvature Bending of Variable-Arc-Length Elasticas. J. Appl. Mech. 1999, 66, 87–94. [Google Scholar] [CrossRef]
- Wang, C.M.; Lam, K.Y.; He, X.Q.; Chucheepsakul, S. Large deflections of an end supported beam subjected to a point load. Int. J. Non-Linear Mech. 1997, 32, 63–72. [Google Scholar] [CrossRef]
- De Bona, F.; Zelenika, S. A generalized elastica-type approach to the analysis of large displacements of spring-strips. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1997, 211, 509–517. [Google Scholar] [CrossRef]
- Coffin, D.W.; Bloom, F. Elastica solution for the hygrothermal buckling of a beam. Int. J. Non-Linear Mech. 1999, 34, 935–947. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R. Stability Analysis of Frame Having FG Tapered Beam–Column. Int. J. Steel Struct. 2019, 19, 446–468. [Google Scholar] [CrossRef]
- Griner, G.M. A Parametric Solution to the Elastic Pole-Vaulting Pole Problem. J. Appl. Mech. 1984, 51, 409–414. [Google Scholar] [CrossRef]
- Panayotounakos, D.E.; Theocaris, P.S. Nonlinear and buckling analysis of continuous bars lying on rigid supports. AIAA J. 1986, 24, 479–484. [Google Scholar] [CrossRef]
- Panayotounakos, D.E.; Theocaris, P.S. Exact solution for an approximate differential equation of a straight bar under conditions of a non-linear equilibrium. Int. J. Non-Linear Mech. 1986, 21, 421–429. [Google Scholar] [CrossRef]
- Panayotounakos, D.E.; Theocaris, P.S. Analytic Solutions for Nonlinear Differential Equations Describing the Elastica of Straight Bars: Theory. J. Frankl. Inst. 1988, 325, 621–633. [Google Scholar] [CrossRef]
- Panayotounakos, D.E.; Theocaris, P.S. Large deflections of buckled bars under distributed axial load. Int. J. Solids Struct. 1988, 24, 1179–1192. [Google Scholar] [CrossRef]
- Panayotounakos, D.E. Non-linear and buckling analysis of bars lying on an elastic foundation. Int. J. Non-Linear Mech. 1989, 24, 295–307. [Google Scholar] [CrossRef]
- Sotiropoulou, A.B.; Panayotounakos, D.E. Exact parametric analytic solutions of the elastica ODEs for bars including effects of the transverse deformation. Int. J. Non-Linear Mech. 2004, 39, 1555–1570. [Google Scholar] [CrossRef]
- Campos, L.M.B.C.; Marta, A.C. On the prevention or facilitation of buckling of beams. Int. J. Mech. Sci. 2014, 79, 95–104. [Google Scholar] [CrossRef]
- Campos, L.M.B.C.; Marta, A.C. On The Vibrations of Pyramidal Beams With Rectangular Cross-Section and Application to Unswept Wings. Q. J. Mech. Appl. Math. 2021, 74, 1–31. [Google Scholar] [CrossRef]
- da Costa Campos, L.M.B. Transcendental Representations with Applications to Solids and Fluids, 1st ed.; Mathematics and Physics for Science and Technology; CRC Press: Boca Raton, FL, USA, 2012; Volume 2. [Google Scholar]
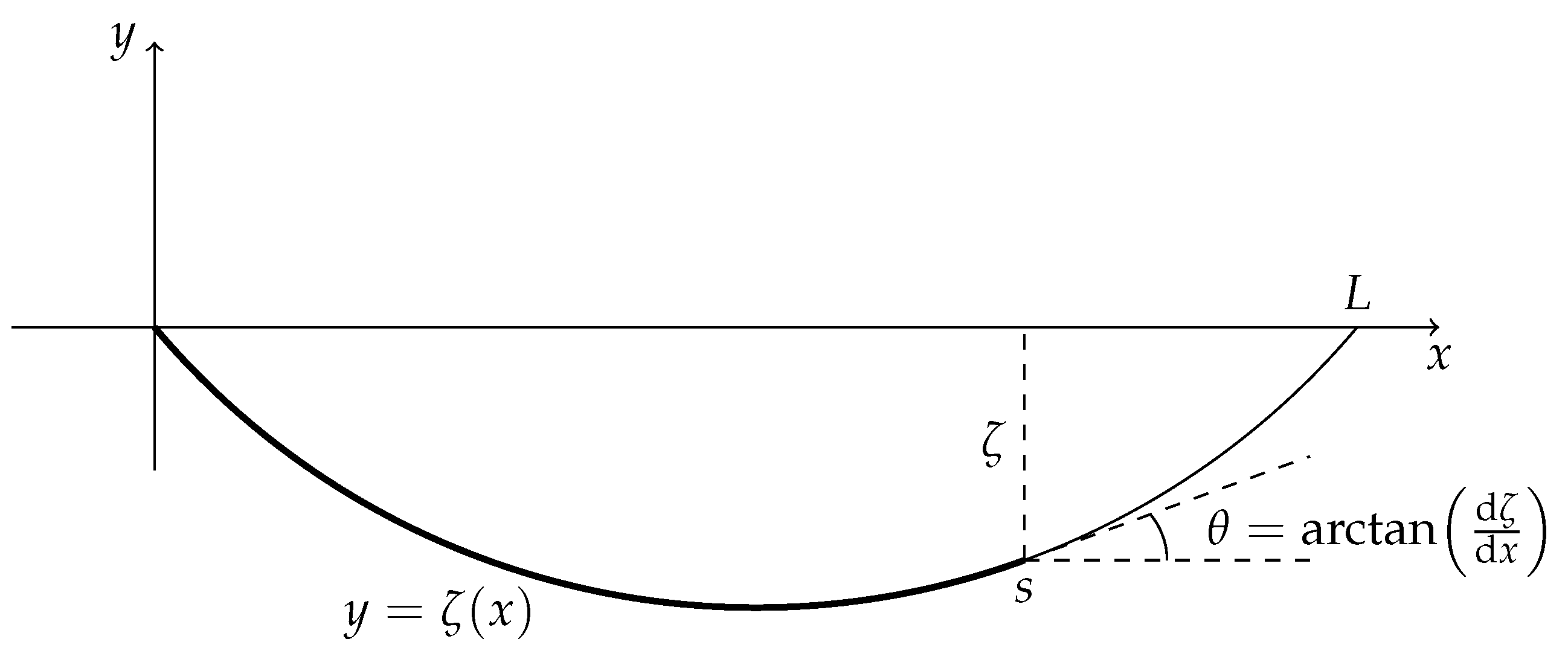

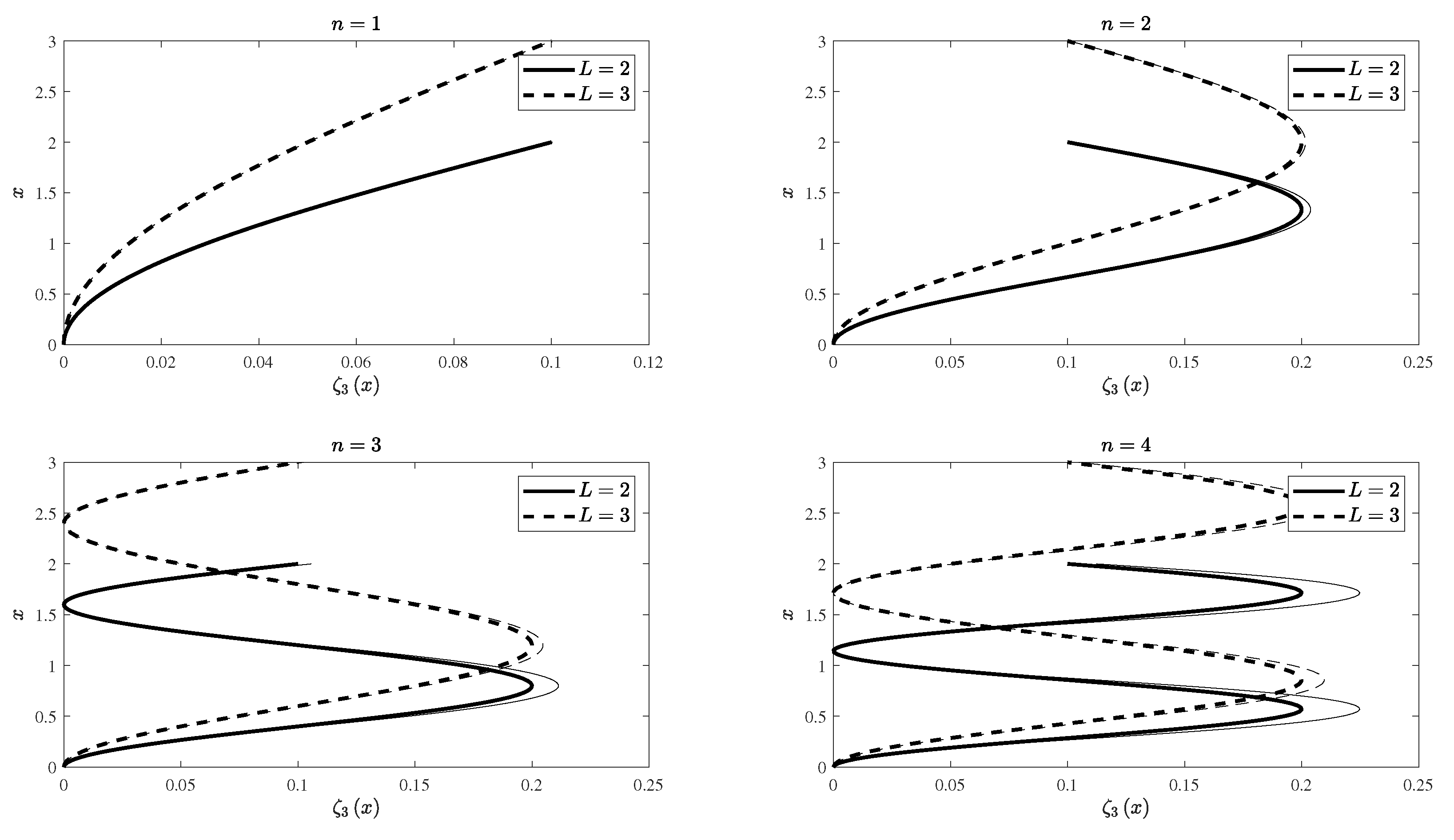

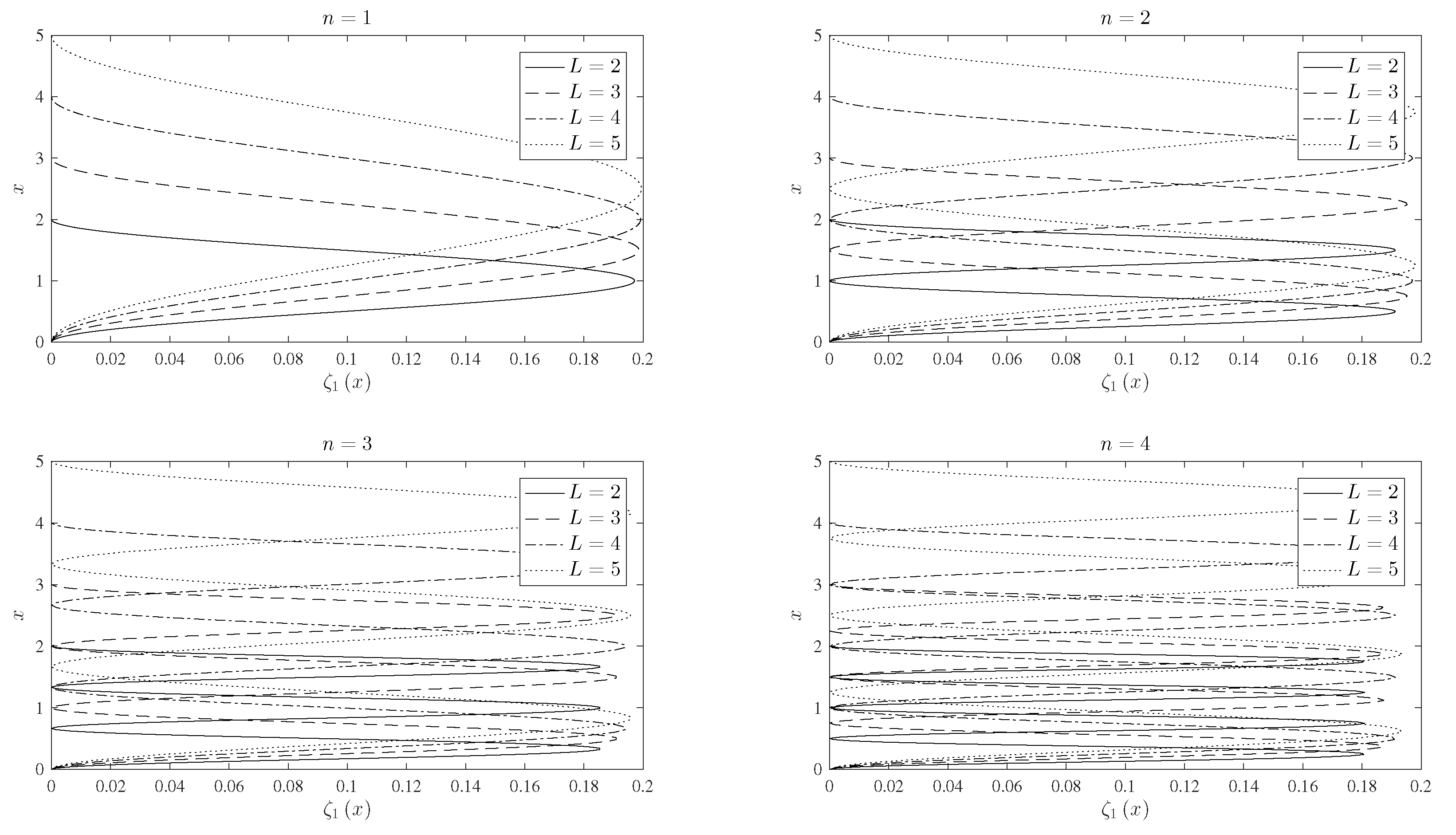
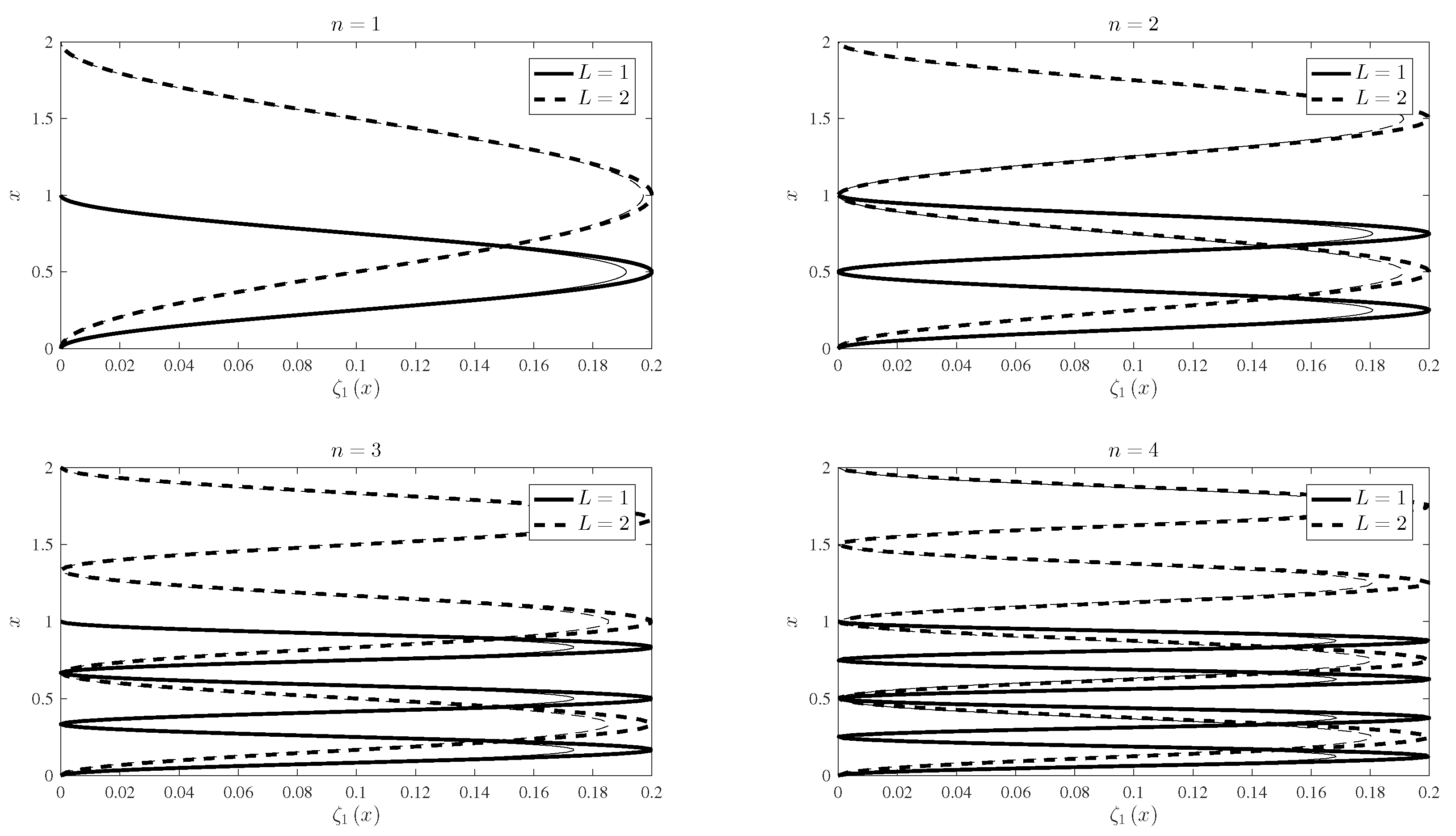
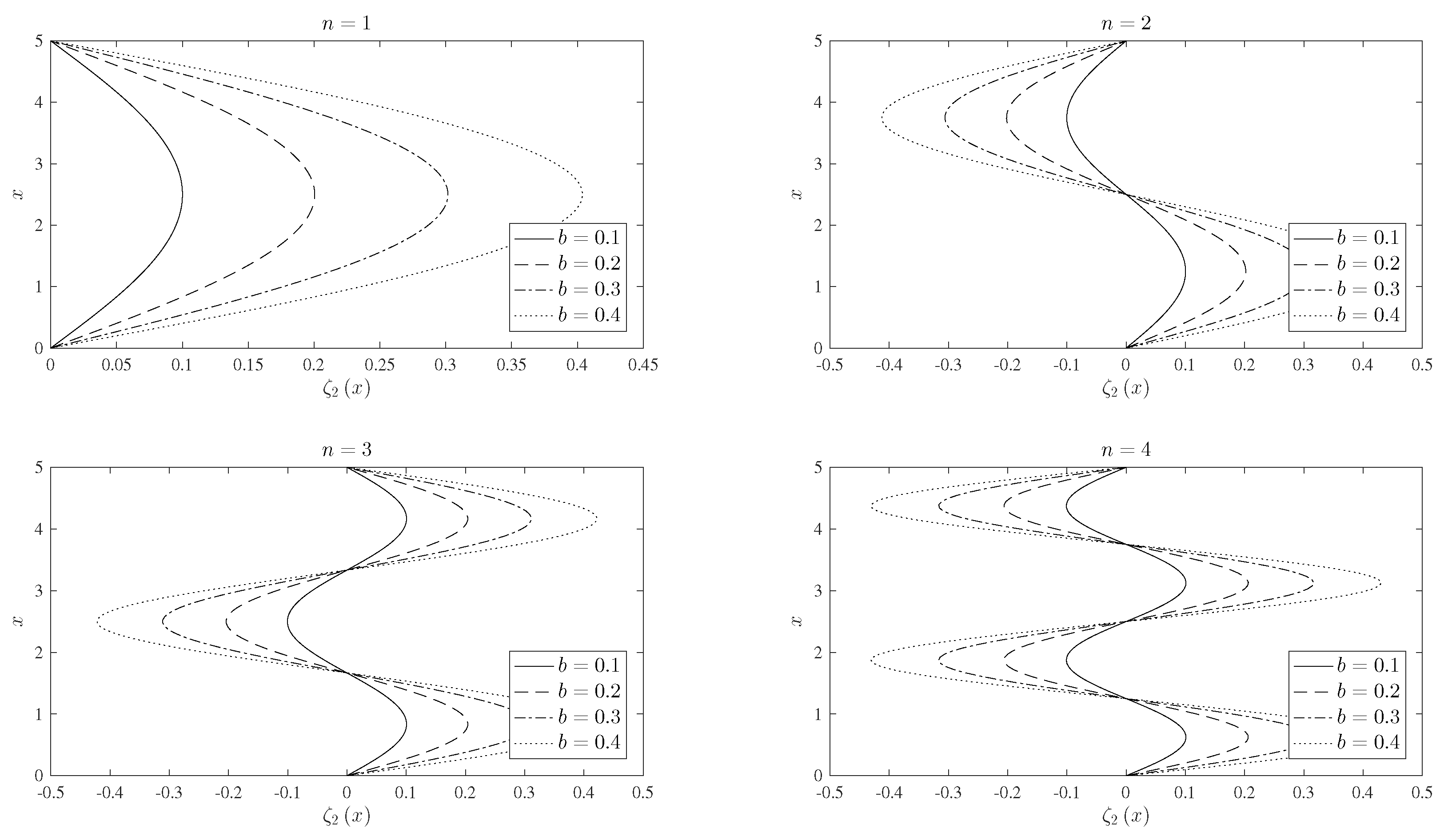
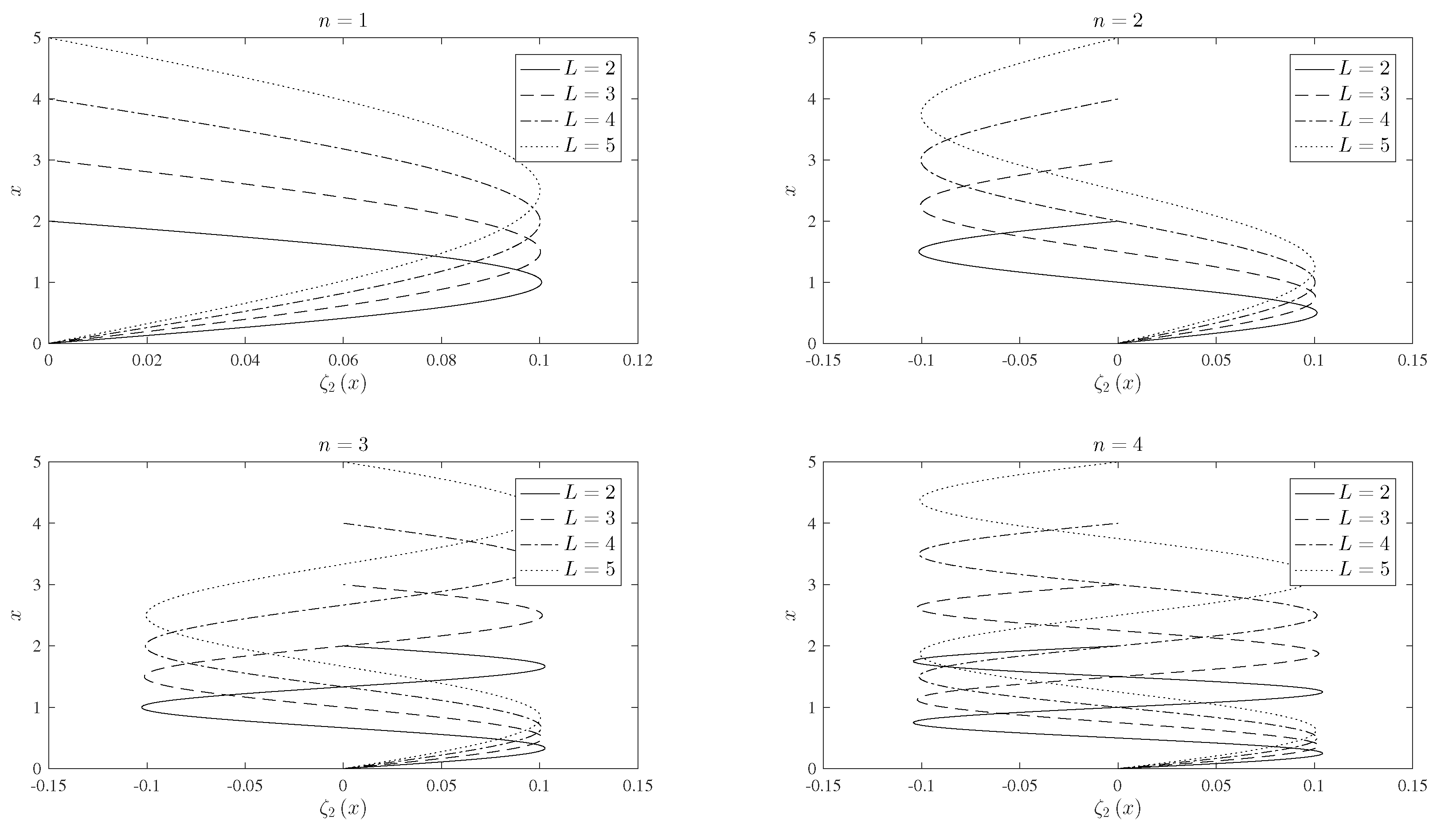
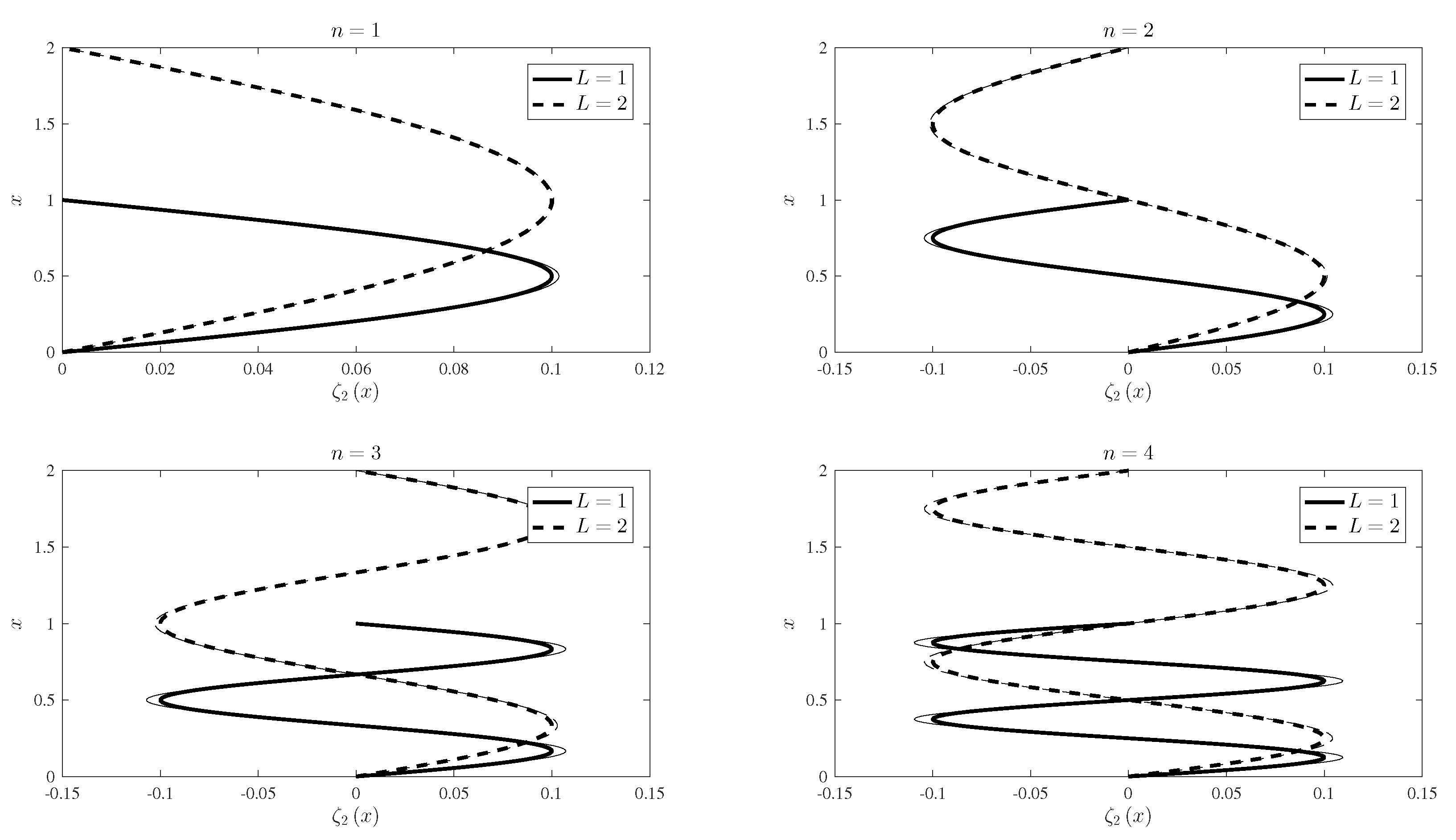
| Coefficient | |||||||
|---|---|---|---|---|---|---|---|
| Numerical value | 1 |
| Number of Terms | Parameter G | ||||||||
|---|---|---|---|---|---|---|---|---|
| Order | Length | |||||||
| 0.8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 10 | 0.196 | 9 | 0.157 | 7 | 0.079 | 6 | 0.052 | 5 | 0.039 | 5 | 0.031 | 5 | 0.026 | 5 | 0.022 |
| 2 | 30 | 0.589 | 21 | 0.471 | 11 | 0.236 | 9 | 0.157 | 8 | 0.118 | 7 | 0.094 | 7 | 0.079 | 6 | 0.067 |
| Buckling orders | ||||||
|---|---|---|---|---|---|---|
| Beam | Reference | 1st | 2nd | 3rd | 4th | 5th |
| Clamped | Present method | 39.478 | 157.914 | 355.306 | 631.655 | 986.960 |
| Literature [3,4,7] | 39.478 | 157.914 | 355.306 | 631.655 | 986.960 | |
| Pinned | Present method | 9.870 | 39.478 | 88.826 | 157.914 | 246.740 |
| Literature [3,4,7] | 9.870 | 39.478 | 88.826 | 157.914 | 246.740 | |
| Cantilever | Present method | 2.467 | 22.207 | 61.685 | 120.903 | 199.859 |
| Literature [3,4,7] | 2.467 | 22.207 | 61.685 | 120.903 | 199.859 | |
| Order n | Length L | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 0.866 | 0.288 | 0.137 | 0.079 | 0.051 | 0.036 | 0.027 |
| 2 | 1.909 | 0.866 | 0.469 | 0.288 | 0.193 | 0.137 | 0.102 |
| 3 | 2.612 | 1.423 | 0.861 | 0.563 | 0.392 | 0.286 | 0.217 |
| 4 | 3.131 | 1.909 | 1.252 | 0.866 | 0.626 | 0.469 | 0.363 |
| Order n | Length L | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 0.144 | 0.040 | 0.018 | 0.010 | 0.007 | 0.005 | 0.003 |
| 2 | 0.433 | 0.144 | 0.069 | 0.040 | 0.026 | 0.018 | 0.013 |
| 3 | 0.0714 | 0.283 | 0.144 | 0.085 | 0.056 | 0.040 | 0.029 |
| 4 | 0.955 | 0.433 | 0.235 | 0.144 | 0.096 | 0.069 | 0.051 |
| Order n | Length L | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | 0.083 | 0.021 | 0.009 | 0.005 | 0.003 | 0.002 | 0.002 |
| 1 | 1.716 | 0.383 | 0.167 | 0.093 | 0.059 | 0.041 | 0.030 |
| 2 | 6.975 | 1.135 | 0.477 | 0.263 | 0.167 | 0.085 | 0.079 |
| 3 | - | 2.484 | 0.976 | 0.528 | 0.332 | 0.229 | 0.167 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campos, L.M.B.C.; Silva, M.J.S. On the Generation of Harmonics by the Non-Linear Buckling of an Elastic Beam. Appl. Mech. 2021, 2, 383-418. https://doi.org/10.3390/applmech2020022
Campos LMBC, Silva MJS. On the Generation of Harmonics by the Non-Linear Buckling of an Elastic Beam. Applied Mechanics. 2021; 2(2):383-418. https://doi.org/10.3390/applmech2020022
Chicago/Turabian StyleCampos, Luiz M. B. C., and Manuel J. S. Silva. 2021. "On the Generation of Harmonics by the Non-Linear Buckling of an Elastic Beam" Applied Mechanics 2, no. 2: 383-418. https://doi.org/10.3390/applmech2020022
APA StyleCampos, L. M. B. C., & Silva, M. J. S. (2021). On the Generation of Harmonics by the Non-Linear Buckling of an Elastic Beam. Applied Mechanics, 2(2), 383-418. https://doi.org/10.3390/applmech2020022






