High-Speed Cutting of Synthetic Trabecular Bone—A Combined Experimental–Computational Investigation
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Methods
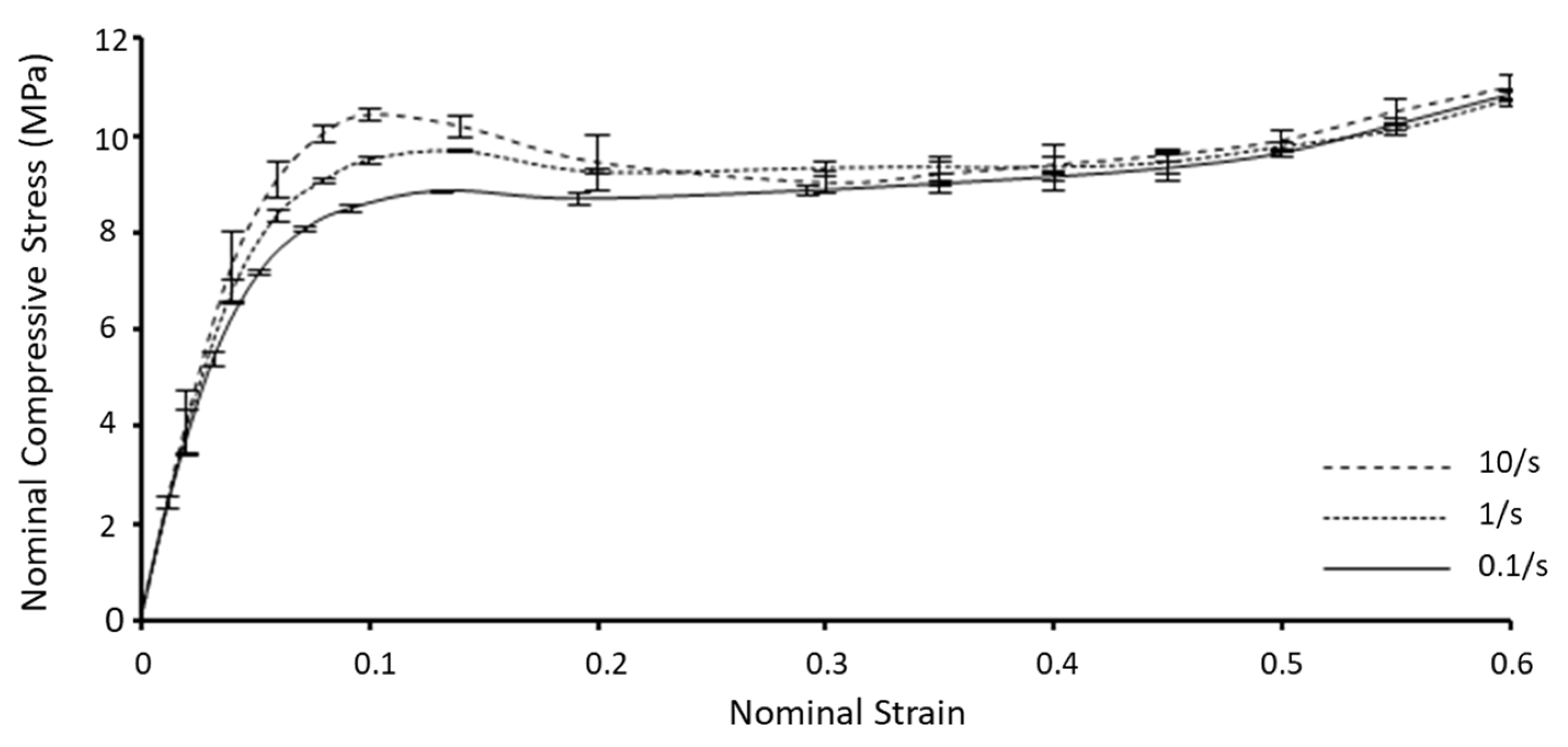
2.1.1. Dynamic Uniaxial Compression Experiments
2.1.2. High-Speed Orthogonal Cutting Experiments
2.2. Computational Analysis
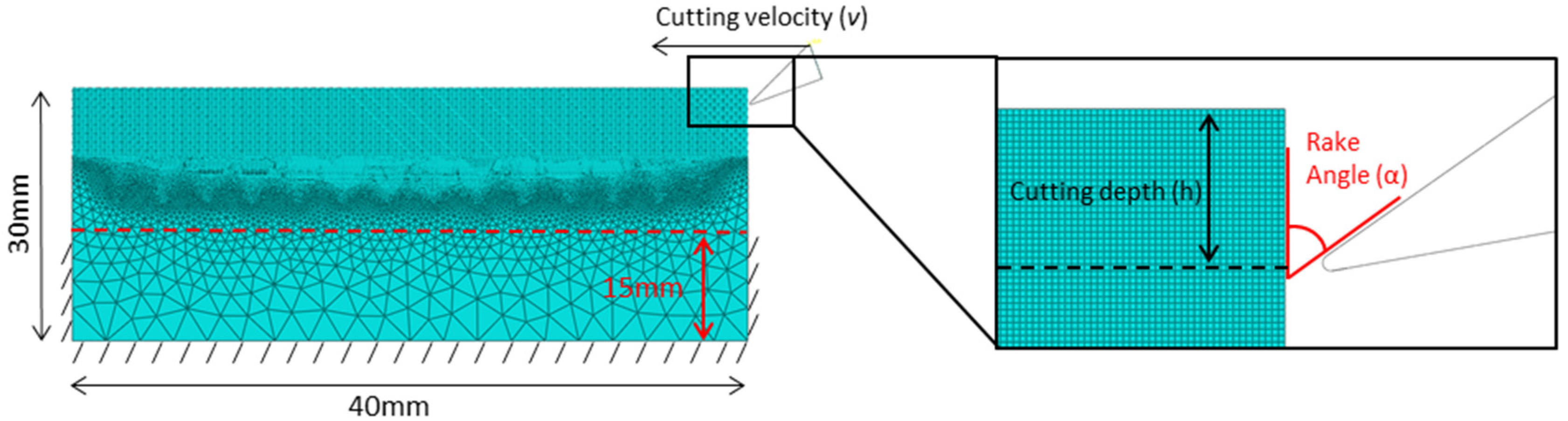
2.2.1. Orthogonal Cutting Geometry
2.2.2. Material Constitutive Model Implementation
2.2.3. High-Speed Orthogonal Cutting Simulations
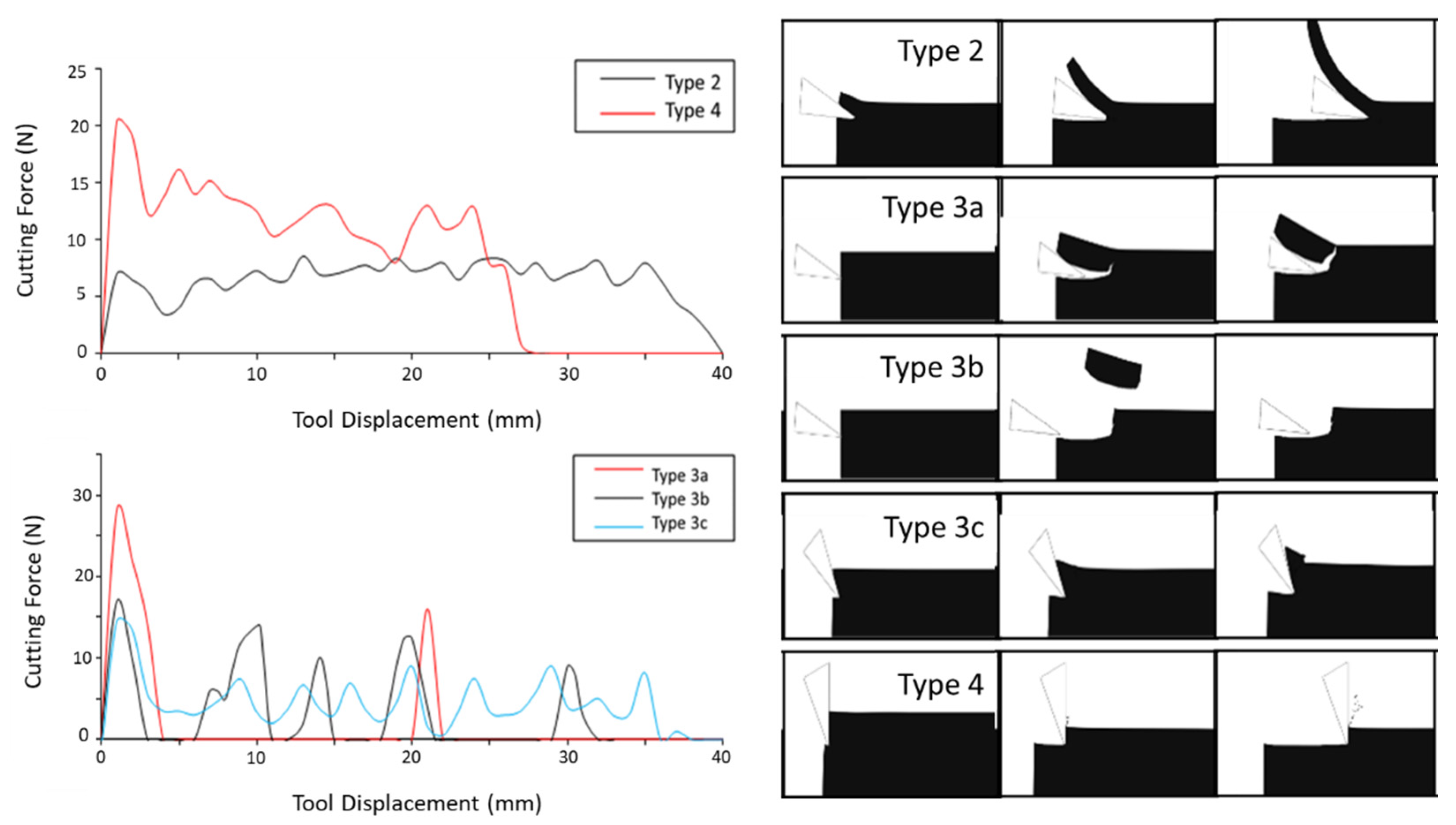
2.3. Categorisation of Chip Formation
3. Results
3.1. Uniaxial Dynamic Compression Tests
3.2. High-Speed Orthogonal Cutting Tests
3.2.1. Chip Formation
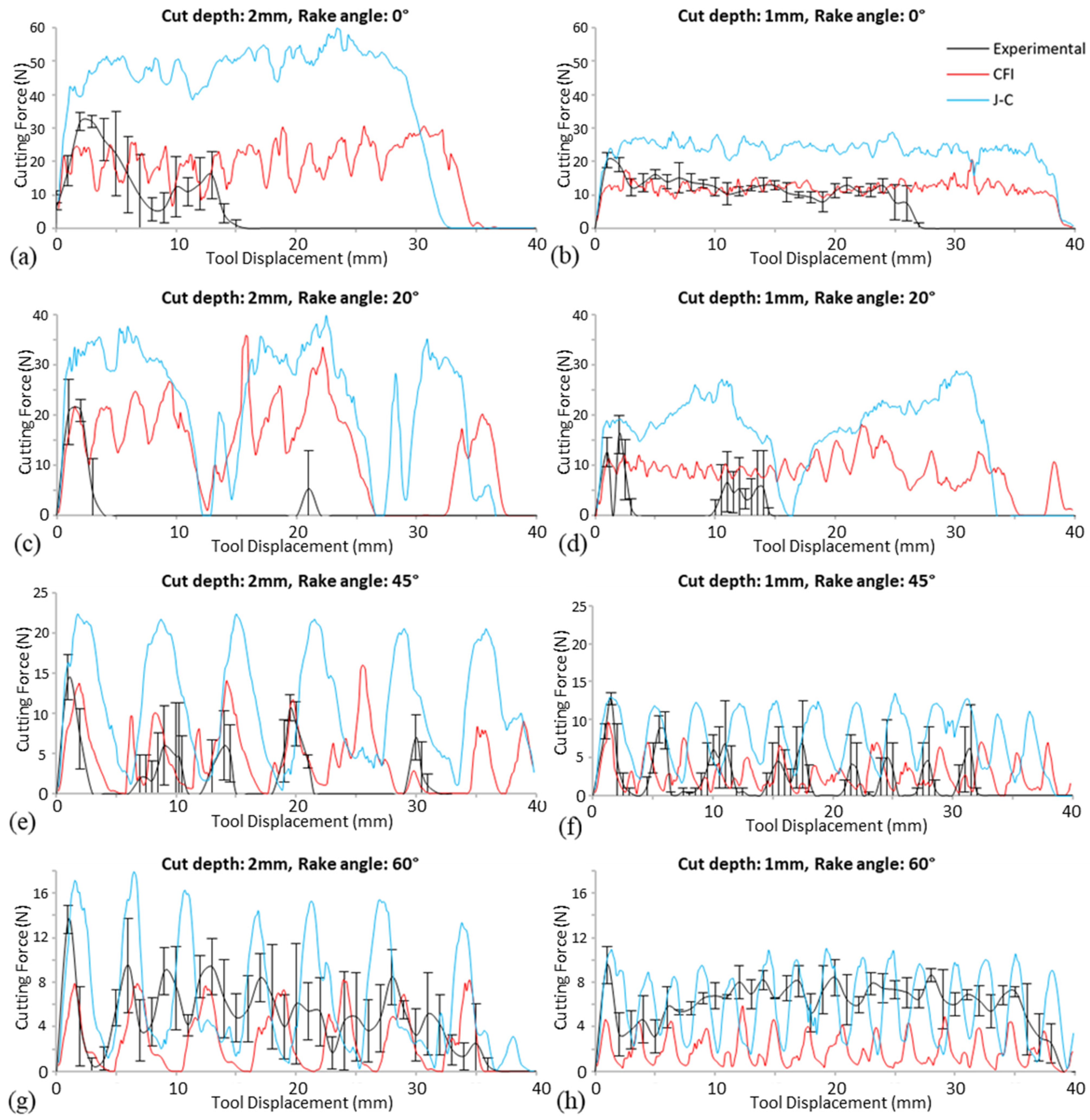
3.2.2. Cutting Force
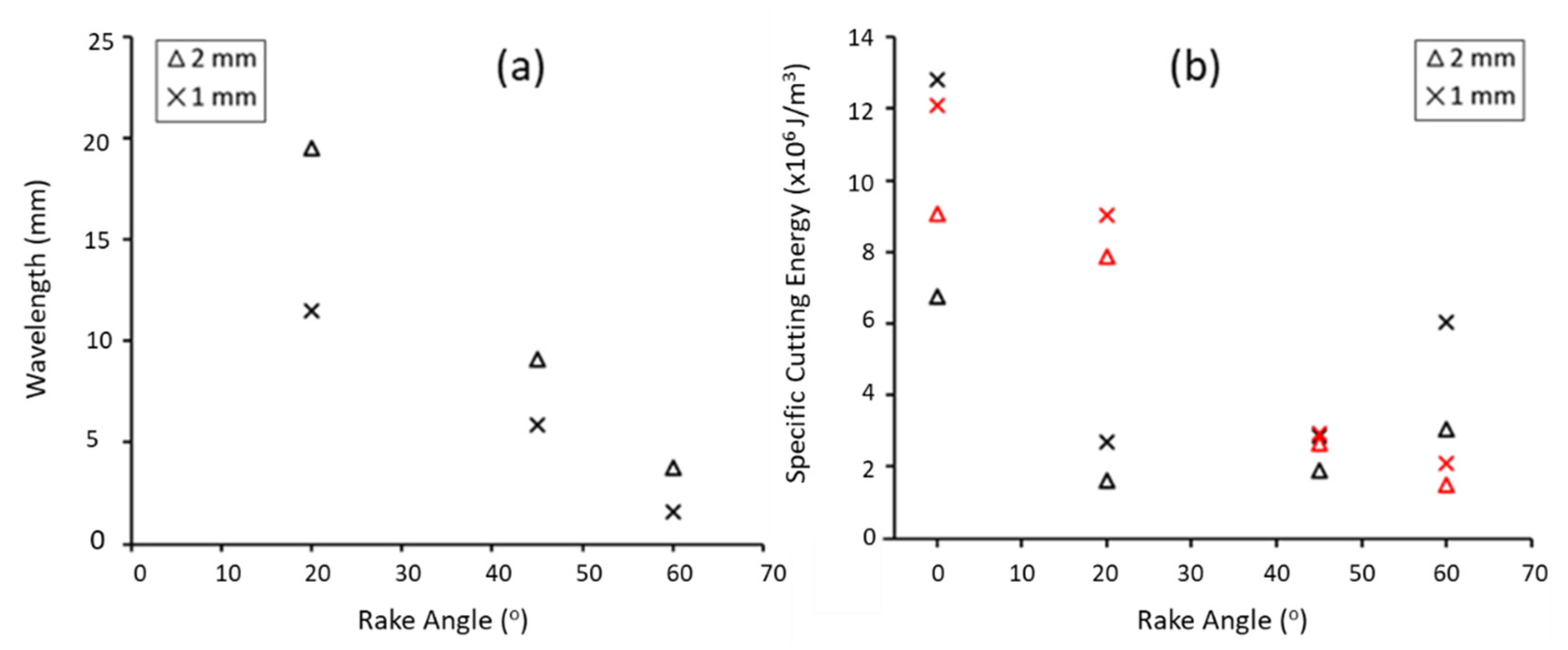
3.2.3. Wavelength of Discontinuous Chip Formation and Specific Cutting Energies
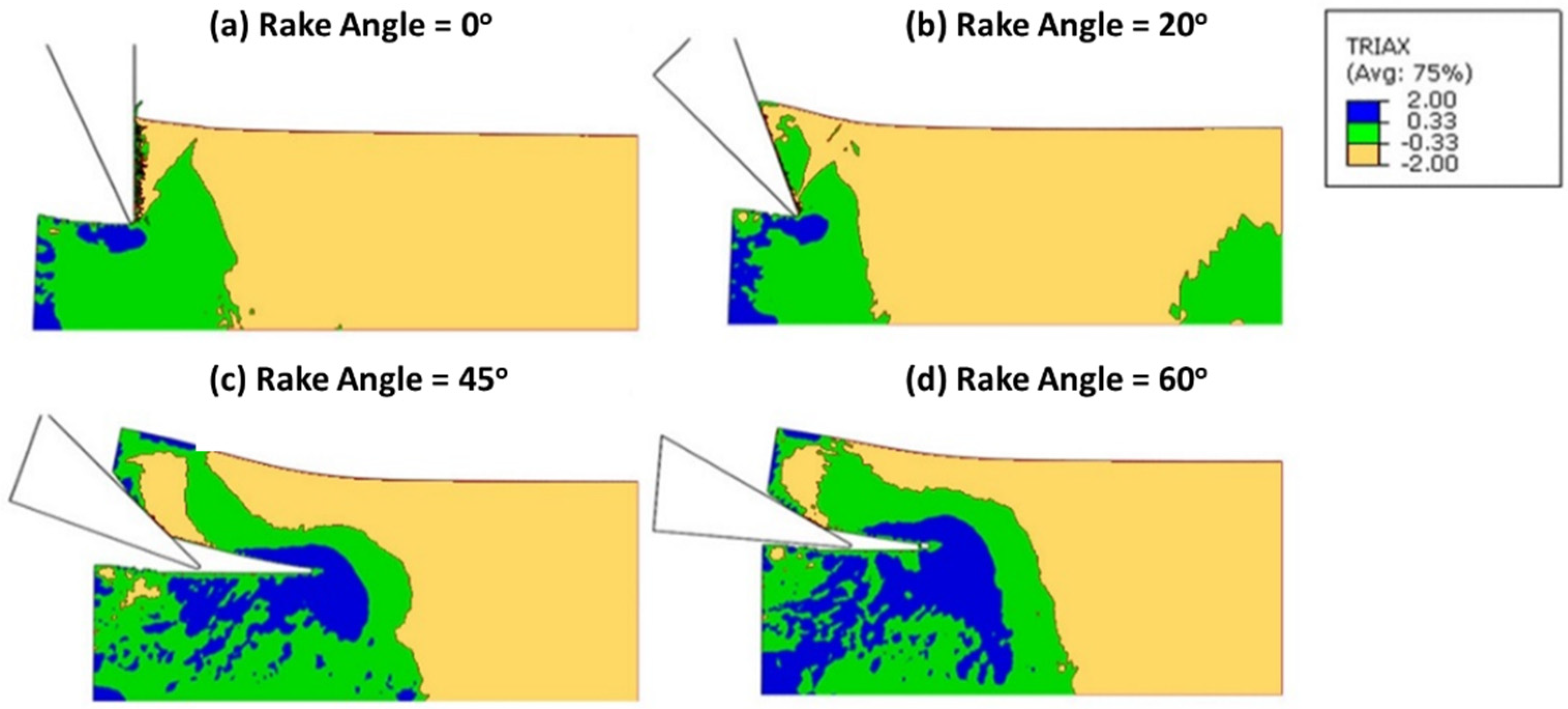
3.2.4. Tool–Bone Interactions
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdel-Wahab, A.A.; Alam, K.; Silberschmidt, V.V. Analysis of anisotropic viscoelastoplastic properties of cortical bone tissues. J. Mech. Behav. Biomed. Mater. 2011, 4, 807–820. [Google Scholar] [CrossRef]
- Vaughan, T.J.; McCarthy, C.T.; McNamara, L.M. A three-scale finite element investigation into the effects of tissue minerali-sation and lamellar organisation in human cortical and trabecular bone. J. Mech. Behav. Biomed. Mater. 2012, 12, 50–62. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Abdel-Wahab, A.; Demirci, E.; Silberschmidt, V.V. Penetration of cutting tool into cortical bone: Experimental and numerical investigation of anisotropic mechanical behaviour. J. Biomech. 2014, 47, 1117–1126. [Google Scholar] [CrossRef] [PubMed]
- Fox, M.J.; Scarvell, J.M.; Smith, P.N.; Kalyanasundaram, S.; Stachurski, Z.H. Lateral drill holes decrease strength of the femur: An observational study using finite element and experimental analyses. J. Orthop. Surg. Res. 2013, 8, 29. [Google Scholar] [CrossRef] [PubMed]
- Dillon, N.P.; Kratchman, L.B.; Dietrich, M.S.; Labadie, R.F.; Webster, R.J.; Withrow, T.J. An Experimental Evaluation of the Force Requirements for Robotic Mastoidectomy. Otol. Neurotol. 2013, 34, e93–e102. [Google Scholar] [CrossRef]
- Krause, W.R. Orthogonal Bone Cutting: Saw Design and Operating Characteristics. J. Biomech. Eng. 1987, 109, 263–271. [Google Scholar] [CrossRef]
- Sui, J.; Sugita, N.; Ishii, K.; Harada, K.; Mitsuishi, M. Force analysis of orthogonal cutting of bovine cortical bone. Mach. Sci. Technol. 2013, 17, 637–649. [Google Scholar] [CrossRef]
- Malak, S.F.F.; Anderson, I.A. Orthogonal cutting of polyurethane foam. Int. J. Mech. Sci. 2005, 47, 867–883. [Google Scholar] [CrossRef]
- Malak, S.F.; Anderson, I.A. Orthogonal cutting of cancellous bone with application to the harvesting of bone autograft. Med. Eng. Phys. 2008, 30, 717–724. [Google Scholar] [CrossRef]
- Yeager, C.; Nazari, A.; Arola, D. Machining of cortical bone: Surface texture, surface integrity and cutting forces. Mach. Sci. Technol. 2008, 12, 100–118. [Google Scholar] [CrossRef]
- Marco, M.; Rodríguez-Millán, M.; Santiuste, C.; Giner, E.; Miguélez, M.H. A review on recent advances in numerical modelling of bone cutting. J. Mech. Behav. Biomed. Mater. 2015, 44, 179–201. [Google Scholar] [CrossRef]
- Goldstein, S. The mechanical properties of trabecular bone: Dependence on anatomic location and function. J. Biomech. 1987, 20, 1055–1061. [Google Scholar] [CrossRef]
- Keaveny, T.M.; Borchers, R.E.; Gibson, L.J.; Hayes, W.C. Trabecular bone modulus and strength can depend on specimen geometry. J. Biomech. 1993, 26, 991–1000. [Google Scholar] [CrossRef]
- Morgan, E.F.; Bayraktar, H.H.; Keaveny, T.M. Trabecular bone modulus–density relationships depend on anatomic site. J. Biomech. 2003, 36, 897–904. [Google Scholar] [CrossRef]
- Cseke, A.; Heinemann, R. The effects of cutting parameters on cutting forces and heat generation when drilling animal bone and biomechanical test materials. Med. Eng. Phys. 2018, 51, 24–30. [Google Scholar] [CrossRef] [PubMed]
- Kusins, J.R.; Tutunea-Fatan, O.R.; Ferreira, L.M. Experimental analysis of the process parameters affecting bone burring operations. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2017, 232, 33–44. [Google Scholar] [CrossRef] [PubMed]
- Umbrello, D.; M’Saoubi, R.; Outeiro, J. The influence of Johnson–Cook material constants on finite element simulation of machining of AISI 316L steel. Int. J. Mach. Tools Manuf. 2007, 47, 462–470. [Google Scholar] [CrossRef]
- Mamalis, A.; Horváth, M.; Branis, A.; Manolakos, D. Finite element simulation of chip formation in orthogonal metal cutting. J. Mater. Process. Technol. 2001, 110, 19–27. [Google Scholar] [CrossRef]
- Rhim, S.-H.; Oh, S.-I. Prediction of serrated chip formation in metal cutting process with new flow stress model for AISI 1045 steel. J. Mater. Process. Technol. 2006, 171, 417–422. [Google Scholar] [CrossRef]
- Zel, T.; Karpat, Y. Identification of Constitutive Material Model Parameters for High-Strain Rate Metal Cutting Conditions Using Evolutionary Computational Algorithms. Mater. Manuf. Process. 2007, 22, 659–667. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Alam, K.; Mitrofanov, A.; Silberschmidt, V.V. Finite element analysis of forces of plane cutting of cortical bone. Comput. Mater. Sci. 2009, 46, 738–743. [Google Scholar] [CrossRef]
- Tu, Y.K.; Chen, L.W.; Ciou, J.S.; Hsiao, C.K.; Chen, Y.C. Finite Element Simulations of Bone Temperature Rise During Bone Drilling Based on a Bone Analog. J. Med. Biol. Eng. 2013, 33, 269–274. [Google Scholar] [CrossRef]
- Santiuste, C.; Rodríguez-Millán, M.; Giner, E.; Miguélez, H. The influence of anisotropy in numerical modeling of orthogonal cutting of cortical bone. Compos. Struct. 2014, 116, 423–431. [Google Scholar] [CrossRef]
- Sezek, S.; Aksakal, B.; Karaca, F. Influence of drill parameters on bone temperature and necrosis: A FEM modelling and in vitro experiments. Comput. Mater. Sci. 2012, 60, 13–18. [Google Scholar] [CrossRef]
- Childs, T.H.C.; Arola, D. Machining of cortical bone: Simulations of chip formation mechanics using metal machining models. Mach. Sci. Technol. 2011, 15, 206–230. [Google Scholar] [CrossRef]
- Kelly, N.; McGarry, J.P. Experimental and numerical characterisation of the elasto-plastic properties of bovine trabecular bone and a trabecular bone analogue. J. Mech. Behav. Biomed. Mater. 2012, 9, 184–197. [Google Scholar] [CrossRef] [PubMed]
- Kelly, N.; Cawley, D.; Shannon, F.; McGarry, J. An investigation of the inelastic behaviour of trabecular bone during the press-fit implantation of a tibial component in total knee arthroplasty. Med. Eng. Phys. 2013, 35, 1599–1606. [Google Scholar] [CrossRef][Green Version]
- Davim, J.P.; Marques, N. Dynamical experimental study of friction and wear behaviour of bovine cancellous bone sliding against a metallic counterface in a water lubricated environment. J. Mater. Process. Technol. 2004, 152, 389–394. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A. Isotropic constitutive models for metallic foams. J. Mech. Phys. Solids 2000, 48, 1253–1283. [Google Scholar] [CrossRef]
- Shaw, M.C. Metal Cutting Principles; Oxford University Press: New York, NY, USA, 1986. [Google Scholar]
- Thaeter, M.; Kobbe, P.; Verhaven, E.; Pape, H.-C. Minimally Invasive Techniques in Orthopedic Trauma. Curr. Trauma Rep. 2016, 2, 232–237. [Google Scholar] [CrossRef]


| A | B | n | C | |
|---|---|---|---|---|
| 5 MPa | 7.5 MPa | 0.55 | 0.04 | 0.1 |
| Compression Yield Stress Ratio (K) | Plastic Poisson’s Ratio (νp) | |
|---|---|---|
| Crushable foam model constants | 0.7 | 0.23 |
| Yield Stress (MPa) | Uniaxial Plastic Strain | |
| Crushable foam piecewise hardening data | 3.7 | 0 |
| 5.2 | 0.01 | |
| 6.5 | 0.02 | |
| 7.1 | 0.04 | |
| 7.2 | 0.06 | |
| 7.47 | 0.08 | |
| 7.56 | 0.1 |
| d1 | d2 | d3 | |
|---|---|---|---|
| −0.77 | 2.5 | −1.75 | 2 × 10−5 |
| Chip Type | Chip Type |
|---|---|
| Surface fragmentation (Type 1) | An accumulation of broken cell walls formed as the tool scrapes along the surface at low cut depths relative to cell size (not observed in this study, so not shown in Figure 3). |
| Continuous chip formation (Type 2) | A continuous plastic deformation of the material without fracture ahead of the cutting edge and results in the smooth flow of the chip up the rake face. |
| Discontinuous chip formation (Type 3) | Fragmented chips forming and may be further subdivided into (i) confined crack propagation and lifting of the chip (Type 3a), (ii) continuous crack propagation (Type 3b) and (iii) shearing (Type 3c). |
| Obliteration (Type 4) | Material ahead of the tool is obliterated, resulting in fine dust. Type 4 chips form a compression failure in the material, ahead of a relatively low rake angle, approaching 0°. This forms an acceptable chip type in the form of fine dust and is a result of the brittle failure of the cell walls within the cellular material. |
| Young’s Modulus, E (MPa) | Yield Stress (MPa) | |||
|---|---|---|---|---|
| Strain rate | 0.1 s−1 | 10 s−1 | 0.1 s−1 | 10 s−1 |
| 155.1 ± 2.6 | 197.9 ± 28.6 | 5.7 ± 0.1 | 6.9 ± 0.3 | |
| 0° | 20° | 45° | 60° | |
|---|---|---|---|---|
| 2 mm cutting depth | Type 4 (Type 4) | Type 3b (Type 3b/3c) | Type 3a (Type 3a) | Type 3a (Type 3a) |
| 1 mm cutting depth | Type 4 (Type 4) | Type 3a/3b (Type 3c) | Type 3a (Type 3a) | Type 3a (Type 3a) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
O’Neill, M.; Vaughan, T.J. High-Speed Cutting of Synthetic Trabecular Bone—A Combined Experimental–Computational Investigation. Appl. Mech. 2021, 2, 650-665. https://doi.org/10.3390/applmech2030037
O’Neill M, Vaughan TJ. High-Speed Cutting of Synthetic Trabecular Bone—A Combined Experimental–Computational Investigation. Applied Mechanics. 2021; 2(3):650-665. https://doi.org/10.3390/applmech2030037
Chicago/Turabian StyleO’Neill, Macdarragh, and Ted J. Vaughan. 2021. "High-Speed Cutting of Synthetic Trabecular Bone—A Combined Experimental–Computational Investigation" Applied Mechanics 2, no. 3: 650-665. https://doi.org/10.3390/applmech2030037
APA StyleO’Neill, M., & Vaughan, T. J. (2021). High-Speed Cutting of Synthetic Trabecular Bone—A Combined Experimental–Computational Investigation. Applied Mechanics, 2(3), 650-665. https://doi.org/10.3390/applmech2030037




