Springback Prediction in Sheet Metal Forming, Based on Finite Element Analysis and Artificial Neural Network Approach
Abstract
1. Introduction
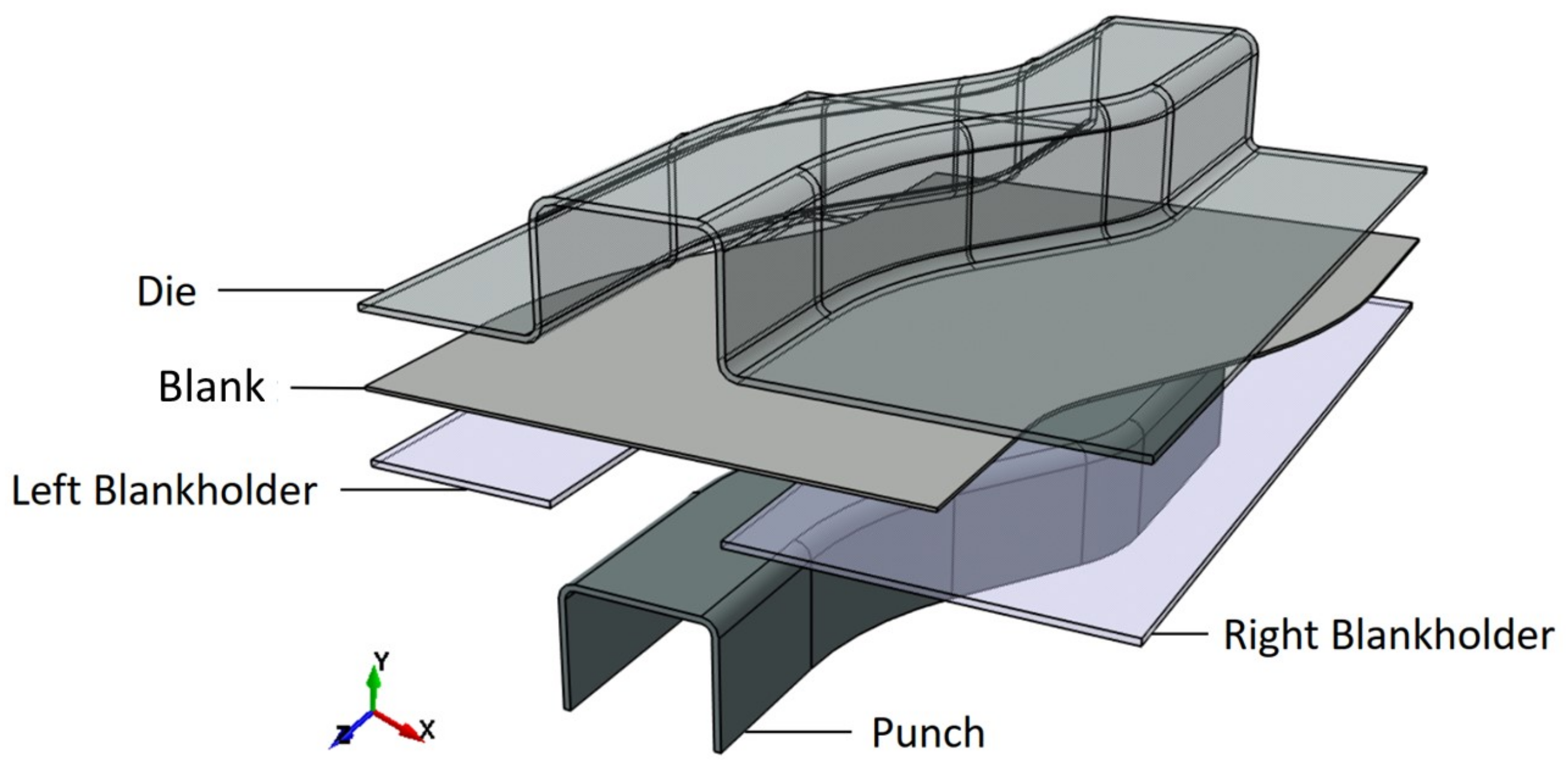
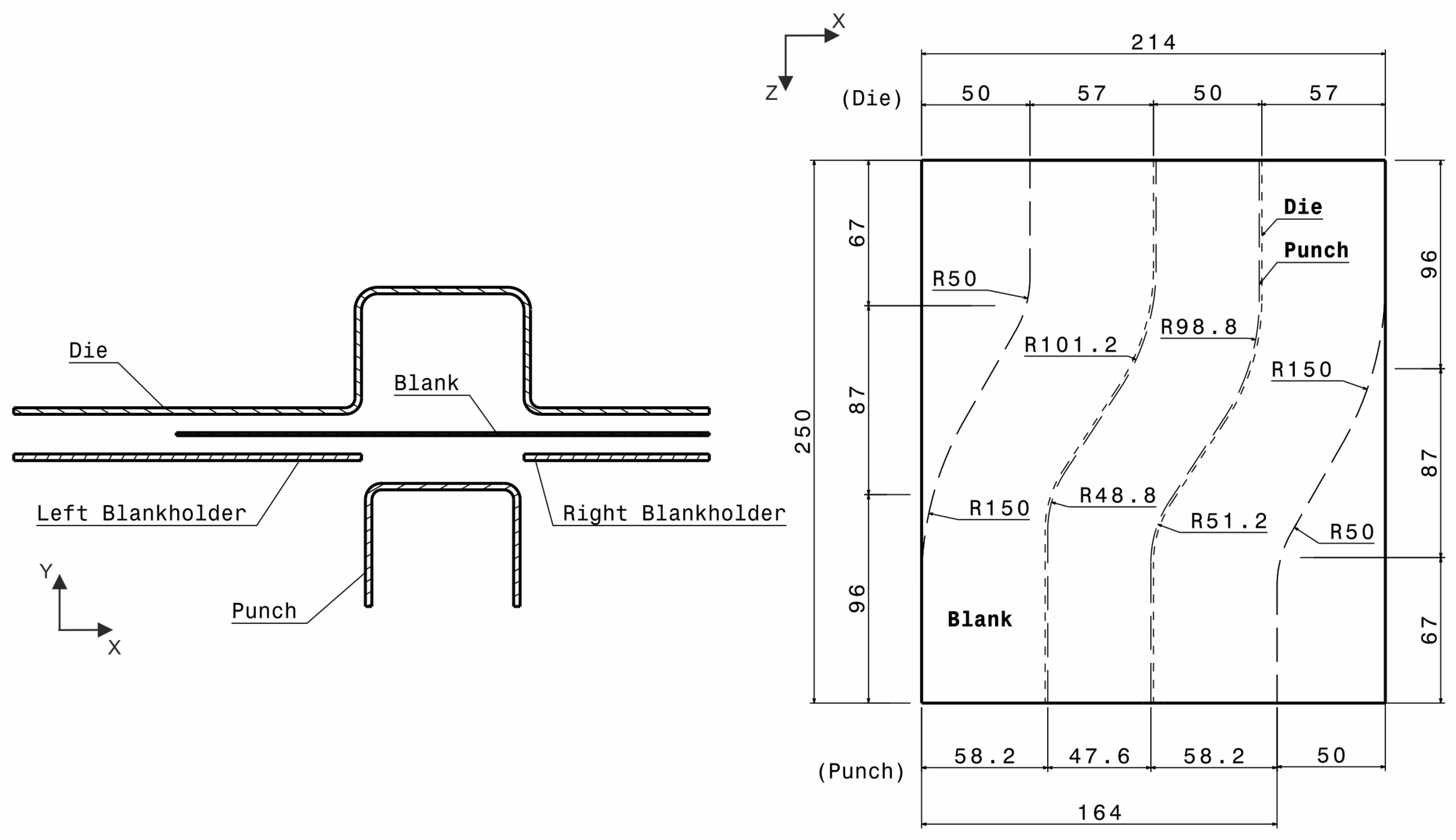
2. S-Rail Simulation
FEA Modelling
3. Analysis Results
3.1. Forming Process Evaluation
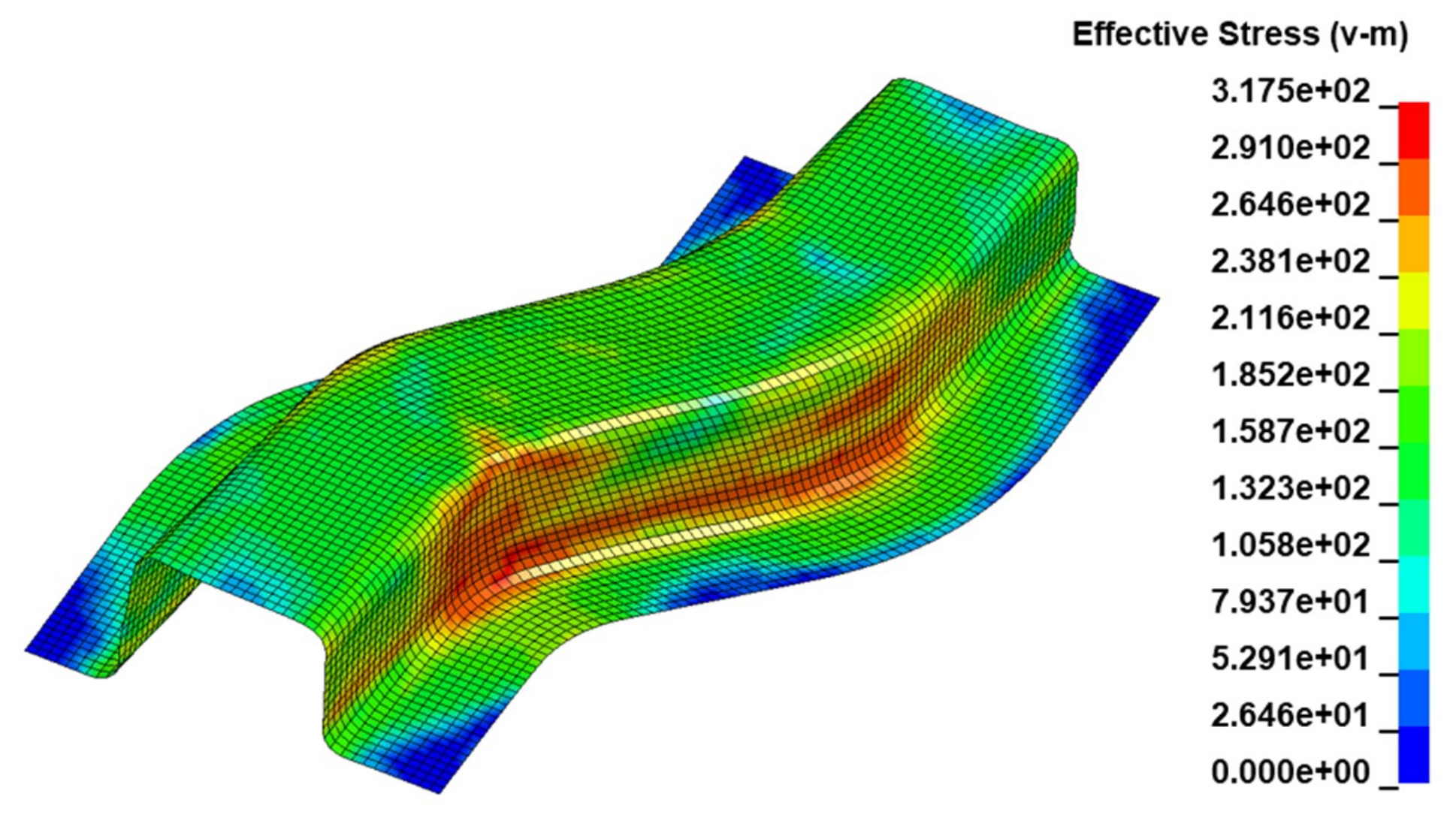
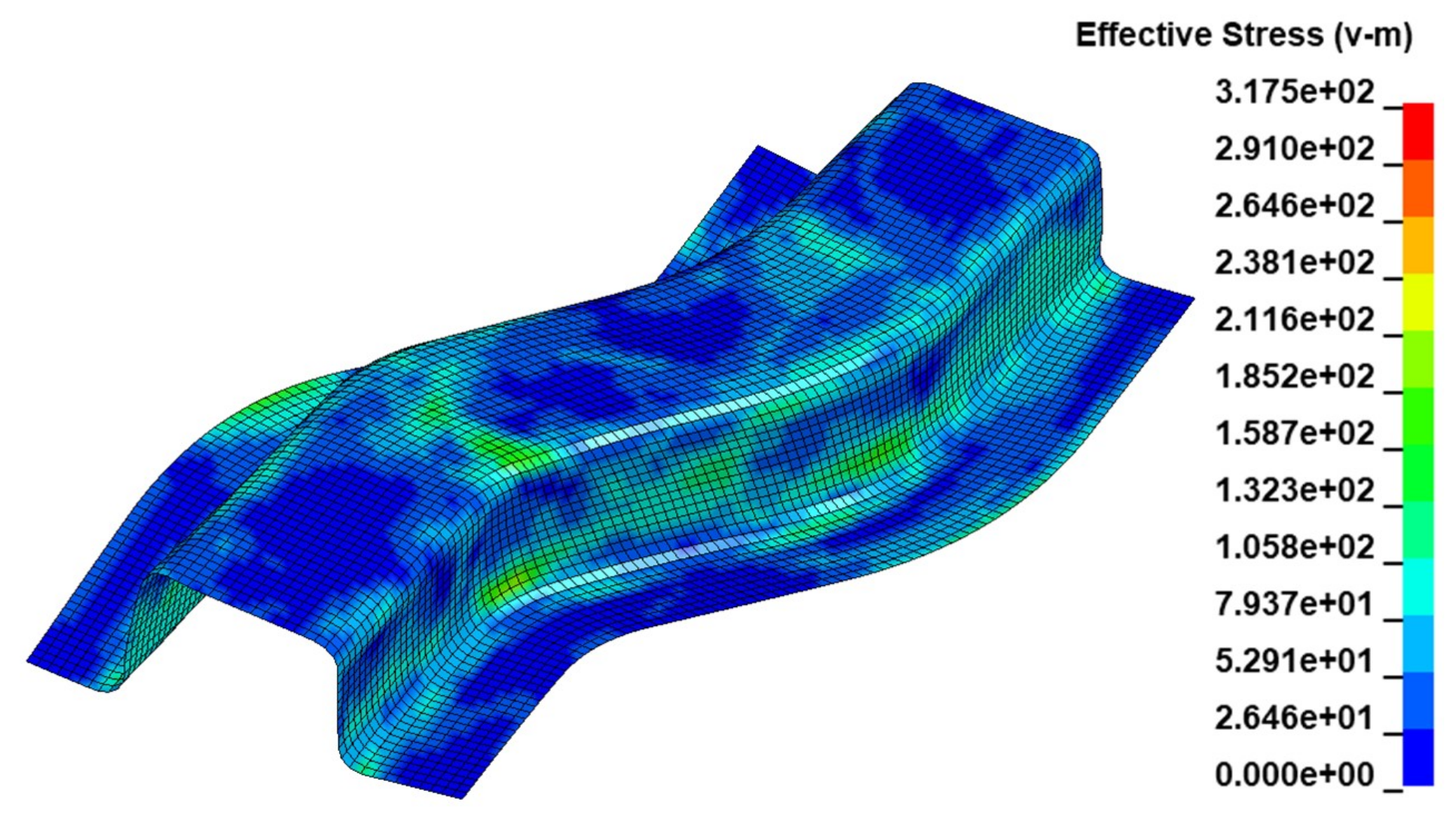
3.1.1. Effective (Von-Mises) Stress
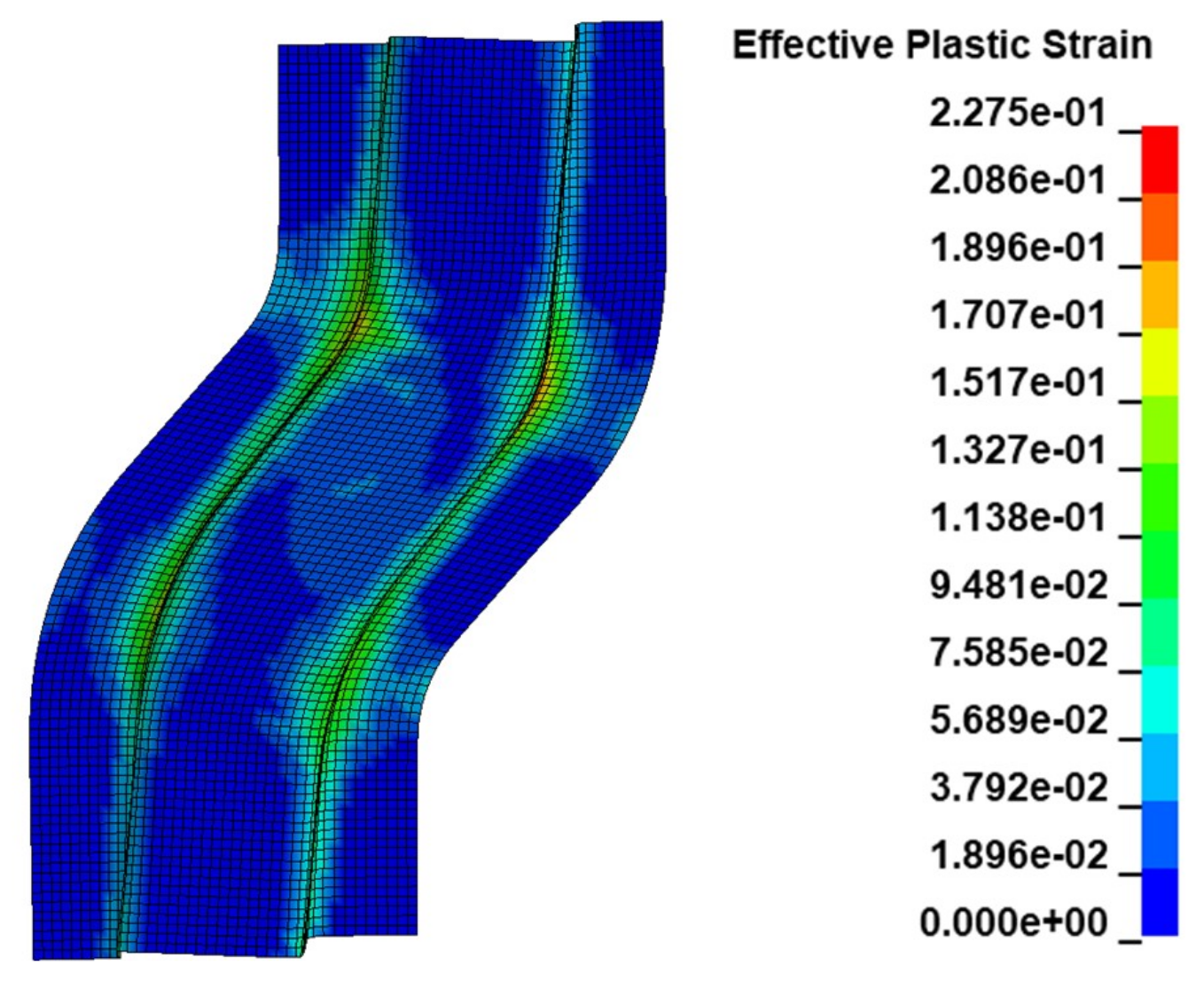
3.1.2. Effective Plastic Strain
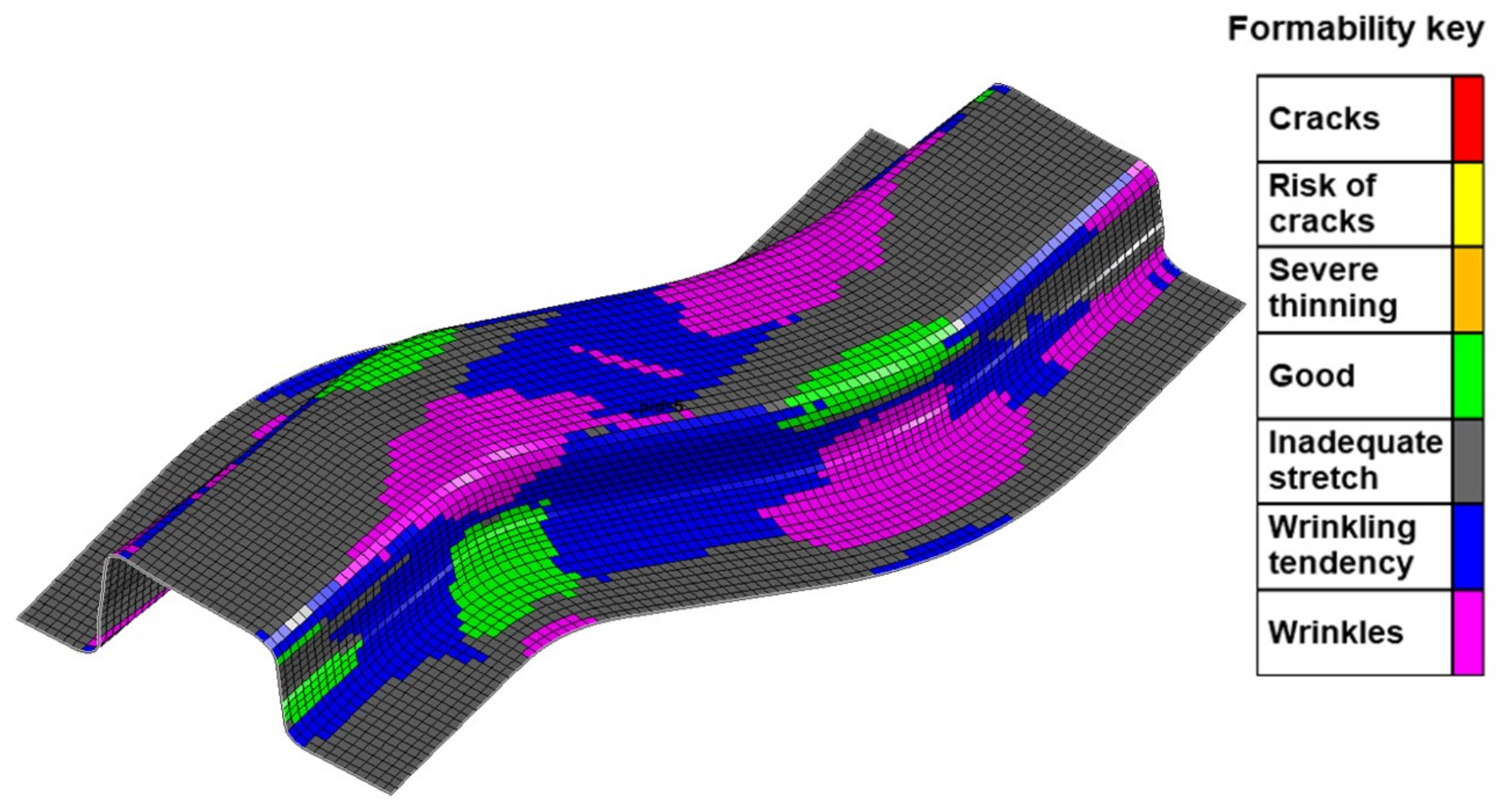
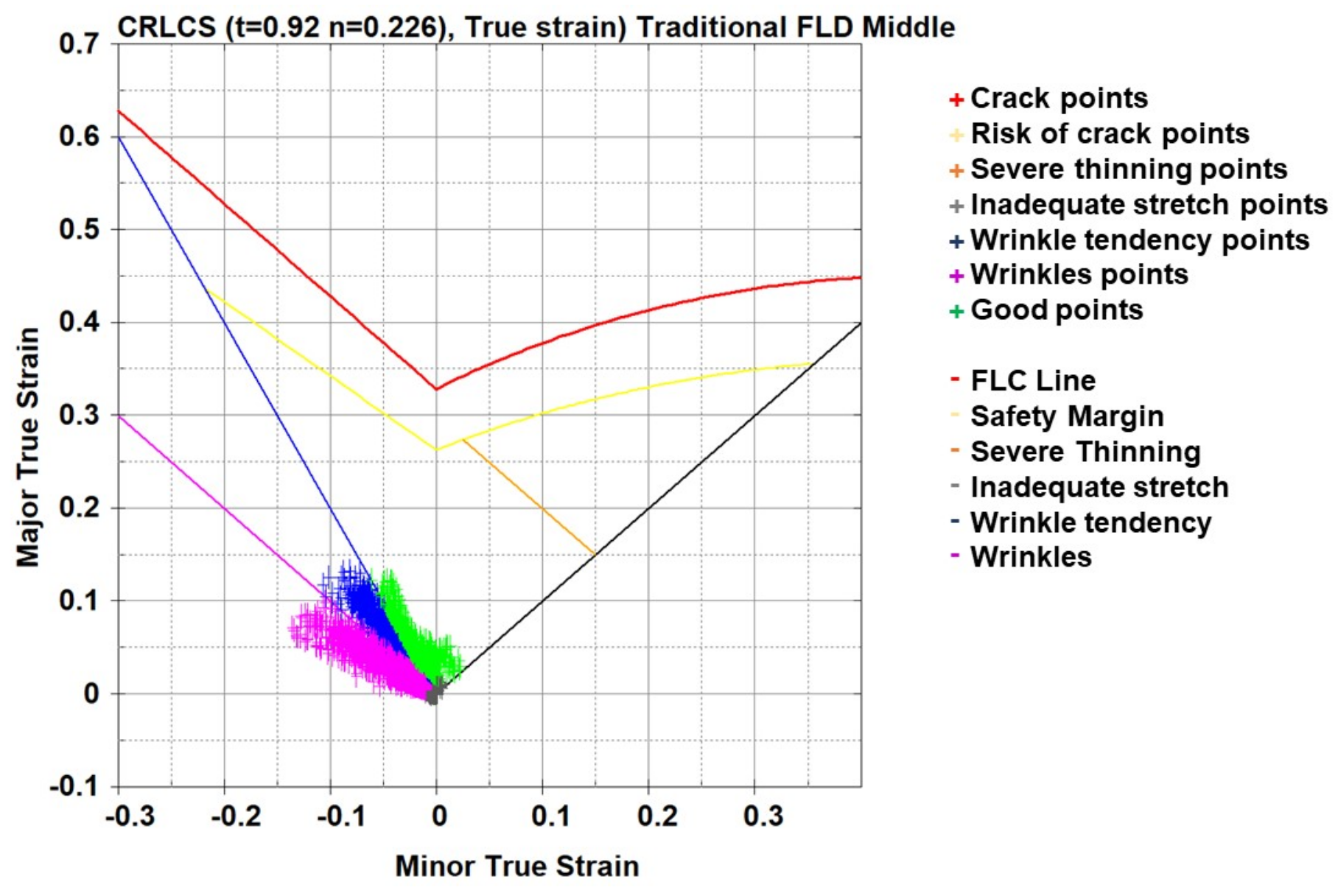
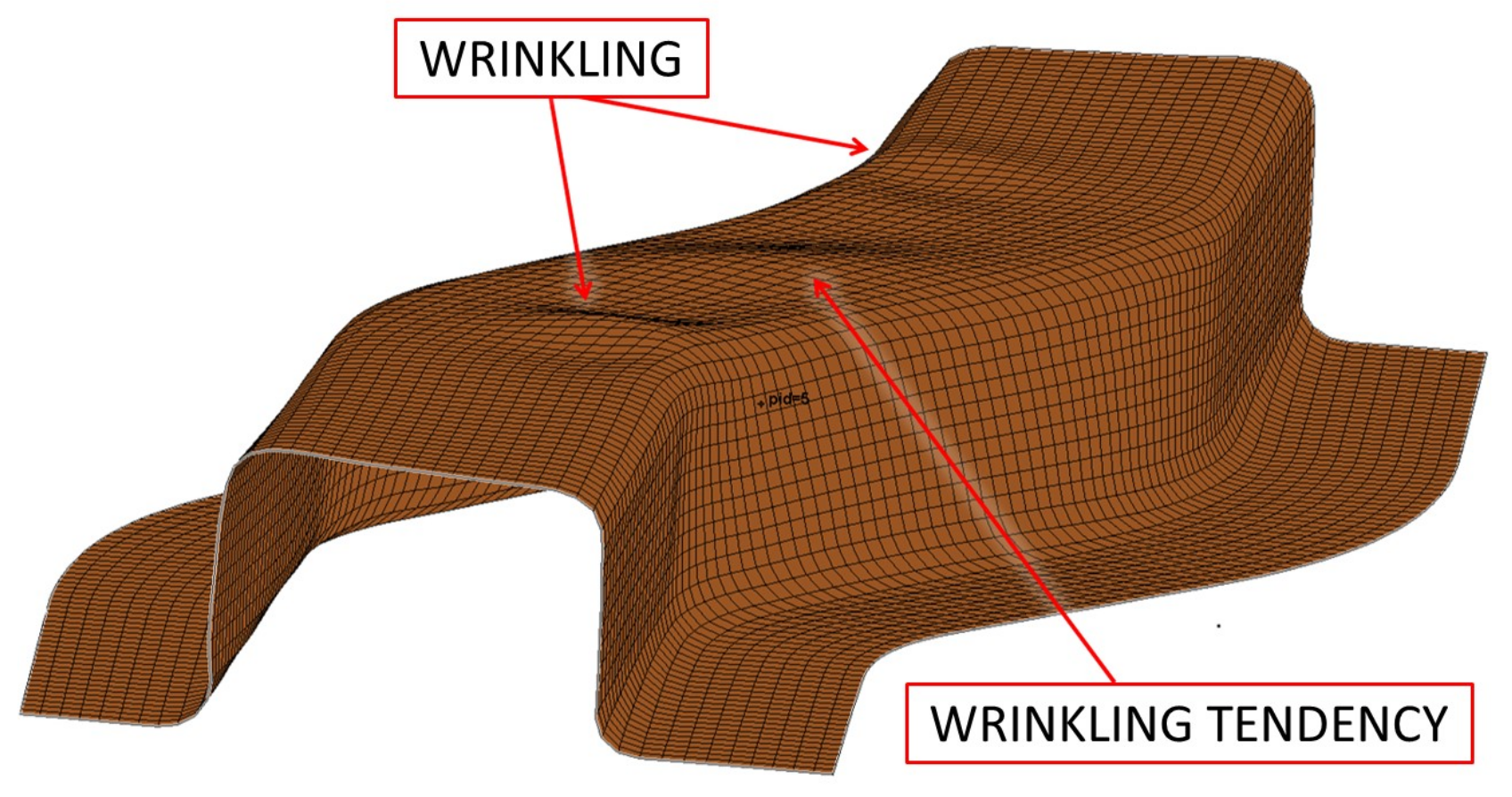
3.1.3. Material Failures Evaluation
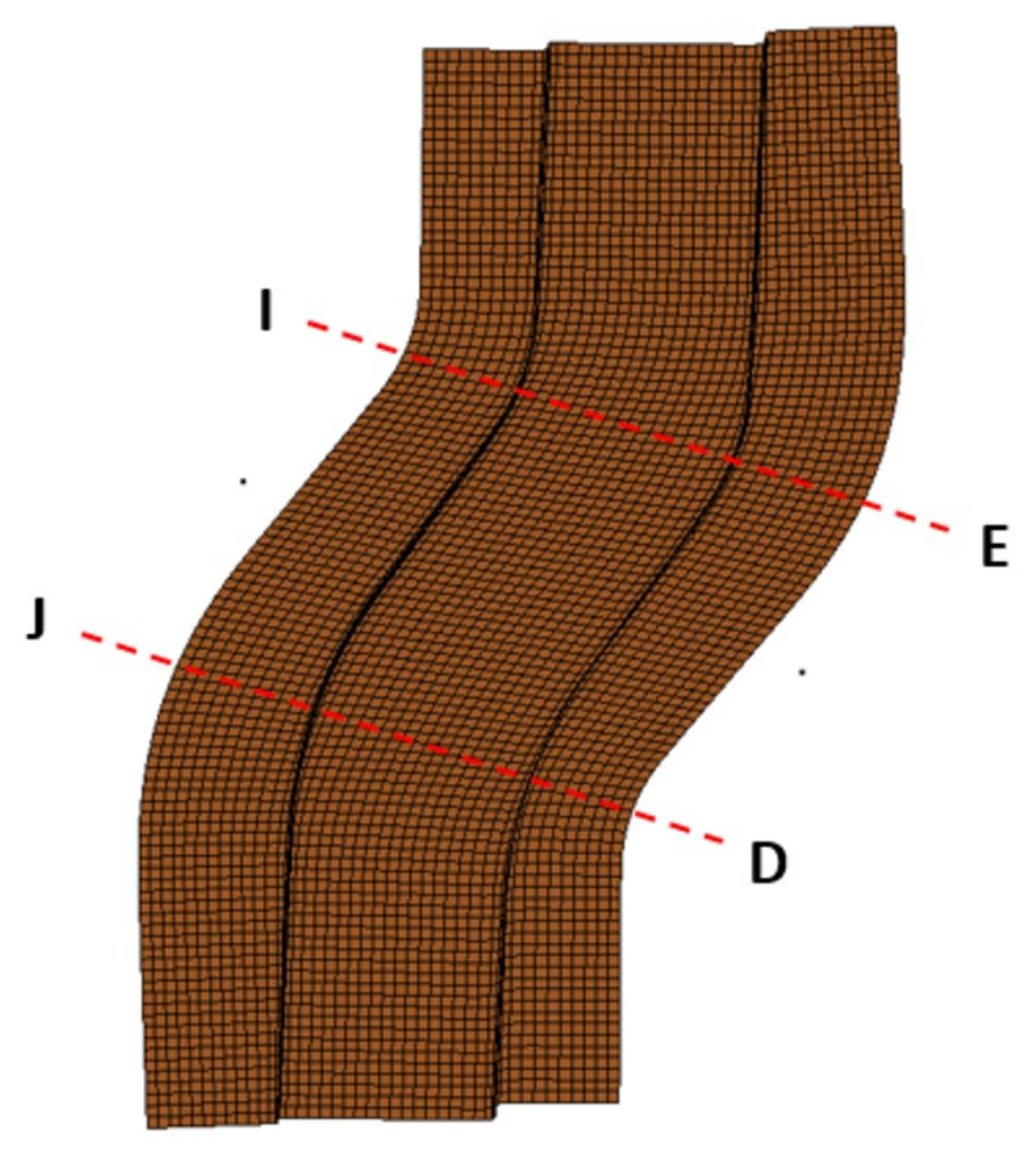
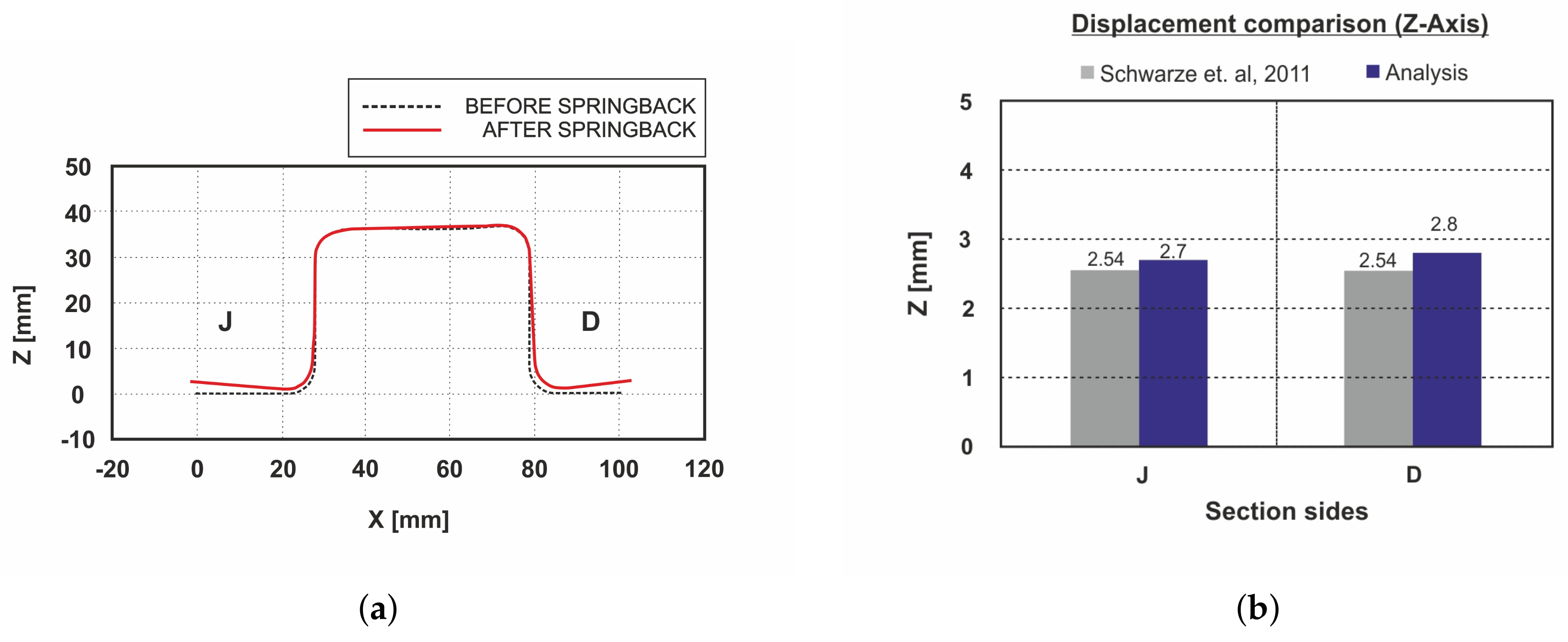
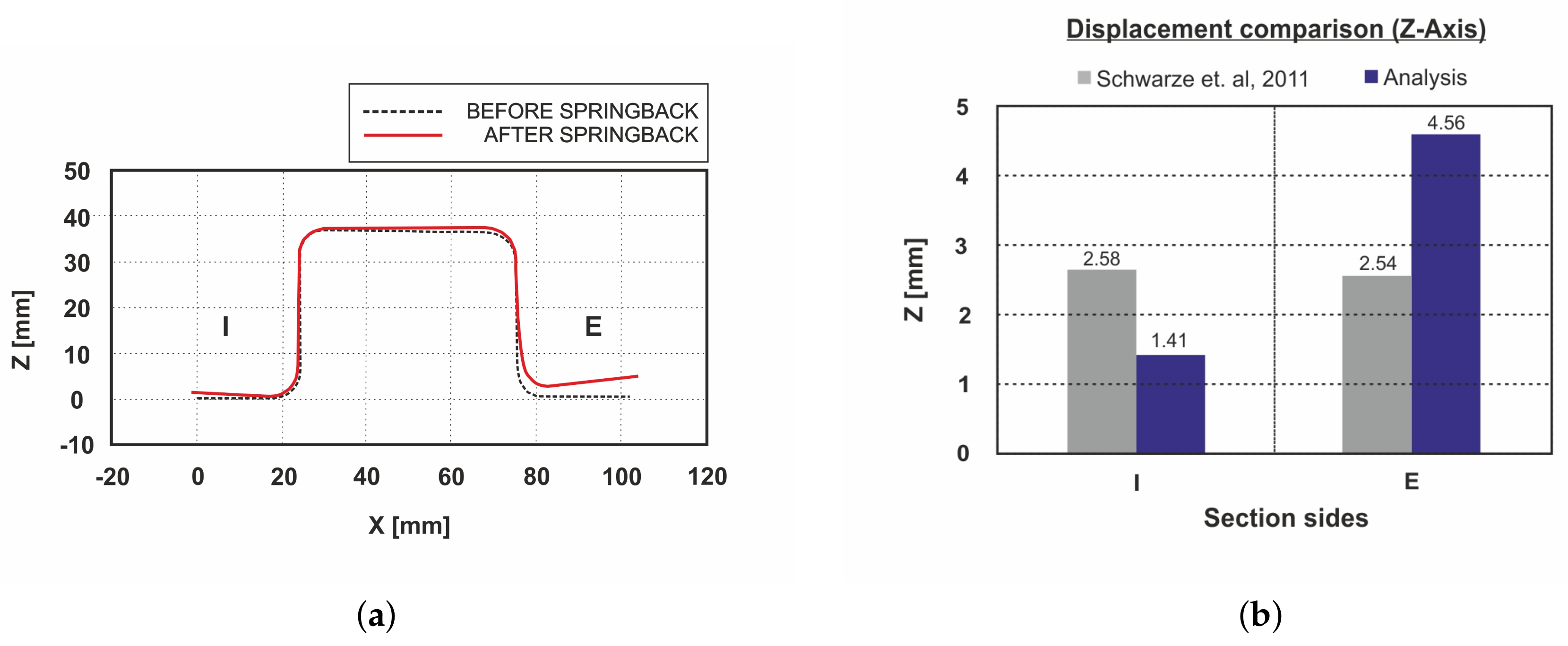
3.2. Springback Prediction
4. Springback Sensitivity Evaluation
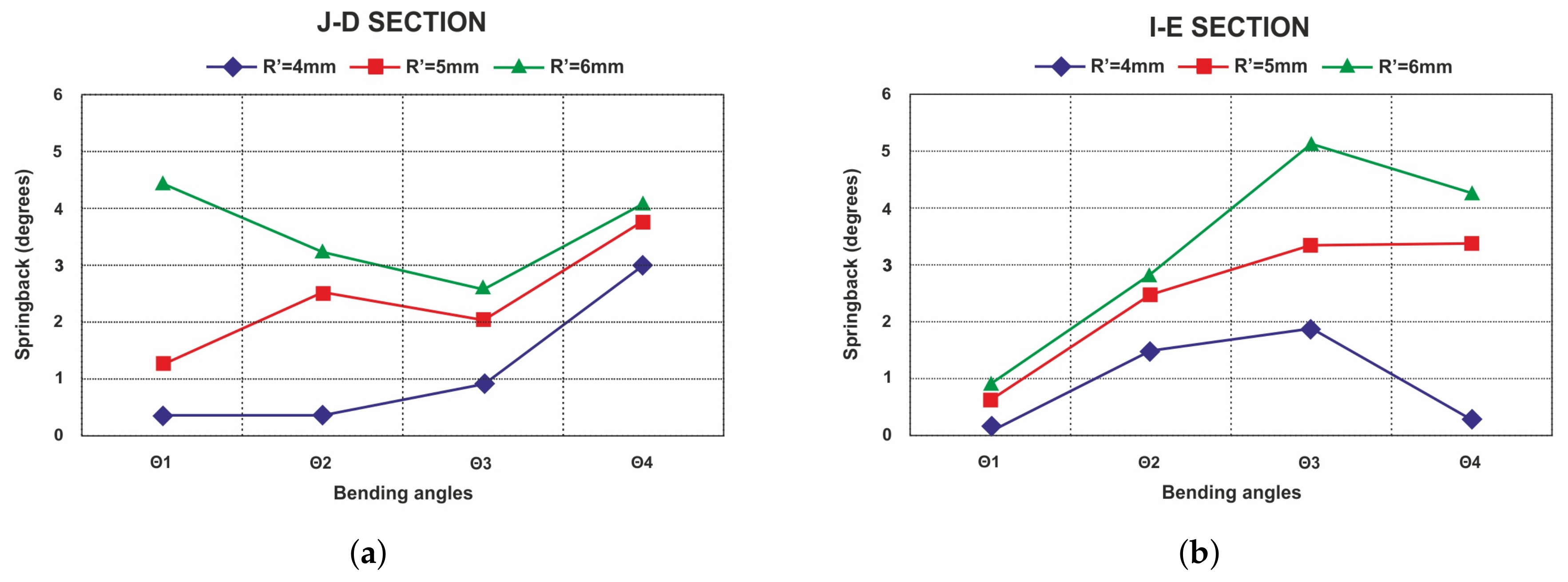
4.1. Effects of Tools Radius
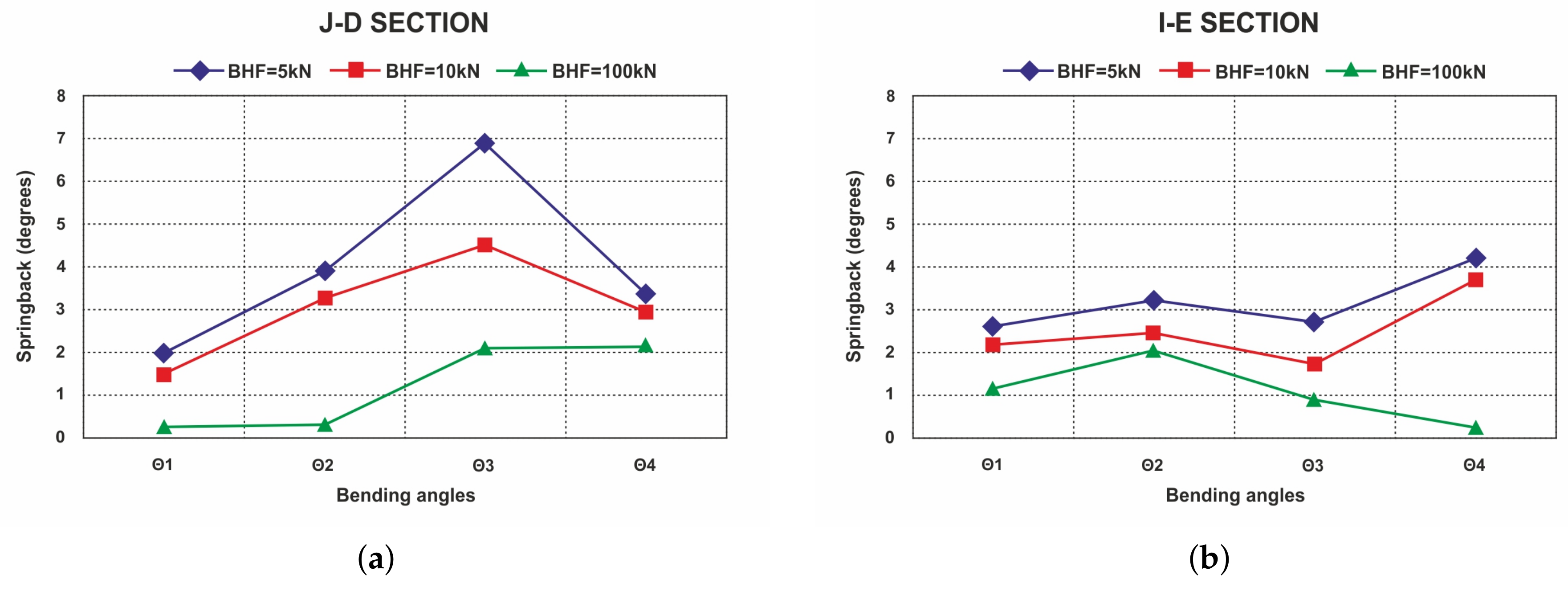
4.2. Effects of BHF
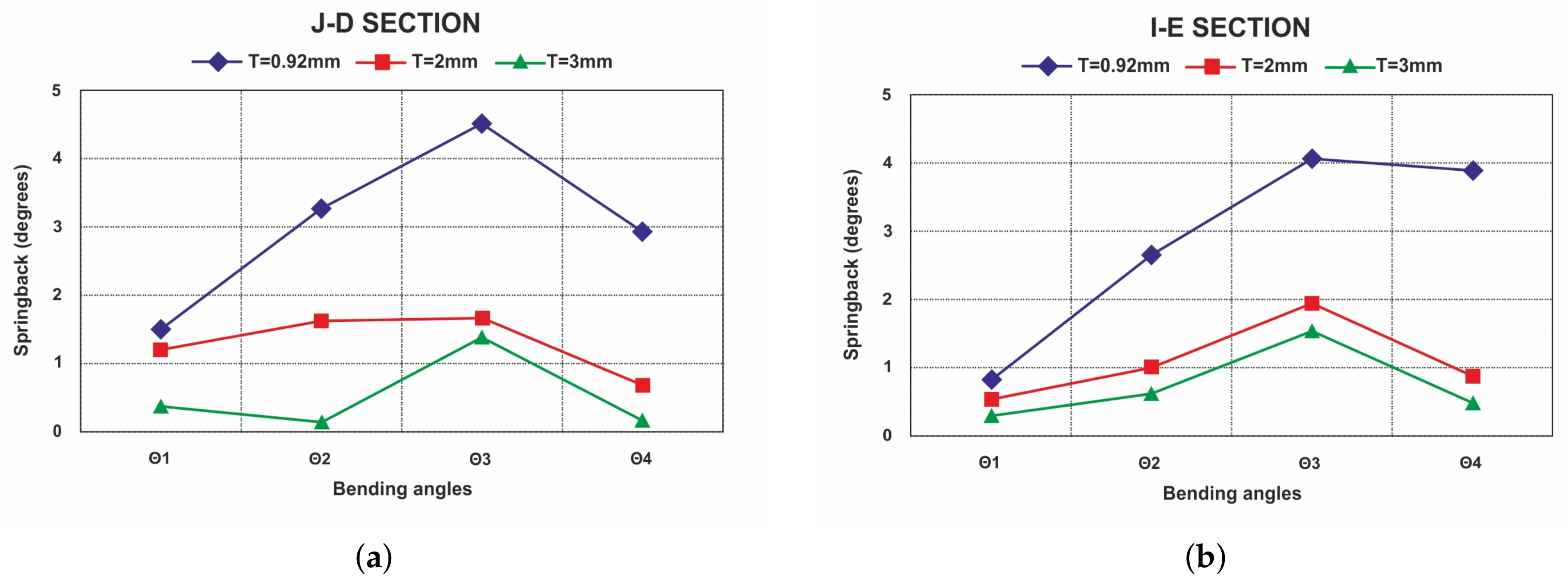
4.3. Effects of Sheet Thickness
5. The Artificial Neural Network Metamodel
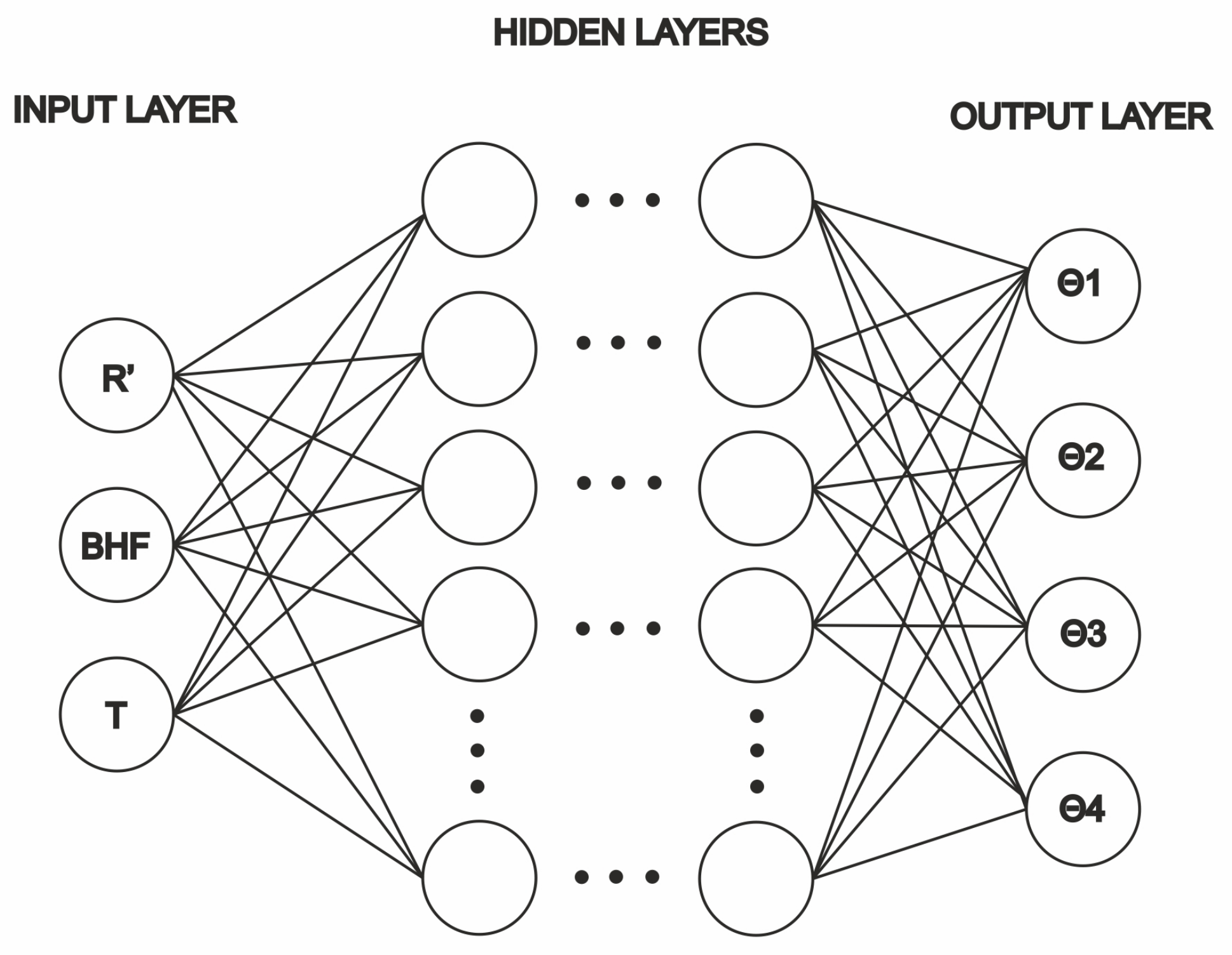
5.1. Artificial Neural Networks
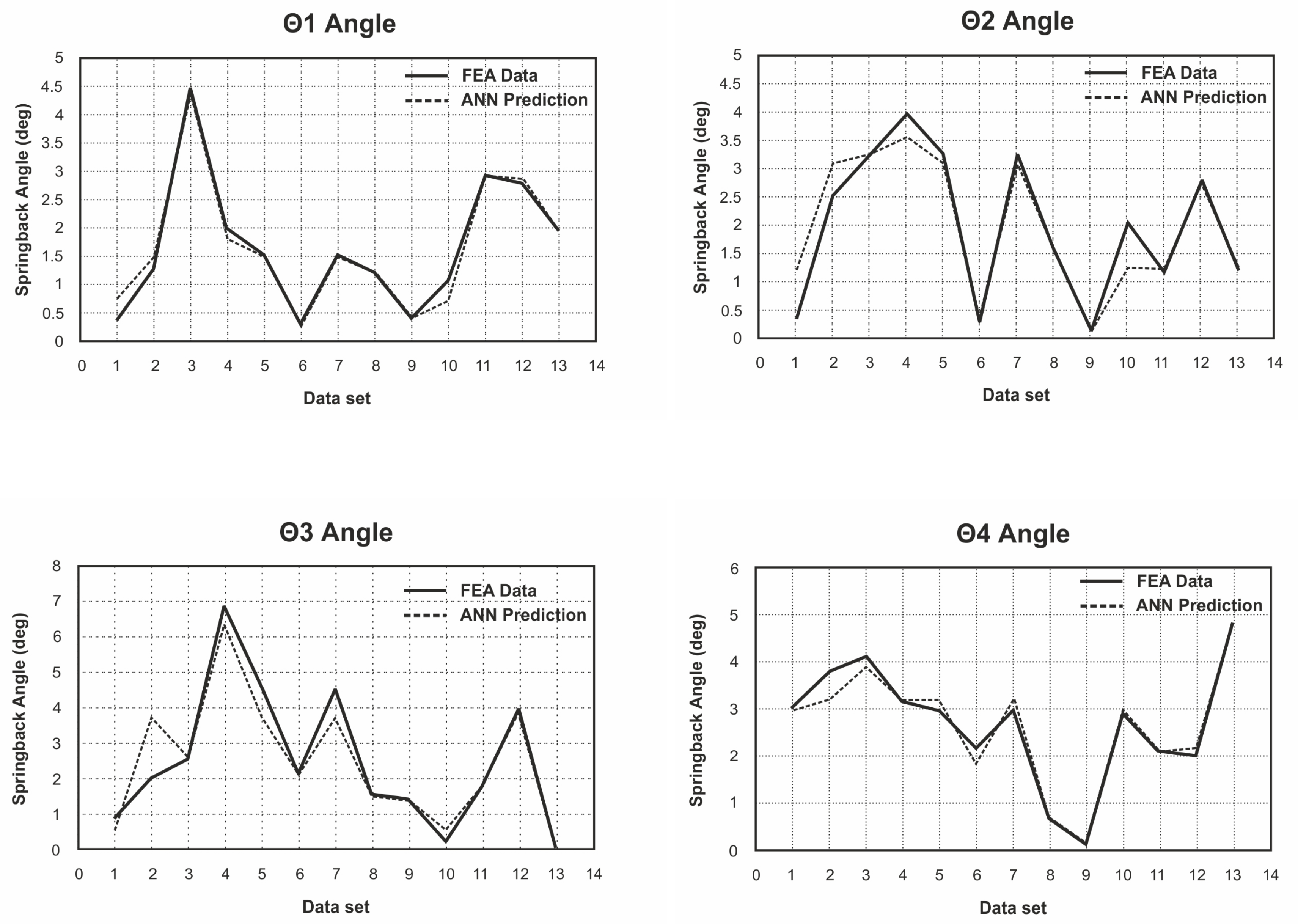
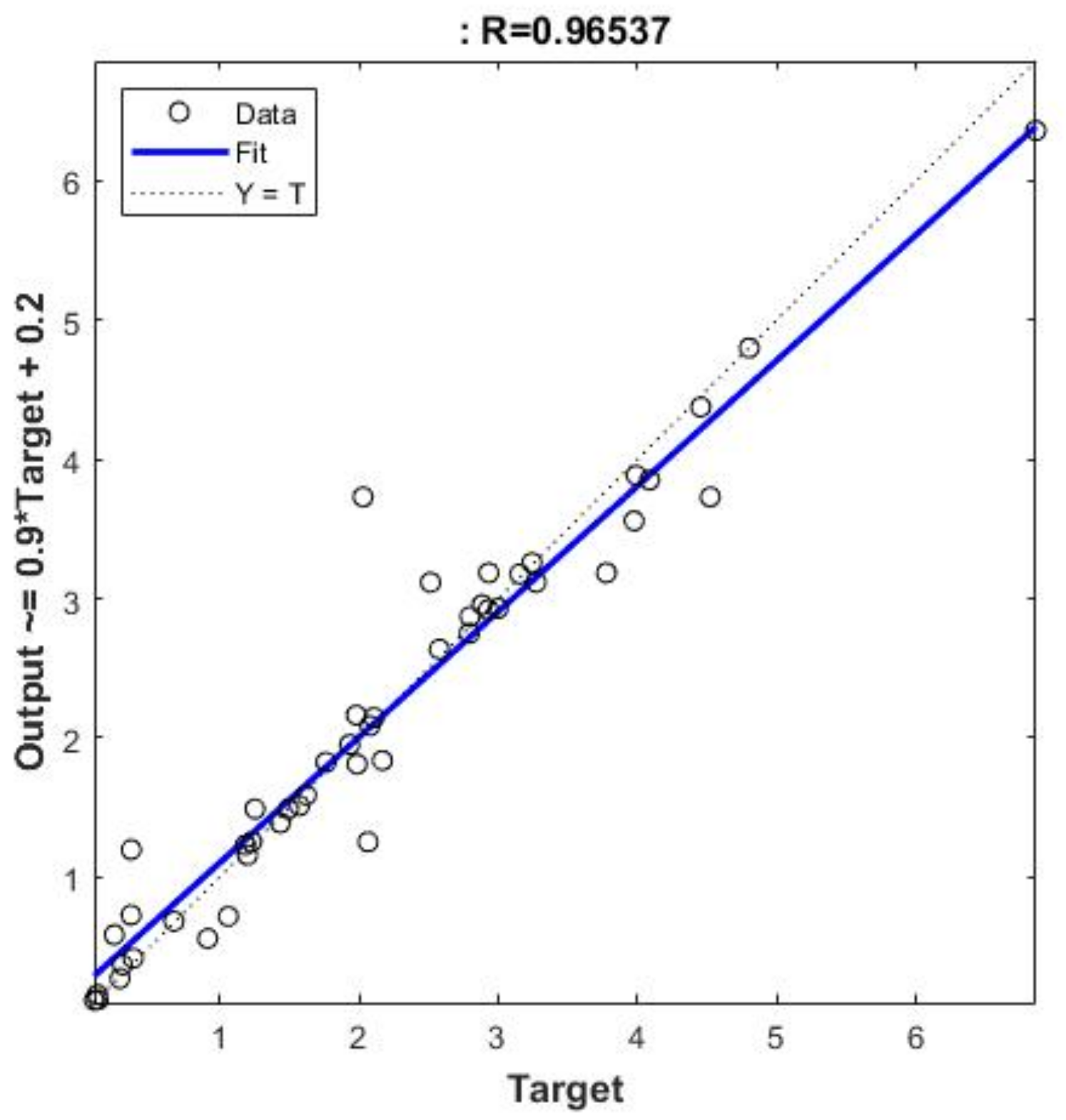
5.2. Springback Prediction with ANN
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| BHF | Blankholder force |
| CAD | Computer Aided Design |
| FEA | Finite Element Analysis |
| FEM | Finite Element Method |
| FLD | Forming Limit Diagram |
| MSE | Mean-Squared Error |
| MLP | Multilayer Perceptron |
| R | Regression coefficient |
| R’ | Tools radius |
| T | Sheet thickness |
| UTS | Ultimate Tensile Strength |
References
- Teti, R.; Engel, U. Numerical Simulation of Metal Sheet Plastic Deformation Processes through Finite Element Method. Ph.D. Thesis, University of Naples Federico II, Naples, Italy, 2006. [Google Scholar]
- Jadhav, S.; Schoiswohl, M.; Buchmayr, B. Applications of Finite Element Simulation in the Development of Advanced Sheet Metal Forming Processes. BHM Berg-und Hüttenmännische Monatshefte 2018, 163, 109–118. [Google Scholar] [CrossRef][Green Version]
- Kazan, R.; Fırat, M.; Tiryaki, A.E. Prediction of springback in wipe-bending process of sheet metal using neural network. Mater. Des. 2009, 30, 418–423. [Google Scholar] [CrossRef]
- Gawade, S.; Nandedkar, V. Investigation of springback in U shape bending with holes in component. Ind. Eng. J. 2018, 11. [Google Scholar] [CrossRef]
- Mulidrán, P.; Šiser, M.; Slota, J.; Spišák, E.; Sleziak, T. Numerical Prediction of Forming Car Body Parts with Emphasis on Springback. Metals 2018, 8, 435. [Google Scholar] [CrossRef]
- Panthi, S.K.; Hora, M.S.; Ahmed, M.; Materials, C.A. Artificial neural network and experimental study of effect of velocity on springback in straight flanging process. Indian J. Eng. Mater. Sci. 2016, 23, 159–164. [Google Scholar]
- Ruan, F.; Feng, Y.; Liu, W. Springback Prediction for Complex Sheet Metal Forming Parts Based on Genetic Neural Network. In Proceedings of the 2008 Second International Symposium on Intelligent Information Technology Application, Shanghai, China, 20–22 December 2008; pp. 157–161. [Google Scholar]
- Han, F.; Mo, J.H.; Qi, H.W.; Long, R.F.; Cui, X.H.; Li, Z.W. Springback prediction for incremental sheet forming based on FEM-PSONN technology. Trans. Nonferrous Met. Soc. China 2013, 23, 1061–1071. [Google Scholar] [CrossRef]
- Marretta, L.; Di Lorenzo, R. Influence of material properties variability on springback and thinning in sheet stamping processes: A stochastic analysis. Int. J. Adv. Manuf. Technol. 2010, 51, 117–134. [Google Scholar] [CrossRef]
- Prates, P.A.; Adaixo, A.S.; Oliveira, M.C.; Fernandes, J.V. Numerical study on the effect of mechanical properties variability in sheet metal forming processes. Int. J. Adv. Manuf. Technol. 2018, 96, 561–580. [Google Scholar] [CrossRef]
- Dib, M.; Ribeiro, B.; Prates, P. Model Prediction of Defects in Sheet Metal Forming Processes. In Engineering Applications of Neural Networks; Pimenidis, E., Jayne, C., Eds.; Springer: Cham, Switzerland, 2018; Volume 893, pp. 169–180. [Google Scholar]
- Dib, M.A.; Oliveira, N.J.; Marques, A.E.; Oliveira, M.C.; Fernandes, J.V.; Ribeiro, B.M.; Prates, P.A. Single and ensemble classifiers for defect prediction in sheet metal forming under variability. Neural Comput. Appl. 2019. [Google Scholar] [CrossRef]
- Schwarze, M.; Vladimirov, I.N.; Reese, S. Sheet metal forming and springback simulation by means of a new reduced integration solid-shell finite element technology. Comput. Methods Appl. Mech. Eng. 2011, 200, 454–476. [Google Scholar] [CrossRef]
- Alghtani, A.H. Analysis and Optimization of Springback in Sheet Metal Forming. Ph.D. Thesis, The University of Leeds, West Yorkshire, UK, 2015. [Google Scholar]
- Papeleux, L.; Ponthot, J.P. Finite element simulation of springback in sheet metal forming. J. Mater. Process. Technol. 2002, 125, 785–791. [Google Scholar] [CrossRef]
- Choi, J.; Lee, J.; Bae, G.; Barlat, F.; Lee, M.G. Evaluation of Springback for DP980 S Rail Using Anisotropic Hardening Models. JOM 2016, 68, 1850–1857. [Google Scholar] [CrossRef]
- Chirita, B.; Brabie, G. Control of Springback Intensity in U-Bending through variation of Blankholder force. In Proceedings of the 9th International Research/Expert Conference Trends in the Development of Machinery and Associated Technology, Antalya, Turkey, 26–30 September 2005; pp. 175–178. [Google Scholar]
- Jiang, K.; Hou, Y.; Lin, J.; Min, J. A springback energy based method of springback prediction for complex automotive parts. IOP Conf. Ser. Mater. Sci. Eng. 2018, 418, 012104. [Google Scholar] [CrossRef]
- Bozdemir, M.; Golcu, M. Artificial Neural Network Analysis of Springback in V Bending. J. Appl. Sci. 2008, 8, 3038–3043. [Google Scholar] [CrossRef][Green Version]
- Okut, H. Bayesian Regularized Neural Networks for Small n Big p Data. In Artificial Neural Networks. Methods and Applications; Rosa, J.L.G., Ed.; Intech Open Book: London, UK, 2016; pp. 16–48. ISBN 978-953-51-2705-5. [Google Scholar] [CrossRef]


| Material Properties | Value |
|---|---|
| Density [g/cm] | 2.71 |
| Young Modulus [N/mm] | 69,000 |
| Poisson ratio | 0.33 |
| Initial yield stress, [N/mm] | 161 |
| Max change in size of elastic range, Q [N/mm] | 207 |
| Rate of change of elastic range size, | 9.74 |
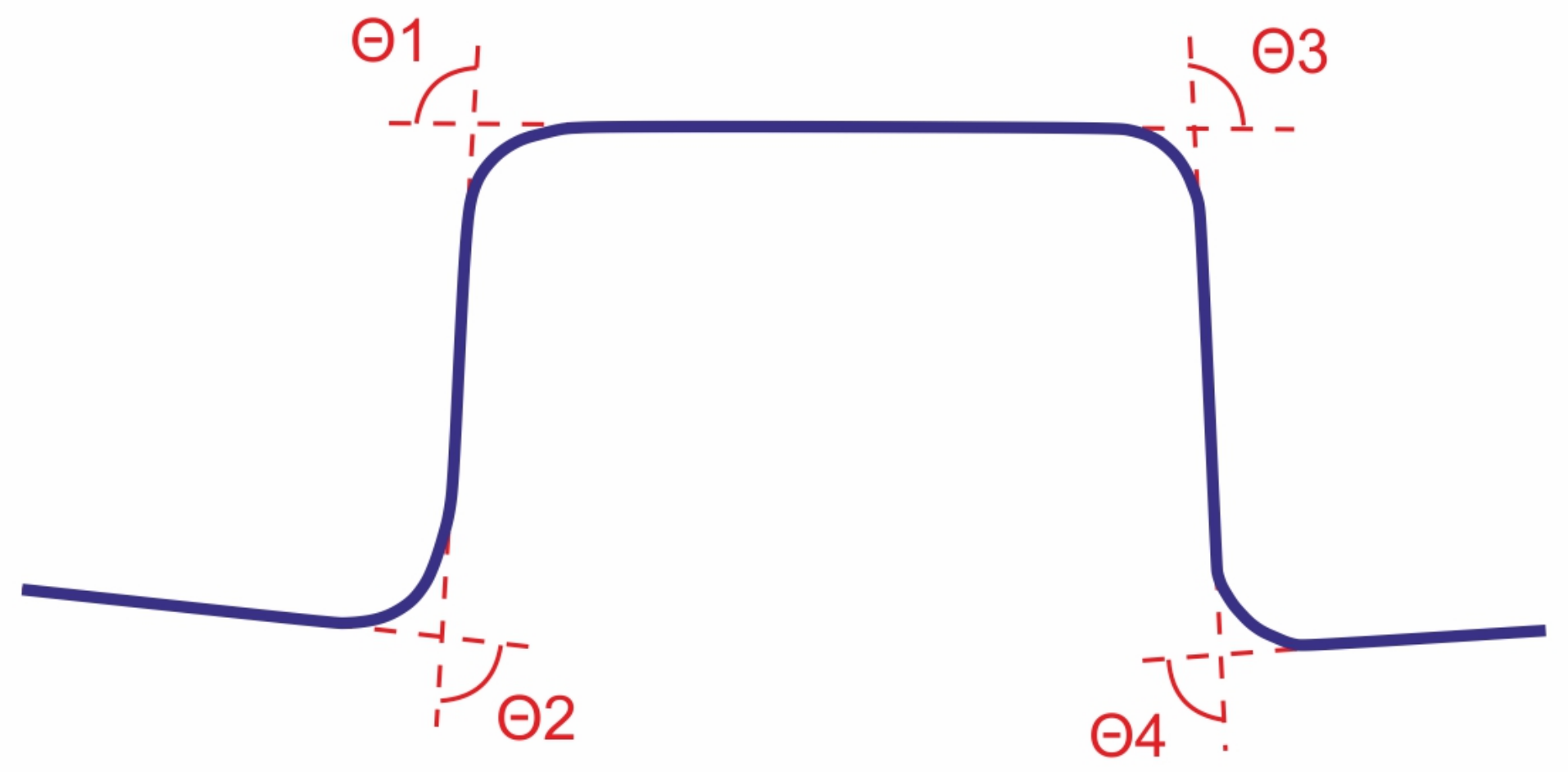
| No. | Tool Radius | Blankholder Force | Sheet Thickness | Angle | Angle | Angle | Angle |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 10 | 0.92 | 0.36 | 0.36 | 0.91 | 3.01 |
| 2 | 5 | 20 | 0.92 | 1.48 | 2.61 | 2.18 | 3.85 |
| 3 | 6 | 10 | 0.92 | 4.45 | 3.24 | 2.57 | 4.08 |
| 4 | 5 | 5 | 0.92 | 1.98 | 3.97 | 6.86 | 3.15 |
| 5 | 5 | 50 | 0.92 | 1.58 | 3.38 | 4.46 | 2.87 |
| 6 | 5 | 100 | 0.92 | 0.28 | 0.30 | 2.10 | 2.16 |
| 7 | 5 | 10 | 0.92 | 1.49 | 3.27 | 4.52 | 2.93 |
| 8 | 5 | 10 | 2 | 1.19 | 1.62 | 1.57 | 0.67 |
| 9 | 5 | 10 | 3 | 0.37 | 0.12 | 1.43 | 0.12 |
| 10 | 4 | 5 | 0.92 | 1.06 | 2.06 | 0.24 | 2.88 |
| 11 | 4 | 100 | 0.92 | 2.92 | 1.18 | 1.76 | 2.07 |
| 12 | 6 | 15 | 0.92 | 2.79 | 2.79 | 3.99 | 1.98 |
| 13 | 6 | 100 | 0.92 | 1.93 | 1.23 | 0.09 | 4.80 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spathopoulos, S.C.; Stavroulakis, G.E. Springback Prediction in Sheet Metal Forming, Based on Finite Element Analysis and Artificial Neural Network Approach. Appl. Mech. 2020, 1, 97-110. https://doi.org/10.3390/applmech1020007
Spathopoulos SC, Stavroulakis GE. Springback Prediction in Sheet Metal Forming, Based on Finite Element Analysis and Artificial Neural Network Approach. Applied Mechanics. 2020; 1(2):97-110. https://doi.org/10.3390/applmech1020007
Chicago/Turabian StyleSpathopoulos, Stefanos C., and Georgios E. Stavroulakis. 2020. "Springback Prediction in Sheet Metal Forming, Based on Finite Element Analysis and Artificial Neural Network Approach" Applied Mechanics 1, no. 2: 97-110. https://doi.org/10.3390/applmech1020007
APA StyleSpathopoulos, S. C., & Stavroulakis, G. E. (2020). Springback Prediction in Sheet Metal Forming, Based on Finite Element Analysis and Artificial Neural Network Approach. Applied Mechanics, 1(2), 97-110. https://doi.org/10.3390/applmech1020007






