Spherical Cavity Expansion Approach for the Study of Rigid-Penetrator’s Impact Problems
Abstract
:1. Introduction
2. Literature Review
- Spherical Cavity Expansion (SCE): Starting with a small hollow sphere in the body of an infinite block of ductile material to determine the pressure that will enlarge the spherical hole indefinitely.
- Cylindrical Cavity Expansion (CCE): Starting with a cylindrical hole of infinite length to find the pressure that will enlarge the hole indefinitely.
Summary of the Literature Review
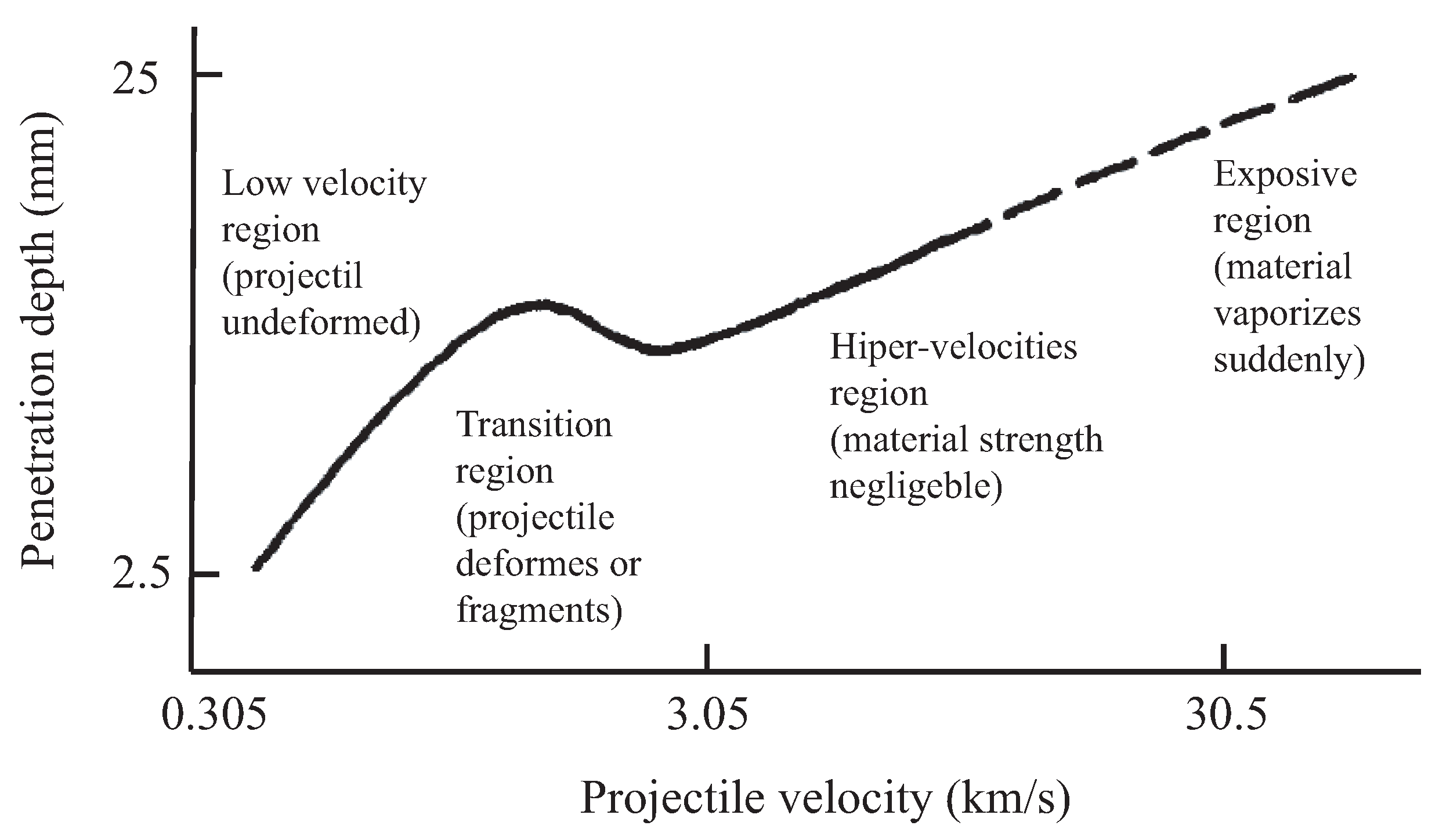
- Penetration of undeformed projectiles into soft targets is valid at low and medium penetration velocities.
- Cavity pressure on the target can be calculated using the spherical cavity expansion theory.
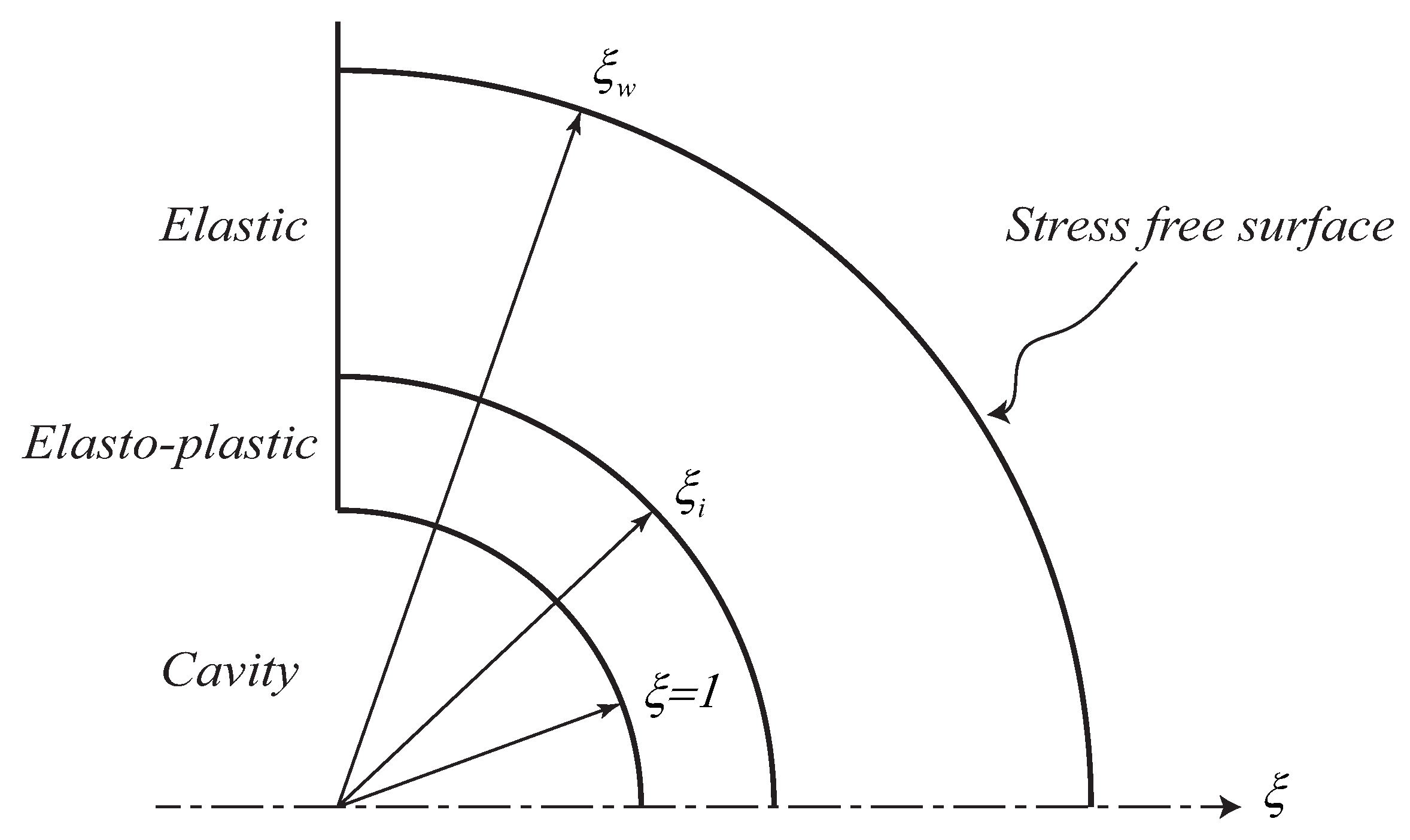
3. Spherical Cavity Expansion Formulation
3.1. Conservation Laws in Spherical Coordinates
3.2. Material Response
3.3. Different Cases of the SCE Theory
3.3.1. Compressible-Dynamical Solution
3.3.2. Incompressible-Dynamical Solution
4. Formulation of the Engineering Model of Penetration
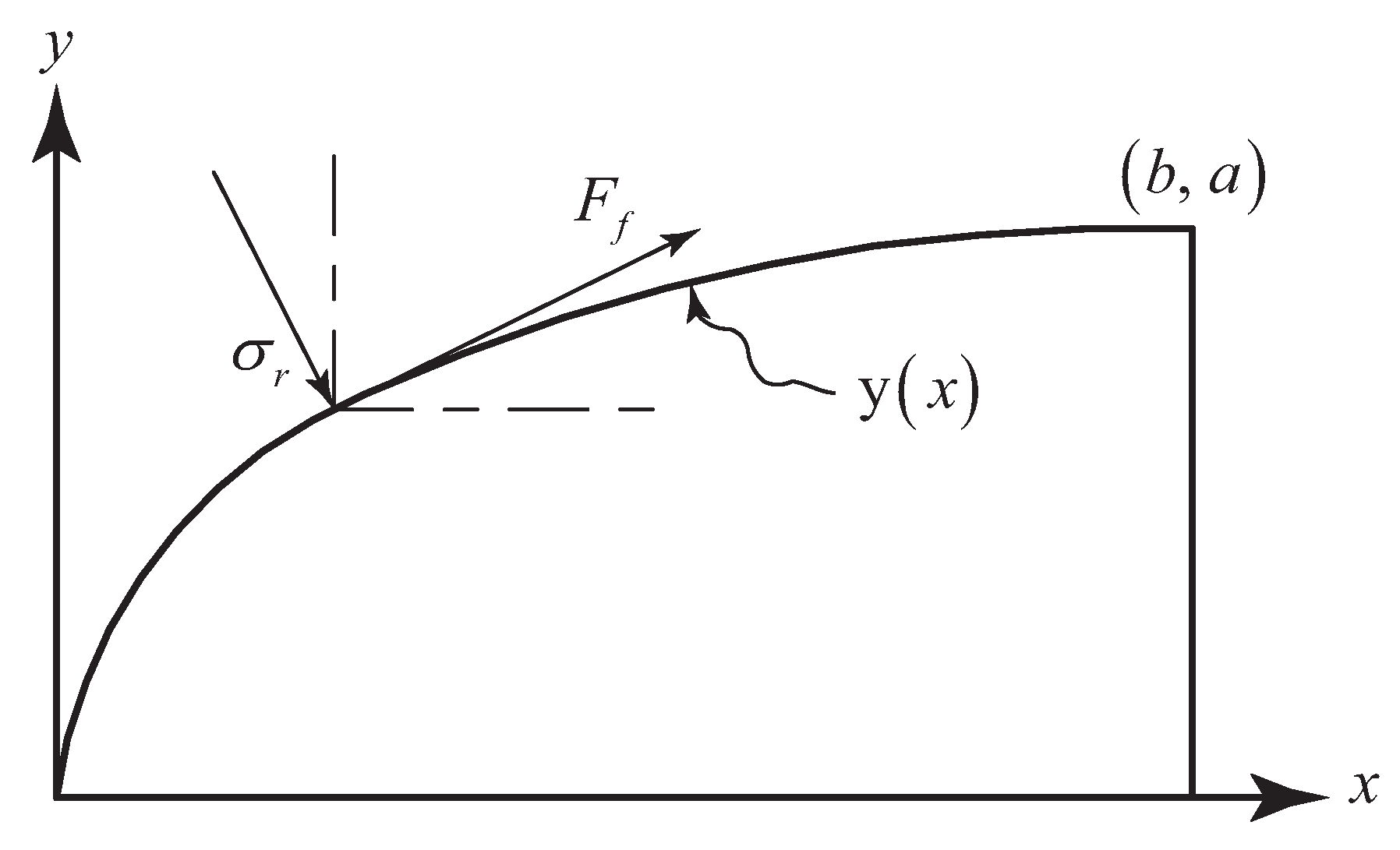
4.1. Projectile Deceleration
4.2. SCE Theory in Penetration Problems
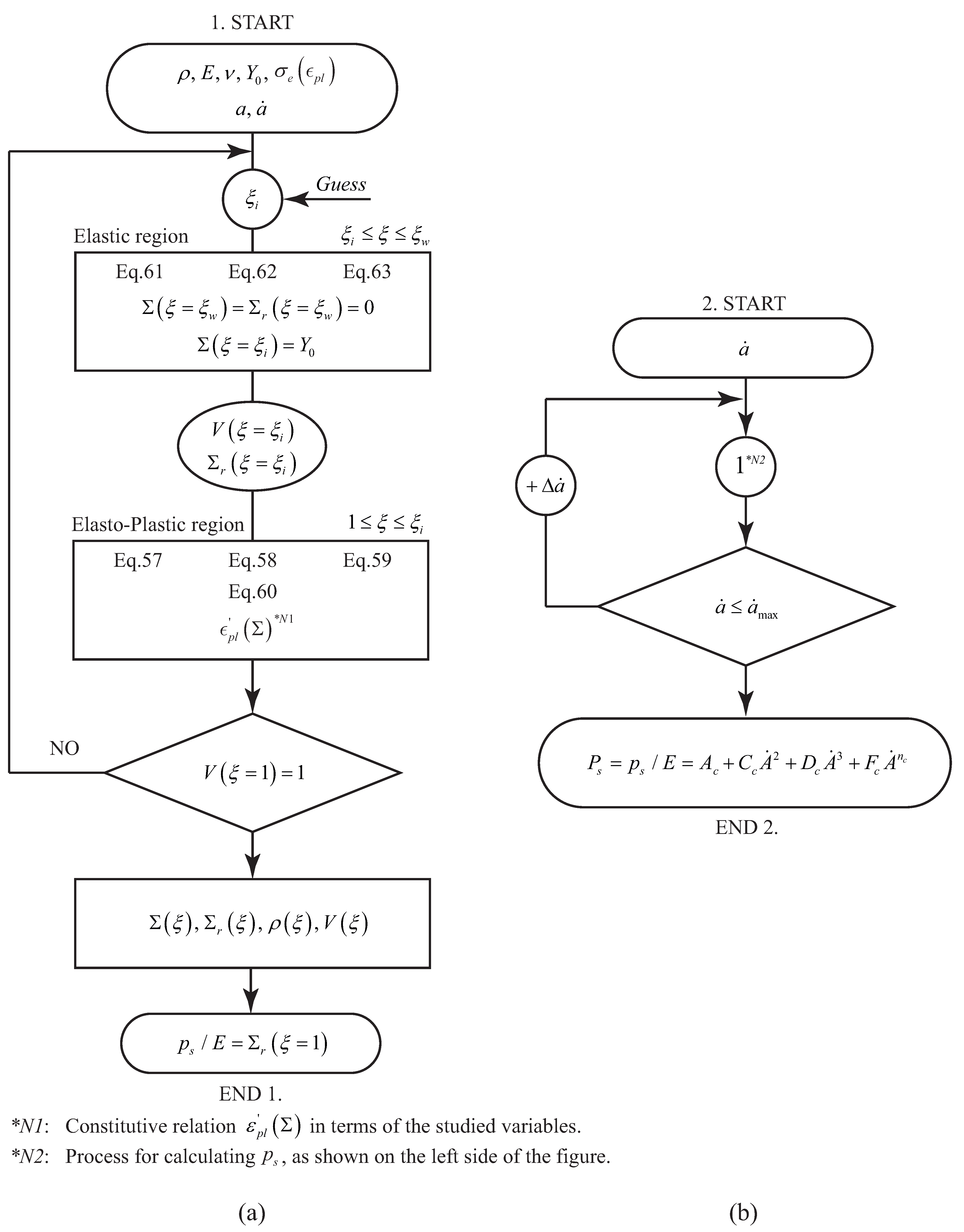
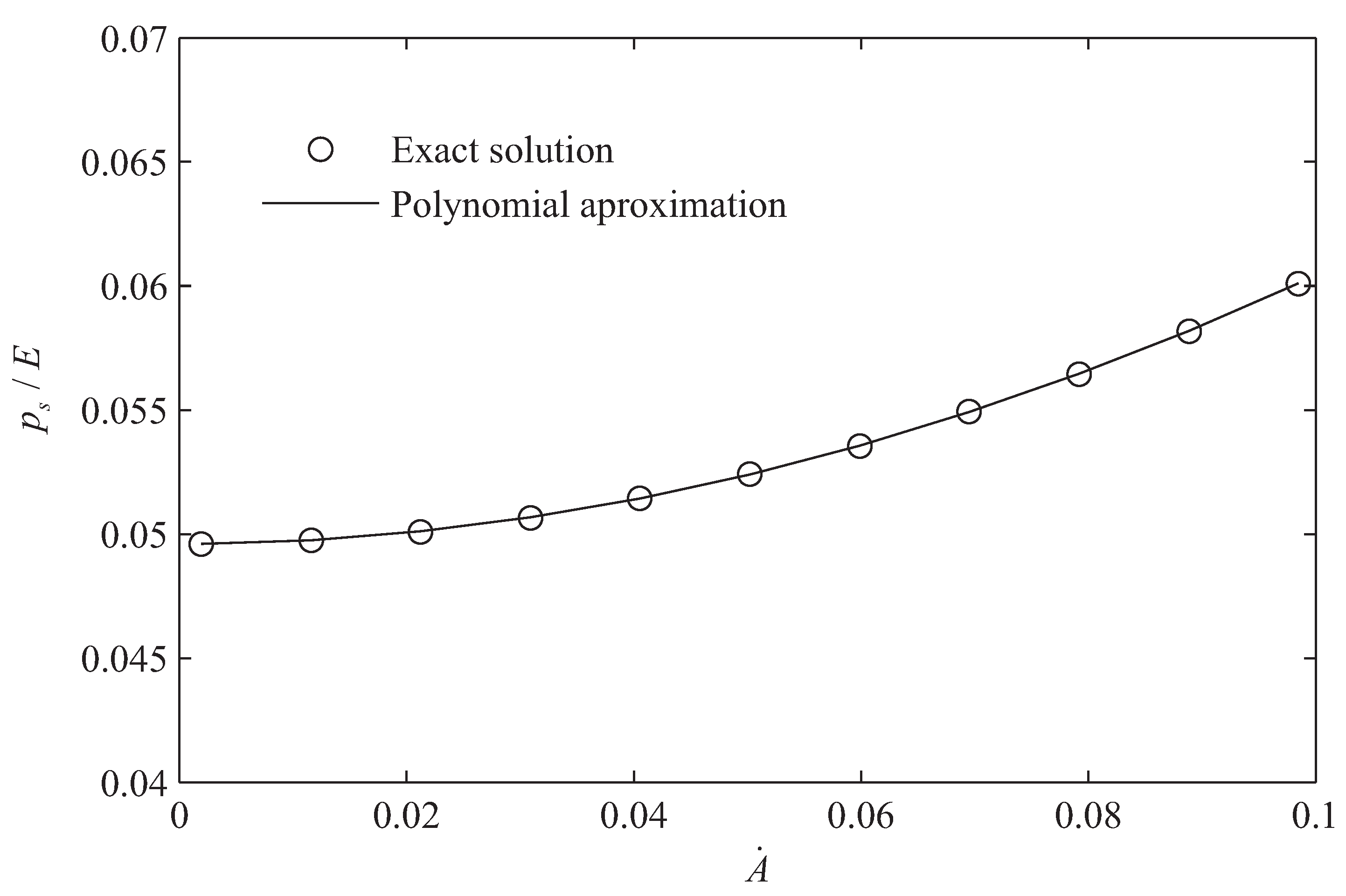
4.3. Model Solution
5. Results and Discussion
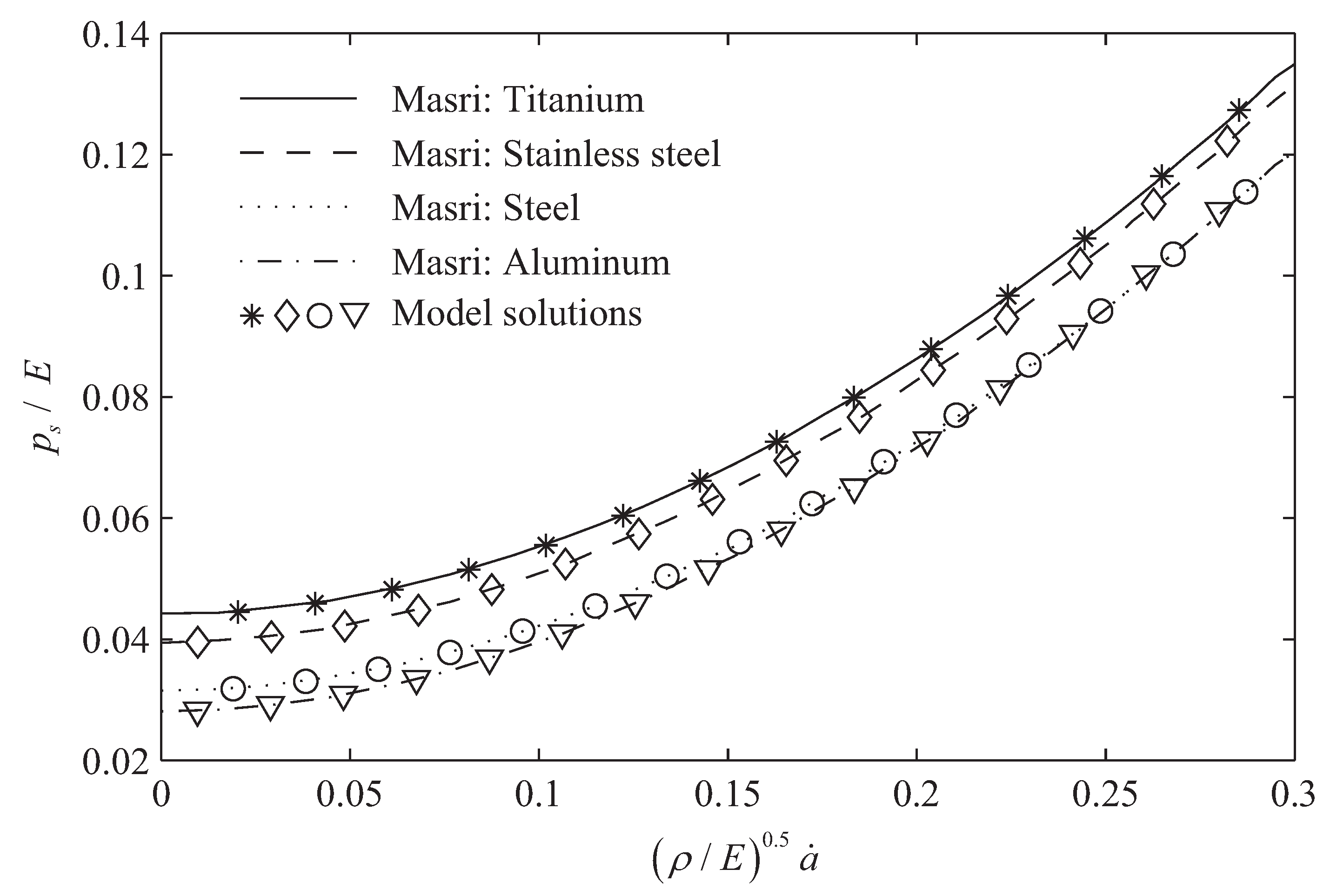
5.1. Comparison to the Forrestal et al. SCE Solution
5.2. Comparison to the Masri and Durban SCE Solution
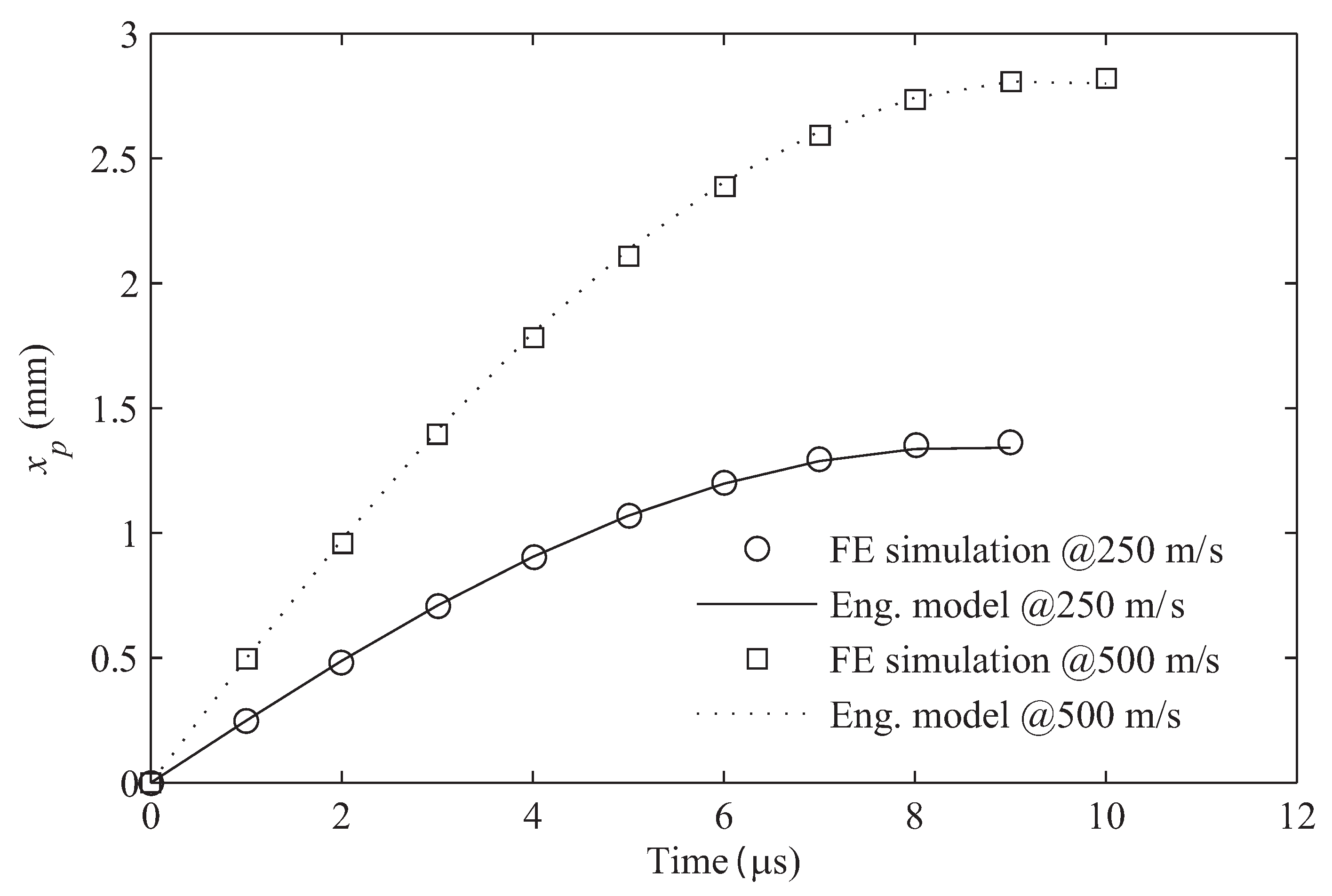
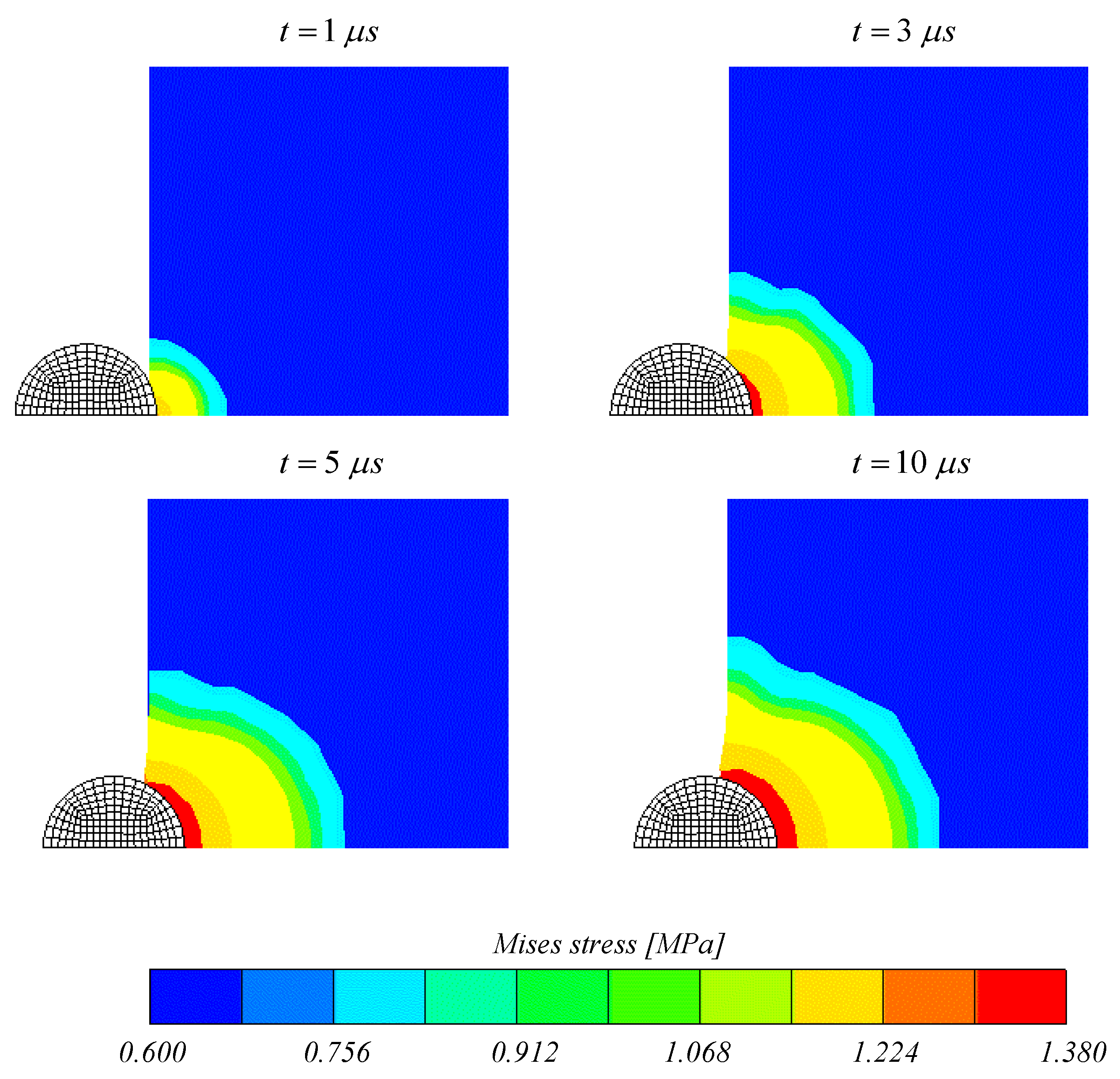
5.3. Results of SCE Model for 7075-T6 Aluminum Alloys and Comparison to FE Models
6. Conclusions
- Verified using elastic, perfectly plastic, 6061-T6 aluminum.
- Verified using four elastic, strain-dependent materials: titanium B120VCA, stainless steel, D6AC steel, and 7076-T6 aluminum.
- Verified and validated by FE numerical simulations and experimental data using semi-infinite, strain-dependent, 7075-T6 aluminum targets in the range of 250 m/s to 500 m/s.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Anderson, C.; Wilbeck, J.; Bodner, S.; Lankford, J.; Mullin, S. A Short Course on Penetration Mechanics; Southwest Research Institute: San Antonio, TX, USA, 2012. [Google Scholar]
- Jonas, G.; Zukas, J. Mechanics of penetration Analysis and Experiment. Int. J. Eng. Sci. 1978, 16, 879–903. [Google Scholar] [CrossRef]
- Hopkins, H.G. Dynamic expansion of spherical cavities in metals. Prog. Solid Mech. 1960, 1, 85–164. [Google Scholar]
- Backman, M.E.; Goldsmith, W. The mechanics of penetration of projectiles into targets. Int. J. Eng. Sci. 1978, 16, 1–99. [Google Scholar] [CrossRef]
- Sun, Y.; Shi, C.; Liu, Z.; Wen, D. Theoretical Research Progress in High-Velocity/Hypervelocity Impact on Semi-Infinite Targets. Shock Vib. 2015, 2015, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.S. Cavity Expansion Methods in Geomechanics; Springer Science & Busines Media: Berlin, Germany, 2013. [Google Scholar]
- Tate, A. A theory for the deceleration of long rods after impact. J. Mech. Phys. Solids 1967, 15, 387–399. [Google Scholar] [CrossRef]
- Tate, A. Further results in the theory of long rod penetration. J. Mech. Phys. Solids 1969, 17, 141–150. [Google Scholar] [CrossRef]
- MacCormack, R. The effect of viscosity in hypervelocity impact cratering. J. Spacecr. Rocket. 2003, 40, 757–763. [Google Scholar] [CrossRef]
- Robertson, H.; Taub, A.; Curtis, C. The Mechanics of Armor Performation. 1. Residual Velocity; Technical Report; DTIC Document: Fort Belvoir, VA, USA, 1943. [Google Scholar]
- Yossifon, G.; Rubin, M.; Yarin, A. Penetration of a rigid projectile into a finite thickness elastic-plastic target. Int. J. Impact Eng. 2001, 25, 265–290. [Google Scholar] [CrossRef]
- Chen, X.; Li, Q. Perforation of a thick plate by rigid projectiles. Int. J. Impact Eng. 2003, 28, 743–759. [Google Scholar] [CrossRef]
- Shaw, A. Penetration of rigid objects into semi-infinite compressible solids. Mech. Mater. 2012, 50, 22–35. [Google Scholar] [CrossRef]
- Durban, D.; Baruch, M. On the problem of a spherical cavity in an infinite elasto-plastic medium. J. Appl. Mech. 1976, 43, 633. [Google Scholar] [CrossRef]
- Bernard, R.S. Depth and Motion Prediction for Earth Penetrators; Technical Report; DTIC Document: Fort Belvoir, VA, USA, 1978. [Google Scholar]
- Yu, H.S.; Houlsby, G.T. Finite cavity expansion in dilatant soils: Loading analysis. Geotechnique 1991, 41, 173–183. [Google Scholar] [CrossRef]
- Su, S.F.; Liao, H.J. Cavity expansion and cone penetration resistance in anisotropic clay. J. Chin. Inst. Eng. 2001, 24, 659–671. [Google Scholar] [CrossRef]
- Houlsby, G.T.; Withers, N.J. Analysis of the cone pressure meter test in clay. Geotechnique 1988, 38, 575–587. [Google Scholar] [CrossRef]
- Osinov, V.A. Large-strain dynamic cavity expansion in a granular material. Math. Mech. Granul. Mater. 2005, 52, 185–198. [Google Scholar]
- Hashmi, M.; Islam, M.; Haque, M.; Sparling, L. High strain-rate properties of material: Design and development of a test equipment and methodology. Int. J. Mach. Tool Des. Res. 1985, 25, 39–50. [Google Scholar] [CrossRef]
- Tirupataiah, Y.; Sundararajan, G. A dynamic indentation technique for the characterization of the high strain-rate plastic flow behaviour of ductile metals and alloys. J. Mech. Phys. Solids 1991, 39, 243–271. [Google Scholar] [CrossRef]
- Dabboussi, W.; Nemes, J.A. Modeling of ductile fracture using the dynamic punch test. Int. J. Mech. Sci. 2005, 47, 1282–1299. [Google Scholar] [CrossRef]
- Carter, J.P. The expansion of a cylinder under conditions of finite plane strain. Nucl. Eng. Des. 1978, 47, 101–106. [Google Scholar] [CrossRef]
- Rubin, M.B.; Kositski, R.; Rosenberg, Z. Essential physics of target inertia in penetration problems missed by cavity expansion models. Int. J. Impact Eng. 2016, 98, 97–104. [Google Scholar] [CrossRef]
- Zhou, H.; Kong, G.; Liu, H.; Laloui, L. Similarity solution for cavity expansion in thermoplastic soil. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 274–294. [Google Scholar] [CrossRef]
- Yankelevsky, D.Z.; Feldgun, V.R. Issues in modelling the penetration of thick targets by rigid long rods. Int. J. Impact Eng. 2020, 137, 103474. [Google Scholar] [CrossRef]
- Anderson, C.E., Jr. Analytical models for penetration mechanics: A Review. Int. J. Impact Eng. 2017, 108, 3–26. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, H.J.; Tan, Z.J.; Huang, F.L. Theoretical Analysis of Dynamic Spherical Cavity Expansion in Reinforced Concretes. In Proceedings of the 9th International Symposium on Impact Engineering, Tainan, Taiwan, 5–9 September 2016; Volume 715, pp. 222–227. [Google Scholar]
- Bavdekar, S.; Parsard, G.; Subhash, G.; Satapathy, S. An improved dynamic expanding cavity model for high-pressure and high-strain-rate response of ceramics. Int. J. Solids Struct. 2017, 125, 77–88. [Google Scholar] [CrossRef]
- Meng, C.; Tan, Q.; Jiang, Z.; Song, D.; Liu, F. Approximate solutions of finite dynamic spherical cavity expansion models for penetration into elastically confined concrete targets. Int. J. Impact Eng. 2018, 114, 182–193. [Google Scholar] [CrossRef]
- Peng, Y.; Wu, H.; Fang, Q.; Kong, X.Z. Modified spherical cavity expansion model for projectile penetration into concrete targets. Acta Mech. Sin. 2019, 35, 518–534. [Google Scholar] [CrossRef]
- Durban, D.; Masri, R. Dynamic spherical cavity expansion in a pressure sensitive elastoplastic medium. Int. J. Solids Struct. 2004, 41, 5697–5716. [Google Scholar] [CrossRef]
- Abrate, S. Ballistic Impacts on Composite and Sandwich Structures. In Major Accomplishments in Composite Materials and Sandwich Structures; Daniel, I., Gdoutos, E., Rajapakse, Y., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 465–501. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Okajima, K.; Luk, V.K. Penetration of 6061-T651 aluminum targets with rigid long rods. J. Appl. Mech. 1988, 55, 755. [Google Scholar] [CrossRef]
- Jones, S.E.; Rule, W.K.; Jerome, D.M.; Klug, R.T. On the optimal nose geometry for a rigid penetrator. Comput. Mech. 1998, 22, 413–417. [Google Scholar] [CrossRef]
- Jones, S.E.; Rule, W.K. On the optimal nose geometry for a rigid penetrator, including the effects of pressure-dependent friction. Int. J. Impact Eng. 2000, 24, 403–415. [Google Scholar] [CrossRef]
- Bishop, R.F.; Hill, R.; Mott, N.F. The theory of indentation and hardness tests. Proc. Phys. Soc. 1945, 57, 147. [Google Scholar] [CrossRef]
- Knowles, J.K.; Jakub, M.T. Finite dynamic deformations of an incompressible elastic medium containing a spherical cavity. Arch. Ration. Mech. Anal. 1965, 18, 367–378. [Google Scholar] [CrossRef]
- Durban, D.; Baruch, M. Behaviour of an incrementally elastic thick walled sphere under internal and external pressure. Int. J. Non-Linear Mech. 1974, 9, 105–119. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Luk, V.K. Dynamic spherical cavity expansion in a compressible elastic-plastic solid. J. Appl. Mech. 1988, 55, 755–760. [Google Scholar] [CrossRef]
- Forrestal, M.J. Penetration into dry porous rock. Int. J. Solids Struct. 1986, 22, 1485–1500. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Tzou, D.Y.; Askari, E.; Longcope, D.B. Penetration into ductile metal targets with rigid spherical-nose rods. Int. J. Impact Eng. 1995, 16, 699–710. [Google Scholar] [CrossRef]
- Luk, V.K.; Forrestal, M.J.; Amos, D.E. Dynamic spherical cavity expansion of strain-hardening materials. J. Appl. Mech. 1991, 58, 1. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Brar, N.S.; Luk, V.K. Penetration of strain-hardening targets with rigid spherical-nose rods. J. Appl. Mech. 1991, 58, 7–10. [Google Scholar] [CrossRef]
- Warren, T.; Forrestal, M. Effects of strain hardening and strain-rate sensitivity on the penetration of aluminum targets with spherical-nosed rods. Int. J. Solids Struct. 1998, 35, 3737–3753. [Google Scholar] [CrossRef]
- Warren, T.; Tabbara, M. Spherical Cavity Expansion Forcing Function in PRONTO 3D for Application to Penetration Problems; Technical Report; Sandia National Labs.: Albuquerque, NM, USA, 1997.
- Warren, T.; Tabbara, M. Simulations of the penetration of 6061-T6511 aluminum targets by spherical-nosed VAR 4340 steel projectiles. Int. J. Solids Struct. 2000, 37, 4419–4435. [Google Scholar] [CrossRef] [Green Version]
- Brown, K.H.; Koteras, J.R.; Longcope, D.B.; Warren, T.L. CavityExpansion: A Library for Cavity Expansion Algorithms, Version 1.0; Technical Report; Sandia National Laboratory: Albuquerque, NM, USA, 2003.
- Chen, X.; Li, Q. Deep penetration of a non-deformable projectile with different geometrical characteristics. Int. J. Impact Eng. 2002, 27, 619–637. [Google Scholar] [CrossRef]
- Teland, J.A.; Moxnes, J.F. Analytical Cavity Expansion Penetration Models Compared with Numerical Simulations; Technical Report; Norwegian Defence Research Establishment: Kjeller, Norway, 2003. [Google Scholar]
- Buchely, M.; Maranon, A. An engineering model for the penetration of a rigid-rod into a Cowper-Symonds low-strength material. Acta Mech. 2015, 226, 2999–3010. [Google Scholar] [CrossRef]
- Buchely, M.; Maranon, A.; Silberschmidt, V. Material model for modeling clay at high strain-rates. Int. J. Impact Eng. 2016, 90, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Buchely, M.; Maranon, A. Study of steady cavitation assumptions in strain-ratesensitive solids for rigid projectile penetrations. Acta Mech. 2016, 227, 2969–2983. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Longcope, D.B. Target strength of ceramic materials for high velocity penetration. J. Appl. Phys. 1990, 67, 3669–3672. [Google Scholar] [CrossRef]
- Satapathy, S. Application of Cavity Expansion Analysis to Penetration Problems; Technical Report; DTIC Document: Fort Belvoir, VA, USA, 1997. [Google Scholar]
- Satapathy, S.; Bless, S.J. Cavity expansion resistance of brittle materials obeying a two curve pressure shear behavior. J. Appl. Phys. 2000, 88, 4004–4012. [Google Scholar] [CrossRef]
- Satapathy, S. Dynamic spherical cavity expansion in brittle ceramics. Int. J. Solids Struct. 2001, 38, 5833–5845. [Google Scholar] [CrossRef]
- Durban, D.; Fleck, N.A. Spherical cavity expansion in a Drucker-Prager solid. J. Appl. Mech. 1997, 64, 743–750. [Google Scholar] [CrossRef]
- Cohen, T.; Durban, D. Hypervelocity Cavity Expansion in Porous Elastoplastic Solids. J. Appl. Mech. 2013, 80, 011017. [Google Scholar] [CrossRef]
- Czarnota, C.; Molinari, A.; Mercier, S. The structure of steady shock waves in porous metals. J. Mech. Phys. Solids 2017, 107, 204–228. [Google Scholar] [CrossRef]
- Rodriguez-Martinez, J.; Cohen, T.; Zaera, R. Approaching steady cavitation: The time scale in hypervelocity cavity expansion in work hardening and transformation hardening solids. Int. J. Impact Eng. 2014, 73, 43–55. [Google Scholar] [CrossRef] [Green Version]
- Masri, R.; Durban, D. Dynamic spherical cavity expansion in an elastoplastic compressible Mises solid. J. Appl. Mech. 2005, 72, 887–898. [Google Scholar] [CrossRef]
- Jacob, P.; Goulding, L. An Explicit Finite Element Primer; NAFEMS: Glasgow, UK, 2002. [Google Scholar]




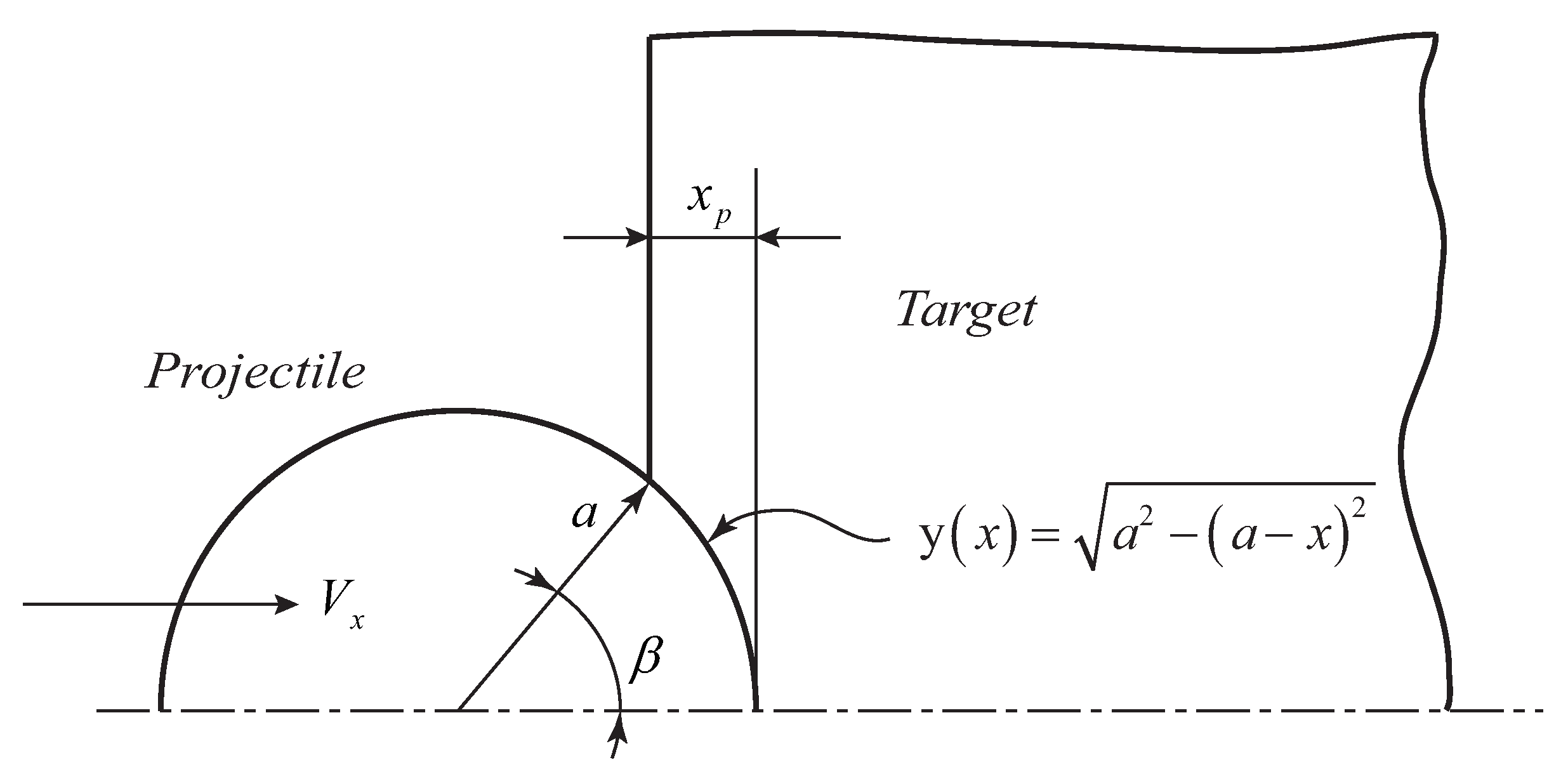
| (kg/m) | E (GPa) | (-) | (MPa) | |
|---|---|---|---|---|
| 6061-T6 Al | 2700 | 68.9 | 0.33 | 300 |
| Material | (kg/m) | E (GPa) | (-) | k (-) | n (-) |
|---|---|---|---|---|---|
| Titanium B120VCA | 4400 | 106 | 0.333 | 2.4 × | 16.5 |
| Stainless steel | 7800 | 206 | 0.3 | 5.78 × | 3 |
| Steel D6AC | 7800 | 213 | 0.27 | 2.52 × | 28 |
| Aluminum7075-T6 | 2700 | 72.4 | 0.32 | 3.94 × | 10.9 |
| (kg/m) | E (GPa) | (-) | Y (MPa) | B (MPa) | n (−) |
|---|---|---|---|---|---|
| 2700 | 72.4 | 0.32 | 601 | 765 | 0.09174 |
| (kg/m) | E (GPa) | (-) |
|---|---|---|
| 2700 | 189 | 0.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buchely, M.; Marañon, A. Spherical Cavity Expansion Approach for the Study of Rigid-Penetrator’s Impact Problems. Appl. Mech. 2020, 1, 20-46. https://doi.org/10.3390/applmech1010003
Buchely M, Marañon A. Spherical Cavity Expansion Approach for the Study of Rigid-Penetrator’s Impact Problems. Applied Mechanics. 2020; 1(1):20-46. https://doi.org/10.3390/applmech1010003
Chicago/Turabian StyleBuchely, Mario, and Alejandro Marañon. 2020. "Spherical Cavity Expansion Approach for the Study of Rigid-Penetrator’s Impact Problems" Applied Mechanics 1, no. 1: 20-46. https://doi.org/10.3390/applmech1010003
APA StyleBuchely, M., & Marañon, A. (2020). Spherical Cavity Expansion Approach for the Study of Rigid-Penetrator’s Impact Problems. Applied Mechanics, 1(1), 20-46. https://doi.org/10.3390/applmech1010003