Machine Learning–Driven Optimization of Photovoltaic Systems on Uneven Terrain for Sustainable Energy Development

Abstract

This study presents an AI-driven computational framework for optimizing the orientation and spatial deployment of photovoltaic (PV) systems installed on uneven terrain, with the objective of enhancing energy efficiency and supporting sustainable energy development. The proposed methodology integrates PVsyst-based numerical simulations with statistical modeling and bio-inspired heuristic optimization algorithms, forming a hybrid machine learning–assisted decision-making approach. A heuristic–parametric optimization strategy was employed to evaluate multiple tilt and azimuth configurations, aiming to maximize specific energy yield and overall system performance, expressed through the performance ratio (PR). The model was validated using site-specific climatic data from Veracruz, Mexico, and identified an optimal azimuth orientation of approximately 267.3°, corresponding to an estimated PR of 0.8318. The results highlight the critical influence of azimuth orientation on photovoltaic efficiency and demonstrate strong consistency between simulation outputs, statistical analysis, and intelligent optimization results. From an industrial perspective, the proposed framework reduces planning uncertainty and energy losses associated with suboptimal configurations, enabling more reliable and cost-effective photovoltaic system design, particularly for installations on uneven terrain. Moreover, the methodology significantly reduces planning time and potential installation costs by eliminating the need for preliminary physical testing, offering a scalable and reproducible AI-assisted tool that can contribute to lower levelized energy costs, enhanced system reliability, and more efficient deployment of photovoltaic technologies in the renewable energy industry. Future work will extend the model toward a multivariable machine learning framework incorporating tilt angle, climatic variability, and photovoltaic technology type, further strengthening its applicability in real-world environments and its contribution to Sustainable Development Goal 7: affordable and clean energy.

1. Introduction

The sustained increase in global energy demand and the urgent need to mitigate greenhouse gas emissions have driven an unprecedented energy transition toward renewable sources, among which photovoltaic (PV) solar energy has emerged as one of the most promising options due to its modularity, scalability, and low environmental impact [1,2]. The rapid deployment of PV systems in urban, industrial, and rural settings has highlighted the critical importance of the geometric design of installations [3], since tilt angle, orientation, shading, and geographical conditions directly determine the amount of incident solar radiation and, consequently, the overall efficiency of the system [4,5].

Several studies have shown that inadequate angular deviations can lead to energy losses ranging from 15% to 30% in annual production [6,7]. This variability directly affects operating costs, return on investment, and component lifetime, particularly in large-scale configurations where cumulative effects become significant [8,9]. For this reason, the optimal design of the orientation and tilt of solar panels has become a central topic in modern photovoltaic engineering [10,11].

In recent years, different methodological approaches have been used to address this challenge. Sidek et al. [12] present an open-loop dual-axis solar tracking system with automated positioning. The solar tracker can be positioned with an accuracy of ±0.5 and generates 26.9% more energy than a fixed photovoltaic system under clear-sky conditions; under very cloudy-sky conditions, it generates 12.8% more energy. Barbón et al. [13] study in detail the energy losses and the distribution of photovoltaic modules installed on flat rooftops when they must be placed in non-ideal positions. Their results show that deviations in the tilt and azimuth of photovoltaic panels can reduce the energy generated; deviations greater than 10° significantly increase losses. They conclude that orientation has a smaller impact on energy losses than the correct system tilt. Ciccozzi et al. [14] present the BIM methodology for the design of photovoltaic systems. The BIM approach enables comprehensive information modeling, accounting for the geometric, energetic, economic, and temporal aspects of the system. The authors emphasize that designing an efficient photovoltaic system requires careful planning that considers various factors, such as the technical characteristics of the system, the positions and shapes of external buildings, and surrounding obstacles. There is growing research interest in optimizing photovoltaic systems through the use of advanced models and computational techniques that can handle multiple complex variables [15,16]. The incorporation of metaheuristic optimization algorithms such as Genetic Algorithms, Particle Swarm Optimization (PSO), or Simulated Annealing has shown promising results for the automatic determination of optimal configurations [17,18,19].

Despite these advances, there is still a lack of an integrated tool that unifies geometric, geographical, and climatic parameters within a single computational environment, with the capability to adapt to irregular terrains and different solar radiation conditions. In this context, the present study aims to design and implement a tool based on mathematical modeling and computational simulations to optimize the positioning of solar panels as a function of global incident radiation, azimuth angle, terrain slope, and geographic location. To this end, the capabilities of PVsyst software (v. 8.0.13) will be integrated with optimization algorithms developed in Python, enabling a systematic analysis of multiple configurations and the identification of the one that maximizes the specific energy yield (kWh/kWp) [20,21].

This article contributes to the field of photovoltaic energy by presenting an advanced computational tool for the optimization of solar panel positioning, with the following main objectives:

• Development of an interactive simulation environment that allows the user to input site parameters, such as geographic coordinates, topography, irradiance, and temperature, to obtain a comparative analysis of energy performance for different orientations and tilt angles.
• Implementation of a heuristic parametric algorithm capable of evaluating multiple angular combinations through automated simulations, identifying the layout with the lowest level of energy losses.
• Model validation by comparing optimized configurations with standard ones, using annual yield and the Performance Ratio (PR) as key metrics.
• Significant reduction of planning time, installation costs, and errors arising from suboptimal configurations, through a precise, scalable methodology that does not require preliminary physical testing.
• Contribution to narrowing the gap between the theoretical potential of solar energy capture and its actual utilization, thereby strengthening sustainable planning and efficiency in the photovoltaic energy sector.

The main objective of this study is to develop and validate a computational tool for the optimization of solar panel positioning based on mathematical modeling and PVsyst simulations. The proposed tool enables the analysis and comparison of the energy performance of a photovoltaic system as a function of its orientation and tilt, while accounting for site-specific parameters such as geographic coordinates, topography, solar irradiance, and ambient temperature. In particular, the study seeks to identify the angular configuration that maximizes specific energy production (kWh/kWp) and minimizes system losses through the application of a heuristic–parametric optimization algorithm. Furthermore, the methodology aims to reduce planning time and design-stage costs by providing a reproducible and scalable framework that eliminates the need for preliminary physical testing, thereby contributing to the efficiency and sustainability of photovoltaic installations. From a methodological perspective, the proposed approach is formulated as a machine learning–assisted multivariable optimization problem, whose mathematical formulation and computational implementation are detailed in Section 2.

To avoid ambiguity between review-oriented and research-oriented content, it is important to clarify the role of the literature analysis within this study. The bibliometric assessment and state-of-the-art discussion are not intended as a comprehensive review, but rather as a contextual tool to systematically identify methodological and practical gaps in existing photovoltaic system optimization approaches. Based on this analysis, the present work explicitly addresses the lack of lightweight, computationally efficient frameworks that integrate physics-based simulation, statistical validation, and intelligent optimization into a unified design methodology. The proposed approach is therefore formulated and presented as a research article, focused on the development, validation, and application of an AI-assisted surrogate-based optimization framework.

Unlike conventional optimization studies focused primarily on numerical tuning, the central intention of this work is to propose a methodological framework that decouples high-fidelity photovoltaic simulations from the optimization stage through surrogate modeling. By combining physics-based simulation (PVsyst), statistical validation, and bio-inspired optimization within a unified workflow, the study aims to provide a transparent, computationally efficient, and reproducible decision-support tool for early-stage photovoltaic system design on uneven terrain. This intention guides the structure of the manuscript and frames the interpretation of the results discussed in later sections.

The remainder of this article is organized as follows. Section 2 describes the materials and methods, detailing the overall methodological framework, the computational tools employed, the bibliometric analysis, and the development of the mathematical and machine learning–assisted optimization model, including the integration of PVsyst simulations, statistical analysis, and bio-inspired optimization. Section 3 presents the results obtained from the photovoltaic system simulations, statistical evaluation, regression modeling, and heuristic optimization, highlighting the identification of the optimal azimuth configuration. Section 4 discusses the main findings in the context of recent literature, emphasizing methodological advantages, limitations, and practical implications. Finally, Section 5 summarizes the main conclusions of the study and outlines future research directions toward multivariable optimization and real-world validation.

2. Materials and Methods

The methodological development of this study is based exclusively on mathematical modeling and computational simulations, without the use of experimental tests or physical prototypes. This approach enables a precise, reproducible, and scalable evaluation of the energy performance of photovoltaic (PV) systems under different geometric, climatic, and topographic configurations. The methodological process is structured into five main phases: energy diagnosis, mathematical model formulation, computational simulation, parametric optimization, and validation of results.

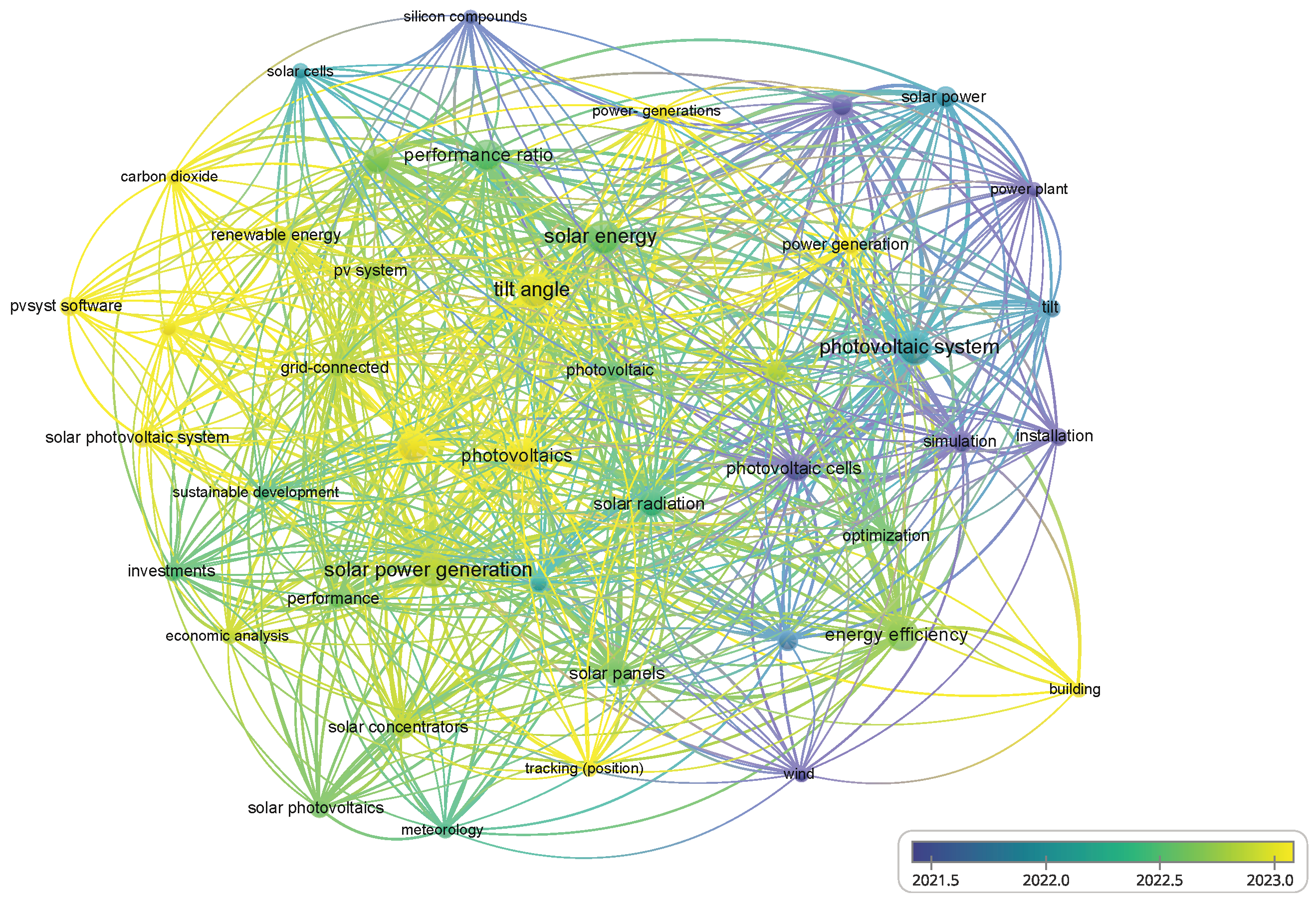
Figure 1 shows the bibliometric map generated with VOSviewer 1.6.20, based on an advanced search in Scopus using the terms included in the query string presented in Listing. The analysis covers publications from 2018 to 2025 related to the optimization of photovoltaic systems, considering orientation, tilt angle, mathematical modeling, and bio-inspired optimization techniques.

Thematic clusters are identified around solar photovoltaic system, optimization, tilt angle, PVsyst software, and energy efficiency, which constitute the main research axes. Peripheral terms such as renewable energy, simulation, and mathematical modeling further reinforce the focus on computational and predictive strategies applied to the enhancement of photovoltaic performance.

The search string used in Scopus was as follows:

TITLE-ABS-KEY( (“photovoltaic system*” OR “solar panel*” OR “PV system*” OR “PV installation*” OR “solar energy optimization”) AND (“orientation optimization” OR “azimuth optimization” OR “tilt angle” OR “panel positioning” OR “terrain irregular*” OR “slope analysis”) AND (“computational modeling” OR “PVsyst” OR “simulation” OR “parametric model*” OR “mathematical modeling” OR “ANOVA” OR “Tukey test” OR “Flower Pollination Algorithm” OR “bio-inspired optimization” OR “polynomial regression” OR “predictive model*”) AND (“energy efficiency” OR “performance ratio” OR “kWh/kWp” OR “energy yield” OR “solar resource assessment”) ) AND PUBYEAR > 2018 AND PUBYEAR < 2026

2.1. General Methodological Framework and Computational Tools

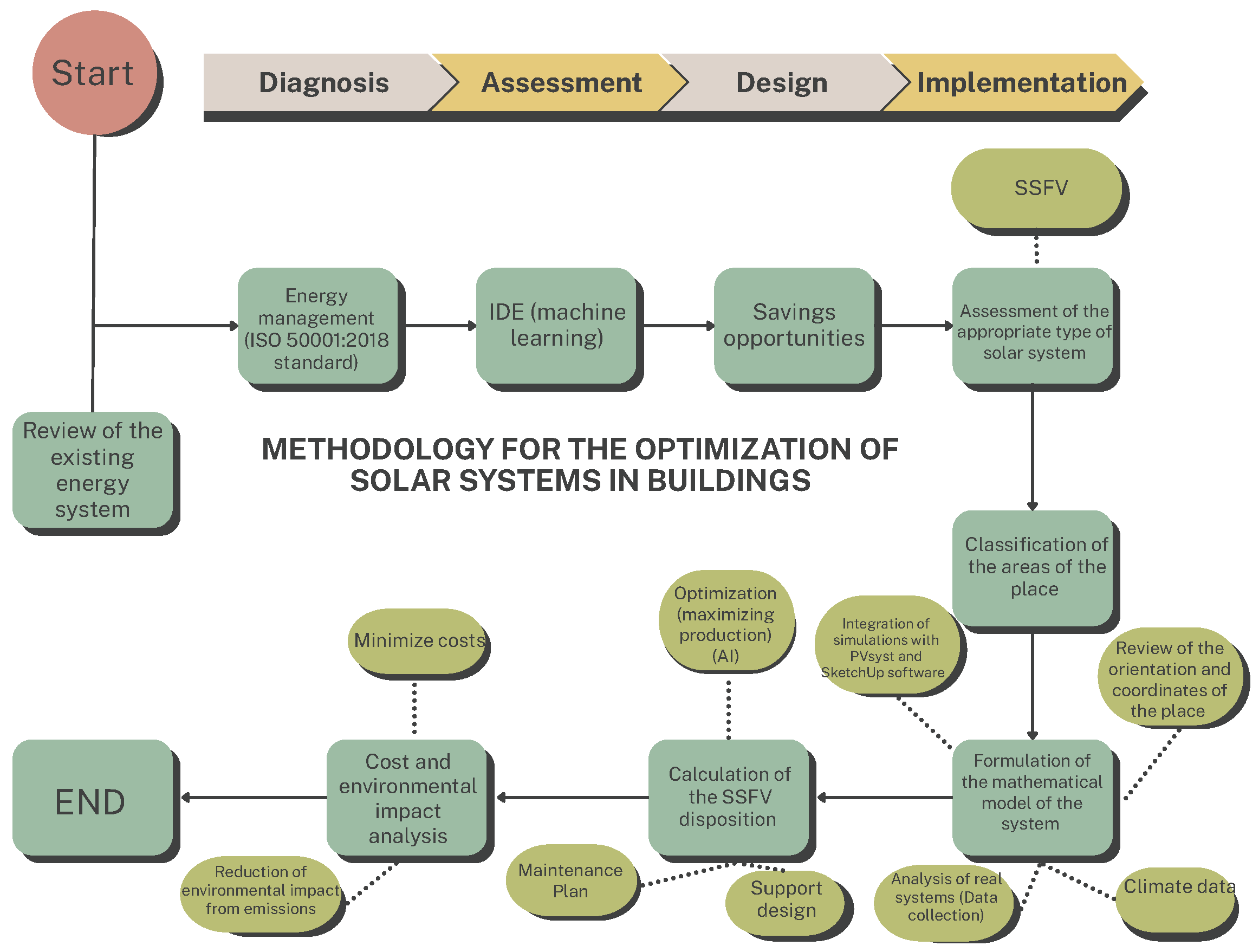
The procedure follows the methodology illustrated in Figure 2 and  Figure 3, which integrates the assessment of the existing energy system, the evaluation of energy-saving opportunities in accordance with ISO 50001:2018 [22], and the optimal design of the solar photovoltaic system (SPVS), considering both technical performance criteria and environmental impact.

In the initial stages, the meteorological data of the study site (Veracruz, Mexico) are analyzed. These data are obtained from the PVsyst and Meteonorm databases and include global irradiance, ambient temperature, and wind speed, all of which are essential for energy modeling.

To implement this framework, specialized computational tools are employed, enabling the integration of photovoltaic performance analysis, data processing, and mathematical and heuristic optimization. The main software packages used in the development of the model are summarized in

Table 1. Summary of technical software used in the project.

Software	Main Function	Expected Output
PVsyst 8.0.13	Simulation of the energy performance of the PV system as a function of orientation and tilt angle.	Annual energy production, losses, and overall performance (PR).
Python 3.10	Development of the parametric optimization algorithm with statistical analysis (ANOVA, Tukey test) and comparative validation.	Optimization curves and statistical validation.
Excel 365	Processing, cleaning, and basic visualization of data exported from PVsyst.	Comparative tables and auxiliary plots.
MATLAB 2022a	Fitting of mathematical models for the continuous representation of the variable PR (azimuth).	Polynomial equation and optimal curve.

.

2.2. Development of the Computational Model

The formulation of the mathematical model is based on the fundamental equation for the energy production of a photovoltaic system (1):

$$E_{\mathrm{total}}=A·G_{\mathrm{opt}}·{\eta }_{\mathrm{sistema}}$$

(1)

where:

• $E_{\mathrm{total}}$ is the annual energy generated [kWh],
• A is the effective area of the photovoltaic array [m²],
• $G_{\mathrm{opt}}$ is the optimized irradiance on the collector plane [kWh/m²],
• ${\eta }_{\mathrm{sistema}}$ is the overall system efficiency, including optical, thermal, and electrical losses.

For clarity and transparency, it is important to explicitly distinguish between third-party tools and original methodological contributions. In this study, established software packages such as PVsyst, Meteonorm, MATLAB, and standard statistical techniques are employed solely as external tools for simulation, data generation, and validation purposes. These components are adopted without modification and do not constitute methodological contributions of the present work.

The originality of the proposed approach lies in the integration and coordination of these tools within a unified AI-assisted optimization framework. In particular, the development of the surrogate-based regression model, the structured coupling of statistical analysis with bio-inspired optimization, and the decoupling between simulation and optimization layers represent contributions conceived and implemented by the authors.

Subsequently, a heuristic–parametric optimization model is developed in Python, which evaluates combinations of tilt and orientation angles through successive iterations, maximizing the specific energy production (kWh/kWp). Each configuration is automatically processed in PVsyst, and the exported results are subjected to statistical analysis (one-way ANOVA and Tukey test) to identify significant differences between configurations.

The mathematical formulation of the proposed model follows a machine learning–based multivariable approach, where the performance ratio (PR) is treated as the target variable and expressed as a nonlinear function of multiple input features, including azimuth angle, tilt angle, site-specific irradiance, ambient temperature, and system configuration parameters. Although the training dataset is generated from physics-based PVsyst simulations rather than experimental measurements, the model operates as a supervised learning framework, where input–output relationships are learned through regression and surrogate modeling techniques. This strategy enables the construction of a predictive metamodel that captures the combined influence of geometric and climatic variables, forming the basis for subsequent heuristic optimization.

To ensure methodological clarity and a clear distinction between adopted tools and original contributions, it is important to explicitly state the role of third-party components within the proposed framework. Established software packages such as PVsyst, Meteonorm, MATLAB, and standard statistical techniques are employed exclusively as supporting tools for high-fidelity simulation, data generation, and validation. These components are not modified and do not constitute methodological contributions of this study.

The original contribution of this work lies in the integration and orchestration of these third-party elements within a unified AI-assisted optimization framework. In particular, the formulation of the surrogate-based regression model, the coupling of statistical validation with heuristic optimization, and the decoupling of simulation and optimization layers represent developments conceived and implemented by the authors. This explicit separation ensures transparency regarding authorship and originality while preserving the reproducibility and robustness of the proposed methodology.

2.3. Problem Formulation and Optimization Model

The optimization problem addressed in this study consists of determining the optimal orientation and spatial deployment of a photovoltaic (PV) system installed on uneven terrain, with the aim of maximizing its annual energy performance. Let x denote the azimuth angle of the PV generator plane, which constitutes the primary decision variable in the present implementation, while the tilt angle is kept fixed according to site-specific design criteria.

The objective function is defined in terms of the performance ratio, $PR\left(x\right)$, which represents the overall efficiency of the PV system and implicitly accounts for optical, thermal, and electrical losses. Since $PR\left(x\right)$ cannot be expressed analytically, it is obtained through physics-based simulations using PVsyst and subsequently approximated by a regression-based surrogate model. The optimization problem can therefore be expressed as:

$$\underset{x}{max}PR\left(x\right)$$

(2)

subject to the feasibility constraints:

$$x_{min}\le x\le x_{max},$$

(3)

where $x_{min}$ and $x_{max}$ define the admissible azimuth range imposed by geometric, climatic, and site-specific considerations. In this study, this range is selected to reflect realistic orientations for the analyzed location.

Within this framework, the surrogate function $PR\left(x\right)$ acts as the objective function evaluated by the optimization algorithm, while feasibility constraints are enforced through bounded search intervals and soft penalty terms. The resulting formulation corresponds to a surrogate-assisted, single-objective optimization problem, where the physical consistency of the system is ensured by the underlying PVsyst simulations and the computational efficiency is achieved through heuristic search on the metamodel.

2.4. Bio-Inspired Optimization Algorithm

In the parametric optimization stage, the search for the optimal azimuth angle is performed using the Flower Pollination Algorithm (FPA), a bio-inspired metaheuristic that mimics the reproductive process of flowering plants. In this framework, each candidate solution is interpreted as a “flower” whose quality is evaluated through the performance ratio $PR$. Global pollination is modelled by Lévy-flight updates guided by the current best solution, whereas local pollination is implemented by small perturbations between neighbouring solutions, with a switching probability p controlling the balance between exploration and exploitation of the search space [23,24].

Once the PV system has been simulated in PVsyst and the relationship between $PR$ and azimuth angle is captured by a fitted polynomial metamodel $PR\left(x\right)$, the optimization problem becomes a continuous, derivative-free search on this surrogate function. The FPA operates exclusively on the polynomial representation, iteratively updating a population of azimuth angles within a feasible interval and converging towards the orientation that maximizes $PR\left(x\right)$. This decoupling between the simulation layer (PVsyst) and the optimization layer (FPA on the metamodel) significantly reduces computational cost, while preserving the physical consistency of the underlying energy model [25,26] (Figure 2).

To ensure realistic solutions, soft penalty terms are incorporated into the objective function so that the algorithm concentrates its search within a predefined azimuth window consistent with the local solar resource (e.g., 240°–300°). In this way, the FPA-based optimizer is fully aligned with the methodological framework of this study, providing an automated and computationally efficient tool for technical design decisions in PV systems installed on irregular terrain [23,27,28].

Algorithmic Description of the Optimization Procedure

Figure 2 schematically illustrates the complete workflow of the surrogate-assisted optimization strategy adopted in this study. The left-hand side of the diagram corresponds to the physics-based modeling stage, where site-specific data (geometry, meteorological conditions, and PV system configuration) are used to perform PVsyst simulations and compute the performance ratio (PR) as a function of the azimuth angle. These simulation results are subsequently employed to construct a polynomial surrogate model $PR\left(x\right)$, which serves as an approximate objective function during the optimization process.

Figure 2. Schematic representation of the FPA-based azimuth optimisation. PVsyst simulations are first used to build a polynomial metamodel $PR\left(x\right)$ as a function of azimuth angle. The Flower Pollination Algorithm (FPA) operates on this surrogate function, alternating global (Lévy-flight) and local updates with soft penalties that restrict the search to a realistic azimuth window (e.g., 240°–300°), until convergence to the orientation that maximises $PR\left(x\right)$.

Figure 2. Schematic representation of the FPA-based azimuth optimisation. PVsyst simulations are first used to build a polynomial metamodel $PR\left(x\right)$ as a function of azimuth angle. The Flower Pollination Algorithm (FPA) operates on this surrogate function, alternating global (Lévy-flight) and local updates with soft penalties that restrict the search to a realistic azimuth window (e.g., 240°–300°), until convergence to the orientation that maximises $PR\left(x\right)$.

The right-hand side of Figure 2 represents the optimization loop based on the Flower Pollination Algorithm (FPA). The procedure begins with the initialization of a population of candidate azimuth angles $\left\{x_i\right\}$. At each iteration, a decision is made between a global or local pollination step, as indicated by the decision diamond “Global or local step?”. Global pollination is implemented through Lévy flights around the current best solution $x*$, promoting exploration of the search space, whereas local pollination relies on neighborhood-based updates to enhance exploitation of promising regions.

After each update, a soft penalty mechanism is applied to enforce realistic azimuth constraints (e.g., 240°–300°), ensuring that candidate solutions remain physically feasible. The surrogate model $PR\left(x\right)$ is then evaluated for each candidate (block “Evaluate $PR\left(x_i\right)$ using $PR\left(x\right)$”), and the best-performing solution is updated accordingly (block “Update best solution $x*,P{R}_{max}$”). The iterative process continues until the convergence criterion represented by the decision block “Converged?” is satisfied, leading to the final output: the optimal azimuth angle and the corresponding maximum PR.

To ensure algorithmic rigor and reproducibility, the operational steps associated with each block of Figure 2 are formally described in Algorithm 1. This explicit pseudocode clarifies the role of the surrogate model, the update rules of the FPA, the enforcement of feasibility constraints, and the stopping criteria, thereby strengthening the transparency and robustness of the proposed optimization framework.

Algorithm 1 Surrogate-assisted FPA-based optimization of PV azimuth orientation

1: Inputs: Site and PV system data (geometry, meteorology, configuration), azimuth bounds $[x_{min},x_{max}]$ (e.g., 240°–300°), FPA parameters $(N,p,{\mathrm{iter}}_{max})$ 2: Outputs: Optimal azimuth angle $x^{*}$ and maximum performance ratio $P{R}_{max}$ 3: (Stage 1: Simulation and surrogate modeling) 4: Generate a discrete set of azimuth angles $\left\{x^{\left(k\right)}\right\}$ in [0°,360°] 5: for each $x^{\left(k\right)}$ do 6:       Run PVsyst simulation and compute $P{R}^{\left(k\right)}=PR\left(x^{\left(k\right)}\right)$ 7: end for 8: Fit a polynomial surrogate model $\widehat{PR}\left(x\right)$ using the dataset $\left\{(x^{\left(k\right)},P{R}^{\left(k\right)})\right\}$ 9: (Stage 2: FPA-based optimization on $\widehat{PR}\left(x\right)$) 10: Initialize a population ${\left\{x_i\right\}}_{i=1}^N$ with $x_i\sim \mathcal{U}(x_{min},x_{max})$ 11: Evaluate $\widehat{PR}\left(x_i\right)$ for all candidates and set $x*\leftarrow arg{max}_i\widehat{PR}\left(x_i\right)$, $P{R}_{max}\leftarrow \widehat{PR}\left(x^{*}\right)$ 12: for $t=1$ to ${\mathrm{iter}}_{max}$ do 13:       for each candidate solution $x_i$ do 14:          Select step type: global with probability p, otherwise local 15:          if global pollination then 16:             $x_i\leftarrow x_i+L(x_i-x^{*})$               ▹ Lévy flight around best solution 17:          else 18:             Randomly select $x_j$ and $x_k$ from the population, $j\ne k\ne i$ 19:             $x_i\leftarrow x_i+ϵ(x_j-x_k)$                ▹ local neighborhood update 20:          end if 21:          Feasibility enforcement: if $x_i\notin [x_{min},x_{max}]$, apply projection or soft penalty 22:          Evaluate $P{R}_i\leftarrow \widehat{PR}\left(x_i\right)$ 23:          if $P{R}_i>P{R}_{max}$ then 24:             $x*\leftarrow x_i$ 25:             $P{R}_{max}\leftarrow P{R}_i$ 26:          end if 27:       end for 28:       if convergence criterion satisfied then 29:          break               ▹ corresponds to the “Converged?” block in Figure 2 30:       end if 31: end for 32: return $x*,P{R}_{max}$

2.5. Integration of Simulations and Validation

The methodological workflow shown in Figure 3 begins with the collection of climatic and geometric data for the site, continues with energy simulations for different orientations, and concludes with the identification of the optimal layout of the PV system.

Figure 3. Methodological workflow for the optimization of solar photovoltaic systems in buildings.

Figure 3. Methodological workflow for the optimization of solar photovoltaic systems in buildings.

The results obtained are validated by comparing the optimized configurations with a standard south-facing orientation, using the performance ratio (PR), overall efficiency, and specific energy as key criteria. In addition, complementary indicators such as the potential reduction in CO₂ emissions and the economic impact associated with improved performance are included, enabling a comprehensive technical and environmental assessment of the proposed design.

2.6. Site-Specific Solar Path Analysis and Methodological Considerations

The adopted approach ensures a reproducible and simulation-based process, free from experimental bias and adaptable to different geographical contexts. Beyond maximizing energy efficiency, the proposed methodology also supports the reduction of installation costs and environmental impact by minimizing energy losses and emissions associated with fossil-fuel-based generation. In this sense, the computational model constitutes a robust tool for the intelligent design of photovoltaic systems in sustainable buildings.

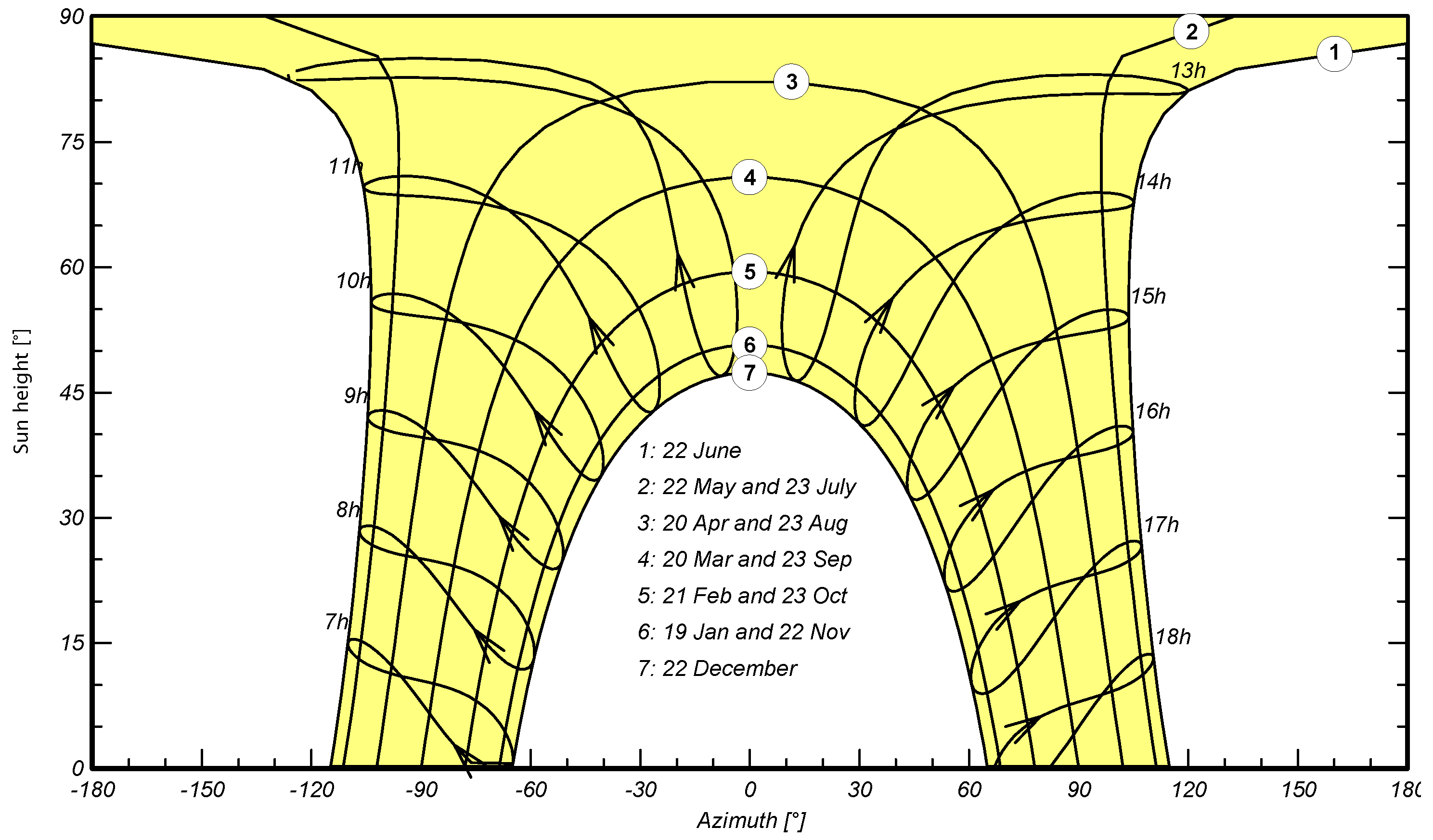
The analysis of solar paths is a key methodological component for determining the optimal orientation and tilt angle of photovoltaic modules. Figure 4 presents the solar path diagram for the city of Veracruz, Mexico, generated using PVsyst V8.0.11. This diagram illustrates the seasonal variation of solar altitude and the apparent motion of the Sun throughout the year, providing essential geometric insight for the subsequent simulation and optimization of photovoltaic system performance.

The graph clearly shows the characteristic solar trajectories for each time of the year, from the summer and winter solstices to the equinoxes. This information provides a geometric basis for the assessment of the solar resource and for the subsequent simulation of the energy performance of photovoltaic panels under different tilt and orientation configurations.

2.7. AI-Assisted Optimization Framework: Purpose and Implementation

In this study, the term AI-assisted refers to the use of data-driven surrogate modeling and intelligent optimization techniques to support decision-making in photovoltaic system design. Rather than relying on black-box machine learning or deep learning architectures, the proposed framework combines physics-based simulations, statistical learning, and bio-inspired optimization into a transparent and computationally efficient workflow.

The purpose of the AI-assisted approach is to decouple high-fidelity photovoltaic simulations from the optimization stage by constructing a surrogate model that approximates the relationship between system performance indicators and design variables. This surrogate model enables continuous evaluation of system performance while significantly reducing computational cost and planning time.

From an implementation perspective, performance data generated through PVsyst simulations are used to train a regression-based metamodel, which captures the nonlinear dependence of the performance ratio on geometric and climatic parameters. Bio-inspired optimization algorithms, such as the Flower Pollination Algorithm, are then applied to this surrogate function to identify optimal design configurations within physically realistic constraints.

The utility of the AI-assisted framework lies in its ability to provide a reproducible, scalable, and interpretable decision-support tool for early-stage photovoltaic system design, particularly in contexts involving uneven terrain or non-ideal installation conditions. By integrating simulation fidelity with intelligent optimization, the framework enhances design robustness while avoiding the computational burden associated with repeated high-resolution simulations.

3. Results

3.1. Simulation Process and Parameter Configuration in PVsyst

Figure 5 shows the initial stage of configuring the geometric conditions of the photovoltaic system in the PVsyst software. In this phase, the parameters of the solar field were defined, including the tilt and azimuth of the generator plane, with the aim of establishing the baseline orientation for the annual performance analysis. This preliminary simulation made it possible to observe the effect of angular position on radiation capture and provided the basis for subsequent model calibration.

Figure 5 illustrates the process of defining the orientation of the photovoltaic field. This methodological step is crucial, since the tilt and azimuth determine the amount of irradiance incident on the modules and, consequently, the accuracy of the energy model. These values were used to configure the initial conditions for the comparative simulations performed in subsequent stages.

Figure 6 presents the graphical results generated after running the annual simulations in PVsyst. At this stage, input–output diagrams of the system, the performance ratio (PR), and power distributions were obtained, enabling a global assessment of the consistency of the model and the energy response under different radiation and temperature scenarios.

Figure 6 highlights how simulations in PVsyst allow the integral behaviour of the system to be represented. These results are used within the methodology as a visual validation of the energy performance prior to formulating the mathematical optimization model. The main objective at this stage is to establish consistent relationships among the simulated variables, rather than focusing on specific numerical values.

The reference geographical location selected for the development of the study is the city of Veracruz, Mexico. This site was defined as the main point of climatic and solar analysis, providing the meteorological data required to feed the energy simulations and ensure the representativeness of the proposed model.

This geographical reference serves as a spatial anchor within the methodology, since the latitude, longitude, and altitude conditions determine the solar path and the available global irradiance. Such information enables a coherent integration of the simulation results with the real operating conditions of the study site. The selection of the inverter is a decisive step to ensure optimal energy transfer and maximum performance of the photovoltaic (PV) generator. As summarised in the design criteria, the inverter must satisfy three main aspects: nominal power ratio, electrical compatibility, and system topology.

With respect to power sizing, for a generator with a nominal capacity of 7.0 kWp, the use of a 6.0 kWac inverter results in a DC/AC ratio of 1.16, which lies within the recommended range of 1.1−1.25 suggested by [29,30]. This slightly oversized configuration on the DC side allows better inverter utilisation at low irradiance levels, minimises clipping losses during peak hours, and maintains high conversion efficiency throughout the day.

Regarding electrical compatibility, it was verified that the voltage at the maximum power point ($V_{\mathrm{mp}}$) and the open-circuit voltage ($V_{\mathrm{oc}}$) of the module strings remain within the maximum power point tracking (MPPT) window of the inverter. Likewise, the string currents remain below the inverter current limits, avoiding power derating due to overcurrent. Finally, considering the modular configuration (two strings of six modules), a topology with multiple MPPT inputs is preferred, as it allows the independent optimisation of the operating point of each string, as discussed in [31].

In the simulated model, two 3.0 kWac inverters connected in parallel were employed to handle the 7.0 kWp DC array, ensuring redundancy and efficient operation under conditions of partial shading or mismatch.

Table 2. Technical summary of the simulated photovoltaic system.

Element	Specification
Location	Veracruz, Mexico
Software	PVsyst 8.0.13
Module	JinkoSolar JKM580M-7RL4-V
Nominal power per module	580 Wp
Number of modules	12 (2 strings of 6)
Total nominal power (Pnom)	7.0 kWp
Generator area	33 m2
Inverters	2 × 3.0 kWac
Total AC power	6.0 kWac
Pnom/inverter ratio	1.16
Tilt angle	20° fixed
Simulated azimuth	0°–360° in 5° steps
Performance ratio (PR) range	0.825–0.831
Optimal orientations	130°–145°
Maximum $E_{\mathrm{grid}}$	≈11,338 kWh/year
Least efficient orientations	0°–30°

summarises the nominal parameters of the photovoltaic system simulated in PVsyst. The selected configuration reproduces a small-scale distributed generator, typical of residential or educational applications in tropical climates. The total DC nominal capacity (7.0 kWp) and the AC capacity (6.0 kWac) result in a DC/AC design ratio consistent with international recommendations for maximising annual energy production. The tilt angle of 20 ° and the azimuth sweep from 0° to 360° enable a comprehensive parametric analysis of energy production as a function of orientation [32,33].

The optimal azimuth range (130°–145°) corresponds to southeast-facing orientations, which achieve the highest annual energy injected into the grid ($E_{\mathrm{grid}}\approx 11,338$ kWh/year) and the highest performance ratio (PR up to 0.831). These results are consistent with local solar path data for Veracruz, where morning irradiance predominates due to lower cloudiness in the afternoon. In contrast, azimuths between 0° and 30° show lower production, confirming the influence of orientation on the annual performance ratio, as reported by [34].

The overall efficiency of 82.8%, expressed in terms of the performance ratio (PR), implicitly accounts for all system losses relative to the reference energy under standard conditions. The remaining ≈17.3% of losses are mainly distributed among thermal losses of the photovoltaic modules due to elevated operating temperatures (typically accounting for about 6–8%), optical and incidence-angle losses associated with reflection effects and non-normal solar incidence on the fixed-tilt plane (approximately 2–3%), DC electrical losses including wiring, mismatch, and soiling effects (around 2–3%), and inverter and AC conversion losses related to power electronics and grid interface (about 3–4%). Minor contributions arise from system availability assumptions and auxiliary consumption. These loss ranges are consistent with those commonly reported for well-designed fixed-tilt photovoltaic systems operating in tropical climates and are implicitly captured within the PR values obtained from the PVsyst simulations.

Table 3. Monthly energy balances and performance indicators of the simulated photovoltaic system.

Month	GlobHor	DiffHor	T_Amb	GlobInc	GlobEff	${\mathit{E}}_{\mathbf{array}}$	${\mathit{E}}_{\mathbf{grid}}$	PR
	(kWh/m2)	(kWh/m2)	(°C)	(kWh/m2)	(kWh/m2)	(kWh)	(kWh)	(Ratio)
January	124.0	57.50	22.10	91.0	84.9	543	523	0.825
February	127.8	55.90	22.40	100.0	94.8	604	582	0.837
March	175.5	75.60	24.40	151.7	146.3	912	881	0.835
April	186.8	75.90	26.30	174.2	170.1	1042	1006	0.830
May	195.8	81.40	28.20	194.9	191.2	1157	1118	0.824
June	183.1	85.10	28.10	187.1	183.5	1114	1077	0.827
July	193.3	80.90	28.10	196.0	192.2	1165	1126	0.825
August	181.6	84.70	28.10	174.4	171.0	1041	1006	0.828
September	148.3	73.40	27.60	135.1	132.4	795	768	0.827
October	136.1	64.40	26.10	117.1	114.4	688	663	0.826
November	122.5	58.20	24.10	98.9	96.6	587	566	0.827
December	121.6	58.00	22.60	89.2	86.9	540	521	0.825
Total	1816.4	—	25.6	1709.6	1669.3	12,188	11,737	0.828

presents the monthly energy balances and performance indicators calculated using PVsyst. The annual global irradiation on the horizontal plane (GlobHor) reaches approximately 1816 kWh/m², while the effective irradiation on the collector plane (GlobEff) is 1669 kWh/m². These values correspond to the local solar potential of the Gulf region and are consistent with NASA-SSE satellite data reported by [35].

The annual energy production of the array ($E_{\mathrm{array}}$) is 12,188 kWh, of which 11,737 kWh are injected into the grid ($E_{\mathrm{grid}}$), resulting in a global performance ratio of 0.828. Seasonal variations are observed, driven by both irradiance and ambient temperature effects: the highest generation occurs between April and July, coinciding with high irradiance and moderate temperatures. In contrast, the winter months (December–January) exhibit reduced generation due to shorter days and lower solar altitude.

The stable monthly PR (0.825–0.837) indicates consistent system efficiency throughout the year, confirming that the inverter sizing and fixed-tilt configuration maintain adequate thermal behaviour. These results fall within the typical PR range (0.80–0.85) for well-designed fixed-tilt systems in tropical climates, as validated by the reference studies of [36,37].

3.2. Statistical Analysis of Photovoltaic System Data

The analysis of data using descriptive and inferential statistics makes it possible to identify relationships, trends, and behaviours that are not evident from energy values alone. In the context of photovoltaic systems, statistical tools such as correlation maps, analysis of variance (ANOVA), and post-hoc tests are essential for validating the impact of design variables—such as orientation or irradiance—on the overall performance of the system [32,37]. This approach provides a quantitative perspective that complements the PVsyst simulations, ensuring coherence between theoretical results and the expected behaviour under real operating conditions.

3.3. Correlation Heat Map

Figure 7 shows the correlation heat map among the main numerical variables analysed: global incident irradiance (GlobInc), effective irradiance (GlobEff), array energy ($E_{\mathrm{array}}$), energy injected into the grid ($E_{\mathrm{grid}}$), overall performance (PR), and orientation angle (degrees).

A near-perfect correlation ($r=0.99$) was observed between $E_{\mathrm{array}}$ and $E_{\mathrm{grid}}$, confirming the energy consistency of the model and the stability of the inverter under different irradiance conditions [36]. Likewise, the high correlation between GlobInc and GlobEff ($r=0.84$) shows that optical and angular losses were minimal, validating the correct geometric configuration of the system.

On the other hand, the correlation between orientation angle (degrees) and performance (PR) was moderate ($r=0.58$), indicating that azimuth variation has a direct, although not dominant, effect on overall efficiency. This behaviour is consistent with the findings of [33,34], who reported that deviations greater than 30° in orientation can reduce performance by 2−4 %. Taken together, the correlation analysis shows that irradiance remains the variable with the greatest statistical weight, while orientation acts as a fine-tuning factor to maximise the energy performance of the system.

3.4. Analysis of Variance (ANOVA) and Tukey Test

To verify whether the differences observed in performance (PR) between orientation groups are statistically significant, a one-way analysis of variance (ANOVA) was applied, followed by Tukey’s post-hoc test for multiple comparisons, as shown in Figure 8 and Figure 9.

The ANOVA yielded an F statistic of 36.91 with $p=5.53\times {10}^{-18}$, confirming highly significant differences among the different orientation intervals. This indicates that azimuth has a systematic effect on overall performance, validating that system efficiency is not homogeneous across the entire angular range [37].

Tukey’s test made it possible to identify which groups exhibit statistically relevant differences. The ranges 120°–180° and 180°–240° show the highest mean PR values (0.830−0.831), whereas orientations between 0° and 120° present lower efficiencies (0.827−0.828). This demonstrates that southeast and south orientations are the most favourable for the solar conditions in Veracruz, a result consistent with the solar path and the seasonal distribution of irradiance.

Overall, the statistical analysis confirms that the behaviour of PR is aligned with the previous polynomial model and with the PVsyst simulation results, strengthening the validity of the angular optimisation method employed [32].

3.5. Polynomial Model and Performance Optimization

The optimisation analysis was carried out on the basis of the statistical results for energy performance (PR) as a function of the orientation angle. From the values obtained with PVsyst, a sixth-order polynomial model was fitted to describe the variation of PR with azimuth (x), allowing the global trend and points of maximum performance to be represented. This type of model is widely used in regression studies applied to photovoltaic systems due to its ability to capture nonlinearities associated with irradiance and solar geometry effects [32,34]. insertar en el manuscrito:

The sixth-order polynomial used in this study does not represent a physical law, but rather a surrogate regression model designed to capture the aggregated and non-linear dependence of the performance ratio (PR) on azimuth, see Figure 10. This nonlinearity arises from the combined effects of solar geometry, seasonal irradiance distribution, and angle-of-incidence losses in a fixed-tilt configuration, leading to an asymmetric and non-monotonic annual response. Lower-order models showed systematic underfitting near the optimum, whereas the selected polynomial provides sufficient flexibility to represent the smooth unimodal trend of the simulation data, making it suitable for optimization purposes.

The resulting model is expressed by Equation (4):

$$PR\left(x\right)=2\times {10}^{-16}{x}^6-2\times {10}^{-13}{x}^5+6\times {10}^{-11}{x}^4-5\times {10}^{-9}{x}^3-3\times {10}^{-7}{x}^2+4\times {10}^{-5}x+0.8275$$

(4)

The coefficient of determination of the model is $R^2=0.846$, indicating a satisfactory fit between simulated and predicted values and confirming that the model correctly describes the angular trend of performance.

Once the mathematical model was defined, the Flower Pollination Algorithm (FPA) was applied to determine the global maximum of performance within a restricted angular range. This metaheuristic method, proposed by Yang (2012) [38] and widely used in energy optimisation due to its rapid convergence and computational simplicity, simulates natural pollination through a balance between global exploration and local exploitation [37].

The FPA was implemented in MATLAB R2022a, configuring a population of 80 solutions and a maximum of 600 iterations. The objective function corresponded to Equation (4), constrained to the feasible domain of 240°–300°, where a local maximum was expected according to the previous statistical analysis. As a result, a maximum performance of $P{R}_{max}\approx 0.8318$ was obtained at $x\approx$ 267.3°.

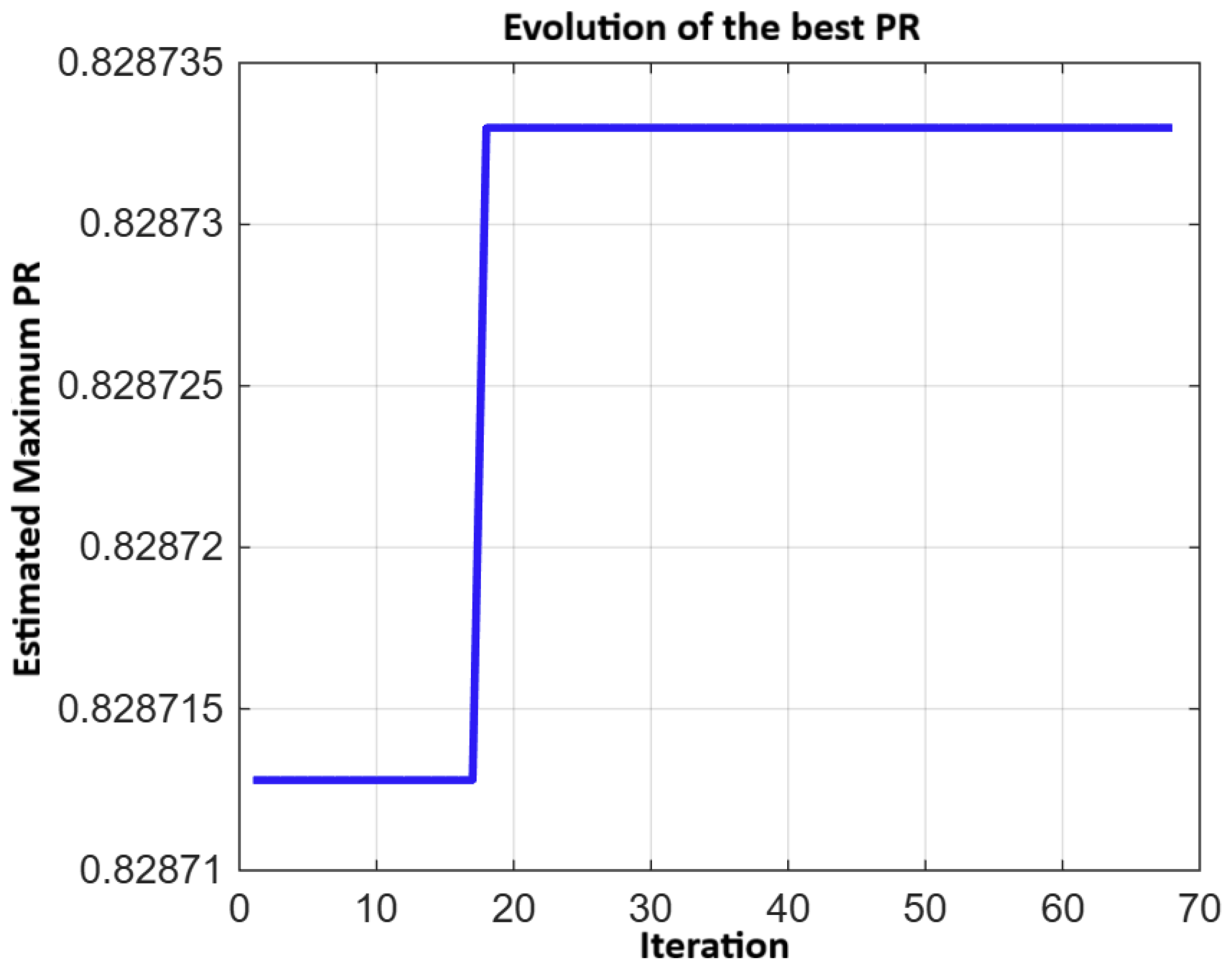
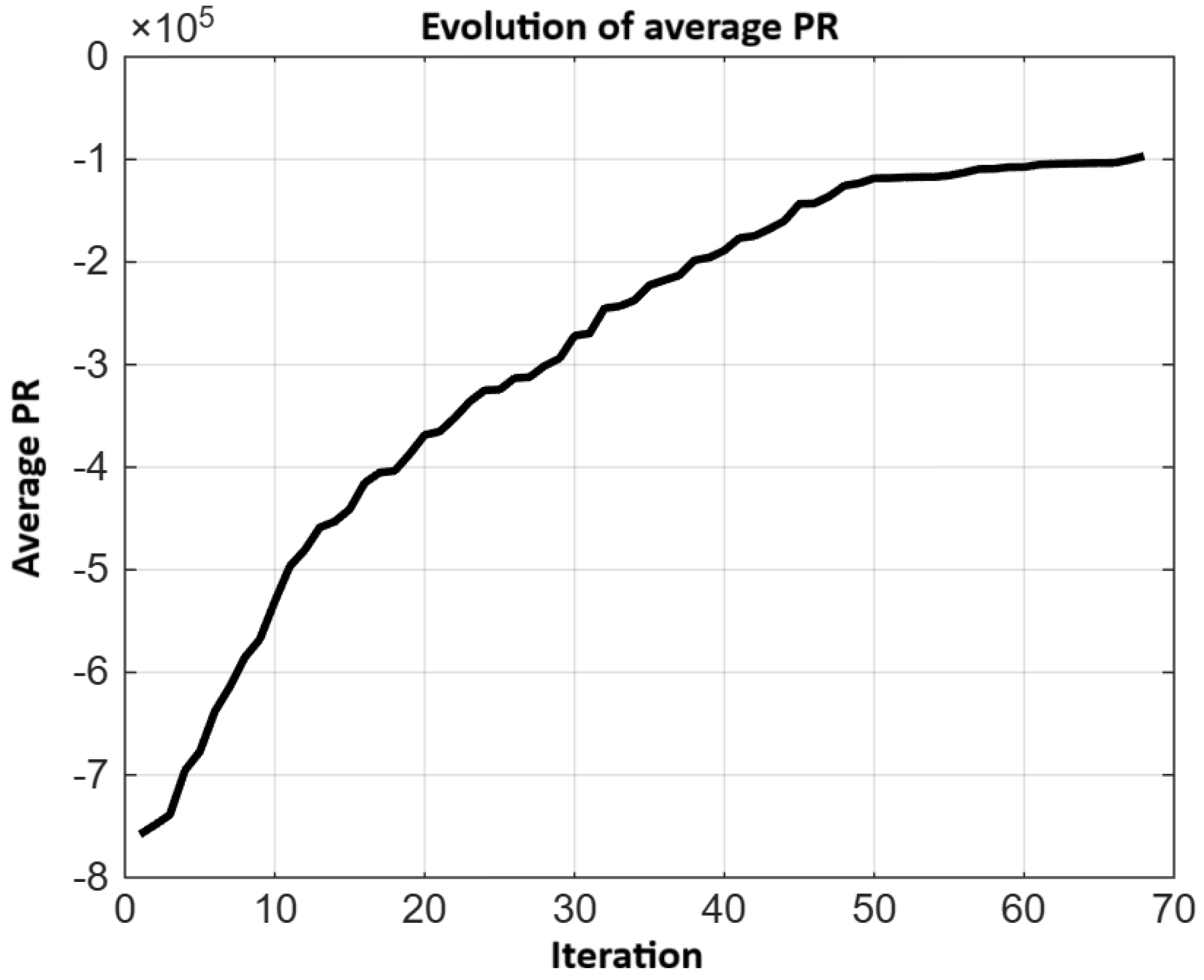
Figure 11 shows the evolution of the best PR value over the iterations, revealing rapid convergence around iteration 20, which indicates algorithm stability and the presence of a well-defined maximum. Figure 12 presents the evolution of the population-averaged performance, where a sustained increase is observed until a steady state is reached, confirming the effectiveness of the global search process.

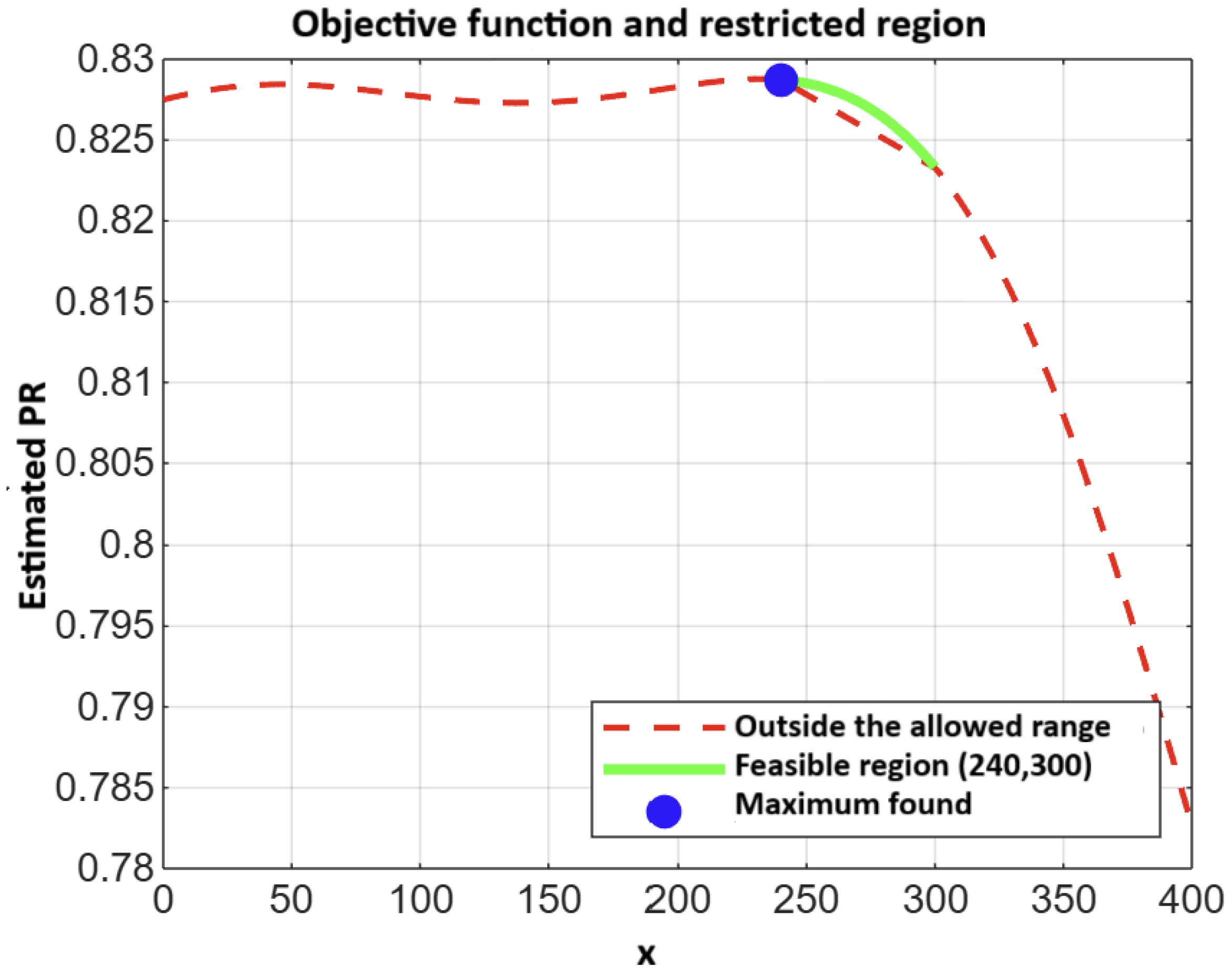
Finally, Figure 13 shows the objective function $PR\left(x\right)$ with the feasible region highlighted (in green) and the global optimum identified (blue point). The smooth and unimodal shape of the polynomial within the admissible range facilitates the search for the maximum and demonstrates that $x$ = 267.3° indeed corresponds to the most efficient orientation under the simulated conditions. This result is consistent with the expected behaviour in tropical regions of the Northern Hemisphere, where slight shifts towards the southwest can maximise annual solar energy capture [33,36].

4. Discussion

The application of the FPA algorithm to the fitted polynomial function made it possible to automate the search for the optimal orientation angle without the need to generate new simulations in PVsyst. Unlike traditional analyses based on the tabulation of discrete cases, this approach provides a continuous alternative capable of exploring the solution space with higher resolution and improved computational efficiency. The model identified a maximum estimated PR value of 0.8318 at an orientation of 267.3°, consistent with the range previously identified as the most efficient in the statistical analysis. This agreement between methods reinforces the validity of the proposed model and positions it as a reliable tool for the technical design phase.

In addition, the implementation of soft penalisation terms allowed the search to be constrained within realistic bounds (240°–300°), avoiding solutions outside the optimal region without compromising the exploratory capacity of the algorithm. The generated plots show rapid convergence, progressive improvement of the population average, and stability in the optimal value reached, which supports the choice of FPA as an effective bioinspired technique for univariate optimisation problems in solar engineering.

However, it is important to acknowledge that the model used is based on a polynomial function fitted to simulated data; therefore, its validity depends on the accuracy of those simulations and the representativeness of the modelled environment. Moreover, by focusing exclusively on the azimuthal variable with a fixed tilt angle, the applicability of the algorithm is limited in scenarios where multiple parameters interact simultaneously. To mitigate this limitation, it is proposed to extend the approach towards multivariable models that integrate tilt angle, local climatology, and photovoltaic technology type, as well as to apply the optimisation to real field data in order to strengthen the transfer of the model to operational applications.

Recent studies have increasingly explored the integration of machine learning techniques with mathematical optimization for photovoltaic-based energy systems, particularly within the context of microgrids and advanced energy management. For instance, Nammouchi et al. [39] propose a hybrid framework combining machine learning forecasting with robust optimization to address uncertainty in the optimal design and operational management of mixed microgrids including photovoltaic generation. Their approach demonstrates strong resilience under asymmetric uncertainties, although it primarily targets operational decision-making rather than geometric or configuration-level optimization of photovoltaic installations.

Similarly, Liu et al. [40] present a comprehensive review and application of machine learning methods combined with heuristic optimization techniques for photovoltaic system optimization in zero-energy buildings. Their work highlights the effectiveness of hybrid learning–optimization strategies in improving energy prediction accuracy and operational efficiency. However, these approaches are largely focused on energy production forecasting, control strategies, and building-level performance optimization, assuming predefined photovoltaic system configurations.

In contrast to these contributions, the present study addresses a complementary and earlier stage of the photovoltaic system lifecycle by focusing on the geometric and orientation optimization of PV installations. By employing physics-based simulations to generate training data and a surrogate regression model to enable computationally efficient optimization, the proposed AI-assisted framework bridges the gap between high-fidelity simulation and intelligent design optimization. This positioning allows the methodology to complement machine learning–driven microgrid and building-level optimization strategies by providing optimized photovoltaic configurations as reliable inputs for subsequent energy management and control applications.

The comparative analysis in

Table 4. Comparison of recent studies on positioning optimisation and digital modelling of photovoltaic systems.

Author/Year	Method or Model	Main Characteristics	Contribution/Limitations
Shirinyan et al. (2024) [41]	Ray-tracing modelling and 3D topographic analysis	Assessment of urban solar potential using 3D CAD radiation modelling, considering large-scale complex shading effects	High spatial accuracy and detailed geometric representation, but with high computational cost and strong dependence on detailed urban models.
Yu, Y., et al. (2024) [42]	Multivariable regression statistical method	Empirical fitting of PV production considering irradiance, tilt, and temperature using field data	Good predictive performance in known environments; limited by its dependence on local calibration and lack of extrapolation capability to new scenarios.
Télesphore et al. (2025) [43]	Optimisation via genetic algorithm (GA) and GIS analysis	Simultaneous search for optimal tilt and orientation with local geometric and climatic constraints	Multivariable coverage with high exploration capability; however, it requires long computation times and careful tuning of population size.
Angelova et al. (2024) [44]	Review of digital twins applied to PV installations	Integration of CFD models, IoT monitoring, and real-time simulation for energy optimisation	Comprehensive overview of digital twin applications in solar energy; lack of experimental studies validating dynamic performance in the field.
Xiang et al. (2024) [45]	Digital twin (DT) model with BiLSTM network	Short-term PV power prediction combining digital twin and deep learning	High predictive accuracy under variable conditions; limited applicability in systems without real-time data infrastructure.
Oss work	Computational modelling with fitted polynomial function and FPA optimisation	Automated search for the optimal azimuth angle without additional simulations in PVsyst; soft penalisation within the 240°–300° range	Reduced computation time and agreement with the maximum PR (0.8318); limited to a single variable but with potential for multivariable extension and application with real data.

Note. Comparison of different optimisation and digital modelling approaches applied to photovoltaic systems, considering accuracy, computational cost, and industrial applicability.

shows that methods based on geometric simulation (ray tracing) and digital twins offer high spatial accuracy, although at the cost of substantial hardware requirements and long processing times. In contrast, heuristic approaches such as genetic algorithms or FPA can explore the search space more efficiently, reducing the need for successive simulations.

A critical comparison with recent literature highlights both the strengths and limitations of existing approaches for photovoltaic system orientation optimization. Simulation-based methods relying on exhaustive parametric sweeps offer high physical fidelity, but they are often computationally expensive and poorly suited for iterative design or early-stage planning. Statistical regression models trained on experimental or site-specific data provide fast predictions, yet their applicability is typically constrained to calibrated environments and limited extrapolation capability.

Heuristic and metaheuristic optimization techniques, such as genetic algorithms or particle swarm optimization, have demonstrated strong global search capabilities and multivariable handling. However, these methods commonly require repeated high-fidelity simulations during the optimization loop, leading to increased computational cost and sensitivity to algorithm tuning. More recent digital twin approaches integrate real-time data, advanced modeling, and control strategies, achieving high accuracy at the expense of significant data infrastructure and implementation complexity.

In contrast, the surrogate-based, AI-assisted framework proposed in this study seeks to balance accuracy, transparency, and computational efficiency. By decoupling the simulation layer from the optimization stage through a fitted metamodel, the approach preserves the physical consistency of PVsyst simulations while enabling continuous optimization at a fraction of the computational cost. This design choice positions the proposed methodology as a practical alternative for early-stage photovoltaic system design, particularly in scenarios involving uneven terrain or limited availability of real operational data.

The proposed model combines simplicity and accuracy by using a fitted polynomial function that acts as a metamodel, enabling continuous evaluation of performance without relying on external tools. Although its current scope is restricted to the azimuthal variable, its coherence with the statistical results and its potential for multivariable extension support its applicability as a decision-support tool in the technical design of photovoltaic installations on irregular terrain.

5. Conclusions

This study demonstrates that the optimization of photovoltaic system orientation on uneven terrain can be effectively addressed through a machine learning–assisted computational framework that integrates physics-based simulations, statistical analysis, and bio-inspired optimization. By coupling PVsyst simulations with regression-based surrogate modeling and the Flower Pollination Algorithm (FPA), the proposed methodology enables an automated and computationally efficient exploration of the design space, overcoming the limitations of conventional trial-and-error or purely tabulated approaches.

From a technical standpoint, the results confirm that azimuth orientation exerts a statistically significant influence on photovoltaic performance, even when system tilt and technology are kept constant. The convergence of outcomes obtained from PVsyst simulations, inferential statistics (ANOVA and Tukey tests), and heuristic optimization provides strong internal consistency and reinforces the robustness of the proposed approach. The identification of an optimal azimuth of approximately 267.3°, associated with a maximum estimated performance ratio of 0.8318, is fully coherent with local solar path conditions and validates the capability of the surrogate-based optimization strategy to capture the underlying physical behavior of the system.

Beyond the numerical results, the main contribution of this work lies in its methodological architecture. The adoption of a machine learning–assisted multivariable formulation despite being implemented here in a univariate optimization context establishes a scalable foundation for intelligent decision-support tools in photovoltaic system design. By decoupling the simulation layer from the optimization layer through a fitted metamodel, the framework significantly reduces computational cost and eliminates the need for repeated high-fidelity simulations, thereby enhancing its practical applicability in early-stage design and planning.

From a sustainability perspective, the proposed approach directly supports Sustainable Development Goal 7 (Affordable and Clean Energy) by enabling more efficient utilization of the solar resource, reducing energy losses associated with suboptimal configurations, and potentially lowering installation costs and material overuse. In this sense, the study illustrates how artificial intelligence and machine learning techniques can move beyond predictive tasks and actively contribute to optimized, resource-efficient energy system design aligned with sustainable development objectives.

Nevertheless, certain limitations must be acknowledged. The current implementation focuses primarily on azimuth optimization with a fixed tilt angle and relies on simulated data rather than long-term field measurements. While this ensures reproducibility and methodological clarity, future research should extend the framework toward fully multivariable optimization, incorporating tilt angle, climatic variability, shading effects, and photovoltaic technology type. Furthermore, validation using real operational data would strengthen the transferability of the model to industrial-scale and real world applications.

Overall, this work contributes a transparent, reproducible, and computationally efficient AI-assisted methodology for photovoltaic system optimization on irregular terrain. It bridges the gap between simulation-based energy analysis and intelligent optimization, offering a practical pathway for integrating machine learning techniques into sustainable energy planning and reinforcing the role of artificial intelligence as an enabling technology for achieving long-term sustainability goals.

The proposed machine learning–assisted optimization framework offers several relevant benefits for the renewable energy industry, particularly for photovoltaic system developers, engineering firms, and energy planners. By combining physics-based simulations with surrogate modeling and bio-inspired optimization, the methodology provides a computationally efficient decision-support tool that can be applied at early design stages, significantly reducing planning time and minimizing the need for extensive trial-and-error simulations or preliminary field testing. This is especially valuable for projects located on uneven or non-ideal terrain, where conventional design rules may lead to suboptimal performance.

From an industrial perspective, the ability to identify optimal orientation configurations with reduced computational cost translates into improved energy yield predictability, lower design uncertainty, and potential reductions in installation and operational costs. Moreover, the surrogate-based approach facilitates rapid scenario evaluation, which is advantageous for feasibility studies, techno-economic assessments, and iterative project development workflows. The methodology is scalable and can be readily extended toward multivariable optimization, allowing its integration into existing digital design environments and supporting the transition toward more intelligent, data-driven practices in the renewable energy sector. Overall, this study demonstrates how artificial intelligence techniques can move beyond forecasting applications and actively contribute to optimized, reliable, and sustainable photovoltaic system deployment at an industrial level.