MST-DGCN: Multi-Scale Temporal–Dynamic Graph Convolutional with Orthogonal Gate for Imbalanced Multi-Label ECG Arrhythmia Classification
Abstract
1. Introduction
- MST-DGCN Framework: Multi-Scale Temporal–Dynamic Graph Convolutional Network (MST-DGCN), integrating dynamic graph learning, temporal modeling, and multi-scale fusion, is proposed for multi-label arrhythmia classification.
- T-DGCN for Spatiotemporal Feature Extraction: This study proposes a novel hybrid architecture that innovatively integrates two complementary components—a Dynamic Graph Convolutional Network (DGCN) for adaptive modeling of inter-lead electrophysiological correlations and a Gated Temporal Convolutional Network (GTCN) for capturing spatiotemporal dependencies, which can effectively overcome the inherent limitation of spatial feature oversight in conventional ECG analytical paradigms.
- OGF for Feature Integration: An orthogonal constraint is proposed to eliminate feature redundancy, while simultaneously implementing adaptive gating mechanisms to dynamically recalibrate the contribution weights of complementary multi-scale representations, so as to optimize classification efficacy in cardiac arrhythmia detection.
2. Related Work
2.1. Deep Learning for ECG Classification
2.2. Feature Fusion Strategies
3. Methods
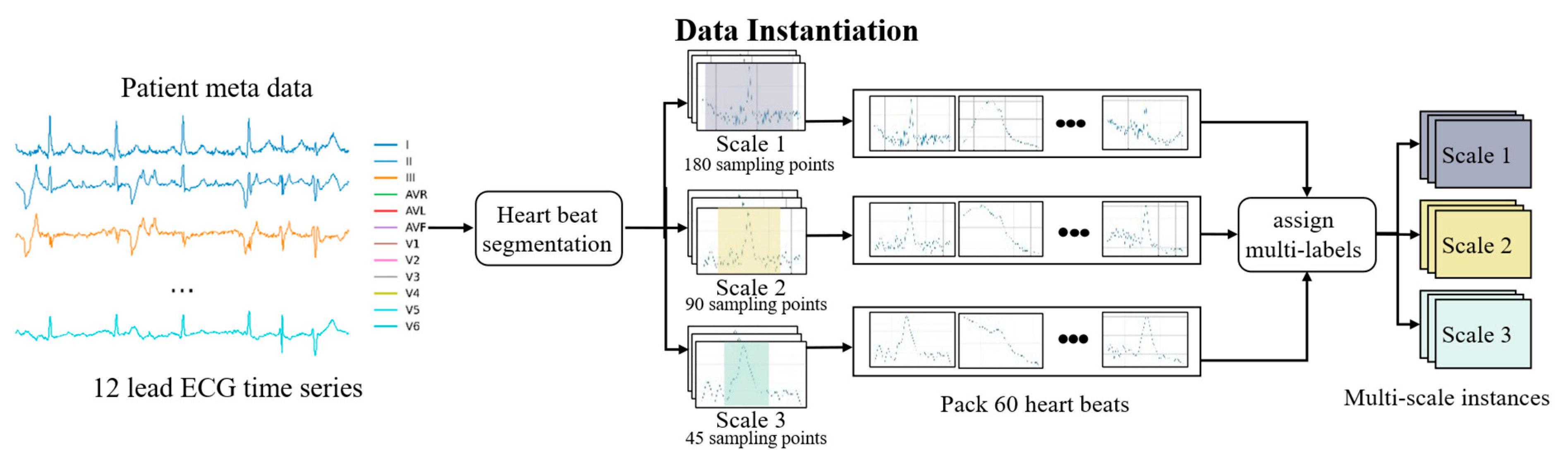
3.1. Overall Framework
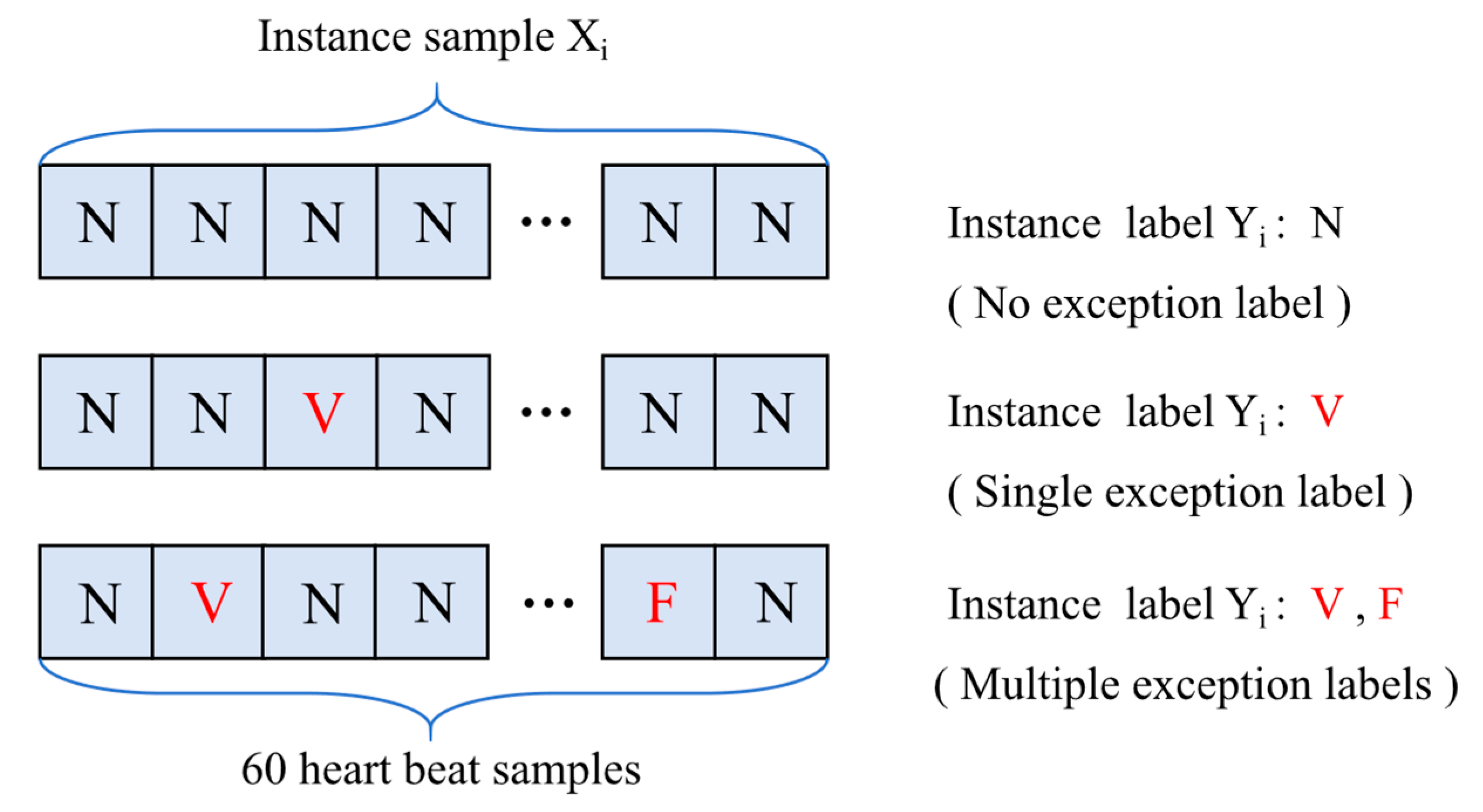
3.2. Multiple Instance Learning (MIL)
3.3. Feature Extractor Method
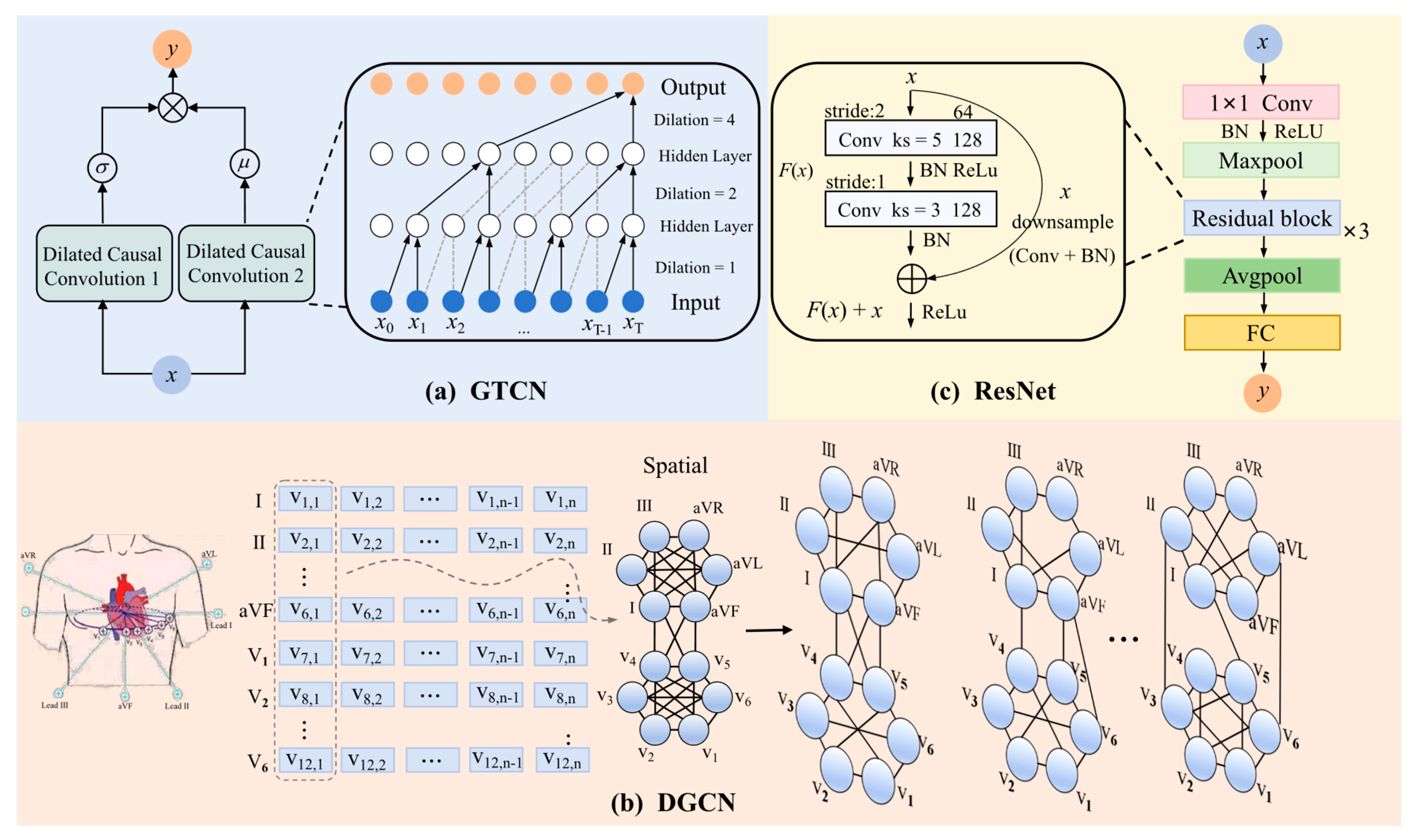
3.3.1. Instance Feature Extraction
- (a)
- Gated Temporal Convolutional Network (GTCN)
- (b)
- Dynamic Graph Convolutional Network (DGCN)
- (c)
- ResNet
3.3.2. Statistical Feature Extraction
3.4. Feature Fusion Method
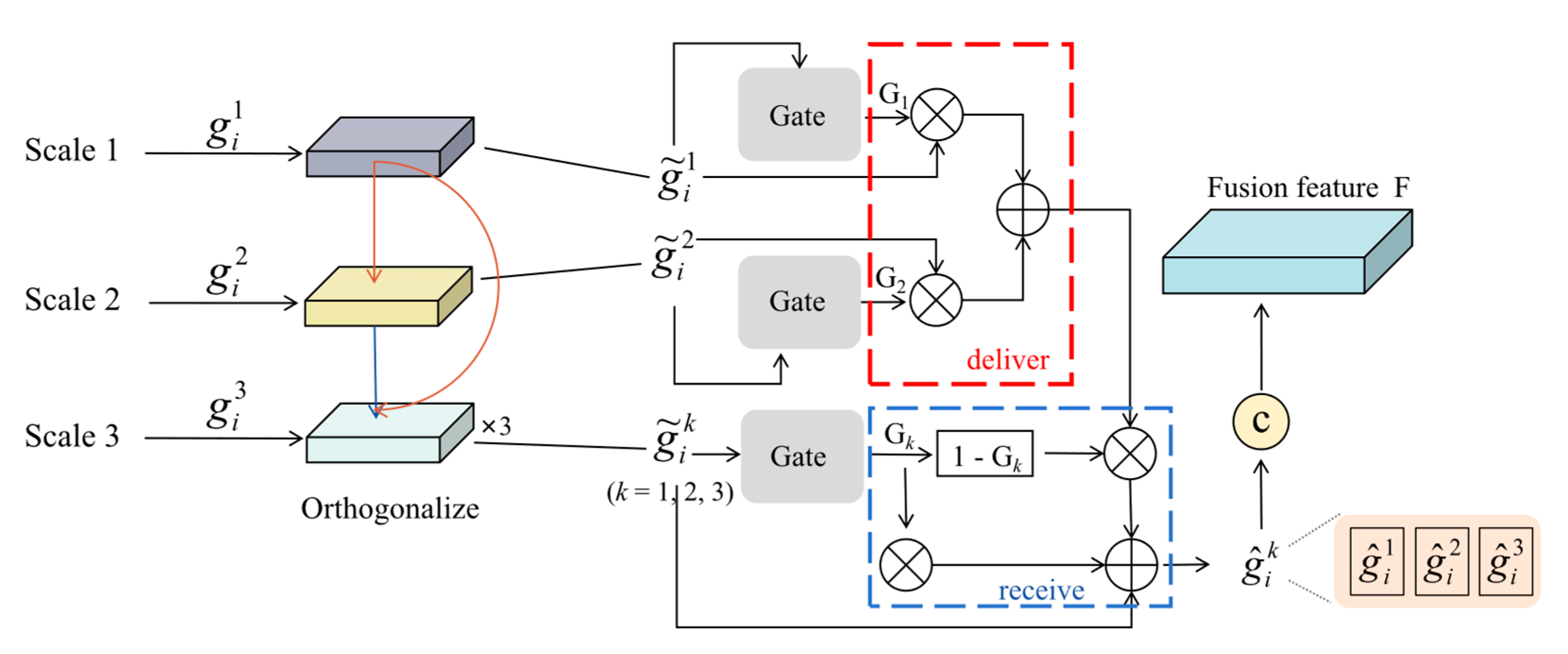
3.4.1. Global–Local Fusion at Specific Scale
3.4.2. Orthogonal Gated Multi-Scale Fusion
4. Experiments
4.1. Dataset
4.2. Evaluation Metrics
4.3. Implementation Details
5. Experimental Result and Discussion
5.1. Comparison with Previous Methods
5.2. Ablation Experiments
5.2.1. Ablation of MIL and Statistical Feature
5.2.2. Ablation of Multi-Scale
5.2.3. Ablation of Feature Extraction Modules
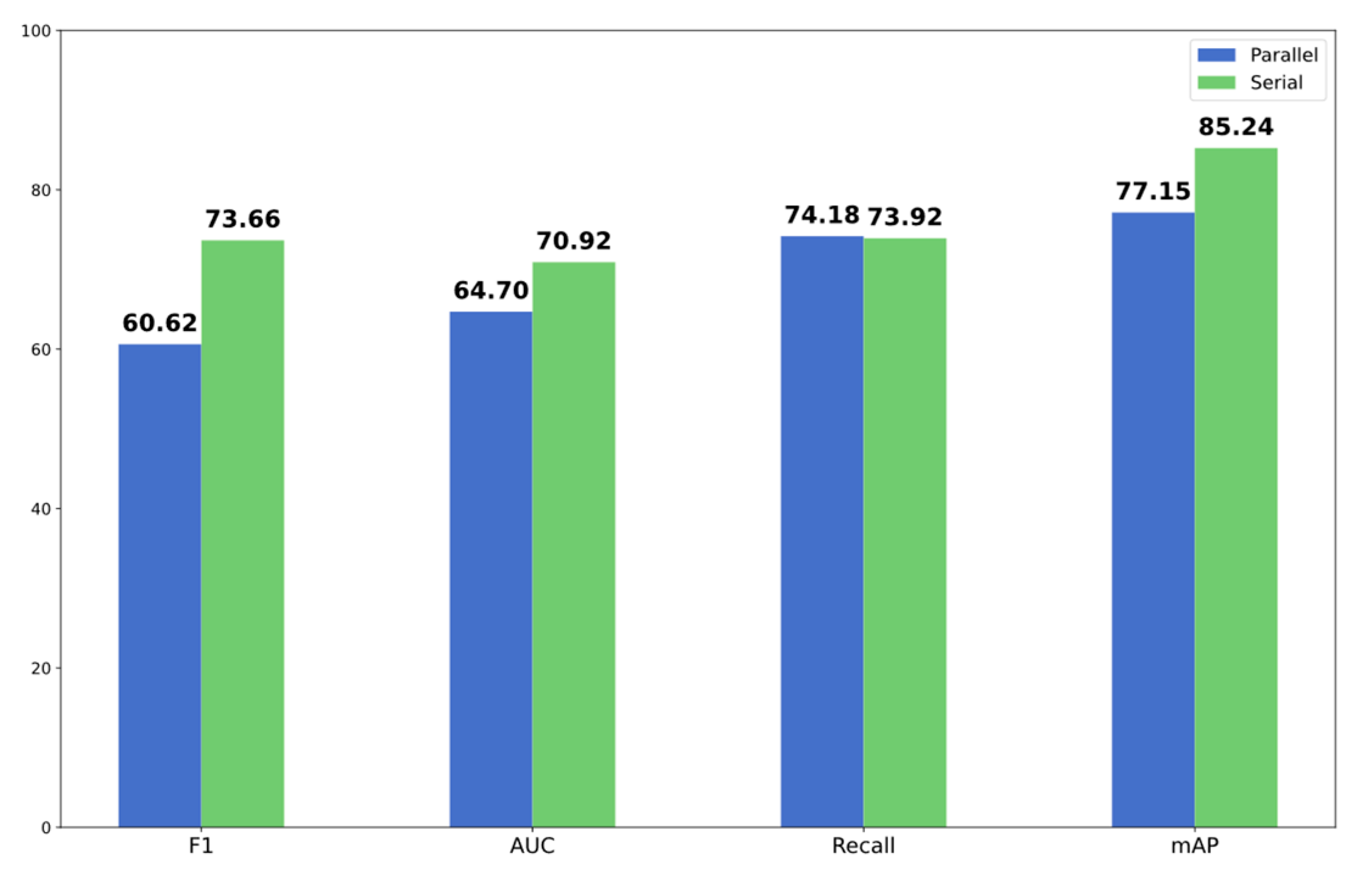
5.3. Serial vs. Parallel Connections of GTCN and DGCN
5.4. Comparison of Fusion Methods
5.5. Lead Importance and Multi-Scale Connectivity Patterns
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MST-DGCN | Multi-Scale Temporal–Dynamic Graph Convolutional |
| T-DGCN | Temporal–Dynamic Graph Convolutional Network |
| OGF | Orthogonal gated fusion |
| MIL | Multiple instance learning |
| TCN | Temporal Convolutional Network |
| GTCN | Gated Temporal Convolutional Network |
References
- Nasef, D.; Nasef, D.; Basco, K.J.; Singh, A.; Hartnett, C.; Ruane, M.; Tagliarino, J.; Nizich, M.; Toma, M. Clinical Applicability of Machine Learning Models for Binary and Multi-Class Electrocardiogram Classification. AI 2025, 6, 59. [Google Scholar] [CrossRef]
- Jiang, M.; Bian, F.; Zhang, J.; Huang, T.; Xia, L.; Chu, Y.; Wang, Z.; Jiang, J. Myocardial infarction detection method based on the continuous T-wave area feature and multi-lead-fusion deep features. Physiol. Meas. 2024, 45, 055017. [Google Scholar] [CrossRef]
- Din, S.; Qaraqe, M.; Mourad, O.; Qaraqe, K.; Serpedin, E. ECG-based cardiac arrhythmias detection through ensemble learning and fusion of deep spatial–temporal and long-range dependency features. Artif. Intell. Med. 2024, 150, 102818. [Google Scholar] [CrossRef] [PubMed]
- El-Ghaish, H.; Eldele, E. ECGTransForm: Empowering adaptive ECG arrhythmia classification framework with bidirectional transformer. Biomed. Signal Process. Control 2024, 89, 105714. [Google Scholar] [CrossRef]
- Sun, L.; Li, C.; Ren, Y.; Zhang, Y. A Multitask Dynamic Graph Attention Autoencoder for Imbalanced Multilabel Time Series Classification. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 11829–11842. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Liu, W.; Chang, S.; Wang, H.; He, J.; Huang, Q. ST-ReGE: A novel spatial-temporal residual graph convolutional network for CVD. IEEE J. Biomed. Health Inform. 2023, 28, 216–227. [Google Scholar] [CrossRef]
- Tao, R.; Wang, L.; Xiong, Y.; Zeng, Y.R. IM-ECG: An interpretable framework for arrhythmia detection using multi-lead ECG. Expert Syst. Appl. 2024, 237, 121497. [Google Scholar] [CrossRef]
- Braman, N.; Gordon, J.W.; Goossens, E.T.; Willis, C.; Stumpe, M.C.; Venkataraman, J. Deep orthogonal fusion: Multimodal prognostic biomarker discovery integrating radiology, pathology, genomic, and clinical data. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2021, Proceedings of the 24th International Conference, Strasbourg, France, 27 September–1 October 2021; Proceedings, Part V 24; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Zhu, Y.; Jiang, M.; He, X.; Li, Y.; Li, J.; Mao, J.; Ke, W. MMDN: Arrhythmia detection using multi-scale multi-view dual-branch fusion network. Biomed. Signal Process. Control 2024, 96, 106468. [Google Scholar] [CrossRef]
- Khalaf, A.J.; Mohammed, S.J. Verification and comparison of MIT-BIH arrhythmia database based on number of beats. Int. J. Electr. Comput. Eng. 2021, 11, 4950. [Google Scholar] [CrossRef]
- Wagner, P.; Strodthoff, N.; Bousseljot, R.D.; Kreiseler, D.; Lunze, F.I.; Samek, W.; Schaeffter, T. PTB-XL, a large publicly available electrocardiography dataset. Sci. Data 2020, 7, 1–15. [Google Scholar] [CrossRef]
- Ge, Z.; Jiang, X.; Tong, Z.; Feng, P.; Zhou, B.; Xu, M.; Wang, Z.; Pang, Y. Multi-label correlation guided feature fusion network for abnormal ECG diagnosis. Knowl.-Based Syst. 2021, 233, 107508. [Google Scholar] [CrossRef]
- Ansari, Y.; Mourad, O.; Qaraqe, K.; Serpedin, E. Deep learning for ECG Arrhythmia detection and classification: An overview of progress for period 2017–2023. Front. Physiol. 2023, 14, 1246746. [Google Scholar] [CrossRef]
- Acharya, U.R.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adam, M.; Gertych, A.; San Tan, R. A deep convolutional neural network model to classify heartbeats. Comput. Biol. Med. 2017, 89, 389–396. [Google Scholar] [CrossRef]
- Cheng, J.; Zou, Q.; Zhao, Y. ECG signal classification based on deep CNN and BiLSTM. BMC Med. Inform. Decis. Mak. 2021, 21, 365. [Google Scholar] [CrossRef]
- Mantravadi, A.; Saini, S.; Mittal, S.; Shah, S.; Devi, S.; Singhal, R. CLINet: A novel deep learning network for ECG signal classification. J. Electrocardiol. 2024, 83, 41–48. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Xie, H.; Liu, Y.; Zhu, H.; Zhang, H.; Wang, Z.; Pan, Y. MrSeNet: Electrocardiogram signal denoising based on multi-resolution residual attention network. J. Electrocardiol. 2025, 89, 153858. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Li, Y. A multi-scale CNN-Transformer parallel network for 12-lead ECG signal classification. Signal Image Video Process. 2025, 19, 611. [Google Scholar] [CrossRef]
- Ranipa, K.; Zhu, W.-P.; Swamy, M.N.S. A novel feature-level fusion scheme with multimodal attention CNN for heart sound classification. Comput. Methods Programs Biomed. 2024, 248, 108122. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhang, P.; Wang, Z.; Chao, L.; Chen, Y.; Li, Q. Multi-feature decision fusion network for heart sound abnormality detection and classification. IEEE J. Biomed. Health Inform. 2023, 28, 1386–1397. [Google Scholar] [CrossRef]
- Maithani, A.; Verma, G. Hybrid model with improved score level fusion for heart disease classification. Multimed. Tools Appl. 2024, 83, 54951–54987. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, W.; Yin, Z.; Hu, S.; Wang, M.; Cai, W. ECG classification based on guided attention mechanism. Comput. Methods Programs Biomed. 2024, 257, 108454. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, K.; Wang, X.; Liu, Y.; Shi, B. Multimodal Emotion Reasoning Based on Multidimensional Orthogonal Fusion. In Proceedings of the 2024 3rd International Conference on Image Processing and Media Computing (ICIPMC), Hefei, China, 17–19 May 2024; IEEE: Piscataway, NJ, USA, 2024. [Google Scholar]
- Chang, P.-C.; Chen, Y.-S.; Lee, C.-H. IIOF: Intra-and Inter-feature orthogonal fusion of local and global features for music emotion recognition. Pattern Recognit. 2024, 148, 110200. [Google Scholar] [CrossRef]
- Petelin, G.; Cenikj, G.; Eftimov, T. Towards understanding the importance of time-series features in automated algorithm performance prediction. Expert Syst. Appl. 2023, 213, 119023. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, L.; Shen, N.; Wu, Y.; Feng, S.; Xu, Y.; Chen, C.; Chen, W. MS-HNN: Multi-scale hierarchical neural network with squeeze and excitation block for neonatal sleep staging using a single-channel EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 2195–2204. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- He, T.; Zhang, Z.; Zhang, H.; Zhang, Z.; Xie, J.; Li, M. Bag of tricks for image classification with convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; PMLR: Brookline, MA, USA, 2019. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Dosovitskiy, A.B.; Kolesnikov, A. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. In Proceeding of the International Conference on Learning Representations, Virtual Conference, 26–30 April 2020. [Google Scholar]
- Xu, Z.; Liu, H. ECG heartbeat classification using convolutional neural networks. IEEE Access 2020, 8, 8614–8619. [Google Scholar] [CrossRef]
- Kuznetsov, V.V.; Moskalenko, V.A.; Zolotykh, N.Y. Electrocardiogram generation and feature extraction using a variational autoencoder. arXiv 2020, arXiv:2002.00254. [Google Scholar] [CrossRef]
- Feng, Y.; Vigmond, E. Deep multi-label multi-instance classification on 12-lead ECG. In Proceedings of the 2020 Computing in Cardiology, Rimini, Italy, 13–16 September 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Shao, Z.; Bian, H.; Chen, Y.; Wang, Y.; Zhang, J.; Ji, X. Transmil: Transformer based correlated multiple instance learning for whole slide image classification. Adv. Neural Inf. Process. Syst. 2021, 34, 2136–2147. [Google Scholar]
- Chen, L.; Lian, C.; Zeng, Z.; Xu, B.; Su, Y. Cross-modal multiscale multi-instance learning for long-term ECG classification. Inf. Sci. 2023, 643, 119230. [Google Scholar] [CrossRef]
- Han, H.; Lian, C.; Zeng, Z.; Xu, B.; Zang, J.; Xue, C. Multimodal multi-instance learning for long-term ECG classification. Knowl.-Based Syst. 2023, 270, 110555. [Google Scholar] [CrossRef]
- Ouyang, D.; He, S.; Zhang, G.; Luo, M.; Guo, H.; Zhan, J.; Huang, Z. Efficient multi-scale attention module with cross-spatial learning. In Proceedings of the ICASSP 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes, Greece, 4–10 June 2023; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar]
- Shaker, A.; Maaz, M.; Rasheed, H.; Khan, S.; Yang, M.H.; Khan, F.S. Swiftformer: Efficient additive attention for transformer-based real-time mobile vision applications. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023. [Google Scholar]
- Strauss, D.G.; Selvester, R.H.; Wagner, G.S. Defining left bundle branch block in the era of cardiac resynchronization therapy. Am. J. Cardiol. 2011, 107, 927–934. [Google Scholar] [CrossRef]
- Wang, A.; Singh, V.; Duan, Y.; Su, X.; Su, H.; Zhang, M.; Cao, Y. Prognostic implications of ST-segment elevation in lead aVR in patients with acute coronary syndrome: A meta-analysis. Ann. Noninvasive Electrocardiol. 2021, 26, e12811. [Google Scholar] [CrossRef] [PubMed]
- Meyers, H.P.; Bracey, A.; Lee, D.; Lichtenheld, A.; Li, W.J.; Singer, D.D.; Rollins, Z.; Kane, J.A.; Dodd, K.W.; Meyers, K.E.; et al. Ischemic ST-segment depression maximal in V1–V4 (versus V5–V6) of any amplitude is specific for occlusion myocardial infarction (versus nonocclusive ischemia). J. Am. Heart Assoc. 2021, 10, e022866. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, T.; Nambu, Y.; Bo, R.; Morichi, S.; Yanagiya, M.; Matsuo, M.; Awano, H. Electrocardiographic R wave amplitude in V6 lead as a predictive marker of cardiac dysfunction in Duchenne muscular dystrophy. J. Cardiol. 2023, 82, 363–370. [Google Scholar] [CrossRef] [PubMed]
- Xiong, P.; Lee, S.M.Y.; Chan, G. Deep learning for detecting and locating myocardial infarction by electrocardiogram: A literature review. Front. Cardiovasc. Med. 2022, 9, 860032. [Google Scholar] [CrossRef]
- Katsushika, S.; Kodera, S.; Sawano, S.; Shinohara, H.; Setoguchi, N.; Tanabe, K.; Higashikuni, Y.; Takeda, N.; Fujiu, K.; Daimon, M.; et al. An explainable artificial intelligence-enabled electrocardiogram analysis model for the classification of reduced left ventricular function. Eur. Heart J.-Digit. Health 2023, 4, 254–264. [Google Scholar] [CrossRef]


| St. Petersburg INCART Arrhythmia Dataset | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Labels | N | V | A | F | Q | R | V, Q | V, F | V, R | Q, F | V, A | Q, R | V, Q, F | Total |
| Train | 480 | 960 | / | 7 | 210 | 41 | 109 | 58 | 12 | 3 | 2 | 1 | 4 | 1887 |
| Test | 344 | 508 | 2 | 7 | 1 | / | 5 | 60 | / | 1 | 2 | / | 1 | 931 |
| Total | 824 | 1468 | 2 | 14 | 211 | 41 | 114 | 118 | 12 | 4 | 4 | 1 | 5 | 2818 |
| St. Petersburg INCART Arrhythmia Dataset | ||||
|---|---|---|---|---|
| Method | F1 | AUC | Recall | mAP |
| Linear SVM | 15.88 | 49.91 | 18.79 | 23.42 |
| Random Forest | 17.27 | 54.45 | 20.57 | 21.91 |
| FCN_wang [27] | 57.95 | 55.15 | 57.5 | 73.19 |
| Restnet1d_wang [27] | 57.9 | 59.21 | 58.33 | 74.29 |
| Restnet1d50 [28] | 58.94 | 56.38 | 60.98 | 75.1 |
| Restnet1d101 [28] | 52.49 | 62.87 | 55.3 | 73 |
| EffcientNet [29] | 54.47 | 56.52 | 54.53 | 71.71 |
| InceptionTime [30] | 57.3 | 58.34 | 58.66 | 73.67 |
| ViT [31] | 63.1 | 65.79 | 61.68 | 77.43 |
| CNN_xu [32] | 58.55 | 66.28 | 59.24 | 75.31 |
| VAE [33] | 59.6 | 57.55 | 61.62 | 75.5 |
| MIC [34] | 57.41 | 66.31 | 56.85 | 76.47 |
| TransMIL [35] | 66.60 | 67.73 | 66.67 | 79.97 |
| CMM [36] | 67.31 | 68.33 | 66.39 | 79.30 |
| MAMIL [37] | 69.42 | 69.74 | 70.57 | 82.58 |
| MST-DGCN (Ours) | 73.66 ↑ 4.24 | 70.92 ↑ 1.18 | 73.92 ↑ 3.35 | 85.24 ↑ 2.66 |
| F1 | AUC | Recall | ||||
|---|---|---|---|---|---|---|
| Class | CMM [36] | Ours | CMM [36] | Ours | CMM [36] | Ours |
| N | 70.12 | 74.54 | 89.33 | 93.14 | 68.25 | 72.40 |
| V | 79.30 | 82.54 | 85.24 | 87.39 | 81.11 | 86.46 |
| A | 24.68 | 60.79 | 76.37 | 88.03 | 14.60 | 53.14 |
| F | 0.00 | 20.00 | 67.97 | 75.12 | 0.00 | 12.86 |
| St. Petersburg INCART Arrhythmia Dataset | ||||
|---|---|---|---|---|
| Method | F1 | AUC | Recall | mAP |
| w/o MIL | 60.96 | 60.38 | 63.15 | 76.52 |
| w/o statistical modality | 71.78 | 68.51 | 72.47 | 83.44 |
| Ours | 73.66 | 70.92 | 73.92 | 85.24 |
| St. Petersburg INCART Arrhythmia Dataset | |||||
|---|---|---|---|---|---|
| Method | F1 | AUC | Recall | mAP | |
| w/o multiscale | 180 sample points | 64.34 | 58.45 | 63.21 | 79.42 |
| 90 sample points | 66.09 | 65.27 | 65.66 | 80.85 | |
| 45 sample points | 67.88 | 64.34 | 67.17 | 81.91 | |
| Ours | 73.66 | 70.92 | 73.92 | 85.24 | |
| Method | St. Petersburg INCART Arrhythmia Dataset | |||||
|---|---|---|---|---|---|---|
| GTCN | DGCN | ResNet | F1 | AUC | Recall | mAP |
| √ | 62.39 | 61.36 | 63.21 | 78.15 | ||
| √ | √ | 64.16 | 64.36 | 64.38 | 79.64 | |
| √ | √ | 71.74 | 70.54 | 71.35 | 84.72 | |
| √ | √ | 70.39 | 67.75 | 72.41 | 83.36 | |
| √ | √ | √ | 73.66 | 70.92 | 73.92 | 85.24 |
| St. Petersburg INCART Arrhythmia Dataset | ||||
|---|---|---|---|---|
| Method | F1 | AUC | Recall | mAP |
| Concat | 69.07 | 65.50 | 70.18 | 82.46 |
| Traditional Attention | 65.85 | 69.02 | 67.50 | 81.08 |
| EMA [38] | 70.31 | 63.33 | 70.01 | 83.28 |
| EAA [39] | 70.85 | 62.58 | 72.08 | 85.19 |
| OGF (Ours) | 73.66 | 70.92 | 73.92 | 85.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Jiang, M.; He, X.; Li, Y.; Zhang, J.; Li, J.; Wu, Y.; Ke, W. MST-DGCN: Multi-Scale Temporal–Dynamic Graph Convolutional with Orthogonal Gate for Imbalanced Multi-Label ECG Arrhythmia Classification. AI 2025, 6, 219. https://doi.org/10.3390/ai6090219
Chen J, Jiang M, He X, Li Y, Zhang J, Li J, Wu Y, Ke W. MST-DGCN: Multi-Scale Temporal–Dynamic Graph Convolutional with Orthogonal Gate for Imbalanced Multi-Label ECG Arrhythmia Classification. AI. 2025; 6(9):219. https://doi.org/10.3390/ai6090219
Chicago/Turabian StyleChen, Jie, Mingfeng Jiang, Xiaoyu He, Yang Li, Jucheng Zhang, Juan Li, Yongquan Wu, and Wei Ke. 2025. "MST-DGCN: Multi-Scale Temporal–Dynamic Graph Convolutional with Orthogonal Gate for Imbalanced Multi-Label ECG Arrhythmia Classification" AI 6, no. 9: 219. https://doi.org/10.3390/ai6090219
APA StyleChen, J., Jiang, M., He, X., Li, Y., Zhang, J., Li, J., Wu, Y., & Ke, W. (2025). MST-DGCN: Multi-Scale Temporal–Dynamic Graph Convolutional with Orthogonal Gate for Imbalanced Multi-Label ECG Arrhythmia Classification. AI, 6(9), 219. https://doi.org/10.3390/ai6090219







